Zadeh^[1]提出二型模糊集合后的很长时间内，由于二型模糊集合的运算复杂性，其理论上的研究较少。直到Mendel等将二型模糊集合简化为区间二型模糊集合，区间二型模糊集合理论及应用得到了广泛关注。Mendel^[2]将二型模糊结合的次隶属度定义为1，利用KM^[3]、EKM等^[4]降阶算法得到区间二型模糊集合的左、右端点，在此基础上进行区间二型模糊逻辑系统的研究^[5-7]。

基于区间二型模糊集合的区间二型模糊控制器在很多方面得到了成功应用，由于其利用不确定域来描述模糊集合，在处理不确定性方面要优于传统的模糊控制器^[8-9]。目前大部分的区间二型模糊控制器都是基于KM等基于迭代运算的降阶算法，KM算法的基本流程是一个不断迭代搜索过程，不断替换上一步的切换点直到最终的切换点满足特定的条件。在区间二型模糊控制器的实现过程中，每一步控制器的计算都要经过这种迭代过程，这不利于实时、在线控制。

由于KM降阶算法的缺陷，一些效率更高的降阶算法也被提出，比如EKM、IASC^[10]、EIASC^[11]、ODSC^[12]等，但这些算法本质上和KM类似，只是它们的效率更高，在实时控制中依然需要进行搜索过程。文献[13]总结了一些替代KM的降阶算法，这些算法不需要进行迭代过程，根据区间二型模糊集合首隶属度的上、下限计算得到降阶结果。

Wu等^[14]基于KM降阶算法，在平衡点附近分析了区间二型模糊PI控制器的一般表达式，说明了在选择特定的模糊隶属度函数的情况下，该控制器在平衡点附件的区域内，其控制器参数与普通PI控制器参数成一定的比例关系。Nie等^[15]基于KM降阶算法，利用模糊划分方法，分析了具有对称结构的区间二型模糊PI和PD控制器，分析了该控制器的一般表达式，说明了区间二型模糊控制器的参数为误差或者误差变化量的函数，并与传统的模糊PI控制器进行了比较。文献[16]研究了一类区间二型模糊Mamdani控制器，分析了其一般性结构，证明了该控制器在采用KM降阶算法的情况下，等价于变增益的PI(PD)控制器。与文献[16]类似，文献[17]基于KM算法分析了首隶属度函数为非线性情况下区间二型模糊PI/PD控制器的一般形式，证明了该区间二型模糊控制器等效为具有变增益的非线性比例积分(PI)或比例微分控制器。与文献[14-17]采用的Zadeh的与推理不同，文献[18]采用乘积推理，基于KM算法，说明了在乘积推理下的区间二型模糊控制器等效于两个PI(或PD)控制器之和。

本文利用一种区间二型动态解模糊化算法，该算法在模糊控制器的输出部分考虑偏差和偏差的变化量^[19]。控制器采用直接降阶算法，其实时性与传统模糊控制器类似而优于基于KM等迭代式降阶算法的区间二型模糊控制器。通过一个二阶迟延对象、一个非线性对象的仿真实验表明，本文算法控制器的输出较为平稳，系统的超调较小，系统到达稳态的时间较短。

1 KM降阶算法

由KM算法，区间二型模糊集合的降阶结果为实数区间[c_l，c_r]。两个端点的计算公式如式(1)、(2)。

${c_l} =\frac{{\displaystyle\sum\limits_{i =1}^L {{x_i}\overline {f({x_i})} + \displaystyle\sum\limits_{i =L + 1}^N {{x_i}\underline {f ({x_i})}} } }}{{\displaystyle\sum\limits_{i =1}^L {\overline {f({x_i})} + \displaystyle\sum\limits_{i =L + 1}^N {\underline {f ({x_i})}} } }}$

(1)

${c_r} =\frac{{\displaystyle\sum\limits_{i =1}^R {{x_i}\underline {f ({x_i})} + \displaystyle\sum\limits_{i =R + 1}^N {{x_i}\overline {f({x_i})}} } }}{{\displaystyle\sum\limits_{i =1}^R {\underline {f ({x_i})} + \displaystyle\sum\limits_{i =R + 1}^N {\overline {f({x_i})}} } }}$

(2)

式中： $ \overline {f\left( {{x_i}} \right)} $ 和 $ \underline {f\left( {{x_i}} \right)} $ 分别为首隶属度函数的上、下限；L和R分别为KM/EKM算法求出的左、右切换点。

式(1)和(2)是将论域为离散情况下的KM降阶算法，当论域为连续的时候，假设论域的区间为[a,b]，连续KM算法表示如式(3)、(4)。

${c_l} =\frac{{\displaystyle\int_a^{{c_l}} {\overline {f(x)}x{\rm{d}}x + \displaystyle\int_{{c_l}}^b {\underline {{f} (x)}x{\rm{d}}x} } }}{{\displaystyle\int_a^{{c_l}} {\overline {f(x)}{\rm{d}}x + \int_{{c_l}}^b {\underline {{f} (x)}{\rm{d}}x} } }}$

(3)

${c_r} =\frac{{\displaystyle\int_a^{{c_r}} {\underline {{f} (x)}x{\rm{d}}x + \int_{{c_r}}^b {\overline {f(x)}x{\rm{d}}x} } }}{{\displaystyle\int_a^{{c_r}} {\underline {{f} (x)}{\rm{d}}x + \displaystyle\int_{{c_r}}^b {\overline {f(x)}{\rm{d}}x} } }}$

(4)

无论离散还是连续的KM算法，都需要进行迭代过程，如果将KM降阶算法用于区间二型模糊控制器的设计，其每一步的控制器输出都要进行迭代运算，实时性将会有一定的影响。

2 区间二型模糊控制系统

区间二型模糊控制器以偏差以及偏差的变化量为输入，在模糊推理结束以后，增加降阶过程，得到控制器的实际增量，结构如图1所示。

区间二型模糊控制器的不确定域通过将一型控制器隶属度进一步模糊化得到，偏差以及偏差的变化量的偏移分别为d₁、d₂，偏差和偏差的变化量分别定义2个模糊变量的三角型隶属度，如图2所示。

当然，偏差或者偏差的变化量也可以定义多个模糊变量，这样模糊规则数也会相应增加，糊控制器的设计难度也会随之增加。

文献[20]证明了当模糊控制器的输入为偏差e和偏差的变化量Δe时，传统一型模糊控制器等价于PID控制器，只要隶属度函数满足特定的条件。具体的满足条件和证明过程可参考文献[20]。

一般的区间二型模糊控制器对偏差和偏差的变化量各定义2个模糊变量，如图2，区间二型模糊控制器共有4条模糊规则，定义如下^[21]：

规则 1：If $\Delta e$ is $\tilde P$ and e is $\tilde P$

then $ {y^1} ={K_{\rm P}} \times (d\dot e) + {K_{\rm I}} \times (de)$

规则 2：If $\Delta e$ is $\tilde P$ and e is $\tilde N$

then $ {y^2} ={K_{\rm P}} \times (d\dot e) + {K_{\rm I}} \times ( - de)$

规则 3：If $\Delta e$ is $\tilde N$ and e is $\tilde P$

then $ {y^3} ={K_{\rm P}} \times ( - d\dot e) + {K_{\rm I}} \times (de)$

规则 4：If $\Delta e$ is $\tilde N$ and e is $\tilde N$

then $ {y^4} ={K_{\rm P}} \times ( - d\dot e) + {K_{\rm I}} \times ( - de)$

3 本文算法

文献[14]提出的区间二型模糊PI控制器基于KM降阶，其控制器的输出为降阶区间的平均值。文献[19]提出的针对区间二型模糊控制器的动态解模糊化算法，其模糊控制器的后件部分是区间二型模糊集合，依然采用的是KM降阶，并不适合于在线实时控制。本文利用的直接降阶算法在计算降阶区间左右端点的时候，利用上、下隶属度函数进行计算，后件部分采用实数，简化了控制器的运算过程，具体描述如下。

假设第k条规则的激发隶属度的上、下限为 ${\bar f^k}$ 和 ${\underline {f} _k}$ ，对应规则的输出为y^k(如前文规则的定义)，4条规则的激发隶属度的上、下限为：

规则 1： $ [{\overline f^1},{\underline {f} _1}] =[\overline \mu _{\Delta e}^{\tilde P} \times \overline \mu _e^{\tilde P},\underline {\mu } _{\Delta e}^{\tilde P} \times \underline {\mu } _e^{\tilde P}]$

规则 2： $ [{\overline f^2},{\underline {f} _2}] =[\overline \mu _{\Delta e}^{\tilde P} \times \overline \mu _e^{\tilde N},\underline {\mu } _{\Delta e}^{\tilde P} \times \underline {\mu } _e^{\tilde N}]$

规则 3： $ [{\overline f^3},{\underline {f} _3}] =[\overline \mu _{\Delta e}^{\tilde N} \times \overline \mu _e^{\tilde P},\underline {\mu } _{\Delta e}^{\tilde N} \times \underline {\mu } _e^{\tilde P}]$

规则 4： $ [{\overline f^4},{\underline {f} _4}] =[\overline \mu _{\Delta e}^{\tilde N} \times \overline \mu _e^{\tilde N},\underline {\mu } _{\Delta e}^{\tilde N} \times \underline {\mu } _e^{\tilde N}]$

偏差e的 $\tilde P$ 变量的首隶属度的上、下限表示为

$\overline \mu _e^{\tilde P} =\left\{ \begin{gathered} 1,\quad{\rm{ }}e > de - {d_1} \\ \frac{{e + de + {d_1}}}{{2 \times de}},\quad {\text{其他}} \\ \end{gathered} \right.$

$\underline {\mu } _e^{\tilde P} =\left\{ \begin{gathered} 0,\quad{\rm{ }}e < - de + {d_1} \\ \frac{{e + de - {d_1}}}{{2 \times de}},\quad{\text{其他}} \\ \end{gathered} \right.$

偏差e的 $\tilde N$ 变量首隶属度的上、下限表示为

$\overline \mu _e^{\tilde N} =\left\{ \begin{gathered} 1,\quad{\rm{ }}e < - de + {d_1} \\ \frac{{de + {d_1} - e}}{{2 \times de}},\quad{\text{其他}} \\ \end{gathered} \right.$

$\underline {\mu } _e^{\tilde N} =\left\{ \begin{gathered} 0,\quad{\rm{ }}e > de - {d_1} \\ \frac{{de - {d_1} - e}}{{2 \times de}},\quad{\text{其他}} \\ \end{gathered} \right.$

偏差变化量Δe的 $\tilde P$ 变量首隶属度函数的上、下限表示为

$\overline \mu _{\Delta e}^{\tilde P} =\left\{ \begin{gathered} 1,\quad{\rm{ }}\Delta e > d\dot e - {d_2} \\ \frac{{\Delta e + d\dot e + {d_2}}}{{2 \times d\dot e}},\quad{\text{其他}} \\ \end{gathered} \right.$

$\underline {\mu } _{\Delta e}^{\tilde P} =\left\{ \begin{gathered} 0,\quad{\rm{ }}\Delta e < - d\dot e + {d_2} \\ \frac{{\Delta e + d\dot e - {d_2}}}{{2 \times d\dot e}},\quad{\text{其他}} \\ \end{gathered} \right.$

偏差变化量Δe的 $\tilde N$ 变量首隶属度函数的上、下限表示为

$\overline \mu _{\Delta e}^{\tilde N} =\left\{ \begin{gathered} 1,\quad{\rm{ }}\Delta e < - d\dot e + {d_2} \\ \frac{{d\dot e + {d_2} - \Delta e}}{{2 \times d\dot e}},\quad{\text{其他}} \\ \end{gathered} \right.$

$\underline {\mu } _{\Delta e}^{\tilde N} =\left\{ \begin{gathered} 0,\quad{\rm{ }}\Delta e > d\dot e - d_2 \\ \frac{{d\dot e - d_2 - \Delta e}}{{2 \times d\dot e}},\quad{\text{其他}} \\ \end{gathered} \right.$

降阶算法中的左、右端点如式(5)、(6)所示，这里的M=4。

${c_l} =\frac{{\displaystyle\sum\limits_{k =1}^M {{{\underline {f} }^k}} {y^k}}}{{\displaystyle\sum\limits_{k =1}^M {{{\underline {f} }^k}} }}$

(5)

${c_r} =\frac{{\displaystyle\sum\limits_{i =1}^M {{\overline{ f^k}}} {y^k}}}{{\displaystyle\sum\limits_{i =1}^M {{\overline {f^k}}} }}$

(6)

二型模糊控制的输出增量Δu表示为

$a(t) =\frac{{e(t) + \Delta e(t)}}{2} + 0.5$

(7)

$\Delta u(t) =a(t) \times {c_l} + (1 - a(t)) \times {c_r}$

(8)

式(8)中c_l表示降阶区间的左端点，c_r表示右端点，在实际控制过程中，由于c_l不一定小于c_r，因此，本文算法实际的控制器输出如式(9)：

$\Delta u(t) =a(t) \times \min ({c_l},{c_r}) + (1 - a(t)) \times \max ({c_l},{c_r})$

(9)

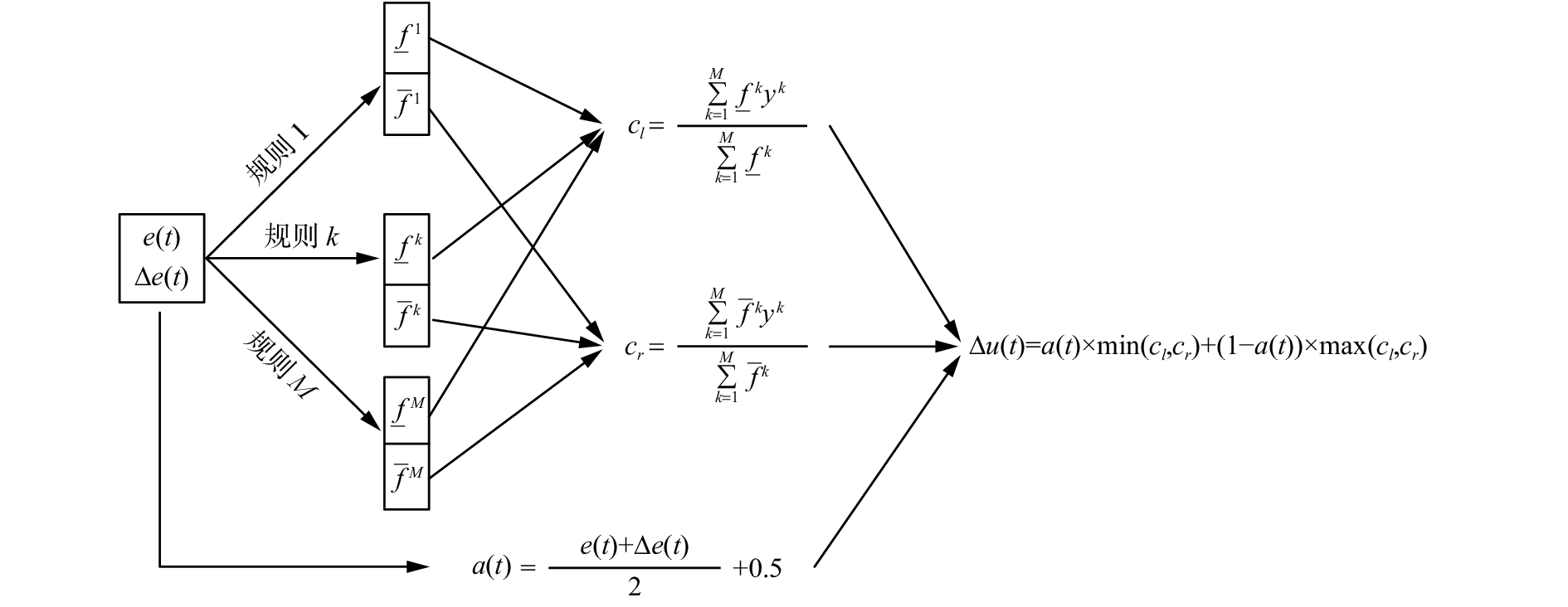
本文算法的控制系统框图如图3所示。

文献[13]也给出了其他的一些替代KM的降阶算法，比如NT算法^[22]等，本文也对其作了比较。

4 仿真实例 4.1 仿真实例1

选取二阶迟延对象，其传递函数为

$G(s) =\frac{K}{{s(Ts + 1)}}{{\rm e}^{ - \tau s}}$

PI控制器参数K_P=0.044 9，K_I=0.001 4，采样周期为0.1 s。

系统参数：K=1，T=1，τ=10 s，d₁=d₂=0.5。

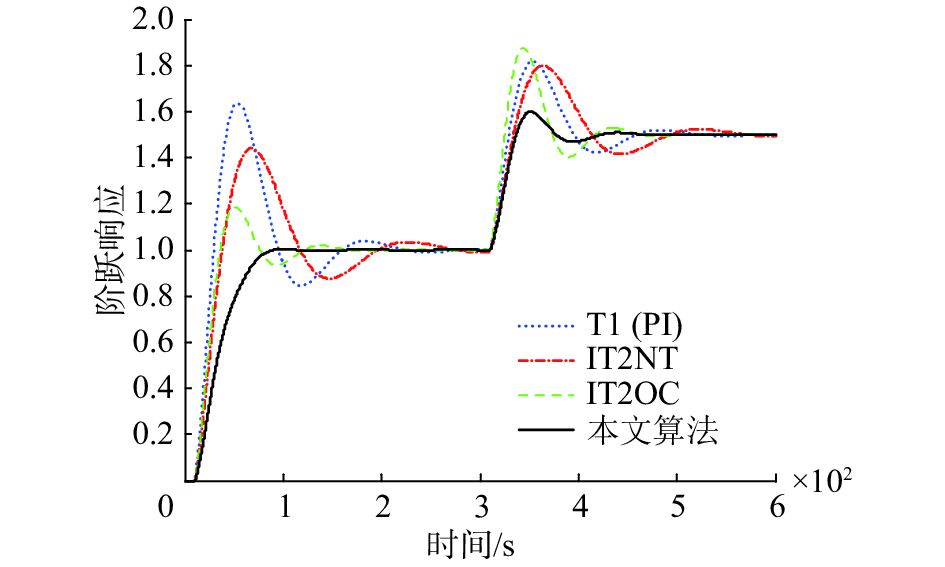
图4中的T1(PI)表示一型模糊控制器(或者PI控制器)的响应曲线，IT2NT表示使用NT降阶算法的区间二型模糊控制器的响应曲线，IT2OC表示使用文献[15]降阶算法的区间二型模糊控制器的响应曲线，本文算法是区间二型模糊控制器响应曲线，以下各例表示相同的含义。

表1显示了针对仿真实例1的线性二阶迟延系统在单位阶跃输入下本文算法和其他几种算法的控制性能比较。其中t_s(s)表示稳定时间(单位为秒)，本文以达到系统偏差绝对值小于稳态值的2%计算。t_r(s)为上升时间(单位为s)，本文以达到系统的稳态值计算。

ISE、ITSE、ITAE为误差积分准则，在单位阶跃扰动下，系统的设定值与输出之间偏差的某个函数的积分数值，分别表示为

${\rm {ISE}} =\int_0^{{t_s}} {e{{(t)}^2}{\rm d}t} $

${\rm {ITSE}} =\int_0^{{t_s}} {t \times e{{(t)}^2}{\rm d}t} $

${\rm{ITAE }}=\int_0^{{t_s}} {t \times \left| {e(t)} \right|{\rm d}t} $

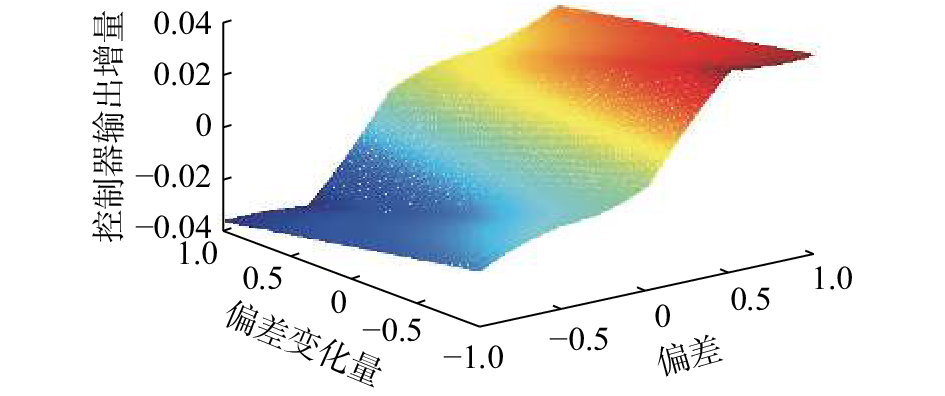
图5和图6分别表示使用PI控制器和本文的区间二型模糊PI控制器的输出增量随着偏差和偏差变化量变化的三维曲线图。

由图5和图6可以看出，本文算法的控制器的输出为非线性形式，其输出量要比PI等控制器的输出量小，这样本文算法的超调量相对较小且达到稳态的时间也相对较短。其他几种比较算法的控制器输出量类似。

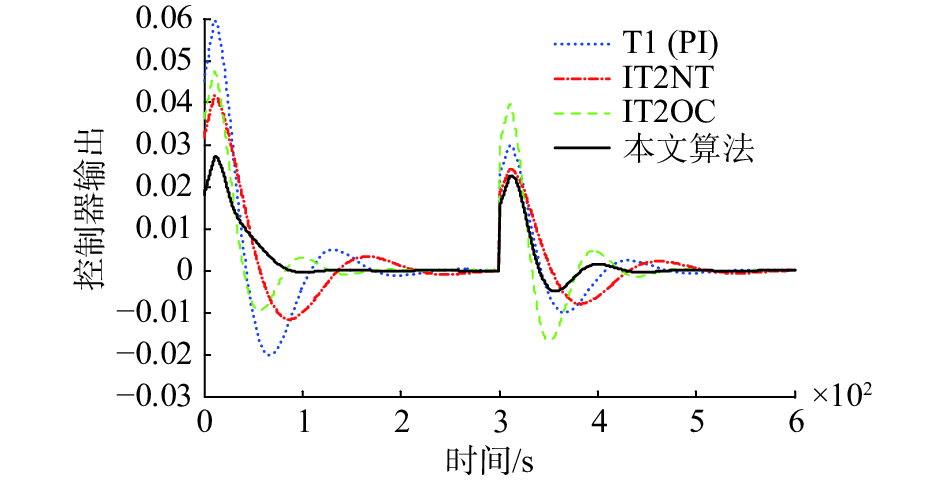
图7显示了几种算法控制器的输出曲线，也进一步说明了上述观点。

4.2 仿真实例2

选取非线性对象：

$ \frac{{y\left( t \right)}}{{dt}} =- y\left( t \right) + 7 \times y{\left( t \right)^2} + u\left( t \right) $

PI控制器参数：K_P=56.25，K_I=669.375，采样周期0.01 s。

参数：d₁=d₂=0.2。

图8显示了几种控制算法对选取的非线性对象阶跃响应的控制效果，具体的曲线定义与仿真实例1中图4中曲线相同。

表2显示了针对仿真实例2的非线性对象在单位阶跃输入下本文算法和其他几种算法的控制性能比较。其中t_s(s)、t_r(s)、ISE、ITSE、IATE的意义同仿真实例1表1的说明。

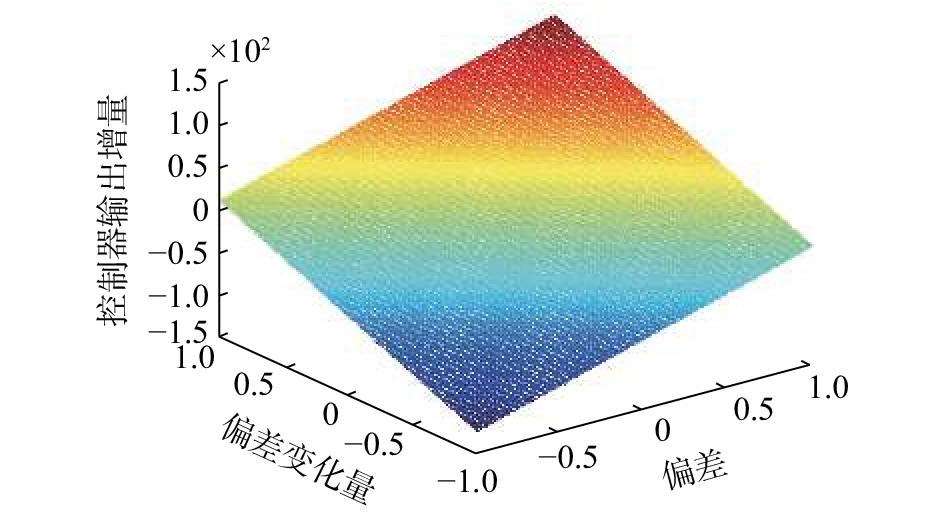
图9和图10分别表示了使用PI控制器和本文的区间二型模糊PI控制器的输出增量随着偏差和偏差变化量变化的三维曲线图。

图11显示了几种算法控制器的输出曲线。

5 结束语

本文提出了一种改进的动态解模糊化区间二型模糊PI控制器设计算法。该算法基于区间二型模糊集合，采用直接降阶算法，避免了KM等常用迭代式降阶算法，其实时性与传统模糊控制器相同，提高了区间二型模糊控制器的实用性。本文算法在计算控制器输出的时候，没有利用降阶区间的平均值作为控制器的输出，而是采用一种动态解模糊化方法，充分利用了偏差和偏差变化量对模糊控制器输出的影响，使得控制器的输出更为平滑。通过线性二阶迟延对象以及一个非线性对象的仿真实验表明，本文算法能够降低系统的超调量，系统达到稳态的时间也相对较短。

本文算法的控制器输出在设定值附近输出更为平滑，抖动量较小。如果想要提高系统的响应速度(减小上升时间)，可以通过减小参数d₁或者d₂来实现，但这样会带来超调和稳定时间的提高。在实际控制过程中，可综合考虑上升时间、稳定时间、超调这几种因素，选择合适的d₁或者d₂值。

本文只考虑了首隶属度函数为三角型，模糊隶属函数还有高斯、钟形等其他形式，下一步将针对其他类型的隶属度函数，进行区间二型模糊PI控制器的研究。