与传统的通信方式相比，激光混沌通信具有很多优点。由于其对初始值的灵敏度具有长期不可预测性，非常适合安全通信应用；通过使用不同的混沌吸引子或相同吸引子的不同初始值和参数产生的混沌信号可以认为是不相关的，因此容易产生大量相互正交的混沌信号，这使得激光混沌信号在多用户通信中具有广泛的应用前景^[1]。然而，在激光通信和信号处理等领域中混沌技术的应用也可能面临一些挑战。对于系统现有的信道间干扰，时变衰落或混合多用户载波，盲源分离是一个必须解决的问题。一些研究人员使用混沌信号的动态属性进行盲源分离^[2-4]，这种方法只能在源信号动态方程的条件下应用,独立分量分析(ICA)方法也用于分离混沌信号^[5-7]。这种方法假设每个源之间是互相统计独立，并通过使用高阶统计性质分离混合信号。然而，激光混沌流信号本质上是确定单一的，并且具有对初始值和宽带光谱非常敏感的特性，因此仅通过使用统计特性难以有效地进行盲源分离。本文使用相空间重构理论描述盲源分离问题,提出了一种针对上述问题的新型混沌信号盲源分离方法。

1 混沌信号的盲源分离方法

激光混沌流信号的盲源分离模型如图1所示， $n$ 个不相关的激光混沌流信号 ${s_j}(t),j = 1,2, \cdots ,n$ 通过传感观测并线性混合。第 $i$ 个传感器观测信号 ${x_i}(t)$ 为每个独立源的线性组合，即

${x_i}(t) = \sum\limits_{j = 1}^n {{a_{ij}}{s_j}(t)} $

(1)

表示为矩阵形式：

${{x}}(t) = {{As}}(t) + {{n}}(t)$

(2)

式中：

${{x}}(t) = {\left[ {{x_1}(t)\,\,\,{x_2}(t) \cdots {x_m}(t)} \right]^{\rm{T}}}$

(3)

${{s}}(t) = {\left[ {{s_1}(t)\,\,\,{s_2}(t) \cdots {s_n}(t)} \right]^{\rm{T}}}$

(4)

式中： ${{A}}$ 称为混合矩阵； ${{n}}(t) = {\left[ {{n_1}(t)\,\,\,{n_2}(t) \cdots {n_m}(t)} \right]^{\rm{T}}}$ 为观测噪声，假设其为高斯白噪声。

根据观测混合信号 ${{x}}(t)$ ，盲源分离算法是为了获得源信号的估计：

$\hat{{ s}}(t) = {{Bx}}(t) = {{BAs}}(t)$

(5)

矩阵 ${{B}}$ 称为分离矩阵。显然，如果不考虑噪声，则 ${{BA}}={{I}}$ ， ${{I}}$ 是单位阵，那么源信号可以被很好地重建。尽管如此，由于盲源分离自身的模糊性^[8]，如果满足式（6）便可得到分离矩阵，然后就可以认为混合信号被成功分离。

${{BA}} = {{\varLambda P}}$

(6)

式中： ${{\varLambda }}$ 是一个随机 $n$ 阶非奇异对角阵， ${{P}}$ 是一个 $n$ 阶置换矩阵。

2 基于相空间的盲源分离理论分析

相空间重建广泛应用于激光混沌序列的分析，如预测、诊断和激光混沌信号的李亚普诺夫指数的计算等。文献[9]通过相空间重建，定义指数来测量流模式混沌序列相空间的生长速率——生长指数。本节将使用生长指数来描述混沌信号的盲源分离问题。

假设由 ${d_A}$ 维混沌吸引子产生的混沌序列 ${{x}}(t)$ ，通过使用延迟为1的相空间重构来估计其相空间的状态向量。

$\begin{align}&{{\varsigma }}(t) = {[{{x}}(t)\,\,\,{{x}}(t + 1) \cdots {{x}}(t + d - 1)]^{\rm{T}}}\end{align}$

(7)

式中： $d$ 表示延迟重建的嵌入维数； $t = 1,2, \cdots ,\sigma + 1 $ ； $\sigma + 1$ 是从观测序列获得的状态向量的数量。当 $d \geqslant 2{d_A}$ 且是整数时， ${{\varsigma }}(t)$ 可以平滑地重构混沌吸引子。在盲源分离问题中，每个源混沌流信号的维数 ${d_A}$ 一般不能预先知道，为了更好地恢复混沌吸引子的性质， $d$ 应尽可能大，当观察序列长度为 $N$ ，例如，可以令 $d = N - \sigma $ 。在相空间中， ${{\varsigma }}(t + 1)$ 和 ${{\varsigma }}(1)$ 之间的距离定义为

$V_{\rm{\varsigma }}(t) = {\left\| {{{\varsigma }}(t + 1) - {{\varsigma }}(1)} \right\|^2}$

(8)

式中 $|| \cdot ||$ 是 ${l^2}$ -规范。不同的激光混沌信号在空间的流模式中具有不同的生长速率，可以通过定义生长指数来描述：

${P_\sigma }({\rm{\varsigma }}) = \frac{{D(V_{\rm{\varsigma }}(t))}}{{{E^2}(V_{\rm{\varsigma }}(t))}},\;\quad t = 1,2, \cdots ,\sigma $

(9)

式中： $D( \cdot )$ 表示方差； $E( \cdot )$ 表示数学期望； $\sigma $ 是控制参数，并且当没有噪声时， $\sigma = 5$ 可以减少 ${P_\sigma }({\rm{\varsigma }})$ 计算负担，当观察噪声不能被忽略时，可令 $\sigma = 100$ 。

文献[9]证明，当重构的观测序列具有零均值时，具有以下性质。

性质1　尺度不变性，即 ${P_\sigma }({{\varsigma }}) = {P_\sigma }(k{{\varsigma }}),\forall k \ne 0\text{。}$

性质2　当 ${{{\varsigma }}_{{1}}}$ 和 ${{{\varsigma }}_{{2}}}$ 是两个不相关的随机序列时，

$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{P_\sigma }({k_1}{{{\varsigma }}_{{1}}}+{k_2}{{{\varsigma }}_{{2}}}) < \max ({P_\sigma }({{{\varsigma }}_{{1}}}),{P_\sigma }({{{\varsigma }}_{{2}}})),\forall {k_1},{k_2} \ne 0\text{。}$

假设有不相关的观测序列 ${{{x}}_1}(t)$ 和 ${{{x}}_2}(t)$ ，并且对其进行时间延迟为1的相位空间重建，分别获得状态向量 ${{{\varsigma }}_1}(t)$ 和 ${{{\varsigma }}_2}(t),\;t = 1,2, \cdots ,\sigma + 1$ 。因此序列 ${k_1}{{x}}_1(t)+{k_2}{{x}}(t)$ 重建的状态向量 ${k_1}{{{\varsigma }}_1}(t)+{k_2}{{{\varsigma }}_2}(t)$ 与 ${P_\sigma }({{\varsigma }})$ 的性质2结合可以得到以下结论：由两个不同的动态系统产生的不相关的时间序列，其线性组合的生长指数总是小于具有较大生长指数的两个时间序列中的一个； $n$ 个不相关序列中的任何一个序列与其余 $n - 1$ 个序列的线性组合无关，因此 $n$ 个不相关序列的线性组合的生长指数总是小于具有最大生长指数的序列。这可以启发我们，可以将包含 $n$ 个混合信号的盲源分离问题转换为具有正交约束的优化问题：

$\left\{ {\begin{aligned}& {\mathop {\max }\limits_{{{B}} \in {R^{n \times n}}} \left\{ {{P_\sigma }({{{\varsigma }}_{\hat{{ s}},1}}) + {P_\sigma }({{{\varsigma }}_{\hat{{ s}},2}})+ \cdots + {P_\sigma }({{{\varsigma }}_{\hat{{ s}},n - 1}})} \right\}\;\;\;} \\ & {E\left[ {\hat{{ s}}(t){{\hat{{ s}}}^{\rm T}}(t)} \right] = {{I}}} \end{aligned}} \right.$

(10)

式中， ${{B}}$ 是分离矩阵， ${P_\sigma }({{{\varsigma }}_{\hat{{ s}},i}})$ 是重构第 $i$ 个信道源 ${\hat s_i}(t)$ 的增长指数，约束条件 $E\left[ {\hat{{ s}}(t){{\hat{{ s}}}^{\rm{T}}}(t)} \right] = {{I}}$ 确保获得的每个信道分离信号 ${\hat s_i}(t)$ 与其他求解分离信号 ${\hat s_j}(t)$ 的解空间正交。

3 盲源分离算法的过程

前一节中生长指数的性质1是在观测序列为零均值时成立的，因此首先要对观测信号进行均值去除：

${x_i}(t) = {x_i}(t) - E\left[ {{x_i}(t)} \right],\;i = 1,2, \cdots ,n$

(11)

生长指数的性质2还要求信号序列彼此不相关，这可以通过预白化观测信号来实现。假设 ${{x}}(t)$ 自相关矩阵特征分解为 $E\left[ {{{x}}(t){{{x}}^{\rm{T}}}(t)} \right] = {{Q\Sigma }}{{{Q}}^{\rm{T}}}$ ，其中， ${{Q}}$ 是正交矩阵， ${{\Sigma }}$ 是对角矩阵，那么 ${{W = }}{{{\Sigma }}^{{{ - 1/2}}}}{{{Q}}^{\rm T}}$ 称为白化矩阵，在线性变换 ${{\tilde x}}(t) = {{Wx}}(t)$ 后， ${{\tilde x}}(t)$ 的每个分量彼此不相关。

通过Cayley变换，任意 $n$ 阶正交矩阵可以被分解为一系列旋转矩阵的乘积，并且包含要表示的 $n(n - 1)/2$ 个参数的参数向量 $\theta = \{ {\theta _1}, {\theta _2},\cdots ,{\theta _{n(n - 1)/2}}\} $ ^[10]。

这种方法可以减少要优化的参数，从而显著提高算法的收敛速度和鲁棒性。本节后续部分采用以下形式的参数化矩阵来表示2阶和3阶正交矩阵：

${{{B}}_{2 \times 2}} = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _1}}&{ - \sin {\theta _1}} \\ {\sin {\theta _1}}&{\cos {\theta _1}} \end{array}} \right]$

(12)

$\begin{aligned}{{{B}}_{3 \times 3}} =& \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos {\theta _1}}&{ - \sin {\theta _1}} \\ 0&{\sin {\theta _1}}&{\cos {\theta _1}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos {\theta _2}}&0&{ - \sin {\theta _2}} \\ 0&1&0 \\ {\sin {\theta _2}}&0&{\cos {\theta _2}} \end{array}} \right] \cdot \\ & \left[ {\begin{array}{*{20}{c}} {\cos {\theta _3}}&{ - \sin {\theta _3}}&0 \\ {\sin {\theta _3}}&{\cos {\theta _3}}&0 \\ 0&0&1 \end{array}} \right]\end{aligned}$

(13)

式中 ${\theta _i} \in [0,2{\text{π}} ]$ 为参数向量。用参数表示，式(10)可以转换为无约束的优化问题：

$\mathop {\max \{ {P_\sigma }({{{\varsigma }}_{{{y}},1}})+{P_\sigma }({{{\varsigma }}_{{{y}},2}})+ \cdots + {P_\sigma }({{{\varsigma }}_{{{y}},n - 1}})\} },{{\theta _i} \in [0,2\text{π} ]}$

(14)

式中 $i=1,2,\cdots,n(n-1)/2$ 。

对于非约束优化问题，粒子群优化算法是一种非常有效的方法。将参数向量视为粒子位置，将目标函数式(14)视为适应度函数，可以使用粒子群优化算法估计最优分离矩阵，以重构每个信道源信号。整个算法过程为：

1) 观测信号 ${{x}}(t)$ 去均值；

2) 预白化观测信号 ${{x}}(t)$ ，得 ${{\tilde x}}(t)$ ；

3) 使用 $[0,2{\text{π}}]$ 上均匀分布的随机数初始化每个粒子的初始位置；

4) 对于每个粒子，根据式(11)、(12)、(13)计算分离矩阵B，根据式(3)计算分离信号，根据式(5)实现相位空间重构；根据式(7)~(9)计算适度函数值；

5) 应用粒子群算法优化式(14)直到满足终止条件，记录优化粒子位置θ_opt；

6) 输出重构的源信号 ${{y}}(t)$ =B_opt ${{\tilde x}}(t)$ ，B_opt为分离矩阵。

4 仿真实验

本节将通过仿真实验来评估盲源分离算法的性能。源信号通过式(1)产生混合信号，混合矩A的元素在每次仿真中通过服从[-1,1]独立均匀分布随机数产生。盲源分离算法的精度将通过性能指标PI来测量：

$\begin{align}{\rm PI} =& \frac{1}{{n(n - 1)}}\sum\limits_{i = 1}^n {\left( {\sum\limits_{j = 1}^n {\frac{{{{\left| {{g_{ij}}} \right|}^2}}}{{{{\max }_k}{{\left| {{g_{ik}}} \right|}^2}}}} } \right)} + \sum\limits_{j = 1}^n {\left( {\sum\limits_{i = 1}^n {\frac{{{{\left| {{g_{ij}}} \right|}^2}}}{{{{\max }_k}{{\left| {{g_{kj}}} \right|}^2}}}} } \right)} \end{align}$

(15)

式中g_ij为 $ {{G}} ={{ BWA}}$ 的元素，PI越小越好，当G满足式(6)时，PI得到最小值0。

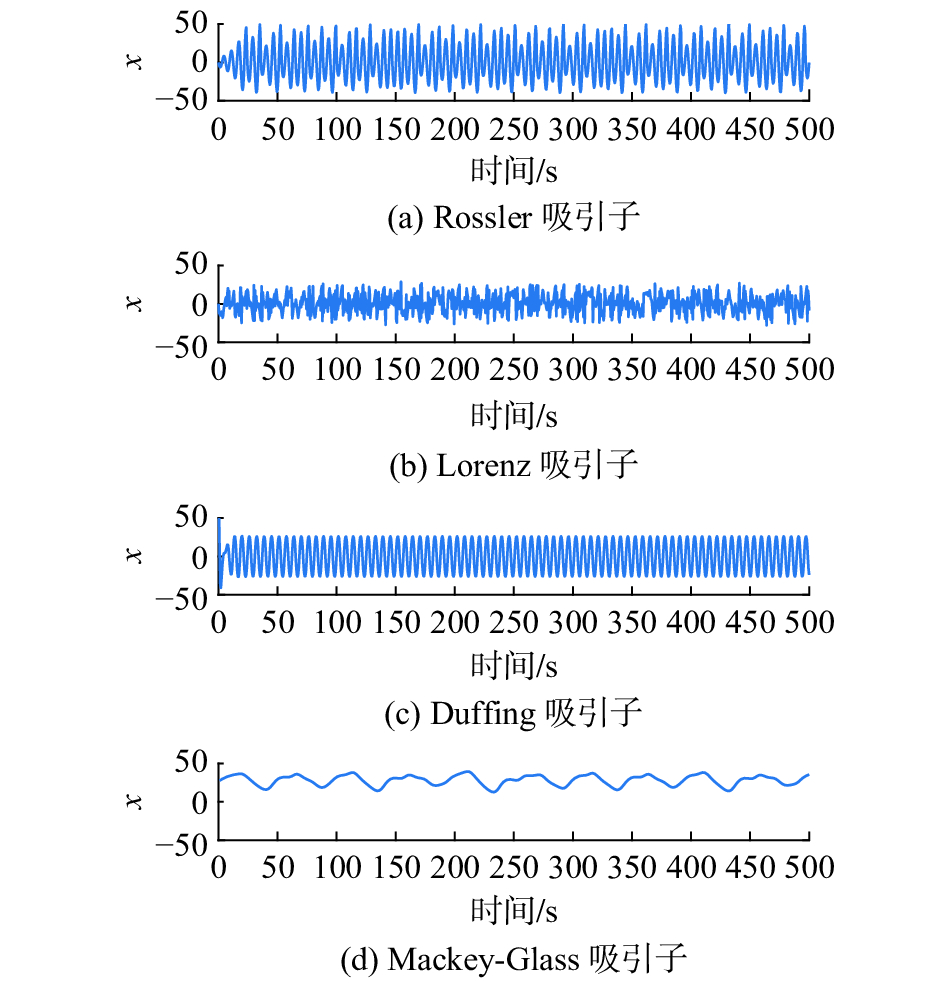
仿真实验中使用的4个源信号分别由Rossler吸引子式(16)、洛伦兹吸引子式(17)、Duffing吸引子式(18)和Mackey-Glass吸引子式(19)产生，前3个信号通过4阶龙格库塔法积分得到，积分步长分别为0.05、0.05、0.01，信号的长度为500 s，如图2所示。利用4个信号组成如表1所示的三通道混合信号和双通道混合信号，用于测试盲源分离效果的。

$\left\{ {\begin{aligned}& {\frac{{{\rm {d}}{x}}}{{{\rm {d}}{t}}} = - y - z}\\& {\frac{{{\rm {d}}{y}}}{{{\rm {d}}{t}}} = x + {\rm{0}}{\rm{.2}}y}\\& {\frac{{{\rm {d}}{z}}}{{{\rm {d}}{t}}} = 0.2 + z\left( {x - 5} \right)}\end{aligned}} \right.$

(16)

$\left\{ {\begin{aligned}& {\frac{{{\rm d}{x}}}{{{\rm d}{t}}} = 16(x-y)}\\& {\frac{{{\rm d}{y}}}{{{\rm d}{t}}} =45.92x-y-xz}\\& {\frac{{{\rm d}{z}}}{{{\rm d}{t}}} = xy-4z}\end{aligned}} \right.$

(17)

$\left\{ {\begin{aligned}& {\frac{{{\rm d}{x}}}{{{\rm d}{t}}} = y}\\& {\frac{{{\rm d}{y}}}{{{\rm d}{t}}} =- 0.5y + x - {x^3} + 0.42\sin t}\\\end{aligned}} \right.$

(18)

$x(i + 1) = x(i) + \frac{{0.2x(i - 17)}}{{1 + {x^{10}}(i - 17)}} - 0.1x(i)$

(19)

4.1 混沌流无噪声信号的盲源分离仿真结果

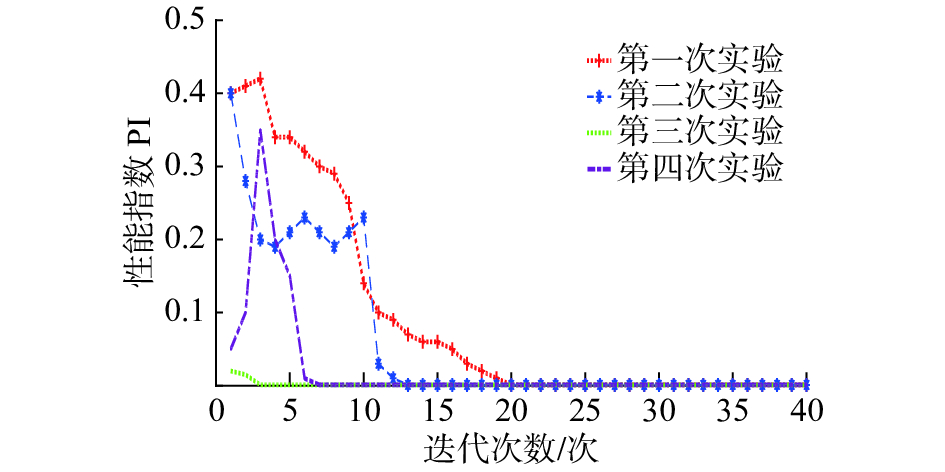
对于表1中的三通道源信号，利用本文提出的方法进行4次盲源分离实验，性能指标PI随迭代步骤变化，如图3所示。随着迭代步长的增加，PI快速减小，在所有实验中，算法可以通过几十次迭代收敛。表2给出了无噪声环境下，对表1中两组源信号进行100次蒙特卡罗模拟之后的实验结果，可以看出，对于组1中的三通道混合信号和组2中的双通道混合信号的分离，提出的算法的分离精度优于快速独立分量分析(FastICA)、蝙蝠算法(BA)和差分进化算法(DEA)。

4.2 噪声环境下混沌流信号的盲源分离仿真结果

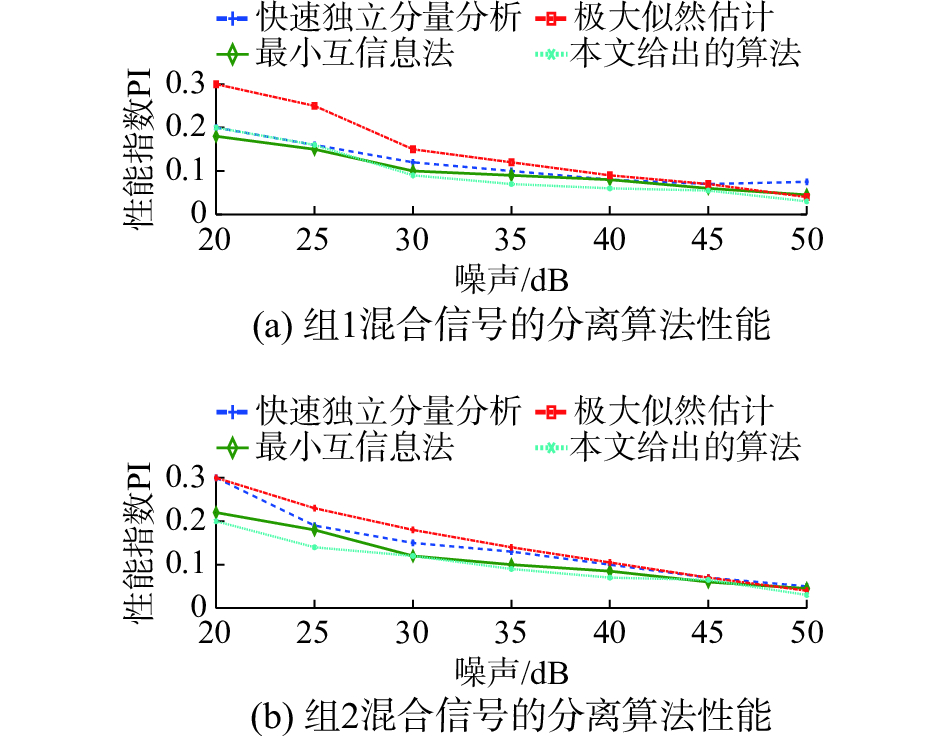
本节将评估基于蚁群技术的多特征值分解盲源分离算法与基于FastICA、最小互信息和极大似然估计法对噪声污染混合信号的分离性能。对于表1中的两组源信号的混合信号加入高斯白噪声。让观测噪声从20 dB变化到50 dB，以5 dB的间隔测试点，在每个测试点重复100次蒙特卡罗模拟，各分离算法的分离性能指数如图4所示。

5 结束语

本文描述了使用相空间重构理论的盲源分离，并为激光混沌流信号提出了一种新的盲源分离算法。该算法通过构建分离信号相位空间中的目标函数，将混沌流信号的盲源分离转换为无约束优化问题，并通过粒子群优化算法求解。同时，它采用分离矩阵上的正交矩阵的参数表示，有效地减少了优化问题的维数，因此该算法可以快速收敛。仿真结果表明，该算法不仅具有快速收敛的特点，其在各种SNR下的精度明显优于FastICA、最小互信息和极大似然算法。