真实世界中的对象通常具有不止一种语义标记，经常表现为多义性，即一个对象可能与多个类别标记相关联。如一幅海边景色图片可以同时标注“蓝天”“白云”“大海”“沙滩”等语义标记，对于多个标记对象的处理方式是为每个图像赋予一个标记子集，并进行建模和学习，这就形成多标记学习框架^[1]。在多标记学习框架下，每个示例由对应的多个标记构成的特征向量进行描述，学习的目标是将多个适当的标记赋予需要预测的未知示例^[2]。

随着信息化的快速发展，数据和资源呈海量特征，数据的标注结构复杂程度也不断增加，单标记方法无法满足分析处理要求^[1]，以机器学习技术为基础的多标记学习技术现已成为一个研究热点，其研究成果广泛地应用于各种不同领域，如图像视频的语义标注、功能基因组、音乐情感分类以及营销指导等^[3]。

在多标记学习过程中，高维数据训练和预测都需要更多的计算时间和空间。降维减少了特征数却提高了算法效率和学习性能，可避免过拟合现象和过滤掉冗余特征^[4-6]。因此，降低数据的维度具有重要意义。

高维数据降维，主要有线性维数约简和非线性维数约简两种方法。线性维数约简的方法有主成分分析方法(principal component analysis, PCA)、独立成分分析方法(independent component correlation algorithm, ICA)、线性判别分析法(linear discriminant analysis, LDA)和局部特征分析法(local feature analysis, LFA)等。非线性降维方法有等距特征映射方法(isometric feature mapping, ISOMAP) 和局部线性嵌入方法(locally linear embedding, LLE)等^[7-8]。多标记学习的有监督降维方法有依赖最大化(MDDM)算法^[5]，半监督方法主要是采用联合降维方法^[9]和依赖最大化方法^[10]。

与一般多标记有监督的降维方法不同，提出一种自编码网络的无监督多标记维数约简方法(multi-label unsupervised dimensionality reduction via autoencoder networks, MUAE)，首先构建自编码神经网络，仅使用特征数据作为输入，进行编码和解码输出以提取特征，在处理过程引入稀疏约束并将输出数据与输入数据对比，计算总体成本误差，应用梯度下降法进行迭代更新，通过深度学习训练获得自编码网络学习模型，提取数据特征，最后以多标记学习ML-kNN算法作为统一的分类评价基准，并在6个公开数据集上与其他4种方法对比。实验结果表明，该方法能够在无监督情况下有效提取特征，降低多标记数据维度，得到较好的学习效果。

1 多标记学习

多标记的样本由一个示例和对应的多个标记构成，多标记学习是一种机器学习框架^[1-2]。下面的内容，简要地介绍多标记学习的问题定义和学习算法。

1.1 多标记问题定义

假设 ${{X}} \in {{{\bf{R}}}^d}$ 代表 $d$ 维的示例空间， ${{Y}} \!=\! \left\{ {{{{y}}_1},{{{y}}_2}, \cdots ,} \right.\left. {{{{y}}_l}} \right\}$ 代表包含 $l$ 个类别的标记空间。给定多标记训练集 ${{D}} = \{ ({{{x}}_i},{{{Y}}_i})|1 \leqslant i \leqslant m\} $ ，其中 ${{{x}}_i}$ 为 $d$ 维的属性向量，即 ${{{x}}_i}={[{x_{i1}}\;{x_{i2}} \cdots {x_{id}}]^{\rm{T}}}$ ，而 ${{{Y}}_i} \in {{Y}}$ 为与 ${{{x}}_i}$ 对应的一组类别标记，多标记学习的目标是从中学习得到一个多标记分类器 $g:{{X}} \to {2^{{Y}}}$ 。因此，对于所有示例 ${{x}} \in {{X}}$ ，分类器预测隶属于该示例的类别标记集合为 $g({{x}}) \subseteq {{Y}}$ ，称多标记学习^[1]。

多标记的集合空间如果太大则会造成学习困难，因此需要充分利用标记之间的“相关性”来辅助学习过程的进行。基于考察标记之间相关性的不同方式，多标记学习问题求解策略有三类^{[1, 11]}。

“一阶(first-order)”策略：只考察每一个单个标记，不考虑标记之间的相关性，将多标记学习问题分解为多个独立的二分类问题。该策略实现简单，效率较高，但学习的泛化性能不高^[11]。

“二阶(second-order)”策略：考察两两标记之间的相关性和交互关系，该类方法的泛化性能较好，但不能很好处理多标记间的二阶以上相关性^[11]。

“高阶(high-order)”策略：考察任一标记对其它所有标记的影响以及一组随机标记集合的相关性等。该类策略较好地反映了真实世界的标记相关性，但复杂度一般过高，难以处理大规模学习问题^[11]。

1.2 多标记学习算法

目前已经涌现出了大量的多标记学习算法，可以分为问题转换和算法适应两类方法^[1]。

问题转换方法的基本思想是将多标记学习问题转换为其他已知的学习问题进行求解，代表性学习算法有Binary Relevance、Calibrated Label Ranking和Random k-labelsets。算法适应方法的基本思想是通过对常用监督学习算法进行改进，将其直接用于多标记学习，代表性学习算法有ML-kNN, Rank-SVM和LEAD^[1]。

ML-kNN算法^[12]是对k近邻(k-nearest neighbors，kNN)算法进行改造以适应多标记数据分类，算法的基本思想是采用kNN分类准则，统计近邻样本的类别标记信息，通过最大化后验概率的方式推理未知示例的标记集合。

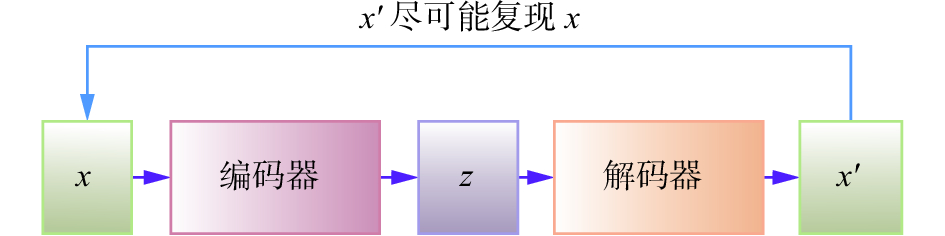
2 自编码网络

自编码网络包含数据输入层、隐藏层、输出重构层。如图1所示，自编码器由编码器(encoder)和解码器(decoder)两部分构成。其作用是将输入样本压缩到隐藏层，然后解压，在输出层重建样本^[13-15] 。

自编码网络是一种不需要标记的无监督学习模型，它试图学习一个函数 $h({{x}}) \approx {{x}}$ ,训练网络使得输出逼近输入，也就是每个样本 ${{x}}$ 的学习目标也是 ${{x}}$ ，这样自编码器自己生成标签，而且标签就是样本数据本身，所以也称为自监督学习或自学习。如图1所示，从输入 $x$ 通过编码器到 ${{z}}$ ，然后经解码器到 ${{x}}'$ ，自编码器的目的是，让输出 ${{x}}'$ 尽可能复现输入 ${{x}}$ 。系统的输出 ${{x}}'$ 能够复原原始数据 ${{x}}$ ，说明 ${{z}}$ 的维度虽然与 ${{x}}$ 的维度不同，但承载了原始数据的所有信息，只是形式不同，是已经变换特征的某种形式。如果对隐含层进行约束使得 ${{z}}$ 的维度小于 ${{x}}$ 的维度，就可以实现无监督数据降维^[16]。

自编码器AE(autoencoder)接受一个输入 ${{x}} \in {{{\bf{R}}}^m}$ ，通过一个编码器将它映射到一个隐藏层，用z表示，如式(1)所示：

${{z}} = s({{Wx}} + {{b}})$

(1)

通常称 ${{z}}$ 为编码，也称为潜在变量或潜在表示， $s$ 是一种基于元素的激活函数，可以是sigmoid函数或双曲正切函数， ${{W}}$ 是一个权重矩阵， ${{b}}$ 是一个偏差向量。

在自编码器的解码阶段，解码器将 ${{z}}$ 映射到与 ${{x}}$ 形状相同的重构 ${{x}}'$ ，即

${{x}}' = s'({{W}}'{{z}} + {{b}}')$

(2)

一般而言，解码器中的 $s'$ 、 ${{W'}}$ 和 ${{b}}'$ 可能与编码器中的 $s$ 、 ${{W}}$ 和 ${{b}}$ 不同，主要取决于自编码器的设计，自编码器的学习函数为 $h({{x}}) = s \circ s'$ 。

重建误差可以用许多方法测量，可根据给定输入的分布假设而制定。一般可以采用样本的代价函数，单个样本的代价函数为

$c({{W}},{{b}},{{{x}}_i},{{x}}_i') = \frac{1}{2}{\left\| {{{x}}_i' - {{{x}}_i}} \right\|^2}$

(3)

$m$ 个样本的整体平方误差成本函数为

$\begin{array}{c} C({{W}},{{b}}) = \displaystyle\frac{1}{m}\sum\limits_{i = 1}^m {\frac{1}{2}{{\left\| {{{x}}_i' - {{{x}}_i}} \right\|}^2}} + \displaystyle\frac{\lambda }{2}\sum\limits_{l = 1}^{n_l - 1} {\sum\limits_{i = 1}^{n_s} {\sum\limits_{j = 1}^{n_s + 1} {({{W}}_{ji}^l} )} } \\ \end{array} $

(4)

式中： $m$ 是样本个数； $n_l$ 是网络层数； $n_s$ 是 $l$ 层的神经元数量； $\lambda $ 是权重衰减参数，用于控制公式中两项的相对重要性。 $C({{W}},{{b}})$ 是整体样本代价函数，第一项是均方差项，第二项是权重衰减项或称为规则化项，其目的是防止过度拟合。

训练目标就是获得总体样本成本误差 $C({{W}},{{b}})$ 最小的 ${{W}},{{b}}$ ，即

$\mathop {\arg \min }\limits_{{{W}},{{b}}} (C({{W}},{{b}}))$

(5)

如果输入是完全随机的，每个输入数据都独立于其他特征的高斯分布，则编码器的压缩任务将非常困难。但是，如果数据中存在结构，有些输入要素是相关或有冗余，则该算法将能够发现一些相关性。自动编码器通常最终会学习与PCA非常相似的低维表示。事实上，如果每两层之间的变换均为线性且训练误差是二次型误差时，该网络等价于PCA。而自编码网络使用非线降维，更符合数据的实际情况，这种机制使得其效果比PCA更优。

自编码网络可以实现无监督的自我学习，把这种自我学习扩展到深度学习网络，即拥有多个隐藏层的神经网络，以提取多标记的数据特征，实现多标记学习的无监督维数约简。

3 多标记维数约简的自编码网络方法 3.1 多标记维数约简

多标记学习与单标记学习一样面临“维度灾难”的挑战，所以维数约简结果的好坏直接影响着分类器的精度和泛化性能，特别是对于基因序列、图像处理等高维数据，影响更加显著。数据维度过大，不仅会增加计算时间和空间的复杂度，还会降低多标记学习性能。如果在多标记学习训练之前，通过一定的特征选择或提取方法，去掉不相关或冗余属性，反而可以获得更令人满意的知识学习模型^[17-18]。降低高维数据的维度是多标记学习中一个重要的研究课题，很多学者研究多标记数据的降维方法以提高多标记学习算法的效果^[19]。

已有的多标记数据维数约简方法可以分为两大类：特征选择(feature selection)和特征提取(feature extraction)。特征选择是给定一个多标记分类算法和训练集，通过优化某个多标记损失函数对属性子集进行评价，选择使损失达到最小的属性子集作为最终结果^[20]。而特征提取是通过空间变换，将某些原始特征映射到其他低维空间，生成一些新的特性^[3，5]，特征提取后的新特征是原来特征的一个变换映射，不是原特征一个子集。

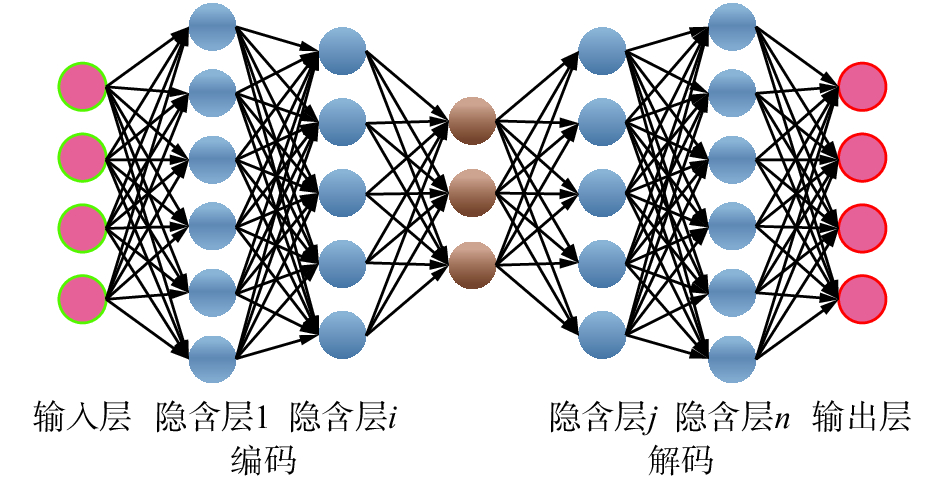
3.2 多标记学习维数约简的自编码网络方法

基本自编码网络可以解决数量很小的隐藏单元问题，而高维数据的隐藏单元数量很大，为此，对隐藏单元进行稀疏约束，使得自编码器可以从大量的隐藏单元中发现高维数据中的相关结构，提取关键特征，实现维数约简。自编码网络，由输入层、隐含层 ${\rm{1,2,}} \cdots {{,i,}} \cdots {{n}}$ 和输出层组成，如图2所示。

如果激活函数采用sigmoid函数，当神经元的输出值接近于1，则神经元是“活动的”，如果它的输出值接近于0，则神经元是“无效的”。

令 ${a_j}$ 表示自编码器中激活隐藏单元 $j$ ，当网络被赋予特定的输入 ${{x}}$ 时，用 ${a_j}({{x}})$ 表示 ${{x}}$ 激活隐藏单元 $j$ 的输出值。如果输入 ${{x}}$ 有 $m$ 个样本，则隐藏单元 $j$ 的平均激活为 ${\bar \rho _j}$ ，即

${\bar \rho _j} = \frac{1}{m}\sum\limits_{i = 1}^m {{a_j}({{{x}}_i})} $

(6)

用稀疏参数 $\rho $ 对每个隐藏神经元的平均激活进行稀疏约束， $\rho $ 的取值接近于零，比如取0.05。为满足这个约束，引入伯努利随机变量KL(Kullback-Leibler)散度来度量平均值 ${\bar \rho _j}$ 和 $\rho $ 之间的距离，即

${\rm{KL}}(\rho ||{\bar \rho _j}) = \rho \log \frac{\rho }{{{{\bar \rho }_j}}} + (1 - \rho )\log \frac{{1 - \rho }}{{1 - {{\bar \rho }_j}}}$

(7)

隐藏层中所有神经元的KL散度之和作为优化目标的处罚项，以惩罚显著偏离 $\rho $ ，即

$\sum\limits_{j = 1}^{n_s} {{\rm{KL}}(\rho ||{{\bar \rho }_j})} $

(8)

式中： $n_s$ 是隐藏层中所有神经元的数量。如果 ${\bar \rho _j} = \rho $ ，那么 ${\rm{KL}}(\rho ||{\bar \rho _j}) = 0$ ；否则 ${\bar \rho _j}$ 会随着偏离 $\rho $ 而单调增加，所以只要使这个惩罚项最小化，就会导致 ${\bar \rho _j}$ 接近于 $\rho $ 。

稀疏约束后，样本的总体成本为

${C_{{\rm{sparse}}}}({{W}},{{b}}) = C({{W}},{{b}}) + \beta \sum\limits_{j = 1}^{n_s} {{\rm{KL}}(\rho ||{{\bar \rho }_j})} $

(9)

式中 $\beta $ 是控制稀疏惩罚项的权重。

稀疏约束后训练目标也是总体成本误差最小，即

$\mathop {\arg \min }\limits_{{{W}},{{b}}} ({C_{{\rm{sparse}}}}({{W}},{{b}}))$

(10)

为了求解上述总体成本误差最小问题，采用反向传播算法计算成本偏导数，先求出成本函数C_sparse（W，b）对 $\partial {{W}}_{ij}^l$ 的偏导数，得到

$\begin{array}{c} \displaystyle \frac{\partial }{{\partial W_{ij}^l}}{C_{{\rm{sparse}}}}({{W}},{{b}}) = \displaystyle \frac{1}{m}\sum\limits_{i = 1}^m {\frac{\partial }{{\partial {{W}}_{ij}^l}}} C({{W}},{{b}},{{{x}}_i},{{x}}_i') + \lambda {{W}}_{ij}^l\end{array} $

(11)

以及对 ${{b}}_{^i}^l$ 求偏导数，得到

$\begin{array}{c} \displaystyle \frac{\partial }{{\partial {{b}}_i^l}}{C_{{\rm{sparse}}}}({{W}},{{b}}) = \displaystyle \frac{1}{m}\sum\limits_{i = 1}^m {\frac{\partial }{{\partial {{b}}_i^l}}} C({{W}},{{b}},{{{x}}_i},{{x}}_i') \\ \end{array} $

(12)

采用梯度下降迭代法，按公式(13)、(14)进行迭代：

${{W}}_{ij}^l = {{W}}_{ij}^l - \alpha \frac{\partial }{{\partial {{W}}_{ij}^l}}{C_{{\rm{sparse}}}}({{W}},{{b}})$

(13)

${{b}}_i^l = {{b}}_i^l - \alpha \frac{\partial }{{\partial {{b}}_i^l}}{C_{{\rm{sparse}}}}({{W}},{{b}})$

(14)

综合上述推导过程和结果，设计多标记学习的自编码网络无监督降维算法MUAE如下。

算法　MUAE

输入　 ${{{X}}^{{{n}} \times {{m}}}}$ 特征矩阵， ${Y^{{{n}} \times {{p}}}}$ 标记矩阵，约简维度 $d$ 。

输出　多标记学习分类结果。

1) 初始化权重矩阵 ${{{W}}^l}$ 和偏离向量 ${{{b}}^l}$ ；

2) for epoch =1:k；

3) 计算样本总成本 ${C_{{\rm{sparse}}}}({{W}},{{b}})$ ；//由式(9)计算；

4) 迭代权重矩阵 ${{W}}^l$ 和偏离向量 ${{b}}^l$ ；//由式(13)和式(14)计算；

5) end for

6) 返回输出层特征矩阵 ${{{X}}^{{{n}} \times {{d}}}}$ ；

7) 多标记算法ML-kNN( ${{{X}}^{{{n}} \times {{d}}}}$ , ${{{Y}}^{{{n}} \times {{p}}}}$ )计算分类结果//按文献[12]计算。

4 实验结果与分析 4.1 实验数据与对比算法

多标记学习数据降维实验采用公开数据集^[21]，各数据集的训练和测试样本数、标记数量与数据特征数量等基本情况如表1所示，表中6个数据集Arts、Business、Computers、Health、Recreation、Reference的名称前面分别用A、B、C、D、E、F对应标注，以方便后续表格使用。

实验过程中，将MUAE算法与4种算法进行对比，对比算法分别是线性维数约简主成分分析PCA算法^[22]、非线性维数约简局部保留投影LPP^[23]算法和拉普拉斯特征映射LE算法^[24]，以及多标记依赖最大化MDDM算法^[5] 。

在维数约简后统一使用ML-kNN算法^[12]进行多标记分类，其中 $k = 10$ ，并以ML-kNN算法在原始特征空间的评价性能作为参照基线，记为Baseline。MDDM算法的 $\mu = 0.5$ ，LLP算法分类时构造邻接图的最近邻个数与ML-KNN算法一样设置 $k = 10$ 。所有维数约简方法降维到相同的维度进行对比，所有算法在6个数据集上的特征降维百分比为10%、20%、30%、40%、50%、60%、70%、80%、90%、100%，共10个百分比的实验对比。

4.2 多标记学习评价指标

在多标记学习问题中，由于每个对象可能同时具有多个类别标记，因此传统监督学习中常用的单标记评价指标无法直接用于多标记学习系统的性能评价。因此，研究者们相继提出了一系列多标记评价指标，一般可分为两种类型，即基于样本的评价指标(example-based metrics)^[25]以及基于类别的评价指标(label-based metrics)^[26]。本文主要采用5种指标，即平均精度(average precision)、汉明损失(Hamming loss)、排名损失(ranking loss)、一错误(oneerror)和覆盖(coverage)，具体的计算公式如下。

1) 平均精度

$\begin{array}{c}{\rm{Averageprecision}}\left( h \right) = \displaystyle\frac{1}{p} \sum \limits_{i = 1}^p \frac{1}{{\left| {{Y_i}} \right|}}\\\displaystyle \sum \limits_{{\rm{y}} \in {Y_{\rm{i}}}} \frac{{\left| {\left\{ {{y'}|{\rm{ran}}{{\rm{k}}_f}\left( {{x_i},{y'}} \right) \leqslant {\rm{ran}}{{\rm{k}}_f}\left( {{x_i},y} \right),{y'} \in {Y_i}} \right\}} \right|}}{{{\rm{ran}}{{\rm{k}}_f}\left( {{x_i},y} \right)}}\end{array}$

(15)

平均精度，是一种最直观的评价方式，评价样本的类别标记排序序列中，排在相关标记之前的标记占标记集合的平均比例，这个指标是相关标记预测的概率平均。

2) 汉明损失

${\rm{Hammingloss}}(h) = \frac{1}{p} \sum \limits_{i = 1}^p \frac{1}{q}|h({x_i})\Delta {Y_i}|$

(16)

汉明损失，是通过计算多标记分类器预测的标记结果与实际的标记差距来度量多标记分类器的性能。

3) 排名损失

$\begin{array}{c}\!\!\!\!\!\!\!\!\!\!\!\!{\rm{Rankingloss}}(f) = \displaystyle\frac{1}{p}\sum\limits_{i = 1}^p {\frac{1}{{\left| {{Y_i}} \right||{{\bar Y}_i}|}}\Bigl| {\left\{ {\left( {{y_1},{y_2}} \right)|f\left( {{x_i},{y_1}} \right) \leqslant } \right.} \Bigr.} \\\!\!\!\!\!\!\!\!\!\!\!\!\left. {\left. {f\left( {{x_i},{y_2}} \right),\left( {{y_1},{y_2}} \right) \in {Y_i} \times {{\bar Y}_i}} \right\}} \right|\end{array}$

(17)

排名损失，评价所有样本的预测标记排名中，不相关标记在相关标记前面的概率平均。

4) 一错误

${\rm{Oneerror}}(f) = \frac{1}{p} \sum \limits_{i = 1}^p \arg \mathop {\max }\limits_{y \in Y} f\left( {{x_i},y} \right) \notin {Y_i}$

(18)

一错误，该指标评价每个样本的预测标记排名中，排在第一位的标记不在该样本的相关标记集中的概率评价。

5) 覆盖

${\rm{Coverage}}(f) = \frac{1}{p} \sum \limits_{i = 1}^p \mathop {\max }\limits_{y \in {Y_i}} {\rm{ran}}{{\rm{k}}_f}\left( {{x_i},y} \right) - 1$

(19)

覆盖，该指标评价每个样本的预测标记排名中需要在标记序列表中最少查找到第几位才可以找出所有与该样本相关的标记。

4.3 实验结果

5种算法和基准算法共6个算法，在6个多标记数据集上用5个评价指标进行对比实验，实验的结果展示在表2~6。

表2是评价平均精度指标的实验结果，其数值是越高越好，最好的结果用黑体表示。实验结果显示，MUAE方法在Business、Computers、Recreation三个数据集上都取得最好结果，PCA在Health和Reference数据集上取得最好结果，MDDM方法在Arts数据集上取得最好结果。能够在平均精度取得好的实验结果，这是由于自编码深度网络能够通过自学习有效提取数据特征，在有监督的多标记数据集上能够通过无监督方法取得好的降维效果。

另外，4个评价指标分别是汉明损失、排名损失、一错误和覆盖，指标数值越小越好，表3~6分别是这4种评价指标的各算法的实验结果，最好的结果用黑体表示。MUAE算法取得最好数据集个数分别为3、3、2、2，4个表中的实验结果显示出MUAE方法总体上比其他4种算法和基准算法好。

综合数据降维的各方法表现，利用自编码进行无监督特征提取，比无监督算法能够取得更好的效果，这应该得益于自编码的思想和设计结构，其能更好地表示输入数据的特征，所以取得好的实验结果。

为了进一步分析自编码在不同降维百分比的性能，以维度数量的10%开始，步长以10%递增至100%，共10组，结果以图的形式展示。图3是平均精度随特征降维百分比变化关系，MUAE在6个数据集上比其他算法能取得更高的精度。图3还显示出平均精度在各个百分比的情况下，MUAE算法精度高且很平稳，没有大幅度变化，而LPP和LE这两个算法随着降维百分比的增加精度反而逐步下降。

另外，除数据集Business外的其他5个数据集，所有算法在特征降维百分比较小的情况下，平均精度的实验结果都比Baseline的结果好，这表明大部分数据集确实存在冗余的特征，各算法提取关键特征而去除了冗余特征，因此，多标记数据降维后，学习精度反而得到不同程序的提高。

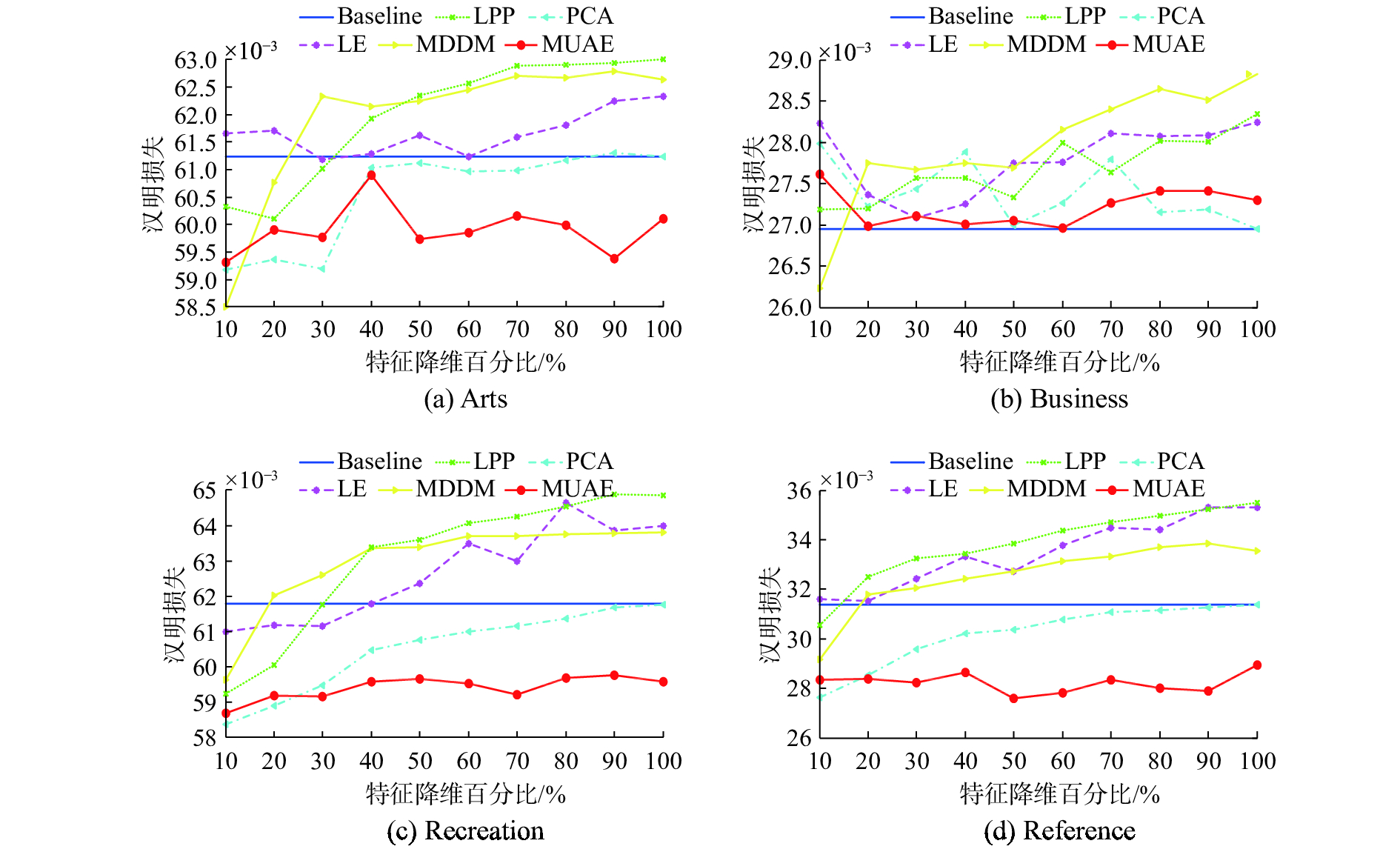
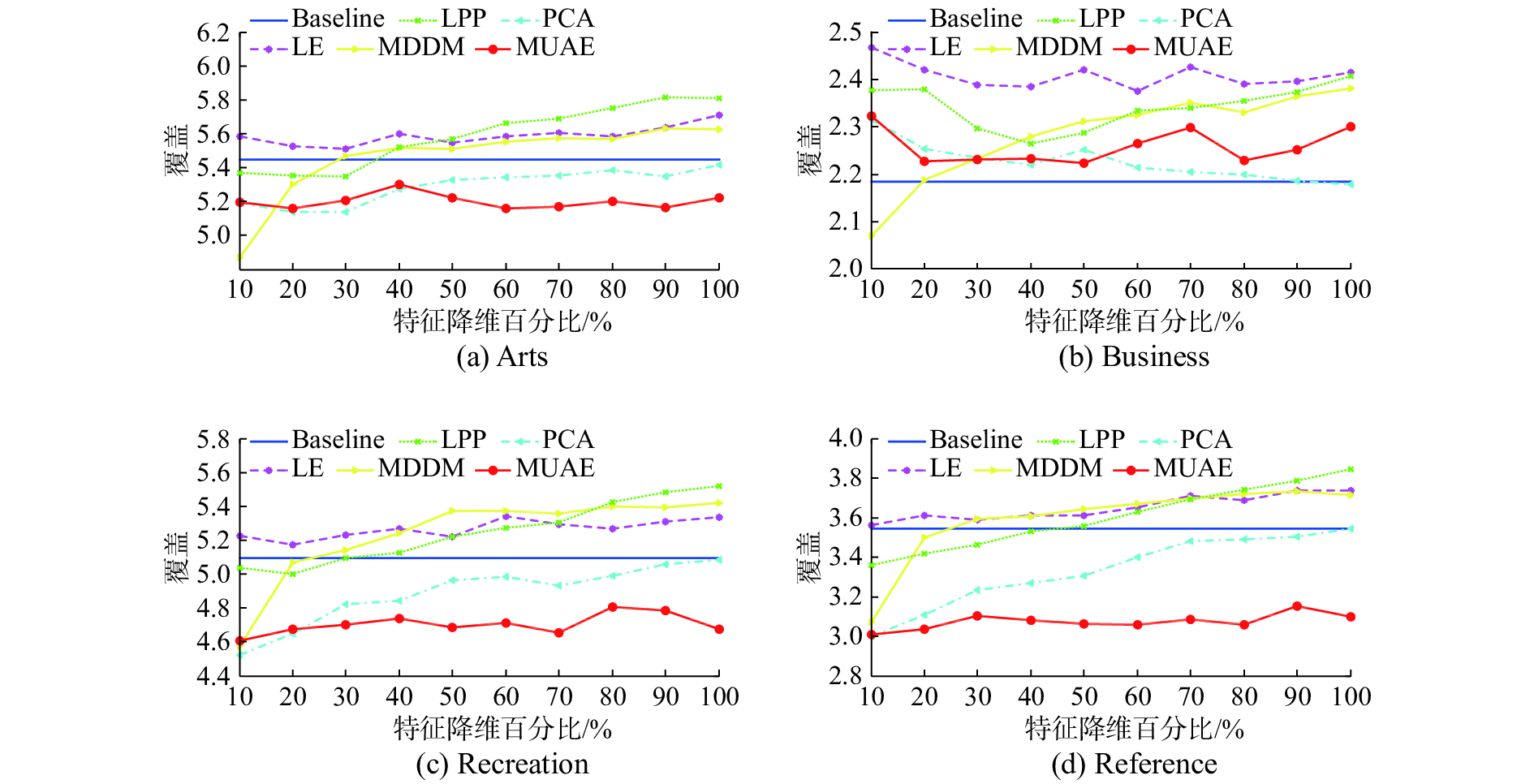
其余4个指标，即汉明损失、排名损失、一错误和覆盖，随特征降维百分比变化关系展示在图4~7中，这4种指标越小越好。从图4~7显示的指标性能，总体上MUAE方法比其他4种方法好，曲线平稳，起伏变化较小，显示出MUAE方法稳定性好。

综合多标记评价5个指标，MUAE方法的结果比其他4种方法和基准算法好，而且在各组提取特征百分比情况下显示出好的稳定性。实验结果进一步证明，自编码网络训练目标在各降维百分比情况下，能保持甚至提取好的数据特征。

5 结束语

针对多标记学习的数据降维问题提出自编码网络维数约简方法，用无监督方法处理有监督的多标记学习降维问题。通过实验验证了所构建自编码深度学习网络能自学习地提取多标记数据特征，降低数据维度，与其他无监督特征降维和多标记有监督降维方法相比，取得了较好的效果，在各百比降维的情况下，降维性能平稳性好。下一步工作，将使用变分自编码和降噪自编码网络对多标记和图像等数据进行无监督降维进行研究。