至今已经有很多种序列模式被提出,包括周期模式[1]、偏序模式[2]、闭合模式[3]、对比序列模式[4]、频繁序列模式[5]等。对比序列模式挖掘作为数据挖掘中重要的一个问题,目前已经积累了大量的研究成果[6-7]。对比序列模式是指在一类数据集中频繁出现,而在另一类数据集中很少出现的序列模式。对比序列模式可以描述不同数据集之间的差异,在很多领域有广泛应用。例如,对比序列模式可以用于纳税人行为分析[8],患者的风险预测[9]等。在对比序列模式挖掘中,Top-k对比序列模式挖掘是一种重要的挖掘策略。Top-k方法是指在给定的标准下挖掘出差异最大的k个模式的方法。该方法被广泛应用在关联规则[10]、序列规则[11]、相关模式[12]和序列模式[7]等领域中。但是,在Top-k策略挖掘结果中依然存在冗余的问题。针对这一问题,本文提出了挖掘去冗余Top-k对比序列模式集合的方法。
1 相关工作对比序列模式挖掘主要包括基于阈值的对比序列模式挖掘和Top-k对比序列模式挖掘两个研究方向。基于阈值的对比序列模式挖掘的目标是找出所有满足给定阈值的模式。最直接挖掘对比序列模式的方法是枚举所有的序列模式,然后统计它们在每个类别上的频率。很明显这种方法的效率太低,不能满足实际应用的需求。Chan等[13]于2003年提出一种基于后缀树的挖掘对比序列模式的算法(emerging substrings mining,ESM)。与朴素的挖掘算法相比,ESM提高了一定的效率。Ji等[14]于2007年定义了MDS (minimal distinguishing subsequence) 的概念,并提出了相应的挖掘算法,即ConSGapMiner (contrast sequences with gap miner)算法。ConSGapMiner是比较经典的对比序列模式挖掘算法,它能以较快的效率挖掘出对比序列模式。但是MDS定义的对比序列模式在正例集中大于一个固定的阈值,在反例集中小于一个固定阈值,这种定义可能使一些有意义的模式没有被挖掘出来。2010年Deng等[15]在ConSGapMiner的基础上利用F-ratio作为对比度;2011年Yu等[16]提出了TSEPsMiner算法;TSEPsMiner利用GrowthRate作为对比度,而且将这个对比度应用在了挖掘对比序列模式的算法中;2014年Wang等[17]提出用gd-DSPMiner算法来解决MDS定义中存在的问题。在不明确数据的差异程度时,使用基于阈值的对比序列模式挖掘难以挖掘出预期的序列模式。在这种情况下,Top-k对比序列模式挖掘是一个可行的办法。Top-k算法不用设定对比度的阈值,只需要设置想要挖掘模式的数目。杨皓等[7]于2015年提出了新的Top-k挖掘算法,即kDSP-Miner(Top-k distinguishing sequential patterns with gap constraint miner)算法。但是kDSP-Miner并没有考虑冗余问题,kDSP-Miner挖掘出的序列模式可能会有大量的冗余。
2 问题定义对于一个给定的数据集
例1 对于序列,
| ${\rm{Sup}}(P,D) = \frac{{\left| {\left\{ {S \in D|P \subseteq S} \right\}} \right|}}{{\left| D \right|}}$ | (1) |
式中
定义1 (对比度)对于给定的数据集
| ${\rm{CR}}(P,{D_ + },{D_ - }) = {\rm{Sup}}(P,{D_ + }) - {\rm{Sup}}(P,{D_ - })$ |
例2 对于表1中给出的DNA数据集,
| 表 1 含有两个类别的基因数据集 Tab.1 A gene data set with two classes |
定义2 (Top-k对比序列模式)给定正例集
Top-k对比序列模式挖掘的目标是找出给定数据集中对比度最大的k个序列模式。
例3 在表1的数据集中,令
| 表 2 表1中基因数据集的Top-5对比序列模式 Tab.2 Top-five discriminative sequential patterns from gene data set in table 1 |
定义3 (冗余对比序列模式) 对于两个给定的对比序列模式
1)
2)
表2的对比序列模式中,
定义4 (去冗余Top-k对比序列模式)集合L满足Top-k对比序列模式集合的要求,同时对于每个序列
例4 在表1的数据集中,令
| 表 3 表1中基因数据集的Top-5去冗余对比序列模式 Tab.3 Top-five non-redundant distinguishing sequential patterns from gene data set in table 1 |
本文中常用的符号及定义总结在表4中。
| 表 4 符号及其含义 Tab.4 Symbols and their meaning |
为了挖掘去冗余Top-k对比序列模式的集合,用本文提出的BFM和PBFM算法,来解决挖掘出的结果集合的冗余问题。BFM和PBFM算法基于广度优先生成树的原理来寻找Top-k序列的集合,树的生成过程就是Top-k集合的更新过程。相比于使用深度优先的方法来生成树结构,使用广度优先的方法每次更新时不改变Top-k集合的大小,所以不会出现冗余的Top-k集合。
3.1 广度优先的生成树算法1) 根据给定的数据集
2) 创建Top-k集合L,设置集合
3) 创建一个队列,将字母表中的每个元素放入队列中。
4) 对于队列的第一个元素,在其末尾分别与字母表中的每个元素连接,形成新的序列。
5) 计算每个新的序列P的支持度和对比度,如果
当
当
6) 将队列的第一个元素弹出。
7) 重复4)~6),直到队列为空。
例5 对表1的数据集进行去冗余Top-k对比序列模式挖掘, 令k=5。找出基因数据集的字母表
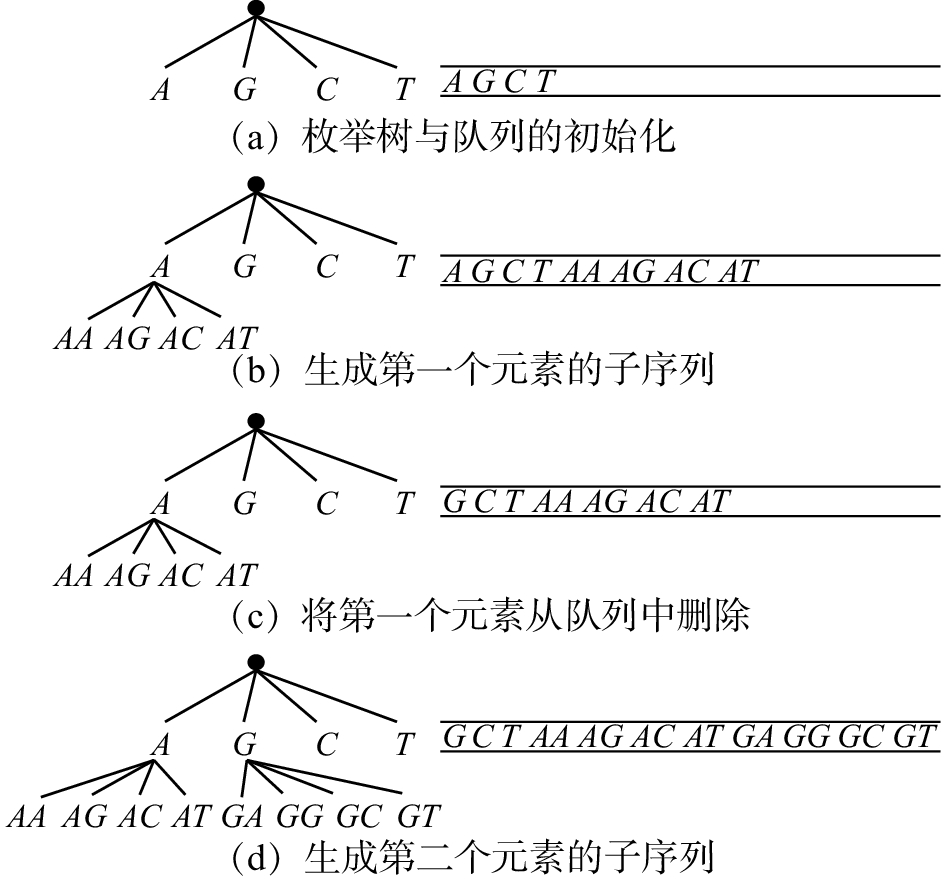
|
Download:
|
| 图 1 生成树和队列的动态变化 Fig. 1 The dynamic change of spanning tree and queue | |
在Top-k对比序列模式挖掘中,去除冗余序列模式是提高挖掘结果质量的重要一步。但是在原有挖掘过程的基础上,加入去冗余的步骤后,一个新的序列可能会替换Top-k集合中的多个序列,使Top-k集合中的序列模式数目小于k个。针对以上问题,本文提出基于广度优先的生成树算法BFM (breadth-first miner)来去除冗余的序列模式。使用BFM算法可以在去除冗余序列模式的同时,保证Top-k集合的大小不发生变化。
算法1 BFM (breadth-first miner)
输入 正例集
输出 包含Top-k对比序列模式的集合
/*初始化*/
1)创建集合
2)创建队列,初始化队列queue为空;
3)计算出字母表
4)创建树的根节点,建立由根节点分别指向字母表中每个元素的连接,令min TopkCR = getMinTopkCR (L);
5)对
如果
如果 P′被找到且 P不是相对于P′的冗余序列模式,则把P加入集合L, 更新
否则把P加入集合L, 更新
6)如果
如果 P′被找到并且P是相对于P′的冗余序列,则用P替换集合L中对比度最小的序列更新
7)重复步骤 5)、6),直到对列为空。
3.2 剪枝策略为了提高算法的性能,本文中应用了一系列剪枝策略来辅助算法的运行[7]。运用这些剪枝策略,可以使程序运行的效率提高,更快地找出Top-k集合。
剪枝策略1 (反例元素剪枝策略)在遍历数据集
这条剪枝策略基于以下原理:如果元素
剪枝策略2 (序列支持度的剪枝策略)当
由
剪枝策略3 (元素支持度的剪枝策略)当
由Top-k对比序列模式的定义可知,包含元素
加入以上3条剪枝策略后,树结构生成的速度会加快,可以在更短的时间内找到Top-k对比序列模式。对于某一类数据集,使用剪枝后,算法的效率会显著提升。加入剪枝后的算法如算法2。
算法2 PBFM(pruning breadth-first miner)
输入 正例集
输出 包含Top-k对比序列模式的集合L。
/*初始化*/
1)创建集合L,设置集合L的最小对比度阈值
2)创建队列,初始化队列queue为空;
3)计算正例集
4)创建树的根节点,建立由根节点分别指向字母表中每个元素的指针,令min TopkCR = getMinTopkCR (L);
5)如果 (
如果
如果
如果
6)如果
如果
7)重复步骤 5)、6),直到队列为空。
4 实验结果 4.1 实验环境本文设计了一系列实验来评估算法的有效性。算法用C++语言来实现。实验中所用到的数据集为4组真实数据。这4组数据分别是:E.Coli数据集,记录了两个不同类型的DNA序列。在E.Coli数据集中,每个DNA序列前面都用“+”和“–”标记出了序列所属的类别。UJI数据集,记录了超过11 000个独立的手写数字。ADLs数据集,记录了一段时间内不同的人在自己家中的活动情况。Question数据集,记录了各种不同的问题,可以将每个问题看作由不同单词组成的序列。前3个数据集来自UCI的机器学习数据集。最后一个数据集是Question的训练数据集。实验运行的环境是:Core i3的处理器,Windows 7操作系统,2GB RAM 的计算机上完成。表5中列出了实验中用到的数据集的特征。
| 表 5 数据集的特征 Tab.5 The characteristics of the data sets |
1) 实验1(去冗余前后Top-k集合对比实验)
实验1的目标是比较去冗余前后Top-k集合中序列模式的变化,来验证去冗余算法的有效性。在该实验中,使用了3组数据来对比去冗余前后Top-k结果集合的不同。每组数据分别找出了含有冗余序列的Top-k集合和不含冗余序列的Top-k集合,并比较其中序列的组成。在实验中,k值设置为5。实验结果如表6~8所示。
| 表 6 去冗余前后Top-k序列模式集合的变化(ADLs数据集) Tab.6 The set of Top-k sequential patterns before and after eliminating redundancy(ADLs data set) |
| 表 7 去冗余前后Top-k序列模式集合的变化(E.Coli数据集) Tab.7 The set of Top-k sequential patterns before and after eliminating redundancy(E.Coli data set) |
| 表 8 去冗余前后Top-k序列模式集合的变化(UJI数据集) Tab.8 The set of Top-k sequential patterns before and after eliminating redundancy(UJI data set) |
通过实验结果可以发现,去冗余Top-k集合中出现了冗余Top-k集合中没有出现的序列模式。同时,去冗余Top-k集合中删去了冗余的序列模式。因此,本文的算法能够有成效地去除冗余对比序列模式。
2) 实验2(加入剪枝策略前后的对比实验)
实验2的目标是比较算法1与加入剪枝策略后算法效率的变化。分别在ADLs数据集和Question数据集上进行对比实验,比较算法1和算法2运行的时间,来衡量算法的效率。
将k的值分别从1取到20,比较算法1(BFM)和算法2(PBFM)运行的时间如图2所示。从图2中可以看出,随着k值的增加,两种算法的运行时间都在增长,但PBFM的运行时间明显少于BFM的运行时间。在ADLs数据集中,随着k值逐渐变大,这一区别越来越明显。在Question 数据集中,当k值较小时,这一区别较为明显。随着k值的增大,Top-k集合的最小对比度minTopkCR逐渐变小,当
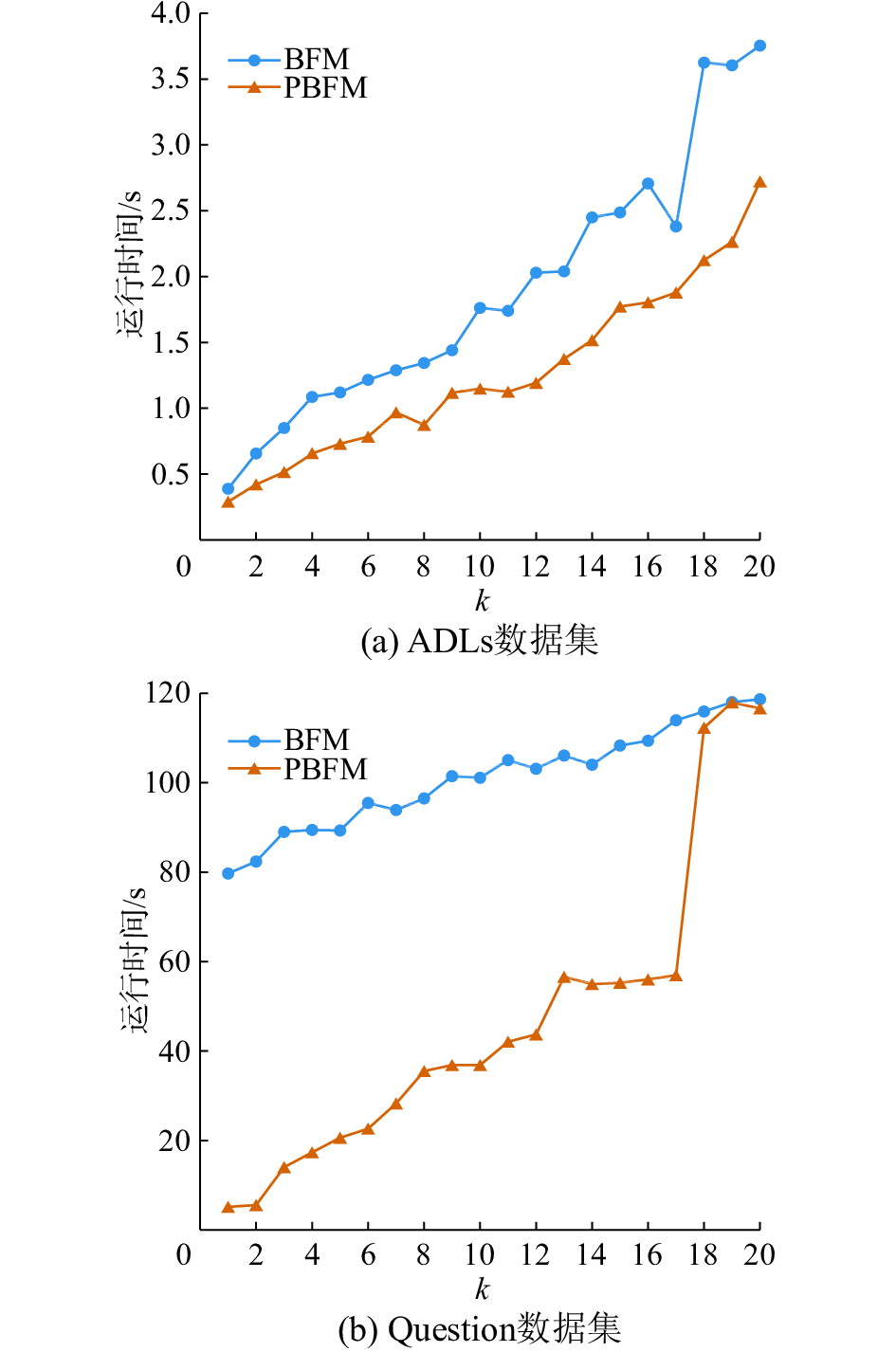
|
Download:
|
| 图 2 BFM和PBFM的效率对比 Fig. 2 Comparison of BFM and PBFM efficiencies | |
本文首先提出了一种挖掘去冗余Top-k对比序列模式的算法BFM,这是一种基于广度优先生成树的算法。通过不断的比较子序列和超序列的对比度,Top-k集合不断地更新,直到树结构的生成过程结束。相比之前的Top-k对比序列模式挖掘算法,BFM算法可以得到去冗余的Top-k集合,并且不需要其他集合的辅助。
在BFM算法的基础上,提出了性能更好的PBFM算法。与BFM算法相比,PBFM算法可以在更短的时间内完成挖掘任务,并且不需要额外的操作。
| [1] |
ZHANG Minghua, KAO Ben, CHEUNG D W, et al. Mining periodic patterns with gap requirement from sequences[J]. ACM transactions on knowledge discovery from data, 2007, 1(2): 7. DOI:10.1145/1267066 ( 0) 0)
|
| [2] |
PEI Jian, WANG Haixun, LIU Jian, et al. Discovering frequent closed partial orders from strings[J]. IEEE transactions on knowledge and data engineering, 2006, 18(11): 1467-1481. DOI:10.1109/TKDE.2006.172 ( 0) 0)
|
| [3] |
YAN Xifeng, HAN Jiawei, AFSHAR R. CloSpan: mining: closed sequential patterns in large datasets[C]//Proceedings of the 3rd SIAM International Conference on Data Mining. San Francisco, USA, 2003: 166–177.
( 0) 0)
|
| [4] |
JI Xiaonan, BAILEY J, DONG Guozhu. Mining minimal distinguishing subsequence patterns with gap constraints[J]. Knowledge and information systems, 2007, 11(3): 259-286. DOI:10.1007/s10115-006-0038-2 ( 0) 0)
|
| [5] |
ZAKI M J. SPADE: an efficient algorithm for mining frequent sequences[J]. Machine learning, 2001, 42(1/2): 31-60. DOI:10.1023/A:1007652502315 ( 0) 0)
|
| [6] |
YANG Hao, DUAN Lei, DONG Guozhu, et al. Mining itemset-based distinguishing sequential patterns with gap constraint[C]//Proceedings of the 20th International Conference on Database Systems for Advanced Applications. Hanoi, Vietnam, 2015: 39–54.
( 0) 0)
|
| [7] |
杨皓, 段磊, 胡斌, 等. 带间隔约束的Top-k对比序列模式挖掘[J]. 软件学报, 2015, 26(11): 2994-3009. YANG Hao, DUAN Lei, HU Bin, et al. Mining Top-k distinguishing sequential patterns with gap constraint[J]. Journal of software, 2015, 26(11): 2994-3009. (  0) 0)
|
| [8] |
ZHENG Zhigang, WEI Wei, LIU Chunming, et al. An effective contrast sequential pattern mining approach to taxpayer behavior analysis[J]. World wide web, 2016, 19(4): 633-651. DOI:10.1007/s11280-015-0350-4 ( 0) 0)
|
| [9] |
GHOSH S, FENG Mengling, NGUYEN H, et al. Risk prediction for acute hypotensive patients by using gap constrained sequential contrast patterns[J]. AMIA annual symposium proceedings, 2014, 2014: 1748-1757. ( 0) 0)
|
| [10] |
FOURNIER-VIGER P, TSENG VS. Mining Top-K Non-redundant association rules[C]//Proceedings of the 20th International Symposium on Foundations of Intelligent Systems. Macau, China, 2012, 7661: 31–40.
( 0) 0)
|
| [11] |
FOURNIER-VIGER P, TSENG V S. TNS: mining top-k non-redundant sequential rules[C]//Proceedings of the 28th Symposium on Applied Computing. Coimbra, Portugal, 2013: 164–166.
( 0) 0)
|
| [12] |
KAMEYA Y, SATO T. RP-growth: Top-k mining of relevant patterns with minimum support raising[C]//Proceedings of the 12th SIAM International Conference on Data Mining. Anaheim, USA, 2012: 816–827.
( 0) 0)
|
| [13] |
CHAN S, KAO B, YIP C L, et al. Mining emerging substrings[C]//Proceedings of 8th International Conference on Database Systems for Advanced Applications. Kyoto, Japan, 2003: 119–126.
( 0) 0)
|
| [14] |
JI Xiaonan, BAILEY J, DONG Guozhu. Mining minimal distinguishing subsequence patterns with gap constraints[J]. Knowledge and information systems, 2007, 11(3): 259-286. DOI:10.1007/s10115-006-0038-2 ( 0) 0)
|
| [15] |
DENG Kang, ZAIANE O R. An occurrence based approach to mine emerging sequences[C]//Proceedings of the 12th International Conference on Data Warehousing and Knowledge Discovery. Bilbao, Spain, 2010: 275–284.
( 0) 0)
|
| [16] |
YU H H, CHEN Chunhao, TSENG V S. Mining emerging patterns from time series data with time gap constraint[J]. International journal of innovative computing information and control, 2011, 7(9): 5515-5528. ( 0) 0)
|
| [17] |
WANG Xianming, DUAN Lei, DONG Guozhu, et al. Efficient mining of density-aware distinguishing sequential patterns with gap constraints[C]//Proceedings of the 19th International Conference on Database Systems for Advanced Applications. Bali, Indonesia, 2014: 372–387.
( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


