2. 东华大学 数字化纺织服装技术教育部工程研究中心,上海 201620
2. Engineering Research Center of Digitized Textile & Apparel Technology, Ministry of Education, Donghua University, Shanghai 201620, China
多移动机器人的协同编队是多机器人研究的关键技术之一,多机器人的协同编队包含三方面内容:队形构建、队形保持和队形重构,其关键在于设计一个高效、高鲁棒性的多机器人编队控制策略。
近年来,随着科学技术的长足进步,多智能体的研究已经得到了广泛的应用,如机场码头转运、大型货物运输、搜索救援、三维地图绘制等。而多机器人协同编队又是多智能体研究中的关键环节。多机器人协同编队的重点是队形控制模型。文献[1]在原有的领航者追随者策略中引入了一个新的队形控制策略,使得追随者的位置相对于领航者不是固定的,而是在以领航者为圆心的适当圆弧中变化。文献[2]分析了两轮机器人的运动模型,并设计摩擦补偿策略,建立低成本高性能的两轮机器人控制模型。文献[3]基于领航者–跟随者控制模型,设计了动态领航者选择策略,可以在领航者失效的情况下,继续编队行进,同时提高了机器人从局部极值点逃离的可能性。文献[4]在编队领航者–跟随者的研究中提出了二维平面下的距离–角度反馈控制器和距离–距离反馈控制器。文献[5]设计了一种基于神经动态优化的非线性模糊预测控制器用于控制领航者追随者编队的形成。文献[6]设计了一种观察者利用视觉和速度信息、领导者的方向和速度信息以及追随者的距离信息等,估计追随者机器人位置信息的方法。文献[7]提出了创建鲁棒图的算法,设计弹性机器人结构方法,提高了机器人结构的稳定性和鲁棒性。文献[8]针对机器人速度受限的情况,提出一种基于锥形方法的几何舵点策略,可以使机器人有效地移动到自己的舵点。文献[9]在领航者追随者策略中引入滚动优化的概念,实验表明可以以较快的误差收敛速度来解决多机器人的编队问题。文献[10]引入了虚拟跟随机器人,将编队控制转化为跟随机器人对虚拟跟随机器人的轨迹跟踪控制,实现实时导航的目的。文献[11]设计了一种基于自治操作条件反射自动机的仿生学习算法,实现机器人的自主平衡学习控制。文献[12] 采用不依赖系统模型的模糊控制方法,对领导者进行路径跟踪控制,设计的控制率可以有效地控制编队。
本文基于领航者–追随者结构的编队控制方法,从军队急行军中得到启发,设计了同列依次替补和末排向内收拢原则,提出多机器人紧密队形保持策略。通过实验验证了该策略的有效性和优越性。
1 急行军编队机制对于多机器人系统的分布控制,研究者们提出了许多方法[4-9, 11]。典型的方法有基于行为和规则的方法、领航者追随者方法、图论方法和物理方法。
领航者追随者方法是将队形中的机器人划分为两种角色,即领航者和追随者,控制追随者跟踪领航者以实现编队控制。其优点是,控制简单,仅给定领航者的运动轨迹就可以控制整个机器人编队。不足之处主要有两点:1)领航者和追随者相对独立,没有明确的队形反馈,实际使用中如果领航者前进速度过快,会产生追随者无法及时跟踪的情况;2)编队中承担领航者角色的机器人如果失效,那么整个编队将无法保持。
本文主要研究的是第二个缺陷,使用多机器人紧密队形保持策略可以消除这一缺点。
在步兵、骑兵或坦克部队行军过程中两个重要的考量因素是行军速度和警戒性。行军速度快慢由任务、敌情、道路、气候条件和部队行军能力确定,行军速度也可依此规定。常言道,兵贵神速,行军途中,在条件允许的情况下,行军速度越快对任务的按时完成越有利。同时,在满足机动性的前提下尽量紧密地编队行进也有利于尽快发现敌情并传播出去。
军队的指挥官们在实战中总结出了部队行军的一般原则,即坦克或步兵行军当中,每一列为一纵队,相邻纵队之间间隔适当的距离,确保出现突发事件,坦克或战士可以在不妨碍行军的前提下撤出编队。同时,最后一排的坦克或士兵应尽量向内收拢,维持紧密行军队形。
受急行军的启发,我们总结出两个行军原则:同列依次替补和末排向内收拢原则。这两个原则可以确保行军的速度和警惕性。
2 多机器人紧密队形保持策略将同列依次替补和末排向内收拢原则提炼并迁移到多机器人协同编队中来,提出了多机器人紧密队形保持策略。下面用图示法论述多机器人紧密队形保持策略的具体实现方法。
2.1 同列依次替补和末排向内收拢原则图示中圆形代表机器人个体,圆中标号代表机器人的标号,线段代表领航者和追随者的跟踪关系,箭头方向代表跟踪方向。例如,图1中C机器人箭头指向A,代表C机器人是追随者,A机器人是其领航者,C机器人跟踪A机器人。

|
Download:
|
| 图 1 同列依次替补原则边缘C机器人失效示意图 Fig. 1 Edge C robot failure with substitution in the same column diagram | |
图1和图2论述同列依次替补原则的具体内容,图3和图4论述末排向内收拢原则的具体内容。

|
Download:
|
| 图 2 同列依次替补原则非边缘C机器人失效示意图 Fig. 2 Non-edge C robot failure with substitution in the same column diagram | |
|
Download:
|
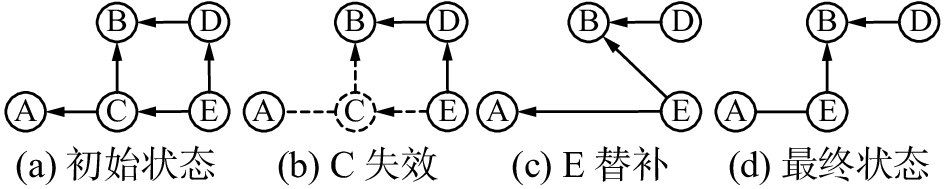
| 图 3 末排向内收拢原则C机器人失效示意图 Fig. 3 C robot failure with inward convergence diagram | |
|
Download:
|
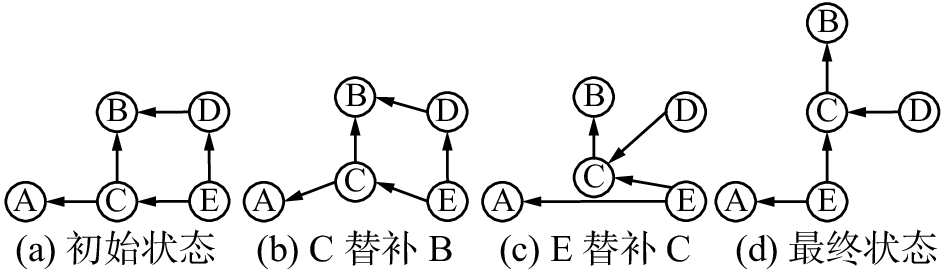
| 图 4 末排向内收拢原则C机器人替补示意图 Fig. 4 C robot substitute with convergence diagram | |
当失效的机器人C位于边缘队列时,如图1所示,作为处于同一列且是C机器人的追随者的机器人D向前替补,同时原来C机器人的参考机器人A和B变为D机器人的参考机器人。随后在机器人运动模型的控制下D机器人完全替补了C机器人原来的位置,紧密编队得以继续。
当失效的机器人C位于非边缘位置时,如图2所示。首先作为处于同一列且是C机器人的追随者的机器人F向前替补,同时原来C机器人的参考机器人A和B变为F机器人的参考机器人,C机器人的追随者机器人D变为机器人F的追随者。最后在机器人运动模型的控制下机器人F和机器人H向前替补了机器人C和机器人F原来的位置,紧密编队得以继续。
当同一列的机器人依次替补完成后,就需要检查是否满足紧密队形约束。如果满足就结束队形重组,如果不满足就需要根据图3和图4所示的不同情况进一步调整。
当末排的机器人C失效时,如图3所示,先判断机器人C是否处于中间位置,如果处于中间位置,则将任意一边的机器人向内收拢,其队形紧密程度相等。否则,就将该机器人向内收拢。假设图3中,机器人C偏向右侧,则将机器人C右侧的机器人E向内收拢。机器人E首先替补了机器人C的位置,同时机器人C原来的参考机器人A和B变成了机器人E 的参考机器人,随后在机器人运动模型的控制下机器人E完全代替了机器人C。紧密编队得以继续。
当末排的机器人C向前替补时,如图4所示,当最后一排中机器人C向前替补后,先判断机器人C是否处于中间位置,如果处于中间位置,则将任意一边的机器人向内收拢,其队形紧密程度相等。否则,就将该机器人向内收拢。假设图4中,机器人C偏向右侧,则将机器人C右侧的机器人E向内收拢。因为机器人C向前替补,机器人A也就不再是机器人C的参考机器人,此时机器人E前来替补机器人C,则机器人A就变成了机器人E的参考机器人。随后在机器人运动模型的控制下机器人E完全替补了机器人C原来的位置。紧密编队得以继续。
2.2 多机器人紧密队形保持策略算法实现本文专注于研究多机器人紧密队形保持策略,对于失效机器人的检测、两轮差动机器人的运动模型、机器人的控制模型等问题不做过多阐述,只是借用当前已有的成熟模型。下面阐述多机器人紧密队形保持策略的算法实现。
1)当检测到编队中有机器人失效时,首先触发同列依次替补原则。将失效机器人所在列的机器人依次向前替补。如果失效机器人或替补后的机器人处于该列的末尾,则同列依次替补原则结束。
2)随后触发末排向内收拢原则,首先判断失效机器人所在列所处的位置,将失效机器人偏向的方向的机器人向内收拢。如果失效机器人或收拢后的机器人处于末排的边缘,则末排向内收拢原则结束。
3)最后机器人个数减1。
2.2.1 同列依次替补算法实现1)首先判断失效或需要替补的机器人是否处于该列的末尾。如果位于列尾,则同列依次替补算法结束。
2)否则就将失效或需要替补的机器人的所有参考关系都转移到替补机器人上面。以领航者追随者控制方法为例,即将失效或需要替补的机器人的领航者变为替补机器人的领航者,同时失效或需要替补的机器人的所有追随者(排除替补机器人)都变为追随替补机器人。
3)因为替补机器人前去替补失效的或需要替补的机器人,替补机器人原来的位置无机器人。接下来将替补机器人原来的位置作为需要替补的机器人位置,将该列下一个机器人作为替补机器人,重新调用步骤1),继续依次替补。直到失效或需要替补的机器人处于该列的末尾。
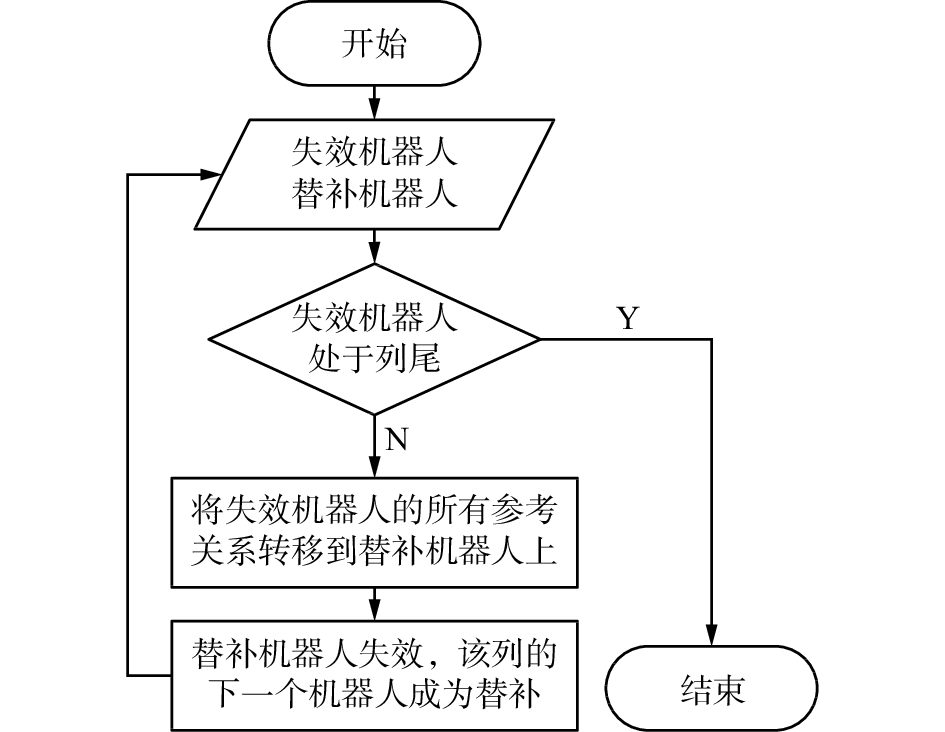
同列依次替补算法的流程图如图5所示。
|
Download:
|
| 图 5 同列依次替补算法流程图 Fig. 5 The algorithm flowchart of substitution in the same column | |
1)首先判断失效或需要替补的机器人是否处于末排的边缘。如果位于边缘,则末排向内收拢算法结束。
2)否则就先判断失效或需要替补的机器人是否处于中间位置,如果处于中间位置,则将任意一边的机器人向内收拢,其队形紧密程度相等。否则,就将该机器人偏向方向的机器人向内收拢。该机器人偏向方向的相邻机器人是其替补机器人。
收拢方法:将失效或需要替补的机器人的所有参考关系都转移到替补机器人上面。
3)因为替补机器人前去替补失效或需要替补的机器人,替补机器人原来的位置无机器人。接下来将替补机器人原来的位置作为需要替补的机器人位置,将末排下一个机器人作为替补机器人,重新调用步骤1),继续收拢队形。直到失效或需要替补的机器人处于末排的边缘。
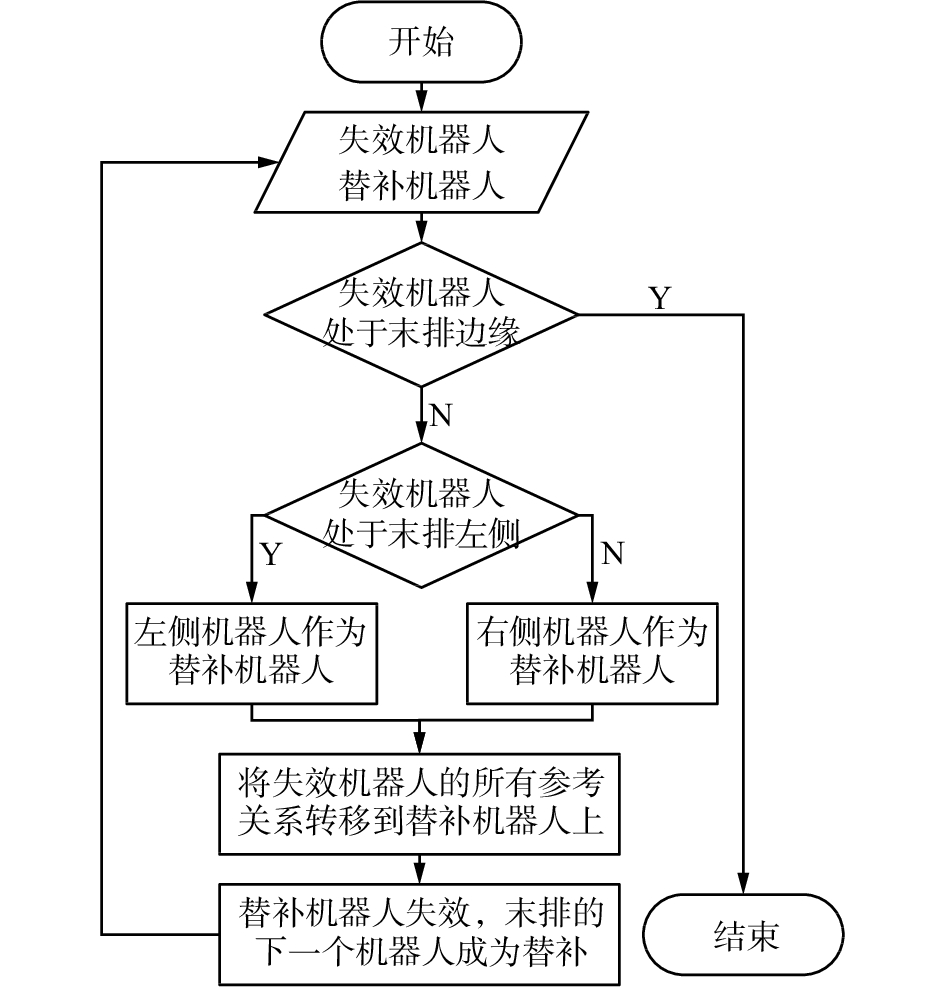
末排向内收拢算法的流程如图6所示。
|
Download:
|
| 图 6 末排向内收拢算法流程 Fig. 6 The algorithm flowchart of approach inward | |
多机器人紧密队形保持策略主要包含两个原则:同列依次替补和末排向内收拢原则。同列替补原则的优化目标是机器人在编队重组过程中的路程最短,末排向内收拢原则的优化目标是更紧密的编队队形。据此我们引入两个队形评价指标:能耗和队形紧密度。
1) 能耗
假设单位路程长度的能耗为1,则能耗就等价于编队在机器人失效时到机器人到达目标点之间走过的路程。定义队列中的各个机器人在失效时的位置为
| ${\rm{min}}\sum\limits_i^N {\sqrt {{{({{\bar x}_i} - {x_i})}^2} + {{({{\bar y}_i} - {y_i})}^2}} } $ | (1) |
2) 队形紧密度
定义队形紧密度为编队中各个机器人到队形几何中心的距离之和的倒数,即各个机器人到队形几何中心的距离之和越大,队形紧密度越小。定义机器人队形的几何中心为
队形紧密度可描述为
| ${\rm{max}}\frac{1}{{\sum\limits_i^N {\sqrt {{{({x_i} - {x_o})}^2} + {{({y_i} - {y_o})}^2}} } }}$ | (2) |
为了直观地比较同列依次替补原则对于能耗的提升效果,本文设计了4个机器人排成一列前进,然后在某一时刻1号追随者机器人失效,随后分别计算使用同列依次替补原则的机器人总路程和不使用该原则的机器人总路程。路程更短的一方能耗更低。
仿真中,0号机器人是领航者机器人,其余的是追随者机器人。领航者机器人设置限速
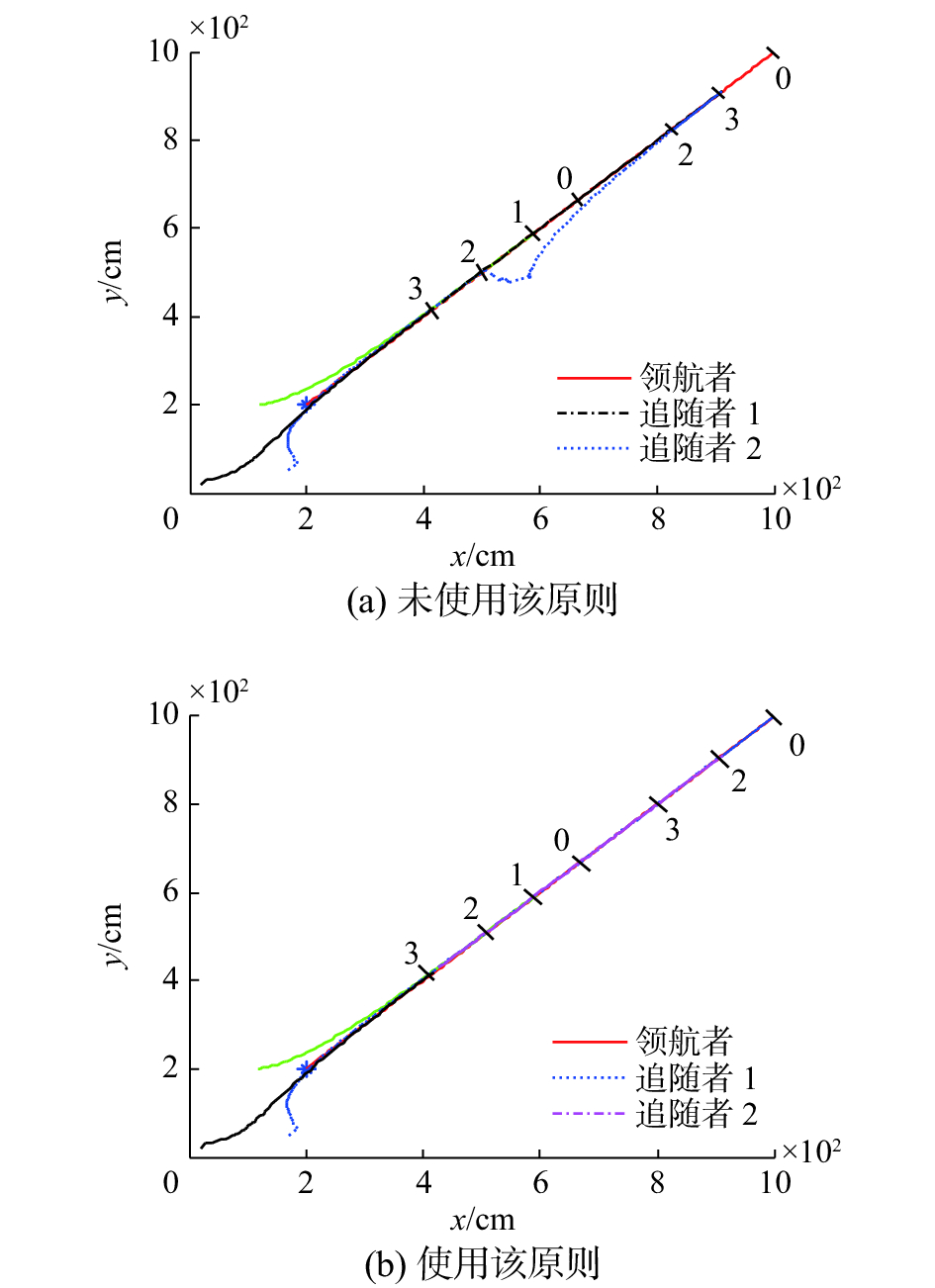
如图7(a)所示,图中的机器人编队未使用同列依次替补原则,而是将该列末端的机器人向前替补。当1号机器人失效时,3号机器人替代了1号机器人的角色。但是因为2号机器人阻挡了3号机器人的前进路线,此时2号机器人会暂时偏离编队轨迹,待3号机器人通过后,2号机器人再回到编队中来。最终成功编队并到达目标点。如图7(b)所示,图中的机器人编队使用了同列依次替补原则。当1号机器人失效时,2号机器人前来替代了1号机器人的角色。同时3号机器人前来替代2号机器人原来的位置。这种策略下,机器人编队依旧保持线性编队。最终成功编队并到达目标点。
|
Download:
|
| 图 7 使用同列依次替补原则的机器人路径对比 Fig. 7 Comparison of robot path using substitution | |
统计结果显示,未使用同列依次替补原则时的总路程是1 662.166 9 cm,而使用同列依次替补原则时的总路程是1 590.560 3 cm。依据假设单位路程的能耗相等,则使用同列依次替补原则能耗更低。
接下来验证使用末排向内收拢原则的效果,如图8所示,当8号机器人失效的时候,左侧是没有使用末排向内收拢原则所形成的队形,右侧是使用末排向内收拢原则所形成的队形。根据公式(2)计算可得,没有使用末排向内收拢原则的紧密度是

|
Download:
|
| 图 8 末排向内收拢原则编队队形比较 Fig. 8 The comparative figure of the formation using inward convergence rule | |
本节中将使用基于同列依次替补和末排向内收拢原则的多机器人紧密队形策略,处理机器人失效情况下的编队重组任务[3, 12-14]。
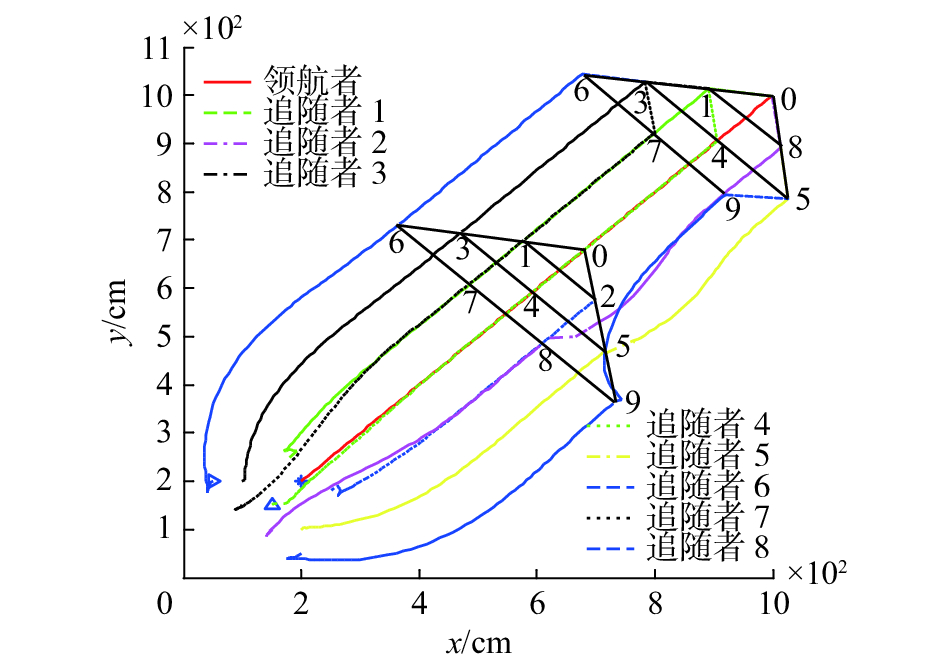
首先仿真编队队形是三角队形的情况。如图9所示,仿真中机器人个数是10个,包含1个领航者和9个追随者。它们共同组成了一个三角形编队。在行进过程中,2号追随者机器人突然失效,按照多机器人紧密队形保持策略,同列的8号机器人遵从同列依次替补原则需要去替补2号机器人,然后9号机器人遵从末排向内收拢原则替补8号机器人。
|
Download:
|
| 图 9 紧密队形保持策略三角队形编队路径 Fig. 9 Triangle formation path using compact formation strategy | |
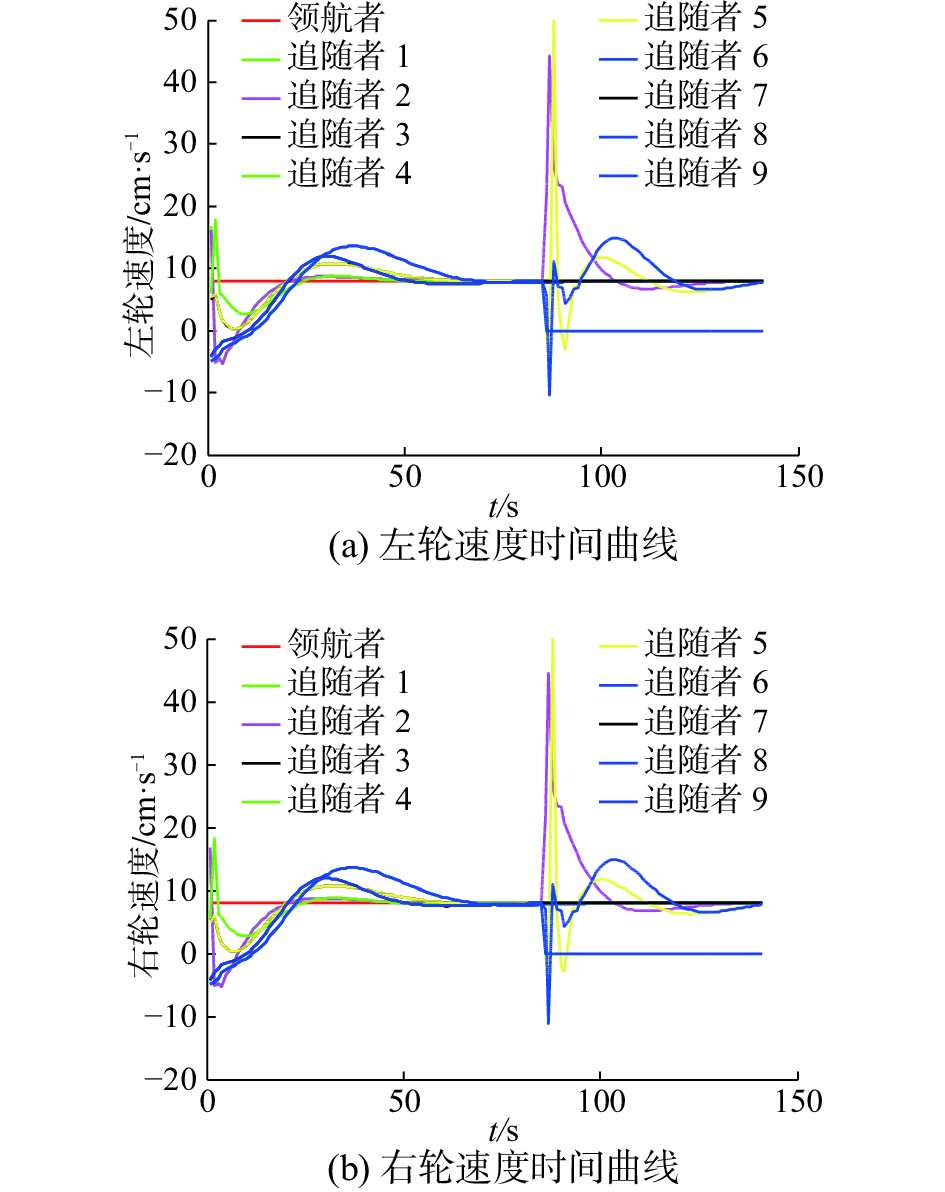
如图9所示,2号机器人失效后,8号机器人快速驶向原来2号机器人的位置,来替换2号机器人。很明显,8号替补2号机器人会比9号前去替换路程更短,能耗更小。同时9号机器人向内收拢来替换8号机器人。假如果9号不前去替补8号的位置,那么形成的队形将较为分散,队形紧密度偏低。5号机器人在这一过程中会稍有偏移。仿真过程中各个机器人左右轮的速度时间曲线如图10所示。在
|
Download:
|
| 图 10 三角队形编队各个机器人左右轮速度时间曲线 Fig. 10 The left and right wheel speed-time curves of each robot using triangle formation | |
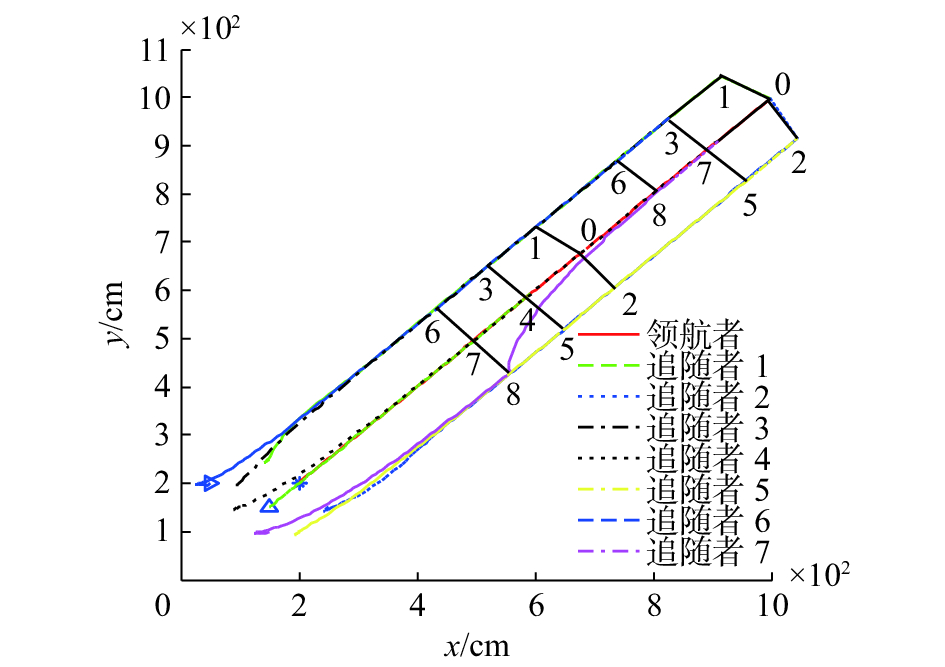
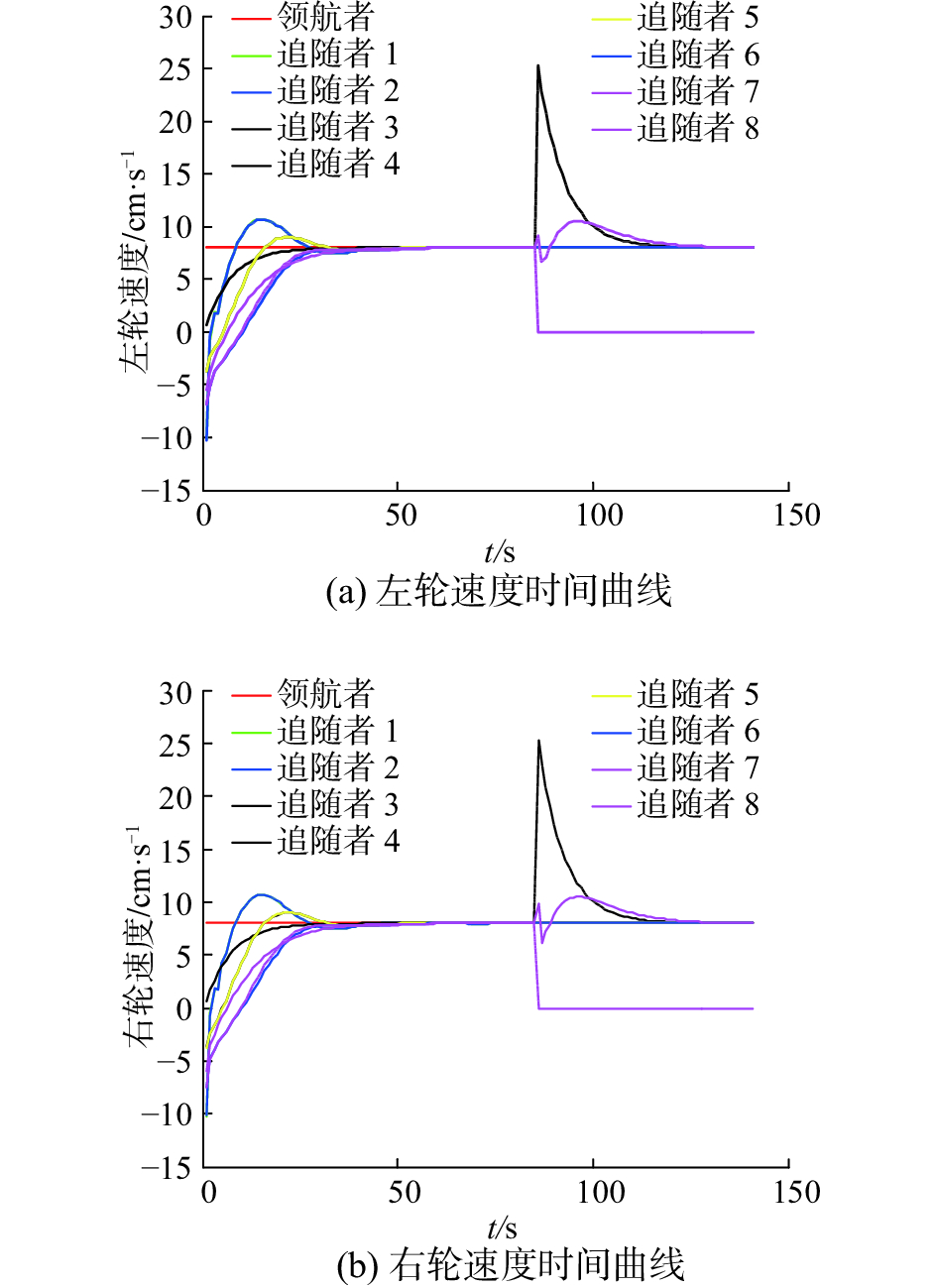
为了说明该策略的可推广性,接下来考虑编队队形是矩形队形的情况。如图11所示,仿真中共有9个机器人,包含1个领航者机器人和8个追随者机器人。它们共同组成了一个矩形编队。在行进过程中,4号追随者机器人突然失效,按照多机器人紧密队形保持策略,同列的7号机器人遵从同列依次替补原则需要去替补4号机器人,然后8号机器人遵从末排向内收拢原则替补7号机器人。如图11所示,4号机器人失效后,7号机器人快速驶向原来4号机器人的位置,来替换4号机器人。很明显,7号替补4号机器人会比8号前去替换路程更短,能耗更小。同时8号机器人向内收拢来替换7号机器人。如果8号不前去替补7号的位置,那么形成的队形将较为分散,队形紧密度偏低。仿真过程中各个机器人左右轮的速度时间曲线如图12所示。在
|
Download:
|
| 图 11 紧密队形保持策略矩形队形编队路径 Fig. 11 Rectangle formation path using compact formation strategy | |
|
Download:
|
| 图 12 矩形队形编队各个机器人左右轮速度时间曲线 Fig. 12 The left and right wheel speed-time curves of each robot using rectangle formation | |
从上述实验结果可以看出,同列依次替补原则会使队形在出现突发事件,更优地实现队形重组,能耗更低。末排向内收拢原则可以确保编队重组之后队形有更好的紧密度。进一步实验表明,行军启发的多机器人紧密队形策略,能够在出现机器人失效的情况下继续实现紧密编队,顺利到达目标点。
4 结束语本文针对领航者–追随者结构队形控制方法中存在的机器人失效,即无法维持编队的缺陷,提出了基于同列依次替补和末排向内收拢原则的多机器人紧密队形保持策略。并通过实验验证了多机器人紧密队形保持策略的有效性和优越性,对多机器人编队研究有一定的参考价值。
| [1] |
CONSOLINI L, MORBIDI F, PRATTICHIZZO D, et al. Leader-follower formation control of nonholonomic mobile robots with input constraints[J]. Automatica, 2008, 44(5): 1343-1349. DOI:10.1016/j.automatica.2007.09.019 ( 0) 0)
|
| [2] |
DAI Fuquan, GAO Xueshan, JIANG Shigong, et al. A two-wheeled inverted pendulum robot with friction compensation[J]. Mechatronics, 2015, 30: 116-125. DOI:10.1016/j.mechatronics.2015.06.011 ( 0) 0)
|
| [3] |
LI Feng, DING Yongsheng, ZHOU Mengchu, et al. An affection-based dynamic leader selection model for formation control in multirobot systems[J]. IEEE transactions on systems, man, and cybernetics: systems, 2017, 47(7): 1217-1228. DOI:10.1109/TSMC.2016.2564931 ( 0) 0)
|
| [4] |
DESAI J P, OSTROWSKI J, KUMAR V. Controlling formations of multiple mobile robots[C]//Proceedings of 1998 IEEE International Conference on Robotics and Automation. Leuven, Belgium, 1998: 2864–2869.
( 0) 0)
|
| [5] |
XIAO Hanzhen, LI Zhijun, CHEN C L P. Formation control of leader-follower mobile robots’ systems using model predictive control based on neuro-dynamics optimization[J]. IEEE transactions on industrial electronics, 2016, 63(9): 5752-5762. DOI:10.1109/TIE.2016.2542788 ( 0) 0)
|
| [6] |
LIANG Xinwu, LIU Yunhui, WANG Hesheng, et al. Leader-following formation tracking control of mobile robots without direct position measurements[J]. IEEE transactions on automatic control, 2016, 61(12): 4131-4137. DOI:10.1109/TAC.2016.2547872 ( 0) 0)
|
| [7] |
GUERRERO-BONILLA L, PROROK A, KUMAR V. Formations for resilient robot teams[J]. IEEE robotics and automation letters, 2017, 2(2): 841-848. DOI:10.1109/LRA.2017.2654550 ( 0) 0)
|
| [8] |
DAI Yanyan, LEE S G. The leader-follower formation control of nonholonomic mobile robots[J]. International journal of control, automation and systems, 2012, 10(2): 350-361. DOI:10.1007/s12555-012-0215-x ( 0) 0)
|
| [9] |
CHEN Jian, SUN Dong, YANG Jie, et al. Leader-follower formation control of multiple non-holonomic mobile robots incorporating a receding-horizon scheme[J]. International journal of robotics research, 2010, 29(6): 727-747. DOI:10.1177/0278364909104290 ( 0) 0)
|
| [10] |
罗京, 刘成林, 刘飞. 多移动机器人的领航-跟随编队避障控制[J]. 智能系统学报, 2017, 12(2): 202-212. LUO Jing, LIU Chenglin, LIU Fei. Piloting-following formation and obstacle avoidance control of multiple mobile robots[J]. CAAL transactions on intelligent systems, 2017, 12(2): 202-212. (  0) 0)
|
| [11] |
戴丽珍, 杨刚, 阮晓钢. 基于AOCA仿生学习模型的两轮机器人自主平衡学习研究[J]. 自动化学报, 2014, 40(9): 1951-1957. DAI Lizhen, YANG Gang, RUAN Xiaogang. Self-balance learning of two-wheeled robot based on autonomous operant conditioning automata[J]. Acta automatica sinica, 2014, 40(9): 1951-1957. (  0) 0)
|
| [12] |
吴垠, 刘忠信, 陈增强, 等. 一种基于模糊方法的领导-跟随型多机器人编队控制[J]. 智能系统学报, 2015, 10(4): 533-540. WU Yin, LIU Zhongxin, CHEN Zengqiang, et al. Formation control of leader-following type multi-robot based on fuzzy control method[J]. CAAI transactions on intelligent systems, 2015, 10(4): 533-540. (  0) 0)
|
| [13] |
俞辉, 王永骥, 徐建省. 非完整移动机器人编队的滑模控制[J]. 机器人, 2006, 28(4): 428-432. YU Hui, WANG Yongji, XU Jiansheng. Sliding mode control for nonholonomic mobile robot formation[J]. Robot, 2006, 28(4): 428-432. DOI:10.3321/j.issn:1002-0446.2006.04.013 (  0) 0)
|
| [14] |
王小亮, 陈健. 多机器人协同队形变换算法与实现[J]. 计算机仿真, 2013, 30(8): 327-330. WANG Xiaoliang, CHEN Jian. Algorithm and implement for formation change based on multi robots cooperation[J]. Computer simulation, 2013, 30(8): 327-330. DOI:10.3969/j.issn.1006-9348.2013.08.077 (  0) 0)
|
 2018, Vol. 13
2018, Vol. 13


