形式概念分析又称概念格[1-2],是由德国Wille教授在20世纪80年代首次提出的,它提供了一种支持数据分析和知识处理的数学工具[3-4]。近些年来,国内外各位学者提出了许多的构造算法。例如:Godin等[5]提出了概念格的渐进生成算法;Ho[6]提出了基于概念格的概念聚类算法;张文修等[7]给出了在保持格同构的条件下建立概念格的属性约简的方法;Elloumi等[8]基于模糊形式背景建立了一个多层次的约简理论。
近几年许多学者从图论方面对概念格进行研究。例如:Amilhastre等[9]与Berry 等[10-12]将二部图与概念格进行了交叉研究;李立峰等[13-14]利用弦二部图和链图对概念格进行表示;张涛等[15-17]利用属性树和属性拓扑图来表示形式背景,简化了形式背景的表示结构,并提出了基于树图的属性约简算法。本文通过二部图的极大完全子图的概念来生成概念格,给出了基于二部图的深度优先的概念格的迭代算法。
1 基本概念
本节主要介绍概念格与二部图的基本知识。关于概念格的更多内容参见文献[1,18],有关图论的详细内容参见文献[19-20]。
1.1 概念格
定义1 1)在形式概念分析中,一个形式背景是一个三元数组
$K = (O,M,I)$
,其中O是对象集合,M是属性集合,I是O与M之间的一个二元关系。用
$oIm$
表示“对象
$o$
有属性
$m$
”。对于
$A \subseteq O$
及
$B \subseteq M$
,定义:
$A' = \left\{ {m \in M|\forall o \in A,oIm} \right\}$
,
$B' = \{ {o \in O|}$
${\forall m \in B,oIm}\}$
。则形式背景
$K = (O,M,I)$
的概念定义为元素对
$(A,B)$
,其中
$A \subseteq O$
,
$B \subseteq M$
,
$A' = B$
,
$B' = A$
。概念
$(A,B)$
的外延是A,内涵是B。
2) 在形式背景
$K = (O,M,I)$
的概念集合间建立一种偏序关系:给定两个概念
${C_1} = ({A_1},{B_1})$
和
${C_2} = ({A_2},{B_2})$
,则
${C_1} < {C_2} \Leftrightarrow {A_1} \subset {A_2}$
(或
${B_1} \supset {B_2}$
),那么
${C_1}$
是
${C_2}$
的子概念,
${C_2}$
是
${C_1}$
的父概念。根据这种偏序关系,形式背景
$K = (O,M,I)$
的概念节点的集合产生一种格结构,称它为
$K = (O,M,I)$
的概念格,记为
$L(K)$
。并且由这种偏序关系可生成
$L(K)$
的Hasse图:对于
$L(K)$
中的两个不同的节点
${C_1}$
和
${C_2}$
,如果
${C_1} < {C_2}$
,并且不存在其他的节点
${C_3}$
,使得
${C_1} < {C_3} < {C_2}$
,则
${C_1}$
与
${C_2}$
之间就存在一条边。此时
${C_1}$
称为
${C_2}$
的直接子概念,
${C_2}$
称为
${C_1}$
的直接父概念。
形式背景
$K = (O,M,I)$
中集合O和M中所含元素的个数直接影响到生成概念格的复杂程度,所以我们有必要对形式背景进行约简。
定义2 1)在形式背景
$K = (O,M,I)$
中,若存在
$m \in M$
,对任意的
$o \in O$
,都有
$oIm$
成立,即属性
$m$
与对象集中每个对象都满足关系I,则可以从形式背景中去掉这个属性
$m$
,所得概念格
$L({K^*})$
与原形式背景所生成的概念格
$L(K)$
同构。要得到
$L(K)$
,只需在
$L({K^*})$
的每个概念的内涵中都添加属性
$m$
即可。
2) 若
$i,j \in M,$
且
$i \ne j$
,
$P = \left\{ {o \in O|oIi} \right\}$
,
$Q = $
$\left\{ {o \in O|oIj} \right\}$
,若
$P = Q$
,则可以将两个属性
$i$
和
$j$
缩写成一个属性
$ij$
。显然,缩写后的形式背景与原形式背景生成的概念格相同。
通过上述两种方法约简形式背景后,就可以有效地减少形式背景中属性集合中的元素个数,从而降低生成概念格的难度,更迅速地生成概念格。
例1 表1给出了形式背景
$K = (O,M,I)$
,其中
$O = \left\{ {{\rm{1}},{\rm{2}},{\rm{3}},{\rm{4}},{\rm{5}},{\rm{6}},{\rm{7}}} \right\}$
,
$M = \left\{ {a,b,c,d,e,f,g} \right\}$
,表2为约简后的形式背景。其中属性的个数由7个约简成5个。
表 1(Tab. 1
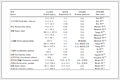
表 1 形式背景
$(O,M,I)$
Tab. 1 Formal context
$(O,M,I)$
| 对象 |
a
|
b
|
c
|
d
|
e
|
f
|
g
|
| 1 |
× |
× |
× |
|
× |
|
× |
| 2 |
|
|
|
× |
× |
× |
× |
| 3 |
|
× |
|
× |
|
× |
× |
| 4 |
|
× |
× |
|
|
|
× |
| 5 |
|
× |
× |
× |
|
× |
× |
| 6 |
× |
× |
× |
|
|
|
× |
| 7 |
|
|
|
|
× |
|
× |
|
表 1 形式背景
$(O,M,I)$
Tab.1 Formal context
$(O,M,I)$
|
表 2(Tab. 2

表 2 约简后的形式背景
$(O,M,I)$
Tab. 2 Reduced formal context
$(O,M,I)$
| 对象 |
a
|
b
|
c
|
df
|
e
|
| 1 |
× |
× |
× |
|
× |
| 2 |
|
|
|
× |
× |
| 3 |
|
× |
|
× |
|
| 4 |
|
× |
× |
|
|
| 5 |
|
× |
× |
× |
|
| 6 |
× |
× |
× |
|
|
| 7 |
|
|
|
|
× |
|
表 2 约简后的形式背景
$(O,M,I)$
Tab.2 Reduced formal context
$(O,M,I)$
|
1.2 图论
定义3 1)设
${V_{\rm{1}}}$
和
${V_{\rm{2}}}$
是图
$G$
的顶点子集,使
${V_{\rm{1}}} \cup {V_{\rm{2}}} = V\left( G \right){\rm{,}}{V_{\rm{1}}} \cap {V_{\rm{2}}} = \phi $
且
$G$
的每一条边都是一个端点在
${V_{\rm{1}}}$
中另一个端点在
${V_{\rm{2}}}$
中,则称
$G$
为二部图,记作
$G = \left( {{V_{\rm{1}}}{\rm{,}}{V_{\rm{2}}}{\rm{;}}E} \right)$
。如果
${V_{\rm{1}}}$
中的顶点与
${V_{\rm{2}}}$
中的每一个顶点都相邻,则称为完全二部图。
2) 设
${V_{\rm{0}}}$
是图G的任一顶点子集,G中与
${V_{\rm{0}}}$
的顶点邻接的所有顶点的集合称为
${V_{\rm{0}}}$
的邻集,记作
$N\left( {{V_{\rm{0}}}} \right)$
。
3) 设
$v \in V\left( G \right)$
,G中与顶点v关联的边的数目称为v(在G中)的度。
4) G与S是两个图,且
$V\left( S \right) \subseteq V\left( G \right){\rm{,}}$
$E\left( S \right)$
$ \subseteq E\left( G \right)$
,则
$S$
是
$G$
的子图,记作
$S \subseteq G$
。设
${V^*}$
是
$G = \left( {V{\rm{,}}E} \right)$
的顶点集的一个非空子集,以
${V^*}$
作为顶点集,以两个端点均在
${V^*}$
中的边的全体为边的子图称为由
${V^*}$
导出的
$G$
的子图,记为
$G\left[ {{V^*}} \right]$
,则
$G\left[ {{V^*}} \right]$
是
$G$
的导出子图。
由概念格和二部图的定义可知,每个形式背景都对应一个二部图,其中二部图的顶点集为
$O \cup M$
,顶点
$o \in O$
与
$m \in M$
之间有一条边当且仅当
$o$
与
$m$
满足关系I。
下面用具体实例来说明以上定义。
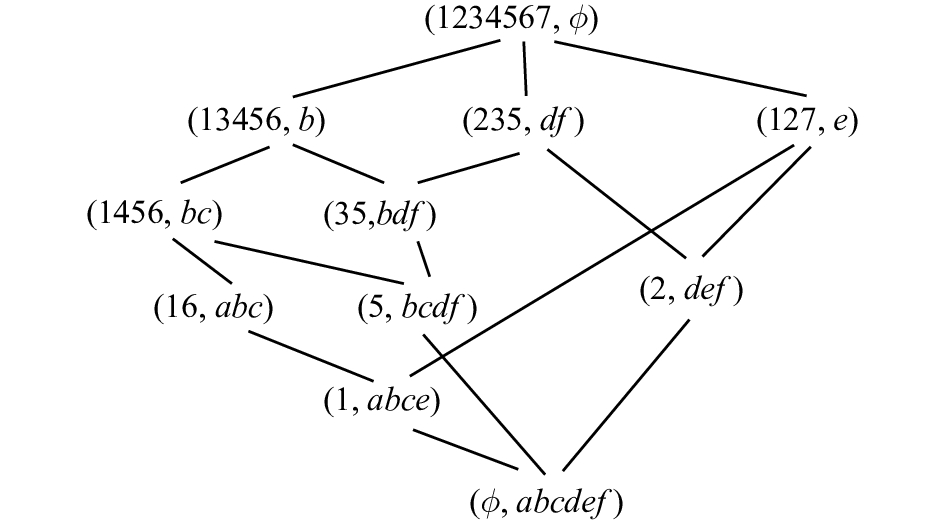
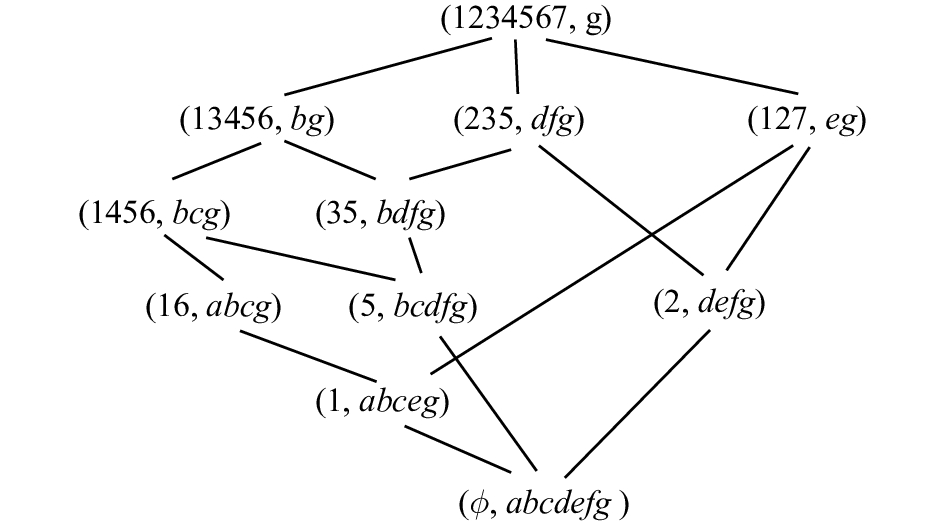
例2 图1是例1中约简后的形式背景表2对应的二部图,图2是表2对应的概念格,原形式背景表1对应的概念格即为图3。
2 利用二部图生成概念格
形式背景中的数据,在很多情况下,对象的个数较大,而属性的个数则相对较少,在这种情况下,基于属性来生成概念格,可以有效地减少算法的执行时间。本文基于属性,利用二部图子图和邻集的知识来生成概念格。
本节中的形式背景是指约简后的形式背景,二部图也指约简后的形式背景所对应的二部图。
首先给出二部图的极大完全子图的定义。
定义4 若
$S$
是二部图
$G$
的子图,且
$S$
是完全二部图,对任意的
$v \in V\left( G \right) - V\left( S \right)$
,
$G$
由
$V\left( S \right) \cup v$
导出的子图
$G\left[ {V\left( S \right) \cup v} \right]$
不是完全二部图,则
$S$
称为二部图
$G$
的极大完全子图。
下面给出二部图的极大完全子图与概念的对应关系。
定理1
$S = \left( {A{\rm{,}}B{\rm{;}}E} \right)$
(其中
$A \subseteq O{\rm{,}}B \subseteq M$
)是二部图
$G = \left( {O,M;E} \right)$
的极大完全子图的充要条件为
$\left( {A{\rm{,}}B} \right)$
是概念。
证明 由概念格的定义知充分性显然成立。
下证必要性,用反证法。假设
$\left( {A{\rm{,}}B} \right)$
不是概念,则有
$A' \ne B$
或
$B' \ne A$
。如果
$A' \ne B$
,因为
$S = $
$\left( {A{\rm{,}}B{\rm{;}}E} \right)$
是完全二部图,所以B中的顶点与A中的每个顶点都相邻,故至少存在一个顶点
$m \in M$
,有m与A中的每个顶点都相邻,即
$A' = B \cup m$
。这样可以得到
${S_1} = \left( {A{\rm{,}}B \cup m{\rm{;}}{E^*}} \right)$
为完全二部图,与S是二部图G的极大完全子图矛盾,故
$A' = B$
。同理可证
$B' = A$
。因此,
$\left( {A{\rm{,}}B} \right)$
是概念。
下面的定理2和定理3就是利用二部图的极大完全子图得到顶层概念
$\left( {O,\phi } \right)$
的直接子概念。
定理2 形式背景
$K = (O,M,I)$
对应的二部图为
$G = \left( {O,M;E} \right)$
,
$i$
为图
$G$
的顶点集
$M$
中度数最大的顶点,
$N\left( i \right) = P$
,则
$i$
与
$P$
构成的
$G$
的导出子图
$G\left[ {P \cup i} \right]$
是
$G$
的极大完全子图,即
$\left( {P,i} \right)$
为概念,且
$\left( {P,i} \right)$
为顶层概念
$\left( {O,\phi } \right)$
的直接子概念。
证明 用反证法。假设
$G\left[ {P \cup i} \right]$
不是
$G$
的极大完全子图,即存在
$o \in O - P$
,有
${S_1} = \left( {P \cup o,i;{E_1}} \right)$
为完全二部图,或存在
$m \in M$
,有
${S_2} = \left( {P,i \cup m;{E_2}} \right)$
为完全二部图。若有第一种情况,则顶点
$i$
与
$P \cup o$
相邻,此与
$N\left( i \right) = P$
矛盾。若有第二种情况,由完全二部图的定义知
$i \cup m$
与P中每个顶点都相邻,如果m的邻集恰好为P,则i与m应约简为im,与i和m是两个顶点矛盾;如果m的邻集包含P,即至少存在
${o_1} \in O$
,使
$m$
与
$P \cup {o_1}$
相邻,则
$m$
的度数大于
$i$
的度数,此与
$i$
为
$M$
中度数最大的顶点矛盾。因此,
$G\left[ {P \cup i} \right]$
是G的极大完全子图,即
$\left( {P,i} \right)$
为概念。且其为顶层概念
$\left( {O,\phi } \right)$
的直接子概念,因为不存在概念
$C$
,使
$\left( {P,i} \right) < C < \left( {O,\phi } \right)$
。
定理3 若
$j$
是形式背景
$K = (O,M,I)$
对应的二部图
$G = \left( {O{\rm{,}}M{\rm{;}}E} \right)$
的顶点集
$M$
中除
$i$
外度数最大的顶点,
$N\left( j \right) = {P^*}$
。若
${P^*} \not\subset P$
,则
$\left( {{P^*},j} \right)$
为顶层概念
$\left( {O,\phi } \right)$
的直接子概念;若
${P^*} \subset P$
,则以
${P^*}$
为外延的概念应为
$\left( {P,i} \right)$
的子概念。
证明同定理2。
由定理2和定理3可以得到顶层概念
$\left( {O,\phi } \right)$
的直接子概念。
以下的定理4给出了利用二部图的子图来求
$\left( {O,\phi } \right)$
的直接子概念
$\left( {P,i} \right)$
的直接子概念及其所有子概念的依据。
定理4 形式背景
$K = (O,M,I)$
对应的二部图为
$G = \left( {O{\rm{,}}M{\rm{;}}E} \right)$
,
$i$
是图
$G$
的属性集
$M$
中度数最大的顶点,
$N\left( i \right) = P$
,则
$\left( {P,i} \right)$
为形式背景
$K$
的概念。
$G$
的导出子图记为
$S = G[P \cup \left( {M - i} \right)]$
,与二部图
$S$
相对应的形式背景约简后记为
${K^*} = \left( {P,\left( {M - i} \right),{I^*}} \right)$
,若
$j$
是
$S$
的顶点集
$M - i$
中度数最大的顶点,
$N\left( j \right)$
$ = Q$
,则
$\left( {Q,j} \right)$
为形式背景
${K^*}$
的概念,
$\left( {Q,i \cup j} \right)$
为形式背景
$K$
的概念,且
$\left( {Q,i \cup j} \right)$
是
$\left( {P,i} \right)$
的直接子概念。
证明
$\left( {P,i} \right)$
为形式背景
$K$
的概念,
$\left( {Q,j} \right)$
为形式背景
${K^*}$
的概念,前文已证。下证
$\left( {Q,i \cup j} \right)$
为形式背景
$K$
的概念,即需证
$G\left[ {Q{\rm{,}}i \cup j} \right]$
为二部图
$G$
的极大完全子图。
用反证法。假设
$G\left[ {Q{\rm{,}}i \cup j} \right]$
不是二部图
$G$
的极大完全子图,那么可能有下列两种情况:1)至少存在
$o \in P - Q$
,使
$G\left[ {Q \cup o{\rm{,}}i \cup j} \right]$
为完全二部图;2)至少存在
$m \in M - i - j$
,使
$G\left[ {Q{\rm{,}}i \cup j \cup m} \right]$
为完全二部图。如果出现第一种情况,由完全二部图的定义知在图
$S$
中顶点
$j$
与
$Q \cup o$
中的每个顶点相邻,此与在形式背景
${K^*}$
中
$N\left( j \right) = Q$
矛盾。如果出现第二种情况,由完全二部图定义知在图S中m与集Q中的每个顶点相邻,那么m在S中的邻集必包含j在S中的邻集,这与形式背景已约简且j是S的顶点集
$M - i$
中度数最大的顶点相矛盾。所以
$\left( {Q,i \cup j} \right)$
为形式背景K的概念,并且不能找到集合B,使
$\left\{ i \right\} \subset B \subset \left\{ {i \cup j} \right\}$
,因此
$\left( {Q,i \cup j} \right)$
是
$\left( {P,i} \right)$
的直接子概念。
根据定理4可以通过求
$G$
的导出子图的概念来简化形式背景,并求出
$\left( {P,i} \right)$
的直接子概念。这样经过反复的分解和约简,使形式背景越来越简化,同时也能求出
$\left( {P,i} \right)$
的所有子概念。
因此便能生成顶层概念的所有直接子概念以及它们各自的子概念。这便是基于二部图的深度优先的概念格的迭代算法。
基于二部图的深度优先的概念格的迭代算法:
1) 最顶层概念为
$\left( {O,\phi } \right)$
,标号为1。
2) 形式背景
$K = (O,M,I)$
(约简后),其对应的二部图为
$G = \left( {O{\rm{,}}M{\rm{;}}E} \right)$
,取属性M中度数最大的顶点
$i$
,
$N\left( i \right) = P$
,则
$\left( {P,i} \right)$
为顶层概念
$\left( {O,\phi } \right)$
的直接子概念,标号为21。
3) 画出
$G$
的导出子图
${S_1} = G[P \cup \left( {N\left( P \right) - i} \right)]$
(约简后),其对应的形式背景为
${K_1}$
。取二部图
${S_1}$
的属性集
$N\left( P \right) - i$
中度数最大的顶点
${i_1}$
,
$N\left( {{i_1}} \right) = $
${P_1}$
,则
$\left( {{P_1},{i_1}} \right)$
为形式背景
${K_1}$
的概念,
$\left( {{P_1},i \cup {i_1}} \right)$
为形式背景
$K$
中概念
$\left( {P,i} \right)$
的直接子概念,标号为31。
4) 画出
${S_1}$
的导出子图
${S_2} = {S_1}[{P_1} \cup \left( {N\left( {{P_1}} \right) - {i_1}} \right)]$
(约简后),其对应的形式背景为
${K_2}$
,取二部图
${S_2}$
的属性集
$N\left( {{P_1}} \right) - {i_1}$
中度数最大的顶点
${i_2}$
,
$N\left( {{i_2}} \right) = {P_2}$
,则
$\left( {{P_2},{i_2}} \right)$
为形式背景
${K_2}$
的概念,故
$\left( {{P_2},i \cup {i_1} \cup {i_2}} \right)$
为形式背景K中概念
$\left( {{P_1},i \cup {i_1}} \right)$
的直接子概念,标号为41。继续下去,直到
${P_l}$
为单点集,则
$\left( {{P_l},i \cup {i_1} \cup {i_2} \cdots \cup {i_l}} \right)$
为形式背景K的倒数第二层概念,它由导出子图
${S_l}$
生成,其直接子概念为最底层概念
$\left( {\phi ,M} \right)$
,标号为
$\left( {l + 2} \right)1$
,最底层概念
$\left( {\phi ,M} \right)$
的标号为
$l + 3$
。
5) 从标号为
$r1$
的概念回到生成它的导出子图
${S_{r - 2}}$
,考察二部图
${S_{r - 2}}$
的属性集中未考虑过的度数最大的顶点
${i_{r - 2}}^*$
。如果
$N\left( {{i_{r - 2}}^*} \right) = {P_{r - 2}}^*$
是已生成的概念的外延,且当此已生成概念的内涵包含
$i \cup {i_1} \cup $
${i_2} \cdots \cup {i_{r - 2}}^*$
时,说明以
${P_{r - 2}}^*$
为外延的概念及其子概念已生成,则不必再考虑此顶点;而当此已生成概念的内涵等于
$i \cup {i_1} \cup {i_2} \cdots \cup {i_{r - 2}}^*$
时,则
$\left( {{P_{r - 2}}^*,{i_{r - 2}}^*} \right)$
是
$\left( {{P_{r - 1}},{i_{r - 1}}} \right)$
的直接子概念,且此概念及其子概念已生成(已标号),此顶点也不必再往下考虑。如果
${P_{r - 2}}^*$
不是已生成概念的外延,则
$\left( {{P_{r - 2}}^*,{i_{r - 2}}^*} \right)$
是
$\left( {{P_{r - 1}},{i_{r - 1}}} \right)$
的直接子概念,标号为
$\left( {r - 1} \right)2$
,然后按步骤3)和步骤4)的方法画出
${S_{r - 2}}$
的导出子图
${S_{r - 1}}^* = $
${S_{r - 2}}[{P_{r - 1}}^* \cup \left( {N\left( {{P_{r - 1}}^*} \right) - {i_{r - 1}}^*} \right)]$
,接着再取未考虑过的最大度数顶点生成概念,直到倒数第二层概念。
6) 从标号为
$\left( {l + 2} \right)1$
的概念起,重复5),便可得到所有概念以及它们之间的父子关系。
3 实例
下面通过例3来具体说明此方法如何产生概念格。
例3 形式背景同例1,其中的对象
$O = \{ {\rm{1}},{\rm{2}},{\rm{3}},{\rm{4}}, $
${\rm{5}},{\rm{6}},{\rm{7}}\} $
表示1班至7班共7个班级,属性
$M = \{ a,b,c,d, $
$e,f,g\} $
表示班级特色,其中a表示团结,b表示纪律严明,c表示学风端正,d表示卫生环境好,e表示干部队伍过硬,f表示英语四六级通过率高,g表示课余活动丰富。
下面用基于二部图的深度优先的概念格的迭代算法来生成概念格。
1) 最顶层概念为
$\left( {1234567,\phi } \right)$
,标号为1。
2) 画出形式背景(约简后)所对应的二部图
$G$
,其属性中度数最大的顶点为
$b$
,
$N\left( b \right) = \{ 1,3,4,5,$
$6\} $
,故
$\left( {13456,b} \right)$
为
$\left( {1234567,\phi } \right)$
的直接子概念,标号为21。
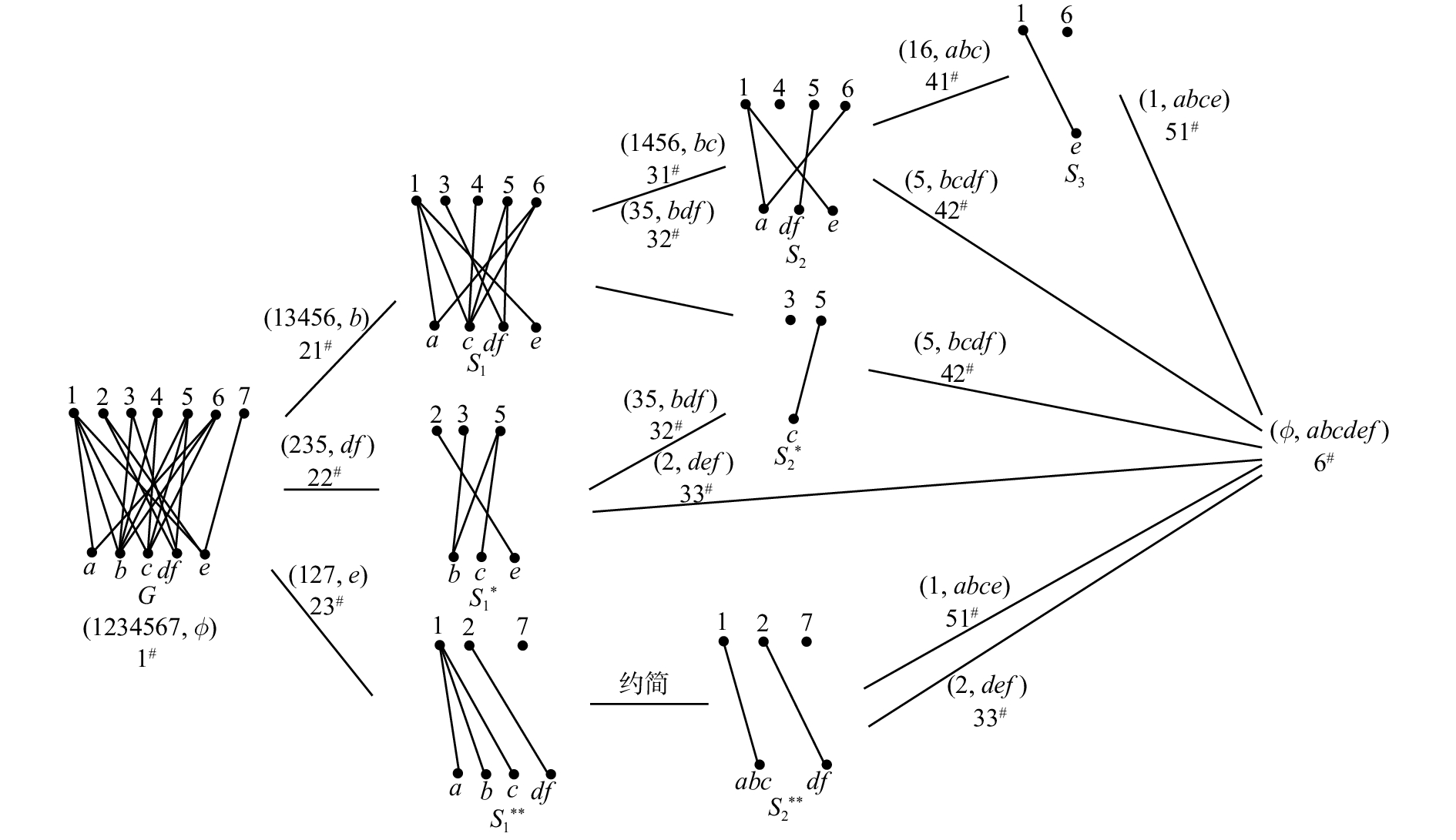
3) 画出
$G$
的由
$P = \left\{ {1,3,4,5,6} \right\}$
和
$N\left( P \right) - b = $
{a,c,
${ df,e} \}$
导出的子图
${S_1}$
,二部图
${S_1}$
的属性集中度数最大的顶点
$c$
,
$N\left( c \right) = \left\{ {1,4,5,6} \right\}$
,故
$\left( {1456,bc} \right)$
为
$\left( {13456,b} \right)$
的直接子概念,标号为31。
4) 画出
${S_1}$
的由
${P_1} = \left\{ {1,4,5,6} \right\}$
和
$N\left( {{P_1}} \right) - c = $
{a,df,
${ e} \}$
导出的子图
${S_2}$
,二部图
${S_2}$
的属性集中度数最大的顶点
$a$
,
$N\left( a \right) = \left\{ {1,6} \right\}$
,故
$\left( {16,abc} \right)$
为
$\left( {1456,bc} \right)$
的直接子概念,标号为41。画出
${S_2}$
的由
${P_2} = \left\{ {1,6} \right\}$
和
$N\left( {{P_2}} \right) - a = \left\{ e \right\}$
导出的子图
${S_3}$
,二部图
${S_3}$
的属性集中度数最大的顶点
$e$
,
$N\left( e \right) = \left\{ 1 \right\}$
,故
$\left( {1,abce} \right)$
为
$\left( {16,abc} \right)$
的直接子概念,标号为51。此时
${P_3} = \left\{ 1 \right\}$
为单点集,故
$\left( {1,abce} \right)$
为倒数第二层概念,其直接子概念只有
$\left( {\phi ,abcdef} \right)$
,
$\left( {\phi ,abcdef} \right)$
为最底层概念,标号为6。
5) 从标号为51的概念
$\left( {1,abce} \right)$
开始返回到生成它的二部图
${S_3}$
,其属性集中除
$e$
外无其他顶点。所以返回到标号为41的概念
$\left( {16,abc} \right)$
的二部图
${S_2}$
,其属性集中除
$a$
外还有顶点
$df$
和
$e$
。先看
$df$
,
$N\left( {df} \right) = \left\{ 5 \right\}$
,未出现过以5为外延的概念,故
$\left( {5,bcdf} \right)$
为
$\left( {1456,bc} \right)$
的直接子概念,标号为42,此时
${P_2}^* = \left\{ 5 \right\}$
为单点集,故
$\left( {5,bcdf} \right)$
为倒数第二层概念,其直接子概念只有
$\left( {\phi ,abcdef} \right)$
。再看
$e$
,
$N\left( e \right) = \left\{ 1 \right\}$
,已出现过以1为外延的概念
$\left( {1,abce} \right)$
,且其内涵
$abce$
真包含
$bce$
,故此处不再考虑。
现在返回到生成标号为31的概念
$\left( {1456,bc} \right)$
的二部图
${S_1}$
,其属性集中除
$c$
外还有顶点
$a,df,e$
。其中
$N\left( a \right) = \left\{ {1,6} \right\}$
,
$N\left( e \right) = \left\{ 1 \right\}$
,已出现过以16和1为外延的概念
$\left( {16,abc} \right)$
和
$\left( {1,abce} \right)$
,且其内涵真包含
$ab$
和
$be$
,故此二顶点不再考虑。而
$N\left( {df} \right) = \left\{ {3,5} \right\} $
,未出现过以35为外延的概念,故
$\left( {35,bdf} \right)$
为
$\left( {13456,b} \right)$
的直接子概念,标号为32。然后接着画出
${S_1}$
的由
${P_1}^* = \left\{ {3,5} \right\}$
和
$N\left( {{P_1}^*} \right) - df = \left\{ c \right\}$
导出的子图
${S_2}\!\!\! ^ {**}$
,二部图
${S_2}\!\!\!^{**}$
的属性集中度数最大的顶点为
$c$
,
$N\left( c \right) = \left\{ 5 \right\}$
,已出现过以5为外延的概念
$\left( {5,bcdf} \right)$
,此概念的内涵恰好为
$bcdf$
,则
$\left( {5,bcdf} \right)$
也为
$\left( {35,bdf} \right)$
的直接子概念,此顶点不再考虑。
现在返回到生成标号为21的概念
$\left( {13456,b} \right)$
的二部图
$G$
,其属性集中除
$b$
外,还有
$ a$
、
$c$
、
$d$
$f $
和
$e$
。其中
$N\left( a \right) = \left\{ {1,6} \right\}$
,
$N\left( c \right) = \left\{ {1,4,5,6} \right\}$
,已出现过以16和1456为外延的概念
$\left( {16,abc} \right)$
和
$\left( {1456,bc} \right)$
,且其内涵真包含
$a$
和
$c$
,故此二顶点不再考虑。
$N\left( {df} \right) = \left\{ {2,3,5} \right\}$
,未出现过以235为外延的概念,故
$\left( {235,df} \right)$
为
$\left( {1234567,\phi } \right)$
的直接子概念,标号为22。然后接着画出
$G$
的由
${P^*} = \left\{ {2,3,5} \right\}$
和
$N\left( {{P^*}} \right) - df$
$ = \left\{ {b,c,e} \right\}$
导出的子图
${S_1}^*$
,二部图
${S_1}^*$
的属性集中度数最大的顶点为
$b$
,
$N\left( b \right) = \left\{ {3,5} \right\}$
,已出现过以35 为外延的概念
$\left( {35,bdf} \right)$
,此概念的内涵恰好为
$bdf$
,则
$\left( {35,bdf} \right)$
也为
$\left( {235,df} \right)$
的直接子概念,此顶点不再考虑。
${S_1}^*$
的属性集中除
$b$
外,还有
$c$
和
$e$
,
$N\left( c \right)$
$ = \left\{ 5 \right\}$
,已出现外延为5的概念
$\left( {5,bcdf} \right)$
,且其内涵真包含
$cdf$
,故此顶点不再考虑。
$N\left( e \right) = \left\{ 2 \right\}$
,未出现过以2为外延的概念,故
$\left( {2,def} \right)$
为
$\left( {235,df} \right)$
的直接子概念,标号为33。此时其外延
${P_1}^* = \left\{ 2 \right\}$
为单点集,其直接子概念只有
$\left( {\phi ,abcdef} \right)$
。
返回二部图
$G$
中的属性
$e$
,
$N\left( e \right) = \left\{ {1,2,7} \right\}$
,未出现过以127为外延的概念,故
$\left( {127,e} \right)$
为
$\left( {1234567,\phi } \right)$
的直接子概念,标号为23。接着画出G的由
${P^{**}} = $
$ \left\{ {1,2,7} \right\}$
和
$N\left( {{P^{**}}} \right) - e = \left\{ {a,b,c,df} \right\}$
导出的子图
${S_1}^{**}$
,二部图
${S_1}^{**}$
的属性集中
$a$
、
$b$
、
$c$
的邻集相等,约简后属性集中度数最大的顶点为
$abc$
和
$df$
,
$N\left( {abc} \right) = \left\{ 1 \right\}$
,
$N\left( {df} \right) = \left\{ 2 \right\}$
,已出现过以1和2为外延的概念
$\left( {1,abce} \right)$
和
$\left( {2,def} \right)$
,其内涵恰好为
$abce$
和
$def$
,则
$\left( {1,abce} \right)$
和
$\left( {2,def} \right)$
也为
$\left( {127,e} \right)$
的直接子概念,此二顶点不再考虑。
到此已生成所有概念,见图4。其概念格见图3。
4 结束语
本文结合图论的内容,将概念格的形式背景和一个二部图相对应,利用二部图的极大完全子图来寻找概念,并且同时得到概念之间的父子关系,最终构造出概念格。此方法同时生成Hasse图,简单直观,能够快速生成概念格。基于概念格的形式背景与图论内容的高度关联性,二者之间其余理论的相互应用是我们下一进努力的方向。
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 2018, Vol. 13
2018, Vol. 13