人脸的三维结构信息广泛地应用在人脸图像处理中，例如人脸识别、人脸跟踪、人脸对齐、人脸表情识别等方面。在过去几年，国内外研究者提出了许多人脸三维重建的方法，一类方法是基于额外的硬件设备进行三维人脸结构的采集，如使用三维激光扫描仪、结构光扫描仪等。这类方法能够获得精度较高的人脸三维结构数据，但是需要使用硬件设备，使得此方法具有造价高、不灵活、复杂度高等诸多限制，并不适合应用于普通场合^[1-2]。另一类方法是基于视频^[3]或者基于多角度照片^[4]的三维人脸重建方法，这类方法成本低，使用灵活，能够应用在日常生活中。

第二类人脸三维重建的方法主要包含基于立体视觉的^[5-6]人脸三维重建方法，基于明暗恢复形状(shape from shading，SFS)^[7-9]的人脸三维重建方法，基于运动的SFM(structure from motion)人脸三维重建方法，和基于三维形变模型(3-D morphable model，3DMM)的人脸三维重建的方法等。

SFS方法假设图像中的样本与参考样本间具有大致相似的形状和反射率，从单幅图像中物体表面的明暗变化来恢复其表面各点的相对高度或表面法向量等参数。虽然该方法使用了不同的限制，但其所求得的解的存在性和唯一性仍然是一个问题^[7-8]。SFM方法根据包含局部运动信号的二维图像序列来估计三维结构信息。王琨等^[9]提出了根据两幅正面人脸图像和一幅侧面图像重建人脸三维模型，虽然此方法能够重建出三维人脸，但是结果并不够准确。H. S. Koo等^[4]提出了对一组不同姿态的人脸图像进行相似变换从而恢复人脸的三维结构的方法，但是该方法计算复杂，运算效率低。Z. L. Sun等^[10-11]提出了基于非线性最小方差(non-linear least-squares，NLS)模型和基于带约束的独立成分分析(constrained independent component analysis，cICA)的方法，通过使用一个正面人脸照片和非正面人脸照片来估计人脸特征点的深度值，该方法提高了运算效率。3-D形变模型^[12-14]是以人脸空间的基向量为基础，建立三维人脸的表示模型，通过将形变模型与输入图像匹配的方式来实现对输入图像的三维重建。这类方法在恢复人脸细节特征方面效果不够理想，并且需要使用通用的模型进行训练。

然而如何使用双目立体图像来重建人脸的三维结构仍然是一个有挑战的问题，这种方法只使用一对图像，它们来自双目摄像头的左摄像头和右摄像头，从而对人脸的三维信息进行恢复。目前存在很多双目匹配的方法，如BM^[15]算法、SGM^[16]算法、Meshstereo^[17]算法等。但是人脸区域的低纹理问题是人脸结构三维重建需要解决的主要问题。因此，提出了专门针对人脸结构的双目立体匹配方法，如基于人脸先验的块匹配方法^[18]、基于种子点增长法^[6]等进行三维人脸结构的恢复，这类方法采用高分辨率(1 380×1 030)的摄像头采集设备，获得较高准确的结果，或者采取普通分辨率(640×480)的摄像头，但是获得的人脸精度比较差。

本文提出了一种通过普通的双目摄像头获取精度较高的三维人脸结构的方法。本文通过立体匹配得到脸部的视差值，从而恢复出脸部对应三维结构。该方法结合脸部具有的拓扑结构，通过获取脸部稀疏点的视差值，进行线性插值，初始化出脸部稠密的视差值，再利用局部匹配方法PatchMatch^[19]对脸部的视差值进行平滑处理，更好地恢复出脸部的曲面特征。

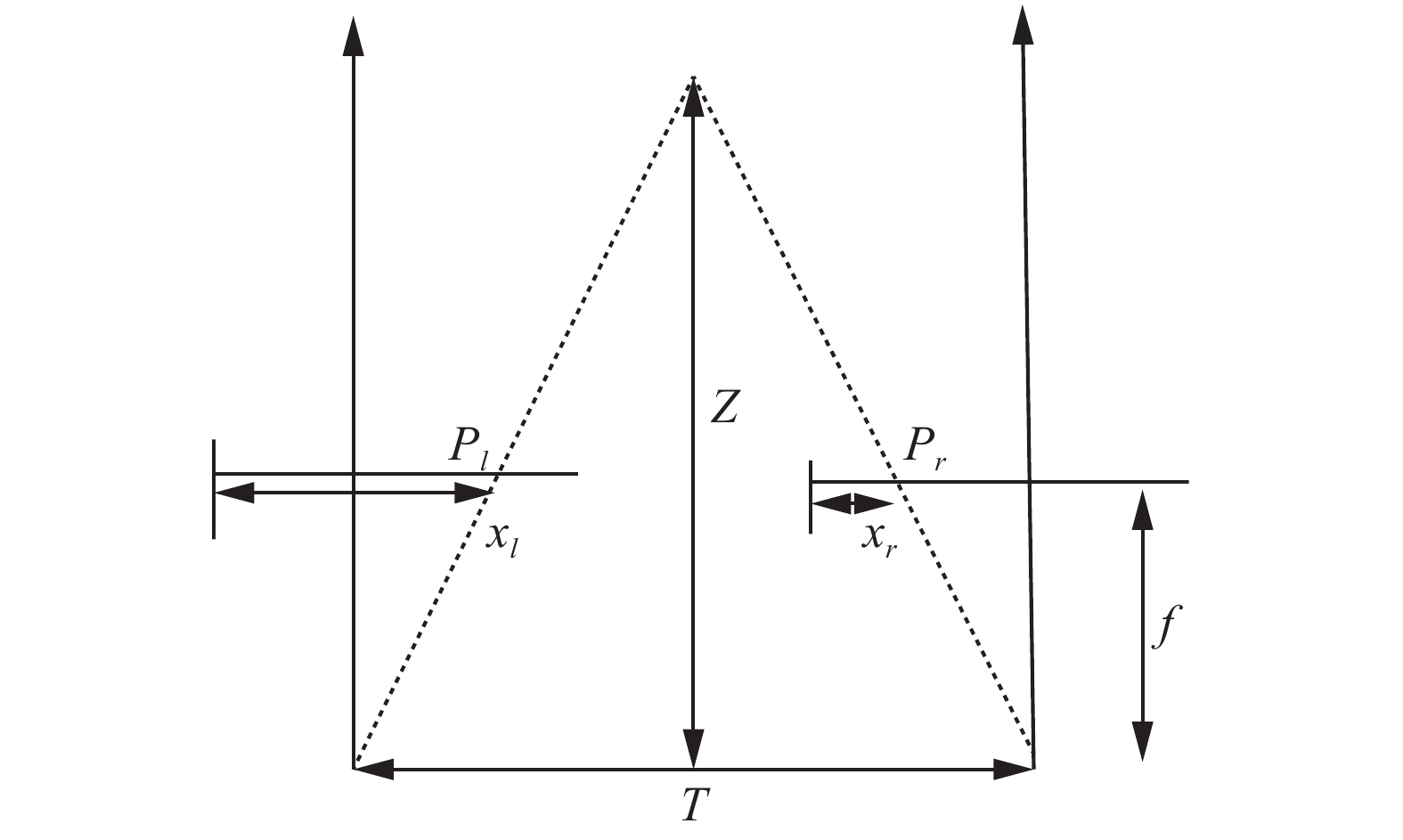
1 双目深度测量原理

在双目视觉系统中，通过立体匹配算法，找到左右两幅图中相匹配的点，如图1所示。

根据相似三角形原理，可以得到式(1)，由此变换后，得到式(2)，从而求得此点对应的深度值。

$\frac{{T - ({x_l} - {x_r})}}{{Z - f}} = \frac{T}{Z}$

(1)

由式(1)经过交叉相乘并化简可得式(2)，其中 ${x_l} - {x_r}$ 定义为视差d。

$Z = \frac{{f \cdot T}}{{{x_l} - {x_r}}} = \frac{{f \cdot T}}{d}$

(2)

式中：Z代表深度值，T代表两个摄像机之间的基线长度，f代表摄像机的焦距， ${x_l}$ 、 ${x_r}$ 分别代表左右摄像机的列坐标，d代表视差值。

由此可知，空间的一点，投射在左右摄像机平面上，该点在左边摄像机的图像平面上具有图像点 ${p_l}$ ，其坐标为 $({x_l},{y_l})$ ，同样此空间点在右边摄像机的图像平面具有图像点坐标 ${p_r}$ ，其坐标为 $({x_r},{y_r})$ ，因为对相机平面进行了校正，使得 ${y_l} = {y_r}$ ，视差值为左右匹配点的横坐标之差 $({x_l} - {x_r})$ 。

在已知两个对应点的坐标的前提下，根据式(2)就可以获取对应点的深度值。

2 基于人脸结构的立体匹配算法

由于人脸具有较多的弱纹理区域，使用常用的立体匹配算法来恢复人脸的三维结构具有一定难度，所以本文利用人脸结构的特殊性，通过人脸检测技术和关键点定位技术，匹配出左右两幅图像中的人脸关键点，获得人脸稀疏的视差值，进而通过插值算法得到整个脸部的粗略的视差值。接着将此视差值作为初值应用到稠密匹配方法Patchmath算法中，调整整个脸部视差值。最后通过三角测量原理恢复出对应点的三维坐标。

为了定位出人脸的关键点信息，本算法采用回归树集合(ensemble of regression trees，ERT)^[20]算法获取人脸的初始形状的关键点。通过ERT算法进行初始定位后，能够得到左右两幅图上的脸部关键点的拓扑结构，计算相应的视差值，再对脸部稀疏的视差值进行线性插值，得到脸部整体的初始视差值，保证了脸部初始结构连续性且有一定的平滑性。通过初始化脸部的视差值，可以减小PatchMatch的迭代次数，使得算法更加快速地计算出准确值。

2.1 脸部稀疏视差计算

为了获得脸部区域的初始视差值，本文首先计算了脸部稀疏的视差值。本文在左右两个图像上分别采用ERT算法定位出关键点，建立脸部关键点的匹配。此算法利用线下训练得到模型，定位检测图像中关键点的位置，恢复人脸的稀疏结构。至此，获得人脸先验的稀疏拓扑信息，得到左图人脸形状SL和右边人脸形状SR，其中包含的左脸特征点坐标 $\{ (l_{x_i},l_{y_i}),i \in [1,n]\} $ ，n代表特征点的总数。右脸特征点坐标 $\{ (r_{x_i},r_{y_i}),i \in [1,n]\} $ 。如图2所示，由于左右图像是经过立体校正的，所以左右的匹配点位于同一行。点 ${p_i}$ 的视差 $D({p_i})$ 的计算如式(3)所示：

$D({p_i}) = \sqrt {{{(l_{x_i} - r_{x_i})}^2}} = {\rm{abs}}(l_{x_i} - r_{x_i})$

(3)

至此得到了n个特征点的视差值，但是对于人脸的结构来说，这样的视差值太过稀疏，不能够很好地描述人脸的结构。

2.2 脸部稠密视差计算

以上述稀疏的脸部关键点的视差值为基础，利用以下两个步骤来计算脸部的稠密视差：1)结合得到的脸部关键点的位置及视差值，对脸部进行Delaunay三角剖分并对三角形内的点进行视差插值，得到脸部稠密的视差初始值；2)通过PatchMatch算法对得到的初始视差值进行平滑处理。

首先利用脸部定位出的关键点对脸部进行Delaunay三角剖分，如图3(a)所示，将脸部划分成n个三角形，此处假设，位于同一三角形内的点的视差与三角形3个顶点的视差成线性关系，从而通过一个三角形的3个顶点视差值获得三角形内点的视差值。如果三角形的3个顶点为 $p_1$ 、 $p_2$ 、 $p_3$ ，对于三角形内的任意点 $p$ ，都存在一个 $u$ 和 $v$ ，使得 $p$ 点与 $p_1$ 、 $p_2$ 、 $p_3$ 存在如式(4)的关系：

$p = (1 - u - v) \cdot p_1 + u \cdot p_2 + v \cdot p_3$

(4)

$p$ 点的坐标为 $({p_x},{p_y})$ ， $p_1$ 点的坐标为 $(p_{1_x},p_{1_y})$ ， $p_2$ 点的坐标为 $(p_{2_x},p_{2_y})$ ， $p_3$ 点的坐标为 $(p_{3_x},p_{3_y})$ ，它们满足式(5)的关系，此时就能解出u和v参数。

$\begin{array}{c}{p_x} = (1 - u - v) \cdot p_{1_x} + u \cdot p_{2_x} + v \cdot p_{3_x}\\{p_y} = (1 - u - v) \cdot p_{1_y} + u \cdot p_{2_y} + v \cdot p_{3_x}\end{array}$

(5)

从而由式(6)进行插值运算得到对p点的视差D(p)：

$D(p) = (1 - u - v) \cdot D(p_1) + u \cdot D(p_2) + v \cdot D(p_3)$

(6)

插值后的脸部视差的伪彩色图如图3(b)所示，图中中间区域代表距离摄像头近，边缘区域代表距离摄像头远。从图中可以看出脸部鼻子区域比眼睛区域距离摄像头更近，脸部轮廓的区域比眼睛区域距离摄像头更远。获得的结构与人脸结构基本符合。

图4(a)和图4(b)分别是未经过初始化和经过插值初始化的视差恢复的三维结构图，图4(b)中的人脸额头部分由于没有关键点，不能通过上述步骤得到，所以采取使用眉毛部位的视差值对其进行初始化。可以看出没有经过初始化的脸部三维结构是一些随机点，而经过插值初始化后的人脸三维结构已经初步具有人脸的基本形状信息，但是仅经过线性初始化的方法得到的人脸三维结构不平滑所以需要通过2.3部分的内容进行进一步优化。

2.3 基于PatchMatch算法的人脸三维结构优化

传统的局部的立体算法以整数视差作为支持窗，此处假设，位于同一个支持窗区域内的像素具有相同的视差值，但是该假设不适用于倾斜的平面，所以会导致重建的前向平行的表面出现一定的偏差。PatchMatch立体算法提出使用倾斜的支持窗策略来解决该问题。因此，对于脸部这样的曲型平面，PatchMatch方法能够较好地恢复。

该算法通过对每个像素构造一个平面，然后找到局部最优平面，再以此平面来描述此点的视差值。该算法与其他的局部立体匹配算法一致，包含代价匹配、代价聚合、代价计算和后处理4个步骤。本文采用的代价匹配算法是census^[21]算法。对于图片上的像素 $({x_0},{y_0})$ ，对应的视差为d，对应的视差平面 $f,{a_f}\text{、}{b_f}\text{、}{c_f}$ 表示平面 $f$ ，单位向量 ${{n}} = ({n_x},{n_y},{n_z})$ 表示平面的法向量。对于某一个像素点的聚合视差代价，如式(7)：

$m(p,f) = \sum\limits_{q \in {W_p}}^{} {w(p,q) \cdot \rho (q,q - {d_q})} $

(7)

式中： ${w_p}$ 代表像素 $p$ 的方形窗口， ${d_q} = {a_f}{q_x} + {b_f}{q_y} + {c_f}$ 代表像素 $q$ 点的视差值。平面参数 ${a_f}\text{、}{b_f}\text{、}{c_f}$ 可通过式(8)转换成平面单位法向量：

$\begin{array}{c}{a_f} = - \displaystyle\frac{{{n_x}}}{{{n_z}}},{b_f} = - \displaystyle\frac{{{n_y}}}{{{n_z}}},{c_f} = \displaystyle\frac{{{n_x}{x_0} + {n_y}{y_0} + {n_z}{z_0}}}{{{n_z}}}\end{array}$

(8)

$\rho (p,q)$ 代表像素p、q之间的匹配代价。定义为: $\rho (p,q) = H({\rm{census}}(p) - {\rm{census}}(q))$ 。其中， ${\rm{census}}(p)$ ， ${\rm{census}}(q)$ 分别代表对像素 $p$ 和 $q$ 进行census编码，然后计算编码后的哈明距离，以此值作为最终的匹配代价。

权重函数 $w(p,q)$ 考虑到方形窗口内的边缘问题，利用两点的颜色相似度来定义权值函数，如果颜色相近则赋予高权重，反之，则赋予低权重，表示如式(9)：

$w(p,q) = {{\rm{e}}^{\frac{{ - \left\| {{{{I}}_p} - {{{I}}_q}} \right\|}}{\gamma }}}$

(9)

式中： $\gamma $ 是定义的参数, $\left\| {{{{I}}_p} - {{{I}}_q}} \right\|$ 表示 $p$ 和 $q$ 的RGB颜色空间的L₁范数。

对于某个像素点选用具有最小的聚合匹配代价的平面作为当前点的最优平面，如式(10)所示：

${f_p} = \mathop {\arg \min m(p,f)}\limits_{f \in F} $

(10)

f代表所有的视差平面，所对应的解是无穷多的。通过下面的方式找到较优的平面参数。

首先初始化平面参数和视差参数，PatchMatch方法采用的是随机初始化方式，但是人脸重建与场景重建之间存在差别，人脸可以通过检测方法确定其所在区域，并且通过关键点检测技术，初步匹配出左右图像人脸的关键点，从而获得稀疏的视差值，结合线性插值方法恢复稠密的视差，为视差提供更好的初始化方式，从而使得算法能够更快地收敛到正确的视差值。本文采用2.1和2.2中的方法得到的脸部视差值进行初始化，图片其余部分视差值进行随机初始化。平面参数采用随机初始化方式。通过迭代步骤和后处理步骤来更新最优平面参数。迭代步骤中包括空间传播、视角传播和平面细化3个步骤。

3 实验结果及分析

该部分中对提出的方法从定性和定量两个方面进行分析。首先，使用双目立体相机采集人脸图像，获取的图像分辨率为640像素×480像素，构建实验室自主人脸数据库，后文用数据库1表示，由于该数据库上缺乏人脸的基准三维坐标，因此，仅从定性方面进行分析。然后在公开的人脸数据库Bosphorus^[22]上进行了脸部深度的定性分析和定量分析。Bosphorus数据库提供了人脸图像和对应点的三维坐标，有利于对人脸三维重建结果做评估，并且与其他在该库上进行的人脸三维重建^{[10-11, 15]}算法进行比较。

3.1 数据库1评估

数据库1包含20人的不同图像对，图像通过双目相机采集，图片大小为640像素×480像素。将该算法与局部立体匹配算法BM和半全局立体匹配算法SGBM(semi-global block matching)进行比较。SGBM是opencv基于SGM算法改进得到的算法。从图5可以看出，BM算法虽然能够得到人脸的总体轮廓，但人脸三维点云很稀疏，说明该算法对弱纹理区域重建较差；SGBM算法相比较BM算法，能够得到更加稠密的点云，但是人脸的下巴与人脸分离，连续性较差，出现了分层现象。而本文提出的算法能够得到更加稠密的人脸点云信息，而且得到的人脸结构也更加真实。可以看出针对人脸结构的双目立体匹配的算法能够更加准确地恢复出人脸的三维结构。

图6展现了本文提出的方法对数据库1中的部分人脸的三维结构恢复，由于侧面信息能够更加直观地展现出人脸的深度信息，所以通过展示人脸的侧脸深度信息来进行比较，前5张图是真实人脸的三维点云效果图，最后一张是人脸照片所得到的三维点云效果图。从图中可以看出，对于不同的人都具有能够区分的三维结构，而人脸照片并不具有人脸结构，说明重建的效果具有一定的区分性。

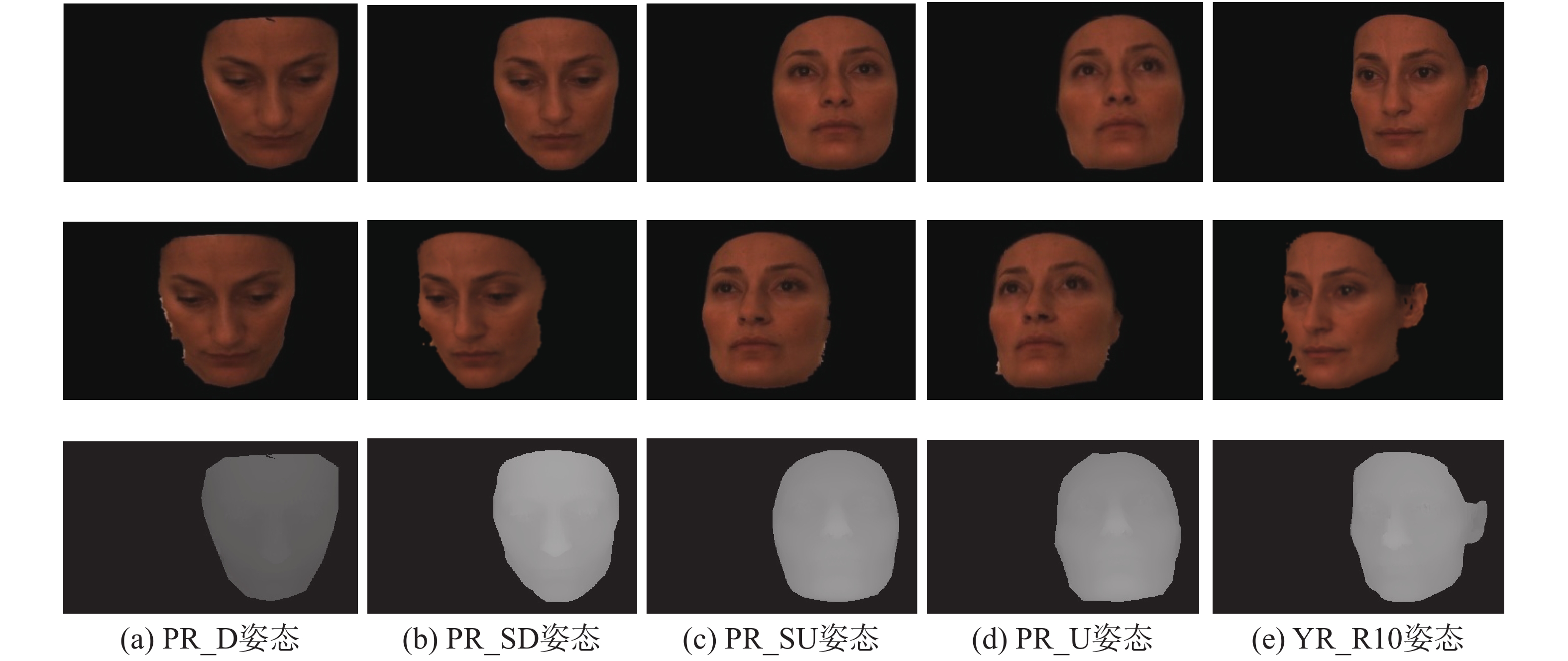
3.2 Bosphorus数据库评估

现在大多数基于双目视觉进行人脸三维重建的方法都只进行了定性分析，为了对本文提出的算法进行定量分析，使用Bosphorus数据库进行实验，但是数据库中只提供了一个摄像头采集的照片，需要对图像进行双目合成。实验中，使用数据库中每个人物的5个模型，这5个模型对应不同的姿态(被命名为PR_D、PR_SD、PR_SU、PR_U和YR_R10，分别代表向下倾斜，轻微向下倾斜，轻微向上倾斜，向上倾斜，向右偏转10°)。利用每一个模型的照片对应的三维坐标，计算了每个照片对应的视差图，从而合成了每一个照片对应的双目图像，即下文提及的左图和右图。其中bs003人物对应的双目图像和对应的视差图像如图7所示。图7中展示了数据库中人物4(命名为bs003人物)5个姿态下(不同列)的图像，第1行图像是数据库中的原图，将此作为双目立体视觉系统中的左摄像头获取的数据；第2行是通过双目立体视觉原理模拟得到的右摄像头获取的数据；第3行是对应双目立体视觉系统下的左图视差值。此值作为后续估计的基准值。

3.2.1 定性分析

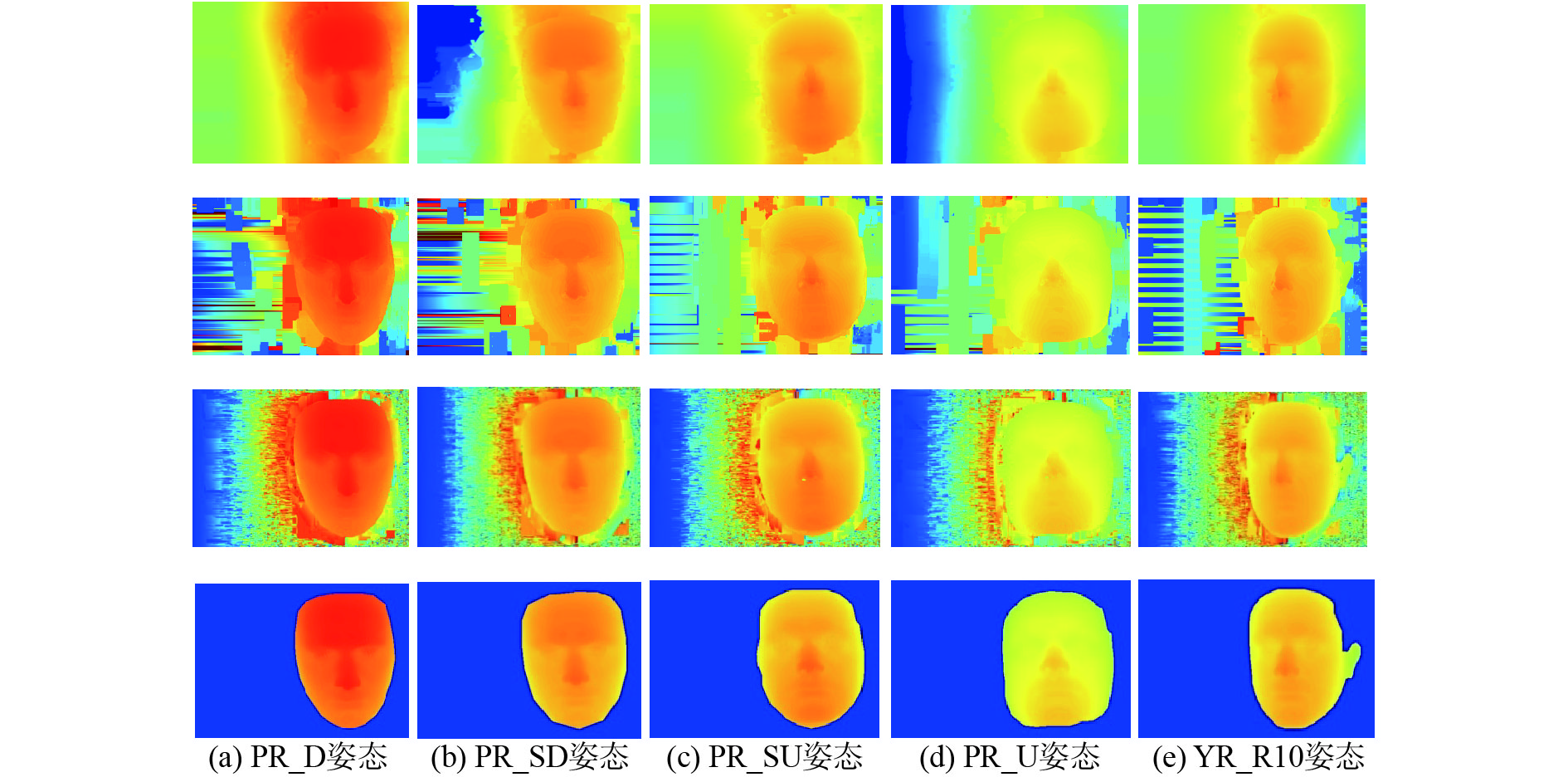
使用数据库中的人物7(命名为bs006人物)5个姿态下的图像为例，将本文方法与其他方法进行比较，(取迭代次数为3)，定性分析如图8所示，第1行是Meshstereo的方法，是一个全局的算法；第2行是原PatchMatch方法；第3行是本文提出的改进方法；第4行是基准图。图8展现了同一个人脸在不同的姿态下人脸视差的恢复，可以看出本文所提出的方法在不同的旋转角度下都最接近基准图，对于同样的迭代次数，按照脸部结构初始化视差的方法使得算法更快地收敛到正确的人脸视差值，使得人脸区域更加接近真实的深度值。

图9中展现了不同方法对不同姿态人脸进行三维重建后的脸部误差分布图。第1行是Meshstereo的方法，第2行是原PatchMatch方法，第3行是本文提出的方法。图中蓝色区域为正确匹配的区域(即视差误差小于等于1个像素)，绿色区域表示视差误差小于2像素大于1个像素，红色区域表示视差误差小于3个像素大于2个像素，黄色区域为视差误差大于3个像素。从错误点的分布来看，Meshstereo蓝色区域比较小，参杂了很多绿色区域，说明视差误差为2个像素的区域偏多，而PatchMatch算法和提出的算法有较多的蓝色区域，说明能获得更准确的视差区域。还可以看出3个算法在鼻子区域和脸部轮廓区域出现了较大误差的区域，这些区域都是遮挡区域，说明算法不能很好地对遮挡区域进行视差的恢复，但是比起前两个方法，本文算法能够减少误差较大区域的面积，从而提高算法的准确率。可以看出结合人脸结构算法有助于人脸区域的重构。

3.2.2 定量分析

将提出的方法与M. Bleyer等提出的PatchMatch方法进行比较，如图10所示。可以看出当迭代次数为4时，两个算法基本收敛，并且迭代次数等于3与等于4差大概3%，差距减小的速度小了很多。本文提出的方法比原方法在同样的迭代次数下能够减小5%的错误率。

表1展示了数据库中前20个人物对应5个姿态下PBM(percentage of bad matching pixel)的平均值，PBM表示错误匹配点的百分比，计算如式(11)所示，PBM值越小表示重建得越准确。可以看出，在每个姿态下，本文提出的方法具有最高的PBM值。

${\rm{PBM}} = \frac{1}{{np}} \times \sum\nolimits_{(x,y)} {D(x,y)} $

(11)

式中 $D(x,y)$ 计算如式(12)：

$D(x,y) = \left\{ \begin{array}{l}\!\!\! 0, \quad \left| {{\rm{d}}E(x,y) - {\rm{d}}T(x,y) \leqslant \delta_d} \right| \\\!\!\! 1, \quad \text{其他}\end{array} \right.$

(12)

式中 ${\delta _d}$ 取值为1。

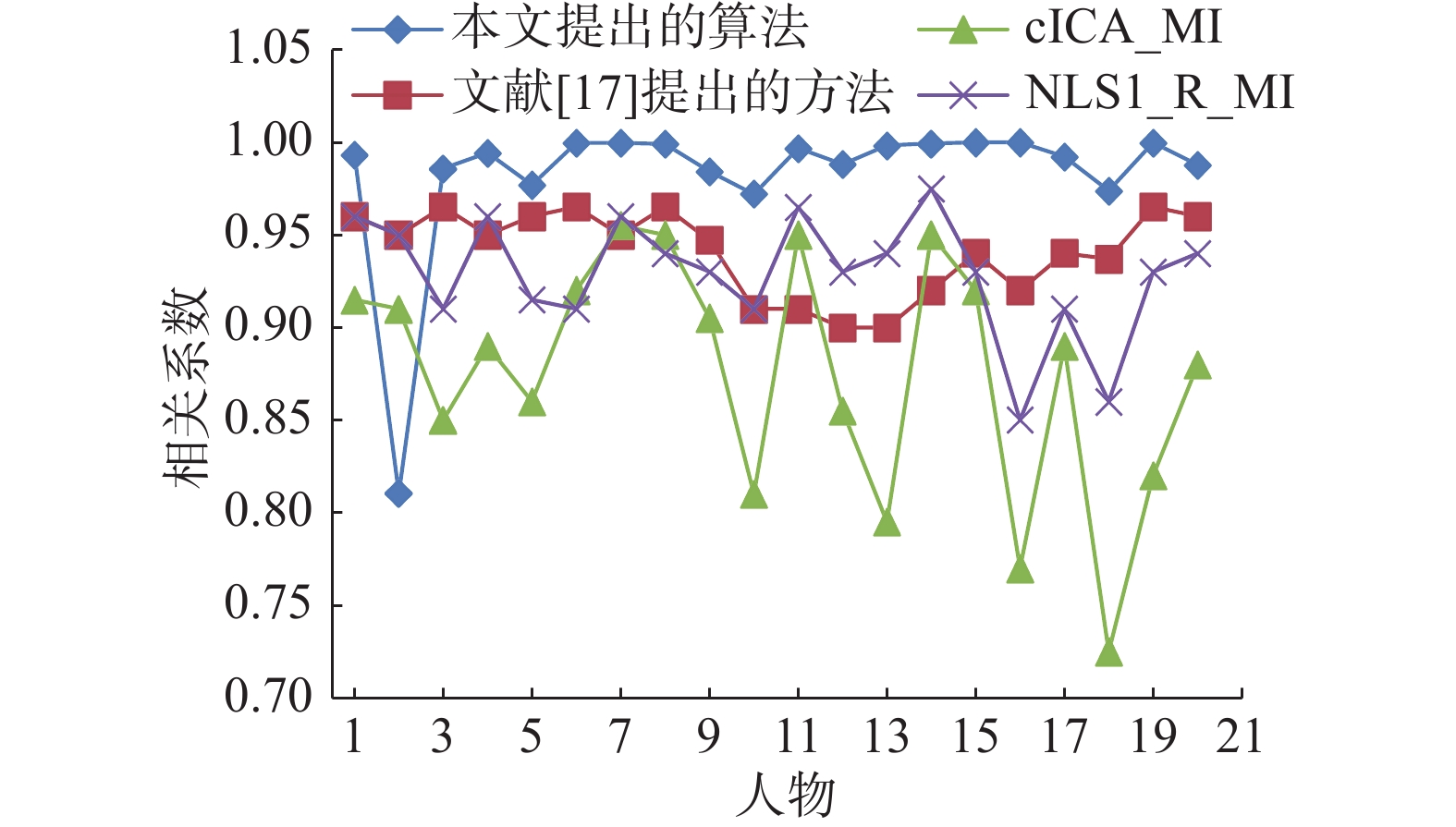
图11将本文所提出的算法与NLS^[10]方法、ICA算法^[11](被称为cICA_MI算法)，以及基于块匹配算法^[18]的双目匹配的算法进行比较。为了与这些算法进行比较，计算脸部基准图中的22个关键点的深度值与本文提出算法建立的深度图中对应点的相关系数。图11比较了数据库中的前20个人物的相关系数。从图7中可以看出，本文算法的相关系数普遍高于另外3种算法，只有人物2的相关性低于别的算法，根据测试结果，分析发现是22点中的右眼内角点与实际差别较大。

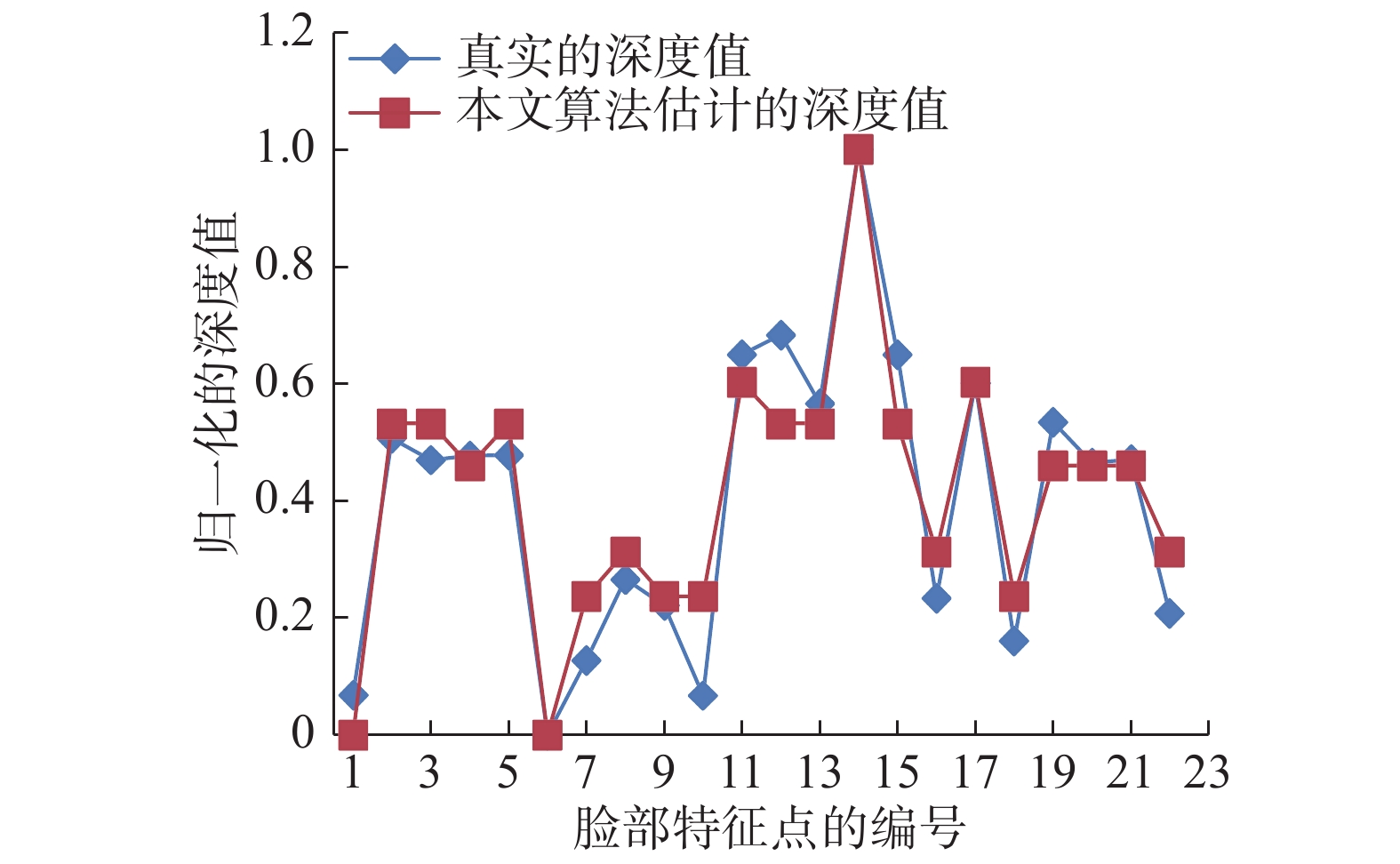
以人物1(bs000的PR_D姿态)为例，比较人物真实的22个特征点的深度值与本文算法重建所得到的值。为了进行比较，将深度值进行了归一化，归一化到[0，1]。通过式(13)对估计的深度值进行归一化^[11]：

$M_z' = \frac{{{M_z} - M_z^{\min }}}{{M_z^{\max } - M_z^{\min }}}$

(13)

式中： $M_z'$ 是 ${M_z}$ 的归一化深度值, $M_z^{\min }$ 和 $M_z^{\max }$ 是最小深度和最大深度。

从图12中可以看出，人脸特征点中的大部分的点得到了正确的估计。可以看出算法能够较好地恢复出人脸的三维深度。

综上所述，无论是与双目匹配算法比较，还是与人脸重建算法进行比较，本文提出的算法都表现出了较好的性能。

4 结束语

本文通过分析人脸的拓扑结构，结合双目立体视觉系统，提出了一种新颖的人脸稠密三维点云的三维重建方法。通过对人脸进行关键点检测，获取稀疏的人脸视差值，然后结合线性插值获得初始的稠密视差初始值，最后使用立体稠密匹配算法PatchMatch对获得的值进行了平滑处理。实验结果证明，本文算法能够得到光滑稠密的三维人脸重建点云模型。下一步研究的问题是人脸的曲面重建工作及其在人脸识别的应用。