无人机(UAV)航迹规划(trajectory planning)是指在初始状态、任务目标、威胁区和一些已知环境信息的情况下获得性能最优的规划问题，是任务规划(mission planning)系统的关键技术之一。其在任务规划系统中起着非常重要的作用，也是实现无人机智能导航并且完成任务的技术保障。基于飞行安全的需要，综合考虑障碍物、无人机自身性能和飞行时间等约束条件，所规划出的航迹既要尽可能减少无人机在飞行中坠毁的概率，又要使得综合性能指标最小，并根据实际需要进行飞行中的局部调整。传统的航迹规划方法是基于预先给定的地图生成一条具有最小代价的航迹，包括A*算法^[1]、人工势场法^[2]、蚁群算法^[3]、概率地图方法^[4](PRM)和快速扩展随机树^[5](RRT)等。这些传统的航迹规划方法一般都用于离线规划，用于在线规划时，需要很长的时间或者极大的内存才能规划出一条最优或次优路径。特别地，无法对环境的变化做出快速的反应，并且在规划的过程中很少涉及无人机自身的动力学约束，比如速度、最大加速度的限制等。因此，很少考虑无人机的安全性和航迹的可行性。

近十年来，滚动时域控制的思想也被用于解决航迹规划问题^[6-9]，采用滚动时域优化策略可以对带有输入和状态约束的线性系统进行最优控制，易于处理约束以及多变量的优化问题。滚动时域控制^[8-13]用于航迹规划，不要求一次规划到达目标，将规划分成多个阶段，成功地绕开障碍物，从而极大地减少了规划的时间，使得该方法可用于在线航迹规划。分布式滚动时域控制方法被提出^[14-16]，进一步减少了多无人机航迹规划的规划时间。然而，上述工作主要集中于采用混合整数线性规划(mixed integer linear programming，MILP)求解航迹规划最优化问题，方法面临以下两个问题：处理带复杂约束问题可扩展性不强和求解时间随着问题规模指数增加。基于以上工作的不足，本文提出了基于RHC-FPSO算法以解决带有动力学约束的多旋翼无人机航迹规划问题。从整个航迹规划看，单次规划属于局部优化，因此需要一个全局的代价图(终端罚函数)来表示航迹端点到目标点的代价估计。区别于文献[8]，本文提出的基于VORONOI图的代价图可以使得规划出的航迹尽可能地远离障碍物，提高了无人机的生存机率。

文献[17]通过空战人工势场确定其威力，将合威力引入PSO算法。通过人工势场启发粒子群算法在当前飞行方向的可机动范围内进行寻优，重点加强对合威力方向的寻优。区别于文献[17]，本文将人工势场法加入到目标函数使无人机远离障碍物，增加了无人机的安全性。此外，结合两种方法的优势，减少了计算量且在环境发生改变时，只需更新势场。RHC-APF是一种非常优秀的航迹规划算法，易于扩展。在优化过程中，计算每个粒子的约束违背量，根据约束违背量来更新粒子的速度，改进后的算法相比文献[18]在计算时间方面有很大提高，单次规划的平均时间减少42.43%，并且在求解结果的稳定性方面具有一致性。仿真结果也表明了RHC-FPSO算法的有效性。

1 相关工作 1.1 滚动时域控制原理

滚动时域控制^[19](RHC)是一种基于模型的反馈控制策略。在每一采样时刻，采集系统当前状态作为初始状态，根据系统状态空间模型和约束，在线求解一个有限时域的最优控制问题，将求解最优控制的第1个控制信号实际作用到系统中，重复以上过程。对于含状态约束和输入约束等限制的系统，滚动时域控制是一种有效的控制方法。随着时间的推移，当无人机执行任务时不断地靠近目标，在此过程中，每一次的输入都是通过求解一个有限时域内带约束的优化问题。因此，相比固定时域能够极大地减少计算时间，满足在线航迹规划。

RHC的基本思想：假设当前时间点为 $k$ ，在有限时域 $[k,k + {H_p}]$ ，通过使某一性能指标最优化来确定其未来的控制作用，选择第一个最优控制输入作为当前的控制输入，在下一时刻 $k + 1$ ，计算 $[k + 1,k + {H_p} + 1]$ 的控制输入，重复以上过程，直到任务完成。具体步骤如下：

1) 根据当前状态 ${{x}}(k)$ ，考虑当前约束和未来约束，计算未来时域 ${H_p}$ 内的输入 $[{{u}}(k)\,\,{{u}}(k+1)\,\, \cdots $ ${{u}}(k + {H_p})]$ 。

2) 选择控制时域 ${H_e}$ ，即 $[{{u}}(k)\,\,{{u}}(k+1)\,\, \cdots \,\,{{u}}(k + {H_e})]$ 作为当前的输入。

3) 当到达 $k + {H_e} + 1$ 时刻时，测量当前状态 $x(k + {H_e} + 1)$ 。

4) 当 $k + {H_e} + 1$ 时刻，在有限时域 $[{{u}}(k + {H_e} + 1),$ ${{u}}(k + {H_e} + {H_p} + 1)]$ 内重复步骤1)～3)直到达到目标。

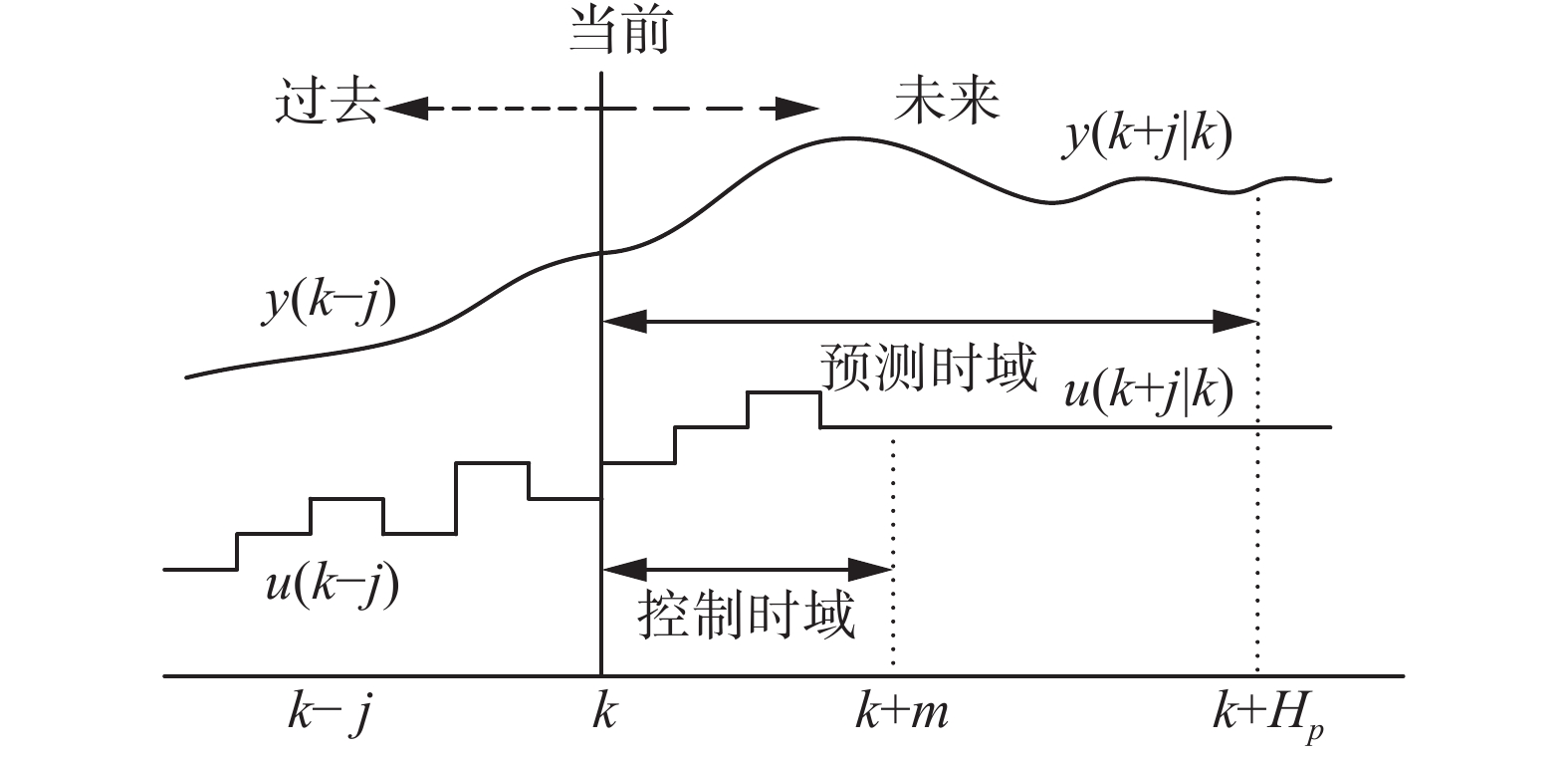
滚动时域优化的基本思想是：首先，根据对应的目标函数和约束条件，RHC利用多旋翼无人机的状态空间模型，预测未来规划时域内的控制输入，将其作用于系统中；然后，测量下一时刻的状态，根据当前的状态进行下一步优化，随着时间的推进反复滚动执行。具体过程如图1所示。

从以上对模型预测控制的介绍和分析，可以看出：RHC是根据当前的状态和目标函数进行不断地迭代，求解该时刻的有限时段的最优输入，采用的是局部优化，不是一个不变的全局最优目标。因此，需要代价图使得规划时跳出局部最优值，完成全局优化。

1.2 人工势场法

人工势场法^[20]是由Khatib在1986提出的一种虚拟力场法。其方法是将研究对象所处的环境用势场来定义，通过位置信息来控制对象的避障运动。将研究对象在实际环境中的运动转换为在虚拟势场的运动，在该势场中目标点对研究对象产生引力，环境中的障碍物产生斥力。引力和斥力的合力决定了研究对象的运动方向和运动速度。人工势场相比其他的算法具有计算量小、描述简单、实时性高、应用广泛。

根据人工势场的理论，对于静态或者动态的环境，都可以计算相应的人工势能图。对于任意状态，研究对象的位姿用 $x$ 表示，则势场可以用 $U(x)$ 表示，目标转态位姿用 ${x_g}$ 表示，因此相应的吸引势为 ${U_{\rm{att}}}(x)$ ，障碍物的位姿用 ${x_o}$ 表示，排斥势 ${U_{\rm{rep}}}(x)$ ，因此空间中的任意位姿的势能场都可以表示为

$U(x) = {U_{\rm{att}}}(x) + {U_{\rm{rep}}}(x)$

(1)

目标点对研究对象产生的势能大小与两者的距离相关，距离大、势能大，反之亦然。当二者之间的距离为零时，表示到达目标点，因此引力势能与距离成正比关系，可表示为

${U_{\rm{att}}}(x) = \frac{1}{2}{k_{\rm{att}}}{d^2}(x,{x_g})$

(2)

与引力势场类似，障碍物对研究对象产生斥力场。斥力场势能大小与障碍物和研究对象的距离有关，距离越近，斥力势能越大，反之越小。因此可以表示为

${U_{\rm{rep}}}(x) = \left\{ {\begin{array}{l} {\displaystyle\frac{1}{2}{k_{\rm{rep}}}(\frac{1}{{d(x,{x_0})}} - \frac{1}{{{d_n}}})}, \quad {d(x,{x_o}) \leqslant {d_n}}\\ 0 , \quad {d(x,{x_o}) > {d_n}} \end{array}} \right.$

(3)

对于势场 $U(x)$ 的定义方式可以有很多种，可以按照实际情况具体定义。势场法在数学的描述上简单，在路径规划中广泛应用。

2 问题描述

以多旋翼无人机为例，讨论其由初始状态出发，在规避障碍物和满足相应的约束条件下，以最小代价到达目标区域。其线性时不变系统动力学描述为^[14]

${{x}}(k + 1) = {{Ax}}(k) + {{Bu}}(k)$

(4)

${{y}}(k) = {{Cx}}(k) + {{Du}}(k) \in {{\gamma }}(k)$

(5)

式中： ${{x}}(k) \in {R^{{N_x}}}$ 是状态向量， ${{u}}(k) \in {R^{{N_u}}}$ 是输入向量，等式(4)为无人机的状态空间模型，等式(5)为状态和输入需要满足的约束条件，其中 ${{\gamma }}(k)$ 为 $k$ 时刻需要满足的约束条件，输出向量 ${{y}}(k) \in {R^{{N_y}}}$ 。

一般的目标函数，采用如下形式：

$J = \sum\limits_{k = 0}^\infty {l({{u}}(k),{{x}}(k),{\chi _F})} $

(6)

式中： $l(*)$ 是代价函数，χ_F是目标集。在RHC框架中，优化是在一个有限域内执行的，第1个控制输入被执行，形成新的状态，基于当前的状态进行下一步优化，直到到达目标集。

因此基于RHC框架的优化完整的描述为

$\begin{array}{c}{J^*} = \mathop {\min }\limits_{u(.)} \{\displaystyle \sum\limits_{j = 0}^{{H_p}} {l({{u}}(k + j|k),{{x}}(k + j|k),{\chi _F})} + \\f({{x}}(k + {H_p} + 1),{\chi _F})\} \end{array}$

(7)

$\begin{array}{c}{{x}}(k + j + 1|k) = {{Ax}}(k + j|k) + {{Bu}}(k + j|k)\\j = 0, 1,\cdots ,{H_p}\end{array}$

(8)

$\begin{array}{c}{{y}}(k + j|k) = {{Cx}}(k + j|k) + {{Du}}(k + j|k) \in {{\gamma }}(k)\\j = 0,1, \cdots ,{H_p}\end{array}$

(9)

式中： ${{x}}(k + j|k)$ 表示在时刻 $k$ ， $(k + j)$ 时刻的预测值， ${{\gamma }} $ 表示输出约束， ${H_p}$ 为滚动时域， $f(*)$ 表示终端惩罚项。

文献[10]使用MILP优化目标函数(7)，如果存在非线性约束条件或者目标函数，通过将其转化为多约束条件进行线性化，将会导致约束条件呈指数增长，会损失一部分求解精度，可扩展性不强。并且对于复杂的环境和目标函数，求解速度进一步降低。PSO可以快速求解一个可行解，因此，使用PSO结合RHC可以平衡求解时间和求解精度。实验结果表明，基于改进的PSO方法(FPSO)能够有效地提高计算效率。

3 RHC-FPSO航迹规划

本文将整个航迹规划分成两个阶段，第1阶段为代价评估阶段，根据当前环境生成代价图，当环境发生改变时，重新计算代价图，使用基于VORONOI图的代价图来表示航迹端点到目标点的代价估计；第2阶段为在线航迹规划阶段，在问题描述中，已经将航迹规划表示成一个优化问题，因此本阶段主要是基于RHC-FPSO在线航迹规划的一个优化过程。

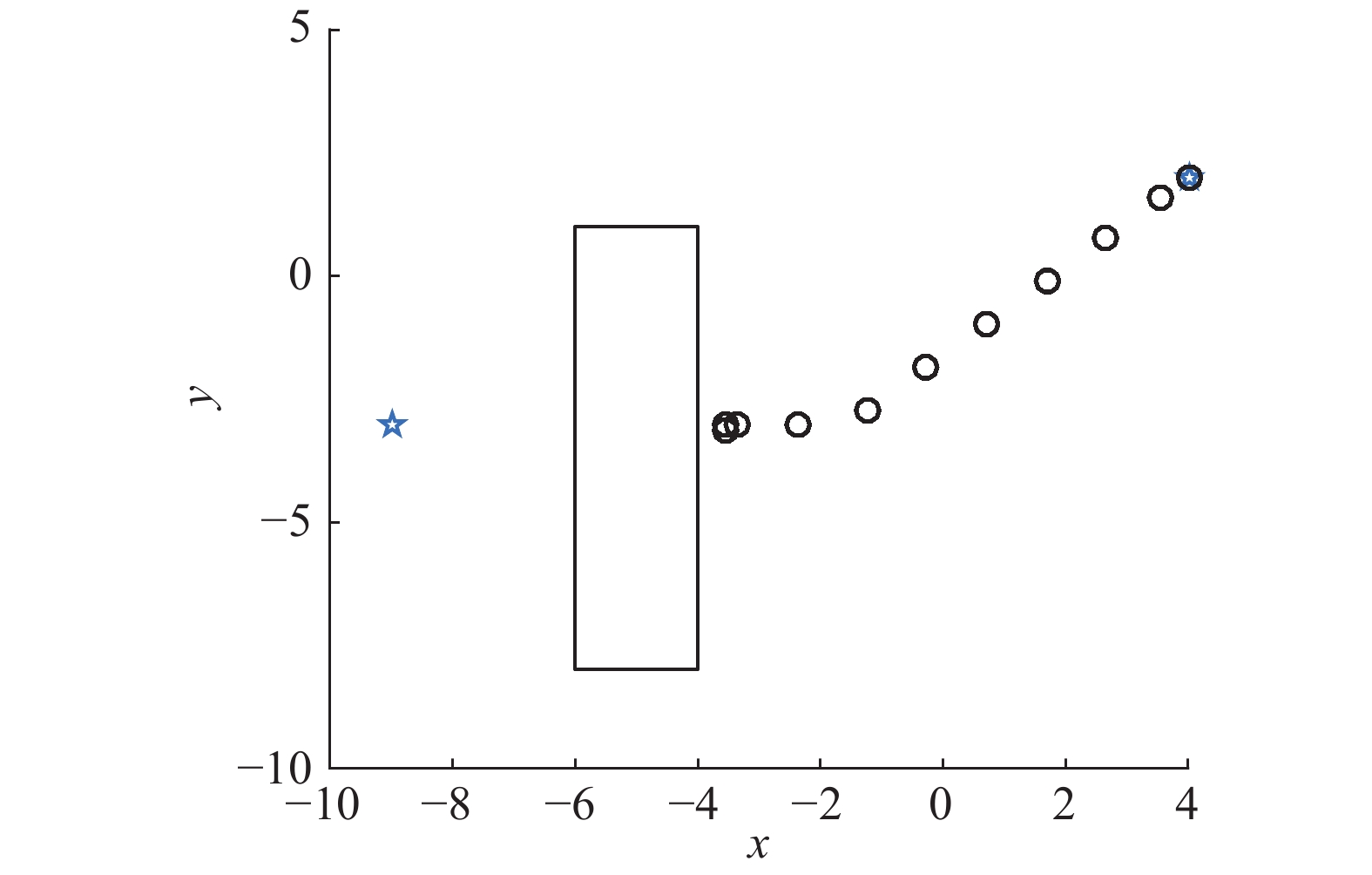
3.1 代价图

根据第1节分析可知，从航迹规划全局看，滚动时域优化是局部优化，因此容易陷入局部最优。如图2所示，这种情况下无人机陷入了局部最优，目标不可达，因此需要估计预测航迹端点到目标点的代价。代价估计阶段根据给出的障碍物和目标预先计算，当探测到环境发生改变将会重新计算。航迹规划阶段使用预先计算的代价图来估计航迹端点到目标点的代价。

文献[8]提出的代价图表示航迹端点到目标点的时间估计值。基本思想为：在不考虑无人机自身的动力学约束条件下，对于多边形的障碍物，连接开始点、障碍物顶点和目标点，如果这些点的连线没有穿过障碍物，则添加一条边，这样形成的图称为可视图。对于可视图使用Dijkstra^[21]单源最短路径算法，搜索从目标点到各个点的最短路径。由第3节问题描述可知，航迹端点为 ${{x}}(k + {H_p} + 1)$ ，因此基于代价图的终端惩罚项 $f(*)$ 可以表示如下：

$f({{x}}(k + {H_p} + 1),{\chi _F})) = d({{x}}(k + {H_p} + 1),{{{x}}_{\rm{vis}}}) + {C_{\rm{vis}}}$

(10)

式中： ${{{x}}_{\rm{vis}}}$ 为基于代价图的可视点， $d({{x}}(k + {H_p} + 1),{{{x}}_{\rm{vis}}})$ 为航迹端点到可视点的代价， ${C_{\rm{vis}}}$ 为可视点到目标点的代价。

然而，基于文献[8]提出的代价图，选择的可视点为障碍物的顶点，这会导致规划出的航迹会沿着障碍物边缘，降低无人机安全性。因此，我们引入基于VORONOI图的可视图，VORONOI图的优点是使得可视点离障碍物的距离尽可能远，VORONOI图使得可视点的选择不再是障碍物的顶点，而是障碍物之间的顶点连线的中点。

定义1　VORONOI图^[22]。任意两点 $p$ 和 $q$ 之间的欧式距离，记作 ${\rm{dist}}(p,q)$ ，假设平面P = $\{ {p_1},{p_2}, \cdots, {p_n}\} $ 为平面上的任意 $n$ 个互异的点， $P$ 所对应的VORONOI图是平面的一个子区域的划分，因此整个平面被划分成 $n$ 个单元，具有以下性质：任意一点 $q$ 位于点 ${P_i}$ 所对应的单元中，当且仅当对于任意的 ${P_j}$ ， $j \ne i$ 都有 ${\rm{dist}}(q,{P_i}) < {\rm{dist}}(q,{P_j})$ 。

根据定义1可知，VORONOI多边形的每条边上的点到相对应的两个点的距离相等，即VORONOI多边形上的点是到障碍物或威胁点的最远点。因此可以得出，飞行器以VORONOI多边形的顶点作为可视点，可以提高飞行器的安全系数。

定理1　VORONOI图定理^[22]：若 $n > 3$ ，则在与平面上任意 $n$ 个基点相对应的VORONOI图中，顶点的数目不会超过 $2n - 5$ ，而且边的数目不会超过 $3n - 6$ 。

由定理1可知，采用基于VORONOI图的可视点的方法，相对于文献[8]，可视点呈线性增长，并且小于 $2n$ 。

3.2 基于RHC-FPSO在线航迹规划

航迹规划是复杂约束条件下的最优化问题，采用粒子群等智能优化算法进行航迹规划时，往往算法迭代初期，控制输入和状态可能存在违反约束的情况，算法需要迭代若干次才能产生满足要求的输入，并在此基础上进一步寻优。粒子群算法中种群最优个体影响着粒子搜索方向，如何缩短搜索到可行输入的时间对提高算法的效率至关重要。因此，我们根据粒子违反约束条件的程度来更新粒子速度。

评价函数设计：评价函数用于给粒子群中每个个体计算适应度。所有约束条件都满足的输入粒子称为可行个体，违反任何一项约束条件的个体称为不可行个体。在进行个体评价时遵循以下准则：

1) 对于可行输入来说，根据式(3)，代价小的输入优于代价大的输入；

2) 对于不可行航迹来说，约束违背小的输入优于约束违背大的输入；

3) 对于可行输入与不可行输入，可行输入总是优于不可行输入；

不可行输入意味着在实际中输入是不可行的，因此没有必要计算它的代价，可以减少计算量。基于以上分析，对任意输入，采用下面的评价函数。

$F({{u}}) = \left\{ {\begin{array}{l}{C({{u}}), \quad {\text{可行解}}}\\{\rm{BigM }}+ C, \quad {\text{不可行解}}\end{array}} \right.$

(11)

式中： $C(u)$ 为式(7)计算的航迹代价，BigM为一个比较大的数。 $C$ 为约束违背量，采用式(12)计算方式：

$C = \sum\limits_{i = 1}^{{H_p}} {({w_1}f({l_i}) + {w_2}g({v_i}) + {w_3}h({a_i}))} $

(12)

式(12)用于计算不可行输入， $f({l_i})$ 表示航迹段 $i$ 穿越禁飞区的约束违背量， $g({v_i})$ 和 $h({a_i})$ 表示速度和加速度的约束违背量， ${w_1}$ 、 ${w_2}$ 、 ${w_3}$ 为权系数。

图3显示了函数 $F(u)$ 的图像，在可行解区域 $F(u)$ 和 $C(u)$ 相等，在不可行区域，离区域边界越远， $F(u)$ 值越大。

假设粒子群种群数为 $N$ ，每个粒子的空间维数为 $D$ ，第 $i$ 个粒子的输入向量和速度为 ${{{u}}_i} \!=\! ({u_{i,1}}, {u_{i,2}},\cdots ,$ ${u_{i,D}})$ ， ${{{v}}_i} \!= \!({v_{i,1}},{v_{i,2}}, \cdots ,{v_{i,D}})$ 。第 $i$ 个粒子最优解为 ${{{P}}_i} \!=\! ({p_{i,1}},$ ${p_{i,2}}, \cdots ,{p_{i,D}})$ ，粒子群最优解为 ${{G}} = ({g_1},{g_2}, \cdots ,{g_D})$ 。因此，根据粒子群优化策略，粒子更新公式为

$\left\{ {\begin{array}{l}\begin{array}{c}\!\!\!\!\!\!\!\!{{{v}}_i}(k + 1) = {{w}}(k){{{v}}_i}(k) + {c_1}{r_1}({{{P}}_i}(k) - {{{x}}_i}(k)) +\\\!\!\!\!\!\!\! \!\!\!\!\!{c_2}{r_2}({{G}}(k) - {{{x}}_i}(k))\end{array}\\\!\!\!\!{{{{x}}_i}(k + 1) = {{{x}}_i}(k) + w{{{v}}_i}(k)}\end{array}} \right.$

(13)

式中： ${c_1}$ 和 ${c_2}$ 为学习因子， ${r_1}$ 和 ${r_2}$ 为区间[0, 1]的随机数，式(13)的第1部分为粒子的全局搜索能力，第2部分为粒子的记忆能力，第3部分为粒子之间信息共享。 $w(k)$ 为粒子的迭代权重:

$w(k) = {w_{\max }} - \frac{{{w_{\max }} - {w_{\min }}}}{{{{\rm{iter}}_{\max }}}}k$

(14)

式中： $k$ 为当前迭代次数， ${{\rm{iter}}_{\max }}$ 为总的迭代次数， ${w_{\min }}$ 和 ${w_{\max }}$ 分别为 $w(k)$ 的最小和最大值，在这里 ${w_{\max }}$ 不再是一成不变的值，而是根据粒子的适应值来更新，如果粒子是可行解，则按照 $w(k)$ 更新，如果粒子是不可行解，则按照式(15)更新：

${w_{\max }}(k,i) = 1 - \frac{{{F_{k,i}}(u)}}{{\mathop {\max }\limits_i ({F_{k,i}}(u))}}$

(15)

式中： ${F_{k,i}}(u)$ 为第 $k$ 次迭代第 $i$ 个粒子的适应度。实验结果表明，相比于文献[15]，这种更新方式在计算时间效率上更快。

3.3 基于RHC-APF在线航迹规划

3.1节介绍的方法中，引入的VORONOI图，构建比较复杂，而且当环境改变的时候，需要重新计算，不利于实时航迹规划。本节结合APF实时计算和计算简单的特点，提出RHC-APF算法。

1) 基于4.1提出的代价图，会导致无人机靠近障碍物飞行。按照APF的思想，让障碍物给无人机一个斥力场，因此此时的目标函数可以表示为式(16)的形式：

$J = {J^*} + {U_{\rm{rep}}}$

(16)

2) 代价图的计算会增加计算负担，而且不利于在线规划，因为当环境发生改变时，需要重新计算代价图，特别突发事件，会降低实时性。人工势场法只需增加障碍物的一个势场，当目标发生改变时，也只需改变目标函数的势场，并且势场的计算非常简单。将RHC和APF结合后能够克服APF的不足，同时增加了实时性。此时的目标函数为

$J = {U_{\rm{att}}} + {U_{\rm{rep}}}$

(17)

3.4 算法实现流程

1) 首先初始化无人机参数，设置最大速度、最大加速等限制，设置滚动时域，以及无人机采样间隔。

2) 初始化粒子群P，包括粒子的位置 ${{{x}}_i} = $ $ ({x_{i,1}},{x_{i,2}}, \cdots ,{x_{i,{H_p}}})$ 和速度 ${{{v}}_i} = ({v_{i,1}},{v_{i,2}}, \cdots ,{v_{i,{H_p}}})$ ，按照表1设置相关参数。

3) 按照式(11)和式(12)分别计算每个粒子的适应度和约束违背量。

4) 更新粒子群最优解和每个粒子的最优解。

5) 如果粒子满足约束条件，按照式(13)和式(14)更新粒子的位置和速度。否则，按照式(13)和式(15)更新粒子的位置和速度。

6) 如果粒子群不满足终止条件，转3)。

7) 取最优结果 ${{{x}}_{\rm{best}}} = ({x_{\rm{best},1}},{x_{\rm{best},2}}, \cdots ,{x_{{\rm{best}},{H_p}}})$ 的第一个控制输入 ${x_{\rm{best},1}}$ 输入模型(4)中。计算无人机下一时刻的状态。

8) 如果到达目标点，完成航迹规划。否则转2)。

4 仿真结果与分析

本文的基本算法已在MATLAB 2016中进行了实现。

多旋翼无人机其动力学可以由具有速度和加速度约束的质点动力学模型近似^[9]。

$\left[ \begin{array}{c}{{r}}(k + 1)\\{{v}}(k + 1)\end{array} \right] = {{A}}\left[ \begin{array}{c}{{r}}(k)\\{{v}}(k)\end{array} \right] + {{Ba}}(k)$

(18)

式中： ${{A}} = \left[ {\begin{array}{*{20}{c}}{{{{I}}_2}} & {\Delta t{{{I}}_2}}\\{{{{O}}_2}} & {{{{I}}_2}}\end{array}} \right]$ ； ${{B}} = \left[ {\begin{array}{*{20}{c}}{{{(\Delta t)}^2}/2{{{I}}_2}}\\{\Delta t{{{I}}_2}}\end{array}} \right]$ ； ${{r}}$ 、 ${{v}}$ 、 ${{a}}$ 分别为位置、速度、加速度向量； ${{{I}}_{2}}$ 和 ${{{O}}_{2}}$ 表示二维单位矩阵和零矩阵。

输出约束：一般的输出约束包括障碍物约束(19)，速度约束(20)，加速度约束(21)

$[{{{I}}_{2}} , {{{O}}_{2}}]x(k + j) \notin {{{O}}}$

(19)

${\left\| {[{{{O}}_{2}},{{{I}}_{2}}]{{{x}}(k + j|k)}} \right\|_2} \leqslant {v_{\max }}$

(20)

${\left\| {{{a}}(k + j|k)} \right\|_2} \leqslant {a_{\max }}$

(21)

式中： ${ {O}} \subset {R^2}$ 为不可飞区域， ${v_{\max }}$ 和 ${a_{\max }}$ 分别为最大速度和最大加速度约束。

仿真环境：处理器：PC (Intel (R)) i3-3240 CPU 3.40 GHz；操作系统：Windows 7；仿真软件：MATLAB 2016。表1为仿真的实验参数，参数设置参考文献[9，18]。本文实验部分为(–25 m，25 m)到(–15 m，12 m)的一个二维规划环境。

实验一　VORONOI代价图与传统代价图对比

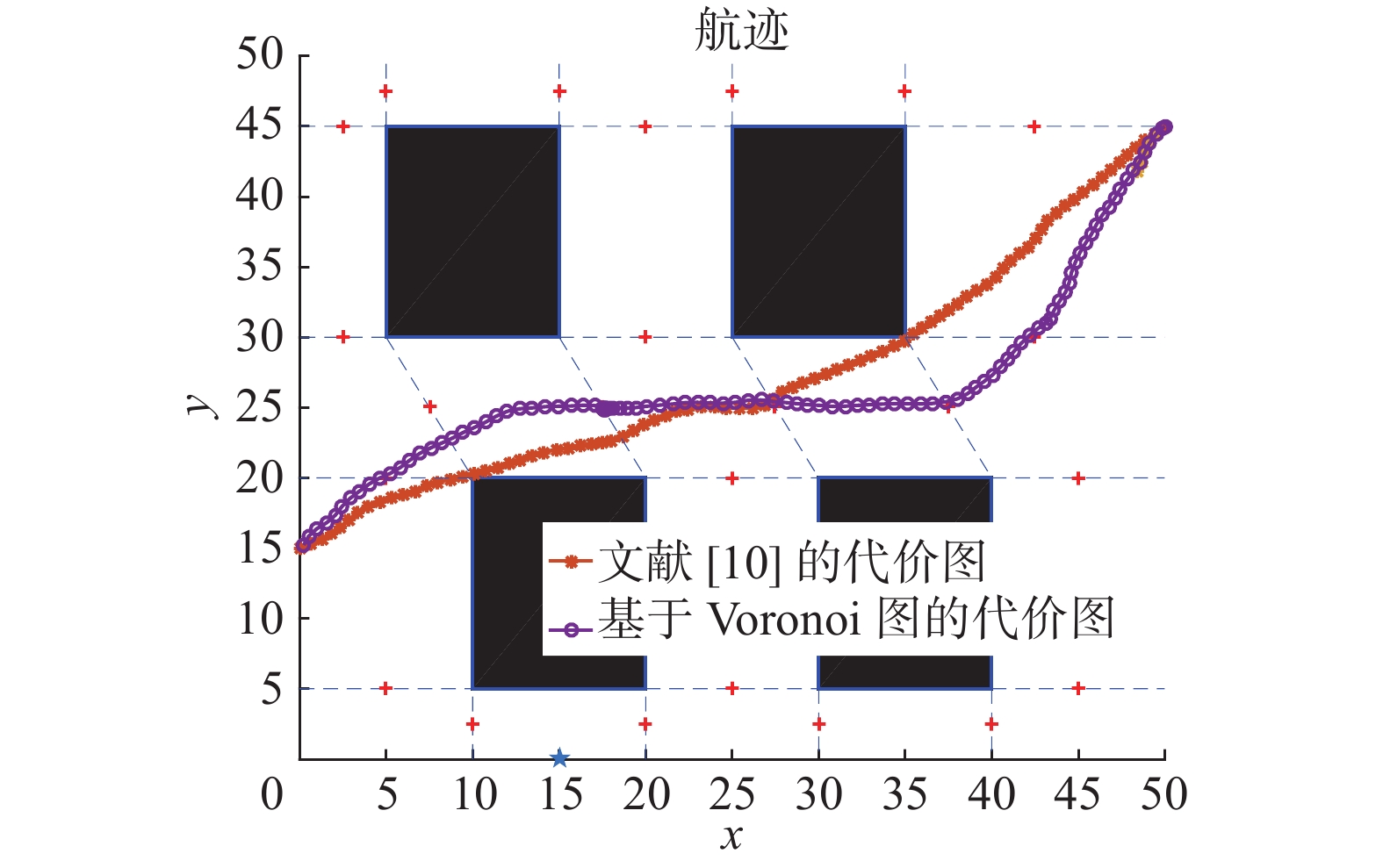
图4为根据文献[8]的代价图和本文提出的基于VORONOI图的代价图的对比。黑色方块表示障碍区域，按照VORONOI图的定义，所选取的可视点都是距离障碍区最远的点，并且地图边框也是不可飞区域，可视点如图4所示。文献[8]的可视点为多边形的顶点。

从实验结果可知，文献[8]的代价图会使得航线尽量靠近障碍物的顶点，在有扰动的情况下，很可能导致飞行器与障碍物发生碰撞。本文提出的代价图可以使得规划出的航迹远离障碍物，提高了无人机生存概率，但是规划出的航迹会比文献[8]的航迹代价高，因此可以综合考虑各种因数，选择合适的代价图。

实验二　RHC-FPSO算法与传统航迹规划算法对比

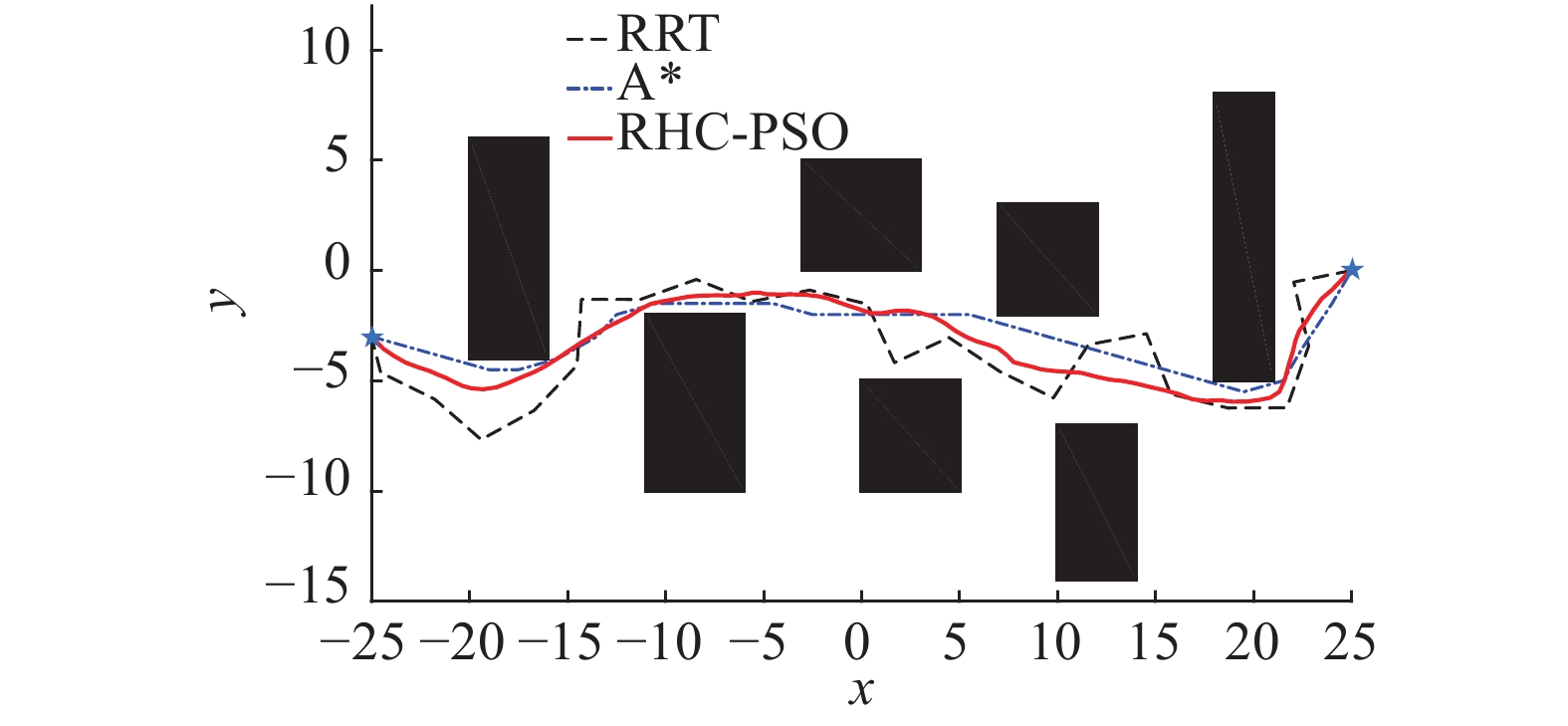
图5将传统经典的航迹规划方法SAS和RRT与本文提出的算法进行了对比。稀疏A*搜索(SAS)算法是启发式搜索算法A*的一种改进，首先将规划环境表示为网格的形式，通过预先确定的代价函数寻找最小代价的航迹。本文在扩展节点时，通过把约束条件结合到搜索算法中去，减少了搜索空间，进一步缩短了规划时间。RRT通过对规划环境中的采样点进行碰撞检测来获取空间中的障碍物的信息,可以避免对规划环境进行建模。RRT首先选择开始点作为随机树的根节点，通过随机探索方向点来扩展随机树，直到扩展到目标点，然后从目标点回溯到根节点，完成航迹规划。因此SAS算法在空间表示精度下是全局最优解，而RRT是局部最优解。

从图5和表2可以看出，在以距离为代价的航迹规划算法中，稀疏A*搜索算法是3种算法里面航迹规划最短的算法，RRT是随机算法，是算法里面航迹最长的，并且不是最优路径，RHC-FPSO算法不是距离最短的算法。从图5可知，本文算法规划出的航迹不是一些直线段的组合，主要是因为需要满足无人机的各种约束，本实验主要是指速度和加速度约束。

实验三　RHC-FPSO与RHC-PSO算法对比

考虑多旋翼无人机，因其具有悬停功能，因此最小速度可以为零，设初始位置为(25, 0)，目标为(–25, –3)。实验结果如图6所示，为将关于未来 ${H_p}$ 步内的预测航迹的计算结果分解开，RHC-FPSO每次预测未来的6个航路点，而将第1个控制输入作为实际的输入值，其他的预测航路点作为参考航路点。图7为将每次预测值的第1个控制输入作为实际输入后规划的完整航迹，可以看出在满足约束条件的前提下，规划出一条穿过障碍物区实际可飞的航迹。

图8显示了改进后的算法比文献[15]在计算时间上有很大的改进。RHC-FPSO算法单次最大计算时间为0.440 0 s，最小计算时间为0.310 0 s，平均计算时间为0.369 5 s，RHC-PSO的最大、最小和平均时间分别为0.800 0 s、0.460 0 s和0.641 9 s。

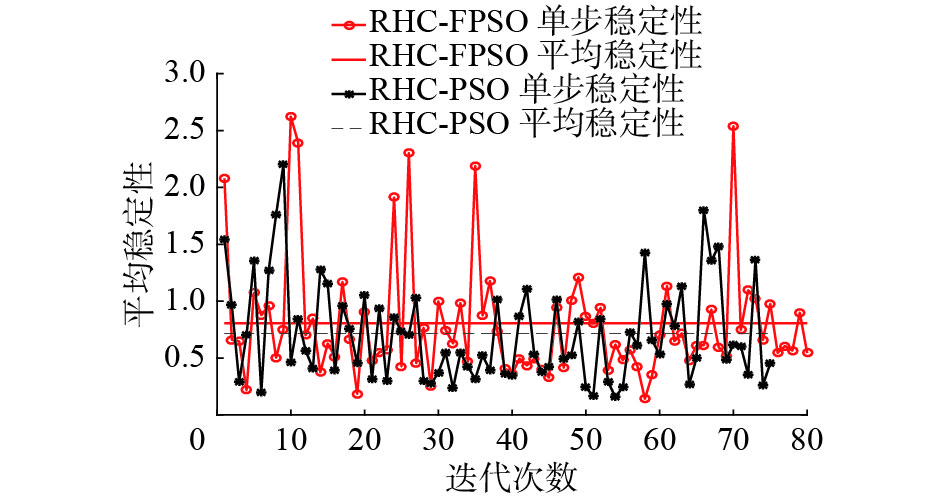
图9和图10显示了RHC-FPSO与RHC-PSO在收敛速度和稳定上几乎相当。图10中，平均稳定性是按照式(22)定义的，分别为0.806 7和0.715 0，对于基于PSO的优化方法可以使用式(22)衡量。

${\rm{Stab}} = (\sum\limits_{k = 1}^{N - 1} {\left\| {{{u}}(*|k) - {{u}}(*|k + 1)} \right\|} )/(N - 1)$

(22)

式中*代表所有的值。

实验四　滚动时域和人工势场相结合(RHC-APF)

实验四主要是结合滚动时域和人工势场的优势规划航迹。实验一中，需要计算代价图，也是一个非常大的代价，而且当环境变化的时候，需要重新计算，代价比较高。如果采用APF的思想，使用势能场作为优化目标，则不需要计算代价图，极大地减少了计算时间，非常适合在线规划。由于使用滚动时域，计算未来有限步的输入，同时使用FPSO优化，成功地解决了APF的两个主要问题。

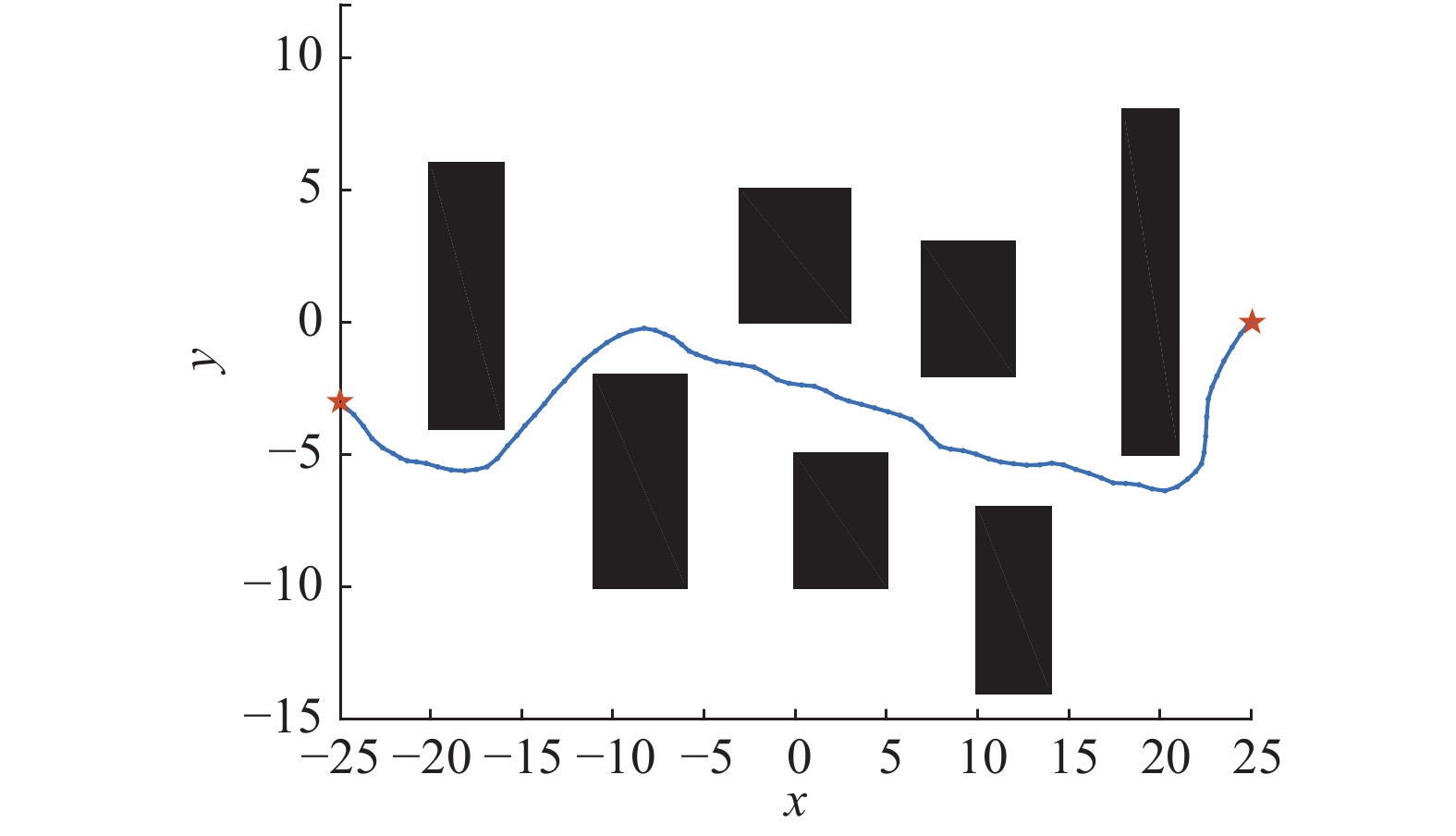
从图10和图11可以得出，由于障碍物对无人机有一个斥力场，使得无人机远离障碍区，提高了无人机的安全性，并且不再需要提前计算代价图，很适合动态的在线规划。

实验五　动态环境中的航迹规划

本文提出的航迹规划算法是适合在动态环境下进行航迹规划的。本实验参数使用表1的参数设置。如图12所示，黑色方框区域为飞行前已经知道的障碍物区域，虚线为飞行器在飞行过程中探测到的障碍物。与图7对比可知，当飞行器靠近图12中下面的浅色虚线的未知障碍物时，飞行探测器探测到新的障碍物，因此需要重新计算代价图，然后根据新的代价图以及当前状态，进行下一个时刻的航迹规划，此时还没有探测到上面的障碍物，因此，飞行器往上面飞行。当探测到上面的障碍物时，飞行器已经不能按照之前的航迹飞行了，此时需要飞出凹型区域，如图12所示。

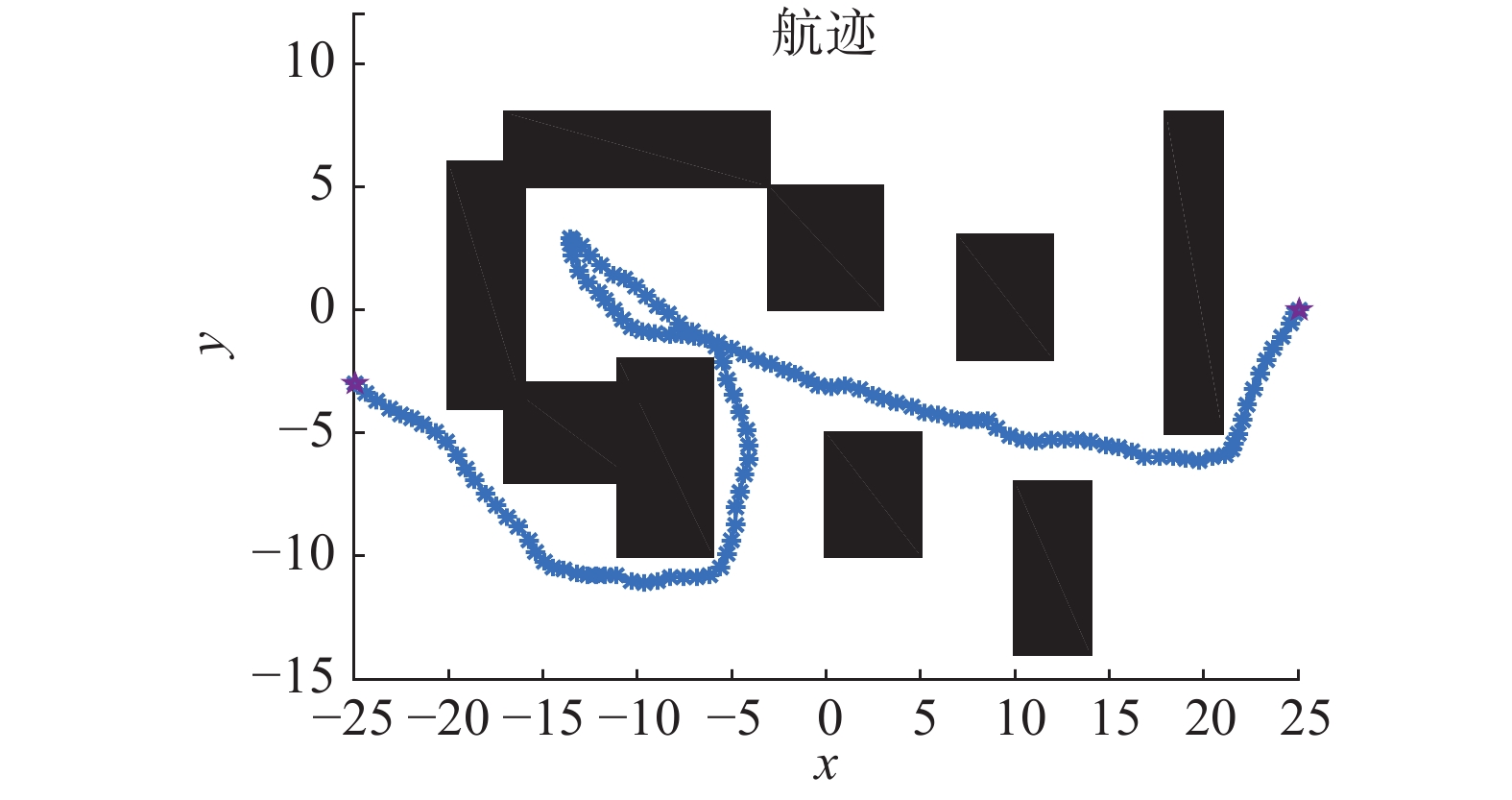
图13显示无人机完整的飞行轨迹，在图11中由于检测到新的障碍物，飞行器需要快速转变方向。在转变方向的时候，无人机的速度接近零，因此，整个的航迹如图13所示。

从以上的5个实验和实验的分析可知，RHC-FPSO在满足障碍物约束和无人机自身约束的条件下，顺利地穿过障碍物区域到达目标区域，并且在时间上有很大提高，是满足在线计算要求的，实验五显示对新检测到的障碍物，本文算法可以做出快速反应，规避障碍物。

5 结束语

首先，将无人机动力学模型进行线性近似，表示为状态空间模型。然后，根据模型和滚动时域优化的思想，将航迹规划表示为一个带约束的优化问题。最后，使用粒子群优化算法进行优化，成功地规划出满足无人机约束和障碍物规避的实际可飞的航迹。将航迹规划分为两个阶段，第1阶段为预先代价估计阶段，第2阶段为在线航迹规划。在代价估计阶段，引入VORONOI图，使得节点离障碍物的距离尽可能远，进一步提高了无人机的生存概率。在第2阶段，通过理论和仿真表明，采用FPSO方法在RHC框架下进行在线航迹规划可以将无人机动力学约束条件很容易地引入到规划问题中来，为带有动态约束的无人机长航程航迹规划提供一种新型的算法，为无人机规划出一条满足约束条件的实际可飞的航迹。滚动时域规划减少了一定的计算量，是一种可行的优化方法。将滚动时域和人工势场法相结合，可以不需要计算代价图，减少了计算量，并且在环境发生改变时，不再需要计算代价图，只需更新势场。因此RHC-APF是非常适合动态在线航迹规划，易于扩展。未来的工作应该把该方法扩展到多机动态三维航迹规划中，以及进一步提高求解算法的速度。