由于如手指静脉、指纹、虹膜等生物特征具有不易被伪造、唯一性且不易丢失等特性[1-2],基于生物特征的识别技术目前已经是一项可靠的、可以替代传统密码识别的普及的技术[3-4]。
然而正因为生物特征的唯一性和不变性,且一个人的生物特征有限,一旦丢失就是永久丢失导致了安全和隐私方面的问题[5],生物特征模板被窃取将会带来比传统身份识别丢失密码更为严重的后果,由此提出了生物特征加密系统的概念[6-7],该系统将被加密技术或其他特定的技术加密过的生物特征模板存储到数据库中[8],这种不可逆的加密过程可以使非法用户无法直接从加密模板中得到原本的生物特征[9-10]。
手指静脉特征具有其他手部特征(如指纹[11]、手形[12]、掌纹[13]等)不具有的独特的优越性:1)非活体无法采集到静脉,所以更安全;2)手指内部的静脉不受到皮肤表面状况的影响,且十根手指均可以用于特征提取,灵活性高;3)静脉特征并不会如人脸一样受年龄影响,而且静脉纹路比指纹清晰,对相机的分辨率要求低于指纹特征采集;4)非接触采集可防止细菌传播且采集设备体积小,采集成本较低且易于被大众接受。
由于静脉识别在生物特征识别方面是后起之秀,尽管其具有良好性能,但是对其研究尚没有像指纹识别那样深入,目前对手指静脉加密的研究则是刚刚起步,公开发表的论文只有我们课题组提出的基于纠错码和细节点提取的指静脉加密算法[14],该算法依赖于静脉图像的细节点,对图像质量要求较高,而在寒冷天气下由于手指冰凉,导致采集到的静脉图像对比度低,静脉不清晰就难以提取有效特征点,致使这种加密方案失效。而局部二进制编码(LBP)直接针对灰度图像进行编码提取图像的纹理特征的方法对图像的质量要求不高,而模糊承诺(fuzzy commitment)加密方案直接使用二进制编码,便于与 LBP相结合,能够给出有效、简单快捷的指静脉加密方法。
基于上述考虑本文提出了对指静脉图像采用多尺度块中心对称局部二进制编码(MB-CSLBP)和模糊承诺相结合的手指静脉加密算法。
模糊承诺方案作为一种传统的加密方法,虽然加解密过程与其他方法相比而言更为简便,但是其效果却很好,因此我们提出将模糊承诺方案与手指静脉的局部二进制模式相结合,研究相关的手指静脉加密算法。局部二进制模式(local binary patem)是由Ojala等[15]提出的一种能有效地描述图像的纹理特征的纹理描述算子。纹理特征是对光照、姿态、背景或者成像等条件因素变化不敏感的图像固有属性,因此很适用于手指静脉特征提取。在改进的多尺度块中心对称的局部二进模式( MB- CSLBP)算法的基础上,利用提取出的二进制编码作为指静脉特征数据,在模糊承诺方案的框架上结合 BCH编码和 SHA-1安全散列算法对密钥进行加密。
1 局部二进制模式(LBP)LBP基本思想:在一个3×3的窗口中依次比较中心点像素灰度值与其相邻的8个点的灰度值,若该邻域位置点的灰度值小则将该像素点置为0,否则置为1,从左上角像素点的位置起依次顺时针(或逆时针)赋权值
| $\operatorname{LBP} ({x_c},{y_c}) = \sum\limits_{i = 0}^7 {s({g_i} - {g_c}){2^i}} $ | (1) |
| $s(x) = \left\{ {\begin{array}{*{20}{c}}{1,\quad x \geqslant 0}\\{0,\quad \text{其他}}\end{array}} \right.$ | (2) |
式中:
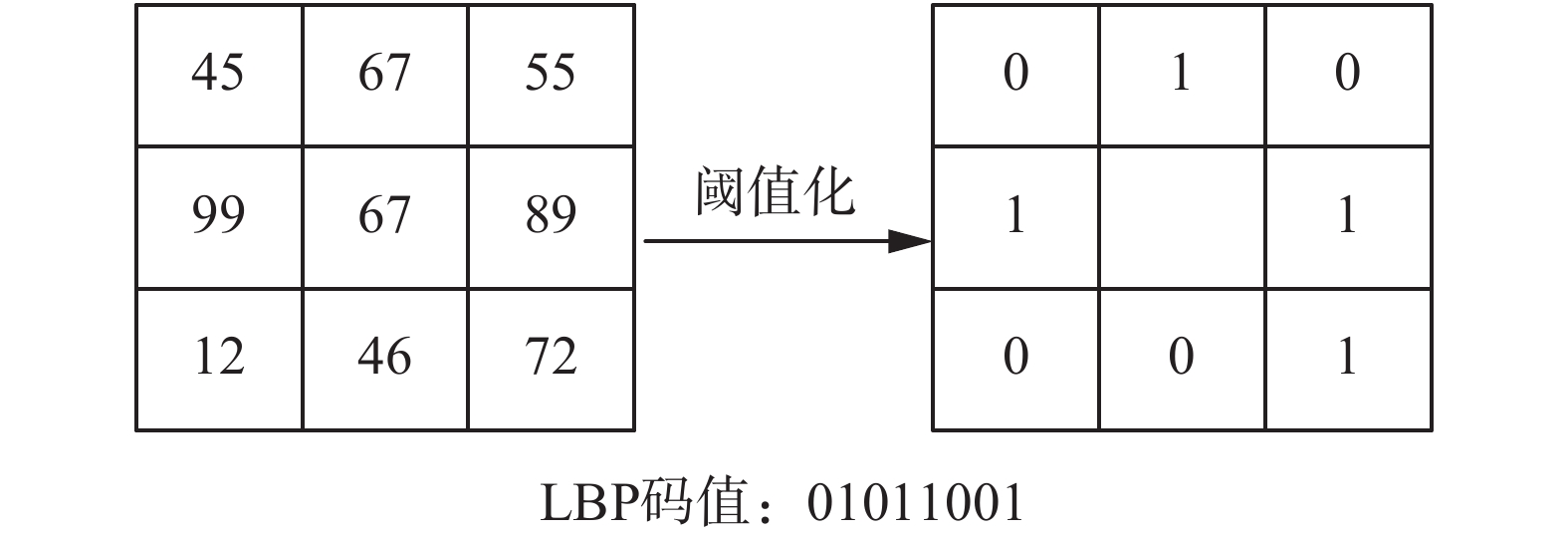
如图1所示,一个3×3的窗口区域中中心像素点的灰度值为67,把该值与邻近的8个像素点比较大小,顺时针得到一个8位的二进制串01011001。
|
Download:
|
| 图 1 LBP算子编码过程 Fig. 1 The encoding process of LBP | |
采用LBP算子遍历一幅大小为
LBP算子具有以下几个显著优点:1)该算子原理简单、运算简洁,且计算复杂度远低于离散小波变换、傅里叶变换等;2)LBP二进制编码是由中心像素点和邻近像素点灰度值比较得到的,这种对图像纹理特征的描述方法对图中的亮暗点和边缘点等细节特征的描述能力较强,符合静脉特征提取的需求;3)基于传统子空间的方法,如ICA(独立成分分析)、LDA(线性判别分析)、PCA(主成分分析)等均需要进行数据训练,而LBP提取到的二进制码或直方图向量不需要,因此便于推广。
虽然LBP算子运算简洁、原理简单、纹理特征描述能力强,但该算子在具体应用中仍存在很多问题,如以下几个方面:
1) LBP二进制特征编码模式过多:在一个大小为3×3的窗口中求得的LBP编码特征是一个8位的二进制数,所以对应的纹理模式有28=256种。虽然越多的纹理模式中提取的纹理细节也越多,但过多的特征模式会降低LBP纹理描述的分辨能力,且并不是所有的纹理细节都对图像信息的描述贡献很大,其中有许多可以被舍弃的纹理特征。
2) LBP算子对剧烈噪声和光照的鲁棒性差:由于LBP码值是由两个单像素点的比较所得,因此剧烈光照和噪声会影响相邻像素的大小比较结果,从而会产生不同的LBP模式,如图2所示。
|
Download:
|
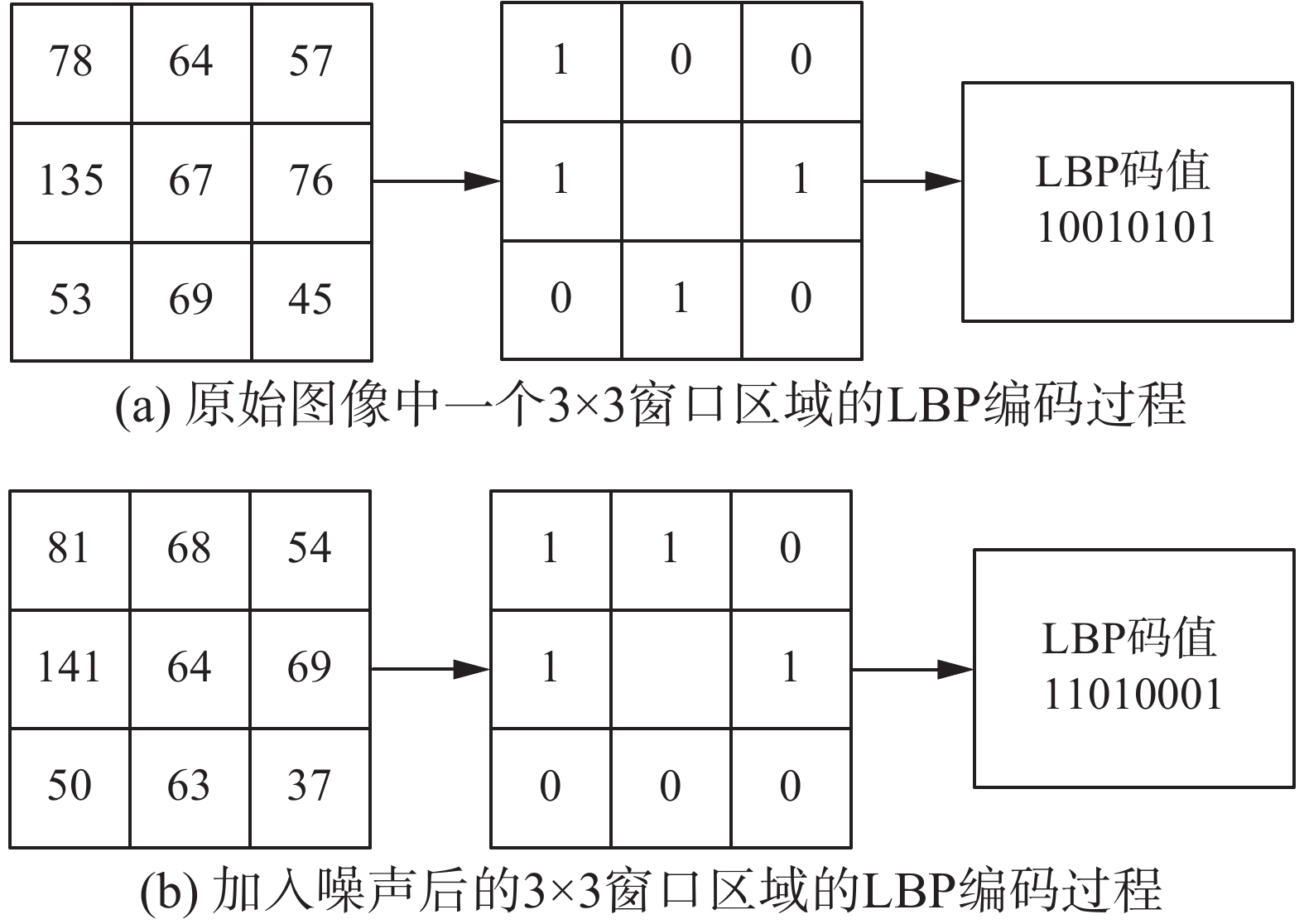
| 图 2 噪声对LBP算子的影响 Fig. 2 The impact of noise on LBP operator | |
图2(a)和图2(b)分别表示原始图像和加入噪声后的图像,对大小为3×3的区域采用LBP算子提取特征编码。图2(a)中阈值为中心像素值67,得到LBP编码值10010101,对应特征值149。图2(b)加入噪声后阈值中心像素值64,得到LBP编码值11010001,对应特征值209。图2(a)和图2(b)本是同一纹理特征,但由于LBP编码值不同故而认为二者是不同纹理,由此可见LBP算子对噪声和光照很敏感。
3) LBP算子对图像拓扑变化(如旋转变化等)的鲁棒性差如图3所示。
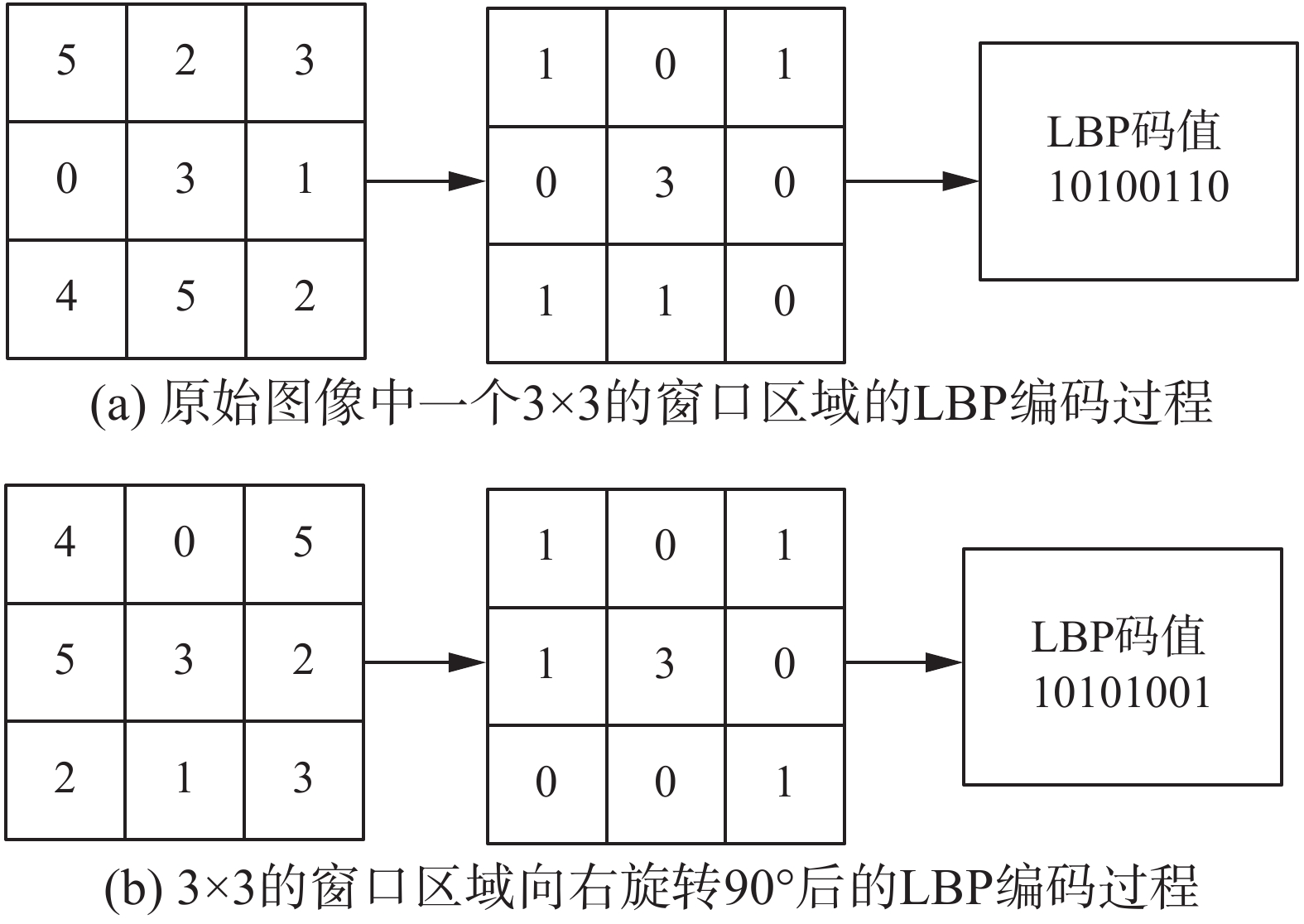
采用窗口大小为3×3的LBP算子对原始图像(图3(a))和原图旋转90°后的图像(图3(b))进行特征提取的过程。图3(a)与图3(b)中阈值均为3,但图3(a)的LBP编码值为10100110,对应特征值166。图3(b)的LBP编码值为10101001,对应特征值169。虽然是同一个纹理却被认为是不同的,由此可见LBP算子对图像拓扑变化的鲁棒性较差。
|
Download:
|
| 图 3 拓扑变化对LBP算子的影响 Fig. 3 The impact of topological changes on LBP operator | |
4)当采用LBP直方图作为特征向量时,模式种类过多,过高的直方图维数会增大计算量,且总特征点数是一定的,使得每种模式特征点数少,从而失去了统计意义降低了识别率。
5)一般的LBP算子对局部区域像素点做的是稀疏采样[15],虽采用了双线性差值方法来计算没有落到像素点上的邻域点的灰度值,但采样过程仍不稳定[19]。
6)专注于图像邻域间的纹理特征的LBP算子没有考虑到图像局部纹理间的联系,并不能有效地处理大型复杂的纹理特征。
因此应当针对以上几点做出某方面性能上的改进,也需要结合实际应用使LBP算子能够得到具有鲜明特征的纹理信息,解决实际具体的问题。
1.2 改进的LBP算子 1.2.1 中心对称局部二进制模式中心对称局部二进制模式(center-symmetric local binary pattern,CSLBP)的基本思想是基于LBP模式,对关于中心点对称的一对像素灰度值做对比,得到的二进制串长度是基本LBP算子的一半[20],减小了需要的存储空间,CSLBP算子计算方法如式(3):
| $\begin{array}{l}{{\rm{CSLBP}}_{R,P,T}} = \displaystyle\sum\limits_{i = 0}^{\frac{P}{2} - 1} {s({g_i} - {g_{i + \frac{P}{2}}}){2^i}} \\s(x) = \left\{ {\begin{array}{*{20}{c}}{1,\quad x > T}\\{0,\quad \text{其他}}\end{array}} \right.\end{array}$ | (3) |
式中:
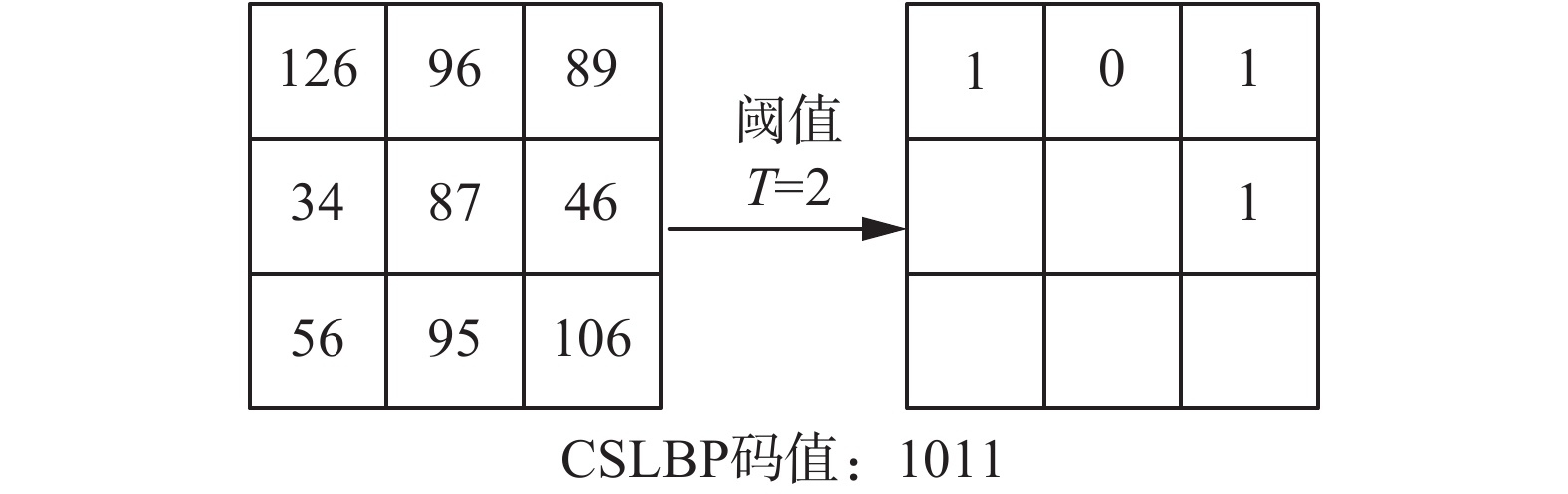
如图4中将阈值T置为2,依次比较3×3的窗口区域内关于中心对称的4对像素点的灰度差值,小于阈值T时相应位置置0,否则置1,得到CSLBP码值1011。
|
Download:
|
| 图 4 CSLBP算子的编码过程 Fig. 4 The encoding process of CSLBP | |
CSLBP算子提取的特征维数为
LBP算子和CSLBP算子计算简单且可以描述图像的微观结构特征,但由于二者均是对图像单个像素点做对比,对噪声和拓扑变化的鲁棒性差,无法描述图像宏观结构特征,影响了识别率。多尺度块中心对称局部二进模式(multi-scale block center- symmetric local binary pattern)[21]用像素块区域的平均灰度值代替CSLBP算子中的单个像素点的灰度值进行编码的求取,MB-CSLBP算子比LBP算子占用存储空间更小、受到噪声的影响更小,同时该算子可同时提取图像的微观结构和宏观结构的特征,可以减小图像宏观特征信息的损失,完整表达图像的信息可增强分类效果,弥补了1.1节中的LBP算子的不足。
MB-CSLBP算子的计算如式(4):
| $\begin{array}{c} {\rm{MB\text{-}CSLBP}} = \displaystyle\sum\limits_{n = 0}^3 {s({B_n} - {B_{n + 4}}){2^n}} \\ B = \displaystyle \sum\limits_{k = 0}^{{L^2} - 1} {{g_k}} \\ s(x) = \left\{ {\begin{array}{*{20}{c}} {1,\quad x \geqslant T} \\ {0,\quad \text{其他}} \end{array}} \right. \\\end{array} $ | (4) |
式中:L表示像素块正方形区域的边长,
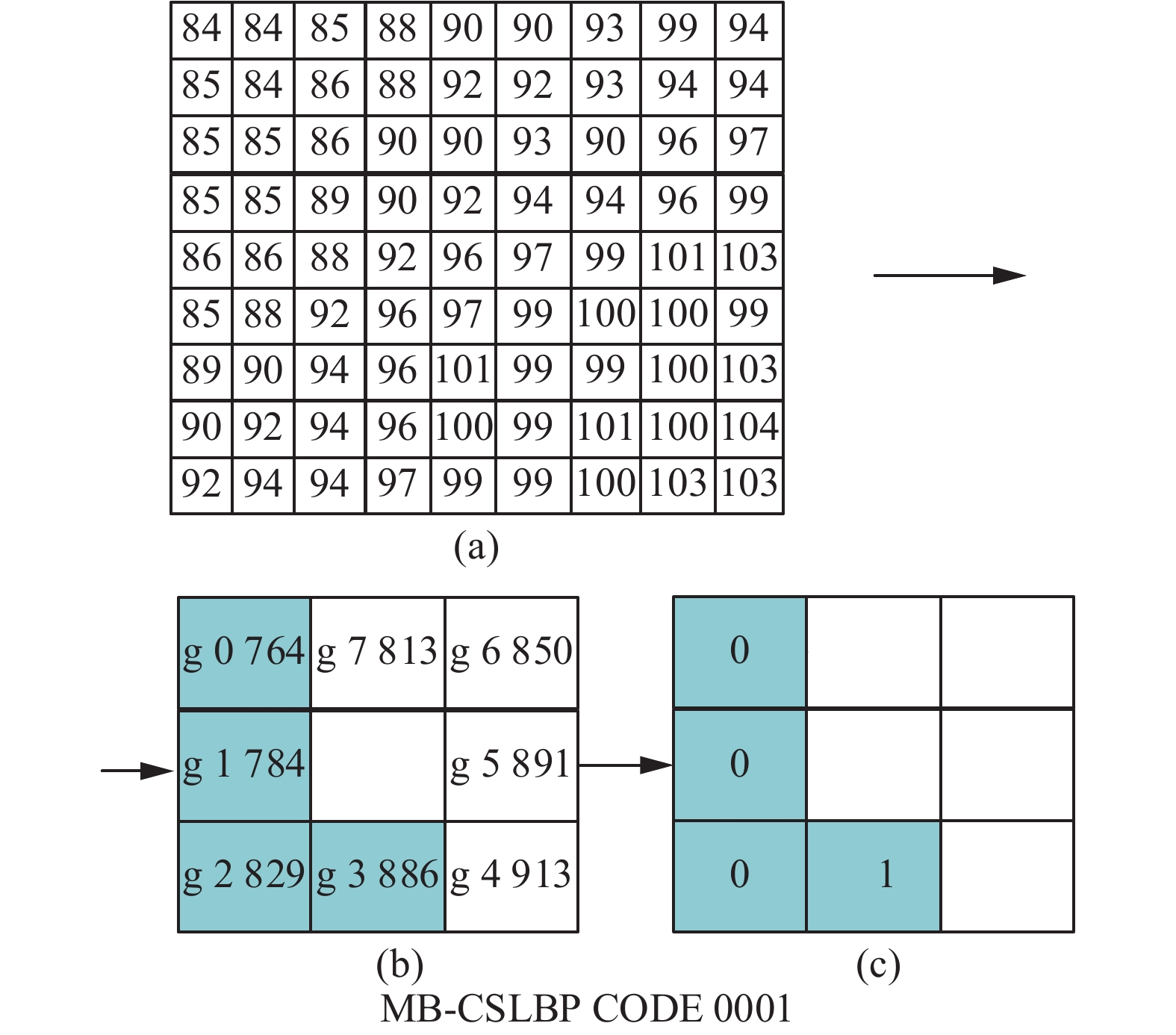
如图5所示,当阈值T=0时,依次比较关于中心正方形区域对称的两个正方形区域的灰度值之和得到二进制编码0001,特征值为1。
|
Download:
|
| 图 5 MB-CSLBP算子的编码过程 Fig. 5 The encoding process of MB-CSLBP | |
模糊承诺方案是利用纠错码的容错能力,在基于汉明距离的度量空间内将生物特征信息和纠错码技术相结合的一种密钥绑定方案。
因为MB-CSLBP编码是长度固定的而本文使用的BCH编码是一种变长数字编码,便于在整个加密解密的过程中进行处理,因此,可以发现基于MB-CSLBP的二进制手指静脉特征编码非常适合于模糊承诺方案的应用。
2.1 BCH码和SHA-1安全散列算法简介在模糊承诺方案中,需要用到密码学中有关的知识和方法,因此首先介绍在本节中需要用到的BCH码以及SHA-1安全散列算法的相关内容。
2.1.1 BCH码自1959年发展起来的BCH码(Bose、Ray-Chaudhuri、Hocquenghem)是一种能纠正多位错误的循环码[22]。这种用来校正多个随机错误的循环、多级、变长数字编码在编码理论尤其是纠错码方面中被广泛地研究和应用。
BCH码把信源待发的信息序列划分为多个长度为固定的
BCH码的编码与解码是建立在有限域的域论和多项式基础上的。在编码过程中还可以构建一个检测多项式,此多项式用于在接受端对接受到的码字进行检测,看是否有错误。以基于有限域
所以
BCH码的解码过程:
1)计算接收到的向量R的
2)计算错误定位多项式;
3)解多项式,得到错误位置;
4)计算非 BCH 码的错误位置的误差值。
2.1.2 SHA-1安全散列算法1993年美国国家标准和技术协会提出SHA算法,这种数据加密算法[23]被定义为安全散列标准。多年来SHA算法经过了一系列的完善并被广泛应用到各个方面,成为了世界公认的最安全的散列算法之一。SHA算法的主要思想:将明文以某种不可逆的变换化为长度更短的一段密文,简言之,就是把一段输入码(预映射或信息)转换位数固定且短的输出序列(散列值或信息摘要)的过程。
1994年,对SHA算法的一个未被公开的缺陷进行了纠正得到了SHA-1算法。该算法要求接收的输入文档大小小于264 bit,并产生160 bit的报文摘要[24]。在SHA-1安全散列算法中,不存在一个文本可使得其散列值与已知文本的散列值相等,举例来说就是如果A对应散列值
基于MB-CSLBP的手指静脉特征加密,是在经过MB-CSLBP算子编码之后,把得到的二进制编码作为手指静脉图像的特征与经过BCH编码的密钥结合,对密钥进行加密。
加密阶段的具体步骤如图6。

|
Download:
|
| 图 6 基于MB-CSLBP手指静脉特征加密流程 Fig. 6 The encryption process of finger vein feature based on MB-CSLBP | |
1)将注册阶段的手指静脉图像进行尺寸归一化为96×64。利用式(4)中的MB-CSLBP算子对图像进行编码,其中取像素块正方形区域的边长
2)假设需要加密的密钥为K,长度为k,首先通过SHA-1安全散列算法将K进行哈希变换,结果记为
3)把编码完成后的密钥
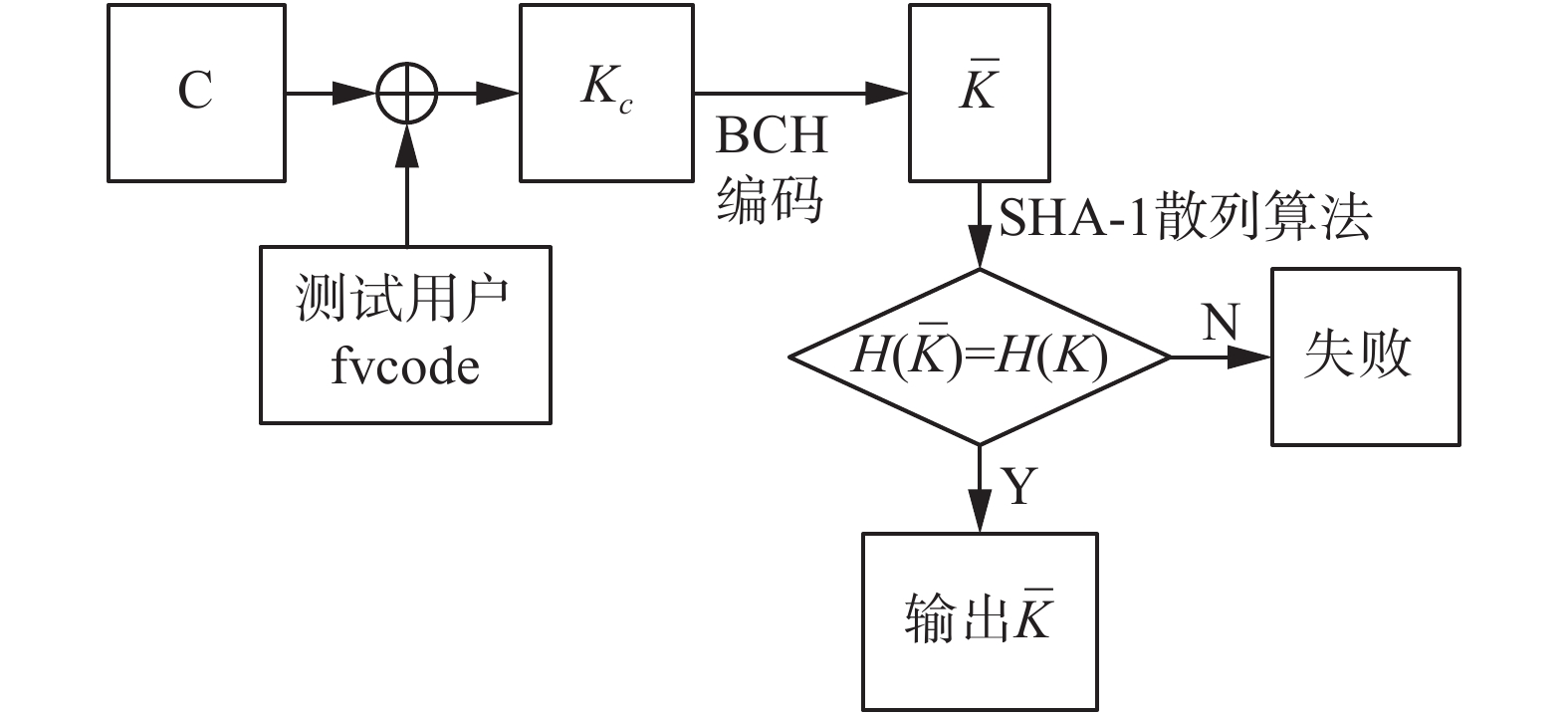
解密阶段步骤如图7。
|
Download:
|
| 图 7 基于MB-CSLBP手指静脉特征解密流程 Fig. 7 The decryption process of finger vein feature based on MB-CSLBP | |
1)与加密阶段一样将用于解密的手指静脉图像进行尺寸归一化处理并用MB-CSLBP算子从图像中提取出用于解密的手指静脉特征编码
2)将
哈尔滨工程大学指静脉库包含105人每人5幅,共525幅大小为320像素×240像素的食指静脉图像,其中每人1幅共105幅作为指静脉图像训练库,用于加密,每人另4幅共420幅图像作为验证库,用于解密。使用BCH纠错编码来更正类内变化,加密系统的性能取决于密钥长度和纠错位数。为了比较不同的密钥长度对系统性能的影响,我们产生长度不同的密钥,用BCH编码对这些密钥分别进行处理,计算不同情况下的拒真率和误识率,计算结果记录在表1中。
| 表 1 不同密钥位数下的拒真率(FRR)和误识率(FAR) Tab.1 FRR and FAR of different keys |
由表1可以得到,密钥的长度越长,系统的误识率FAR(系统错误识别非真实用户的概率)越低,拒真率FRR(系统不识别真实用户的概率)越高。当密钥长度为400 b时,FAR达到了0.47%,充分说明该加密系统的加密效果非常好。
当密钥长度为400 b,采用BCH(511,400,24)来进行纠错编码,我们结合实验数据来分析在不同的可能存在的攻击下,系统的安全性能。
1)若非法用户尝试使用多张手指静脉图像来尝试攻击系统,由于错误接受率为0.47%,那么非法用户需要至少尝试使用213(1/0.47%)张不同的手指静脉图像对系统进行攻击,在短时间内一般不可能找到这么多张不同的手指静脉图像。
2)若非法用户尝试直接生成手指静脉特征编码从而攻击系统的话,对于一个511 b,容错位数为24 b的编码,需要生成487 b的正确序列才能成功,此概率为2–487,这是不太可能的。
3)若非法用户想直接生成密钥的话,生成一个正确的长度为400 b的密钥的概率为2–400,这也是不太可能的。
4)若非法用户想要通过生成SHA-1散列编码反求出正确的密钥来攻击系统,因为散列编码的长度为128 b,所以生成正确密钥的概率为2–128,这几乎是不可能做到的。
通过结合实验数据,我们对不同的可能存在的非法用户的攻击尝试进行了可行性的分析,不管是哪一种攻击方式,想要成功攻击系统在一定程度上来说都是不可能的,也充分说明了基于MB-CSLBP编码的手指静脉特征加密系统有很好的安全性。
4 结束语本文提出了基于MB-CSLBP编码的手指静脉加密方案。该方法弥补了LBP算子的不足,结合了BCH纠错码和SHA-1散列算法对指静脉图像进行了加密和解密,得到了很好的结果。首先,介绍了LBP算子以及MB-CSLBP算子。然后,把得到的手指静脉的MB-CSLBP二进制编码作为手指静脉图像的特征,与经过BCH编码之后的密钥结合,对密钥进行加密。最后对其进行解密,得到了密钥长度不同时,加密系统的拒真率和误识率。实验结果表明,密钥的长度越长,系统的误识率越低,满足了系统安全性要求。结合实验数据和理论数据对系统进行分析,结果表明本文提出的基于MB-CSLBP编码的手指静脉加密方案具有很高的鲁棒性和安全性。本文仅使用了BCH码进行编码,而实际还有几种纠错码可以应用于加密,使用多种纠错码进行对比实验是接下来要做的主要工作。
| [1] |
DAUGMAN J G. High confidence visual recognition of persons by a test of statistical independence[J]. IEEE transactions on pattern analysis and machine intelligence, 1993, 15(11): 1148-1161. DOI:10.1109/34.244676 ( 0) 0)
|
| [2] |
AHADULLAH M, SAID M R M, BANERJEE S. History, development and trend of fractal based biometric cryptography[M]//ERÇETIN Ş Ş, BANERJEE S. Chaos, Complexity and Leadership 2013. Cham: Springer, 2015: 27–33.
( 0) 0)
|
| [3] |
NAVEEN K H N, JAGADEESHA S, AMITH K J. Human facial expression recognition from static images using shape and appearance feature[C]//Proceedings of the 2nd International Conference on Applied and Theoretical Computing and Communication Technology. Bangalore, India, 2016: 598–603.
( 0) 0)
|
| [4] |
HUANG Di, ZHANG Renke, YIN Yuan, et al. Local feature approach to dorsal hand vein recognition by centroid-based circular key-point grid and fine-grained matching[J]. Image and vision computing, 2017, 58: 266-277. DOI:10.1016/j.imavis.2016.07.001 ( 0) 0)
|
| [5] |
RATHA N K, CONNELL J H, BOLLE R M. An analysis of minutiae matching strength[C]//Proceedings of the 3rd International Conference on Audio- and Video-Based Biometric Person Authentication. Halmstad, Sweden, 2001: 223–228.
( 0) 0)
|
| [6] |
JAIN A K, NANDAKUMAR K, NAGAR A. Biometric template security[J]. EURASIP journal on advances in signal processing, 2008, 2008: 279416. ( 0) 0)
|
| [7] |
张宁, 臧亚丽, 田捷. 生物特征与密码技术的融合——一种新的安全身份认证方案[J]. 密码学报, 2015, 2(2): 159-176. ZHANG Ning, ZANG Yali, TIAN Jie. The integration of biometrics and cryptography—a new solution for secure identity authentication[J]. Journal of cryptologic reseatch, 2015, 2(2): 159-176. (  0) 0)
|
| [8] |
LI Peng, YANG Xin, CAO Kai, et al. An alignment-free fingerprint cryptosystem based on fuzzy vault scheme[J]. Journal of network and computer applications, 2010, 33(3): 207-220. DOI:10.1016/j.jnca.2009.12.003 ( 0) 0)
|
| [9] |
CHUNG Y, MOON D, LEE S, et al. Automatic alignment of fingerprint features for fuzzy fingerprint vault[C]//Proceedings of the 5st SKLOIS Conference Information Security and Cryptology. Beijing, China, 2005: 358–369.
( 0) 0)
|
| [10] |
ULUDAG U, PANKANTI S, PRABHAKAR S, et al. Biometric cryptosystems: issues and challenges[J]. Proceedings of the IEEE, 2004, 92(6): 948-960. DOI:10.1109/JPROC.2004.827372 ( 0) 0)
|
| [11] |
PERALTA D, TRIGUERO I, SANCHEZ-REILLO R, et al. Fast fingerprint identification for large databases[J]. Pattern recognition, 2014, 47(2): 588-602. DOI:10.1016/j.patcog.2013.08.002 ( 0) 0)
|
| [12] |
CHAUDHARY D R, SHARMA A. Hand geometry based recognition system[C]//Proceedings of 2012 Nirma University International Conference on Engineering. Ahmedabad, India, 2012: 1–5.
( 0) 0)
|
| [13] |
JING Xiaoyuan, LI Sheng, ZHANG D, et al. Optimal subset-division based discrimination and its kernelization for face and palmprint recognition[J]. Pattern recognition, 2012, 45(10): 3590-3602. DOI:10.1016/j.patcog.2012.04.001 ( 0) 0)
|
| [14] |
王科俊, 曹逸, 姜博威, 等. 基于纠错码的指静脉加密算法[J]. 智能系统学报, 2017, 12(1): 55-59. WANG Kejun, CAO Yi, JIANG Bowei, et al. Finger vain encryption algorithm based on an error-correcting code[J]. CAAI transactions on intelligent systems, 2017, 12(1): 55-59. (  0) 0)
|
| [15] |
YOU Lin, WANG Jiawan, YAN Bin. A secure finger vein recognition algorithm based on MB-GLBP and Logistic mapping[J]. Journal of information hiding and multimedia signal processing, 2016, 7(6): 1231-1242. ( 0) 0)
|
| [16] |
ZHANG D, ZUO Wangmeng, YUE Feng. A comparative study of palmprint recognition algorithms[J]. ACM computing surveys (CSUR), 2012, 44(1): 2. ( 0) 0)
|
| [17] |
OJALA T, PIETIKÄINEN M, HARWOOD D. A comparative study of texture measures with classification based on featured distributions[J]. Pattern recognition, 1996, 29(1): 51-59. DOI:10.1016/0031-3203(95)00067-4 ( 0) 0)
|
| [18] |
OJALA T, PIETIKAINEN M, MAENPAA T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns[J]. IEEE transactions on pattern analysis and machine intelligence, 2002, 24(7): 971-987. DOI:10.1109/TPAMI.2002.1017623 ( 0) 0)
|
| [19] |
AHONEN T, PIETIKÄINEN M. A framework for analyzing texture descriptors[C]//Proceedings of the 3rd International Conference on Computer Vision Theory and Applications. Madeira, Portugal, 2008: 1.
( 0) 0)
|
| [20] |
HEIKKILA M, PIETIKAINEN M. A texture-based method for modeling the background and detecting moving objects[J]. IEEE transactions on pattern analysis and machine intelligence, 2006, 28(4): 657-662. DOI:10.1109/TPAMI.2006.68 ( 0) 0)
|
| [21] |
HEIKKILÄ M, PIETIKÄINEN M, SCHMID C. Description of interest regions with local binary patterns[J]. Pattern recognition, 2009, 42(3): 425-436. DOI:10.1016/j.patcog.2008.08.014 ( 0) 0)
|
| [22] |
MALOFEY O P, MALOFEY A O, SHANGINA A E. Enhancing the functionality of the procedures of encoding and decoding BCH codes[C]//Proceedings of 2017 International Conference " Quality Management, Transport and Information Security, Information Technologies”. Petersburg, Russia, 2017: 243–246.
( 0) 0)
|
| [23] |
SLIMANE N B, BOUALLEGUE K, MACHHOUT M. A novel image encryption scheme using chaos, hyper-chaos systems and the secure Hash algorithm SHA-1[C]//Proceedings of 2017 International Conference on Control, Automation and Diagnosis. Hammamet, Tunisia, 2017: 141–145.
( 0) 0)
|
| [24] |
SLIMANE N B, BOUALLEGUE K, MACHHOUT M. Nested chaotic image encryption scheme using two-diffusion process and the Secure Hash Algorithm SHA-1[C]//Proceedings of the 4th International Conference on Control Engineering and Information Technology. Hammamet, Tunisia, 2016: 1–5.
( 0) 0)
|
| [25] |
MAKKAD R K, SAHU A K. Novel design of fast and compact SHA-1 algorithm for security applications[C]//Proceedings of IEEE International Conference on Recent Trends in Electronics, Information and Communication Technology. Bangalore, India, 2016: 921–925.
( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


