粒子群优化算法是Kennedy等^[1]在1995年提出的一种群体搜索的随机优化算法。由于PSO算法的参数少而且易操作，所以在实际问题中得到了广泛的应用。对PSO算法的研究主要有以下几个方面：1）对PSO算法自身参数的改进，这方面的工作主要关于惯性权重的自适应改进^[2-9]和对学习因子的改进^[9-11]；2）将其他进化算法与PSO相结合，比如，遗传算法与PSO算法结合^[12-13]，差分进化算法与PSO算法结合^[14]，模拟退火算法与PSO算法结合^[15]；3）在PSO算法引入一些改进PSO算法性能的其他算子，比如，把高斯扰动策略加入粒子群优化算法中^[16]，把均匀设计方法引入到粒子群优化算法中^[17]，把变异策略^[18]、精英策略^[19]、局部搜索策略^[20]及邻域搜索策略^[21]引入到粒子群优化算法中；4）PSO算法的理论分析，比如，基于线性系统理论研究PSO收敛性^[22-25]，基于随机过程研究PSO收敛性^[26]，但是粒子群算法不依概率收敛^[26]。本文给出了一种依概率1收敛的PSO算法，该算法在标准粒子群优化算法实施位置更新后按一定概率对较好的粒子实施具有开发能力的变异操作，对较差的粒子实施具有探索能力的变异操作，从而平衡了算法的全局搜索能力和局部搜索能力，提高了算法的效率，另外，证明了该算法依概率1收敛到ε-最优解。实验结果表明，提出的算法能够提高全局搜索能力，算法的收敛速度明显加快。

1 标准PSO算法

标准粒子群算法中，粒子群由N_p个粒子组成，在时刻k，第i个粒子在d维空间中速度和位置的更新公式为

$ v_{id}^{k + 1} = \omega v_{id}^k + {c_1}{r_1}\left( {p_{id}^k - x_{id}^k} \right) + {c_2}{r_2}\left( {p_{gd}^k - x_{id}^k} \right) $

(1)

$ x_{id}^{k + 1} = x_{id}^k + v_{id}^{k + 1} $

(2)

式中：i=1, 2, …, N_p，d=1, 2, …, D，D为决策变量的维数，ω为惯性权重，$\mathit{\boldsymbol{x}}^k_i=(x^k_{i1},x^k_{i2},…,x^k_{iD})$表示粒子i的当前的位置；$\mathit{\boldsymbol{v}}^k_i=(v^k_{i1},v^k_{i2},…,v^k_{iD})$是粒子i的当前的速度；$\mathit{\boldsymbol{P}}^k_i=(p^k_{i1},p^k_{i2},…,p^k_{iD})$是粒子i当前最优位置，$\mathit{\boldsymbol{P}}^k_g=(p^k_{g1},p^k_{g2},…,p^k_{gD})$是全局最优位置；c₁、c₂是加速度因子，r₁、r₂是0~1之间的随机数。第k次迭代的惯性权重表示为

$ {\omega _k} = \left( {{\omega _{{\rm{start}}}} - {\omega _{{\rm{end}}}}} \right)\left( {\frac{{{K_{\max }} - k}}{{{K_{\max }}}}} \right) + {\omega _{{\rm{end}}}} $

(3)

式中：ω_start、ω_end分别为最初和最终的惯性权重，K_max是最大迭代步。

2 改进的PSO算法

提高PSO算法性能的有效方法之一就是平衡算法的探索能力和开发能力。我们的目的是对粒子所经历的最好位置进行操作，一方面能够使其跳出局部最优；另一方面使其具有一定的局部搜索能力。为此，给出两个变异算子：

$ \bar P_{id}^k = P_{id}^k \cdot {\rho _1}N\left( {0,{\sigma ^2}} \right) $

(4)

$ \bar P_{id}^k = P_{id}^k + {\rho _2}N\left( {0,{\sigma ^2}} \right) $

(5)

式中：ρ₁>1和ρ₂>1是常数，N(0, σ²)是具有时变标准差σ的高斯分布的随机变量，σ表示为

$ \sigma = {\sigma _{\max }} - \left( {{\sigma _{\max }} - {\sigma _{\min }}} \right)\frac{k}{{{K_{\max }}}} $

(6)

式中：σ_max和σ_min是标准差σ的最终和初始值，k是当前迭代步，K_max是最大迭代步。因为ρ₁N(0, σ²)的值比1大或比1小，又因为$P^k_{id}$·ρ₁N(0, σ²)是一个随机值，所以它比$P^k_{id}$大或小，这样$\bar P^k_{id}$可能远离$P^k_{id}$，因此说式（4）具有一定的全局搜索能力。另一方面，式（5）表明在$P^k_{id}$附近搜索，因此式（5）具有一定的局部搜索能力。

如果每次都对$\mathit{\boldsymbol{P}}^k_{i}$实施式（4）或式（5）的变异操作，那么导致算法运行时间长，因此按一定概率μ对$\mathit{\boldsymbol{P}}^k_{i}$实施式（4）或式（5）的变异操作，即当$f(\mathit{\boldsymbol{P}}^k_{i})$≤f_ave时，对$\mathit{\boldsymbol{P}}^k_{i}$按概率μ实施式（5）的变异操作，当$f(\mathit{\boldsymbol{P}}^k_{i})$>f_ave时，对$\mathit{\boldsymbol{P}}^k_{i}$按概率μ实施式（4）的变异操作，其中

$ {f_{{\rm{ave}}}} = \frac{1}{{{N_p}}}\sum\limits_{j = 1}^{{N_p}} {f\left( {\mathit{\boldsymbol{P}}_j^k} \right)} , $

(7)

$ \mu = \left\{ \begin{array}{l} \frac{{\alpha \left( {{f_{{\rm{ave}}}} - f\left( {\mathit{\boldsymbol{P}}_i^k} \right)} \right)}}{{{f_{{\rm{ave}}}} - f\left( {\mathit{\boldsymbol{P}}_g^k} \right)}},\;\;\;\;f\left( {\mathit{\boldsymbol{P}}_i^k} \right) \le {f_{{\rm{ave}}}}\\ \frac{{\alpha \left( {f\left( {P_i^k} \right) - {f_{{\rm{ave}}}}} \right)}}{{{f_{\max }} - {f_{{\rm{ave}}}}}},\;\;\;\;\;f\left( {\mathit{\boldsymbol{P}}_i^k} \right) > {f_{{\rm{ave}}}} \end{array} \right. $

(8)

式中：f_max=$\max\limits_{1≤i≤N_p}{f(\mathit{\boldsymbol{P}}^k_i)}$, α是一个自适应参数，它被定义为

$ \alpha = 1 - 0.8\frac{k}{{{K_{\max }}}} $

(9)

由式（8）知，对适应值较好的粒子实施局部搜索的概率较大，而对适应值较差的粒子实施全局搜索的概率较大。由于当算法迭代到后期，粒子比较集中，从而导致$\frac{f_\text{ave}－f(\mathit{\boldsymbol{P}}^k_i)}{f_\text{ave}－f(\mathit{\boldsymbol{P}}^k_g)}$或$\frac{f(\mathit{\boldsymbol{P}}^k_i)－f_\text{ave}}{f_\max－f_\text{ave}}$接近1，若α大，那么实施式（4）或式（5）的变异操作的粒子较多，从而导致算法运算时间长，因此按式（9）实行单调递减策略。

位置与速度越界处理：

$ x_{id}^{k + 1} = \left\{ \begin{array}{l} x_{id}^{k + 1},\;\;\;\;\;{l_d} \le x_{id}^{k + 1} \le {u_d}\\ {l_d} + {\rm{rand}}\left( \; \right) \cdot \left( {{u_d} - {l_d}} \right),\;\;\;\;\;其他 \end{array} \right. $

(10)

$ v_{id}^{k + 1} = \left\{ \begin{array}{l} v_{id}^{k + 1},\;\;\;{v_{\min }} \le v_{id}^{k + 1} \le {v_{\max }}\\ {v_{\min }},\;\;\;\;v_{id}^{k + 1} < {v_{\min }}\\ {v_{\max }},\;\;\;\;v_{id}^{k + 1} > {v_{\max }} \end{array} \right. $

(11)

式中：$v^\min_d=0.5l_d,v^\max_d=0.5u_d$。

改进PSO算法的流程如下：

1) 设置参数，随机初始化粒子的位置和速度，计算各粒子的适应度，确定每个粒子的经历过的最优位置及全局最优位置，令k=1；

2）按式（3）计算惯性权重，并按式（1）和式（2）进行速度与位置更新；

3) 按式（10）和式（11）进行越界处理；

4) 对粒子i(i=1, 2, …, N_p)计算其适应值，更新其经历过的最优位置$\mathit{\boldsymbol{P}}^{k+1}_i$和全局最优位置$\mathit{\boldsymbol{P}}^{k+1}_g$，并按式（7）计算f_ave；

5）若$f(\mathit{\boldsymbol{P}}^{k+1}_i)≤f_\text{ave}$，按式（9）计算α，按式（8）计算μ，在[0, 1]选取一个随机数rand，若ran < μ，则按式(6) 计算σ，按式（5）更新粒子经历过的最优位置，得到$\bar {\mathit{\boldsymbol{P}}}^{k+1}_i$，转7）；

6）若$f(\mathit{\boldsymbol{P}}^{k+1}_i)>f_\text{ave}$，按式（9）计算α，按式（8）计算μ，在[0, 1]选取一个随机数rand，若rand < μ，则按(6) 式计算σ，按（4）式更新粒子经历过的最优位置，得到$\bar {\mathit{\boldsymbol{P}}}^{k+1}_i$；

7）令

$ \mathit{\boldsymbol{P}}_i^{k + 1}\left( {{\rm{new}}} \right) = \left\{ \begin{array}{l} \mathit{\boldsymbol{\bar P}}_i^{k + 1},\;\;f\left( {\mathit{\boldsymbol{\bar P}}_i^{k + 1}} \right) < f\left( {\mathit{\boldsymbol{P}}_i^{k + 1}} \right)\\ \mathit{\boldsymbol{P}}_i^{k + 1},\;\;f\left( {\mathit{\boldsymbol{\bar P}}_i^{k + 1}} \right) \ge f\left( {\mathit{\boldsymbol{P}}_i^{k + 1}} \right) \end{array} \right.; $

8）令$\mathit{\boldsymbol{P}}^{k+1}_i=\mathit{\boldsymbol{P}}^{k+1}_i$(new)，更新$\mathit{\boldsymbol{P}}^{k+1}_g$；

9）判断是否满足终止条件（本文采用最大迭代步），若满足则输出结果，否则令k=k+1，转2）。

3 收敛性分析

本文考虑如下全局优化问题：

$ \begin{array}{*{20}{c}} {\min {\rm{imize}}\;f\left( x \right)}\\ {{\rm{subject}}\;{\rm{to}}\;x \in S} \end{array} $

式中：f:S→R是实值函数, S={x_min≤x≤x_max}，x_min=(l₁, l₂, …, l_D)，x_max=(u₁, u₂, …, u_D)。

定义1 设f(x)是实值函数，x^*∈S，若对任意x∈S，

$ f\left( {{x^ * }} \right) \le f\left( x \right) $

则称x^*为S的全局最优解。

定义2 对任意ε>0，设

$ {B_\varepsilon } = \left\{ {x \in S\left| {\left| {f\left( x \right) - f\left( {{x^ * }} \right)} \right| < \varepsilon } \right|} \right\} $

则称B_ε为ε最优解集，x∈B_ε被称为ε-最优解。

本文假设μ(B_ε)>0, 其中μ为勒贝格测度。

由定义1和2得:

$ x_{id}^{k + 1} = x_{id}^k + {\omega _k}v_{id}^k + {c_1}{r_1}\left( {p_{id}^k - x_{id}^k} \right) + {c_2}{r_2}\left( {p_{gd}^k - x_{id}^k} \right) $

(12)

由式（12）可看出，在第k+1代粒子群中第i个粒子的状态由$\mathit{\boldsymbol{x}}^k_i、\mathit{\boldsymbol{v}}^k_i、\mathit{\boldsymbol{P}}^k_i、\mathit{\boldsymbol{P}}^k_g$决定，所以令φ_i=(x_i, v_i, P_i, P_g)∈Γ，其中Γ=S×V×S×S∈R^4D。

定义3 设$ \mathit Φ_{N_p}=\{\mathit Φ丨\mathit Φ=(\mathit φ_1，…，\mathit φ_{N_p}）,\mathit φ_i∈\mathit Γ,i=1,…,N_p\}，$则称Φ_Np为状态空间，Φ∈Φ_Np称为状态。

定义4 设Ω={ω|ω=(ω₁, ω₂, ω₃, …), Φ_k∈Φ_Np, $\forall k\}，$则称Ω为样本空间，ω∈Ω称为状态序列，其中Φ_k=$(\mathit{\mathbf{φ}}^k_1,\mathit{\mathbf{φ}}^k_>2,…,\mathit{\mathbf{φ}}^k_{N_p})，\mathit{\mathbf{φ}}^k_i=(x^k_i,v^k_i, \mathit{\boldsymbol{P}}^k_i,\mathit{\boldsymbol{P}}^k_g)$。

由改进算法可知，$f(\mathit{\boldsymbol{P}}^{k+1}_g)≤f(\mathit{\boldsymbol{P}}^k_g)$，所以有如下引理。

引理1 对$\forall k≥1$，若$\mathit{\boldsymbol{P}}^k_g∈B_ε$，则$\mathit{\boldsymbol{P}}^{k+1}_g∈B_ε$。

引理2 对$\forall i，k$，若$\bar {\mathit{\boldsymbol{P}}}^k_i∈B_ε$，那么$\mathit{\boldsymbol{P}}^{k+1}_i(\text{new}) ∈B_ε$。

证明 如果$\mathit{\boldsymbol{P}}^k_i(\text{new})=\mathit{\boldsymbol{P}}^k_i$，由算法7) 知$f(\bar {\mathit{\boldsymbol{P}}}^k_i)≥f(\mathit{\boldsymbol{P}}^k_i)$，再由$\bar{\mathit{\boldsymbol{P}}}^k_i∈B_ε$有$\mathit{\boldsymbol{P}}^k_i∈B_ε$，从而$\mathit{\boldsymbol{P}}^{k+1}_i(\text{new})∈B_ε$；如果$\mathit{\boldsymbol{P}}^k_i(\text{new})=\bar{\mathit{\boldsymbol{P}}}^k_i$，则结论是显然的。

引理3 $\forall $Φ∈Φ_Np，$\mathit{\boldsymbol{P}}^{k+1}_g$由算法生成的，则存在ρ>0，使得

$ {\rm{pr}}\left( {\mathit{\boldsymbol{P}}_g^{k + 1} \in {\mathit{\boldsymbol{B}}_\varepsilon }\left| {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \right.} \right) \ge \rho $

式中pr表示概率测度。

证明 如果$\mathit{\boldsymbol{P}}^k_i$实施变异算子（4）或（5）操作，则令$χ(\bar{\mathit{\boldsymbol{P}}}^k_i)=1$，否则令$χ(\bar{\mathit{\boldsymbol{P}}}^k_i)=0$，由算法步骤5）和步骤6）及式（8）有

$ {\rm{pr}}\left( {\chi \left( {\mathit{\boldsymbol{\bar P}}_g^{k + 1}} \right) = 1} \right) = \alpha ,{\rm{pr}}\left( {\chi \left( {\mathit{\boldsymbol{\bar P}}_g^{k + 1}} \right) = 0} \right) = 1 - \alpha $

于是

$ \begin{array}{*{20}{c}} {{\rm{pr}}\left( {\mathit{\boldsymbol{P}}_g^{k + 1} \in {B_\varepsilon }\left| {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \right.} \right) \ge {\rm{pr}}\left( {\chi \left( {\mathit{\boldsymbol{\bar P}}_g^{k + 1}} \right) = 1} \right) \cdot }\\ {{\rm{pr}}\left( {\left( {\mathit{\boldsymbol{P}}_g^{k + 1} \in {B_\varepsilon }\left| {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \right.} \right)\left| {\chi \left( {\mathit{\boldsymbol{\bar P}}_g^{k + 1}} \right) = 1} \right.} \right) = }\\ {\alpha \cdot {\rm{pr}}\left( {\left( {\mathit{\boldsymbol{P}}_g^{k + 1} \in {B_\varepsilon }\left| {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \right.} \right)\left| {\chi \left( {\mathit{\boldsymbol{\bar P}}_g^{k + 1}} \right) = 1} \right.} \right) = }\\ {\alpha \cdot {\rm{pr}}\left( {\mathit{\boldsymbol{P}}_g^{k + 1}\left( {{\rm{new}}} \right) \in {B_\varepsilon }\left| {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \right.} \right)} \end{array} $

由引理2有

$ {\rm{pr}}\left( {\mathit{\boldsymbol{P}}_g^{k + 1} \in {B_\varepsilon }\left| {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \right.} \right) \ge \alpha \cdot {\rm{pr}}\left( {\mathit{\boldsymbol{\bar P}}_g^{k + 1} \in {B_\varepsilon }\left| {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \right.} \right) $

由于$\bar{\mathit{\boldsymbol{P}}}^{k+1}_g$的每个分量是独立的，再由式（5）知，随机变量$\bar{\mathit{\boldsymbol{P}}}^{k+1}_g$的密度函数为

$ g\left( {{x_1},{x_2}, \cdots ,{x_D}} \right) = {\left( {\frac{1}{{\sqrt {2{\rm{\pi }}} \sigma {\rho _2}}}} \right)^D}\exp \left( { - \sum\limits_{d = 1}^D {\frac{{{{\left( {{x_d} - p_{gd}^{k + 1}} \right)}^2}}}{{2{\sigma ^2}\rho _2^2}}} } \right) $

于是

$ \begin{array}{*{20}{c}} {{\rm{pr}}\left( {\mathit{\boldsymbol{\bar P}}_g^{k + 1} \in {B_\varepsilon }\left| {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \right.} \right) = }\\ {\int_{{B_\varepsilon }} {g\left( {{x_1},{x_2}, \cdots ,{x_D}} \right){\rm{d}}{x_1},{\rm{d}}{x_2}, \cdots ,{\rm{d}}{x_D}} \ge }\\ {{{\left( {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} {\sigma _{\max }}{\rho _2}}}} \right)}^D}\exp \left( { - D\frac{{2{m^2}}}{{\sigma _{\max }^2\rho _2^2}}} \right)\mu \left( {{\mathit{\boldsymbol{B}}_\varepsilon }} \right)} \end{array} $

式中$m=\max\limits_{1≤i≤D}\{|l_i|,|u_i|\}$。

令$ρ=\left(\frac 1{\sqrt{2π}σ_\maxρ_2}\right)^D\exp(－D\frac{2m^2}{σ_\min\ ^2ρ^2_2})μ(\mathit{\boldsymbol{B}}_ε)$，则

$ {\rm{pr}}\left( {\mathit{\boldsymbol{P}}_g^{k + 1} \in {B_\varepsilon }\left| {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \right.} \right) \ge \rho > 0。$

定理1 设(Φ₁, Φ₂, Φ₃, …)∈Ω是由算法任意生成的状态序列，则序列{$p^k_g$}依概率1收敛到ε-最优解，即

$ \mathop {\lim }\limits_{k \to \infty } {\rm{pr}}\left\{ {p_g^k \in {\mathit{\boldsymbol{B}}_\varepsilon }} \right\} = 1 $

证明 由算法可知，Φ_k+1只与Φ_k有关，所以Φ₁, Φ₂, Φ₃, …是马尔可夫过程，由马尔可夫过程性质及引理1可知

$ \begin{array}{*{20}{c}} {{\rm{pr}}\left( {\mathit{\boldsymbol{P}}_g^{k + 1} \notin {\mathit{\boldsymbol{B}}_\varepsilon }} \right) = {\rm{pr}}\left( {\mathit{\boldsymbol{P}}_g^1 \notin {\mathit{\boldsymbol{B}}_\varepsilon }} \right) \cdot }\\ {\prod\limits_{t = 1}^k {{\rm{pr}}\left( {\mathit{\boldsymbol{P}}_g^{t + 1} \notin {\mathit{\boldsymbol{B}}_\varepsilon }\left| {\mathit{\boldsymbol{P}}_g^t \notin {\mathit{\boldsymbol{B}}_\varepsilon }} \right.} \right)} \le }\\ {\prod\limits_{t = 1}^k {{\rm{pr}}\left( {\mathit{\boldsymbol{P}}_g^{t + 1} \notin {\mathit{\boldsymbol{B}}_\varepsilon }\left| {\mathit{\boldsymbol{P}}_g^t \notin {\mathit{\boldsymbol{B}}_\varepsilon }} \right.} \right)} } \end{array} $

令

$ \Delta = \left\{ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left| {{\mathit{\boldsymbol{P}}_g} \notin {\mathit{\boldsymbol{B}}_\varepsilon }} \right.} \right\} \subset {\mathit{\Phi }_{{N_p}}} $

则$\forall \mathit{\boldsymbol{\varPhi}}∈\mathit{\boldsymbol{\varPhi}}_{N_p}$，由引理3有

$ \begin{array}{*{20}{c}} {{\rm{pr}}\left( {\mathit{\boldsymbol{P}}_g^{t + 1} \notin {\mathit{\boldsymbol{B}}_\varepsilon }\left| {\mathit{\boldsymbol{P}}_g^t \notin {\mathit{\boldsymbol{B}}_\varepsilon }} \right.} \right) \le }\\ {{\rm{pr}}\left( {\mathit{\boldsymbol{P}}_g^{k + 1} \notin {\mathit{\boldsymbol{B}}_\varepsilon }\left| {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_t} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \right.} \right) = 1 - \rho } \end{array} $

于是pr$(\mathit{\boldsymbol{P}}^{k+1}_g∈\mathit{\boldsymbol{B}}_ε)≤1－(1－ρ)^k$，故

$ \mathop {\lim }\limits_{k \to \infty } {\rm{pr}}\left\{ {p_g^k \in {\mathit{\boldsymbol{B}}_\varepsilon }} \right\} = 1 $

4 数值实验

为了评价改进算法（简称，IPSO）的性能，我们选取文献[24]中的13个测试函数进行实验研究。前7个函数为高维单峰函数，后6个函数是高维多峰函数。在本文中13个问题的维数都取30。IPSO算法的实验结果与LDIWPSO^[2]、CDIWPSO^[3]、DAPSO^[4]、和SSRDIWPSO^[5]实验结果进行比较。所有算法的共同参数设置如下：ω_start=0.9，ω_end=0.4，Np=30，c₁=c₂=2，v_min=0.5x_min，v_max=0.5x_max，K_max=3 000，IPSO算法的其他参数设置如下：ρ₁=2, ρ₂=0.1, σ_max=1, σ_min=0.2。所有算法的程序都是由MATLAB2007实现，且每个实验独立运行30次，实验结果见表 1和表 2。

从表 1可以看出，除了测试函数F₁、F₅和F₆外, IPSO算法与其他4种算法相比，在寻优能力和稳定性方面明显优于其他4种算法，特别是测试函数F₃和F₄，其他4种算法不能获得到最优解，而IPSO算法能够得到较理想的最优解，且稳定性也非常好。对于测试函数F₁来说，IPSO算法不如SSRDIWPSO算法，但是优于其他3种算法。对于测试函数F₅来说，IPSO算法的最好收敛值不如其他4种算法，但是对于平均收敛值和方差来说，IPSO算法优于其他4种算法。对于测试函数F₆，IPSO算法与其他4种算法获得相同的结果。总之，对于高维单峰函数来说IPSO算法有一定优势，其原因如下：函数F₁~F₇都单峰函数，由于IPSO算法有较好的局部搜索能力，所以IPSO算法对于单峰函数具有一定优势。函数F₁是非线性简单的单峰函数，所以大多数算法都能够找到最优解；函数F₅是很难极小化的典型病态二次函数，由于其全局最优解与可达到的局部最优之间有一道狭窄的山谷，所以算法很难辨别搜索方向，找到全局最优解的机会很小，因此5种算法都没有找到全局最优解，而函数F₇是含有随机变量的函数，由于目标函数不确定，找到非常理想的全局最优解也是较困难的。

从表 2可以看出，除了测试函数F₁₂和F₁₃外IPSO算法与其他4种算法相比，在寻优能力和稳定性方面明显优于其他4种算法，特别是测试函数F₉和F₁₁，其他4种算法不能获得较好最优解，而IPSO算法能够得到非常理想的最优解，且稳定性也非常好。对于测试函数F₁₂来说，关于最好收敛值，IPSO算法不如SSRDIWPSO和CDIWPSO算法，但是优于其他两种算法，而关于最差收敛值、平均收敛值和方差，IPSO算法远好于其他4种算法。对于测试函数F₁₃来说，对于最好收敛值IPSO算法不如SSRDIWPSO和CDIWPSO算法，对于平均收敛值，IPSO算法与SSRDIWPSO算法一样优于其他3种算法。总之，除了函数F₈~F₁₃外，对于其他函数IPSO算法都能够得到满意结果，其原因如下：函数F₈~F₁₃都是多峰函数且有较多局部最优解，由于IPSO算法按一定概率对适应值较差的粒子实行全局搜索，对于适应值较好的粒子实行局部搜索，所以IPSO算法对于解决多峰函数有一定优势。但是由于函数F₈的全局最优解与局部最优相距较远，且有一定的欺骗性，导致算法朝着错误方向搜索，因此不易找到满意的全局最优解；函数F₁₃含有大量深度不同的“坑”，导致算法陷入第一个坑后不易跳出来，因此也不易找到满意的全局最优解。

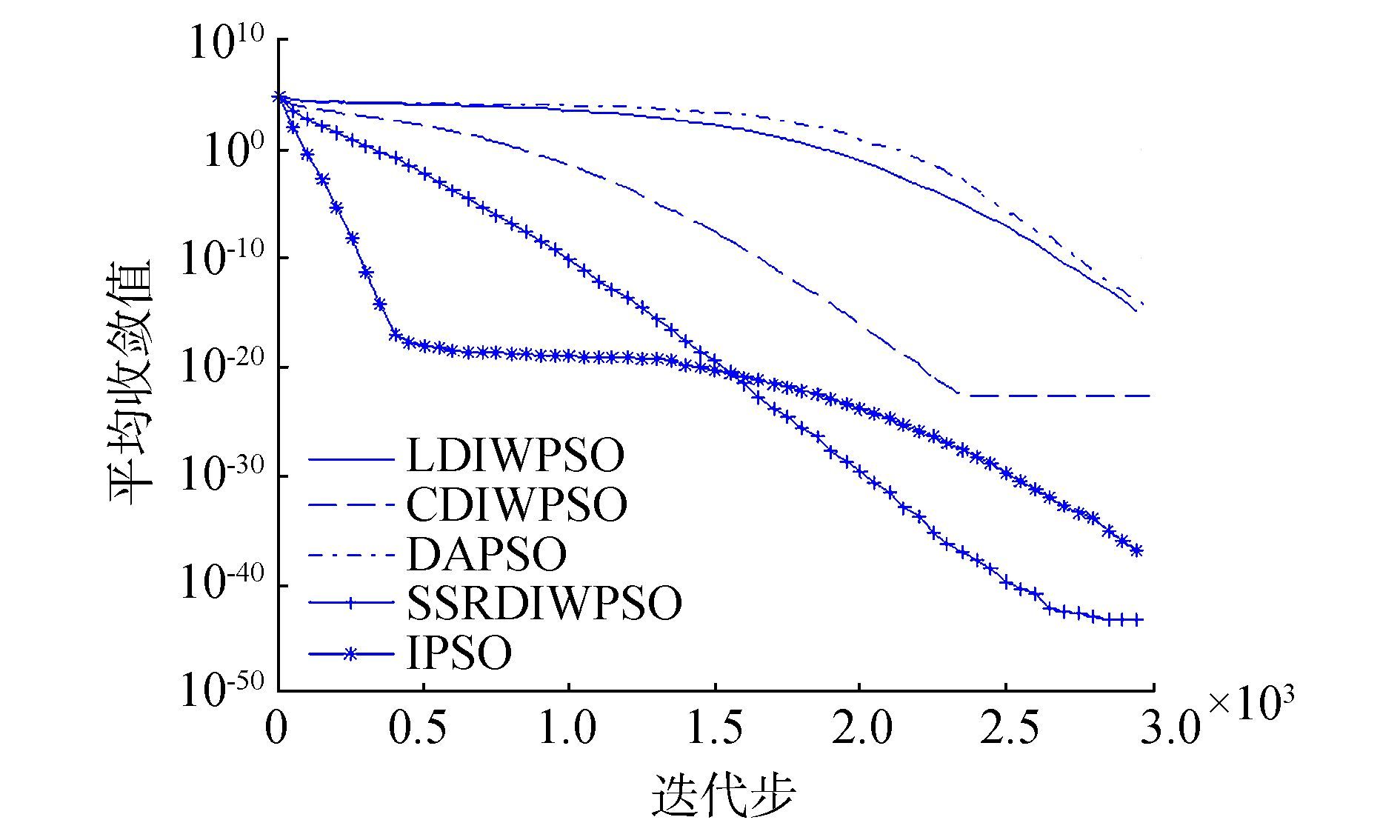
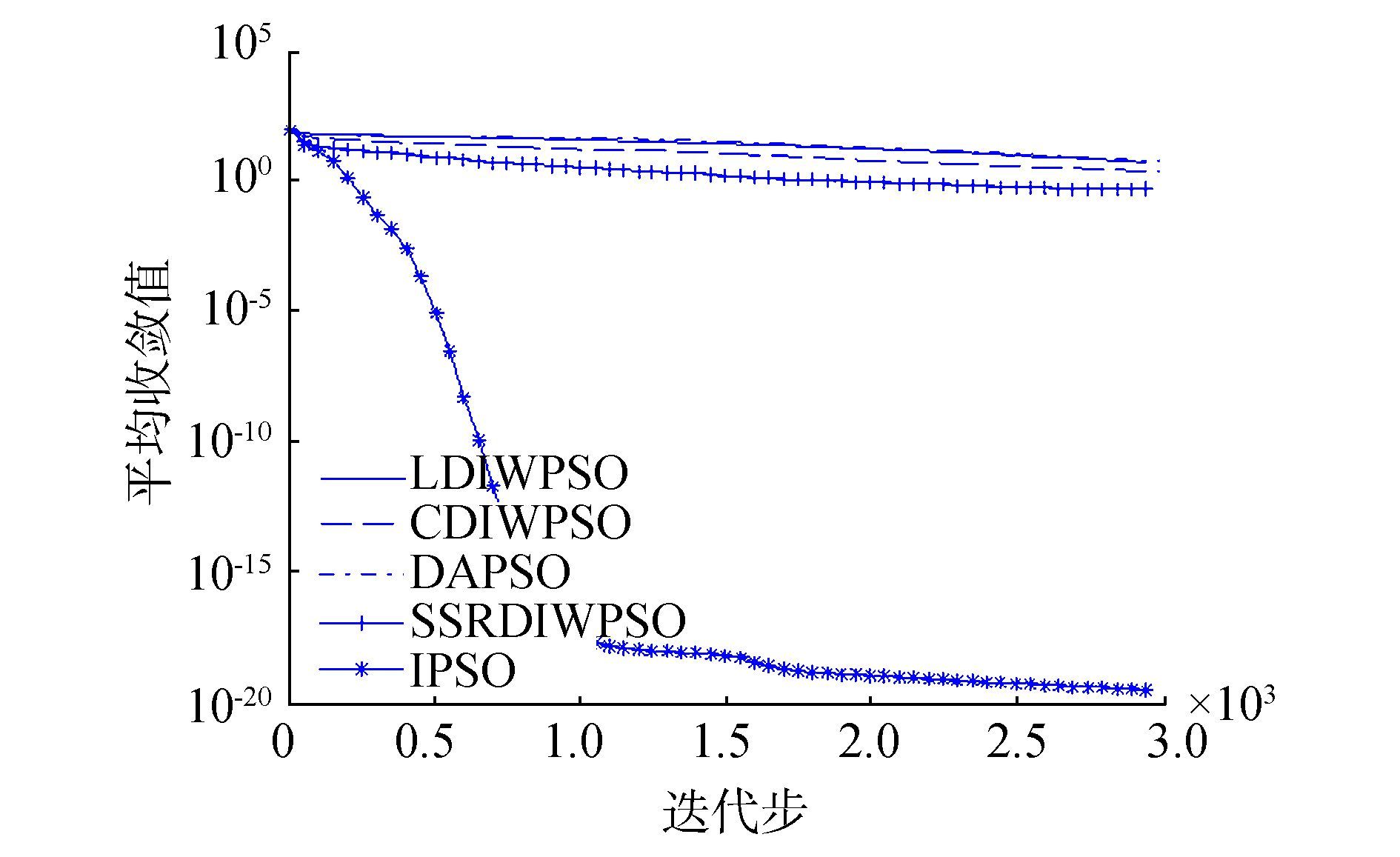
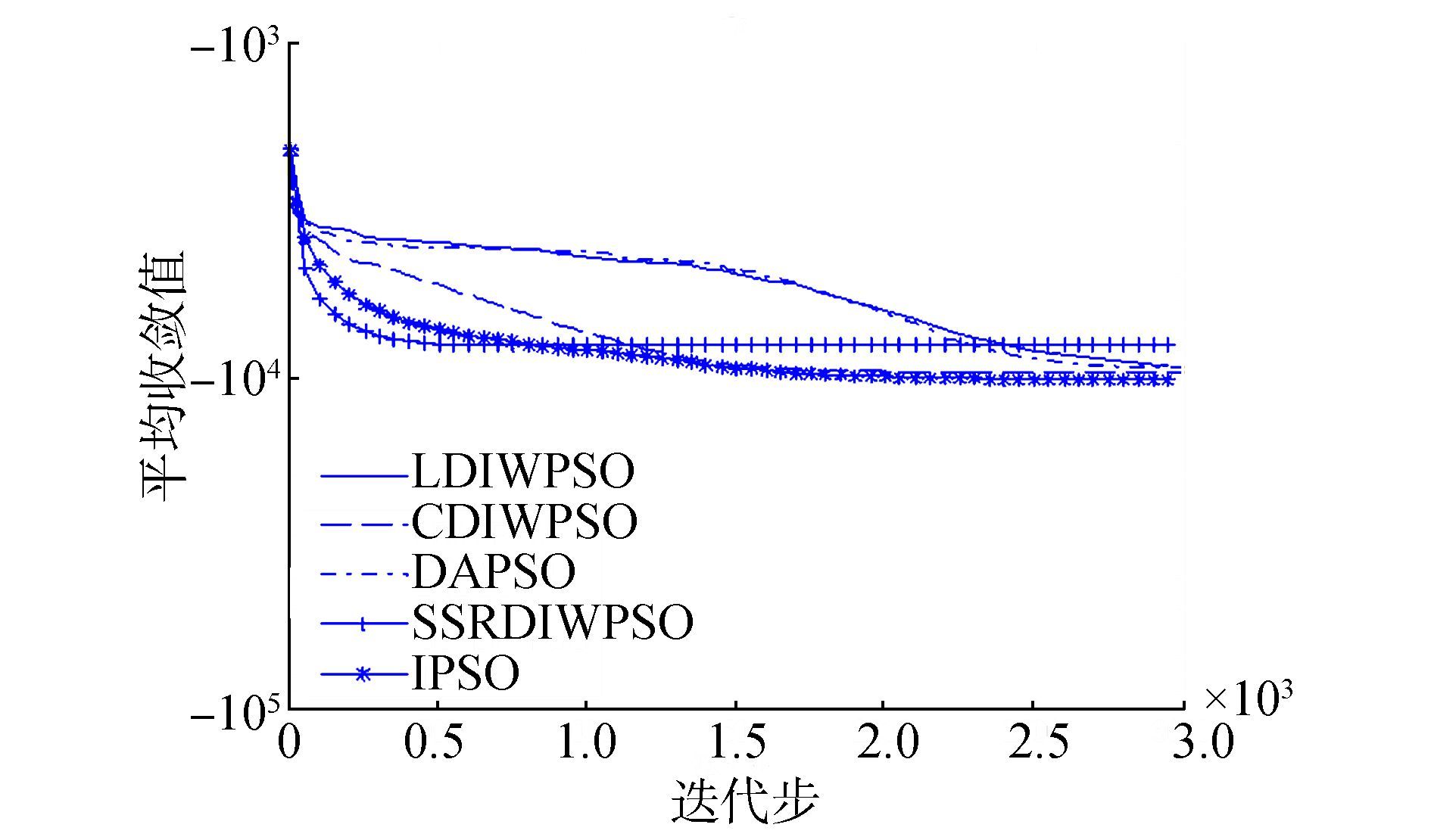
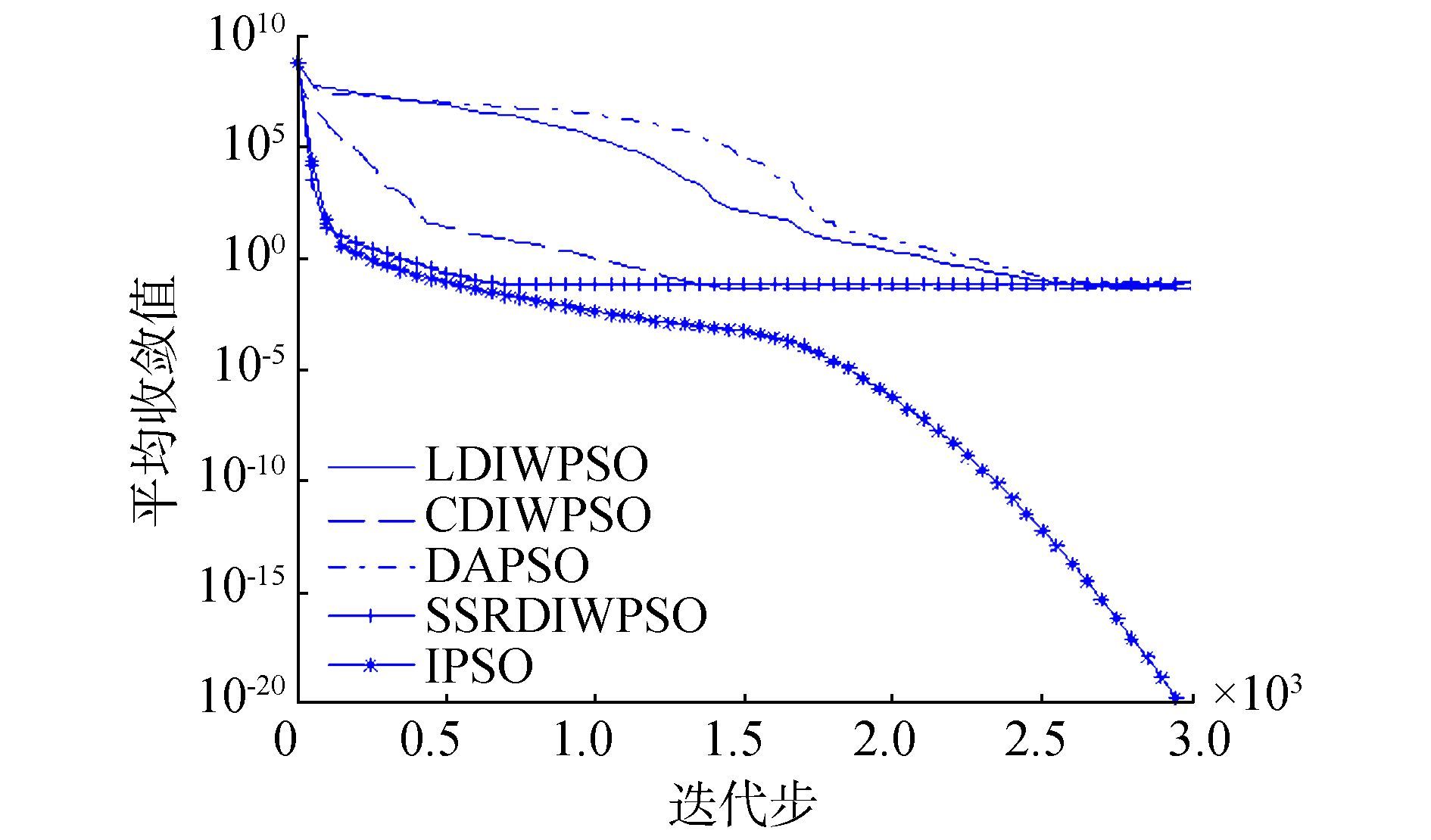
为了更清楚且直观地比较各种算法的收敛性，我们分别从高维单峰函数和高维多峰函数中选取3个函数进行收敛曲线分析，图 1~图 3分别表示测试函数F₁、F₄、和F₆的收敛曲线，其中用100^-100代替0。图 4~图 6分别表示测试函数F₈、F₁₀和F₁₂的收敛曲线。

从图 1~6中可以看出，对于函数F₄、F₁₀和F₁₂，IPSO算法的收敛速度及求解精度明显优于其他4种算法，对于函数F₆，虽然求解精度一样，但是IPSO算法的收敛速度明显比其他4种算法收敛快，对于函数F₁，虽然收敛精度IPSO算法不如SSRDIWPSO算法，但是他较快收敛到人们比较满意精度，对于函数F₈，IPSO算法的求解精度略优于其他4种算法。总之，IPSO算法有较好的收敛速度和求解精度。

5 结束语

针对标准PSO算法不依概率收敛和易出现早熟收敛等缺点，提出了标准粒子群优化算法中增加了具有开发能力和探索能力两个变异算子，其目的是平衡算法的全局探索能力和局部搜索能力。并且从理论上证明所提出算法依概率1收敛到ε-最优解。数值结果表明，所提出的算法较大提高了全局寻优能力且具有较好的鲁棒性。在未来的工作中，将对变异算子中的参数设置进一步研究，以便提高算法收敛精度与收敛速度。