2. 辽宁师范大学 数学学院, 辽宁 大连 116081
2. School of Mathematics, Liaoning Normal University, Dalian 116081, China
自从Zadeh[1]提出模糊集以来,模糊理论就受到人们的高度关注,并取得了丰富的研究成果[2-3]。随着科学研究的不断深入,传统的模糊集理论已经不能完整地表达研究问题的全部信息,因此,Atanassov对模糊集进行了拓展,提出了直觉模糊集[4-5]的概念。直觉模糊集同时考虑了隶属度、非隶属度和犹豫度3个方面的信息,在不确定性研究方面中做出了巨大的贡献[6-8]。在现实生活中,人类在做评价时更喜欢用模糊语言形式给出。因此,结合人类自然语言的特点,文献[9-10]提出了语言真值格蕴涵代数及语言真值命题逻辑系统。在此基础上,文献[11]建立了语言真值直觉模糊格,可以从正反两方面处理语言值模糊信息,且能够同时处理语言值信息的可比性和不可比性。
在决策领域,有很多种排序方法,逼近理想解(TOPSIS)的方法是其中常用的一种排序法。该方法由HWang等[12]提出,其主要思想是一个理想的方案应该距离正理想解近,同时又远离负理想解。由于该方法具有运算量小、几何意义直观以及信息失真小等优点,因此,该方法自从被提出,便引起了各领域研究人员的广泛关注,并被迅速地应用到实践中。文献[13]提出在直觉模糊环境中进行决策,基于距离测度和直觉模糊熵,建立了直觉模糊TOPSIS方法的多准则决策模型;在此基础上,文献[14]基于TOPSIS方法和相似度,提出了一种新的直觉模糊环境中的多准则决策方法,文中利用案例将该方法和文献[13]方法的实验结果进行对比,文献[13]出现了除零问题,并且无法获得方案的偏好排序,而文献[14]克服了此问题,因此说明文献[14]方法具有创新性;文献[15]将TOPSIS方法拓展到单值中智环境下进行多属性群决策,利用单值中智集表示各属性值,提出了单值中智加权平均算子,并利用该算子对中智决策矩阵进行聚合,最后根据聚合结果对待选方案进行排序和择优。TOPSIS方法不仅限于在数值上的运用,还被拓展到模糊语言值中。文献[16]利用语言值的形式表达属性值和权重,将语言值转换成三角模糊数的形式进行计算,构建了模糊环境下基于TOPSIS方法的群决策模型,并给出了在人才选拔方面的应用。之后,文献[17]提出了一种新的基于TOPSIS的多属性决策模型,该方法将语言值转换成梯形模糊数进行计算,并给出了正负理想方案的确定方法,最后,根据各方案的相对贴近度对方案进行排序。
由于客观事物的复杂性和人类思维的模糊性,使决策者很难用精确的数值去表达待选方案的评价,因此更习惯于用模糊的语言信息去表达。基于语言真值直觉模糊格进行表达,既可以从正反两方面处理模糊语言值信息,又能够同时处理信息的可比性和不可比性,是一种很好的表达方法。
针对在语言真值直觉模糊格上如何计算格值之间的距离,以及如何确定正、负理想点,本文提出了语言真值直觉模糊对之间的归一化距离,并构建了一种基于TOPSIS的语言真值直觉模糊多属性决策模型,探讨了模糊语言的正、负理想点确立方法,从而使决策者在以语言值形式评估的决策中可以确定最佳方案。
1 预备知识定义1[11] 在2n元语言真值格蕴涵代数LV(n×2)={ (hi, t), (hj, f) | hi∈Ln, t, f∈L2}中,对任意(hi, t), (hj, f)∈LV(n×2),称((hi, t), (hj, f))是一个语言真值直觉模糊对,则S={((hi, t), (hj, f)) | i, j∈{1, 2, …, n}}是一个2n元语言真值直觉模糊对集合。
定理1[11] 对任意(hi, t), (hj, f)∈LV(n×2),((hi, t), (hj, f))是一个语言真值直觉模糊对当且仅当i ≤ j。
推论1[11] 对任意((hi, t), (hj, f)), ((hk, t), (hl, f))∈LI2n的关系:
1)((hi, t), (hj, f)) ≥ ((hk, t), (hl, f)),当且仅当i ≥ k且j≥l;
2)((hi, t), (hj, f))与((hk, t), (hl, f))不可比,当且仅当i>k且j<l,或i<k且j>l。
推论2[11] 2n元语言真值直觉模糊格LI2n=(LI2n, ∪, ∩)是一个有界分配格,((hn, t), (hn, f))和((h1, t), (h1, f))分别为LI2n中的最大元和最小元。
定义2[11] 基于语言真值直觉模糊格LI2n=(LI2n, ∪, ∩),对任意((hi, t), (hj, f)), ((hk, t), (hl, f))∈LI2n,有
1)((hi, t), (hj, f))∪((hk, t), (hl, f))=((hmax(i, k), t), (hmax(j, l), f));
2)((hi, t), (hj, f))∩((hk, t), (hl, f))=((hmin(i, k), t), (hmin(j, l), f))。
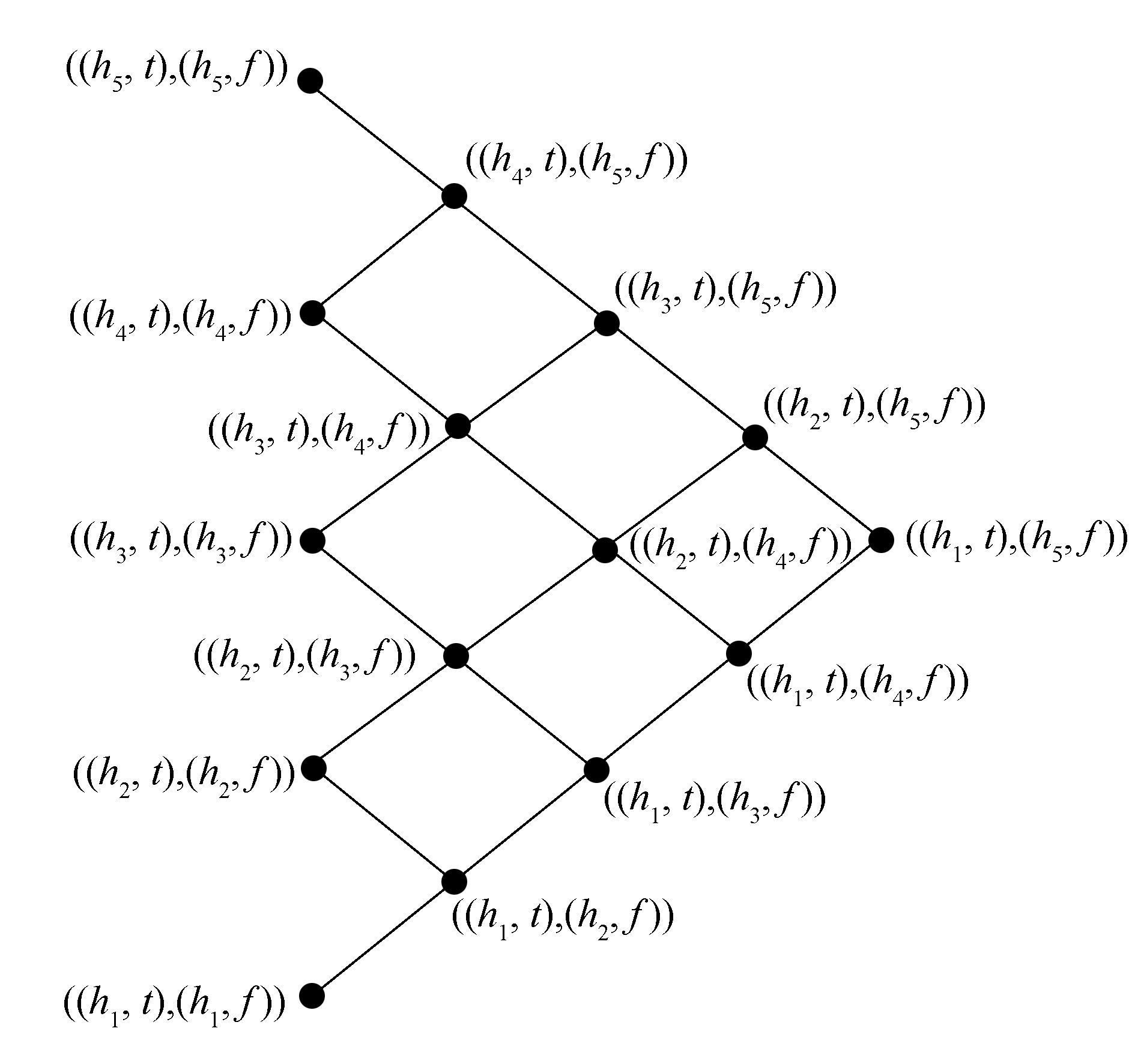
令语气词集合L5={hi| i=1, 2, 3, 4, 5},其中,语气词h1表示“稍微”,h2表示“有点”,h3表示“一般”,h4表示“很”,h5表示“非常”,且h1<h2<h3<h4<h5,元语言真值集{t, f},其中,t表示“真”,即对肯定的评价,f表示“假”,即对否定的评价,可得十元语言真值直觉模糊格LI10,其哈斯图如图 1。
|
图 1 十元语言真值直觉模糊格的哈斯图 Fig.1 Hasse diagram of 10-element linguistic truth-valued intuitionistic fuzzy lattice |
为进行语言真值直觉模糊格上方案的排序,借鉴TOPSIS方法的思想,需计算各方案与正、负理想点之间的距离,因此,下面提出了语言真值直觉模糊正、负理想点及语言真值直觉模糊对之间的归一化距离。
定义3 对任意((hi, t), (hj, f)), ((hk, t), (hl, f))∈LI2n,定义语言真值直觉模糊对((hi, t), (hj, f))和((hk, t), (hl, f))之间的归一化距离为
| $ \begin{array}{*{20}{c}} {{d_{{\rm{LIF}}}}\left( {\left( {\left( {{h_i},t} \right),\left( {{h_j},f} \right)} \right),\left( {\left( {{h_k},t} \right),\left( {{h_l},f} \right)} \right)} \right) = }\\ {\frac{{\left| {i - k} \right| + \left| {j - l} \right|}}{{2n - 2}}} \end{array} $ |
例1 在十元语言真值直觉模糊格上,两个语言真值直觉模糊对((h1, t), (h1, f))和((h3, t), (h4, f))之间的归一化距离为
| $ \begin{array}{*{20}{c}} {{d_{{\rm{LIF}}}}\left( {\left( {\left( {{h_1},t} \right),\left( {{h_1},f} \right)} \right),\left( {\left( {{h_3},t} \right),\left( {{h_4},f} \right)} \right)} \right) = }\\ {\frac{{\left| {1 - 3} \right| + \left| {1 - 4} \right|}}{8} = \frac{5}{8}} \end{array} $ |
定理2 对任意的((hi, t), (hj, f)), ((hk, t), (hl, f)), ((hp t), (hq, f))∈LI2n,具有如下性质:
1)0≤dLIF(((hi, t), (hj, f)), ((hk, t), (hl, f)))≤1;
2)dLIF(((hi, t), (hj, f)), ((hk, t), (hl, f)))=0当且仅当((hi, t), (hj, f))=((hk, t), (hl, f));
3)dLIF(((hi, t), (hj, f)), ((hk, t), (hl, f)))=dLIF(((hk, t), (hl, f)), ((hi, t), (hj, f)));
4) 若((hi, t), (hj, f))≥((hk, t), (hl, f))≥((hp, t), (hq, f)),则有dLIF(((hi, t), (hj, f)), ((hp, t), (hq, f)))≥dLIF(((hi, t), (hj, f)), ((hk, t), (hl, f)))且dLIF(((hi, t), (hj, f)), ((hp, t), (hq, f)))≥dLIF(((hk, t), (hl, f)), ((hp, t), (hq, f)))。
证明1 在2n元语言真值直觉模糊格上,由推论2可知,((h1, t), (h1, f))与((hn, t), (hn, f))分别是最小值与最大值;
由定义3可知,任意一个语言真值直觉模糊对与本身之间的距离最小,即
| $ \begin{array}{*{20}{c}} {{d_{{\rm{LIF}}}}\left( {\left( {\left( {{h_i},t} \right),\left( {{h_j},f} \right)} \right),\left( {\left( {{h_i},t} \right),\left( {{h_j},f} \right)} \right)} \right) = }\\ {\frac{{\left| {i - i} \right| + \left| {j - j} \right|}}{{2n - 2}} = 0} \end{array} $ |
最小值((h1, t), (h1, f))与最大值((hn, t), (hn, f))之间的距离最大,即
| $ \begin{array}{*{20}{c}} {{d_{{\rm{LIF}}}}\left( {\left( {\left( {{h_n},t} \right),\left( {{h_n},f} \right)} \right),\left( {\left( {{h_1},t} \right),\left( {{h_1},f} \right)} \right)} \right) = }\\ {\frac{{\left| {n - 1} \right| + \left| {n - 1} \right|}}{{2n - 2}} = \frac{{2n - 2}}{{2n - 2}} = 1} \end{array} $ |
因此,0≤dLIF(((hi, t), (hj, f)), ((hk, t), (hl, f)))≤1。
2) 对任意((hi, t), (hj, f)), ((hk, t), (hl, f))∈LI2n,由定义3可得,两个语言真值直觉模糊对之间的归一化距离为
| $ \begin{array}{*{20}{c}} {{d_{{\rm{LIF}}}}\left( {\left( {\left( {{h_i},t} \right),\left( {{h_j},f} \right)} \right),\left( {\left( {{h_k},t} \right),\left( {{h_l},f} \right)} \right)} \right) = }\\ {\frac{{\left| {i - k} \right| + \left| {j - l} \right|}}{{2n - 2}}} \end{array} $ |
若dLIF(((hi, t), (hj, f)), ((hk, t), (hl, f)))=0,则i=k,j=l,即((hi, t), (hj, f))=((hk, t), (hl, f))。
若((hi, t), (hj, f))=((hk, t), (hl, f)),
则dLIF(((hi, t), (hj, f)), ((hk, t), (hl, f)))=dLIF(((hi, t), (hj, f)), ((hi, t), (hj, f)))=
3) 根据定义3可知:
| $ \begin{array}{l} {d_{{\rm{LIF}}}}\left( {\left( {\left( {{h_i},t} \right),\left( {{h_j},f} \right)} \right),\left( {\left( {{h_k},t} \right),\left( {{h_l},f} \right)} \right)} \right) = \\ \frac{{\left| {i - k} \right| + \left| {j - l} \right|}}{{2n - 2}}; \end{array} $ |
| $ \begin{array}{l} {d_{{\rm{LIF}}}}\left( {\left( {\left( {{h_k},t} \right),\left( {{h_l},f} \right)} \right),\left( {\left( {{h_i},t} \right),\left( {{h_j},f} \right)} \right)} \right) = \\ \frac{{\left| {k - i} \right| + \left| {l - j} \right|}}{{2n - 2}}; \end{array} $ |
因为|i-k|=|k-i|, |j-l|=|l-j|,所以,dLIF(((hi, t), (hj, f)), ((hk, t), (hl, f)))=dLIF(((hk, t), (hl, f)), ((hi, t), (hj, f)))。
4) 对任意(hi, t), (hj, f)),((hk, t), (hl, f)),((hp, t), (hq, f))∈LI2n,由定义3可得:
| $ \begin{array}{*{20}{c}} {{d_{{\rm{LIF}}}}\left( {\left( {\left( {{h_i},t} \right),\left( {{h_j},f} \right)} \right),\left( {\left( {{h_p},t} \right),\left( {{h_q},f} \right)} \right)} \right) = }\\ {\frac{{\left| {i - p} \right| + \left| {j - q} \right|}}{{2n - 2}} = \frac{{\left| {i + j} \right| - \left| {p + q} \right|}}{{2n - 2}}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{d_{{\rm{LIF}}}}\left( {\left( {\left( {{h_i},t} \right),\left( {{h_j},f} \right)} \right),\left( {\left( {{h_k},t} \right),\left( {{h_l},f} \right)} \right)} \right) = }\\ {\frac{{\left| {i - k} \right| + \left| {j - l} \right|}}{{2n - 2}} = \frac{{\left| {i + j} \right| - \left| {k + l} \right|}}{{2n - 2}}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{d_{{\rm{LIF}}}}\left( {\left( {\left( {{h_k},t} \right),\left( {{h_l},f} \right)} \right),\left( {\left( {{h_p},t} \right),\left( {{h_q},f} \right)} \right)} \right) = }\\ {\frac{{\left| {k - p} \right| + \left| {l - q} \right|}}{{2n - 2}} = \frac{{\left| {k + l} \right| - \left| {p + q} \right|}}{{2n - 2}}} \end{array} $ |
若((hi, t), (hj, f))≥((hk, t), (hl, f))≥((hp, t), (hq, f)),
则有i≥k≥p且j≥l≥q,所以i+j≥k+l≥p+q,且(i+j)-(p+q) ≥(i+j)-(k+l),(i+j)-(p+q) ≥ (k+l)-(p+q);
因此,dLIF(((hi, t), (hj, f)), ((hp, t), (hq, f)))≥dLIF(((hi, t), (hj, f)), ((hk, t), (hl, f)))且dLIF(((hi, t), (hj, f)), ((hp, t), (hq, f)))≥dLIF(((hk, t), (hl, f)), ((hp, t), (hq, f)))。
定义4 设决策矩阵R=(rij)m×n,rij∈S,S为2n元语言真值直觉模糊对集合,则定义语言真值直觉模糊正理想点rj+和负理想点rj-分别为
| $ r_j^ + = \left\{ \begin{array}{l} \bigcup\limits_i {{r_{ij}}} ,\;\;\;\;\;\;j \in {\mathit{\Omega }_1}\\ \bigcap\limits_i {{r_{ij}}} ,\;\;\;\;\;\;\;j \in {\mathit{\Omega }_2} \end{array} \right. $ |
| $ r_j^ - = \left\{ \begin{array}{l} \bigcap\limits_i {{r_{ij}}} ,\;\;\;\;\;\;j \in {\mathit{\Omega }_1}\\ \bigcup\limits_i {{r_{ij}}} ,\;\;\;\;\;\;\;j \in {\mathit{\Omega }_2} \end{array} \right. $ |
式中:i=1, 2, …, m,j=1, 2, …, n,Ω1和Ω2分别表示效益型、成本型属性的下标集。
3 基于TOPSIS的语言真值直觉模糊多属性决策方法在2n元语言真值直觉模糊格上,提出了一种基于TOPSIS的语言真值直觉模糊多属性决策方法,其中,Ω1和Ω2分别表示效益型、成本型属性的下标集,决策方法具体步骤如下:
1) 对于某一多属性决策问题,设A={A1, A2, …, Am}为方案集,G={G1, G2, …, Gn}为属性集。w=[w1 w2 … wn]T为属性权重向量,其中,wj∈[0, 1],
2) 利用定义4确定语言真值直觉模糊正、负理想方案:
① 语言真值直觉模糊正理想方案为
| $ {A^ + } = \left( {r_1^ + ,r_2^ + , \cdots ,r_n^ + } \right) $ |
② 语言真值直觉模糊负理想方案为
| $ {A^ - } = \left( {r_1^ - ,r_2^ - , \cdots ,r_n^ - } \right) $ |
3) 分别计算各方案与语言真值直觉模糊正、负理想方案之间的距离:
① 方案Ai与语言真值直觉模糊正理想方案之间的距离为
| $ d\left( {{A_i},{A^ + }} \right) = \sum\limits_{j = 1}^n {{w_j}{d_{{\rm{LIF}}}}\left( {{r_{ij}},r_j^ + } \right)} $ |
② 方案Ai与语言真值直觉模糊负理想方案之间的距离为
| $ d\left( {{A_i},{A^ - }} \right) = \sum\limits_{j = 1}^n {{w_j}{d_{{\rm{LIF}}}}\left( {{r_{ij}},r_j^ - } \right)} $ |
4) 计算方案Ai与理想方案之间的相对贴近度:
| $ C\left( {{A_i}} \right) = \frac{{d\left( {{A_i},{A^ - }} \right)}}{{d\left( {{A_i},{A^ + }} \right) + d\left( {{A_i},{A^ - }} \right)}} $ |
5) 按照相对贴近度C(Ai)(i=1, 2, …, m)由大到小的顺序对方案Ai(i=1, 2, …, m)进行排序,C(Ai)值越大,则方案Ai越优。
4 案例考虑某个风险投资公司进行的高科技项目投资问题,有4个备选企业(方案)Ai(i=1, 2, 3, 4) 可供选择。从企业能力角度对企业进行评价,首先制定了6项评估指标(属性):
G1为销售能力;G2为管理能力;G3为生产能力;G4为技术能力;G5为资金能力;G6为风险承担能力。
依据决策者对每个企业的各项指标的评估结果(表示为十元语言真值直觉模糊对形式,如表 1所示),试确定最佳企业。
| 表 1 公司各项指标的评估 Tab.1 Assessment of each company index |
在十元语言真值直觉模糊格上,利用本文提出的基于TOPSIS的语言真值直觉模糊多属性决策方法确定最佳企业:
1) 将表格1转换成语言真值直觉模糊对决策矩阵R:
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {\left( {\left( {{h_3},t} \right),\left( {{h_4},f} \right)} \right)}&{\left( {\left( {{h_3},t} \right),\left( {{h_3},f} \right)} \right)}&{\left( {\left( {{h_3},t} \right),\left( {{h_5},f} \right)} \right)}&{\left( {\left( {{h_3},t} \right),\left( {{h_4},f} \right)} \right)}&{\left( {\left( {{h_5},t} \right),\left( {{h_5},f} \right)} \right)}&{\left( {\left( {{h_2},t} \right),\left( {{h_2},f} \right)} \right)}\\ {\left( {\left( {{h_5},t} \right),\left( {{h_5},f} \right)} \right)}&{\left( {\left( {{h_3},t} \right),\left( {{h_5},f} \right)} \right)}&{\left( {\left( {{h_2},t} \right),\left( {{h_3},f} \right)} \right)}&{\left( {\left( {{h_3},t} \right),\left( {{h_4},f} \right)} \right)}&{\left( {\left( {{h_3},t} \right),\left( {{h_3},f} \right)} \right)}&{\left( {\left( {{h_2},t} \right),\left( {{h_5},f} \right)} \right)}\\ {\left( {\left( {{h_4},t} \right),\left( {{h_4},f} \right)} \right)}&{\left( {\left( {{h_2},t} \right),\left( {{h_4},f} \right)} \right)}&{\left( {\left( {{h_3},t} \right),\left( {{h_4},f} \right)} \right)}&{\left( {\left( {{h_4},t} \right),\left( {{h_5},f} \right)} \right)}&{\left( {\left( {{h_3},t} \right),\left( {{h_3},f} \right)} \right)}&{\left( {\left( {{h_3},t} \right),\left( {{h_3},f} \right)} \right)}\\ {\left( {\left( {{h_3},t} \right),\left( {{h_5},f} \right)} \right)}&{\left( {\left( {{h_3},t} \right),\left( {{h_3},f} \right)} \right)}&{\left( {\left( {{h_4},t} \right),\left( {{h_5},f} \right)} \right)}&{\left( {\left( {{h_1},t} \right),\left( {{h_3},f} \right)} \right)}&{\left( {\left( {{h_2},t} \right),\left( {{h_4},f} \right)} \right)}&{\left( {\left( {{h_4},t} \right),\left( {{h_5},f} \right)} \right)} \end{array}} \right] $ |
2) 该决策中的6个属性均为效益型属性,确定语言真值直觉模糊正、负理想点。
语言真值直觉模糊正理想点为
| $ {A^ + } = \left( {r_1^ + ,r_2^ + , \cdots ,r_n^ + } \right) $ |
式中:
| $ \begin{array}{l} r_1^ + = \left( {\left( {{h_5},t} \right),\left( {{h_5},f} \right)} \right),r_2^ + = \left( {\left( {{h_3},t} \right),\left( {{h_5},f} \right)} \right)\\ r_3^ + = \left( {\left( {{h_4},t} \right),\left( {{h_5},f} \right)} \right),r_4^ + = \left( {\left( {{h_4},t} \right),\left( {{h_5},f} \right)} \right)\\ r_5^ + = \left( {\left( {{h_5},t} \right),\left( {{h_5},f} \right)} \right),r_6^ + = \left( {\left( {{h_4},t} \right),\left( {{h_5},f} \right)} \right) \end{array} $ |
语言真值直觉模糊负理想点为
| $ {A^ - } = \left( {r_1^ - ,r_2^ - , \cdots ,r_n^ - } \right) $ |
式中:
| $ \begin{array}{l} r_1^ - = \left( {\left( {{h_3},t} \right),\left( {{h_4},f} \right)} \right),r_2^ - = \left( {\left( {{h_2},t} \right),\left( {{h_3},f} \right)} \right)\\ r_3^ - = \left( {\left( {{h_2},t} \right),\left( {{h_3},f} \right)} \right),r_4^ - = \left( {\left( {{h_1},t} \right),\left( {{h_3},f} \right)} \right)\\ r_5^ - = \left( {\left( {{h_2},t} \right),\left( {{h_3},f} \right)} \right),r_6^ - = \left( {\left( {{h_2},t} \right),\left( {{h_2},f} \right)} \right) \end{array} $ |
3) 取权重w=(0.1, 0.2, 0.15, 0.2, 0.15, 0.2),分别计算各方案与语言真值直觉模糊正、负理想方案之间的距离:
① 方案Ai与语言真值直觉模糊正理想方案之间的距离为
| $ \begin{array}{*{20}{c}} {d\left( {{A_1},{A^ + }} \right) = }\\ {\sum\limits_{j = 1}^n {{w_j}{d_{{\rm{LIF}}}}\left( {{r_{1j}},r_j^ + } \right)} = }\\ {0.1{d_{{\rm{LIF}}}}\left( {{r_{11}},r_1^ + } \right) + 0.2{d_{{\rm{LIF}}}}\left( {{r_{12}},r_2^ + } \right) + }\\ {0.15{d_{{\rm{LIF}}}}\left( {{r_{13}},r_3^ + } \right) + 0.2{d_{{\rm{LIF}}}}\left( {{r_{14}},r_4^ + } \right) + }\\ {0.15{d_{{\rm{LIF}}}}\left( {{r_{15}},r_5^ + } \right) + 0.2{d_{{\rm{LIF}}}}\left( {{r_{16}},r_6^ + } \right) = }\\ {0.1 \times \frac{3}{8} + 0.2 \times \frac{2}{8} + 0.15 \times \frac{1}{8} + 0.2 \times \frac{2}{8} + }\\ {0.15 \times 0 + 0.2 \times \frac{5}{8} = 0.281\;25} \end{array} $ |
同理可得,d(A2, A+)=0.25,d(A3, A+)=0.262 5,d(A4, A+)=0.275。
② 方案Ai与语言真值直觉模糊负理想方案之间的距离为
| $ \begin{array}{*{20}{c}} {d\left( {{A_1},{A^ - }} \right) = }\\ {\sum\limits_{j = 1}^n {{w_j}{d_{{\rm{LIF}}}}\left( {{r_{1j}},r_j^ - } \right)} = }\\ {0.1{d_{{\rm{LIF}}}}\left( {{r_{11}},r_1^ - } \right) + 0.2{d_{{\rm{LIF}}}}\left( {{r_{12}},r_2^ - } \right) + }\\ {0.15{d_{{\rm{LIF}}}}\left( {{r_{13}},r_3^ - } \right) + 0.2{d_{{\rm{LIF}}}}\left( {{r_{14}},r_4^ - } \right) + }\\ {0.15{d_{{\rm{LIF}}}}\left( {{r_{15}},r_5^ - } \right) + 0.2{d_{{\rm{LIF}}}}\left( {{r_{16}},r_6^ - } \right) = }\\ {0.1 \times 0 + 0.2 \times \frac{1}{8} + 0.15 \times \frac{3}{8} + 0.2 \times \frac{3}{8} + }\\ {0.15 \times \frac{5}{8} + 0.2 \times 0 = 0.25} \end{array} $ |
同理可得,d(A2, A-)=0.281 25,d(A3, A-)=0.268 875,d(A4, A-) =0.256 25。
4) 计算方案Ai与理想方案的相对贴近度为
| $ \begin{array}{*{20}{c}} {\left( {{A_1}} \right) = \frac{{d\left( {{A_1},{A^ - }} \right)}}{{d\left( {{A_1},{A^ + }} \right) + d\left( {{A_1},{A^ - }} \right)}} = }\\ {\frac{{0.25}}{{0.281\;25 + 0.25}} = 0.470\;6} \end{array} $ |
同理可得,C(A2)=0.529 4,C(A3)=0.505 9,C(A4)=0.472 9。
5) 根据相对贴近度C(Ai)对方案Ai进行排序:
| $ {A_2} > {A_3} > {A_4} > {A_1} $ |
因此,最佳企业是A2。
表 2和表 3分别为属性权重的语言值变量和属性的语言值变量。
| 表 2 属性权重的语言值变量 Tab.2 Linguistic variables for weight of attributes |
| 表 3 属性的语言值变量 Tab.3 Linguistic variables for attributes |
1) 取案例评估值的真值部分,且转换成三角模糊数形式表示,则决策矩阵R′及属性权重如表 4所示。
| 表 4 决策矩阵R′及属性权重 Tab.4 The decision matrix R′ and weights of attributes |
2) 对决策矩阵进行规范化并加权,得到模糊加权规范化决策矩阵V,如表 5所示。
| 表 5 模糊加权规范化矩阵V Tab.5 The fuzzy weighted normalized decision matrix V |
针对上面例子,我们根据文献[16]中的决策方法计算,并将两种算法进行对比,如表 6所示。由表 6可知,两种方法均选择A2作为最佳企业,说明本文方法具有合理性。在最终的排序过程中,A1、A3、A4的排序有稍微的不同,有两方面原因:1) 利用文献[16]的方法对案例进行计算过程时,由于文献[16]的语言值只是从正面对属性进行评价,因此只取语言真值直觉模糊对的真值部分,假值部分的信息在计算过程中缺失,对最终的排序结果有一定的影响;2) 本文案例的权重为数值形式,而文献[16]的权重为语言值形式,因此权重在转换成三角模糊数过程中,信息有一定的缺失,对最终的排序结果有相对的影响。
| 表 6 算法对比 Tab.6 Algorithm comparison |
与文献[16]的决策方法相比,本文方法具有:
1) 文献[16]的语言值只是从正面对属性进行评价,而本文使用的语言真值直觉模糊对形式的语言值既可以从正反两方面进行评估,也可同时处理信息的可比性与不可比性;文献[16]将语言值转换成三角模糊数形式进行运算,而本文直接对语言值进行运算。
2) 文献[16]中的模糊正、负理想点为固定值,即(1, 1, 1) 和(0, 0, 0),而本文中的语言真值直觉模糊正、负理想点需要计算进行确定,该理想点确定方法可以同时确定可比的和不可比的语言值信息的理想点。
3) 相对于文献[16]中的三角模糊数之间的距离公式,本文提出了语言真值直觉模糊对之间的归一化距离算法,利用该距离公式得到相对贴近度,并进行决策排序,使该决策方法具有较高的实用价值。
5 结束语为解决具有模糊语言值信息的决策问题,提出了基于TOPSIS的语言真值直觉模糊多属性决策方法。将传统的TOPSIS方法拓展到语言真值直觉模糊格上,给出了语言真值直觉模糊正、负理想点的计算公式及语言真值直觉模糊对之间的归一化距离公式,通过相对贴近度的大小排序进行择优。以评选最佳风险投资公司为例,说明本文方法的有效性及可行性。
本文所提出的决策方法可操作性强,适合在实际中应用。下一步将对属性权重的确立方法进行深入研究,并将其运用到决策、评价等领域中。
| [1] |
ZADEH L A. Fuzzy sets[J]. Information and control, 1965, 8(3): 338-353. DOI:10.1016/S0019-9958(65)90241-X ( 0) 0)
|
| [2] |
王跃, 杨燕, 王红军, 等. 一种基于少量标签的改进迁移模糊聚类[J]. 智能系统学报, 2016, 11(3): 310-317. WANG Yue, YANG Yan, WANG Hongjun, et al. An improved transfer fuzzy clustering with few labels[J]. CAAI transactions on intelligent systems, 2016, 11(3): 310-317. (  0) 0)
|
| [3] |
李滔, 王士同. 适合大规模数据集的增量式模糊聚类算法[J]. 智能系统学报, 2016, 11(2): 188-199. LI Tao, WANG Shitong. Incremental fuzzy (c+p)-means clustering for large data[J]. CAAI transactions on intelligent systems, 2016, 11(2): 188-199. (  0) 0)
|
| [4] |
ATANASSOV K. Intuionistic fuzzy sets[J]. Fuzzy sets and systems, 1986, 20(1): 87-96. DOI:10.1016/S0165-0114(86)80034-3 ( 0) 0)
|
| [5] |
ATANASSOV K. More on intuionistic fuzzy sets[J]. Fuzzy sets and systems, 1989, 33(1): 37-45. DOI:10.1016/0165-0114(89)90215-7 ( 0) 0)
|
| [6] |
SZMIDT E, KACPRZYK J. Entropy for intuitionistic fuzzy sets[J]. Fuzzy sets and systems, 2011(118): 467-477. ( 0) 0)
|
| [7] |
WANG Y, WEN X, ZOU L. 10-Elements linguistic truth-valued intuitionistic fuzzy first-order logic system[M]. Springer Berlin Heidelberg, 2015: 407-417.
( 0) 0)
|
| [8] |
牛强. 基于区间直觉集的互联网金融模式择优方法[J]. 统计与决策, 2016(1): 66-68. NIU Qiang. Internet financial model optimizing method based on interval intuitionistic sets[J]. Statistics and decision, 2016(1): 66-68. (  0) 0)
|
| [9] |
XU Y, LI X, LIU J, et al. Determination of α-resolution for lattice-valued first-order logic based on lattice implication algebra[C]//2007 International conference on Intelligent Systems and Knowledge Engineering. 2007:1567-1574.
( 0) 0)
|
| [10] |
XU Yang, MA Jun. Linguistic truth-valued lattice implication algebra and its properties[C]//The Proceedings of the IMACS Multi-conference on Computational Engineering in Systems Applications. Beijing, 2006:1413-1418.
( 0) 0)
|
| [11] |
邹丽. 基于语言真值格蕴涵代数的格值命题逻辑及其归结自动推理研究[D]. 成都: 西南交通大学, 2010: 1-160. ZOU Li. Studies on lattice-valued propositional logic and its resolution-based automatic reasoning based on linguistic truth-valued lattice implication algebra[D]. Cheng Du:Southwest Jiaotong University, 2010:1-160. http://cdmd.cnki.com.cn/Article/CDMD-10613-1011234257.htm (  0) 0)
|
| [12] |
HWANG C L, YOON K. Multiple attribute decision making:methods and applications[M]. NewYork: Springer-Verlag, 1981.
( 0) 0)
|
| [13] |
JOSHI D, KUMAR S. Intuitionistic fuzzy entropy and distance measure based TOPSIS method for multi-criteria decision making[J]. Egyptian informatics journal, 2014, 15(2): 97-104. DOI:10.1016/j.eij.2014.03.002 ( 0) 0)
|
| [14] |
CHEN S M, CHENG S H, LAN T C. Multicriteria decision making based on the TOPSIS method and similarity measures between intuitionistic fuzzy values[J]. Information sciences, 2016, 367: 279-295. ( 0) 0)
|
| [15] |
BISWAS P, PRAMANIK S, GIRI B C. TOPSIS method for multi-attribute group decision-making under single-valued neutrosophic environment[J]. Neural computing and applications, 2016, 27(3): 727-737. DOI:10.1007/s00521-015-1891-2 ( 0) 0)
|
| [16] |
CHEN C T. Extensions of the TOPSIS for group decision-making under fuzzy environment[J]. Fuzzy sets and systems, 2000, 114(1): 1-9. DOI:10.1016/S0165-0114(97)00377-1 ( 0) 0)
|
| [17] |
MAHDAVI I, HEIDARZADE A, SADEGHPOUR-GILDEH B, et al. A general fuzzy TOPSIS model in multiple criteria decision making[J]. The international journal of advanced manufacturing technology, 2009, 45(3/4): 406-420. ( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


