特征选择是指在原始特征空间中选择能让给定任务的评价准则达到最优的特征子集的过程,是模式识别、机器学习等领域中数据预处理的关键步骤之一[1-3]。其主要目标是在不显著降低分类精度和不显著改变类分布情况下选择一个重要特征子集并且移除不相关或不重要的特征,使留下的特征具有更强的分辨率[4]。其中评价准则是特征选择算法中的关键步骤,国内外研究者已设计了多种评价准则,包括距离度量[5]、信息度量[6]和谱图理论[7-8]等方法。由于基于谱图理论的特征选择模型的可理解性及其完备的数学理论,受到了广泛的关注[8-9]。
根据数据是否带有标记,基于谱图理论的特征选择可分为有监督特征选择和无监督特征选择[8-12]。无监督特征选择算法在构造相似性矩阵时不考虑类信息,通常对给出的样本值采用核函数构造相似性矩阵。有监督特征选择算法将类信息引入相似性矩阵中,常根据类别个数来构造对应的相似性矩阵。利用谱图理论进行特征选择的主要思想是对邻接图Laplacian矩阵进行谱分解,其特征向量反映了样本的类属关系[11]。基于该思想,Zhao等[8]设计了一个谱特征选择框架,框架根据相似性矩阵是否考虑类标记信息分别应用于有监督和无监督算法,而选择特征子集过程与具体学习器无关,利用特征对样本分布的影响对特征进行排序。He等[10]结合谱图理论和特征的局部保持能力提出了基于Laplacian得分的特征选择算法。Zhao[8]和He[10]等基于谱图理论的特征选择均仅考虑每个单独的特征按一定的可分性或统计判据进行排队以形成特征序列,并取靠前的特征子集进行学习。该策略仅在各个特征间统计独立且类别正态分布时较优,但特征间具有这种关系仅仅是极少数[13],实际上特征空间中特征之间存在较为紧密的关联性。
针对已有的基于谱图理论有监督特征选择算法存在的上述问题,我们提出融合特征相关的谱特征选择算法,在原始的整个特征空间中不仅考虑每一个特征的区分力,还考虑特征组的区分性能,迭代地寻找对保持数据的局部结构比上一组特征更强的特征组合。由此,提出了基于特征相关的谱特征选择算法(spectral feature selection based on feature correlation,SPFC)。实验结果表明,该算法不仅提高了特征选择的分类性能,而且获得了较高的分类精度下所需特征子集的数量较少。
1 谱特征选择算法谱特征选择算法的主要理论是谱图理论,本文研究的算法是以Laplacian Score特征选择算法为基础,因此本节只介绍图Laplacian矩阵谱分析。
假设训练样本集X=[x1 x2 … xm]T, 类标记y=[y1 y2 … ym]T。用标量Fi(1≤i≤n)记为第i个特征,向量fi表示所有样本在第i个特征上的取值,第j个样本可以表示成xj=(
| $ \mathit{\boldsymbol{S}} _{ij}= \left\{ \begin{array}{l} \frac 1 {{n}_{k}},\ \ {y}_{i}={y}_{j}=k\\ 0,\ \ 其他 \end{array} \right. $ |
式中nk为类别为k的样本个数。
令G为一无向有权图,则邻接矩阵Wij=Sij(1≤i, j≤m), 且W为对称矩阵。令度矩阵D为
| $ \mathit{\boldsymbol{D}}= \left\{ \begin{array}{l} \sum\limits^{m} _{j=1} \mathit{\boldsymbol{W}}_{ji},\ \ j=i\\ 0,\ \ j\ne i \end{array} \right. $ | (1) |
由式(1)可以看出度矩阵D是一个对角矩阵,对角线上的每个元素是邻接矩阵W每一行或每一列的和。度矩阵可以解释为每个样本周围围绕的其他样本的密集度,度矩阵中的元素越大,意味着有更多的样本靠近这个元素代表的样本。
由邻接矩阵和度矩阵得到相应的Laplacian矩阵L和正则化的Laplacian矩阵
| $\mathscr{L}=\mathit{\boldsymbol{D}}-\mathit{\boldsymbol{S}}, \mathscr{L}=\mathit{\boldsymbol{D}}^{-\frac 1 2} \mathit{\boldsymbol{LD}}^{-\frac 1 2}$ |
根据Laplacian矩阵的性质[5],给出下面定义:
定义1 Laplacian矩阵的最小特征值为0,对应特征向量为单位向量
| $\text{let}\ \mathit{\boldsymbol{I}} ={[1 1 \cdots 1]}^\text{T}, \mathit{\boldsymbol{L}}*\mathit{\boldsymbol{I}}=0$ |
定义2 对于任意一个n维向量x(数据集中的特征列),都满足下式成立:
| $\forall \mathit{\boldsymbol{x}}∈\mathit{\boldsymbol{R}}^n, \mathit{\boldsymbol{x}}^\text{T}\mathit{\boldsymbol{Lx}} =\frac 1 2\sum\limits{ \mathit{\boldsymbol{w}}}_{ij}{ (\mathit{\boldsymbol{x}}_i- \mathit{\boldsymbol{x}} _j})^2$ |
定义3 对于任意一个n维向量x(数据集中的特征列),任意一个实数,都有(特征列中的每个元素减去一个相同的值得到的新特征列仍然保持结果不变):
| $\forall x∈{\mathit{\boldsymbol{R}}}^{n}, {\forall t∈R, (\mathit{\boldsymbol{x}}- \mathit{\boldsymbol{t}}*\mathit{\boldsymbol{e}}})^{\text{T}}L( \mathit{\boldsymbol{x}}-\mathit{\boldsymbol{t}}*\mathit{\boldsymbol{e}})={ \mathit{\boldsymbol{x}}}^{\text{T}} \mathit{\boldsymbol{Lx}}$ |
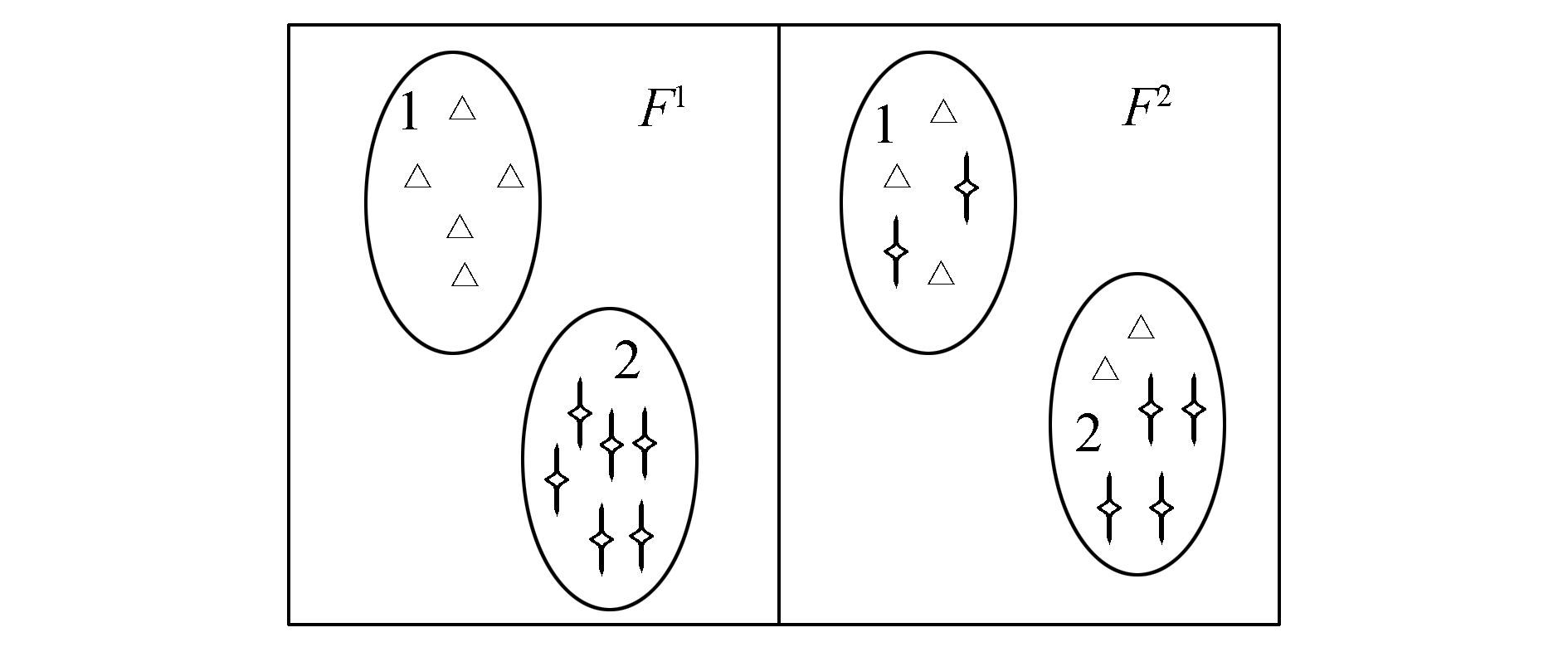
谱图理论说明,Laplacian矩阵的特征值与特征向量包含着数据集的样本分布结构。谱特征选择在选取有强识别度的特征时,以特征取值的分布是否与样本分布的结构保持一致作为特征选择的评价标准。例如在图 1中,每个图形(三角和星)表示一个样本,形状不同意味样本在同一特征上的取值不同,各圆形分别为类1和类2的区域,即同一区域内的样本属于同一类别。在图 1左侧中属于同一类的样本在特征F1上取值近似相同,而不属于同一类的样本在特征F1上取值不同,因此特征F1对类1和类2就有很好的识别能力,此时称特征F1的取值分布与样本分布一致。在图 1右侧中特征F2的取值分布则与样本分布不一致,F2对类1和类2不具有很好的识别能力。因此在谱特征选择算法中会选取F1而不选F2。
|
图 1 特征与样本分布一致性示意图 Fig.1 The characteristics and the sample distribution consistency schematic diagram |
而谱特征选择算法将选择那些与样本分布结构一致的特征,即选择那些使得式(2)取较小值的特征[7]:
| $φ(F^r)=\frac{\sum_{i,j}S_{ij}(f_{ri}-f_{rj})^2} {V(\mathit{\boldsymbol{f}}_r)}$ | (2) |
式中:Fr表示第r个特征, fr是第r个特征向量,fri和frj表示第r个特征上的i, j(1≤i, j≤m)个样本的取值,V(fr)表示第r个特征fr的方差。
一个随机变量x的方差定义为[7]:
| $V(x)=∫\limits_ {M}{(x-u)}^2\text{d}P(x)$ |
式中:M是数据的流行结构,u表示x期望值,dP是一个概率度量。根据谱图理论[7],dP可以用对角矩阵D估计出来,因此特征fr的方差V(fr)为
| $V(\mathit{\boldsymbol{f}}_r)=\sum_i{(f_{ri}-u_r)}^2D_{ii}$ |
式中ur表示第r个特征fr的期望值,定义为
| $u_r=\sum_i \left( f_{ri}\frac{D_{ii}} {\sum_iD_{ii}} \right) =\frac{\sum_if_{ri}D_{ii}} {\sum_i{D}_{ii}}$ |
传统的谱特征选择算法采用单独最优特征组合的启发式搜索策略,用式(2)对每个特征单独度量其重要度,该策略并未考虑特征间的冗余度和交互性,因此需要考虑候选特征与已选特征之间的冗余性和交互性。本文在式(2)的基础上定义了特征组的重要度公式如式(3)。为了度量每个候选特征对已选特征的贡献程度,同时定义了式(4)来计算候选特征的重要度。模型思想是:首先利用传统谱特征选择算法选出使目标函数式(2)最好的一个特征,然后以这个特征为核心据点作为已选特征,依次逐个评价候选特征与已选特征的相关性,即依次根据目标函数(式(3))评价特征组合后的图的保持能力,然后根据式(4)选出保持能力优于未组合时的最强一个特征,并将该特征加入到已选特征中形成新的组合,接着对余下候选特征进行下一轮的迭代。该算法不仅考虑了特征间的相关效应,而且通过式(4)避免了特征间的冗余。
定义特征组相关的目标函数为
| $φ(\mathit{\boldsymbol{F}}_S)=\frac{\text{sqrt}(\sum\limits^k _{r=1}\sum_{i,j}(S_{ij}(f_{ri}-f_{rj})^2)} {\frac{\sum\limits^k _{r=1}\sum_i(f_{ri}-u_r)^2 D_{ii}} k}$ | (3) |
式中:FS表示已选出的特征子集,k表示已选出的特征子集中的特征个数,φ(Fs)表示已选出的特征子集对数据的识别能力。
在式(3)的基础上通过式(4)评估候选特征中能提升已有特征子集的区分能力的特征,其目标函数定义为
| $\text{argminRed}(\mathit{\boldsymbol{f}}_i)_{f_i∈F_U}=φ(\mathit{\boldsymbol{F}}_S∪\mathit{\boldsymbol{F}}_i)-φ(\mathit{\boldsymbol{F}}_S)$ | (4) |
式中:FU表示候选特征集合,fi∈FU,通过评估一个新的特征fi能否使得同类样本距离小而不同类样本距离大来衡量是否加入已选Fs。又在候选特征集合里可能有多个fi能提升已选子集的能力,由式(3)知新加入的fi使得φFS越小越好,因此在多个具有提升子集能力的候选特征中选择使φFS∪fi-φFS最小的一个特征。
根据式(4),可提出基于特征相关的谱特征选择算法(SPFC)的伪代码如算法1所示。
算法1 基于特征相关的谱特征选择算法(SPFC)
输入 样本集X,类标记Y;
输出 FS特征相关后的特征序列。
1)FS=
2)依据X、Y计算每两个样本间的相似度矩阵Sij(1≤i, j≤m);
3)依据相似度构建Laplacian图G,并计算W、D、L;
4)根据传统谱特征选择算法求出最具有识别力的一个特征fi
| $\mathit{\boldsymbol{F}}_S=\mathit{\boldsymbol{F}}_S∪\mathit{\boldsymbol{f}}_i,\mathit{\boldsymbol{F}}_U= \mathit{\boldsymbol{F}}_U-\{\mathit{\boldsymbol{f}}_i\};$ |
5)while FU不为空
6)根据式(3)计算φ(FS);
7)for i=1 to length(FU)
if (φ(FS)∪fi)-φ(FS))>0 then
L(j)=φ(FS)∪(fi)-φ(FS);
j=j+1;
end if
8) end for
9) 将L按升序排序
FS=FS∪fL(1),FU=FU-{fL(1)};
10) end while
3 实验设计与对比 3.1 实验数据为了进一步验证SPFC算法的有效性,本文从UCI (http://www.ics.uci.edu)中选择8个数据集,各数据集相应的描述信息见表 1, 在表 1~3中australian_credit数据集简写为AC,VeteranLungCancer数据集简写为VE。
| 表 1 实验数据描述 Tab.1 Experimental data description |
为了验证SPFC算法的性能,实验分为两部分。第1组实验与CFS[14]、ChiSquare[15]、FCBF[16]、Laplacian[10]、NRS[17]以及Relief[18]算法进行比较由特征子集诱导出来的分类精度。另一组实验采用Friedman test[19]和Bonferroni-Dunn test[20]在统计上对比SPFC与其他算法在8个数据集上的实验结果。由于ChiSquare、Laplacian、FCFS、Relief这4种算法得到的是一个特征序列,而CFS、FCBF、NRS 3种算法得到的是子集约简,因此,ChiSquare、Fisher、FCFS、Relief这4种算法得到的特征序列取前k个特征作特征子集,其中k为CFS、FCBF、NRS算法中得到的3个约简子集数量的最小值。此外,NRS算法中的邻域参数值δ为0.10。在实验中,采用十折交叉验证法进行评价特征子集的优劣,用KNN(K=10)、CART 2个不同的基分类器来评价分类精度。
实验1 为了比较特征选择后的分类精度,在表 2~4中,分别采用KNN(K=10)、CART这2个不同的基分类器进行特征子集分类精度的评价。此外,为了更加直观地比较不同方法得到的特征子集的性能,表 2、3中加粗的数值表示最高分类进度,下划线表示精度次优,最后一行表示不同算法得到的特征子集的平均分类精度,最后一行中加下划线的数值表示平均分类精度最高的值。另外,括号里面的数值表示数据的标准差,括号外面的数值表示分类精度。
| 表 2 不同特征选择算法在KNN分类器下的分类精度比较 Tab.2 Classification accuracies of feature selection with different algorithms based on KNN |
| 表 3 不同特征选择算法在CART分类器下的分类精度比较 Tab.3 Classification accuracies of feature selection with different algorithms based on CART |
1)从总体上看,SPFC算法相比CFS、ChiSquare、FCBF、Laplacian、NRS以及Relief算法在KNN、CART基分类器下表现稳定,且均获得最高平均分类精度。相比考虑类信息的传统谱特征选择算法Laplacian, SPFC算法优于Laplacian。
2)相比ChiSquare、Laplacian、Relief这3种同样获得特征系列的算法,SPFC算法以相同的前k个特征在不同的基分类器下获得的平均分精度明显较高,相比子集约简的算法CFS、FCBF、NRS,SPFC取它们子集约简数量的最小值在两个基分类器下分类精度明显要高于NRS,在CART基分类器下SPFC的分类精度高于CFS、FCBF达两个百分点以上,而在KNN基分类器下也显著高于CFS、FCBF。
3)每一种算法均会在某一个分类器上某个数据集上获得最高分类精度,但只有SPFC能在两个基分类器上多个数据集上获得最高分类精度。SPFC算法在数据集ICU、rice、zoo上性能提升更为明显,在两个分类器上均达到最高。而ICU为混合型数据,rice为连续型数据、zoo为离散型数据。说明SPFC可以处理多类型数据集,在大部分各类型数据集上SPFC均能达到较好的稳定表现。
实验2 为了进一步研究比较SPFC算法与其他算法在两个分类器下的分类性能是否明显不同,我们采用Friedman test和Bonferroni-Dunn在统计上进行验证。Friedman统计值定义为
| $x^2_F=\frac{12N} {k(k+1)} \left[ \sum\limits^{k} _{i=1} {R}^2_i-\frac{k{(k+1)}^2} 4\right]\\ F_F=\frac{(N-1)x^2_F} {N(k-1)-x^2_F}$ | (5) |
式中:k代表对比算法个数,N表示数据集个数,Ri表示第i个算法在8个数据集上的排序均值(见表 4)。由表 4结合式(5)算出KNN分类器下FF的值为2.18,cart分类器下FF的值为3.05,又当显著性水平a=0.1时F(6, 42)=1.87,因此在两个分类器下都拒绝了零假设(所有算法性能相等),这时还需要结合特定的post-hoc test来进一步分析各个算法性能的差异。本文采用显著性水平为0.1的Bonferroni-Dunn test。在这里定义两个算法的不同用下面的临界差:
| ${\text{CD}}_α=q_α \sqrt{\frac{k(k+1)} {6N}}$ |
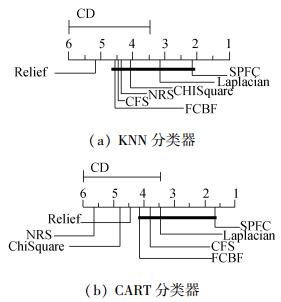
在Bonferroni-Dunn test里显著性水平为0.1且7个算法对比时qα=2.394,因此CD=2.58(k=7, N=8)。如果两个算法在所有数据集上的平均排序的差不低于临界差CD,则认为它们有显著性差异。图 2给出了在两个分类器下SPFC算法与其他算法的比较,其中,每个子图中最上行为临界值,坐标轴画出了各种算法的平均排序且最左(右)边的平均排序最高(低)。用一根加粗的线连接性能没有显著差异的算法组。
从图 2可以直观看出在KNN分类器下,SPEC算法显著优于Relief算法,虽然与其他算法没有显著差别,但可以看出SPFC算法性能要高于其他算法;在CART分类器下SPFC算法性能显著优于算法NRS、ChiSquare、Relief,而与算法Laplacain、CFS、FCBF性能相当,但性能相当的同一组里SPFC算法要远远优于算法Laplacain、CFS、FCBF。
| 表 4 不同算法在两个分类器下的排序均值表 Tab.4 Different algorithms under the two classifiers the mean of sorting table |
|
图 2 在KNN和CART分类器下SPEC与其他算法的比较 Fig.2 SPEC compared with other algorithms Under the CART and KNN classifier |
本文针对传统的谱特征选择只考虑特征的单独最优组合问题进行改进,提出基于谱图理论的特征相关的特征选择算法,本文研究发现:1) 引入特征之间的统计相关性到谱特征选择中,能有效地解决有用特征可能是冗余的问题;2)在公开的UCI数据集上的实验结果表明, 本文算法能够选择较少的特征,获得较好的分类精度;3)由表 2~4中的数据亦看出考虑特征间的相关性算法(SPEC)比不考虑特征间相关性算法(Laplacian)能显著提高特征子集的分类性能。但由于本文实验采用欧式距离统计特征间的相关性,而欧式距离对于高维特征的计算差值变化不大,因此对于高维特征间的相关性的设计有待进一步研究。
| [1] |
LIN Yaojin, Li Jinjin, LIN Peirong, et al. Feature selection via neighborhood multi-granulation fusion[J]. Knowledge-based systems, 2014, 67: 162-168. DOI:10.1016/j.knosys.2014.05.019 ( 0) 0)
|
| [2] |
MANORANJAN D, LIU Huan. Consistency-based search in feature selection[J]. Artificial intelligence, 2003, 151(1): 155-176. ( 0) 0)
|
| [3] |
ZHANG C, ARUN K, CHRISTOPHER R. Materialization optimizations for feature selection workloads[J]. ACM transactions on database systems, 2016, 41(1): 2. ( 0) 0)
|
| [4] |
曹晋, 张莉, 李凡长. 一种基于支持向量数据描述的特征选择算法[J]. 智能系统学报, 2015, 10(2): 215-220. CAO Jin, ZHANG li, LI Fanchang. A feature selection algorithm based on support vector data description[J]. CAAI transactions on intelligent systems, 2015, 10(2): 215-220. (  0) 0)
|
| [5] |
MANORANJAN D, LIU Huan. Feature selection for classification[J]. Intelligent data analysis, 1997, 1(3): 131-156. ( 0) 0)
|
| [6] |
SUN Yujing, WANG Fei, WANG Bo, et al. Correlation feature selection and mutual information theory based quantitative research on meteorological impact factors of module temperature for solar photovoltaic systems[J]. Energies, 2016, 10(1): 7. DOI:10.3390/en10010007 ( 0) 0)
|
| [7] |
CVETKOVIC D M, ROWLINSON P. Spectral graph theory[J]. Topics in algebraic graph theory, 2004: 88-112. ( 0) 0)
|
| [8] |
ZHAO Zheng, LIU Huan. Spectral feature selection for supervised and unsupervised learning[C]//Proceedings of the 24th international conference on Machine learning. ACM, 2007:1151-1157.
( 0) 0)
|
| [9] |
ZHAO Zhou, HE Xiaofei, CAI Deng, et al. Graph regularized feature selection with data reconstruction[J]. IEEE transactions on knowledge and data engineering, 2016, 28(3): 689-700. DOI:10.1109/TKDE.2015.2493537 ( 0) 0)
|
| [10] |
HE Xiaofei, CAI Deng, NIYONGI P. Laplacian score for feature selection[M]. Cambridge: MIT Press, MA, 2005: 507-514.
( 0) 0)
|
| [11] |
BELABBAS M A, WOLFE P J. Spectral method in machine learning and new strategies for very large datasets[J]. Proceedings of the national academy of sciences, 2009, 106(2): 369-374. DOI:10.1073/pnas.0810600105 ( 0) 0)
|
| [12] |
WANG Xiaodong, ZHANG Xu, ZENG Zhiqiang, et al. Unsupervised spectral feature selection with l 1-norm graph[J]. Neurocomputing, 2016, 200: 47-54. DOI:10.1016/j.neucom.2016.03.017 ( 0) 0)
|
| [13] |
边肇祺, 张学工. 模式识别[M]. 2版. 北京: 清华大学出版社, 2000.
( 0) 0)
|
| [14] |
HALL M A. Correlation-based feature selection for discrete and numeric class machine learning[C]//the 17th International Conference on Machine Learning. San Francisco:Morgan Kaufmann, 2000:359-366.
( 0) 0)
|
| [15] |
ANDREAS W, ANDREAS P. Attacks on stegan ographic systems[M]. Heidelberg, Berlin: Springer-Verlag, 2000: 61-76.
( 0) 0)
|
| [16] |
YU Lei, LIU Huan. Efficient feature selection via analysis of relevance and redundancy[J]. Journal of machine learning research, 2004, 5(1): 1205-1224. ( 0) 0)
|
| [17] |
HU Qinghua, YU Daren, LIU Jinfu, et al. Neighborhood rough set based heterogeneous feature subset selection[J]. Information sciences, 2008, 178(18): 3577-3594. DOI:10.1016/j.ins.2008.05.024 ( 0) 0)
|
| [18] |
CRAMMER K, GILAD-BACHRACH R, NAVOT A. Margin analysis of the lvq algorithm[C]//Advances in Neural Information Processing Systems. 2002, 14:462-469.
( 0) 0)
|
| [19] |
FRIEDMAN M. A comparison of alternative tests of significance for the problem of m rankings[J]. The annals of mathematical statistics, 1940, 11(1): 86-92. DOI:10.1214/aoms/1177731944 ( 0) 0)
|
| [20] |
DUNN O J. Multiple comparisons among means[J]. Journal of the american statistical association, 1961, 56(293): 52-64. DOI:10.1080/01621459.1961.10482090 ( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


