M气田为渤海湾盆地大型变质岩潜山凝析气田,主要含气段位于太古界潜山裂缝性储层[1-2],钻井揭示潜山裂缝储层发育规律复杂,裂缝带发育主要受古地貌与微古地貌、断裂期次、潜山内幕高陡断缝体三个主控因素共同控制,实现多尺度裂缝带预测是M气田开发阶段储量动用与井位部署面临的核心问题[3]。
地震裂缝预测方法分为叠前、叠后两大类,预测结果通常为大、中尺度裂缝带,尺度范围在数十米至千米之间[4-6]。叠前裂缝预测结果预测尺度相对更精细[7-8],但该方法完全基于地震数据驱动,地质模式认识难以干预裂缝预测过程,因此常导致预测结果缺乏地质意义。叠后裂缝预测主要表征宏观、大尺度裂缝带或断裂带分布[9-11],可以根据不同地质主控因素应用相应的地球物理技术,从而有效提升预测结果与地质认识的吻合度。例如,当裂缝发育主要受地层构造作用控制时,用于刻画地层变形程度的面曲率属性能较好地预测断裂带分布[12-13]。以区域断裂主要发育方向和角度作为先验约束,应用蚂蚁体等断裂检测属性对微断裂带预测效果较好[14-15],通过表征构造缝发育带主控断裂的特征,能够有效预测构造裂缝区带发育规律[16-17]。现有各类地震预测方法多从相同尺度预测裂缝储层发育特征,针对多尺度裂缝带综合预测问题也有相关研究报道[18-19],但是聚焦不同尺度预测结果有效融合的研究相对较少,而实现多尺度裂缝带综合表征对于反映潜山裂缝储层发育规律具有重要意义。
地震属性融合是综合反映多种预测信息的有效途径,可用于多尺度裂缝带综合预测。目前有基于简单线性加权[20-21]、小波变换[14, 22]以及机器学习神经网络[23-24]三类属性融合手段。近年来,随着小波变换的不断升级、衍化,基于小波变换衍化技术的多属性融合在灵活表达多尺度信息(如局部性和方向性)方面的优势进一步突出,因而得到广泛应用。
本文提出基于主控因素的潜山裂缝储层多尺度预测与有效融合技术。首先,分析不同尺度裂缝主控因素并采用对应属性进行表征。太古界潜山沟—脊微地貌形态是M气田潜山风化缝的主控因素[25],利用曲率属性预测潜山风化成因宏观尺度裂缝富集条带;燕山—喜山期发育的近EW向高陡断缝体是潜山构造缝发育的主控断裂[26],基于Radon变换技术预测大尺度潜山内幕高陡断缝体;以区域断裂发育方向与倾角为约束,利用蚂蚁体属性预测中、小尺度潜山微断裂带。其次,利用Contourlet变换技术依次分解上述三种属性并获得低频端与高频端分量,通过设计低频端与高频端融合规则,实现三种不同尺度预测结果的有效融合,从而综合反映M气田太古界潜山裂缝储层多尺度发育特征[27]。
1 沟—脊微地貌演化与风化缝富集条带预测M气田潜山风化缝的发育受古地貌影响,同时也受沟—脊微地貌形态的控制。沟—脊微地貌的演化可以描述为:①潜山内幕发育大量古断层,使潜山顶面呈现高、低起伏的初始地貌特征;②古断层附近岩体风化剥蚀速度快,古断层上、下盘与断面逐渐被侵蚀成为沟谷形态;③随着地层年代推移,古断层被持续风化剥蚀,最后造就潜山顶面高、低起伏的沟—脊残留地貌。“沟”与“脊”通常相伴出现,其中“脊”为古断层剥蚀残留后上升盘的高部位,风化缝集中发育;“沟”则对应古断层下降盘。钻井资料证实,钻在“脊”部位的探井揭示风化带储层发育(图 1左),因此对“脊”地貌的刻画能够反映M气田潜山风化缝富集条带。
|
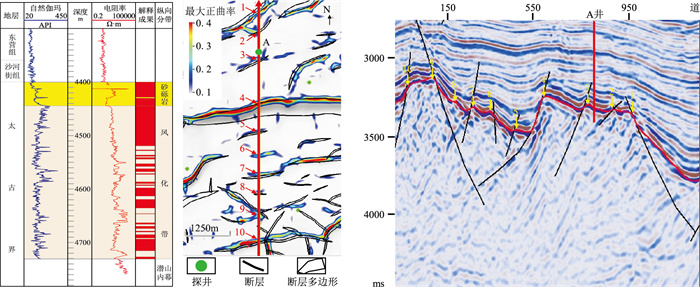
图 1 “脊”部位A井测井解释结果(左)、最大正曲率属性(中)及地震剖面刻画潜山沟―脊地貌(右) |
曲率属性为地震数据或构造面的二阶导数运算结果,常用于刻画地层挠曲程度。M气田太古界潜山沟—脊微地貌特征表现为潜山顶面高、低起伏,适合利用曲率属性表征。首先通过三维自动追踪精细解释潜山顶面,然后利用最大正曲率属性预测沟—脊地貌中“脊”的平面分布(图 1中)。与地震剖面的标定结果显示(图 1右):最大正曲率属性与潜山顶面“脊”的位置匹配较好。同时,最大正曲率值较大区域附近均有断层发育。沟—脊地貌与断层发育部位对应关系较好,进一步说明最大正曲率属性能够相对客观地预测潜山风化缝富集条带。
2 断裂期次与潜山高陡断缝体预测曲率属性描述了宏观尺度潜山风化缝富集条带平面分布,而针对更细一级的大尺度断裂带平面分布描述,厘清影响M气田潜山构造缝发育的主控断层是关键。
前人研究表明,M气田历经印支、燕山、喜山三期构造运动,太古界潜山构造主要受燕山期(晚三叠—白垩纪)和喜山期(新生代)两期构造运动所控制。燕山期太平洋板块沿NWW方向向东亚大陆俯冲,郯庐断裂发生左旋挤压,派生出大量NE向断层。喜山早期渤海湾盆地进入拉张裂陷阶段,在近SN向的拉张作用下,形成大量EW向张性正断层[28-29]。在此构造背景下,断裂系统主要分为四类(图 2):Ⅰ类为燕山早期发育的太古界潜山内幕断层,以近EW向和NE-SW向为主,具有高角度(35°~70°)特征,对潜山裂缝发育起重要控制作用;Ⅱ类为燕山中期—喜山早期发育的长期活动断裂,以南倾为主,与Ⅰ类断层走向、倾角一致,对裂缝发育也起到重要控制作用;Ⅲ类为喜山期活动的走滑断层,近SW向展布,将M气田分割为不同构造带,对裂缝发育起局部改造作用;Ⅳ类断裂为喜山中、晚期活动的晚期断层,以北倾为主,对裂缝发育影响有限。

|
图 2 M气田太古界潜山主要断层分类平面(左)、剖面(右)显示 |
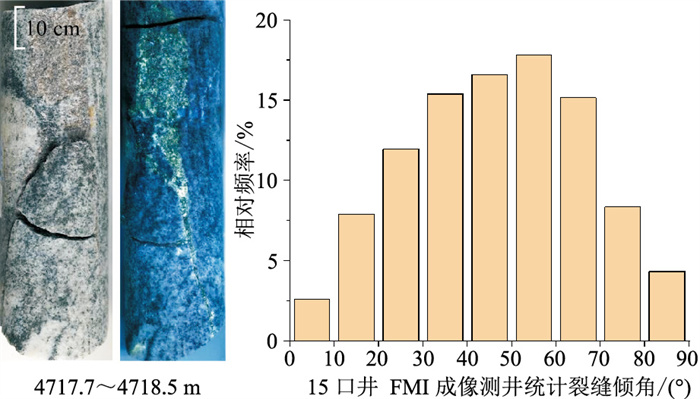
另一方面,FMI成像测井与岩心资料证实M气田太古界潜山内幕以中—高角度构造缝发育为主(图 3),通过野外露头调研、类比现代花岗岩地貌认为,该地区地震剖面上潜山内幕高陡、断续、强反射(图 4)的主要成因可能是规模发育的高角度及垂直的断裂节理面,裂缝依附于节理面发育,节理控制裂缝整体发育格局。节理面历经沉降、活化形成高陡断缝体,对应地震剖面上看到的潜山内幕高角度反射。
|
图 3 A井岩心(左)与FMI测井裂缝统计(右) |
|
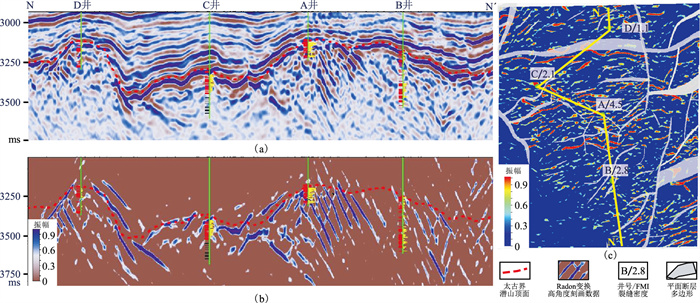
图 4 地震剖面(a)、Radon变换高陡反射刻画数据剖面(b)及沿潜山顶面振幅切片(c) 井柱左侧为流体解释结论,红色代表气层,黑色代表干层;右侧曲线为裂缝密度。 |
此外,井—震标定结果显示(图 4): 地震剖面上高角度反射发育部位井上储层含气性相对较好,如A井附近地震高角度反射最发育,含气性较好,裂缝密度为4口井中最高。C、D井附近地震高角度反射不发育,含气性一般、裂缝密度较低。说明地震高角度反射与潜山高陡断缝体具有一定程度相关性。
目前没有直接证据表明地震高角度反射是潜山内幕高陡断缝体的响应,但现阶段渤海湾盆地2个太古界潜山油气田勘探开发实践表明,地震高角度反射预测结果与探井、开发井认识基本吻合,预测的高陡断缝体发育部位裂缝储层相对发育,说明对高陡断缝体的识别与刻画是M气田裂缝储层预测的重要方向。此外正演模型实验结果[7]表明,潜山内幕发育高陡断层会在地震剖面上形成高角度反射特征。
Radon变换是数字信号处理领域经典技术,常用于解决数据保幅重建等问题[30-31],通过对数据沿特定空间路径积分,将具有规律排列的信号分解为Radon域的稀疏散点,进一步改变积分路径,就能够追踪地震数据中具有不同几何形态的反射信息,最后利用反Radon变换实现时—空域反射信号的分离。将Radon变换技术引入地震资料解释领域,可实现潜山内幕高陡反射信号的刻画与预测。Radon变换表达式为
| $ m({p}_{x}, {p}_{y}, \tau )=\sum\limits _{x}\sum\limits _{y}d(x, y, t=\tau +{p}_{x}x+{p}_{y}y) $ | (1) |
反Radon变换公式为
| $ d(x, y, t)=\sum\limits _{{p}_{x}}\sum\limits _{{p}_{y}}m({p}_{x}, {p}_{y}, \tau =t-{p}_{x}x-{p}_{y}y) $ | (2) |
式中:m(·)为三维地震数据体d(·)在Radon域的变换结果;x、y、t分别代表主测线、联络测线和时间;
通过Fourier变换将式(2)用经典矩阵—向量系统表达为
| $ \boldsymbol{d}=\boldsymbol{L}\boldsymbol{m} $ | (3) |
式中:d为t-x-y域三维地震数据;L为Radon变换算子矩阵;m为d经过Radon变换后的Radon域系数矩阵。
利用最小二乘反演框架可求解得到式(3)中系数矩阵m。首先在Radon域压制非高角度反射信号,然后通过反Radon变换将系数阈值结果变换至t-x-y域,从而实现高陡断缝体的刻画。刻画结果如图 4b所示,可以看到通过Radon变换技术刻画的高角度反射与地震剖面(图 4a)吻合。进一步从Radon变换结果中提取地震属性预测高陡断缝体平面分布(图 4c),结果显示潜山高陡断缝体具有局部集中发育、内部不均匀、不连续特征,同时与FMI成像测井解释裂缝密度整体趋势基本一致。
3 基于蚂蚁体属性的微断裂带预测针对比高陡断缝体更细一级的断层衍生的中、小尺度微断裂,利用蚂蚁体属性开展预测。
M气田太古界潜山主要断裂为近EW向、倾角为中—高角度(35°~70°),以此构造背景为约束计算蚂蚁体属性(图 5),属性预测结果显示:微断裂带围绕大断层集中发育,同时蚂蚁体属性与FMI成像测井解释裂缝密度具有一定程度相关性。A、B井区蚂蚁体属性值整体高,对应成像测井裂缝密度也高;C、D井区蚂蚁体属性值相对低,成像测井密度也较低。同时,蚂蚁体属性预测的微断裂发育方向与邻近断层走向具有较高的一致性(图中黄色箭头标记处),证实蚂蚁体属性预测的微断裂带相对可靠。

|
图 5 蚂蚁体属性沿潜山顶面切片 |
结合多个潜山地震工区测量得到的各种尺度预测裂缝带长度统计结果,本文定性评估了前述三种裂缝带预测结果的尺度范围:①最大正曲率属性预测的风化缝富集条带尺度范围约为10~400 m;②基于Radon变换预测的高陡断缝体尺度范围约为50~200 m;③蚂蚁体属性预测的微断裂带尺度范围约为30~50 m。有效融合这三种尺度地震预测属性对于综合反映M气田太古界潜山裂缝带发育特征具有重要意义。
本文利用Contourlet变换实现多尺度地震预测属性保结构融合,Contourlet变换是近年提出的一种二维信号稀疏表示新方法,与小波变换相比能够较好地捕捉信号的轮廓特征,具有灵活的局部性和方向性,以及多尺度信息表征优势,在图像融合领域应用广泛[22]。Contourlet变换实质是对一维或二维信号进行拉普拉斯金字塔变换(LP)的多尺度分解,再利用方向滤波器组(DFB)对分解得到的各层信号进行二次分解,从而捕获信号的轮廓信息。
在LP多尺度分解程序中,每一层LP分解产生一个下采样低通信号和一个带通信号(即原始信号与下采样低通信号的差值),后续层的LP分解在每层的下采样低通信号上循环进行,N层分解后形成第N层低通信号和N个不同尺度的带通信号。
DFB二次分解程序包括双通道梅花扇形滤波器组与Shearing算子,前者将带通信号频谱分解为水平、垂直、对角线方向,反映相对高频的信息变化;后者实现信号的旋转、平移与拉伸。DFB通过一个l层树形分解实现方向滤波,树形分解将产生2l个锲形频率分割子带,具有方向性与局部化特性。
Contourlet逆变换(重构)通过对第N层的低通信号与DFB二次分解得到的水平、垂直、对角线方向的高频信号进行LP重构(即LP分解的逆过程)来实现。
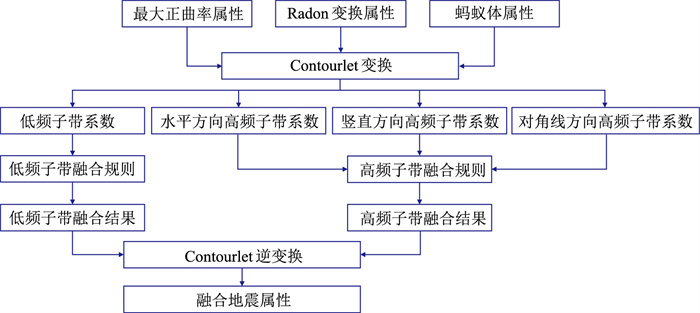
4.1 基于Contourlet变换的多属性融合原理基于Contourlet变换的属性融合流程如图 6所示。首先利用Contourlet变换将最大正曲率、Radon变换属性、蚂蚁体属性进行多级分解,得到三种属性的低频子带系数与不同方向的高频子带系数。然后分别设计低频子带与高频子带融合规则,进一步将分解得到的最大正曲率、Radon变换属性、蚂蚁体属性低频子带系数与高频子带系数分别按照设计规则进行融合,得到Contourlet域的低频子带、高频子带融合结果,最后利用反Contourlet变换得到x-y域三种属性融合结果。
|
图 6 基于Contourlet变换的属性融合流程图 |
经Contourlet变换分解得到三种属性的低、高频子带系数分别为
Contourlet变换得到的低频子带是原始属性的近似表达,反映属性整体特征,基于拉普拉斯能量的低频子带融合规则具有高对比度、自适应的优势,能有效保持各属性的主要信息,拉普拉斯能量计算公式为
| $ \begin{array}{l}{E}_{k}^{L}(i, j)=\left|2{L}_{k}(i, j)-{L}_{k}(i-\mathrm{\Delta }s, j)-{L}_{k}(i+\mathrm{\Delta }s, j)\right|+\\ \left|2{L}_{k}(i, j)-{L}_{k}(i, j-\mathrm{\Delta }s)-{L}_{k}(i, j+\mathrm{\Delta }s)\right|\end{array} $ | (4) |
式中:
| $ {M}_{L}(i, j)={L}_{1}(i, j)\frac{{E}_{1}^{L}(i, j)}{\sum {E}_{1}^{L}(i, j)}+ \\ {L}_{2}(i, j)\frac{{E}_{2}^{L}(i, j)}{\sum {E}_{2}^{L}(i, j)}+ \\ {L}_{3}(i, j)\frac{{E}_{3}^{L}(i, j)}{\sum {E}_{3}^{L}(i, j)} $ | (5) |
式中:
Contourlet变换得到的高频子带主要反映属性的细节与边缘特征,本文基于三种属性高频子带系数的均方根能量分别设计了水平方向、竖直方向、对角线方向高频子带融合规则,从整体上保证为均方根能量更大的高频子带系数配置更大的融合权重,以此强化各个地震属性边缘特征与细节信息在融合过程中的表现。高频子带融合权重计算公式为
| $ {E}_{k}^{n}(i, j)=\frac{{\left[{H}_{k}^{n}(i, j)\right]}^{2}}{{\left[{H}_{k}^{h}(i, j)\right]}^{2}+{\left[{H}_{k}^{v}(i, j)\right]}^{2}+{\left[{H}_{k}^{d}(i, j)\right]}^{2}} $ | (6) |
式中:
| $ \left\{\begin{array}{l}{M}_{\mathrm{h}}(i, j)=\frac{\sum\limits _{k}{E}_{k}^{\mathrm{h}}(i, j){H}_{k}^{\mathrm{h}}(i, j)}{\sum\limits _{k}{E}_{k}^{h}(i, j)}\\ {M}_{\mathrm{v}}(i, j)=\frac{\sum\limits _{k}{E}_{k}^{\mathrm{v}}(i, j){H}_{k}^{\mathrm{v}}(i, j)}{\sum\limits _{k}{E}_{k}^{v}(i, j)}\\ {M}_{\mathrm{d}}(i, j)=\frac{\sum\limits _{k}{E}_{k}^{\mathrm{d}}(i, j)\cdot {H}_{k}^{\mathrm{d}}(i, j)}{\sum\limits _{k}{E}_{k}^{d}(i, j)}\end{array}\right. $ | (7) |
式中
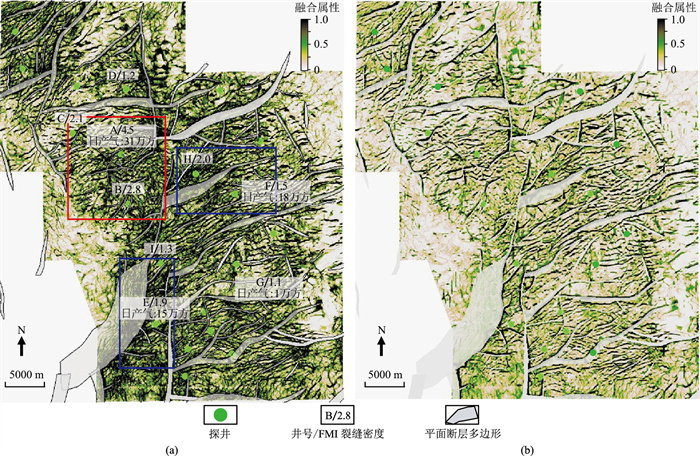
根据式(4)~式(7)得到最大正曲率属性、Radon变换高陡断缝体预测属性、蚂蚁体属性的低频子带及高频子带融合系数,最终利用Contourlet逆变换得到x-y域融合地震属性(图 7a)。由图可见,融合属性在消除多属性冗余的同时,进一步反映了M气田太古界潜山裂缝带多尺度发育特征,整体表现为中、小尺度缝网围绕大尺度断裂带集中发育的特点。对比三种属性按照1:1:1简单线性加权融合的结果(图 7b),本文方法融合结果具有更丰富的边缘轮廓和细节信息,裂缝带多尺度特征表达相对更佳。
|
图 7 基于Contourlet变换的属性融合结果(a)与简单线性加权融合结果(b)对比 |
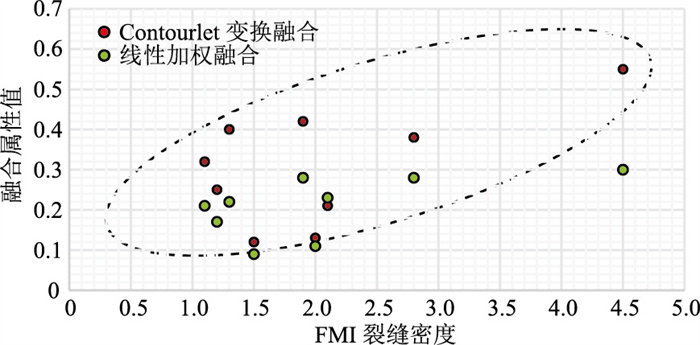
研究区融合属性预测结果整体表现为:以SN向走滑断层为界,西区裂缝带发育优于东区,这与研究区古地貌认识吻合。预测A、B、C井区裂缝储层最发育(红框区域),而FMI测井显示A、B、C井区裂缝密度整体较高,生产测试资料揭示A井测试日产气达31万方,证实预测结果合理;E、F井区预测裂缝储层较为发育(蓝框区域),E井测试日产气达15万方,F井测试日产气达18万方,与预测结果吻合;G井区预测裂缝储层不发育,该井生产测试日产气仅1万方,说明融合属性能够反映潜山裂缝储层多尺度发育特点。此外,9口井的FMI测井解释裂缝密度与基于Contourlet变换的融合属性交会(图 8)相关性整体较好,相关系数达到0.72,较简单线性加权的融合属性相关系数0.54有明显提升。
|
图 8 两种方法融合属性与FMI测井解释裂缝密度交会 |
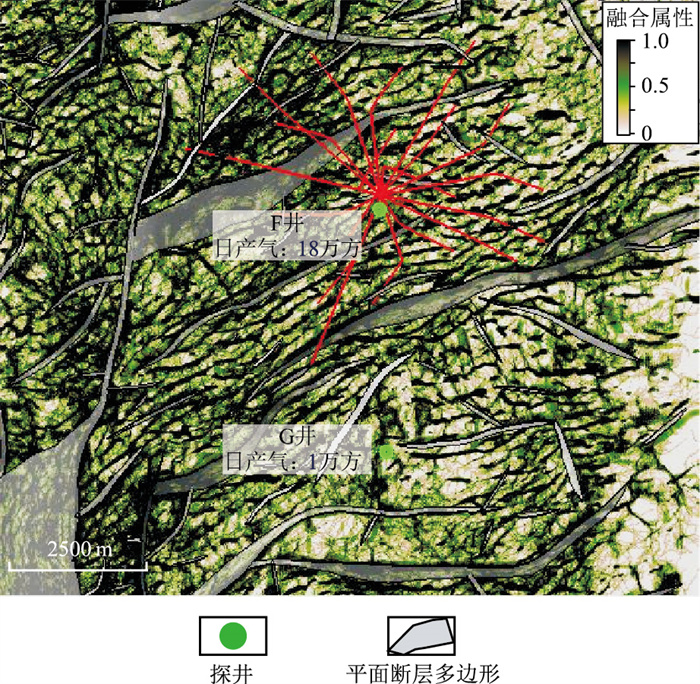
本文方法融合属性有效指导了M气田开发井位设计与井轨迹优化,以F、G井区域为例(图 9),基于融合属性认为探井F周围裂缝储层较发育,设计了一座包含18口开发井的平台,开发井轨迹考虑了第一、第二靶点之间尽可能多地穿过预测裂缝带发育区,注、采井之间与局部裂缝带走向呈一定夹角,以此增大泄油面积,提高单井产量。
|
图 9 本文方法融合属性指导F井区平台设计与井轨迹优化 |
基于主控因素的太古界潜山裂缝储层多尺度预测、有效融合技术,利用曲率、Radon变换高角度反射刻画以及蚂蚁体属性分别预测宏观尺度潜山风化缝富集条带、大尺度高陡断缝体以及中、小尺度微断裂带平面分布;基于Contourlet变换的上述多尺度裂缝带预测融合结果有效地描述了太古界潜山裂缝储层多尺度特征。该技术组合在一定程度上将地震裂缝预测从分析裂缝发育强度向描述多尺度裂缝带推进,使裂缝预测尺度进一步精细化。该技术在M气田的应用结果表明,地质主控因素驱动地球物理潜山裂缝储层预测的技术思路具有一定实用意义。
| [1] |
徐长贵, 于海波, 王军, 等. 渤海海域渤中19-6大型凝析气田形成条件与成藏特征[J]. 石油勘探与开发, 2019, 46(1): 25-38. XU Changgui, YU Haibo, WANG Jun, et al. Formation conditions and accumulation characteristics of Bozhong 19-6 large condensate gas field in offshore Bohai Bay Basin[J]. Petroleum Exploration and Development, 2019, 46(1): 25-38. |
| [2] |
薛永安, 王德英. 渤海湾油型湖盆大型天然气藏形成条件与勘探方向[J]. 石油勘探与开发, 2020, 47(2): 260-271. XUE Yongan, WANG Deying. Formation conditions and exploration direction of large natural gas reservoirs in the oil-prone Bohai Bay Basin, East China[J]. Petroleum Exploration and Development, 2020, 47(2): 260-271. |
| [3] |
张志军, 肖广锐, 李尧. 渤中19-6油田变质岩潜山内幕裂缝地震响应特征及预测技术[J]. 石油地球物理勘探, 2021, 56(4): 845-852. ZHANG Zhijun, XIAO Guangrui, LI Yao. Seismic response characteristics and prediction of fractured inside metamorphic buried hill of Bozhong 19‑6 oilfield[J]. Oil Geophysical Prospecting, 2021, 56(4): 845-852. |
| [4] |
刘振峰, 刘忠群, 郭元玲, 等. "断缝体"概念、地质模式及其在裂缝预测中的应用——以四川盆地川西坳陷新场地区须家河组二段致密砂岩气藏为例[J]. 石油与天然气地质, 2021, 42(4): 973-980. LIU Zhenfeng, LIU Zhongqun, GUO Yuanling, et al. Concept and geological model of fault-fracture reservoir and their application in seismic fracture prediction: A case study on the Xu 2 Member tight sandstone gas pool in Xinchang area, Western Sichuan Depression in Sichuan Basin[J]. Oil & Gas Geology, 2021, 42(4): 973-980. |
| [5] |
黄保纲, 汪利兵, 赵春明, 等. JZS油田潜山裂缝储层形成机制及分布预测[J]. 石油与天然气地质, 2011, 32(5): 710-717. HUANG Baogang, WANG Libing, ZHAO Chunming, et al. Formation mechanism and distribution of fractured buried hill reservoir in JZS oilfiled[J]. Oil & Gas Geology, 2011, 32(5): 710-717. |
| [6] |
杨勉, 徐梓洋, 杨柏松, 等. 贝尔凹陷基岩潜山致密储层裂缝分布预测[J]. 石油与天然气地质, 2014, 35(2): 253-257. YANG Mian, XU Ziyang, YANG Baisong, et al. Fracture prediction of bedrock buried hill tight reservoirs in Beier Depression[J]. Oil & Gas Geology, 2014, 35(2): 253-257. |
| [7] |
范廷恩, 杜昕, 马淑芳, 等. 高角度断裂约束的方位傅里叶系数裂缝预测方法及在M气田的应用[J]. 石油地球物理勘探, 2022, 57(6): 1436-1444. FAN Tingen, DU Xin, MA Shufang, et al. Application of the high-angle-fault constrained azimuthal Fourier coefficients fracture prediction in M gas field[J]. Oil Geophysical Prospecting, 2022, 57(6): 1436-1444. |
| [8] |
刘俊州, 韩磊, 时磊, 等. 致密砂岩储层多尺度裂缝地震预测技术——以川西XC地区为例[J]. 石油与天然气地质, 2021, 42(3): 747-754. LIU Junzhou, HAN Lei, SHI Lei, et al. Seismic prediction of tight sandstone reservoir fractures in XC area, western Sichuan Basin[J]. Oil & Gas Geology, 2021, 42(3): 747-754. |
| [9] |
王威, 凡睿, 黎承银, 等. 川东北地区须家河组"断缝体"气藏有利勘探目标和预测技术[J]. 石油与天然气地质, 2021, 42(4): 992-1001. WANG Wei, FAN Rui, LI Chengyin, et al. Exploration and prediction of promising fault‑fracture reservoirs in the Xujiahe Formation, northeastern Sichuan Basin[J]. Oil & Gas Geology, 2021, 42(4): 992-1001. |
| [10] |
李蒙, 商晓飞, 赵华伟, 等. 基于likelihood地震属性的致密气藏断裂预测——以四川盆地川西坳陷新场地区须二段为例[J]. 石油与天然气地质, 2020, 41(6): 1299-1309. LI Meng, SHANG Xiaofei, ZHAO Huawei, et al. Prediction of fractures in tight gas reservoirs based on likelihood attribute: A case study of the 2nd member of Xujiahe Formation in Xinchang area, Western Sichuan Depression, Sichuan Basin[J]. Oil & Gas Geology, 2020, 41(6): 1299-1309. |
| [11] |
王明飞, 苏克露, 肖伟, 等. 泥页岩应力场约束的叠后地震裂缝预测技术——以焦石坝区块五峰组-龙马溪组一段为例[J]. 石油与天然气地质, 2018, 39(1): 198-206. WANG Mingfei, SU Kelu, XIAO Wei, et al. Post-stack seismic fracture prediction under constraint of shale stress field: A case from the shale reservoir in Wufeng Fm-1st member of Longmaxi Fm in Jiaoshiba area[J]. Oil & Gas Geology, 2018, 39(1): 198-206. |
| [12] |
印兴耀, 马正乾, 向伟, 等. 地震岩石物理驱动的裂缝预测技术研究现状与进展(Ⅰ)——裂缝储层岩石物理理论[J]. 石油物探, 2022, 61(2): 183-204. YIN Xingyao, MA Zhengqian, XIANG Wei, et al. Review of fracture prediction driven by the seismic rock physics theory(Ⅰ): Effective anisotropic seismic rock physics theory[J]. Geophysical Prospecting for Petroleum, 2022, 61(2): 183-204. |
| [13] |
姜晓宇, 张研, 甘利灯, 等. 花岗岩潜山裂缝地震预测技术[J]. 石油地球物理勘探, 2020, 55(3): 694-704. JIANG Xiaoyu, ZHANG Yan, GAN Lideng, et al. Seismic techniques for predicting fractures in granite buried hills[J]. Oil Geophysical Prospecting, 2020, 55(3): 694-704. |
| [14] |
汤韦, 李景叶, 王建花, 等. 基于非下采样剪切波变换―参数自适应脉冲耦合神经网络的属性融合裂缝预测方法[J]. 石油地球物理勘探, 2022, 57(1): 52-61. TANG Wei, LI Jingye, WANG Jianhua, et al. Attribute fusion method based on NSST-PAPCNN for fracture prediction[J]. Oil Geophysical Prospecting, 2022, 57(1): 52-61. |
| [15] |
朱光辉, 李忠城, 师素珍, 等. 鄂尔多斯盆地东缘MG区块煤层裂缝发育多尺度预测[J]. 煤田地质与勘探, 2022, 50(3): 173-182. ZHU Guanghui, LI Zhongcheng, SHI Suzhen, et al. Multi-scale prediction of coal seam fracture development in MG block, eastern margin of Ordos Basin[J]. Coal Geology & Exploration, 2022, 50(3): 173-182. |
| [16] |
张继标, 张仲培, 汪必峰, 等. 塔里木盆地顺南地区走滑断裂派生裂缝发育规律及预测[J]. 石油与天然气地质, 2018, 39(5): 955-963, 1055. ZHANG Jibiao, ZHANG Zhongpei, WANG Bifeng, et al. Development pattern and prediction of induced fractures from strike-slip faults in Shunnan area, Tarim Basin[J]. Oil & Gas Geology, 2018, 39(5): 955-963, 1055. |
| [17] |
丁中一, 钱祥麟, 霍红, 等. 构造裂缝定量预测的一种新方法——二元法[J]. 石油与天然气地质, 1998, 19(1): 1-7, 14. DING Zhongyi, QIAN Xianglin, HUO Hong, et al. A new method for quantitative prediction of tectonic fractures: Two-factor method[J]. Oil & Gas Geology, 1998, 19(1): 1-7, 14. |
| [18] |
王峣钧, 郑多明, 李向阳, 等. 碳酸盐岩裂缝-孔洞型储层缝洞体系综合预测方法及应用[J]. 石油物探, 2014, 53(6): 727-736. WANG Yaojun, ZHENG Duoming, LI Xiangyang, et al. The fracture-cavern system prediction method and its application in carbonate fractured-vuggy reservoirs[J]. Geophysical Prospecting for Petroleum, 2014, 53(6): 727-736. |
| [19] |
CHEN S, ZENG L, HUANG P, et al. The application study on the multi‑scales integrated prediction method to fractured reservoir description[J]. Applied Geophysics, 2016, 13(1): 80-92. |
| [20] |
吴海波, 王江, 李军辉. 地震多属性融合技术在贝尔凹陷储层预测中的应用[J]. 岩性油气藏, 2014, 26(2): 96-101. WU Haibo, WANG Jiang, LI Junhui. Application of seismic multi-attribute fusion technique to the reservoir prediction in Beier Depression[J]. Lithologic Reservoirs, 2014, 26(2): 96-101. |
| [21] |
王成泉, 王孟华, 周佳宜, 等. 多属性融合定量储层预测方法研究与应用——以廊固凹陷杨税务潜山为例[J]. 物探与化探, 2022, 46(1): 87-95. WANG Chengquan, WANG Menghua, ZHOU Jiayi, et al. Application of multi-attribute fusion in quantitative prediction of reservoirs: A case study of Yangshuiwu buried hill in Langgu sag[J]. Geophysical and Geochemical Exploration, 2022, 46(1): 87-95. |
| [22] |
谢成芳, 彭真明, 周晶晶, 等. 基于Contourlet变换的地震多属性融合方法[J]. 石油地球物理勘探, 2014, 49(4): 739-744. XIE Chengfang, PENG Zhenming, ZHOU Jingjing, et al. Seismic multi-attribute fusion based on Contourlet transform[J]. Oil Geophysical Prospecting, 2014, 49(4): 739-744. |
| [23] |
杨宏伟, 吴海燕, 魏国华, 等. 基于概率核地震属性融合的砂体预测方法研究[J]. 地球物理学进展, 2020, 35(1): 216-221. YANG Hongwei, WU Haiyan, WEI Guohua, et al. Research on sand body prediction method based on seismic attributes integrating of probabilistic kernel[J]. Progress in Geophysics, 2020, 35(1): 216-221. |
| [24] |
李芳, 王守东, 陈小宏, 等. 基于模糊逻辑的多属性融合油气预测方法[J]. 石油地球物理勘探, 2014, 49(1): 197-204. LI Fang, WANG Shoudong, CHEN Xiaohong, et al. Oil-gas prediction with multi-attributes fusion based on fuzzy logic[J]. Oil Geophysical Prospecting, 2014, 49(1): 197-204. |
| [25] |
范廷恩, 牛涛, 范洪军, 等. 渤中19-6凝析气田太古界潜山储层地质模式及开发策略[J]. 中国海上油气, 2021, 33(3): 85-92. FAN Tingen, NIU Tao, FAN Hongjun, et al. Geological model and development strategy of Archean buried hill reservoir in BZ19-6 condensate field[J]. China Offshore Oil and Gas, 2021, 33(3): 85-92. |
| [26] |
范廷恩, 牛涛, 范洪军, 等. 渤中19-6凝析气田太古宇潜山储层发育主控因素及地质模式[J]. 海洋地质与第四纪地质, 2021, 41(4): 170-178. FAN Tingen, NIU Tao, FAN Hongjun, et al. Archaeozoic buried-hill reservoir of Bozhong 19-6 condensate field: Main controlling factors and development model[J]. Marine Geology & Quaternary Geology, 2021, 41(4): 170-178. |
| [27] |
施和生, 王清斌, 王军, 等. 渤中凹陷深层渤中19-6构造大型凝析气田的发现及勘探意义[J]. 中国石油勘探, 2019, 24(1): 36-45. SHI Hesheng, WANG Qingbin, WANG Jun, et al. Discovery and exploration significance of large condensate gas fields in BZ19-6 structure in deep Bozhong sag[J]. China Petroleum Exploration, 2019, 24(1): 36-45. |
| [28] |
吕丁友, 杨明慧, 周心怀, 等. 辽东湾坳陷辽西低凸起潜山构造特征与油气聚集[J]. 石油与天然气地质, 2009, 30(4): 490-496. LYU Dingyou, YANG Minghui, ZHOU Xinhuai, et al. Structural characteristics and hydrocarbon accumulation in the buried hills of the Liaoxi low salient, the Liaodong Bay Depression[J]. Oil & Gas Geology, 2009, 30(4): 490-496. |
| [29] |
谢玉洪, 张功成, 沈朴, 等. 渤海湾盆地渤中凹陷大气田形成条件与勘探方向[J]. 石油学报, 2018, 39(11): 1199-1210. XIE Yuhong, ZHANG Gongcheng, SHEN Piao, et al. Formation conditions and exploration direction of large gas field in Bozhong sag of Bohai Bay Basin[J]. Acta Petrolei Sinica, 2018, 39(11): 1199-1210. |
| [30] |
SABBIONE J I, SACCHI M D. Restricted model domain time Radon transforms[J]. Geophysics, 2016, 81(6): A17-A21. |
| [31] |
GHOLAMI A, ZAND T. Three‑parameter Radon transform based on shifted hyperbolas[J]. Geophysics, 2018, 83(1): V39-V48. |



 杜昕, 北京市朝阳区太阳宫南街6号院中海油研究总院有限责任公司,100028。Email:
杜昕, 北京市朝阳区太阳宫南街6号院中海油研究总院有限责任公司,100028。Email: