② 赛吉纪技术服务(北京)有限公司, 北京 100020
② CGG Technical Services (Beijing) Co., Ltd., Beijing 100020, China
渤海湾盆地M气田是全球储量最大的变质岩潜山凝析气田,已探明天然气地质储量超千亿立方米[1-2]。M气田主要含气层段发育太古界变质岩潜山裂缝型储层,勘探阶段探井钻遇储层品质差异大,存在复杂裂缝。在M气田开发进程中发现,太古界潜山裂缝型储层主要受内幕高角度断裂控制,高角度断裂区域普遍发育裂缝。因此,裂缝预测是开发阶段储层预测与井位部署面临的核心问题。2019年,M气田主体完成宽方位海底电缆(OBC)采集,覆盖次数为1200,纵横比达0.72,高品质的宽方位地震数据为叠前定量预测裂缝奠定了基础。
与叠后裂缝预测方法相比,叠前裂缝预测方法具有定量预测裂缝密度与方向的优势[3-4],构建方位反射系数特征方程是后者的理论基础。M气田潜山的裂缝多呈近垂直高角度[5],基于等效介质理论可将裂缝介质抽象为HTI介质[6]。构建HTI介质的方位反射系数近似方程主要有两类方法:①基于传统的HTI介质Ruger振幅方位各向异性反射系数近似方程;②基于杨氏模量表征的方位反射系数近似方程[7]。其中方法①应用广泛[8-9],并且是多种改进算法的基础。然而,方法①预测的裂缝方向存在90°的不确定性,并且要求叠前道集的炮检距与方位角信息丰富,计算效率较低,在一定程度影响了其在三维实际资料中的应用效果[10]。方位傅里叶系数裂缝预测方法[11-12]可缓解方法①的预测裂缝方向不确定性问题,同时解耦振幅随炮检距与振幅随方位角的变化关系,并使用特定炮检距的分方位叠加数据预测裂缝,显著提高了计算效率,且预测精度与方法①相当。但是方法①完全基于地震数据,预测过程没有考虑宏观地质模式约束,预测结果的稳定性以及与构造背景的吻合程度有待提升。
本文改进了方位傅里叶系数裂缝预测方法。利用f-k滤波、高分辨率Radon变换从叠后地震数据中提取高角度断裂信息,并映射为方位傅里叶系数裂缝预测中各采样点的先验权重,以此建立高角度断裂约束的方位傅里叶系数裂缝预测反演目标泛函,最后求解得到裂缝密度与方向。新方法的裂缝预测结果与井上解释的裂缝特征以及各井生产测试情况吻合较好。
1 方法原理 1.1 HTI介质振幅方位各向异性反射系数公式近炮检距Ruger纵波方位各向异性反射系数近似公式[9]为
| $ R(\phi, \theta)=A+\left[B_{\mathrm{iso}}+B_{\mathrm{ani}} \cos ^2\left(\phi-\phi_{\mathrm{sym}}\right)\right] \sin ^2 \theta $ | (1) |
式中:R(ϕ, θ)为随方位角ϕ与平均入射角θ变化的纵波反射系数;A为振幅截距;Biso为各向同性梯度;Bani为各向异性梯度;ϕsym为观测方位角。Hudson理论揭示,各向异性梯度与裂缝密度呈正相关关系,观测方位则与裂缝走向垂直[13-15]。
方法①通常利用三角函数变换将式(1)改写为cos2ϕ与sin2ϕ的线性组合函数,之后采用最小二乘反演得到裂缝密度与裂缝方位估计。由于式(1)中sin2θ项的影响,导致预测的ϕsym存在90°的不确定性。
1.2 方位傅里叶反射系数公式基于式(1),Shaw等[14]利用傅里叶级数展开给出了随ϕsym变化的纵波反射系数公式
| $ \begin{aligned} R_{\mathrm{PP}}(\phi, \theta)= & r_0(\theta)+r_2(\theta) \cos 2\left(\phi-\phi_{\mathrm{sym}}\right)+ \\ & r_4(\theta) \cos 4\left(\phi-\phi_{\mathrm{sym}}\right) \end{aligned} $ | (2) |
其中
| $ r_0(\theta)=A+B \sin ^2 \theta+C \sin ^2 \theta \tan ^2 \theta $ | (3) |
| $ r_2(\theta)=\frac{1}{2}\left[B_{\mathrm{ani}}+g(g-1) \Delta \delta_{\mathrm{N}} \tan ^2 \theta\right] \sin ^2 \theta $ | (4) |
| $ r_4(\theta)=\frac{1}{8} g^2\left(\Delta \delta_{\mathrm{T}}-g \Delta \delta_{\mathrm{N}}\right) \sin ^2 \theta \tan ^2 \theta $ | (5) |
式中:B、C为由Thomsen各向异性参数组成的各向异性系数;ΔδT、ΔδN分别为切向弱度与法向弱度;g=β2/α2,α与β分别为反射界面附近纵波速度α、横波速度β的平均值。
式(2)实现了振幅随炮检距变化关系(AVO)与振幅随方位角变化关系(AVAZ)的解耦。其中r0(θ)等价表达了第三类AVO变化关系,r2(θ)及r4(θ)为AVAZ项cos2(ϕ-ϕsym)与cos4(ϕ-ϕsym)的系数。一般情况下,叠前地震道集的最大公共炮检距存在上限,因此θ≤35°。在此条件下,式(4)中g(g-1)ΔδNtan2θsin2θ项以及高阶项r4(θ)可忽略,则式(2)可近似为[15]
| $ R_{\mathrm{PP}}(\phi, \theta) \approx r_0(\theta)+r_2(\theta) \cos 2\left(\phi-\phi_{\mathrm{sym}}\right) $ | (6) |
其中
| $ r_2(\theta) \approx 0.5 B_{\text {ani }} \sin ^2 \theta $ | (7) |
式(6)为拟线性方程组,输入特定入射角(炮检距)的分方位叠前道集或部分方位角叠加数据,通过最小二乘反演求解得到Bani(表征裂缝密度)与ϕsym(表征裂缝方向)。
1.3 基于f-k滤波与高分辨率Radon变换的高角度断裂信息提取f-k滤波的理论基础是二维傅里叶变换,常用于地震资料去噪[16-17]。核心原理为:时—空域的反射波与线性噪声存在较明显视速度差异;经过f-k变换反射波与线性噪声在f-k域的斜率与分布区间显著不同;在f-k域压制噪声,再经过反f-k变换得到去噪后的时—空域信号。
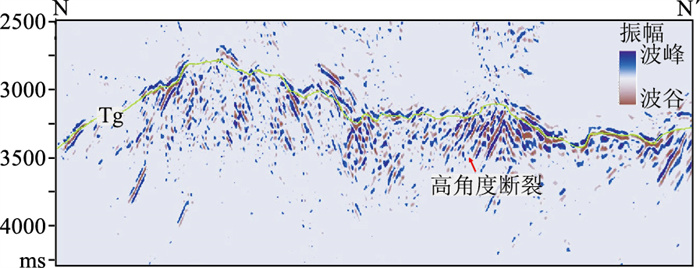
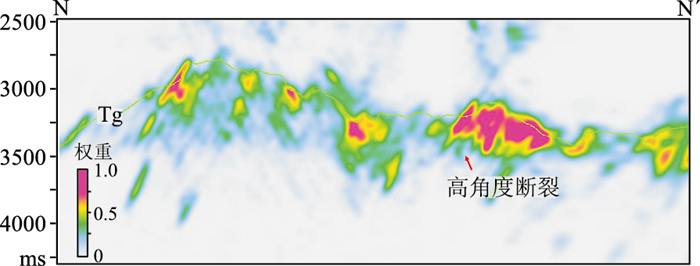
M气田潜山内幕高角度断裂在地震剖面上表现为大斜度(60°~70°)、近似呈线性反射形态的几何学特征(图 1),本质上反映了潜山内幕高角度断裂与围岩的显著速度差异。因此,可利用对视速度差异敏感性强的f-k滤波从偏移成果数据中提取高角度断裂信息。

|
图 1 M气田典型地震剖面Tg为潜山顶面 |
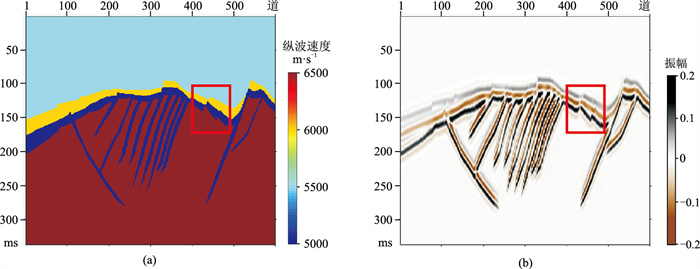
首先利用二维模型测试f-k滤波提取效果。采用主频为15Hz的Ricker子波与由模型(图 2a)计算的反射系数(密度为常数)褶积,得到合成地震剖面(图 2b)。利用f-k滤波方法从图 2b中提取的高角度断裂信息(图 3a)与图 2a基本一致,但分辨率较低,同时存在假象(图 3a的红框区域)。这是由于红框区域潜山顶面地层反射倾角较大,并与潜山内幕高角度断裂的共轭方向相近,通过设计滤波器形态难以有效去除f-k域中的地层响应所致。
|
图 2 潜山高角度断裂二维模型 (a)纵波速度;(b)合成地震剖面 模拟潜山内幕高角度断裂的反射倾角约为65° |
|
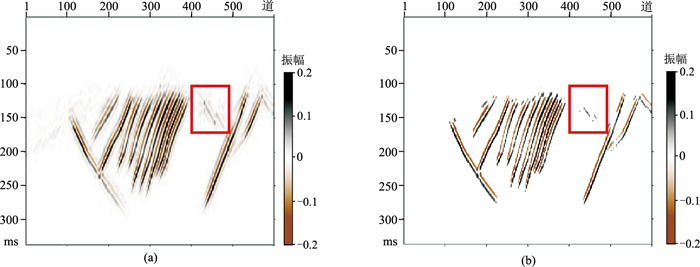
图 3 基于f-k滤波(a)与高分辨率Radon变换(b)提取的高角度断裂 f-k滤波提取的高角度断裂存在假象(红色方框区域),即与真实高角度断裂响应相比,f-k滤波结果的连续性较差、能量较弱 |
Radon变换广泛应用于地震信号处理领域[18-19],包括多次波压制、地震反射同相轴识别、数据保幅重建等。三维Radon变换的实质是对输入数据沿特定空间路径积分,从而将具有规律排列的信号分解为Radon域内的稀疏散点,以此实现信号识别与分离。通过改变积分路径,Radon变换能够追踪地震数据中不同形态的地层反射信息。三维线性Radon正变换为
| $ m\left(p_x, p_y, \tau\right)=\sum\limits_x \sum\limits_y d\left(x, y, t=\tau+p_x x+p_y y\right) $ | (8) |
其反变换为
| $ d(x, y, t)=\sum\limits_{p_x} \sum\limits_{p_y} m\left(p_x, p_y, \tau=t-p_x x-p_y y\right) $ | (9) |
式中m为三维地震数据体d(x,y,t)在τ-px-py域中的变换结果,x、y、t分别代表主测线、联络测线、时间,而px、py、τ分别为主测线方向斜率、联络测线方向斜率、时间截距。通过傅里叶变换,可将式(9)写为矩阵形式
| $ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{Lm}} $ | (10) |
式中:d为t-x-y域三维地震数据;L为Radon变换算子;m为待求解的τ-px-py域Radon变换系数矩阵。基于最小二乘反演框架,通过正则化约束条件求解m。
高分辨率Radon变换应用稀疏正则化约束项替代传统最小二乘约束项,使反演结果具有突出强信号、压制弱信号的稀疏形态特点,较传统Radon变换的分辨率更高[20],适合精细提取高角度断裂信息。高分辨率Radon变换目标泛函为
| $ J(\boldsymbol{m})=\|\boldsymbol{d}-\boldsymbol{L} \boldsymbol{m}\|_2^2+\lambda\|\boldsymbol{m}\|_1 $ | (11) |
式中:‖d-Lm‖22为最小二乘数据误差项;‖m‖1为正则化约束项;λ为约束项权重超参数。对式(11)的最小化问题一般采用迭代重加权最小二乘算法(IRSL)或交替方向乘子法(ADMM)等最优化算法求解[21]。
针对f-k滤波方法提取高角度断裂信息存在假象的不足,应用三维高分辨率Radon变换方法从f-k滤波结果(图 3a)中进一步提取高角度断裂信息,通过在τ-px-py域中压制非高角度反射信号,然后将只保留高角度反射信号的τ-px-py域阈值结果利用反Radon变换转换至t-x-y域(图 3b),以此优化高角度断裂提取结果。可见,与图 3a相比,图 3b的分辨率更高,同时能够较好地分离高角度断裂反射与地层反射。
根据M气田裂缝发育程度主要受潜山内幕高角度断裂控制的认识,将f-k滤波与高分辨率三维Radon变换提取的高角度断裂信息映射为三维地震数据各采样点参与AVAZ裂缝预测的先验权重,使高角度断裂发育区域的数据样点对裂缝预测结果的影响更大。另一方面,加入先验权重本身也是一种平滑机制,可提升裂缝预测结果的横向稳定性。
权重计算公式为
| $ \left\{\begin{array}{l} w_{x, y, t}=S_{\mathrm{Gauss}}\left(\sum\limits_{x-r_x}^{x+r_x} \sum\limits_{y-r_y}^{y+r_y} \sum\limits_{t-r_t}^{t+r_t} a_{x, y, t}\right) \\ a_{x, y, t}= \begin{cases}d_{x, y, t} & d_{x, y, t} \geqslant c_{\text {threshold }} \\ 0 & d_{x, y, t}<c_{\text {threshold }}\end{cases} \end{array}\right. $ | (12) |
式中:wx, y, t为各采样点参与AVAZ裂缝预测的先验权重;SGauss为高斯平滑算子;rx、ry、rt分别为主测线、联络测线、时间方向的权重计算半径;ax, y, t为对dx, y, t以cthreshold作为门槛值的阈值结果,而dx, y, t为由f-k滤波与高分辨率Radon变换综合提取的高角度断裂信息。进一步对wx, y, t归一化处理
| $ \bar{w}_{x, y, t}=\frac{w_{x, y, t}-\min \left(w_{x, y, t}\right)}{\max \left(w_{x, y, t}\right)-\min \left(w_{x, y, t}\right)} $ | (13) |
将式(6)与式(13)结合,建立高角度断裂约束的方位傅里叶系数裂缝预测公式
| $ w \boldsymbol{R}=\boldsymbol{w}\left(\boldsymbol{r}_0+\boldsymbol{F}_\phi \boldsymbol{r}_2\right) $ | (14) |
式中:w为先验权重;R为方位各向异性反射系数;r0为方位各向同性项;r2为方位各向异性项,代表裂缝发育密度信息;Fϕ为方位角函数项cos2(ϕ-ϕsym)组成的角度矩阵算子。基于式(14)利用最小二乘反演建立高角度断裂约束的方位傅里叶系数裂缝预测目标泛函
| $ J\left(\boldsymbol{r}_2\right)=\left\|\boldsymbol{w}\left(\boldsymbol{R}-\boldsymbol{r}_0-\boldsymbol{F}_\phi \boldsymbol{r}_2\right)\right\|_2^2+\mu\left\|\boldsymbol{r}_2\right\|_2^2 $ | (15) |
式中μ为最小二乘约束项的超参数。式(15)的解析解为
| $ \boldsymbol{r}_2=\left(\boldsymbol{F}_\phi^{\mathrm{T}} \boldsymbol{w}^{\mathrm{T}} \boldsymbol{w} \boldsymbol{F}{ }_\phi+\mu \boldsymbol{I}\right)^{-1} \boldsymbol{F}_\phi^{\mathrm{T}} \boldsymbol{w}^{\mathrm{T}} \boldsymbol{w}\left(\boldsymbol{R}-\boldsymbol{r}_0\right) $ | (16) |
式中I为单位矩阵。
可通过IRSL、共轭梯度等算法求解式(16)。基于高角度断裂约束的方位傅里叶系数裂缝预测技术流程如图 4所示。

|
图 4 基于高角度断裂约束的方位傅里叶系数裂缝预测技术流程 |
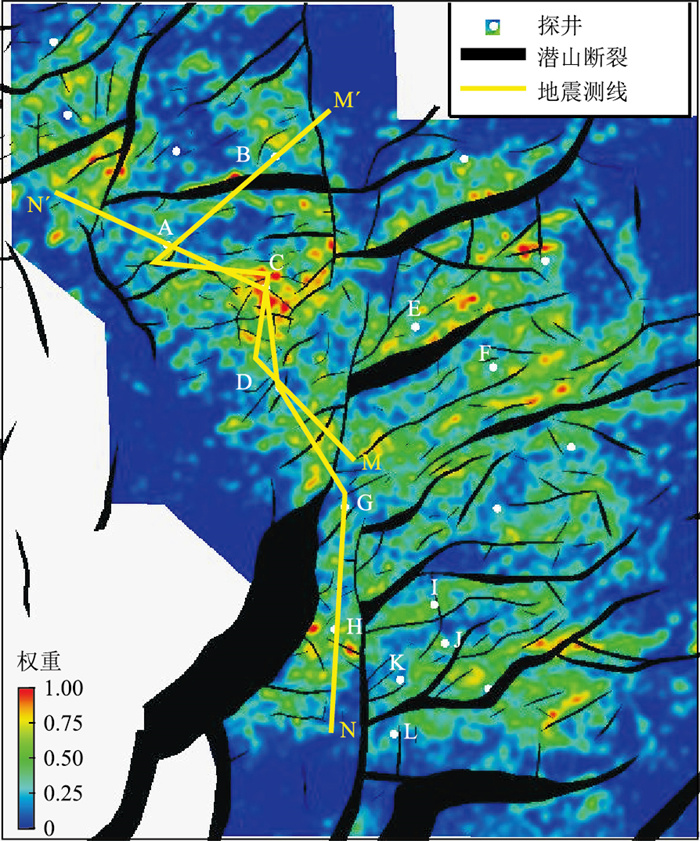
M气田位于渤中凹陷渤中19构造脊上,该构造脊同其西侧的渤中13构造脊及东侧的渤中21-22构造脊共同构成面积近440km2的古潜山群[1],整体发育在太古界基底之上并受郯庐走滑断裂带后期切割改造,形成了大型复杂构造脊(图 5)。
|
图 5 M气田潜山顶面裂缝预测先验权重平面图 |
M气田裂缝型储层受潜山内幕的高角度断裂控制,沿高角度断裂走向呈“漏斗状”分布。准确预测高角度断裂的空间展布是裂缝型储层描述突破的关键。图 6为MM′地震剖面。可见:A、B井附近高角度断裂发育程度一般,由A、B井的测井响应解释的内幕带储层含气性较差;C、D井附近的高角度断裂较发育,与C、D井的测井响应解释的储层含气性较好相吻合。

|
图 6 MM′地震剖面 红色为气层、黑色为干层;井位及剖面位置见图 5 |
图 7为基于f-k滤波提取的潜山内幕高角度断裂信息。可见,f-k滤波结果分辨率较低,同时提取的高角度反射信号连续性较差。图 8为应用三维高分辨率Radon变换对图 7进一步提取的高角度断裂信息。可见,提取效果得到一定改善,分辨率较高,高角度反射更连续。

|
图 8 应用三维高分辨率Radon变换对图 7进一步提取的高角度断裂信息 |
基于式(12)与式(13)计算各采样点参与裂缝预测的先验权重,得到高角度断裂先验约束权重剖面(图 9)。可见,高角度断裂带发育区域对应更大的约束权重值,对式(15)、式(16)的干预作用更强。此外,潜山顶面裂缝预测先验权重平面图(图 5)表明:D、C、A、B四口井中,C、D井先验权重值较大,A、B井先验权重值较小,这与图 6反映的高角度断裂发育规律相吻合,验证了先验权重估计的合理性。
|
图 9 高角度断裂先验权重剖面 |
通过AVAZ特性分析以及对比不同入射角道集叠加地震剖面,优选裂缝预测的最佳部分入射角叠加数据。A井风化带顶面AVAZ分析结果表明,原始叠前道集最大入射角约为35°,AVAZ特性随着入射角增大而更明显(图 10)。进一步采用不同入射角范围数据叠加形成部分入射角叠加地震数据(图 11),其中20°~35°叠加地震数据的高角度断裂特征明显(图 11c)。根据上述分析,确定以20°~35°叠加数据作为特定入射角(平均入射角为28°)的叠加地震数据,开展方位傅里叶系数裂缝预测。

|
图 10 A井风化带顶面AVAZ特性分析(左)及30°入射角的分方位道集(右) 正东方向为0°,正北方向为90°。东、西向方位地震道集振幅更大,表明该方向的各向异性最强 |

|
图 11 部分入射角道集叠加地震剖面 (a)0°~15°;(b)10°~25°;(c)20°~35° |
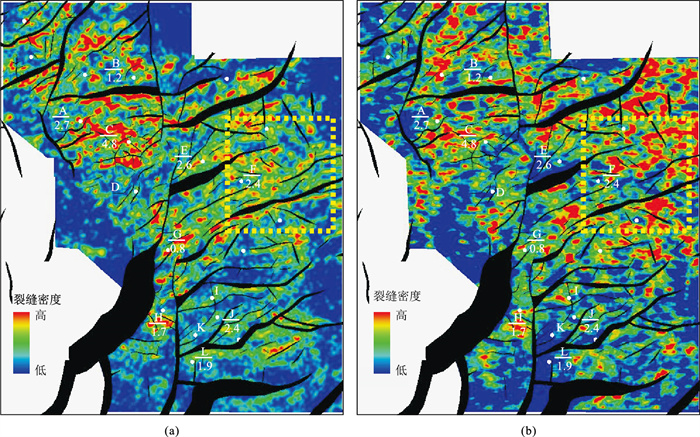
将20°~35°入射角道集资料以30°为间隔分为6组分方位角(0°~30°、30°~60°、60°~120°、120°~150°、150°~180°)数据并叠加,作为叠前裂缝预测的基础输入数据,基于式(15)实现高角度断裂约束的方位傅里叶系数裂缝预测,得到裂缝密度与裂缝方向预测数据体。图 12为风化带裂缝密度预测结果。可见:①与未考虑高角度断裂约束的方法(图 12b)相比,考虑高角度断裂约束的方法预测的裂缝密度(图 12a)与电成像测井解释结果整体较吻合,均表现为A、C井区裂缝最发育,G、H井区次之。②图 12b的裂缝密度在研究区东侧偏高,如F井(图 12黄框区域)的测井解释裂缝密度(2.4)明显低于C井(4.8),但F井与C井附近的裂缝密度差异并不大。
|
图 12 风化带裂缝密度预测结果 (a)考虑高角度断裂约束;(b)未考虑高角度断裂约束 井号下的数字表示电成像测井解释的裂缝密度 |
图 13为预测裂缝密度连井剖面。可见:①考虑高角度断裂约束的方法预测的裂缝密度与测井流体解释结果一致(图 13a),井上解释气藏较发育部位的裂缝密度也较高;同时由A井生产测试解释的干层对应较低的裂缝密度值(图 13a蓝色方框),结果较合理。②未考虑高角度断裂约束的方法在G井与D井附近预测的裂缝密度相对偏低(图 13b)。图 14为考虑高角度断裂约束的风化带裂缝方向预测结果。可见,风化带裂缝发育方向整体以近东西向为主,局部存在北东、南西向,这与电成像测井揭示的裂缝发育方向较吻合。

|
图 13 不同方法预测裂缝密度连井剖面 (a)考虑高角度断裂约束;(b)未考虑高角度断裂约束 |

|
图 14 考虑高角度断裂约束的风化带裂缝方向预测结果 |
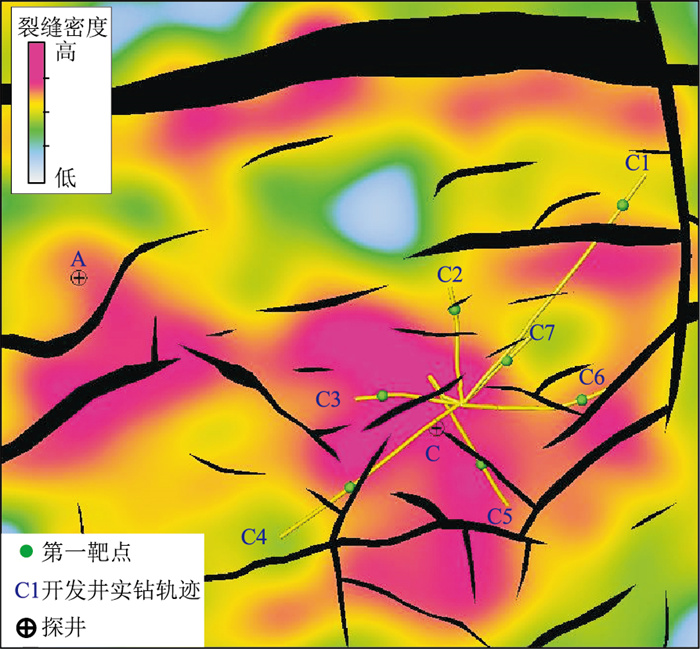
进一步利用已投产开发井验证所提方法的裂缝预测结果(图 15)。目前各开发井钻遇的储层普遍存在裂缝,而开发井实钻轨迹与预测裂缝密度叠合表明,各井第一靶点基本着陆于裂缝密度较高区域,说明预测结果较可靠。
|
图 15 开发井实钻轨迹与预测裂缝密度叠合图 |
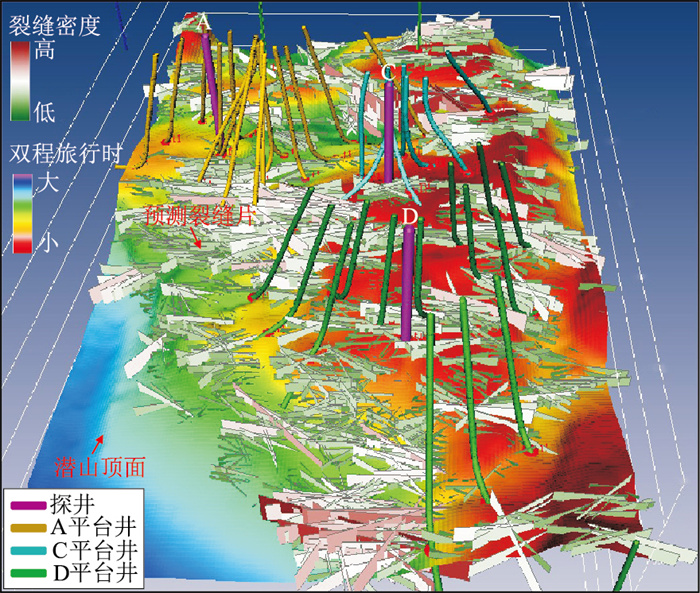
将新方法获得的裂缝预测成果应用于M气田开发井井位设计与优化。图 16为设计井轨迹与预测裂缝密度、方向以及潜山顶面等T0图的三维叠合显示。可见,设计开发井靶点坐标位于裂缝密度较高区域,同时井轨迹与裂缝方向呈一定角度。后期将基于裂缝预测成果进一步建立M气田潜山立体缝网,持续评价与优化设计井位及轨迹。
|
图 16 设计井轨迹与预测裂缝密度、方向以及潜山顶面等T0图的三维叠合显示 裂缝片颜色代表预测裂缝密度,裂缝片走向代表预测裂缝方向 |
本文提出了基于高角度断裂约束的方位傅里叶系数裂缝预测方法,考虑了裂缝沿着高角度断裂呈带状分布的宏观地质认识,增强了预测结果的地质意义。运用该方法预测M气田太古界潜山裂缝型储层,探井及开发井数据验证了所提方法的可靠性,为具有类似高角度构造特征的油气田的裂缝型储层预测提供了新思路。
| [1] |
徐长贵, 于海波, 王军, 等. 渤海海域渤中19-6大型凝析气田形成条件与成藏特征[J]. 石油勘探与开发, 2019, 46(1): 25-38. XU Changgui, YU Haibo, WANG Jun, et al. Formation conditions and accumulation characteristics of Bozhong 19-6 large condensate gas field in oil offshore Bohai Bay Basin[J]. Petroleum Exploration and Development, 2019, 46(1): 25-38. |
| [2] |
薛永安, 王德英. 渤海湾油型湖盆大型天然气藏形成条件与勘探方向[J]. 石油勘探与开发, 2020, 47(2): 260-271. XUE Yong'an, WANG Deying. Formation conditions and exploration direction of large natural gas reservoirs in the oil-prone Bohai Bay Basin, East China[J]. Petroleum Exploration and Development, 2020, 47(2): 260-271. |
| [3] |
姜晓宇, 张研, 甘利灯, 等. 花岗岩潜山裂缝地震预测技术[J]. 石油地球物理探, 2020, 55(3): 694-704. JIANG Xiaoyu, ZHANG Yan, GAN Lideng, et al. Seismic techniques for predicting fractures in granite buried hills[J]. Oil Geophysical Prospecting, 2020, 55(3): 694-704. |
| [4] |
陈怀震, 印兴耀, 高成国, 等. 基于各向异性岩石物理的缝隙流体因子AVAZ反演[J]. 地球物理学报, 2014, 57(3): 968-978. CHEN Huaizhen, YIN Xingyao, GAO Chengguo, et al. AVAZ inversion for fluid factor based on fracture anisotropic rock physics theory[J]. Chinese Journal of Geophysics, 2014, 57(3): 968-978. |
| [5] |
张志军, 肖广锐, 李尧. 渤中19-6油田变质岩潜山内幕裂缝地震响应特征及预测技术[J]. 石油地球物理勘探, 2021, 56(4): 845-852. ZHANG Zhijun, XIAO Guangrui, LI Yao. Seismic response characteristics and prediction of fractured inside metamorphic buried hill of Bozhong 19-6 oilfield[J]. Oil Geophysical Prospecting, 2021, 56(4): 845-852. |
| [6] |
王建花, 张金淼, 吴国忱. 宽方位杨氏模量反演和裂缝预测方法及应用[J]. 石油地球物理勘探, 2021, 56(3): 593-602. WANG Jianhua, ZHANG jinmiao, WU Guochen. Wide-azimuth Young's modulus inversion and fracture prediction: An example of H structure in Bozhong sag[J]. Oil Geophysical Prospecting, 2021, 56(3): 593-602. |
| [7] |
宗兆云, 印兴耀, 张峰, 等. 杨氏模量和泊松比反射系数近似方程及叠前地震反演[J]. 地球物理学报, 2012, 55(11): 3786-3794. ZONG Zhaoyun, YIN Xingyao, ZHANG Feng, et al. Reflection coefficient equation and pre-stack seismic inversion with Young's modulus and Poisson ration[J]. Chinese Journal of Geophysics, 2012, 55(11): 3786-3794. |
| [8] |
王康宁, 孙赞东, 侯昕晔. 基于傅里叶级数展开的纵波方位各向异性裂缝预测[J]. 石油物探, 2015, 54(6): 755-761. WANG Kangning, SUN Zandong, HOU Xinye. Fracture prediction by P-wave azimuthal anisotropy based on Fourier series decomposition[J]. Geophysical Prospecting for Petroleum, 2015, 54(6): 755-761. |
| [9] |
宋维琪, 徐月森, 张云银, 等. 基于傅里叶级数分析的各向异性参数估计及裂缝预测[J]. 石油物探, 2020, 59(1): 108-113. SONG Weiqi, XU Yuesen, ZHANG Yunyin, et al. Anisotropy parameter estimation and fracture prediction based on Fourier series analysis[J]. Geophysical Prospecting for Petroleum, 2020, 59(1): 108-113. |
| [10] |
PAN X P, ZHANG G, YIN X Y. Amplitude variation with offset and azimuth inversion for fluid indicator and fracture weakness in an oil-bearing fractured re-servoir[J]. Geophysics, 2019, 84(3): N41-N53. |
| [11] |
ZHANG G Z, LI L, PAN X P, et al. Azimuthal Fourier coefficient inversion for horizontal and vertical fracture characterization in weakly orthorhombic media[J]. Geophysics, 2020, 85(6): C199-C214. |
| [12] |
RUGER A. P-wave reflection coefficients for transversely isotropic models with vertical and horizontal axis of symmetry[J]. Geophysics, 1997, 62(3): 713-722. |
| [13] |
HUDSAON J A. Wave speeds and attenuation of elastic waves in material containing cracks[J]. Geophysical Journal of the Royal Astronomical Society, 1981, 64(1): 133-150. |
| [14] |
SHAW R K, SEN M K. Use of AVOA data to estimate fluid indicator in a vertically fractured medium[J]. Geophysics, 2006, 71(3): C15-C24. |
| [15] |
DOWNTON J, RUSSELL H. Azimuthal Fourier coefficients: A simple method to estimate fracture parameters[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 269-273.
|
| [16] |
李庆忠. 地震信号内插与噪音剔除(二)[J]. 地球物理学报, 1988, 31(3): 329-341. LI Qingzhong. Seismic signal interpolation and noise deletion(Ⅱ)[J]. Chinese Journal of Geophysics, 1988, 31(3): 329-341. |
| [17] |
谭军, 宋鹏, 李金山, 等. 基于同相轴追踪的三维地震资料多次波压制方法[J]. 石油地球物理勘探, 2017, 52(5): 895-905. TAN Jun, SONG Peng, LI Jinshan, et al. 3D multiple suppression based on event tracing[J]. Oil Geophysical Prospecting, 2017, 52(5): 895-905. |
| [18] |
SABBIONE J I, SACCHI M D. Restricted model domain time Radon transforms[J]. Geophysics, 2016, 81(6): A17-A21. |
| [19] |
GHOLAMI A, ZAND T. Three-parameter Radon transform based on shifted hyperbolas[J]. Geophy-sics, 2018, 83(1): V39-V48. |
| [20] |
杜昕, 范廷恩, 董建华, 等. 基于多层感知机网络的薄储层预测[J]. 石油地球物理勘探, 2020, 55(6): 1178-1187. DU Xin, FAN Ting'en, DONG Jianhua, et al. Characterization of thin sand reservoirs based on a multi-layer perceptron deep neural network[J]. Oil Geophysical Prospecting, 2020, 55(6): 1178-1187. |
| [21] |
DU X, LI G F, ZHANG M, et al. Multichannel band-controlled deconvolution based on a data-driven structural regularization[J]. Geophysics, 2018, 83(5): R401-R411. |



 杜昕, 北京市朝阳区太阳宫南街6号院中海油研究总院有限责任公司开发地质研究室,100020。Email:
杜昕, 北京市朝阳区太阳宫南街6号院中海油研究总院有限责任公司开发地质研究室,100020。Email: