② 油气资源与探测国家重点实验室, 北京 102249;
③ 海洋石油勘探国家工程实验室, 北京 100028;
④ 华北油田公司勘探开发研究院, 河北任丘 062552
② State Key Laboratory of Petroleum Resources and Prospecting, Beijing 102249, China;
③ National Engineering Laboratory for Offshore Oil Exploration, Beijing 100028, China;
④ Research Institute of Exploration&Development, Huabei Oilfield Company, PetroChina, Renqiu, Hebei 062552, China
裂缝是影响油气藏岩石物性参数的重要因素,精确预测裂缝对油气勘探、开发具有重要意义[1-2]。不同尺度的裂缝对地下油气藏的影响程度不同,基于叠后地震数据预测的大尺度裂缝(断裂)通常改变油气的储存状态[3-5],因此精确预测大尺度裂缝是油气勘探的重要组成部分[3]。
叠后地震数据与储层地质信息具有相关性[6-8],大尺度裂缝使叠后地震数据波形明显突变或不连续[4]。提取有效的叠后地震属性,可从几何动力学角度预测储层中的大尺度裂缝。常用的叠后地震属性主要有相干体(描述波形相似性)[9-13]、曲率体(表征构造应力引起的地层弯曲程度)[14-16]、倾角体(刻画地层构造变化特征)[17]等。然而,仅仅依靠单一属性很难准确预测地下裂缝分布情况,因此属性融合技术显得极其重要。通过数学方法综合考虑多种属性特征,将它们组合为更全面、可靠的裂缝表征属性,可以降低单一属性预测的多解性[18-20],提高裂缝预测精度。
目前,属性融合方法较多,且应用较广泛。在属性色彩技术方面,Guo等[21]将属性分量映射到色彩模型中,通过红、绿、蓝(Red-Green-Blue, RGB)和色调、亮度、色饱和度(Hue-Intensity-Saturation, HIS)模型进行属性融合;为了准确确定融合属性,丁峰等[22]结合主成分分析与红、绿、蓝、透明度(Red-Green-Blue-Alpha, RGBA)颜色融合方法分析属性融合,很好地识别了断裂区域。在神经网络方面,徐丽萍[23]利用人工神经网络方法进行非线性融合,以预测储层的发育程度。曹琳昱等[24]将粒子群优化的BP神经网络方法用于属性融合,但需要优选属性训练网络,且会陷入极小值。李全忠等[25]首次利用脉冲耦合神经网络(Pulse Coupled Neural Networks, PCNN)进行地震属性融合,以指示油气发育情况,然而PCNN模型中的大量参数需要人为干预设置,导致融合结果不准确及不能准确突出单属性的细节特征。因此,参数自适应PCNN(Parameter-Adaptive PCNN, PA-PCNN)模型[26]应运而生并用于图像融合领域,很好地避免了人为设置参数带来的误差。此外,基于多尺度几何分析的PCNN模型在图像融合领域的应用效果很好,通过非下采样小波变换[27]或非下采样剪切波变换[28](Non-Subsampled Shearlet Transform, NSST)分割原图像,可更好地提取细节信息进行融合。基于NSST-PCNN模型的多信息融合技术广泛用于医学[29-30]、遥感[31-32]等领域,且融合效果尤为突出。
本文在前人理论研究的基础上,结合NSST和PA-PCNN的优点,建立了基于NSST-PAPCNN的属性融合裂缝预测方法,以降低属性多解性,消除原属性中的部分冗余成分,可最大限度地保留有用信息,为地质解释提供相对准确的裂缝预测数据。首先,通过NSST将多属性分解为高、低频子带,其中高频子带包含更多的裂缝细节信息,低频子带可更好地刻画裂缝轮廓且具有丰富的能量信息。其次,对高频子带运用PA-PCNN模型进行融合,无需人工设置参数,得到更全面的高频数据;结合八邻域的改进拉普拉斯算子加权和(Weighted Sum of Eight-neighbor-hood-based Modified Laplacian,WSEML)与局部能量加权(Weighted Local Energy,WLE)方法对低频子带进行融合,使低频数据更好地保留细节及能量信息,以得到丰富的低频数据。最后,通过逆NSST方法完成属性融合裂缝预测。应用实例较好地证明了本文方法的有效性,通过对比不同方法的属性融合裂缝预测效果,突出了所提方法的优势。
1 理论方法 1.1 NSST属性融合过程中,为了获得细节信息更丰富的结果,通过数学变换进行多尺度、多方向分解提取相同位置的不同属性、不同空间细节信息进行融合。NSST具有位移不变性及方向灵敏性等特点[32],计算相对简单,能够准确提取目标边缘及空间信息,在医学和图像处理领域应用广泛。因此,将其应用于裂缝单属性分解,提取细节信息进行融合,可以更全面、准确地预测裂缝。
NSST分解主要包含基于非下采样金字塔滤波(Non-Subsampled Pyramid Filters, NSPFs)的多尺度分解、基于平移不变剪切滤波器组(Shift-invaria-nt Shearlet Filter Banks, SFBs)的多方向分解两个部分(图 1)。假设通过NSPFs将单属性数据X分解为多尺度K层数据,得到K+1个大小相同的子带数据,即包括K个高频子带和1个低频子带。对每个分解的高频子带运用SFBs获得对应子带的多方向表示数据{HXk, m, LX},其中HXk, m表示经过k层和m方向分解得到的高频子带,LX表示经过分解得到的低频子带,从而更全面且稀疏地表征融合信息并用于后续的融合处理。其中低频子带近似于原属性数据,具有丰富的能量信息,高频子带主要包含数据中的多方向、多尺度信息,可更好地刻画裂缝分布的细节[31]。

|
图 1 NSST分解框架 |
对高、低频子带分别融合后的数据运用逆NSST进行数据组合重构,主要分两个步骤:首先,通过SFBs对各个方向分解的滤波结果进行累加,生成非下采样金字塔;然后,使用重构滤波器对非下采样金字塔由粗到细地进行数据组合重构,获得融合后的数据结果。
1.2 PA-PCNN高频子带融合PCNN是一种基于文献[33]的皮质模型,是依据哺乳动物大脑皮层中同步脉冲发放的现象提出的,具有全局耦合和脉冲同步等特点,适用于数据融合领域。
PCNN模型是由若干神经元连接而成的单层反馈网络[34],输入的单个属性中数据的个数与神经元一一对应,每个神经元都受相邻神经元影响,从而进行信息传递和耦合,且主要由接收、调制和脉冲发生三部分组成。在传统的PCNN模型中,存在大量的自由参数设置且非线性较强,求解过程繁琐、计算量大,因此简化的PCNN模型[26]应运而生。
简化的PCNN单个神经元工作流程(图 2)可描述为
| $ \boldsymbol{F}_{i j}(\eta)=\boldsymbol{S}_{i j} $ | (1) |
| $ \boldsymbol{L}_{i j}(\eta)=V_{\boldsymbol{L}} \sum\limits_{n, l} \boldsymbol{W}_{i j n l} \boldsymbol{Y}_{n l}(\eta-1) $ | (2) |
| $ \boldsymbol{U}_{i j}(\eta)=\mathrm{e}^{-\alpha_{f}} \boldsymbol{U}_{i j}(\eta-1)+\boldsymbol{F}_{i j}(\eta)\left[1+\beta \boldsymbol{L}_{i j}(\eta)\right] $ | (3) |
| $ \boldsymbol{Y}_{i j}(\eta)= \begin{cases}1 & \boldsymbol{U}_{i j}(\eta)>\boldsymbol{E}_{i j}(\eta-1) \\ 0 & \text { 其他 }\end{cases} $ | (4) |
| $ \boldsymbol{E}_{i j}(\eta)=\mathrm{e}^{-\alpha_{e}} \boldsymbol{E}_{i j}(\eta-1)+V_{\boldsymbol{E}} \boldsymbol{Y}_{i j}(\eta) $ | (5) |

|
图 2 简化的PCNN工作流程 |
式中:Fij(η)为第η次迭代后(i, j)位置的反馈输入项;Sij为(i, j)位置输入数据;Lij为连接项,将周围神经元依据不同权重值相连;Ynl为周围(n, l)位置神经元的输出脉冲值;Wijnl为(i, j)位置输入数据周围(n, l)位置神经元的权重;Uij为内部活动项,e-αf×Uij(η-1)为上一次内部活动的衰减项,e-αf为Uij(η-1)的指数衰减系数;Fij(η)[1+βLij(η)]为反馈输入和连接项的非线性调制,β为连接系数;e-αe为Eij(η-1)的指数衰减系数;Eij为动态阈值项;VL和VE分别为连接项和动态阈值项的幅值。
在属性融合中,将各属性经过NSST分解后的高频子带数据HSk, m(S为属性集合)作为反馈输入项F(即Fij(η)=Sij=HSk, m(i, j)),将单个子带中每个数据看成神经元,因此总神经元个数即为输入单个子带中的数据个数。迭代开始前,需要初始化所有神经元脉冲值、内部活动和动态阈值项(Yij(0)=0,Uij(0)=0,Eij(0)=0),才能保证第一次迭代后所有的神经元都产生脉冲输出,能被点火(内部活动项大于动态阈值时,Yij=1点火;否则,Yij=0不点火)。一旦神经元被点火后,动态阈值迅速增加,抑制下一次点火脉冲产生;随后,动态阈值随着迭代不断衰减,直到小于内部活动项,并再次产生下一次点火脉冲。每当点火脉冲产生后,周围的神经元都被激励,从而产生点火脉冲。在多次迭代中,可以通过神经元点火脉冲产生的次数进行属性融合。
在式(1)~式(5)中,主要涉及五个自由参数(VL、αf、β、αe、VE)和一个权重矩阵(Wijnl)。在常规方法中,这些参数往往都由人为设定,会导致不准确的融合预测结果。因此本文运用PA-PCNN方法,无需人为设定,根据输入数据自有特征自适应地求解参数进行融合处理。分析式(1)~式(5)可知,β和VL可以整体视为连接项的权值系数,因此定义κ=βVL为连接权重强度。此外,权重矩阵主要计算周围神经元对目标神经元的影响作用,可通过距离定义权值。根据文献[26]可知,所有自由参数都通过自适应计算获得,即
| $ \boldsymbol{W}_{i j n l}= \begin{cases}\frac{1}{\|(i, j)-(n, l)\|_{2}} & (i, j) \neq(n, l) \\ 0 & (i, j)=(n, l)\end{cases} $ | (6) |
| $ \alpha_{f}=\lg \frac{1}{\sigma\left(\boldsymbol{H}_{\boldsymbol{S}}^{k, m}\right)} $ | (7) |
| $ \kappa=\frac{\frac{\boldsymbol{H}_{\boldsymbol{S}}^{k, m} \max }{\left(\boldsymbol{H}_{\boldsymbol{S}}^{k, m}\right)^{\prime}}-1}{6} $ | (8) |
| $ V_{\boldsymbol{E}}=\mathrm{e}^{-\alpha_{f}}+1+6 \kappa $ | (9) |
| $ \alpha_{e}=\ln \frac{\frac{V_{\boldsymbol{E}}}{\left(\boldsymbol{H}_{\boldsymbol{S}}^{k, m}\right)^{\prime}}}{\frac{1-\mathrm{e}^{-3 \alpha_{f}}}{1-\mathrm{e}^{-\alpha_{f}}}+6 \kappa \mathrm{e}^{-\alpha_{f}}} $ | (10) |
式中:σ(HSk, m)为输入高频子带数据HSk, m的标准方差;HSk, mmax和(HSk, m)′分别为输入数据的最大值和大津(Otsu)阈值。
为了便于求解计算,需将权重矩阵近似为
| $ \boldsymbol{W}_{i j n l} \approx\left[\begin{array}{ccc} 0.5 & 1 & 0.5 \\ 1 & 0 & 1 \\ 0.5 & 1 & 0.5 \end{array}\right] $ |
由上述PA-PCNN过程得到每个属性迭代后在所有神经元处产生的脉冲点火次数,由此可以获得各个神经元处的融合权重系数
| $ \left\{\begin{array}{l} \boldsymbol{\omega}_{i j, \mathrm{PA}-\mathrm{PCNN}}^{p}=\frac{\boldsymbol{T}_{i j}^{p}}{\boldsymbol{T}_{i j}^{1}+\boldsymbol{T}_{i j}^{2}+\cdots+\boldsymbol{T}_{i j}^{{N}}} \quad p \leqslant N \\ \text {s. t. }\left\{\begin{array}{l} \boldsymbol{T}_{i j}(\eta)=\boldsymbol{T}_{i j}(\eta-1)+\boldsymbol{Y}_{i j}(\eta) \quad \eta \geqslant 1 \\ \boldsymbol{T}_{i j}(0)=0 \end{array}\right. \end{array}\right. $ | (11) |
式中:Tijp为第p个高频子带位置(i, j)经过η次迭代神经元产生的脉冲点火总次数;N为属性总个数。根据PA-PCNN求解的子带权重系数,将NSST分解后不同属性的高频子带融合,得到最终多尺度、多方向的高频子带数据
| $ \boldsymbol{H}_{\mathrm{Fusion}}^{k, m}(i, j)=\sum\limits_{p=1}^{N} \boldsymbol{H}_{p}^{k, m}(i, j) \boldsymbol{\omega}_{i j, \mathrm{PA}-\mathrm{PCNN}}^{p} $ | (12) |
经过NSST分解后的各属性数据低频子带包含大量能量和细节信息,因此低频段的融合策略对最终融合质量具有重要影响。传统方法通常直接对低频数据进行简单加权平均融合,然而不同属性在同一位置的能量不同,易造成低频融合结果能量损失。为了在低频融合数据中尽可能保留原数据能量和细节信息,引入WLE和WSEML算法融合低频子带数据[35-36]。
WLE算法根据区域内各数据之间的相关性,最大限度地保留原数据能量信息
| $ \begin{aligned} \operatorname{WLE}_{\boldsymbol{S}}(i, j)=& \sum\limits_{u=-R}^{R} \sum\limits_{v=-R}^{R} \boldsymbol{W}(u+R+1, v+R+1) \times \\ & \boldsymbol{L}_{\boldsymbol{S}}(i+u, j+v)^{2} \end{aligned} $ | (13) |
式中:W是大小为(2R+1)×(2R+1)、半径为R的权重矩阵,矩阵中每个元素值设为22R-r,其中r是(i, j) 位置到矩阵中心四邻域的距离;LS为NSST分解后各属性的低频子带。以一个3×3阶矩阵为例,设R=1,r=0, 1, 2,则
| $ \boldsymbol{W}=\frac{1}{16}\left(\begin{array}{lll} 1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1 \end{array}\right) $ |
由于计算效率问题,对NSST分解层数进行一定限制,因此低频子带中仍然包含一定细节信息。为了尽可能地保存原数据中的细节信息,引入WSEML算法
| $ \begin{gathered} \operatorname{WSEML}_{\boldsymbol{S}}(i, j)=\sum\limits_{u=-R}^{R} \sum\limits_{v=-R}^{R} \boldsymbol{W}(u+R+1, v+ \\ R+1) \times \operatorname{EML}_{\boldsymbol{S}}(i+u, j+v) \end{gathered} $ | (14) |
其中
| $ \begin{gathered} \operatorname{EML}_{\boldsymbol{S}}(i, j)=\mid 2 \boldsymbol{L}_{\boldsymbol{S}}(i, j)-\boldsymbol{L}_{\boldsymbol{S}}(i-1, j)-\boldsymbol{L}_{\boldsymbol{S}}(i+ \\ 1, j)|+| 2 \boldsymbol{L}_{\boldsymbol{S}}(i, j)-\boldsymbol{L}_{\boldsymbol{S}}(i, j-1)-\boldsymbol{L}_{\boldsymbol{S}}(i, j+1) \mid+\\ \frac{1}{\sqrt{2}}\left|2 \boldsymbol{L}_{\boldsymbol{S}}(i, j)-\boldsymbol{L}_{\boldsymbol{S}}(i-1, j-1)-\boldsymbol{L}_{\boldsymbol{S}}(i+1, j+1)\right|+ \\ \frac{1}{\sqrt{2}}\left|2 \boldsymbol{L}_{\boldsymbol{S}}(i, j)-\boldsymbol{L}_{\boldsymbol{S}}(i-1, j+1)-\boldsymbol{L}_{\boldsymbol{S}}(i+1, j-1)\right| \end{gathered} $ | (15) |
结合WLE和WSEML算法,充分提取了原属性数据中的能量和细节信息,可求取低频子带融合权重,最终获得低频子带数据
| $ \boldsymbol{\omega}_{i j}^{p}{}_\mathrm{\ W}=\frac{\mathrm{WLE}_{i j}^{p} \times \mathrm{WSEML}_{i j}^{p}}{\sum\limits_{q=1}^{N}\left(\mathrm{WLE}_{i j}^{q} \times \mathrm{WSEML}_{i j}^{q}\right)} \quad p \leqslant N $ | (16) |
| $ \boldsymbol{L}_{\text {Fusion }}(i, j)=\sum\limits_{p=1}^{N} \boldsymbol{L}_{p}(i, j) \boldsymbol{\omega}_{i j}^{p}{}_ \mathrm{\ W} $ | (17) |
根据上述理论算法,总结了NSST—PAPCNN属性融合裂缝预测结构框架的具体流程(图 3)。
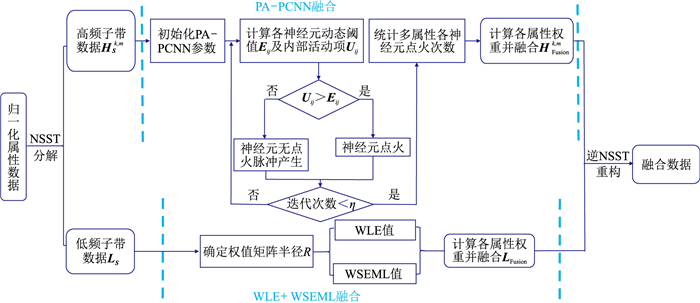
|
图 3 NSST-PAPCNN属性融合裂缝预测结构框架 |
(1) 从叠后地震数据中提取表征大尺度裂缝的属性(包括相干A、最大曲率B和倾角C),并对各属性数据进行归一化处理。由于不同的属性其量纲及数量级不同,不能直接融合,需要将多属性数据归一化到[0, 1]。
(2) 利用NSST算法分解各属性数据,得到各属性多尺度、多方向的高频子带HSk, m及低频子带LS,即
| $ \boldsymbol{S} \rightarrow\left\{\boldsymbol{H}_{S}^{k, m}, \boldsymbol{L}_{\boldsymbol{S}}\right\} \quad \boldsymbol{S} \in\{\boldsymbol{A}, \boldsymbol{B}, \boldsymbol{C}\}, k \in[1, K], $ |
| $ m \in[1, M(k)] $ |
数据分解过程中需要确定分解的层数K及每层方向数M(k)。
(3) 对各属性高频子带进行PA-PCNN融合,以提取高频细节信息。首先,初始化PA-PCNN模型中的各项参数,确定迭代次数η;其次,融合各属性每层、每个方向的数据,得到融合后的高频数据HFusionk, m。
(4) 对各属性低频子带进行WLE+WSEML融合,最大限度地保留能量和细节信息。融合前,需确定式(13)中的权重矩阵半径R,最终得到融合的低频子带LFusion。
(5) 逆NSST重构。将融合后的多尺度、多方向高、低频子带进行数据重构,得到最终的多属性融合结果{HFusionk, m, LFusion},可更全面地预测裂缝。
2 应用实例为了验证NSST-PAPCNN多属性融合裂缝预测方法的可行性和有效性,对M区地震数据进行测试,数据范围为Crossline1~Crossline751、Inline1~Inline751。该区裂缝较发育,大尺度裂缝(小断裂)分布广泛。为了有效预测大尺度裂缝,从叠后地震数据中准确提取了目的层段的相干、最大曲率和倾角等三种属性,并分别做归一化处理,然后进行属性融合处理,具体过程(图 4)如下。

|
图 4 M区多属性融合步骤 |
(1) 将三种属性分别进行NSST多尺度、多方向分解处理。测试并分析该区的数据特征可知,分解的层数超过4时,计算较稳定,但是层数过多会导致计算耗时较长。经权衡计算效果及效率,设定分解层数为5,每层的分解方向由细到粗为{16, 16, 8, 8, 4}。
(2) 对分解后的高频子带数据进行PA-PCNN融合。测试结果表明,迭代次数过多,融合结果差异不明显。因此通过试验,选取迭代次数为110。融合前,需要将PCNN模型中的各项参数初始化为0,并根据实际数据特征自适应地计算各融合参数。通过点火次数确定各属性高频子带数据权重系数,融合得到最终高频子带。
(3) 对分解后的低频子带数据进行WLE+WSEML融合。综合考虑计算效率及对结果的影响程度,设定式(13)中权重矩阵半径R为1,计算相应的WLE及WSEML值,并确定各属性低频子带数据权重系数,融合得到最终低频子带。
(4) 对分别融合后的高、低频子带数据进行逆NSST重构,获得最终的属性融合结果。
由M区归一化叠后均方根振幅属性切片(图 5)可以大致看出裂缝的发育特征,以此验证融合结果。为了更全面、准确地预测裂缝,需要最大限度保留三种属性的轮廓、能量及细节特征。图 6为M区目的层段归一化属性切片,图 7为相干、最大曲率和倾角多尺度、多方向分解的部分切片。由图可见,本文的NSST-PAPCNN方法能够对三种属性进行多尺度、多方向分解,充分提取了裂缝细节及能量信息,分别获得了低频(图 7a)、浅层分解(粗化分解,图 7b)、中层分解(逐渐细化,图 7c)及深层分解(细化分解,图 7d)等信息,从而得到了全面表征裂缝信息的融合结果。

|
图 5 M区归一化叠后均方根振幅属性切片 |

|
图 6 M区目的层段归一化属性切片
(a)相干;(b)最大曲率;(c)倾角 属性数值越大,则裂缝越发育,红框区域展示了三种属性的明显差异 |
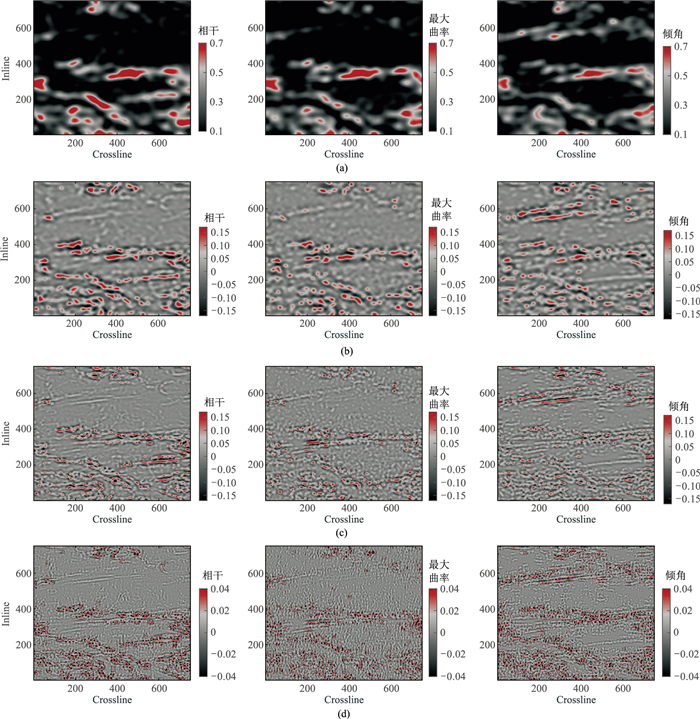
|
图 7 相干(左)、最大曲率(中)和倾角(右)多尺度、多方向分解的部分切片 (a)低频分量;(b)浅层分解;(c)中层分解;(d)深层分解 |
为了验证NSST—PAPCNN方法的属性融合裂缝预测效果,对比了不同方法的属性融合裂缝预测结果(图 8)。对比图 8与图 5可见,NSST-PAPC-NN方法具有明显的优势,消除了部分冗余成分(图 8a红框区域),很好地保留了原属性的能量、轮廓及细节信息(图 5),全面刻画了大尺度裂缝的发育情况,为地质解释人员提供了较精确的裂缝预测数据。实际数据测试结果表明,本文提出的基于NSST-PAPCNN的属性融合裂缝预测方法能够更有效地预测裂缝。
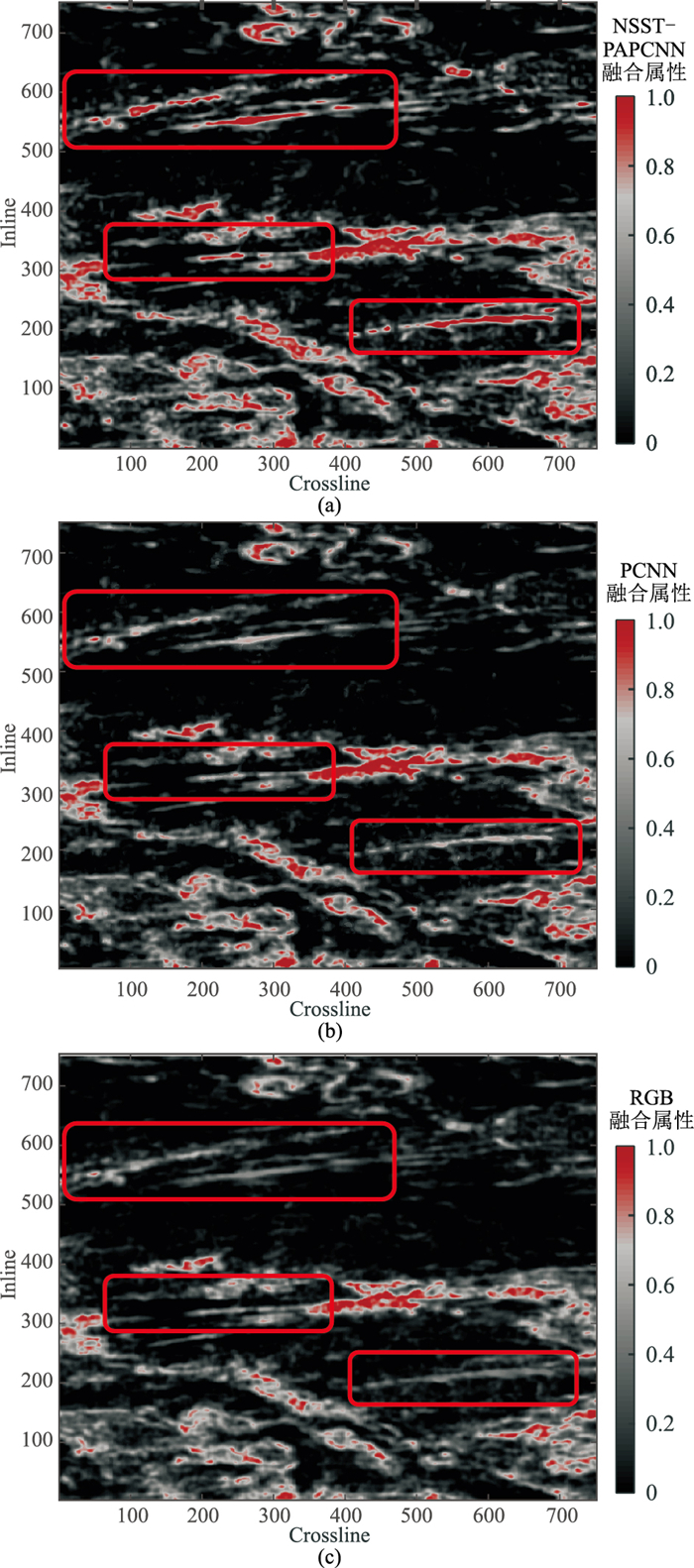
|
图 8 不同方法的属性融合裂缝预测结果
(a)NSST-PAPCNN;(b)PCNN;(c)RGB 红框区域展示了三种结果的明显差异 |
本文基于NSST及PA-PCNN方法提出了一种属性融合方法用于裂缝预测。该方法基于NSST分解算法,将多种属性数据分解为高、低频子带,对融合后的多尺度、多方向高、低频子带进行数据重构,得到最终的多属性融合结果,可进一步提取裂缝的轮廓及细节信息。
针对包含丰富细节信息的高频子带数据,采用PA-PCNN算法自适应调节自由参数,降低人为设置带来的误差。根据各子带数据各元素的点火脉冲产生次数,确定融合系数进行高频子带融合。针对包含能量、轮廓及残存细节信息的低频子带,结合WLE和WSEML算法,最大限度保留低频子带的能量和细节信息,确定融合系数进行低频子带融合。将融合后的高、低频子带数据进行逆NSST重构,获得最终的融合结果,降低了原属性的多解性,消除了部分冗余成分,很好地保留了原属性的细节和能量信息,能够综合多属性特征,全面、准确地预测裂缝,从而为地质解释人员提供较为精确的裂缝预测数据。运用本文方法对M区属性数据进行测试,并对比了不同方法的属性融合裂缝预测结果,证明基于NSST-PAPCNN的属性融合裂缝预测方法能够更有效地预测裂缝。
尚需指出,所提方法由于需要经过NSST多尺度、多方向分解,并对各尺度、各方向数据分别进行属性融合,导致计算量较大,耗时较长。因此,经权衡计算效率和融合效果,认为NSST分解的层数不能过多。此外,在尽量保留原属性中的有用细节成分时,往往无法保证融合后的所有细节信息都可靠,因此还需要依靠地质解释人员的专业经验及实际工区的数据特征准确预测裂缝,以进一步降低细节信息的多解性。
| [1] |
CHEN S Q, ZENG L B, HUANG P, et al. The application study on the multi-scales integrated prediction method to fractured reservoir description[J]. Applied Geophysics, 2016, 13(1): 80-92. DOI:10.1007/s11770-016-0531-7 |
| [2] |
姜晓宇, 张研, 甘利灯, 等. 花岗岩潜山裂缝地震预测技术[J]. 石油地球物理勘探, 2020, 55(3): 694-704. JIANG Xiaoyu, ZHANG Yan, GAN Lideng, et al. Seismic techniques for predicting fractures in granite buried hills[J]. Oil Geophysical Prospecting, 2020, 55(3): 694-704. |
| [3] |
王玲玲, 魏建新, 黄平, 等. 依托物理模型的叠后裂缝敏感地震属性优选与应用[J]. 石油地球物理勘探, 2019, 54(1): 127-136. WANG Lingling, WEI Jianxin, HUANG Ping, et al. Fracture-sensitive poststack seismic attribute optimization based on the physical model[J]. Oil Geophysical Prospecting, 2019, 54(1): 127-136. |
| [4] |
吕文雅, 曾联波, 陈双全, 等. 致密低渗透砂岩储层多尺度天然裂缝表征方法[J]. 地质论评, 2021, 67(2): 543-556. LYU Wenya, ZENG Lianbo, CHEN Shuangquan, et al. Characterization methods of multi-scale natural fractures in tight and low-permeability sandstone reser-voirs[J]. Geological Review, 2021, 67(2): 543-556. |
| [5] |
刘建军, 吴明洋, 宋睿, 等. 低渗透油藏储层多尺度裂缝的建模方法研究[J]. 西南石油大学学报(自然科学版), 2017, 39(4): 90-103. LIU Jianjun, WU Mingyang, SONG Rui, et al. Study on simulation method of multi-scale fractures in low permeability reservoirs[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2017, 39(4): 90-103. |
| [6] |
曹占宁. 碳酸盐岩多尺度裂缝预测方法及应用研究[D]. 北京: 中国石油大学(北京), 2018.
|
| [7] |
李付雷. 叠后地震属性分析技术在神泉地区微小断裂识别中的应用[D]. 四川成都: 西南石油大学, 2016.
|
| [8] |
张志军, 肖广锐, 李尧. 渤中19-6油田变质岩潜山内幕裂缝地震响应特征及预测技术[J]. 石油地球物理勘探, 2021, 56(4): 845-852. ZHANG Zhijun, XIAO Guangrui, LI Yao. Seismic response characteristics and prediction of fractured re-servoir inside metamorphic buried hill of Bozhong 19-6 oilfield[J]. Oil Geophysical Prospecting, 2021, 56(4): 845-852. |
| [9] |
崔正伟, 程冰洁, 徐天吉, 等. 基于构造导向滤波与梯度结构张量相干属性的储层裂缝预测方法及应用[J]. 石油地球物理勘探, 2021, 56(3): 555-563. CUI Zhengwei, CHENG Bingjie, XU Tianji, et al. Re-servoir fracture prediction method and application based on structure-oriented filtering and coherent attri-butes of gradient structure tensor[J]. Oil Geophysi-cal Prospecting, 2021, 56(3): 555-563. |
| [10] |
窦喜英. 裂缝储层高精度弹性阻抗预测与相干体属性增强方法研究[D]. 吉林长春: 吉林大学, 2015.
|
| [11] |
王永刚, 刘礼农. 利用相干数据体检测断层与特殊岩性体[J]. 石油大学学报(自然科学版), 2000, 24(1): 69-72. WANG Yonggang, LIU Linong. Automatic detection of faults and special lithologic body by using cohe-rence algorithm[J]. Journal of the University of Petroleum (Edition of Natural Science), 2000, 24(1): 69-72. DOI:10.3321/j.issn:1000-5870.2000.01.017 |
| [12] |
刘传虎. 地震相干分析技术在裂缝油气藏预测中的应用[J]. 石油地球物理勘探, 2001, 36(2): 238-243. LIU Chuanhu. Application of seismic coherent analysis technology to prediction of fractured reservoir[J]. Oil Geophysical Prospecting, 2001, 36(2): 238-243. DOI:10.3321/j.issn:1000-7210.2001.02.015 |
| [13] |
王志军, 黄军斌. 利用相干技术和三维可视化技术识别微小断层和砂体[J]. 石油地球物理勘探, 2001, 36(3): 378-381. WANG Zhijun, HUANG Junbin. Identification of micro-fault and sandbody by using coherence technique and 3-D visualization[J]. Oil GeophysicalProspecting, 2001, 36(3): 378-381. DOI:10.3321/j.issn:1000-7210.2001.03.018 |
| [14] |
王雷, 陈海清, 陈国文, 等. 应用曲率属性预测裂缝发育带及其产状[J]. 石油地球物理勘探, 2010, 45(6): 885-889. WANG Lei, CHEN Haiqing, CHEN Guowen, et al. Application of curvature attributes in predicting fracture-developed zone and its orientation[J]. Oil Geophysical Prospecting, 2010, 45(6): 885-889. |
| [15] |
杨威, 贺振华, 陈学华. 三维体曲率属性在断层识别中的应用[J]. 地球物理学进展, 2011, 26(1): 110-115. YANG Wei, HE Zhenhua, CHEN Xuehua. Application of three-dimensional volumetric curvature attri-butes to fault identification[J]. Progress in Geophysi-cs, 2011, 26(1): 110-115. DOI:10.3969/j.issn.1004-2903.2011.01.011 |
| [16] |
孔选林, 唐建明, 徐天吉. 曲率属性在川西新场地区裂缝检测中的应用[J]. 石油物探, 2011, 50(5): 517-520. KONG Xuanlin, TANG Jianming, XU Tianji. Application of curvature attribute in fracture detection of new area in Western Sichuan[J]. Geophysical Prospecting for Petroleum, 2011, 50(5): 517-520. DOI:10.3969/j.issn.1000-1441.2011.05.015 |
| [17] |
王峣钧, 郑多明, 李向阳, 等. 碳酸盐岩裂缝—孔洞型储层缝洞体系综合预测方法及应用[J]. 石油物探, 2014, 53(6): 727-736. WANG Yaojun, ZHENG Duoming, LI Xiangyang, et al. The fracture-cavern system prediction method and its application in carbonate fractured-vuggy reservoirs[J]. Geophysical Prospecting for Petroleum, 2014, 53(6): 727-736. DOI:10.3969/j.issn.1000-1441.2014.06.014 |
| [18] |
闫家伟, 王文庆, 吕芳芳, 等. 复杂碳酸盐岩储层多数据融合预测技术——以千米桥潜山奥陶系为例[J]. 石油地球物理勘探, 2021, 56(3): 583-592. YAN Jiawei, WANG Wenqing, LYU Fangfang, et al. Fusion of multiple data for predicting complex carbonate reservoirs and its application: A case study on Ordovician of Qianmiqiao buried hills[J]. Oil Geophysical Prospecting, 2021, 56(3): 583-592. |
| [19] |
王磊, 沈金松, 邹榕, 等. 融合地震属性和成像测井信息优化的储层缝洞带评价与钻井轨迹[J]. 吉林大学学报(地球科学版), 2021, 51(2): 607-623. WANG Lei, SHEN Jinsong, ZOU Rong, et al. Evaluation of fracture zones and optimazation of borehole tracks in carbonate formations through information fusion of seismic attributes and electric image well logging[J]. Journal of Jilin University (Earth Science Edition), 2021, 51(2): 607-623. |
| [20] |
史维, 李伟波. 多属性融合技术在裂缝储层预测中的应用[J]. 中国锰业, 2019, 37(2): 106-110. SHI Wei, LI Weibo. An application of multi-attribute fusion technique in prediction of fracture reservoir[J]. China's Manganese Industry, 2019, 37(2): 106-110. |
| [21] |
GUO H, LEWIS S, MARFURT K J. Mapping multiple attributes to three- and four-component color models-A tutorial[J]. Geophysics, 2008, 73(3): W7-W19. DOI:10.1190/1.2903819 |
| [22] |
丁峰, 年永吉, 王志国, 等. 地震多属性RGBA颜色融合技术的应用研究[J]. 石油物探, 2010, 49(3): 248-252. DING Feng, NIAN Yongji, WANG Zhiguo, et al. App-lication of seismic multi-attributes RGBA color blending[J]. Geophysical Prospecting for Petroleum, 2010, 49(3): 248-252. DOI:10.3969/j.issn.1000-1441.2010.03.007 |
| [23] |
徐丽萍. 多属性融合技术在塔中碳酸盐岩缝洞储层预测中的应用[J]. 工程地球物理学报, 2010, 7(1): 23-26. XU Liping. The application of multi-attribute fusion technology to the reservoir prediction of carbonate fracture and cavity in Tazhong area[J]. Chinese Journal of Engineering Geophysics, 2010, 7(1): 23-26. DOI:10.3969/j.issn.1672-7940.2010.01.006 |
| [24] |
曹琳昱, 朱仕军, 周强. 基于粒子群优化的BP网络在地震属性融合技术中的应用[J]. 石油与天然气地质, 2010, 31(5): 685-688. CAO Linyu, ZHU Shijun, ZHOU Qiang. Application of particle swarm optimization-based BP neural network to multi-attribute fusion techniques[J]. Oil & Gas Geology, 2010, 31(5): 685-688. |
| [25] |
李全忠, 彭真明, 周晶晶, 等. 基于脉冲耦合神经网络的地震多属性融合方法[J]. 石油地球物理勘探, 2014, 49(2): 316-321. LI Quanzhong, PENG Zhenming, ZHOU Jingjing, et al. Seismic multi-attribute fusion based on pulse coupled neural networks[J]. Oil Geophysical Prospecting, 2014, 49(2): 316-321. |
| [26] |
CHEN Y L, PARK S K, MA Y D, et al. A new automatic parameter setting method of a simplified PCNN for image segmentation[J]. IEEE Transactions on Neural Networks, 2011, 22(6): 880-892. DOI:10.1109/TNN.2011.2128880 |
| [27] |
ZHANG Q, GUO B L. Multifocus image fusion using the nonsubsampled contourlet transform[J]. Signal Processing, 2009, 89(7): 1334-1346. DOI:10.1016/j.sigpro.2009.01.012 |
| [28] |
GAO G, XU L, FENG D. Multi-focus image fusion based on non-subsampled shearlet transform[J]. IET Image Processing, 2013, 7(6): 633-639. DOI:10.1049/iet-ipr.2012.0558 |
| [29] |
黄陈建, 戴文战. NSST域内结合UDWT与PCNN医学图像融合算法[J]. 光电子·激光, 2020, 31(11): 43-51. HUANG Chenjian, DAI Wenzhan. Medical image fusion algorithm based on UDWT and PCNN in NSST domain[J]. Journal of Optoelectronics·Laser, 2020, 31(11): 43-51. |
| [30] |
DAS M, GUPTA D, RADEVA P, et al. NSST domain CT-MR neurological image fusion using optimised bio-logically inspired neural network[J]. IET Image Processing, 2020, 14(16): 4291-4305. DOI:10.1049/iet-ipr.2020.0219 |
| [31] |
张康, 黄永东, 王国芬. 基于NSST变换与自适应PCNN的多特征遥感图像融合[J]. 激光与红外, 2018, 48(6): 775-781. ZHANG Kang, HUANG Yongdong, WANG Guofen. Multi-feature remote sensing image fusion based on NSST transform and adaptive PCNN[J]. Laser & Infrared, 2018, 48(6): 775-781. DOI:10.3969/j.issn.1001-5078.2018.06.019 |
| [32] |
李敏, 苑贤杰, 骆志丹, 等. 基于NSST与改进PCNN的红外与可见光图像融合方法[J]. 光电子·激光, 2019, 30(2): 185-191. LI Min, YUAN Xianjie, LUO Zhidan, et al. Infrared and visual image fusion method based on NSST and improved PCNN[J]. Journal of Optoelectronics·Laser, 2019, 30(2): 185-191. |
| [33] |
ECKHORN R, REITBOECK H J, ARNDT M, et al. Feature linking via synchronization among distributed assemblies: Simulations of results from cat visual cortex[J]. Neural Computation, 1990, 2(3): 293-307. DOI:10.1162/neco.1990.2.3.293 |
| [34] |
赵丹, 戴文战, 李俊峰. 基于NSST和改进PCNN的医学图像融合[J]. 光电子·激光, 2018, 29(1): 95-104. ZHAO Dan, DAI Wenzhan, LI Junfeng. Medical ima-ge fusion based on NSST and improved PCNN[J]. Journal of Optoelectronics·Laser, 2018, 29(1): 95-104. |
| [35] |
CHANG L H, MA W, JIN Y, et al. An image decomposition fusion method for medical images[J]. Mathematical Problems in Engineering, 2020. DOI:10.1155/2020/4513183 |
| [36] |
DING Z, ZHOU D, NIE R, et al. Brain medical image fusion based on dual-branch CNNs in NSST domain[J]. BioMed Research International, 2020. DOI:10.1155/2020/6265708 |



 李景叶, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院, 102249。Email:
李景叶, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院, 102249。Email: 