2. 贵州省交通规划勘察设计研究院股份有限公司, 贵阳 550001
2. Guizhou Transportation Planning Survey Design Academy Co., LTD, Guiyang 550001, China
0 引言
滑坡的产生受地形地貌、地层构造、地质水文、降雨、人类活动等多种因素的影响,导致模型预报的结果具有高度的不确定性[1-2]。单一滑坡预报的模型难以取得理想的预报效果,因而多模型融合预警是当今研究热点。
滑坡位移-时间序列可以直接反映滑坡动态变化过程[3-4],利用该序列构建的多种临滑时刻预报模型(如Verhulst反函数模型、福囿模型等[5-8])可以从不同侧面反映滑坡机理,同时其互相之间又具有互补性。信息融合能综合多源互补信息以提高决策的准确性和可靠性[9-10],在滑坡多模型融合方面,采用的方法有:1)利用滑坡实际位移-时间序列与模型预报位移-时间序列形成拟合残差矩阵,通过求取残差矩阵的最优解来确定模型权重,实现多模型融合的预报[11-12]。但该权重一方面未考虑模型的最终预报误差;另一方面,因滑坡所处环境条件及其内部地质结构等要素各不相同,在不同的预报时间点,模型预报的滑坡位移误差波动较大。由于上述两方面原因,该权重作为模型的可靠性评估不够准确,难以取得理想的融合效果。2)通过已知滑坡预报的结果建立模糊隶属度函数,并对模型进行可靠性评估,再用模糊积分方法实现多模型融合的预报[13]。该隶属度函数需要滑坡发生时刻作为参照点,当滑坡未发生时,其发生时刻是未知的。因此,该隶属度函数不适用于滑坡预警实践。
针对目前多模型融合预警方法未能充分体现个体模型预报特征、缺乏实用性等问题。本文针对单一模型预报结果可能提前或延迟的情况,结合模糊积分方法处理不确定性决策融合的优势[14-15],构建了一种新的无需滑坡发生时刻作为参照点的模糊隶属度函数——预警隶属度函数,并利用模糊积分方法实现多模型滑坡预警。
1 滑坡预报模型与模糊积分融合 1.1 滑坡临滑时刻预报模型常用的滑坡临滑时刻预报模型有福囿模型、Verhulst函数模型和Verhulst反函数模型,表达式及参数确定方法见表 1。
| 模型名称 | 模型表达式 | 变量及参数 | 参数确定方法 |
| 福囿模型 |  |
v为滑动速度;tf为临滑时刻;t为监测时刻序列;C,α为常数 | α取值范围为1.5~2.2;C,α通过实验确定 |
| Verhulst函数模型 |  |
x(0)(1)为原始监测累加位移序列;t0为初始监测时刻;a,b为待定系数 | a, b可利用最小二乘法计算求取;选择预测曲线与监测曲线相距最小时刻作为t0值 |
| Verhulst反函数模型 | 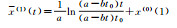 |
当预测累积位移系列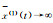 时,临滑时刻tf=(a/b)-t0, 其他参数同上 时,临滑时刻tf=(a/b)-t0, 其他参数同上 |
选择预测曲线与监测曲线相距最小时刻作为t0值 |
经典测度需要满足可加性,模糊测度无需严格满足可加性,能较好地对存在测量误差的信息进行度量。模糊积分是建立在模糊测度基础上的不确定性信息求和。
设Y是任意集合,R是Y的子集所构成的Borel域,对于所有的A, B⊂Y,且A∩BØ,Sugeno积分定义模糊测度gλ满足下面的可加性:
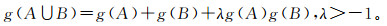 (1)
(1) 其中:λ为测度参数。
设Y={y1, y2, …, ym},定义映射g:yi∈Y→[0, 1]为gλ的模糊密度,令gi=gλ({yi}), i=1, 2, …, m,那么,当λ≠0时,有限集Y的gλ测度可由下式计算:
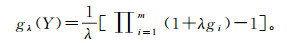 (2)
(2) 根据边界条件g(Y)=1,λ可由下式计算:
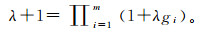 (3)
(3) 设(Y, R, g)是模糊测度空间,A∈R,f:Y→[0, 1]为R上的可测函数,当0≤f(y1), f(y2), …, f(ym)时,Sugeno积分可由下式计算:
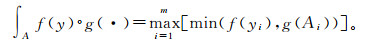 (4)
(4) 其中g(Ai)由下式递归计算:
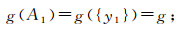 (5)
(5) 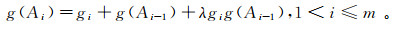 (6)
(6) 模糊积分融合多滑坡预报模型中,Y为滑坡预报模型的集合,g(Ai)为模型可靠性,f(yi)为模型yi当次预报隶属于预警论域子集的程度,模糊积分
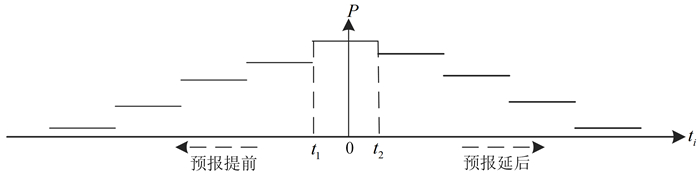
把模型预报滑坡发生时间视为随机变量,以滑坡实际发生时刻为参照点划分时间区间,时段概率为模型预报时刻落入某一时段区间的次数与模型预报总数的比值;时段概率与随机变量的分布函数密切相关,其可作为模型可靠性评价依据,若模型具有实用性,其时段概率应大致呈正态分布(图 1)。
|
| P为模型时段概率。 图 1 模型预报时段概率分布示意图 Fig. 1 Figure of probability distribution of model forecast period |
|
|
图 1中,0点表示滑坡发生时刻,时段区间[t1, t2]越小对模型预报可靠性评价的精度越高,区间大小受样本数量的限制,样本数量充分情况下可用较小的区间,样本数量较少宜用较大区间。对于滑坡预报需要解决滑坡具体发生时刻,而对于滑坡预警只需要解决预警时段内是否发生滑坡。因此,利用时段概率分布进行滑坡预警是可行的。
2.2 预警隶属度函数构建滑坡预警是评估预警时刻以后一定时间段发生滑坡和不发生滑坡的可能性,由于滑坡是否发生具有高度不确定性,可以把发生滑坡和不发生滑坡作为滑坡预警论域中的2个模糊子集,预警就是求取模型预报结果隶属于2个模糊子集的程度。如某滑坡预报模型最大延迟误差为50 d,假设模型当次预报是延迟的(滑坡发生提前),其预报滑坡发生时刻为第65天,可以确定从预警时刻起15 d以内,该斜坡发生滑坡的可能性趋近于0。依据上述思路,结合模型预报时段概率,构建模型预报隶属于发生滑坡和不发生滑坡模糊子集的隶属度函数,分别用实线和虚线表示,设模型预报提前和预报延迟的最大误差分别为σmaxa,σmaxb,模型预警隶属度函数如图 2所示。

|
| u为隶属度。 图 2 模型预警隶属度函数 Fig. 2 Model early warning membership function |
|
|
假设模型预报发生滑坡时刻为当前预报时刻后第L天,对于尚未发生的滑坡,滑坡发生时刻是未知的,不能确定模型该次预报时刻是提前还是延后,因此,也无法计算预警时效W天内发生滑坡的可能性。现分情况讨论如下:
1) 若预报提前,预报时间L取负值,在预警时间内发生滑坡的隶属度为:
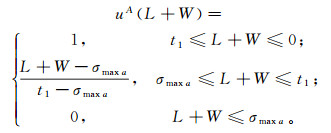 (7)
(7) 预报提前不发生滑坡的隶属度为
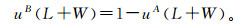 (8)
(8) 2) 若预报延后,预报时间L取正值,在预警时间内发生滑坡的隶属度为:
 (9)
(9) 预报延后不发生滑坡的隶属度为
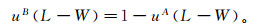 (10)
(10) 为降低滑坡发生的风险,模型在预警时间内发生滑坡的隶属度uA(L, W)取预报提前发生滑坡隶属度和延后发生滑坡隶属度二者较大值,不发生滑坡的隶属度uB(L, W)取二者较小值,那么预警隶属度函数为:
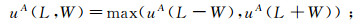 (11)
(11)  (12)
(12) 上述隶属度函数表达式中的t1、t2和σmaxa、σmaxb已通过模型可靠性评价确定,其反映了模型预报特征;因此模型预警隶属度函数只与预警时间W及模型预报时刻L有关,与实际发生滑坡时刻无关,这较好地解决了模型预报是提前还是延迟的问题。
3 验证 3.1 实验数据与预警隶属度函数确定收集20个已知滑坡位移监测数据,其中的16个用表 1中的滑坡预报模型计算滑坡临滑时刻,模型评价参数见表 2。从表 2可见,受已知样本数量限制,难以取得较高的模型评价精度,因此,隶属度函数的提前和延后最大值均采用3个模型的最大值,即σmaxb=-45,σmaxa=61,选用15 d时段精度,即t1=-15,t2=15,W=15。用另外的4个已知滑坡(卧龙寺、黄茨、晴隆和新滩滑坡)进行模拟预警验证实验,滑坡基本情况及位移监测数据见表 3。
| 模型名称 | 提前最大值/d | 延后最大值/d | 15 d时段精度/% | 10 d时段精度/% |
| 福囿模型 | 36 | 48 | 50 | 35 |
| Verhulst函数模型 | 45 | 61 | 45 | 25 |
| Verhulst反函数模型 | 31 | 27 | 60 | 42 |
| 滑坡名称 | 地质特性及诱发因素 | 累积位移曲线 |
| 卧龙寺滑坡 | 土质滑坡。土体疏松,裂隙纵横,滑动面坡度较陡,亚黏土层起伏较大。地表排水、地下水补给引发 | 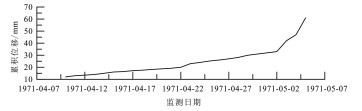 |
| 黄茨滑坡 | 土质滑坡。结构疏松,垂直节理发育,岩层产状变化较大,具强自重湿陷性。灌溉水引发 | 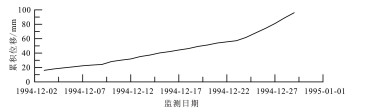 |
| 晴隆滑坡 | 岩质滑坡。土质松散,强风化层岩体破碎,节理裂隙发育,遇水易软化,地层起伏大。施工爆破、降雨引发 | 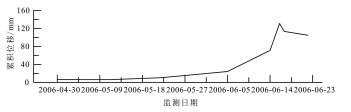 |
| 新滩滑坡 | 堆积体滑坡。长江岸坡发育,崩塌活动严重, 崩塌物来源充分。降雨是主要诱发因素 | 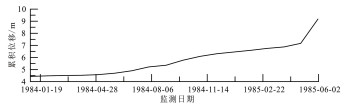 |
模拟预警时刻为滑坡发生3 d前、预警15 d内发生滑坡的可能性,多模型融合预警步骤如下:
1) 计算模型预报时刻及其提前或延后预警隶属度。根据表 1中滑坡预报模型,求取滑坡自预报时刻起到发生滑坡的时间L,根据式(7)和式(8)求取uA(L+W)和uB(L+W),根据式(9)和式(10)计算uA(L-W)和uB(L-W),结果见表 4(uB未列出)。
| 模型名称 | 卧龙寺滑坡 | 黄茨滑坡 | 晴隆滑坡 | 新滩滑坡 |
| 福囿模型 | (54, 0.20, 0.478) | (46, 0.46, 0.652) | (36, 0.80, 0.870) | (31, 0.967, 0.978) |
| Verhulst函数模型 | (56, 0.133, 0.435) | (51, 0.30, 0.543) | (55, 0.167, 0.457) | (28, 1.0, 0.0) |
| Verhulst反函数模型 | (47, 0.433, 0.63) | (62, 0.0, 0.304) | (25, 1.0, 0.0) | (56, 0.133, 0.435) |
| 注:括号中数据为L, uA(L+W), uA(L-W)。 | ||||
2) 计算模型预报发生滑坡和不发生滑坡预警的隶属度。根据式(11)和式(12),求取uA(L, W)和uB(L, W),并对3个预报模型按隶属度值大小排序,分别得到uA(yi)和uB(yi), 其中yi表示第i个预报模型。
3) 以模型15 d时段精度(表 2)作为模型模糊密度,根据式(3)求取λ值,得λ=-0.80。
4) 计算模糊测度。按照步骤3)的排序结果,结合表 2中精度,根据式(5)和式(6)计算模糊测度g(A)。
5) 计算模糊积分。按式(4)计算发生滑坡和不发生滑坡的模糊积分,当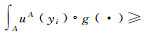
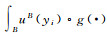
| i | 卧龙寺滑坡 | 黄茨滑坡 | 晴隆滑坡 | 新滩滑坡 |
| 1 | (0.435, 0.45, 0.45) | (0.304, 0.6, 0.6) | (0.457, 0.45, 0.45) | (0.435, 0.6, 0.6) |
| 2 | (0.478, 0.5, 0.77) | (0.543, 0.45, 0.83) | (0.870, 0.5, 0.77) | (0.978, 0.5, 0.86) |
| 3 | (0.630, 0.6, 1) | (0.652, 0.50, 1) | (1.0, 0.6, 1) | (1.0, 0.45, 1) |
| 积分结果 | 0.630 | 0.652 | 1.000 | 1.000 |
| 注:括号中数据为uA(yi),gi,g(Ai)。 | ||||
| i | 卧龙寺滑坡 | 黄茨滑坡 | 晴隆滑坡 | 新滩滑坡 |
| 1 | (0.37, 0.6, 0.6) | (0.348, 0.5, 0.5) | (0.0, 0.6, 0.6) | (0.0, 0.45, 0.45) |
| 2 | (0.552, 0.5, 0.86) | (0.457, 0.45, 0.77) | (0.13, 0.55, 0.86) | (0.022, 0.55, 0.77) |
| 3 | (0.565, 0.45, 1) | (0.696, 0.6, 1) | (0.543, 0.45, 1) | (0.565, 0.6, 1) |
| 积分结果 | 0.565 | 0.696 | 0.543 | 0.565 |
| 注:括号中数据为uA(yi),gi,g(Ai)。 | ||||
根据表 5和表 6模糊积分计算结果,滑坡发生3 d前模拟预警15 d内是否发生滑坡结果见表 7,1 d前模拟预警结果见表 8。
| 模型/方法 | 卧龙寺滑坡 | 坡黄茨滑 | 晴隆滑坡 | 新滩滑坡 |
| 福囿模型 | 不预警 | 预警 | 预警 | 预警 |
| Verhulst函数模型 | 不预警 | 预警 | 不预警 | 预警 |
| Verhulst反函数模型 | 预警 | 不预警 | 预警 | 不预警 |
| 模糊积分融合 | 预警 | 不预警 | 预警 | 预警 |
| 模型/方法 | 卧龙寺滑坡 | 黄茨滑坡 | 晴隆滑坡 | 新滩滑坡 |
| 福囿模型 | 不预警 | 预警 | 预警 | 预警 |
| Verhulst函数模型 | 预警 | 预警 | 不预警 | 预警 |
| Verhulst反函数模型 | 预警 | 预警 | 不预警 | 预警 |
| 模糊积分融合 | 预警 | 预警 | 预警 | 预警 |
1) 若虚警率采用错误预警次数与总预警次数的比值,那么,滑坡发生3 d前模拟预警模糊积分融合方法比单一模型平均虚警率降低16.6%,1 d前模糊积分融合法比单一模型降低25.0%;基于预警隶属度函数的模糊积分综合多模型综合预警能提高预警精度,虚警率降低20.0%左右。
2) 采用的监测数据越接近滑坡发生时刻,越能反映滑坡滑动特征,预警精度越高。
4 结语1) 利用滑坡预报模型的预报结果,构建了滑坡预警隶属度函数,函数充分反映了滑坡预报模型特征,实现了预报与预警的有机结合,且有效地解决了模型预报是提前还是延迟的问题。
2) 利用模糊积分方法,实现了基于预警隶属度函数多模型综合预警,多模型预警比单一模型预警准确。
3) 需要注意的问题是:基于预警隶属度函数的模糊积分融合多模型滑坡预警方法与单个模型预报精度、监测样本数量、预警时段的长短以及最大最小提前和延迟误差密切相关,方法直接应用于滑坡预警实践还需在滑坡预报模型适应性评价、收集已知滑坡实例等方面进行大量工作。
| [1] |
Ma G, Kirby J T, Hsu T J, et al. A Two-Layer Granular Landslide Model for Tsunami Wave Generation:Theory and Computation[J]. Ocean Modelling, 2015, 93: 40-55. DOI:10.1016/j.ocemod.2015.07.012 |
| [2] |
杜光波, 倪万魁. 降雨诱发型残坡积土滑坡形成机理分析[J]. 防灾减灾工程学报, 2016, 36(4): 565-571. Du Guangbo, Ni Wankui. Analysis of the Formation Mechanism of Rainfall-Induced Residual Soil Landslide[J]. Journal of Disaster Prevention and Mitigation Engineering, 2016, 36(4): 565-571. |
| [3] |
黄海峰, 易武, 易庆林, 等. 滑坡位移分解预测中的平滑先验分析方法[J]. 水文地质工程地质, 2014, 41(5): 95-100. Huang Haifeng, Yi Wu, Yi Qinglin, et al. Smoothness Priors Approach in Displacement Decomposition and Prediction of Landslides[J]. Hydrogeology & Engineering Geology, 2014, 41(5): 95-100. |
| [4] |
唐鹏, 陈国庆, 黄润秋, 等. 基于物理模拟试验的岩质滑坡地表位移分析[J]. 水文地质工程地质, 2017, 44(4): 105-110. Tang Peng, Chen Guoqing, Huang Runqiu, et al. Surface Displacement Analysis of Rock Slope Based on Physical Simulation Tests[J]. Hydrogeology & Engineering Geology, 2017, 44(4): 105-110. |
| [5] |
张俊, 殷坤龙, 王佳佳, 等. 基于时间序列与PSO-SVR耦合模型的白水河滑坡位移预测研究[J]. 岩石力学与工程学报, 2015, 34(2): 382-391. Zhang Jun, Yin Kunlong, Wang Jiajia, et al. Displacement Prediction of Baishuihe Landslide Based on Time Series and PSO-SVR Model[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(2): 382-391. |
| [6] |
龙万学, 林剑, 许湘华, 等. Verhulst反函数模型滑坡起始预测时刻的选择[J]. 岩石力学与工程学报, 2008, 27(增刊1): 3298-3304. Long Wanxue, Lin Jian, Xu Xianghua, et al. Selection of Initial Prediction Time for Landslide with Verhulst Inverse Function Model[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(Sup.1): 3298-3304. |
| [7] |
Lian C, Zeng Z G, Yao W, et al. Displacement Prediction Model of Landslide Based on a Modified Ensemble Empirical Mode Decomposition and Extreme Learning Machine[J]. Natural Hazards, 2013, 66(2): 759-771. DOI:10.1007/s11069-012-0517-6 |
| [8] |
Lian C, Zeng Z G, Yao W, et al. Ensemble of Extreme Learning Machine for Landslide Displacement Prediction Based on Time Series Analysis[J]. Neural Computing & Applications, 2014, 24(1): 99-107. |
| [9] |
王萌, 姜元俊, 黄栋, 等. 基于小流域的地震扰动区降型滑坡泥石流危险性评价方法[J]. 吉林大学学报(地球科学版), 2015, 45(6): 1781-1788. Wang Meng, Jiang Yuanjun, Huang Dong, et al. Hazard Assessment on Rainfall-Triggered Landslide and Debris Flow in the Seismic Disturbance Area at Watershed Level[J]. Journal of Jinlin University (Earth Science Edition), 2015, 45(6): 1781-1788. |
| [10] |
Zhai J H, Wang J G, Hu W X. Combination of OSELM Classifiers with Fuzzy Integral for Large Scale Classification[J]. Journal of Intelligent & Fuzzy Systems, 2015, 28(5): 2257-2268. |
| [11] |
徐则民, 梅雪峰, 王礼荣, 等. 滑坡预警中的降水时空变异性:以云南头寨沟为例[J]. 吉林大学学报(地球科学版), 2017, 47(1): 154-162. Xu Zemin, Mei Xuefeng, Wang Lirong, et al. Precipitation Temporal and Variability of Landslide Earthy Warning Research:A Case Study on Touzhai Gully in Yunnan Province[J]. Journal of Jinlin University (Earth Science Edition), 2017, 47(1): 154-162. |
| [12] |
沈玲玲, 刘连友, 许冲, 等. 基于多模型的滑坡易发性评价:以甘肃岷县地震滑坡为例[J]. 工程地质学报, 2016, 24(1): 19-28. Sheng Lingling, Liu Lianyou, Xu Chong, et al. Multi-Models Based Landslides Susceptibility Evaluation-Illustrated with Landslides Ttriggered by Minxian Earthquake[J]. Journal of Engineering Geology, 2016, 24(1): 19-28. |
| [13] |
李艳华, 林剑, 龙万学, 等. 基于位移的滑坡临滑时刻多模型综合预测模糊积分方法[J]. 自然灾害学报, 2013, 22(4): 209-212. Li Yanhua, Lin Jian, Long Wangxue, et al. Displace-ment Based Fuzzy Integral Method for Multi-Model Comprehensive Forecast of Landslide-Approaching Time[J]. Journal of Natural Disasters, 2013, 22(4): 209-212. |
| [14] |
Yin X X, Lin Y G, Li W, et al. A Novel Fuzzy Integral Sliding Mode Current Control Strategy for Maximizing Wind Power Extraction and Eliminating Voltage Harmonics[J]. Energy, 2015, 85: 677-686. DOI:10.1016/j.energy.2015.04.005 |
| [15] |
Yoo B S, Kim J H. Fuzzy Integral-Based Gaze Control of a Robotic Head for Human Robot Interaction[J]. IEEE Transactions on Cybernetics, 2015, 45(9): 1769-1783. DOI:10.1109/TCYB.2014.2360205 |


