2. 西南交通大学地质工程系, 成都 610031;
3. 昆明理工大学地球科学系, 昆明 650093
2. Department of Geological Engineering, Southwest Jiaotong University, Chengdu 610031, China;
3. Department of Earth Science, Kunming University of Science and Technology, Kunming 650093, China
0 前言
滑坡,尤其是大型滑坡,由于其地质过程、形成条件的复杂性、多样性及变化的随机性,往往会给人们带来惨重的损失。大量学者研究了诱发滑坡的众多因子。吴树仁等[1]对三峡库区与巴东县的滑坡进行分析后指出,有92%的滑坡与降水有关,66%的滑坡直接由降水诱发,当每小时降水量大于50 mm、或日降水量大于100 mm、或次降水大于150 mm时,滑坡发生的概率会显著增加。张珍等[2]报道,降水(雨)型滑坡占滑坡总数70%以上。1987年在意大利Valtellina谷坡区,180 mm强降水诱发了大量滑坡,仅80 km2的调查区就有500余处曾发生过滑坡[3]。1997年7月1998年3月,美国旧金山湾区高达1 115 mm降水量诱发数千处的滑坡及泥石流灾害,造成经济损失1.5亿美元[4]。1998年8月,日本福岛达正常水平4~6倍的1 200 mm强降水在100 km2范围内诱发滑坡1 000余处[5]。文献[6]报道,洪都拉斯900 mm的强降水诱发了50 000余处滑坡。因此,滑坡与降水在时间和空间上具有较高的一致性,特别是极端降水事件,“滑坡尾随降水,降水量越大的地区滑坡越发育”[7]。
鉴于滑坡的巨大危害性,20世纪70年代各国学者就已陆续开展了滑坡灾害的区域性预报或单体滑坡的早期预警[8]。基于大多数滑坡尾随强降水这一现象,通过大气降水的观测,借助降水量、降水强度和降水过程与滑坡在空间上、时间上的对应关系开展预警预报,是目前国内外区域降水型滑坡预警的主要手段。国内外学者研究的内容包括雨强-持续时间(I-D)、降雨量-持续时间(CR-D)及降雨量-雨强(CR-I)关系[9-14];但诱发降雨(水)型滑坡、流域群发性滑坡的I、CR、D临界阈值及相互关系在空间上大多随机性极大,而既有滑坡群中心区及其附近往往缺乏足够的雨量站,滑坡发生时间也多是基于推测(难以精准到小时水平)。
尽管目前已有大量不同尺度的临界标准对区域性滑坡进行预警;但是还存在预警时间精度低、空间外延性差等问题,原因主要在于所构建的临界降水量、降水强度阈值及降水持时并非来自滑坡区域或滑坡群中心区附近,即没有考虑降水(量)的时空变异性。为了提升基于降水的滑坡预警水平,本文以1991年9月曾经发生过特大滑坡灾害的云南昭通市头寨沟盘河流域为依托,对降水的时空变异性进行了深入的研究。
1 研究区概况和研究方法 1.1 研究区概况研究区位于云南省昭通市北东方向约30 km处的盘河乡头寨村(27°33′11″N27°33′16″N,103°52′33″E103°52′38″E),金沙江二级支流--盘河在头寨沟村以东自北向南径流,受河流侵蚀及切割作用,形成典型的“V”型河谷。1991年9月23日18时10分,盘河支流--头寨沟沟头部位发生大型高速远程滑坡碎屑流灾害,造成216人死亡,直接经济损失达1 200万元[15]。头寨沟全长约4 km,流域面积约3.2 km2。流域最高点海拔2 940 m,与盘河汇合处最低点海拔1 820 m,相对高差1 120 m。头寨沟沟谷两侧岸坡陡峭,坡度在30°以上,岸坡植被发育,植被覆盖率90 %以上。区内山上与山下年均气温分别为10.8、8.3 ℃,最高分别为30.2、27.1 ℃,最低分别为-6.7、-19.3 ℃。降水主要以降雨的方式出现,12月至次年2月有少量冻雨。
1.2 研究方法为了研究降水的时空变异特征,考虑研究区流域面积仅为3.2 km2,故在头寨沟布设2台自动气象站(图 1)。其中一台布设于滑坡碎屑流堆积扇左侧的头寨新村,编号1#站,标高1 820 m,坐标27°33′15″N、103°52′36″E,采用220 V工频交流电供电,计雨分辨率0.2 mm;另外一台布设于滑源区左侧附近,编号2#站,标高2 230 m,坐标27°34′11″N、103°51′43″E,采用64 V蓄电池供电,计雨分辨率0.2 mm。两站海拔高差410 m,直线距离约2.23 km。监测目标主要包括降水量、蒸发量、温度和湿度。监测数据可通过GPRS传输至位于昆明指定IP地址的接收器。监测从2013年10月开始,至2014年10月结束,历时约1 a。

|
| 图 1 气象站及布设位置图 Figure 1 Location of the weather station layout and schematic diagram |
|
|
为期1 a的监测结果(图 2)表明:1#站全年降水量970.0 mm,平均月降水量80.8 mm;2#站全年降水量1 751.0 mm,平均月降水量145.9 mm。2#站年降水总量是1#站的1.8倍。降水梯度高达190.5 mm/hm,大于王菱[16]所认为的在南方山地不同山、不同坡向降水梯度介于24.9~144.9 mm/hm范围的最大值。其中:1#站59月降水量751.0 mm,占全年降水量77.4 %;2#站59月降水量1 252.0 mm,占全年降水量71.5 %。2#站59月降水量是1#站的1.5倍。两站降水量均在8月达最大,分别为273.0 mm和394.0 mm。观测期内2#站共发生9次暴雨、1次大暴雨,1#站共发生2次暴雨,且1#站发生暴雨时2#站均为暴雨。2#站其他场次暴雨及大暴雨,1#站同时段对应发生6次大雨、2次中雨。两站最大小时降水强度分别为23.2、53.2 mm/h。总体上,两站年降水量以及降水强度的差异,因海拔关系而极为显著。

|
| 图 2 两站月降水量及降水量比值 Figure 2 Ratio of mouthly precipitation and the sum of precipition |
|
|
按气象部门规定,日降水量大于或等于0.1 mm为一个降水日。统计结果表明,一年观测期内1#站和2#站的降水日数分别为232 d和261 d,2#站站降水日数略大于1#站降水日数。1#站与2#站日降水序列在时间上存在较强的对应关系,即1#站发生降水时,一般而言2#站也会降水。日降水序列皮尔逊(Pearson)相关系数为0.871。1#站与2#站最大日降水量分别为55.2与66.6 mm。1#站无降水时2#站共发生82.0 mm累计降水量,对2#站高于1#站的降水量贡献率为10%左右,其中大部分为5.0 mm以下;这表明,2#站降水量远高于1#站的原因并非由2#站单独降水引起的。就日降水量而言,1#站日降水量5.0 mm以下共99.6 mm,2#站日降水量5.0 mm以下共270.0 mm,分别占全年降水量的10.3%和15.4%。就连续无降水日数而言,1#站出现16 d连续无降水日,而2#站最长出现7 d连续无降水日。运用统计学原理对日降水量频率分布进行研究,结果表明,日降水空间变化服从两参数伽马分布(图 3)。设某一时段的降水量为x,则:
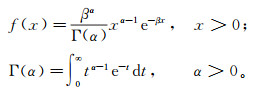
其中:f(x)为日降水密度函数;α为形状参数;β为尺度参数;t为时间;Γ(α)为伽马函数。伽马分布的具体形状受控于形状参数α和尺度参数β。

|
| 图 3 两站日降水量伽马分布拟合曲线 Figure 3 Precipitation of gamma distribution fitting curve |
|
|
用逐日降水样本对研究区伽马分布模式参数进行极大似然法估计,1#站和2#站的形状参数和尺度参数α1、α2、β1、β2分别为0.341 3、0.433 6、12.422 9、15.183 5。对1#站和2#站日降水量进行分布拟合,采用柯尔莫哥洛夫-斯米诺夫(Kolmogorov-Smirnovtest)拟合优度检验,在置信水平σ=0.01时均通过显著性检验。研究区两站α均小于1.0,表明日降水量分布最常出现在水量值较小的量级范围内。其中:α1 < α2,表明1#站气象站概率密度大值区较2#站左偏;β1 < β2,表明1#站气象站日降水分布较2#站更分散。
2.3 次降水变异性特征为了详细探讨研究区降水空间变异性特征,基于年降水观测资料对两站次降水量的变异性进行研究。关于次降水事件首先应解决的问题是如何从观测资料中分离出“次降水事件”。次降水事件是指一次天气系统过境引起的降水,一次降水事件过程中可能有短时间的间歇。因此,需定义降水间隔时间作为两次降水事件的分界,即如果降水间隔大于某一时间,则属于两次降水事件,反之则属同一降水事件。美国通用水土流失模型(USLE)定义6 h为两次降水事件的分界。E. C. Cutrim等[17]的研究采用1 h作为分界标准。D. Koutsoyiannis等[18]通过对希腊降水的研究,利用柯尔莫哥洛夫-斯米诺夫检验(Kolmogorov-Smirnovtest)确定5~7 h为两次降水事件的分界。Thorp[19]指出,降水事件的降水间隔的长短与不同季节的降水特性密切相关:美国大部分地区在春末、夏季和秋初易发生对流性降水,其具有强度大、历时短的特点,故降水间歇长度确定为1~2 h;而冬季以锋面雨(水)为主,一般持续时间较长,故降水间隔应更长。依据研究区降水特性,并参考以上研究成果,本研究的降水间隔标准定义为:59月降水强度大,降水间隔标准定为2 h;其他月份降水强度小,降水历时长,降水间隔标准定为6 h。两站次降水量变异性研究结果(表 1,2)表明:2#站中雨及以上降水事件比例均高于1#站;观测期内1#站共发生179次降水事件,2#站共204次,1#站和2#站最大次降水量分别为52.0、116.6 mm,持续时长分别为8、16 h;2#站无论是降水次数、累积降水时长及降水量都明显高于1#站,以上指标2#站分别是1#站的1.14、1.73和1.77倍。对两站次降水量进行检验,其中两站次降水持续时间和降水量之间均存在着显著差异(P < 0.050),2#站平均次降水时间和降水量显著高于1#站,尤其是平均次降水时间的差异达到极显著水平。而两站平均小时降水量无显著差异,这可能是由于1#站次降水事件划分过程中降水间歇时间较长和较多导致的。故造成两气象站之间的次平均降水量及累计降水量差异的主要贡献因素为次降水持续时长。
| 站点 | 小雨 | 中雨 | 大雨 | 暴雨 |
| 1#站 | 87.0 | 10.4 | 2.2 | 0.4 |
| 2#站 | 78.7 | 16.0 | 3.7 | 1.5 |
| 降水 次数 |
累积降水时间/ h |
累积降水量/ mm |
最大次降水量/ mm |
持续时间/ h |
次平均降水量/ mm |
平均次降水时间/ h |
平均小时降水量/ mm |
|
| 1#站 | 179 | 1 292.0 | 905.4 | 52.0 | 8 | 5.058±9.075 | 7.218±6.754 | 0.697±1.090 |
| 2#站 | 204 | 2 236.6 | 1 604.6 | 116.6 | 16 | 7.866±12.722 | 10.961±12.712 | 0.828±1.243 |
| P | - | - | - | - | - | 0.015 | 0.000 | 0.279 |
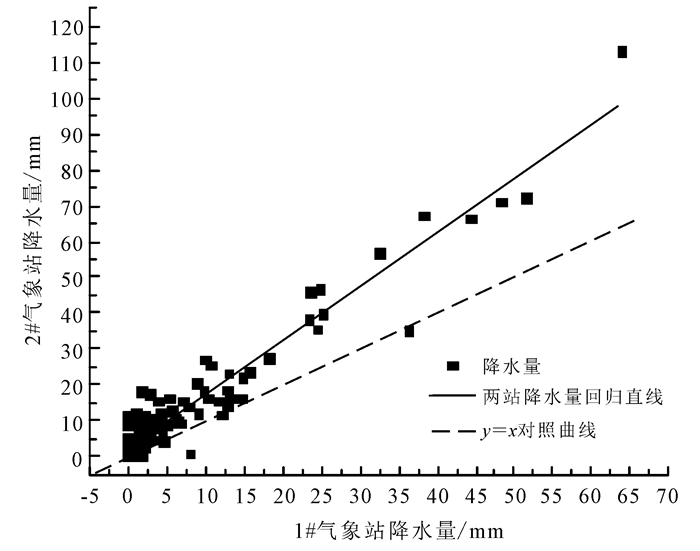
相关性分析(图 4)表明,在相同时段内,1#站气象站和2#站气象站的降水量呈现出了极显著的相关性,两者的Pearson相关系数为0.966(P=0.000 < 0.010)。以1#站气象站的降雨量为横坐标x、2#站气象站的降雨量为纵坐标y进行回归分析。结果表明,1#站15 mm与2#站20 mm的降水场次较为集中,两站降水量有明显的线性相关效应,线性函数关系为y=1.774+1.517x(R2=0.932)。两站降水坐标基本位于对照曲线y=x上方;这表明,相同时间内2#站气象站的降雨量基本大于1#站气象站。从拟合函数的趋势看,1#站气象站的降水量越大,2#站较1#站降水量增加的幅度越明显。
|
| 图 4 两站降水量线性回归 Figure 4 Liner regression analysis of precipitation |
|
|
采用GRI (generalized Rule Induction)关联规则对两站降水级别之间的关系进行分析,以高于50%置信度为标准,分别对两站的降水进行双向关联规则分析。首先,以相同时段内2#站降水级别为目标项、1#站的降水级别为控制项,获得了4条50%以上置信度的关联规则(表 3)。4个规则分别为:当1#站为暴雨时,2#站为暴雨的概率是100.00%;1#站无雨时,2#站为小雨概率是95.00%;1#站小雨时,2#站也有72.12%的可能性为小雨;1#站中雨时,2#站是大雨的概率是59.26%。GRI关联规则表明:相对1#站来说,2#站基本处于有雨的状态,当1#站为小雨或者暴雨时,两站降水级别相同的概率大; 而当1#站为中雨时,2#站有59.26%的概率达到大雨甚至暴雨级别。进一步将目标项和控制项倒置后,以1#站降水级别为目标项,2#站降水级别为控制项进行GRI关联分析。结果表明:当2#站为小雨时,1#站降水与2#站级别相同的概率为78.95%;2#站为大雨时,1#站中雨的概率为76.19%;2#站为中雨时,1#站小雨的概率为72.97%。即,2#站为小雨时,1#站小雨或无雨的概率大;当2#站达到中雨或大雨级别时,1#站的降水等级有较大概率比2#站低一个等级。在两站降水量等级关联规则的基础上,将降水量的实际数值作为条件项进行关联效应分析,明确了条件项为数值变量的重要关联规则,获得控制项为1#站与2#站降水级别的重要关联规则4条和5条(表 4)。结果表明:当1#站降雨量 > 9.10 mm时,2#站有76.00%~88.89%的概率发生大雨;当1#站降雨量 > 33.60 mm时,2#站一定发生暴雨;当2#站降雨量 < 9.20 mm,即发生接近中雨水平的降雨事件时,1#站也有较大概率发生小雨;而当2#站存在0.70 mm及以下降雨事件时,1#站有80.00%的概率不发生降雨。即当1#站发生中雨及以上等级的降雨时,2#站一般要比1#站高出1~2个降雨等级。
| 规则编号 | 前项(控制项) | 后项(目标项) | 支持度/% | 置信度/% | ||
| 关联目标 | 降水级别 | 关联目标 | 降水级别 | |||
| 1 | 1#站降水等级 | 中雨 | 2#站降水等级 | 大雨 | 17.09 | 59.26 |
| 2 | 暴雨 | 暴雨 | 1.27 | 100.00 | ||
| 3 | 无雨 | 小雨 | 12.66 | 95.00 | ||
| 4 | 小雨 | 小雨 | 65.82 | 72.12 | ||
| 1 | 2#站降水等级 | 小雨 | 1#站降水等级 | 小雨 | 60.13 | 78.95 |
| 2 | 大雨 | 中雨 | 13.29 | 76.19 | ||
| 3 | 中雨 | 小雨 | 23.42 | 72.97 | ||
由以上分析可见,表 4结论与表 3相似。两种不同的关联分析均表明,两站在小雨时变异性不明显,但当发生较大降水事件时,两站降水变异性显著。
| 规则编号 | 前项(控制项) | 后项(目标项) | 支持度/% | 置信度/% | ||
| 关联目标 | 降水级别 | 关联目标 | 降水量/mm | |||
| 1 | 1#站降水量 | < 1.30 | 2#站降水等级 | 小雨 | 53.80 | 96.47 |
| 2 | 9.10~24.60 | 大雨 | 11.39 | 88.89 | ||
| 3 | >9.10 | 大雨 | 15.82 | 76.00 | ||
| 4 | >33.60 | 暴雨 | 2.53 | 100.00 | ||
| 1 | 2#站降水量 | >12.1 | 1#站降水等级 | 中雨 | 21.52 | 61.76 |
| 2 | 1.30~9.20 | 小雨 | 50.00 | 92.41 | ||
| 3 | < 0.70 | 无雨 | 6.33 | 80.00 | ||
| 4 | >61.9 | 大雨 | 1.27 | 100.00 | ||
| 5 | < 9.20 | 小雨 | 70.25 | 81.08 | ||
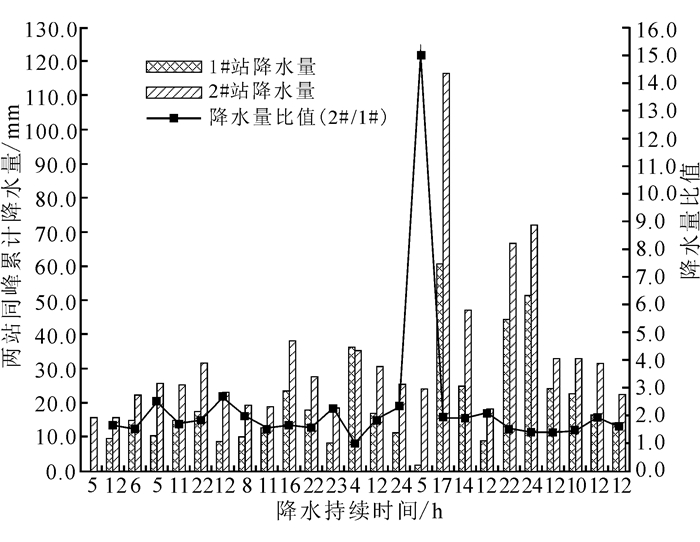
大雨及暴雨等极端降水事件下滑坡发生的概率会陡然增加。为研究极端降水情形下两站降水空间的变异特征,选取观测期内的典型降水事件进行比对分析。基于中国气象部门通用降水等级划分标准,以2#站为降水中心,选出2#站发生大雨、暴雨、大暴雨的降水事件,与对应1#站同步降水资料的主雨峰作为比对组(图 5)。如图 5所示:1)在所有选取的次降水事件及相同的累计降水时段内,1#站累计降水497.6 mm,占全年降水的49.8%;2#站累计降水836.6 mm,占全年降水量47.8%。2#站累计降水量为1#站的1.68倍。2)研究区降水表现出较强的“集中度”效应。2#站共9场暴雨累计降水504.0 mm,占全年降水的28.8%。挑选出的2#站共16场大雨,对应1#站发生3场小雨、12场中雨、1场无降水;2#站9场暴雨,对应1#站3场中雨、4场大雨、2场暴雨;2#站1场大暴雨,对应1#站为大雨。其中,2#站最大降水强度为时长达17 h的116.6 mm降水,而同时段1#站仅为60.6 mm,2#站降水量是1#站的1.92倍。3)两站降水差异最大的一次降水事件是相同5 h时段内,2#站发生24.0 mm降水,而1#站同时段降水量仅为1.6 mm,2#站降水量是1#站的15倍。
|
| 图 5 两站强降水空间变异性特征 Figure 5 Characteristics of heavy precipitation spatial variability |
|
|
对1#站与2#站做差异性相关分析,采用χ2检验。结果表明,两站降水量存在显著差异(P < 0.050),两站降水量线性回归方程为y=1.393 8x+6.724 9(R2=0.852)。
3 降水时间变异性特征据气象部门对昼夜划分标准,当日820时、20时次日8时为一个昼夜。由中国常用12小时降水强度等级划分的降水事件结果(表 5)表明:1#站与2#站白昼与夜间降水场次分别为132、166次,180、199次,降水量分别为266.4,705.8 mm,634.8,1 079.4 mm,分别占年降水的27.4%,72.6%,37.0%,63.0%。两站不同级别的降水事件及降水量均表现为夜间降水场次高于白昼。从1#站组来看,1#站白天12 h无大雨及暴雨场次的降水事件发生;但夜间1#站共发生了8次大雨和4次暴雨,而2#站夜间共发生14次大雨、7次暴雨,2#站夜间无论是降水场次还是降水量均明显高于白天。通过对1#站与2#站的纵向比对,2#站大雨以上级别的降水场次与累计降水量均远高于1#站。对两站温度、湿度资料分析发现,2#站平均湿度较1#站大,温度较1#站低。故在夜间,由于谷风盛行、空气湿度较大、气温较低,所以导致了2#站降水量较1#站明显增加。另外,从次连续降水间隔时间来看,1#站连续性降水过程中,降水间隔次与间隔时长略大于2#站。因此,从时间变异性看,研究区两不同位置处的降水时间变异性较强。对文献[20]中的滑坡进行完全统计发现:90多个大型滑坡大多由降水诱发,而在有具体时间记录的17个降水型滑坡中,共有10个发生在夜间20时以后,其中5个发生在凌晨;4个发生在早上89时之间;3个发生在下午15时左右。基于本文研究,可合理解释降水型滑坡夜间发生频次高于白昼的现象。
| 场次 | 累计降水量/mm | 降水量均值/mm | |||||
| 白昼 | 夜间 | 白昼 | 夜间 | 白昼 | 夜间 | ||
| 1#站 | 小雨 | 116 | 129 | 115.2 | 157.8 | 1.0 | 1.2 |
| 中雨 | 16 | 25 | 151.2 | 237.6 | 9.5 | 9.5 | |
| 大雨 | 0 | 8 | 0.0 | 158.4 | 0.0 | 19.8 | |
| 暴雨 | 0 | 4 | 0.0 | 152.0 | 0.0 | 38.0 | |
| 2#站 | 小雨 | 146 | 144 | 173.4 | 226.4 | 1.2 | 1.6 |
| 中雨 | 27 | 34 | 277.4 | 283.4 | 14.4 | 8.3 | |
| 大雨 | 6 | 14 | 126.8 | 290.8 | 21.1 | 20.8 | |
| 暴雨 | 1 | 7 | 57.2 | 278.8 | 57.2 | 39.8 | |
基于区域性降水资料推算临界降水阈值是降水型滑坡预警的主要手段,但降水站点最大控制面积研究仍然存在不足,外围站点布设的疏密,会直接影响滑坡预警的精度,甚至导致预警的失败。针对当前通过构建临界降水阈值模型的区域性预报或单体滑坡的早期(实时)预警,对不同海拔高度的两气象站资料做了深入研究,得出以下结论:
1)受地形及海拔控制,研究区直线距离为2.32 km的两气象站降水梯度高达190 mm /hm,降水空间变异性极显著。
2)研究区日降水量的空间频率分布服从两参数伽马分布,两站日降水量分布最常出现在水量值较小的量级范围内,且2#站日降水序列分散度较1#站高。
3)两个气象站次降水持续时间和降水量之间均存在着显著差异(P < 0.050),2#站平均次降水持续时间与降水量均显著高于1#站气象站,尤其是降水持续时间的差异达到极显著水平。因此降水持续时间是造成降水空间变异性的主要原因。
4)1#站为小雨或者暴雨级别时,两站降水级别相同的概率大,而1#站为中雨时,2#站有59.26%的概率达到大雨甚至暴雨级别;1#站为暴雨时,2#站有100.00%的概率发生暴雨,甚至有可能发生大暴雨。1#站的降水量越大,2#站较1#站降水量增加的幅度越明显。2#站与1#站降水在小雨以上级别时差异性显著,而强降水是诱发滑坡最重要的因素,故构建预警降水临界阈值时需特别考虑强降水时空变异性。
5)受谷风影响,两站不同级别的降水事件及降水量均表现为夜间降水场次高于白昼降水场次。其中2#站无论是降水场次还是降水量均明显高于1#站。对1#站与2#站的纵向比对表明,2#站大雨以上级别的降水事件多发于夜晚,这对滑坡的预警极为不利。
6)地形复杂的山区进行滑坡预报或建立降雨-滑坡预报预警模型时,要充分考虑降水的空间变异性问题,即气象站点所能控制的有效相关域。在降水空间变异性较大且存在潜在滑坡区域增大气象站设点密度;在坡体处于变形蠕变阶段或者已发生较大变形的潜在滑源区附近单独布设站点;雨量接收站可以放在就近的村、乡或县。
| [1] | 吴树仁, 金逸民, 石菊松, 等. 滑坡预警判据初步研究:以三峡库区为例[J]. 吉林大学学报(地球科学版), 2004, 34 (4) : 596-600. Wu Shuren, Jin Yimin, Shi Jusong, et al. A Primary Study of Landslide Warning Criterion:An Example from the Reservoir Region of the Three Gorges[J]. Journal of Jilin University (Earth Science), 2004, 34 (4) : 596-600. |
| [2] | 张珍, 李世海, 马力. 重庆地区滑坡与降雨关系的概率分析[J]. 岩石力学与工程学报, 2005, 24 (17) : 3185-3191. Zhang Zhen, Li Shishai, Ma Li. Probability Analysis of Relationship Between Landslide and Rainfall in Chongqing Area[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24 (17) : 3185-3191. |
| [3] | Guzzetti F, Crosta G, Marchetti M, et al. Debris Flows Triggered by the July, 17-19, 1987 Storm in the Valtellina Area (Northern Italy)[C]//Internationales Symposion, Tagungspublikation, Band 2, Seite. Bern:Interpraevent, 1992:193-204. |
| [4] | Coe J A, Godt J W, Brian D, et al. Map Showing Locations of Damaging Landslides in Alameda County, California, Resulting from 1997-1998 EL Nino Rainstorms[Z/OL]. (1999-07-12)[2015-02-08].http://greenwood.cr.usgs.gov. |
| [5] | Chigira M. Geologic Factors Contributing to Landslide Generation in a Pyroclastic Area:August 1998 Nishigo Village, Japan[J]. Geomorphology, 2002, 46 (1/2) : 117-128. |
| [6] | Schuster R L, Lynn M H. Socioeconomic Impacts of Landslides in the Western Hemisphere[R]. Reston:United States Geological Survey, 2001. |
| [7] | 张友谊, 胡卸文, 朱海勇. 滑坡与降雨关系研究展望[J]. 自然灾害学报, 2007, 16 (1) : 104-108. Zhang Youyi, Hu Xiewen, Zhu Haiyong. Prospect of Reseach on Relationship Between Landslide and Rainfall[J]. Journal of Natural Disasters, 2007, 16 (1) : 104-108. |
| [8] | 徐则民, 黄润秋. 山区流域高盖度斜坡对极端降雨事件的地下水响应[J]. 地球科学进展, 2011, 26 (6) : 598-607. Xu Zemin, Huang Runqiu. The Response of the Groundwater in Vegetated Slopes in Mountainous Catchments to Heavy Rain Events[J]. Advances in Earth Science, 2011, 26 (6) : 598-607. |
| [9] | Chleborad A F, Baum R L, Godt J W. Rainfall Thres-holds for Forecasting Landslides in the Seattle, Washington, Area:Exceedance and Probability[R].Reston:U S Geological Survey, 2006:1064. |
| [10] | Fiorillo F, Wilson R C. Rainfall Induced Debris Flows in Pyroclastic Deposits Campania (Southern Italy)[J]. Engineering Geology, 2004, 75 (3/4) : 263-289. |
| [11] | Guzzettil F, Peruccacci1 S, Rossi1 M, et al. Rainfall Thresholds for the Initiation of Landslides in Central and Southern Europe[J]. Meteorology and Atmospheric Physics, 2007, 98 (3/4) : 239-267. |
| [12] | 柳源. 滑坡临界暴雨强度[J]. 水文地质工程地质, 1998, 25 (3) : 43-45. Liu Yuan. Critical Precipitation of Landslide[J]. Hydrogeology and Engineering Geology, 1998, 25 (3) : 43-45. |
| [13] | 王萌, 姜元俊, 黄栋, 等. 基于小流域的地震扰动区降雨型滑坡泥石流危险性评价方法[J]. 吉林大学学报(地球科学版), 2015, 45 (6) : 1781-1788. Wang Meng, Jiang Yuanjun, Huang Dong, et al. Hazard Assessment on Rainfall-Triggered Landslide and Debris Flow in the Seismic Disturbance Area at Watershed Level[J]. Journal of Jilin University (Earth Science), 2015, 45 (6) : 1781-1788. |
| [14] | 高华喜, 殷坤龙. 降雨与滑坡灾害相关性分析及预警预报阀值之探讨[J]. 岩土力学, 2007, 28 (5) : 1055-1060. Gao Huaxi, Yin Kunkong. Discussion on Correlations Between Landslides and Rainfall and Threshold for Landslide Early-Warning and Prediction[J]. Rock and Soil Mechanics, 2007, 28 (5) : 1055-1060. |
| [15] | 唐川. 昭通头寨沟特大型灾害性滑坡研究[J]. 云南地理环境研究, 1991, 3 (2) : 64-70. Tang Chuan. A Study on Large-Scale Catastrophic Landslide at Touzhai Gully of Zhaotong[J]. Yunnan Geographic Environment Research, 1991, 3 (2) : 64-70. |
| [16] | 王菱. 华北山区年降水量的推算和分布特征[J]. 地理学报, 1996, 51 (2) : 164-170. Wang Ling. Calculation and Distributional Characteristics of Annual Rainfall Amount in Mountainous Regions of North China[J]. Acta Georaphical Sinica, 1996, 51 (2) : 164-170. |
| [17] | Cutrim E C, Martin D W, Butzow D G, et al. Pilot Analysis of Hourly Rainfall I Central and Eastern Amazonia[J]. Journal of Climate, 2000, 13 (7) : 1326-1334. DOI:10.1175/1520-0442(2000)013<1326:PAOHRI>2.0.CO;2 |
| [18] | Koutsoyiannis D, Xanthopoulos T. A Dynamic Model for Short Scale Rainfall Disaggregation[J]. Hydrdogical Sciences Journal, 1990, 35 : 305-322. |
| [19] | Thorp J M. Mesoscale Storm and Dry Period Paramen-ters from Hourly Precipitation Data[J]. Atmospheric Environment, 1986, 20 (9) : 1683-1689. DOI:10.1016/0004-6981(86)90115-0 |
| [20] | 黄润秋, 许强. 中国典型灾难性滑坡[M]. 北京: 科学出版社, 2008 . Huang Runqiu, Xu Qiang. Catastrophic Landslides in China[M]. Beijing: Science Press, 2008. |



