2. 海洋信息获取与安全工业和信息化部重点实验室(哈尔滨工程大学), 黑龙江 哈尔滨 150001;
3. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001
2. Key Laboratory of Marine Information Acquisition and Security (Harbin Engineering University), Ministry of Industry and Information Technology, Harbin 150001, China;
3. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
研究水下目标声散射物理机理,建立散射信号参数与目标属性之间的函数关系是获取目标属性信息的关键。根据目标声散射特性,回波可分为几何声散射回波与弹性声散射回波[1]。声呐目标回波亮点模型是目标散射回波分析的有效工具[2-3]。结合该模型中的理论,根据不同声波入射角度下目标声散射成分的时序关系可以对回波角度进行识别。
分数阶傅里叶变换是一种具有良好的脉冲压缩性能的时频分析方法[4],适用于分析具有线性调频特性的非平稳信号,在主动声呐目标探测识别中具有的广泛应用[5]。在发射线性调频信号的情况下,目标回波具有与发射信号相似的调频特性,在分数阶变换域中回波成分具有最佳变换阶数[6]。根据变换关系,利用最佳变换域的结果可以进行信号的参数估计[7]。
基于浅层学习的传统模式识别方法依赖于人为提取的特征向量,且参数无法进行自学习,对于大样本、高维数据的分类识别效果有限。深度学习方法克服了传统方法在高维数据表征能力的不足,根据训练数据调整参数,提取数据的深层特征,准确地实现分类任务[8]。深度学习方法在水声领域已得到广泛地应用。Fischell提取目标回波的几何散射强度和三维散射场特征,实现对球体和圆柱体目标形状和成分的分类[9]。多模态深度学习分类识别方法将长短时记忆系统与卷积神经网络结合,对信号的一维和二维特征并行处理,提高水下目标识别精度[10]。将二阶池化与卷积神经网络相结合,可以从声信号的时频表示中获取目标分类信息[11]。
本文基于声呐目标回波亮点模型对有限长半球头圆柱目标声散射回波信号进行分析,利用分数阶傅里叶变换提取不同入射角度下的目标回波特征。将传统特征与深度学习方法结合,以获取的特征作为深度学习网络模型的输入,通过对网络结构和参数的优化实现不同入射角度下回波的分类识别。
1 水下目标声散射机理目标声散射是入射声波与目标作用的结果,声散射回波中包含目标形状、尺寸、结构、材质等信息。目标声散射的求解方法包括严格的理论解析解和近似理论解,对简单形状的目标,可以将声散射归结为波动方程和边界条件描述的数学物理问题[12]。实际水下目标受限于复杂的形状以及边界条件,可采用共振散射理论对声散射机理和回声成分和特性进行研究[13]。声呐目标回波亮点模型理论是在此基础上发展的一种高频近似方法,能够直观地分析目标回波特性,可以作为声散射回波处理方法研究的信号模型,符合实际的工程应用。
亮点模型将复杂目标的回波近似为多个子回波叠加的结果,子回波从目标某个等效的散射点产生,这些散射点即为亮点。根据形成机理分为几何亮点与弹性亮点[13],其中几何亮点成分服从线性声学规律,包括镜反射和棱角反射。弹性亮点回波包含目标结构和材质信息,产生机理复杂。不同声散射成分间的时延信息可以作为不同入射角度下目标回波特征提取的依据。
在亮点模型的理论框架下,每个亮点回波信号可以看作入射信号的时延拷贝,对于复杂目标,多亮点的传递函数表示为单个亮点传递函数的线性叠加:
| $ H(\boldsymbol{r}, {\omega})=\sum\limits_{m=1}^{N} A_{m}(\boldsymbol{r}, \omega) \mathrm{e}^{\mathrm{j} \omega \tau_{m}} \mathrm{e}^{\mathrm{j} \varphi_{m}} $ | (1) |
式中:Am(r, ω)为第m个幅度因子,与频率有关;r为声波入射方向矢量;τm为目标各亮点与接收点间的时延;φm是相位因子。工程中,回波信号可表示为随不同入射角度变化的参数组合。其中时延因子携带了目标的尺寸信息,可以用来分析目标的几何结构和声波入射角。
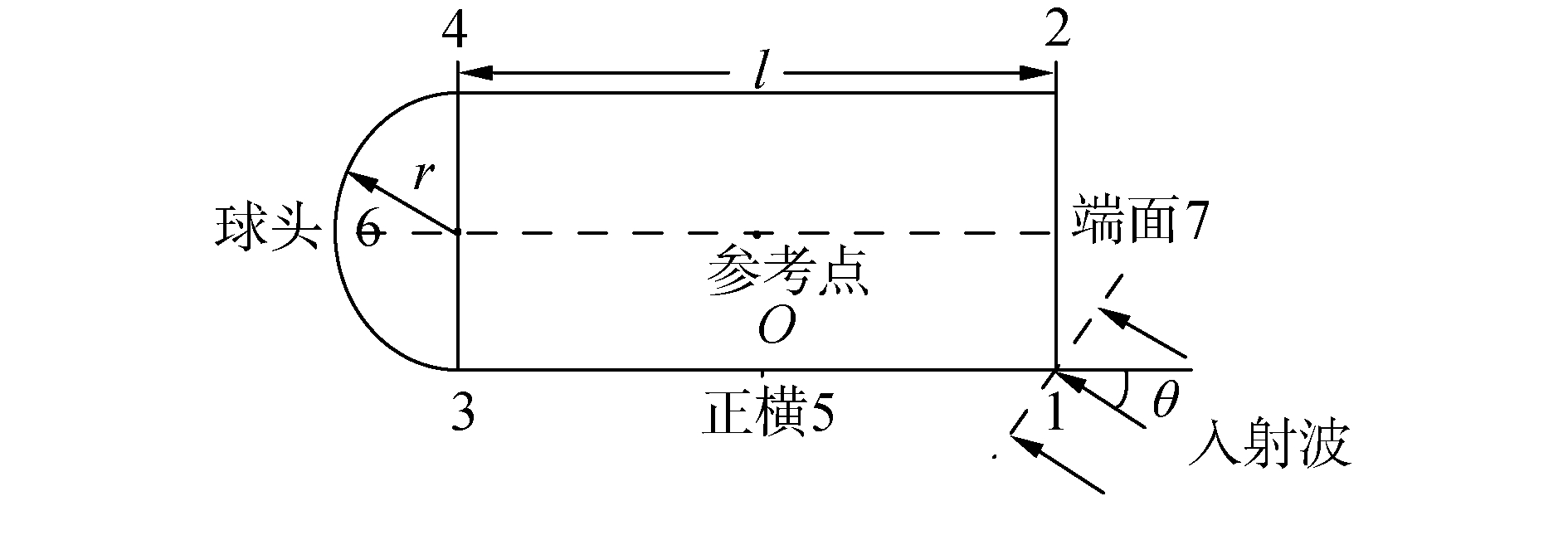
本文研究的目标模型结构示意图如图 1。根据亮点模型理论,其声散射回波可以等效为半球和有限长圆柱2个子目标声散射回波的组合。
|
Download:
|
| 图 1 目标模型结构 Fig. 1 Schematic diagram of target model | |
图 1中目标回波主要为棱角波和镜面反射波,由于目标模型具有对称结构,简化分析0~180°内的变化情况。声波垂直入射目标端面时角度记为θ=0°,正横入射时记为θ=90°。在图 1中,几何散射回波主要由圆柱端面、球冠、圆柱正横以及棱角1、2的回波成分组成,由于目标表面不够光滑,在3、4处同样也会产生几何声散射回波。在观察范围内棱角4处于影区,故棱角散射回波包含棱角1、棱角2和棱角3,镜反射回波则包含端面正横7、正横5和球冠6。不同的声波入射角度会导致目标几何散射回波中含有的目标种类和数目显著变化,在观测范围内,亮点出现位置与入射角度关系见表 1。
| 表 1 入射角度与亮点关系 Table 1 Relationship between incident angle and highlight |
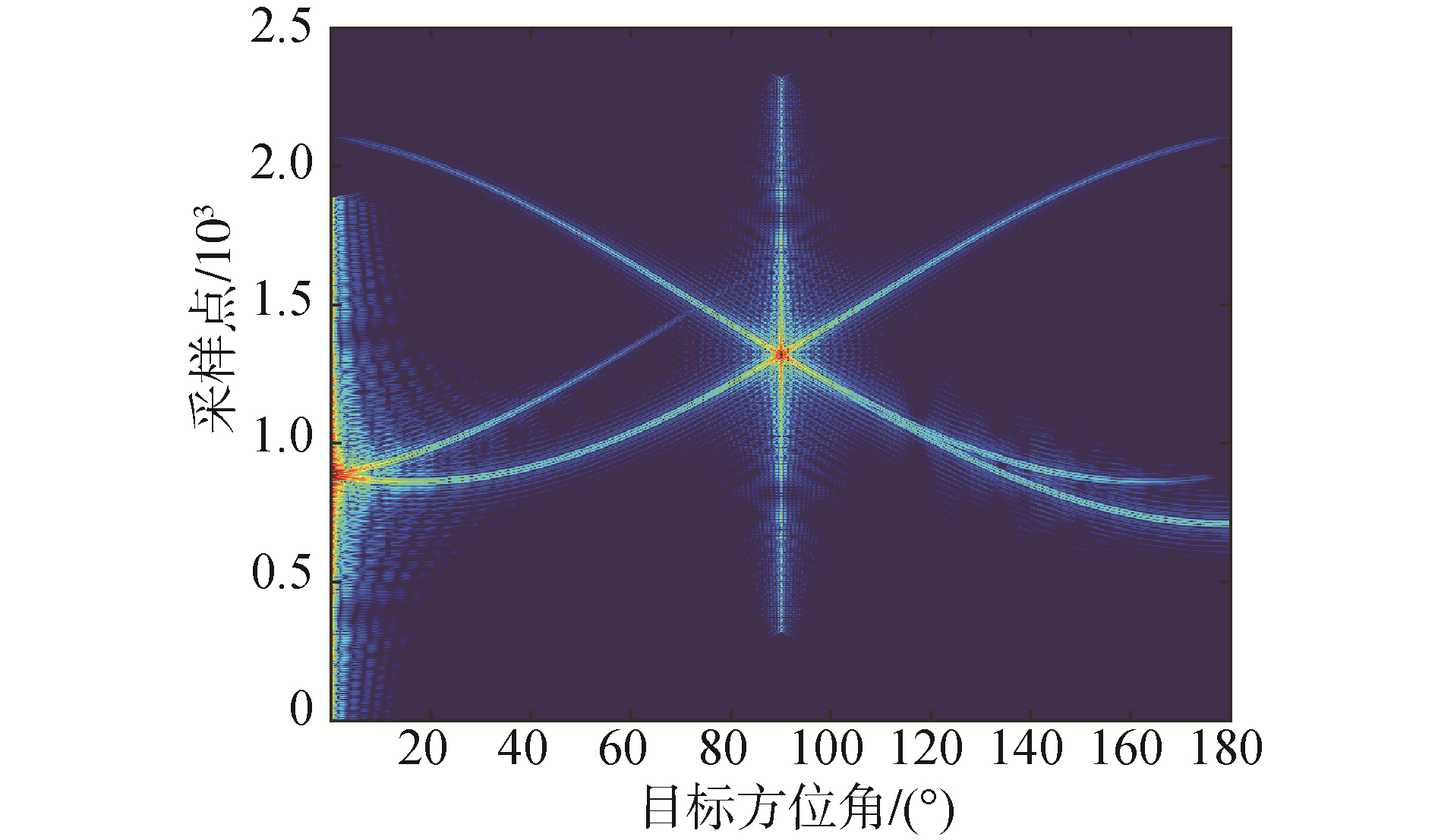
结合幅度因子和时延因子对目标模型不同入射角度的几何回波进行仿真,仿真信号归一化频率为0.02~0.08,仿真结果如图 2。图中不同目标方位角条件下,亮点的成分和数量均有差异,可以作为角度与回波特性之间的映射关系进行深度神经网络的学习特征。
|
Download:
|
| 图 2 目标模型几何亮点回波仿真 Fig. 2 Simulation of geometric highlight spot echo of target model | |
实际目标探测中,若发射信号的脉宽大于2个相邻散射成分间的时延,各散射成分在时域上存在混叠,在时域或频域无法为不同角度回波的识别提供有效特征。时频分析可以给出信号在时间和频率2个维度上的信息,其中分数阶傅里叶变换可以获得有效的信号特征。在最佳分数阶傅里叶变换域,各声散射回波分量的时延因子与形成脉冲的位置构成映射关系,通过极大值位置可以计算得到各分量的时延关系[14],将获得的时延关系称为信号的时序结构特征。
2.1 分数阶傅里叶变换根据分数阶傅里叶变换的定义,x(t)的p阶分数阶傅里叶变换可表述为:
| $ X_{p}(u)=F^{p}[x(t)]=\int_{-\infty}^{+\infty} K_{p}(t, u) x(t) \mathrm{d} t $ | (2) |
式中Kp(t, u)为分数阶傅里叶变换的核函数:
| $ \begin{aligned} &\tilde{K}_{p}(u, t)= \\ &\left\{\begin{array}{l} A_{\alpha} \exp \left[\mathrm{j} \pi\left(u^{2} \cot \alpha-2 u t \csc \alpha+t^{2} \cot \alpha\right)\right], \alpha \neq n \pi \\ \delta(t-u), \alpha=2 n \pi \\ \delta(t+u), \alpha=(2 n+1) \pi \end{array}\right. \end{aligned} $ | (3) |
式中
当坐标旋转角度对应最佳分数阶变换阶次,单个亮点回波的最佳分数阶傅里叶变换为
| $\begin{array}{*{20}{c}} {F(u) = AT\exp \left[ {{\rm{j}}{\rm{ \mathit{ π} }} T\left( {{f_0} - k{\tau _i} - u\csc \alpha } \right)} \right]} ·\\ {{\mathop{\rm sinc}\nolimits} \left[ {{\rm{ \mathit{ π} }} T\left( {{f_0} - k{\tau _i} - u\csc \alpha } \right)} \right]} \end{array} $ | (4) |
式中:T为发射信号长度;f0为信号初始频率;k为调频斜率;τi为第i个亮点分量的时延,可以看出单亮点的最佳分数阶傅里叶变换为sinc函数形式,其幅度极大值及其在分数阶域对应的位置为:
| $ |F(u)|_{\max }=\frac{A_{0} A_{i} T}{\sqrt{|\sin \alpha|}} $ | (5) |
| $ u_{\max }=\left(f_{0}-k \tau_{i}\right) \sin \alpha $ | (6) |
式中:A0为发射信号的幅度;Ai为回波信号中第i个亮点的幅度。对于不同回波成分,经分数阶傅里叶变换后的脉冲幅值大小取决于幅度因子,sinc函数位置取决于时延因子。从时频投影的角度来看,变换后的信号在时频平面为一条斜线,在最佳分数阶傅里叶变换域的投影结果存在峰值。在(p, u)平面上,与发射信号参数对应的最佳阶次附近,通过搜索最大值的方法确定最佳分数阶傅里叶变换阶次,获得回波信号在最佳分数阶傅里叶变换域的时序结构特征。
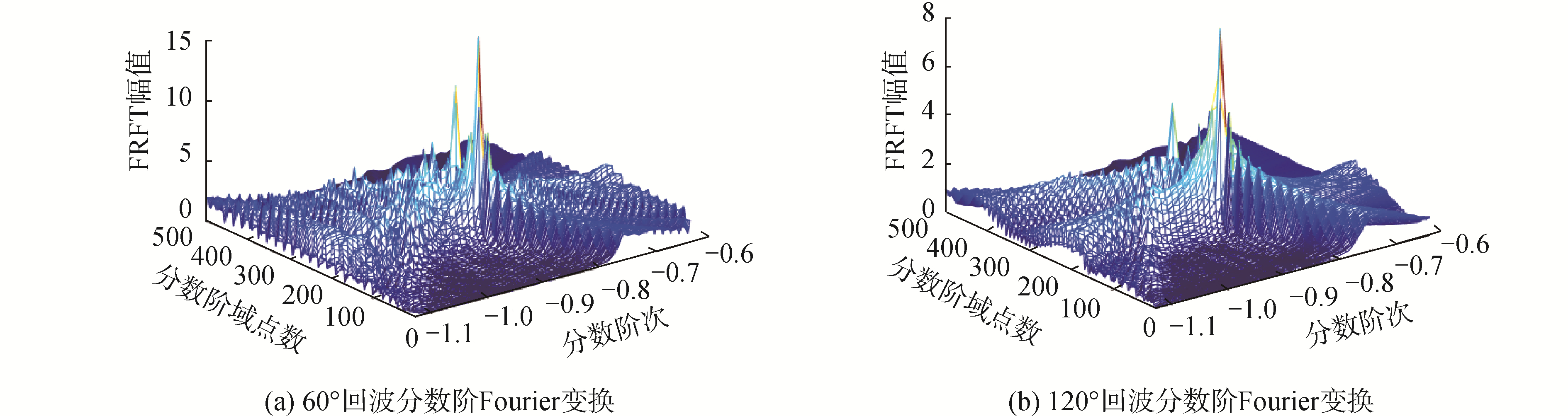
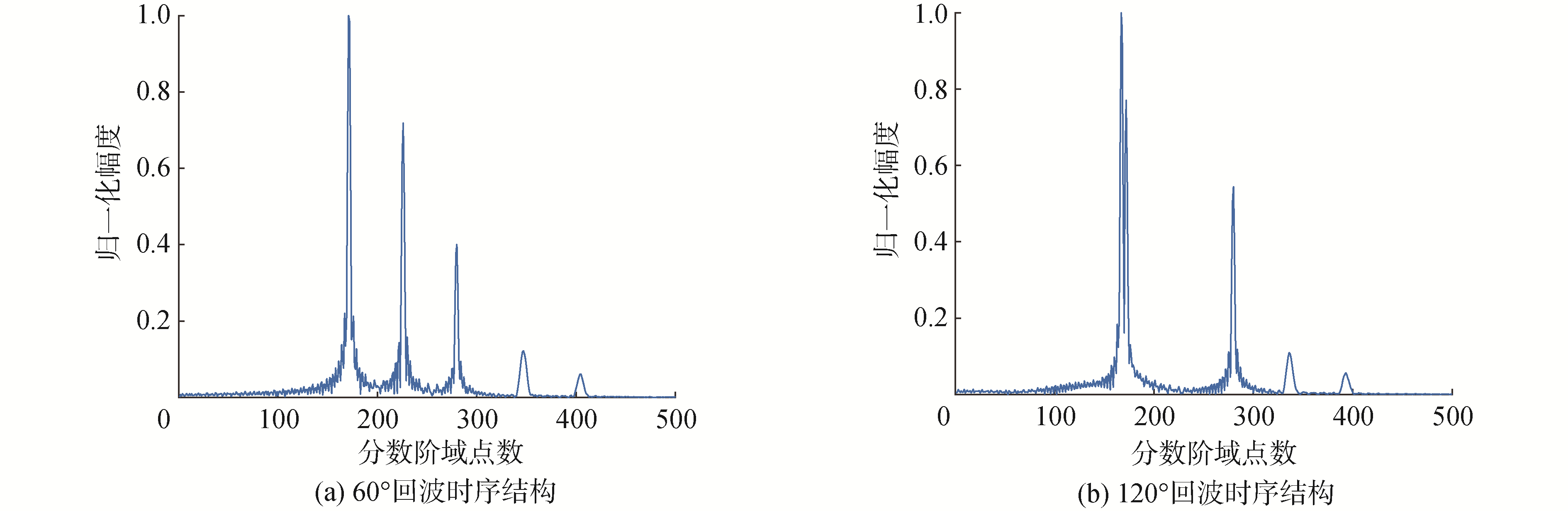
仿真线性调频信号,脉宽1 000点,归一化频率0.02~0.08,声波入射角度分别为θ=60°和θ=120°,根据仿真信号参数计算可知,最佳分数阶次为-0.886 6,在最佳分数阶次附近的[-1.126 6, -0.636 6]范围内得到的分数阶傅里叶变换结果如图 3所示。选取最佳分数阶次下的分数阶傅里叶变换结果如图 4所示。利用最佳分数阶次下得到的分数阶傅里叶变换能够获得不同入射角度下目标回波精细的时序结构。2个角度下的时序结构中均出现5个峰值,其中θ=60°时3个几何散射回波对应棱角1、2、3,第4、第5个峰值为弹性环绕波。θ=120°时第1个峰值对应球冠的镜反射回波,第2个峰值对应棱角3的散射回波。由于2个亮点时延间隔很小,导致峰值接近重叠。同时2个角度下几何散射成分对应峰的聚集性都比较好,弹性环绕波对应的峰值相对于几何散射成分较小且聚集性较差。不同声波入射角度下,各散射成分对应的幅度极大值具有显著差异,各亮点成分的时延也具有差异性。目标回波在分数阶域的时序结构在不同入射角度下的差异,可以作为不同入射角度回波的识别特征。
|
Download:
|
| 图 3 仿真目标回波的分数阶傅里叶变换 Fig. 3 Fractional Fourier transform of simulated target echo | |
|
Download:
|
| 图 4 仿真目标回波的分数阶傅里叶域时序结构 Fig. 4 Time series structure of simulated target echo in fractional Fourier domain | |
长短期记忆神经网络(long short-term memory networks, LSTMs)是循环神经网络(recurrent neural networks, RNN)的一种特殊形式[15]。循环神经网络是为有效处理时间序列数据而设计的,时间序列数据的显著特征是相邻信号帧与长距离帧之间特征存在密切关联,因此循环神经网络的神经元被设计成具有环路的网络结构,其输出由存储过去信息的状态变量与当前的输入共同决定,是一类具有短期记忆能力的神经网络。循环神经网络可以将时间序列信息间的特征保存在网络的隐藏状态中,完成对序列信号的动态建模。但当输入序列比较长时,按照时间的逆序将错误信息逐步向前传递时会存在梯度爆炸和消失问题,引入了门控机制的LSTMs可以有效地解决这个问题。
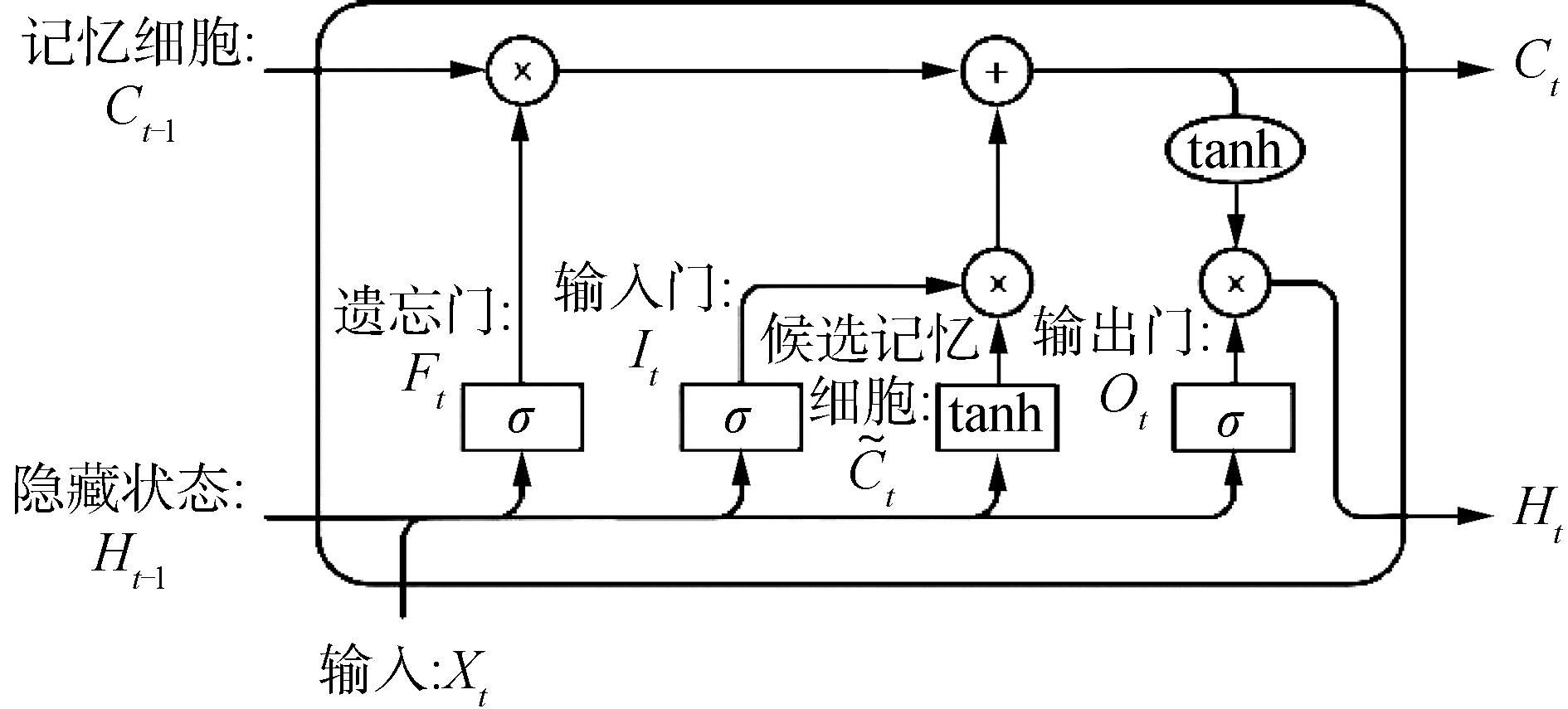
长短期记忆神经网络中引入了遗忘门Ft、输入门It和输出门Ot的3个门结构,以及用于记录额外的信息、进行线性循环信息传递的记忆细胞Ct[15],长短期记忆神经网络的内部结构如图 5。
|
Download:
|
| 图 5 LSTMs结构 Fig. 5 Structure of LSTMs | |
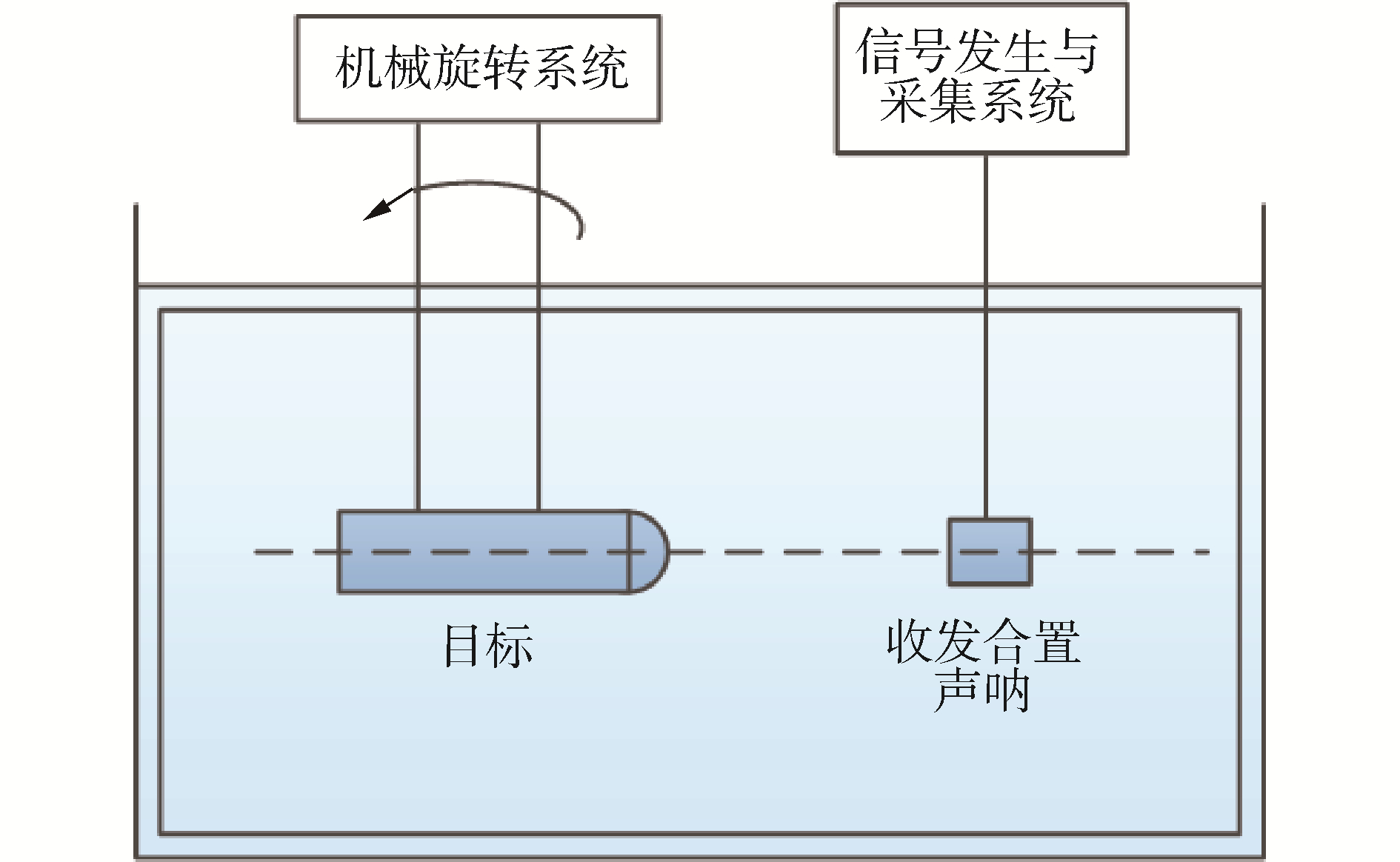
数据源自消声水池中模拟自由场环境对目标散射回波的测量实验。实验水池六面铺设吸声尖劈,在工作频率内能够减弱由反射引起的多途,避免目标散射回波的干扰。实验系统布放如图 6所示。目标模型与收发合置换能器处于相同水平位置,发射信号归一化频率为0.02~0.08,脉宽为1 000采样点,目标由机械系统控制匀速旋转,信号发生与采集装置由同步信号控制,目标反向散射回波信号经基阵接收后由信号采集器存储。
|
Download:
|
| 图 6 实验系统布放 Fig. 6 The setup of the experiment | |
考虑水平旋转情况下,全角度目标反向散射信号的采集,定义声波自半球一侧沿壳体轴向入射为θ=0°,从平面一端为θ=180°,而正横入射为θ=90°。
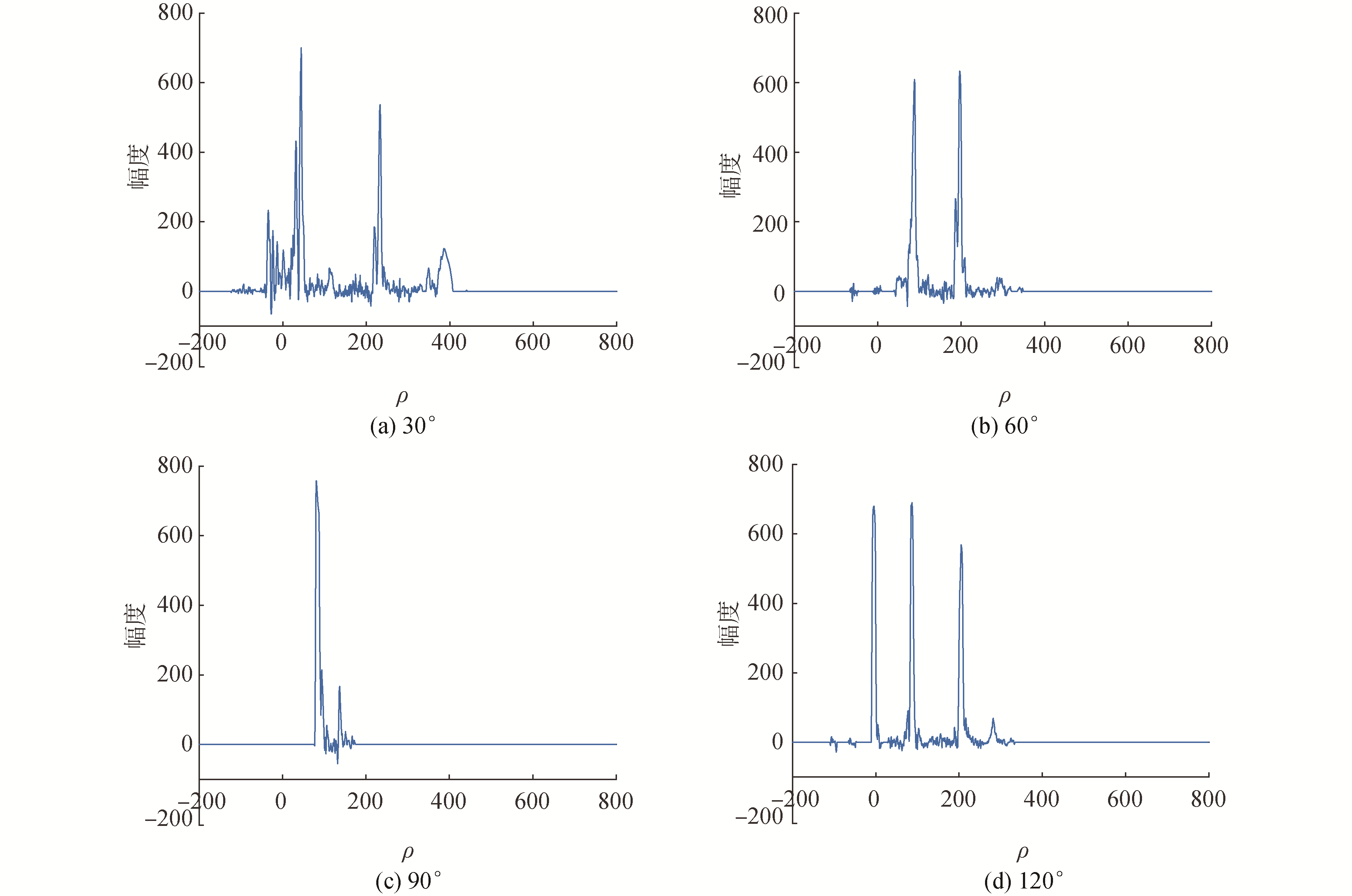
在最佳分数阶次下,利用分数阶傅里叶变换获取不同入射角度下目标回波的时序结构,作为不同入射角度回波的识别特征。在0~180°内,每间隔15°,共13类角度的目标回波信号求取相应的最佳分数阶傅里叶域的时序结构特征,图 7中为观测范围内典型角度的时序结构示意图。
|
Download:
|
| 图 7 0°~180°范围内最佳分数阶域时序结构 Fig. 7 Optimal time sequence structure in fractional Fourier domain from 0°~180° | |
实际探测中存在环境干扰和声场分布不均匀等问题,目标回波的波形可能产生畸变。对不同时刻接收到的回波,分数阶傅里叶变换所得到结果不同,时序结构的特征会随之改变。并且对不同角度下弹性环绕波间的时延研究,缺乏明确函数关系的量化,对高维时序结构数据进行降维处理会导致特征信息的丢失。这些问题都将增加分类识别的难度,深度学习中的循环神经网络适合处理此类时间序列数据。循环神经网络可以将时间序列信息间的特征保存在网络的隐藏状态中,学习复杂的函数映射关系,完成对序列信号的动态建模。
利用分数阶傅里叶变换提取不同入射角度下目标回波在最佳分数阶域的一维时序结构,采用LSTMs进行训练学习,与采用频谱结构作为输入数据训练得到的模型进行对比,训练所得模型验证集的混淆矩阵如图 8。混淆矩阵表明模型预测过程中,对哪一部分产生混淆,用以判断模型分类预测的优劣。文中实现13类标签的分类任务,混淆矩阵的尺度为13×13,混淆矩阵在对角线上的值越大,表明模型的分类性能越好。

|
Download:
|
| 图 8 频谱结构-LSTMs的混淆矩阵 Fig. 8 Confusion matrix of spectrum structure- LSTMs | |
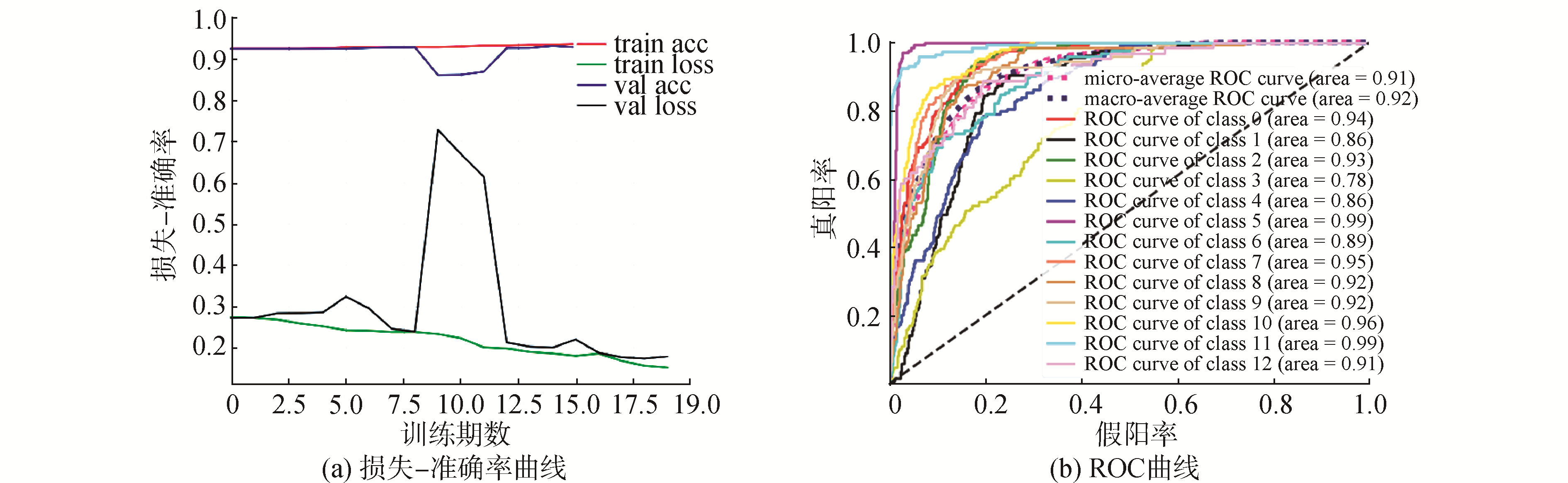
使用频谱结构数据构建模型的混淆矩阵表明,在多数角度下的模型分类性能表现不佳。损失-准确率变化曲线以及ROC曲线(受试者操作特性曲线)如图 9所示。损失-准确率曲线描述模型的传播损失和准确率随训练期数(epoch)的变化规律,曲线评价模型(receiver operating characteristic,ROC)在不同阈值下的表现情况,曲线的横、纵坐标分别表示假阳率和真阳率。(area under curve,AUC)表示ROC曲线下方面积,用来表征模型正确预测为正例的值高于将其预测为负例的值的概率,越接近1则模型性能越好。
|
Download:
|
| 图 9 频谱结构-LSTMs模型性能 Fig. 9 Performance of spectrum structure-LSTMs | |
图 9描述了模型整体性能以及模型对每一类样本的识别能力。图 9(a)中,随着训练期数的增加,训练集的误差呈下降趋势,但训练集的准确率在93%的基础上只有小幅度的上升,且验证集的误差表现不稳定。图 9(b)中AUC值普遍较小,说明频谱结构数据仍不足以作为表征不同角度回波的特征。这是因为回波各散射成分存在相似的调频性质,而几何散射回波的频谱范围更广,导致其完全覆盖了弹性回波的频谱,深度神经网络也难以学习到深层特征。
将分数阶域下的时序结构作为LSTMs的输入数据,训练所得模型的验证集混淆矩阵如图 10。图 10中混淆矩阵结果表明,利用时序结构训练得到的模型,其混淆矩阵对角线上的值接近100%,在150°时有一定错误分类的概率,但分类错误样本主要集中在与样本临近的角度,相比于频谱结构数据下混淆矩阵所呈现出的模型分类性能,采用FRFT-LSTMs的模型分类性能具有显著增强。进一步采用损失-准确率变化曲线以及ROC曲线对模型进行评估,结果如图 11所示。

|
Download:
|
| 图 10 FRFT-LSTMs的混淆矩阵 Fig. 10 Confusion matrix of FRFT-LSTMs | |
|
Download:
|
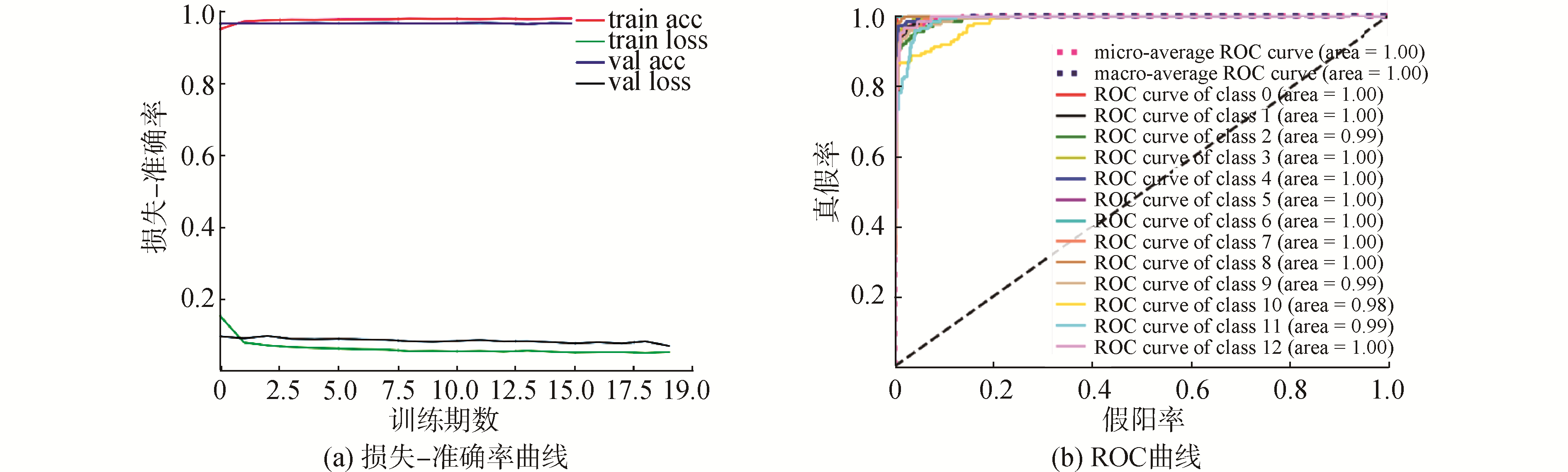
| 图 11 FRFT-LSTMs模型结果 Fig. 11 Results of FRFT-LSTMs | |
图 11(a)中损失-准确率曲线表明,模型在第2次迭代后损失准确率曲线即得到了收敛,训练集和验证集的准确率稳定在98.92%和98.53%;图 11(b)中的ROC-AUC曲线表明,AUC值均接近1,众多评估指标表明FRFT-LSTMs的模型可以实现对不同角度回波的精准分类识别。频谱结构-LSTMs和FRFT-LSTMs两种模型的详细评估指标如表 2所示。
| 表 2 模型各项评估指标 Table 2 Evaluation indicators of the model |
与频谱结构-LSTMs模型相比,FRFT-LSTMs模型在上述评估指标中均有更佳的性能表现。将分数阶域下时序结构的特征作为LSTMs的输入数据,并与使用频谱结构数据的LSTMs模型进行对比,FRFT-LSTMs的识别准确率达到了98.53%。通过调节优化网络参数,构建了2种对水下目标回波角度识别稳定、精确的深度神经网络模型。
4 结论1) 本文基于亮点模型理论,利用分数阶傅里叶变换对不同入射角度下的水下目标回波数据进行时序特征提取,获得与声波入射角度相关的目标回波时序结构。通过构建深度学习神经网络,将时序结构特征作为LSTMs网络的输入进行训练,实现对不同声波入射角度下目标回波的识别。
2) 与采用目标信号频谱结构作为输入特征的模型进行对比,采用LSTMs的深度神经网络模型的识别率可达98.53%。综合模型查准率、召回率、AUC等指标,FRFT-LSTMs深度学习模型性能均优于传统频谱结构-LSTMs。实验数据处理结果表明,FRFT-LSTMs网络模型可以实现实验条件下对水下目标姿态的精准分类与识别。
| [1] |
汤渭霖. 声呐目标回波的亮点模型[J]. 声学学报, 1994, 19(2): 92-100. TANG Weilin. Highlight model of echoes from sonar targets[J]. Acta acustica, 1994, 19(2): 92-100. (  0) 0)
|
| [2] |
陈云飞, 李桂娟, 王振山, 等. 水中目标回波亮点统计特征研究[J]. 物理学报, 2013, 62(8): 084302. CHEN Yunfei, LI Guijuan, WANG Zhenshan, et al. Statistical feature of underwater target echo highlight[J]. Acta physica sinica, 2013, 62(8): 084302. (  0) 0)
|
| [3] |
刘建设, 朱广平, 刘冰, 等. 时频域去模糊提取目标回波亮点[J]. 哈尔滨工程大学学报, 2020, 41(9): 1340-1345. LIU Jianshe, ZHU Guangping, LIU Bing, et al. Time-frequency domain deblurring for target echo highlight extraction[J]. Journal of Harbin Engineering University, 2020, 41(9): 1340-1345. (  0) 0)
|
| [4] |
TAO Ran, LI Xuemei, LI Yanlei, et al. Time-delay estimation of chirp signals in the fractional Fourier domain[J]. IEEE transactions on signal processing, 2009, 57(7): 2852-2855. DOI:10.1109/TSP.2009.2020028 (  0) 0)
|
| [5] |
JACOB R, THOMAS T, UNNIKRISHNAN A. Applications of fractional Fourier transform in sonar signal processing[J]. IETE journal of research, 2009, 55(1): 16-27. DOI:10.4103/0377-2063.51323 (  0) 0)
|
| [6] |
TANT K M M, MULHOLLAND A J, LANGER M, et al. A fractional Fourier transform analysis of the scattering of ultrasonic waves[J]. Proceedings of the royal society a: mathematical, physical and engineering sciences, 2015, 471(2175): 20140958. DOI:10.1098/rspa.2014.0958 (  0) 0)
|
| [7] |
JIA Hongjian, LI Xiukun, MENG Xiangxia. Rigid and elastic acoustic scattering signal separation for underwater target[J]. The journal of the acoustical society of America, 2017, 142(2): 653-665. DOI:10.1121/1.4996127 (  0) 0)
|
| [8] |
张健. 基于深度学习的水下目标识别的研究[D]. 成都: 电子科技大学, 2020. ZHANG Jian. Research on underwater target recognition based on deep learning[D]. Chengdu: University of Electronic Science and Technology, 2020. (  0) 0)
|
| [9] |
FISCHELL E M, SCHMIDT H. Classification of underwater targets from autonomous underwater vehicle sampled bistatic acoustic scattered fields[J]. The journal of the acoustical society of America, 2015, 138(6): 3773-3784. DOI:10.1121/1.4938017 (  0) 0)
|
| [10] |
曾赛, 杜选民. 水下目标多模态深度学习分类识别研究[J]. 应用声学, 2019, 38(4): 589-595. ZENG Sai, DU Xuanmin. Multimodal underwater target recognition method based on deep learning[J]. Applied acoustics, 2019, 38(4): 589-595. (  0) 0)
|
| [11] |
CAO Xu, TOGNERI R, ZHANG Xiaomin, et al. Convolutional neural network with second-order pooling for underwater target classification[J]. IEEE sensors journal, 2019, 19(8): 3058-3066. DOI:10.1109/JSEN.2018.2886368 (  0) 0)
|
| [12] |
汤渭霖, 范军, 马忠成. 水中目标声散射[M]. 北京: 科学出版社, 2018: 14-49. TANG Weilin, FAN Jun, MA Zhongcheng. Target sound scattering in water[M]. Beijing: Science Press, 2018: 14-49. (  0) 0)
|
| [13] |
FLAX L, DRAGONETTE L R, ÜBERALL H. Theory of elastic resonance excitation by sound scattering[J]. The journal of the acoustical society of America, 1978, 63(3): 723-731. DOI:10.1121/1.381780 (  0) 0)
|
| [14] |
李秀坤, 孟祥夏, 夏峙. 水下目标几何声散射回波在分数阶傅里叶变换域中的特性[J]. 物理学报, 2015, 64(6): 064302. LI Xiukun, MENG Xiangxia, XIA Zhi. Characteristics of the geometrical scattering waves from underwater target in fractional Fourier transform domain[J]. Acta physica sinica, 2015, 64(6): 064302. (  0) 0)
|
| [15] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


