2. 海洋信息获取与安全工业和信息化部重点实验室(哈尔滨工程大学), 黑龙江 哈尔滨 150001;
3. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001;
4. 广东海洋大学 电子与信息工程学院, 广东 湛江 524000
2. Key Laboratory of Marine Information Acquisition and Security (Harbin Engineering University), Ministry of Industry and Information Technology, Harbin 150001, China;
3. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China;
4. College of Electronic and Information Engineering, Guangdong Ocean University, Zhanjiang 524000, China
中尺度涡是海洋中以封闭式环流为主体的旋转水体,类似于大气中的气旋或风暴,对于中心水温低于外围海水的涡称为冷涡(气旋涡),反之称为暖涡(反气旋涡)。中尺度涡旋半径尺度为10~100km量级,寿命可长达几个星期到几个月、甚至几年。在其生命周期中,涡旋会移动几十公里到几百公里的距离[1]。海洋涡旋的存在会使一定区域内的声速垂直剖面结构出现明显变化,进而使声波导传播形式和声场能量分布规律发生改变,从而对声呐的水下探测和反探测产生影响[2-3]。海洋涡旋的三维结构建模及其对声传播的影响也是近年来研究的热点问题之一[4-6]。研究显示,与不存在涡旋时的声场相比,涡旋使声场的主要特性发生明显改变:汇聚区的偏移,多路径到达次序的改变和水平折射问题等[7]。涡旋将引起会聚区结构特性的改变和表面声道效应的出现或者消失[8-9]。
Watson等[10]和Henrick等[11-12]从海洋动力学原始方程出发,利用小参数摄动展开法,建立了准地转位涡方程,通过求解此方程可以得到流函数,根据流函数可以得到无量纲涡诱导的密度和压强,再利用Eckart状态方程,得到温度的分布,并利用Wilson声速经验公式,可得到声速分布。此模型将声速与涡旋参数:如涡旋半径、影响深度、旋转方向、旋转速度等联系起来,研究了中尺度涡的强度、尺度等特征量同声传播的关系,获得了很好的结果。Baer[13-14]之后引用了这个模型,并将其与三维声学模型联合使用,研究声波穿过涡旋时的水平和垂直折射,研究表明较强的冷涡存在会使声波水平传播方向改变超过0.5°。Jian等[15]考虑涡的分布随方向角的变化对模型进行完善,推导了关于原点非对称理论下涡场的计算,取得了很好的效果。姬莉莉等[16]利用此涡旋模型研究了中尺度涡影响下目的层地震成像的畸变。
基于上述研究,本文采用海洋动力学模型计算出温度场,并与现场实测水文数据对比,调整涡旋参数,利用抛物方程模型,计算了不同声源深度与接收深度时,暖涡有无时传播损失的变化特点。
1 单个中尺度涡旋模型假设所研究海域的水平尺度远小于地球半径,局部卡氏坐标系以纬度Ф处为中心。x轴指向正东,y轴指向正北,深度z从海表面向正下方测量。通过海洋的重要特征来简化方程,进而求得密度和压力的解可表示为:
| $ \rho = {\rho _s}\left( z \right) + M\bar \rho \left( {x, y, z, t} \right) $ | (1) |
| $ P = {P_s}\left( z \right) + M\bar P\left( {x, y, z, t} \right) $ | (2) |
式中:静态密度ρs和压强Ps与深度有关,马赫数M=U0/c0,表示流体速度与声速的比值。水平方向的涡流可以用流函数ψ表示:
| $ u = - {\psi _y}, v = {\psi _x} $ | (3) |
通过方程(2)和(3)可以求得流速、密度和压力场。其中涡的流速为:
| $ {V^ * } = {U_0}{\chi _r} $ | (4) |
密度为:
| $ {\rho ^ * } = {\rho _0}\left\{ {1 + \Delta \left[ {z + \pi \left( z \right)} \right] + M{\chi _z}} \right\} $ | (5) |
压强为:
| $ {P^ * } = {\rho _0}gD\left\{ {z + \Delta \int_0^z {\left[ {s + \pi \left( s \right)} \right]} {\rm{ds}} + M\chi } \right\} $ | (6) |
式中分层参数Δ为等熵、静力学平衡条件下深度随密度的变化,其值为Δ=gD/c02。
再利用Eckart状态方程,求得温度为:
| $ {T^ * } = - {a_2}{\left( {2{a_1}} \right)^{ - 1}} + {\left[ {a_2^2{{\left( {2{a_1}} \right)}^{ - 2}} - {a_3}a_1^{ - 1}} \right]^{1/2}} $ | (7) |
其中:
| $ \left\{ \begin{array}{l} {a_1} = - 0.375 + 0.33625{\rho ^ * }\\ {a_2} = 38 - 37.42{\rho ^ * }\\ {a_3} = \left( {1.033} \right){P^ * }\left( {1 - 0.698{\rho ^ * }} \right) + 5995 - 5831.01{\rho ^ * } \end{array} \right. $ |
假设盐度为常数35.0‰,利用Wilson声速经验公式,即可获得声速分布。Wilson声速经验公式为:
| $ \begin{array}{l} {c^ * } = 1.449.30 + 1.5848 \times {10^{ - 1}}{P^ * } + 1.572 \times \\ \;\;\;\;\;\;{10^{ - 5}}{P^{{ * ^2}}} - 3.46 \times {10^{ - 12}}{P^{{ * ^4}}} + 4.587{T^ * } - \\ \;\;\;\;\;\;5.356 \times {10^{ - 2}}{T^{{ * ^2}}} + 2.604 \times {10^{ - 4}}{T^{{ * ^3}}} + \\ \;\;\;\;\;\;1.354 \times {10^{ - 5}}{T^{{ * ^2}}}{P^ * } - 7.19 \times {10^{ - 7}}{T^ * }{P^{{ * ^2}}} \end{array} $ | (8) |
对于一个特定的涡旋来说,模型中的涡旋参数(如涡旋半径、深度、旋转方向等)、表面流速等参数的选取由实测的数据来确定。模型推导的详细过程过程及其中用到参数无量纲化见文献[10-12, 15]。
2 单个中尺度暖涡对声传播的影响 2.1 海洋环境数据介绍关于南海北部涡旋的研究大多采用卫星遥感数据或者数值模拟,少量的研究使用现场观测资料[17-18, 20-23]。Liu等[19]依托2009-2010年冬季908项目补充调查“南海北部坡折带水体环境调查与研究”对南海北部陆架与陆坡海域进行了观测,发现在调查海域东侧存在一个反气旋暖涡。
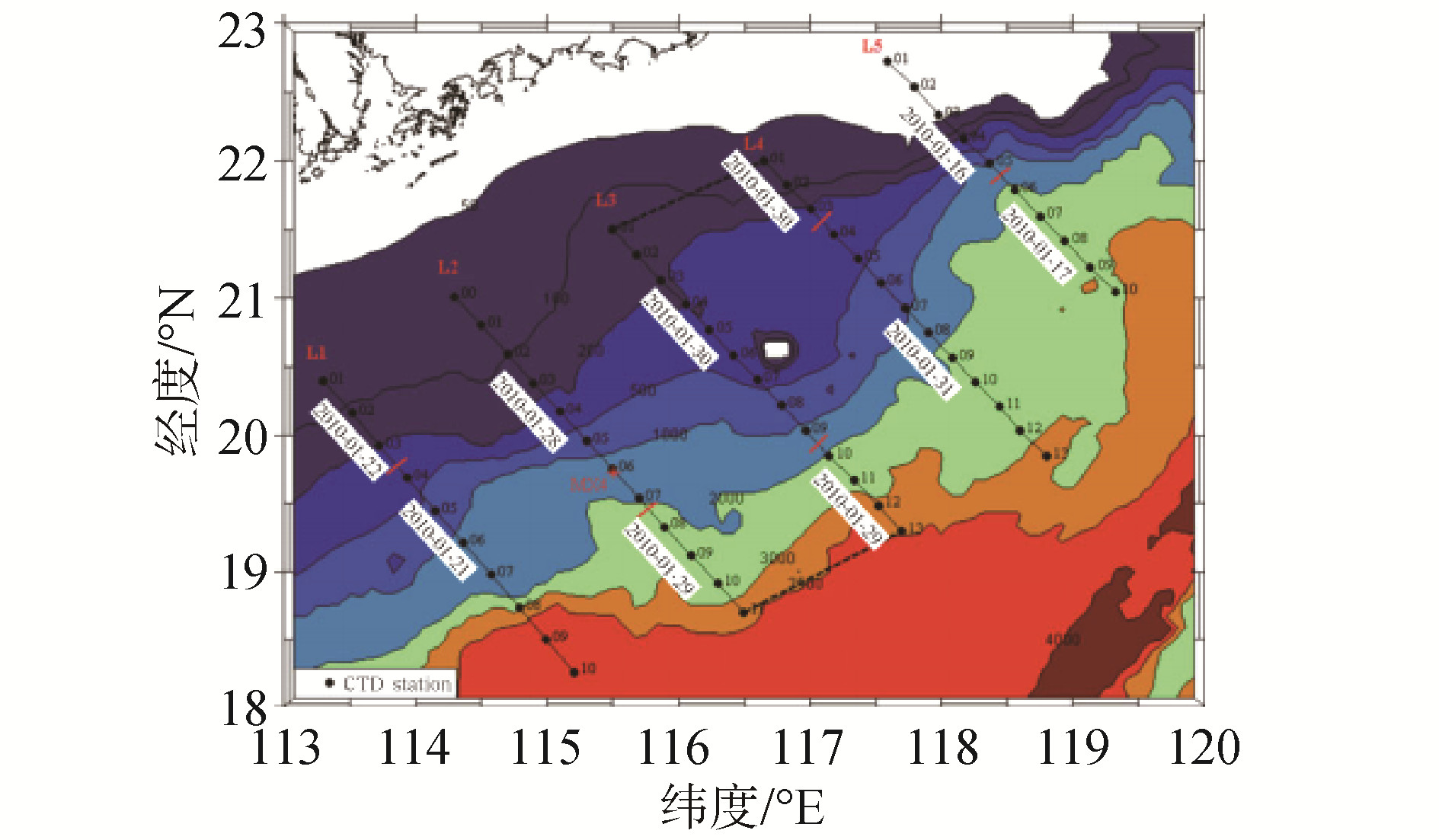
图 1是项目调查时的走航观测站位图[19]。通过数据处理,发现L4断面第8个观测站位出现明显的下凹结构,符合暖涡的特点。涡的位置大致在北纬20.75°N,东经118°E附近,涡的结构呈中间深,两侧浅的下凹型分布,具有显著的正压结构,涡所在海区的深度为2 500m,其影响深度大约为1 000m,水平方向的影响半径为150 km。根据现场测量数据,最大表面流速度、表面声速以及密度分别为1.0m/s、1 532m/s、1020.7kg/m3。
|
Download:
|
| 图 1 观测站位 Fig. 1 Survey station | |
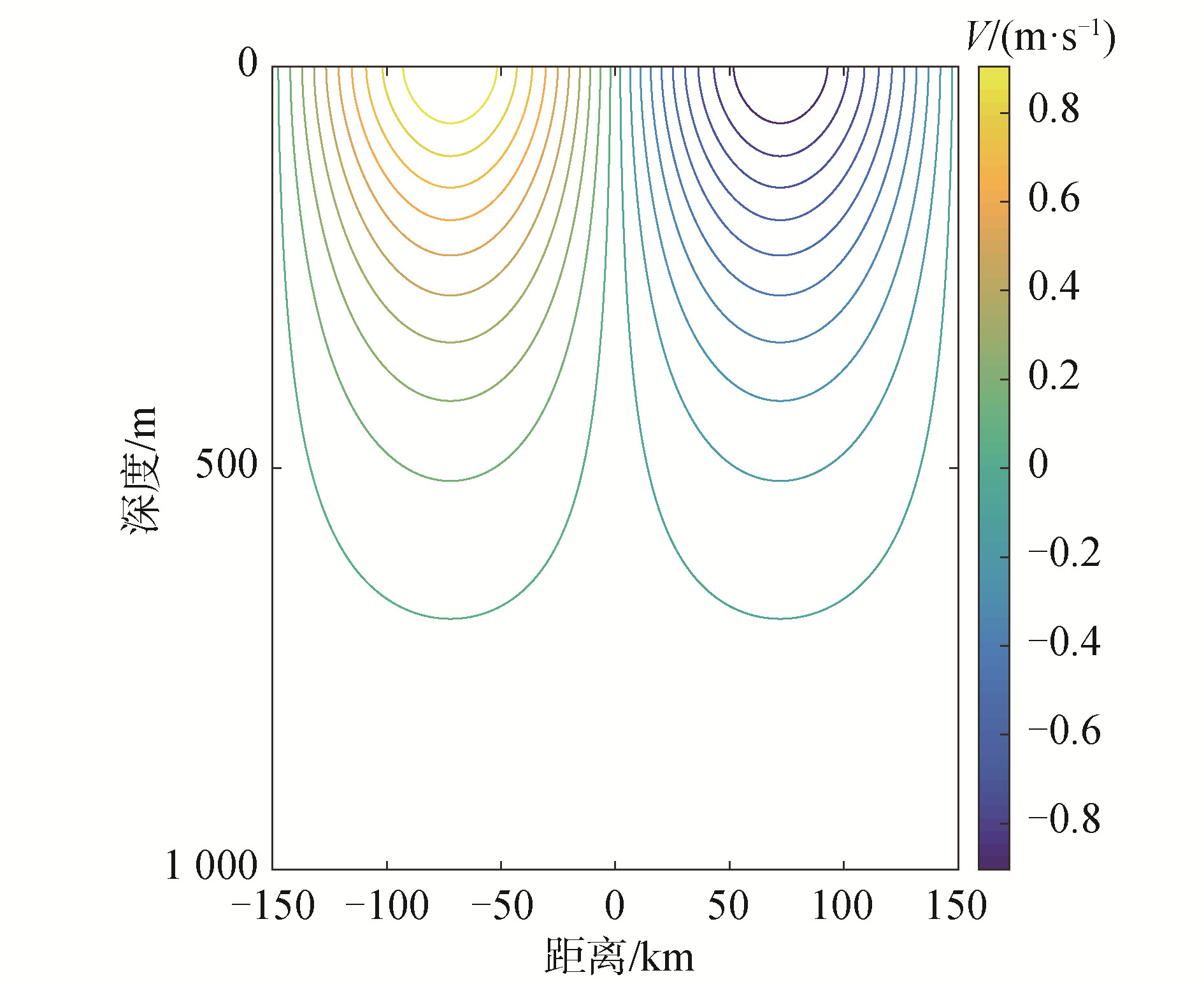
图 2是经过计算得到的暖涡海流结构剖面图,从图中可以看到,暖涡中心,流速较小,在边界处随涡旋半径的减小而减小,减小至零,然后在涡旋的中心处随半径的增加从零开始逐渐增加。暖涡的旋转流速随深度增加而减小。
|
Download:
|
| 图 2 暖涡中心流结构 Fig. 2 Current structure of warm eddy | |
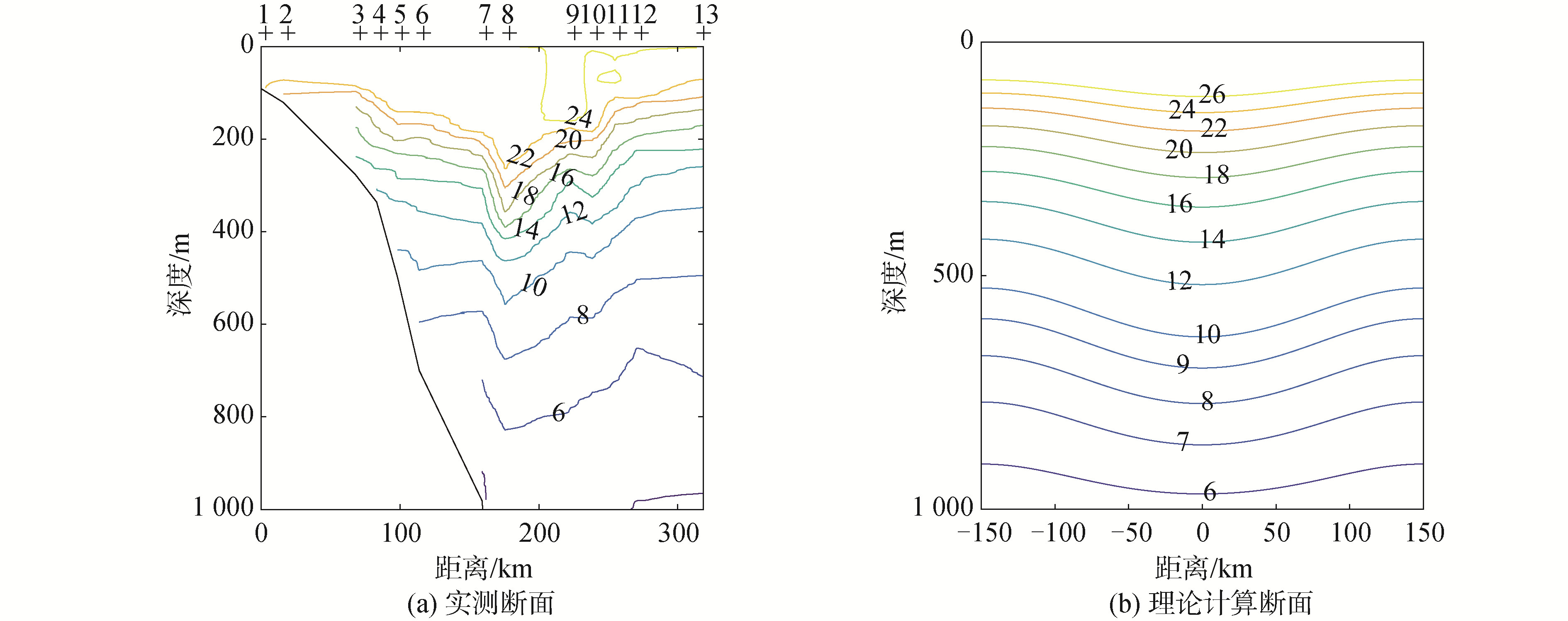
图 3(a)是实测断面的温度分布,这种温度在23℃以上,盐度小于34.5的淡水和暖水团与西太平洋的水特征相似,表明涡中心的水可能来自黑潮东部,而在300m深处,暖淡水只存在于L4断面附近,说明暖涡的次表层存在黑潮水[19],说明了涡旋是一个移动的旋转水体。图 3(b)是理论计算获得的断面温度分布,温度的计算利用Eckart状态方程,求解的过程是首先求得扰动下的密度和压强,带入状态方程即可获得。理论计算的涡呈对称分布,计算时没有考虑地形的影响,而且理论计算的图形与计算时所用的环境参数关系较大,海域的环境参数A和B的选取与海区的温度、盐度和压强有关,A、B参数的变化对理论结果影响显著,关于参数的选取可以参考文献[10]。通过对观测温度断面与理论计算温度断面进行比较,可以看出理论计算和实测断面基本符合,实测的涡中心向下凹陷,对称良好。只是计算得到的涡强度比实测稍微有一点小。
|
Download:
|
| 图 3 温度场的实测断面与模型计算的结果 Fig. 3 Observation section and theoretical calculation of temperature section | |
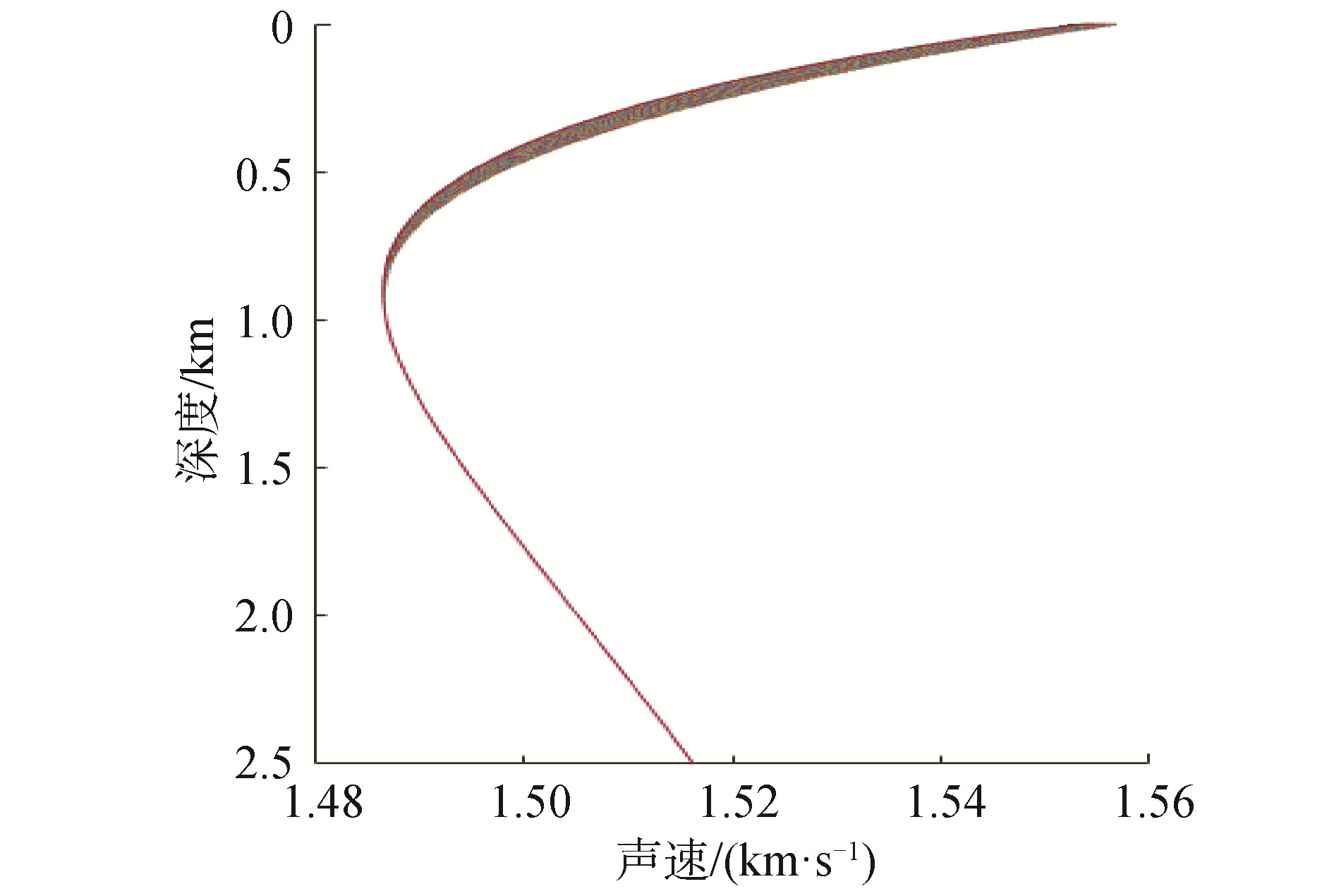
根据计算的温度场数据,利用Wilson声速经验公式,可以计算出声速场。图 4是理论计算声速的垂直分布,在1 000m以上,随深度增加,水平方向的声速有一定的扰动;1 000m之下,水平方向的声速基本没有变化。这也对应了此处涡旋的影响深度大致1 000m。
|
Download:
|
| 图 4 声速的垂直分布 Fig. 4 Vertical distribution of sound speed | |
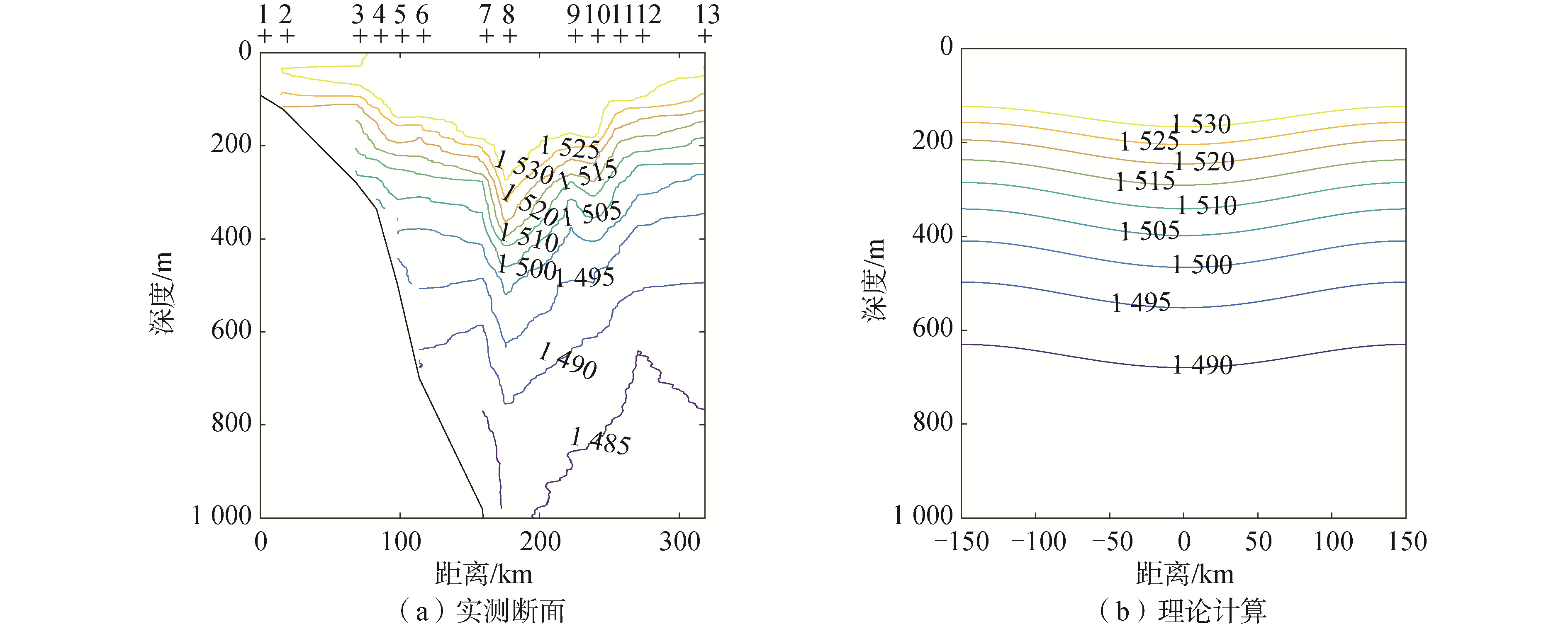
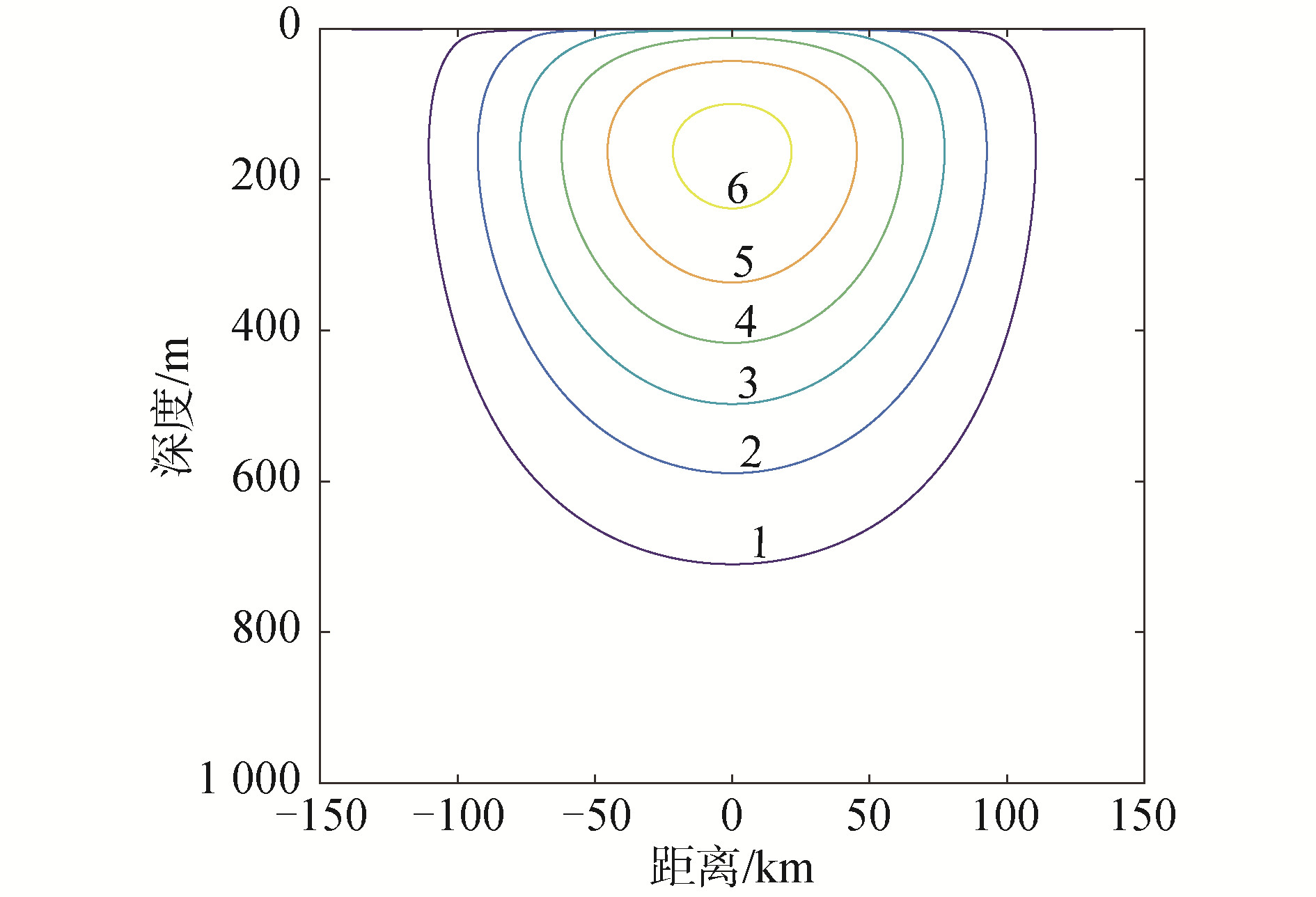
图 5(a)是观测的声速断面图,图 5(b)是理论计算获得的声速断面分布图。对比2图,可以看出声速断面图也基本符合海域环境设定。图 6是声速扰动曲线,在涡旋中心处,扰动幅度最大为6m/s,扰动不是很大。
|
Download:
|
| 图 5 温度场的实测断面与模型计算的结果 Fig. 5 Observation section and theoretical calculation of sound speed section | |
|
Download:
|
| 图 6 声速扰动等值线 Fig. 6 Sound speed perturbation contours | |
根据前面获得的声速场,利用PE算法计算传播损失。计算时设定声源发射频率为100 Hz,讨论声源位于暖涡中心线上,声源深度500m及800m这2种情况,接收器位于暖涡的外部。
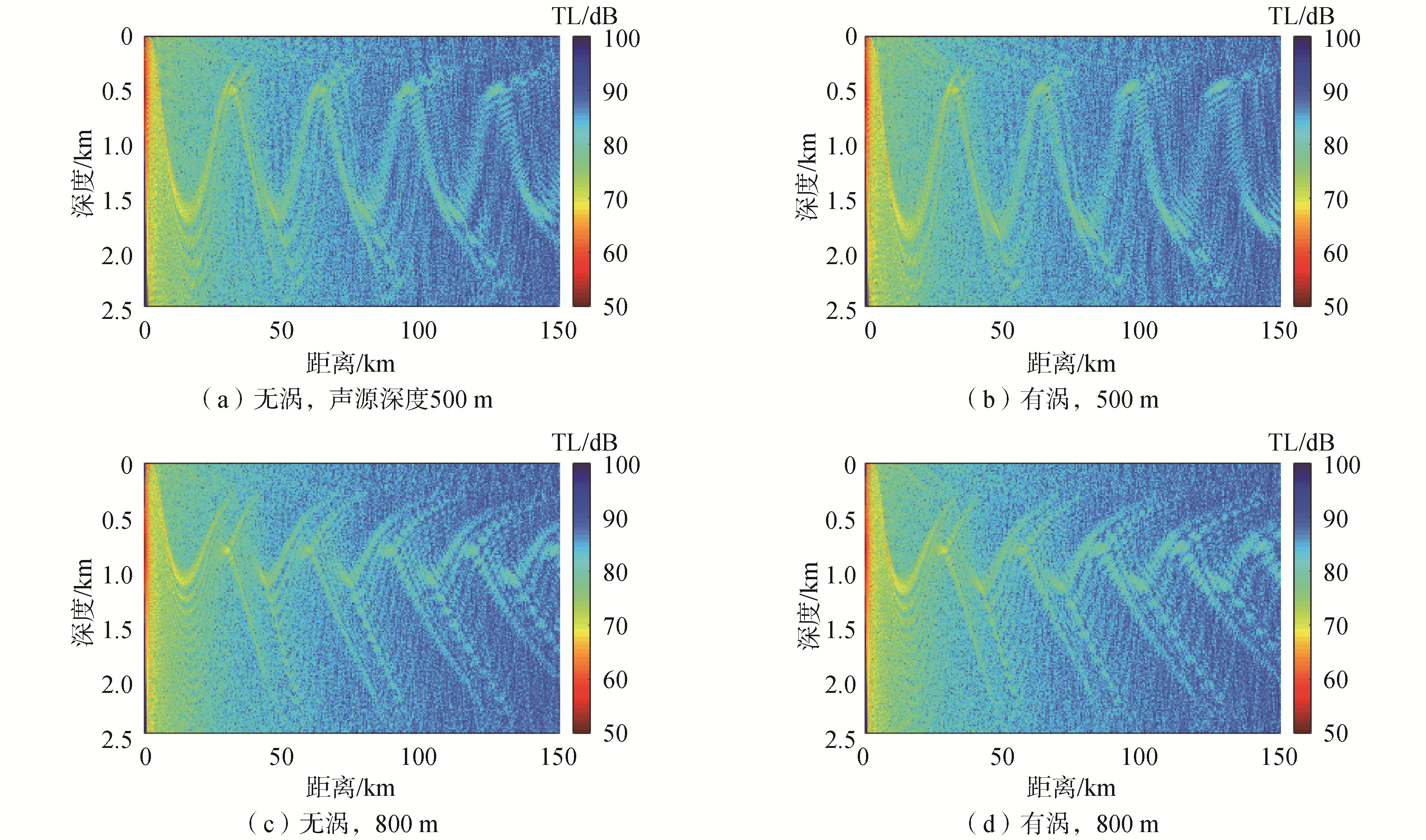
从图 7(a)可以看出,当声波从暖涡中心向暖涡外部传播时,由于暖涡的存在,声道轴加深,和图 7(b)相比,有涡时声线的翻转深度加深,图 7(c)是声源深度为800m时传播损失图,800m深度靠近声道轴附近,有一部分声线向上弯折,部分向下弯折,声道轴会聚区的位置前移,宽度有减小趋势。以第5会聚区为例,无涡旋的背景环境下,第5会聚区的距离在大约150km处,而当声源经过有暖涡的背景环境时,第5会聚区的距离大约在140km处,大致前移10km左右。由于暖涡的存在导致了声速分布的变化,中心处为温度极大值区的暖涡环境,致使暖涡区声速增大,声波折射路线改变,从而使得会聚区位置往前推移。
|
Download:
|
| 图 7 不同声源深度的传播损失 Fig. 7 TL with and without eddy at different source depths | |
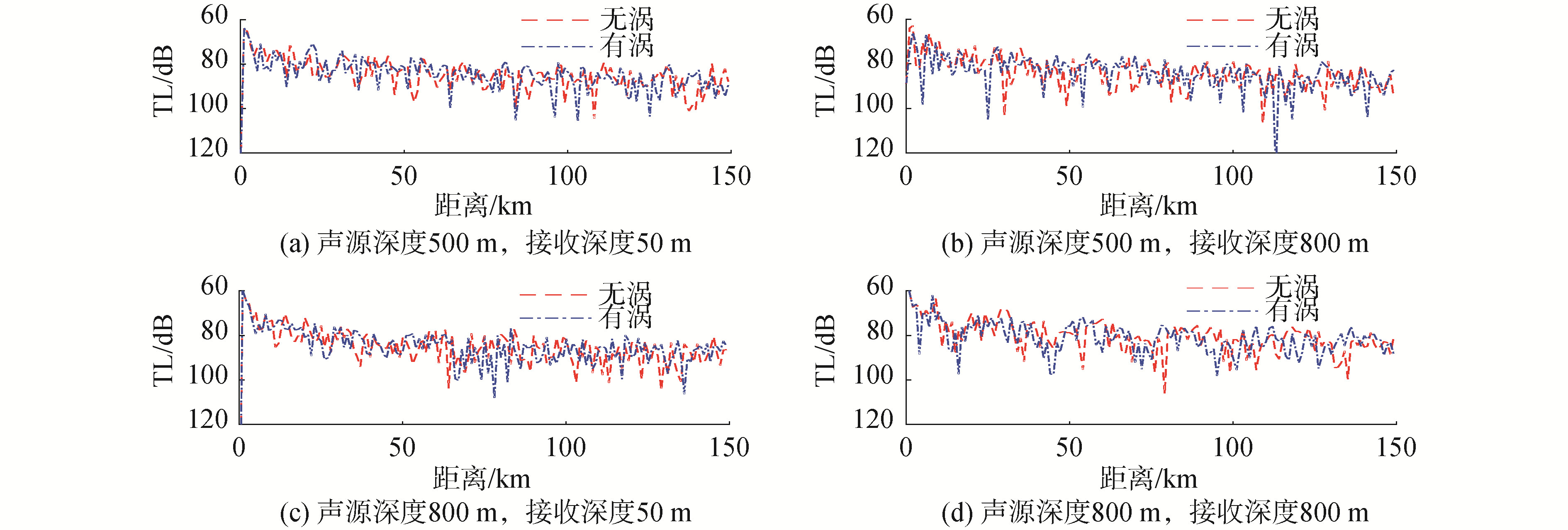
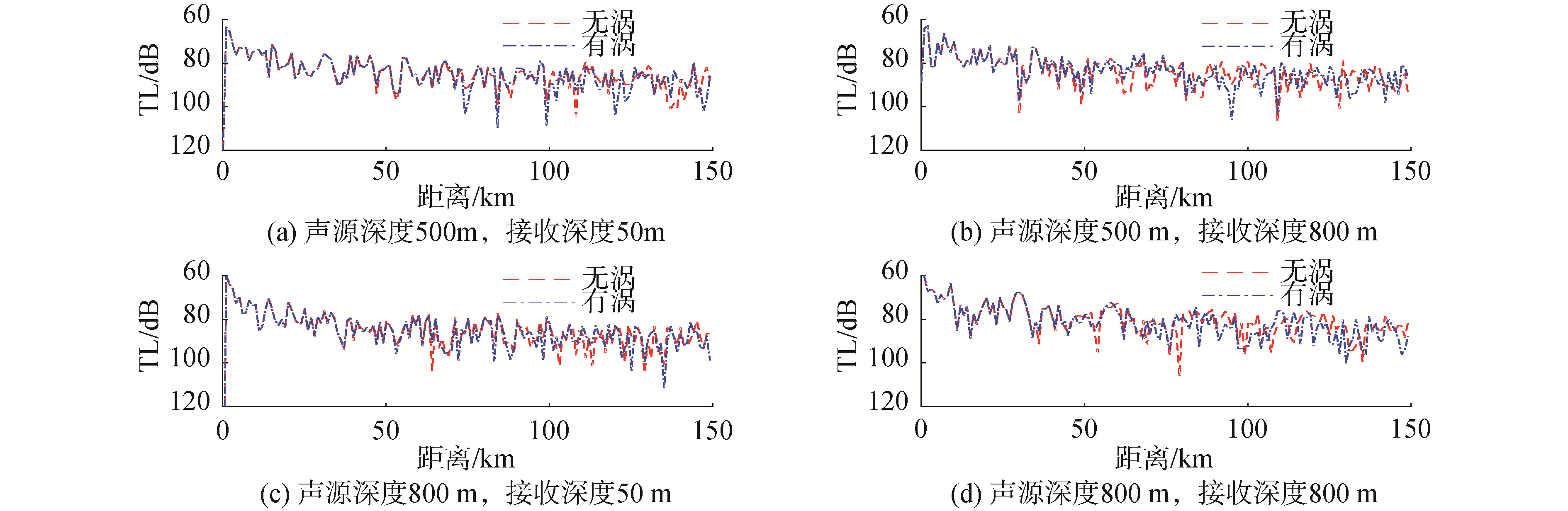
图 8是声源频率100 Hz,声源深度为500m与800m,声波从暖涡中心向暖涡外部传播时,深度分别为50m和800m的声传播损失曲线。从图 9中可以看出,50m深度处,距离涡中心70km以内,有涡的传播损失相比无涡环境下的传播损失比较明显,在水平距离116km左右相差36 dB。深度800m时,在水平距离124km左右,传播损失差值可达到30 dB,通过观察图 8可以发现,124km处正好对应无涡时的会聚区,对应有涡时的影区,这也正是因为涡旋的存在使会聚区发生前移。随着水平传播距离的增大,有涡的传播损失曲线衰减规律与无涡的相比,峰值逐步前移,70km以外,传播损失相差不大,因为涡对远处的影响逐渐减弱。图 9是声波从暖涡的外部向暖涡中心传播的损失曲线。
|
Download:
|
| 图 8 从暖涡内向外,不同声源深度及接收深度下的传播损失 Fig. 8 Transmission Losses at different depth of source and receive from the center of the warm eddy to outside | |
|
Download:
|
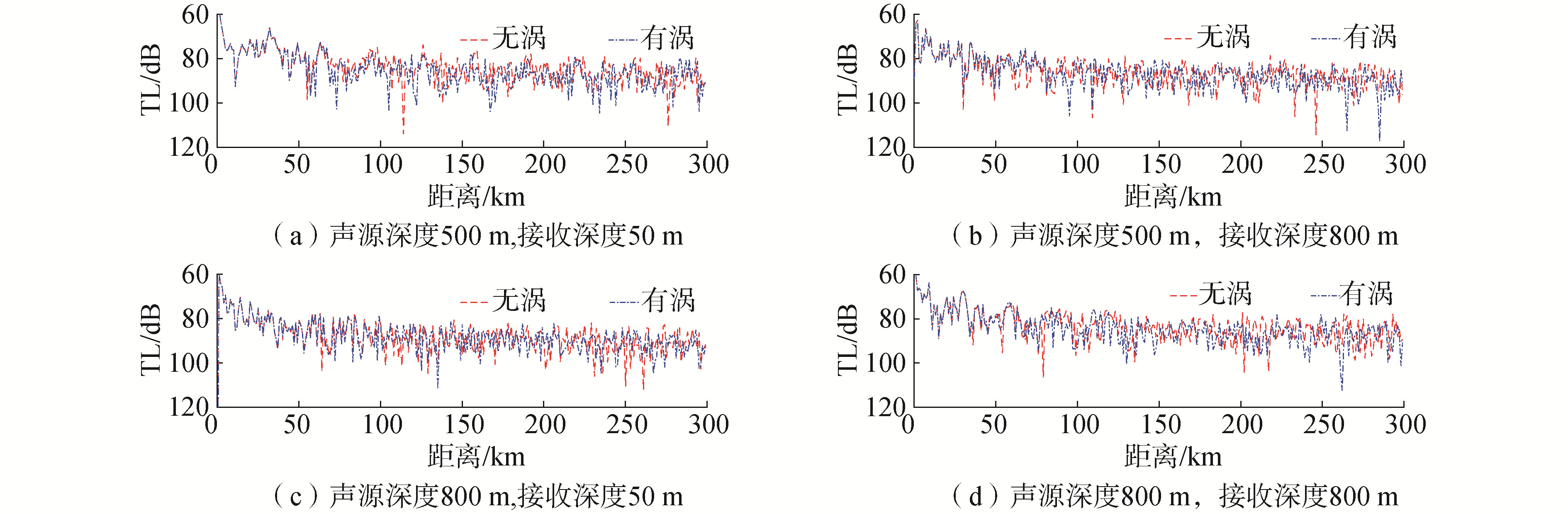
| 图 9 从暖涡外向内,不同声源深度及接收深度下的传播损失 Fig. 9 Transmission Losses at different depth of source and receive from outside to the center of the warm eddy | |
在暖涡的边缘,水温的水平梯度较小,随着往暖涡中心推进,在水平方向,水温逐渐增大,暖涡的效果愈发明显。水下50m深度处,在水平方向100km的距离上,传播损失开始显著变化,涡的有效影响距离大致100km。而在800m深度处,在水平方向50km的距离上,传播损失就开始显著变化,涡的有效影响距离大致200km。
声波由暖涡的左侧穿越暖涡向右侧传播时,和没有暖涡相比,穿越左侧时,从声速小的区域到声速大的区域,会聚区后移,穿越右侧时,会聚区前移,穿越左右两侧具有类似的“对称性”,这一点从图 10中的传播损失曲线可以看出。
|
Download:
|
| 图 10 从左右两侧分别穿越涡旋时的TL Fig. 10 TL of eddy crossing from left and right sides | |
1) 暖涡的存在,改变声道轴深度,从而对声线的弯折产生影响。
2) 暖涡的存在使从暖涡中心出发的声线会聚区宽度减小,汇聚位置前移。
3) 通过研究南海北部中尺度暖涡引起的声场变化,可以发现,发射频率100 Hz,声源深度800m,接收深度800m处有涡和无涡的传播损失可以达到30 dB以上。
4) 根据对观测数据分析发现,暖涡在移动,对于不断移动演变的暖涡的声场环境分析将在以后的工作中开展。
| [1] |
董昌明. 海洋涡旋探测与分析[M]. 北京: 科学出版社, 2015. DONG Changming. Oceanic eddy detection and analysis[M]. Beijing: Science Press, 2015. (  0) 0)
|
| [2] |
笪良龙. 海洋水声环境效应建模与应用[M]. 北京: 科学出版社, 2012. DA Lianglong. Modeling and application of underwater acoustic environmental effect[M]. Beijing: Science Press, 2012. (  0) 0)
|
| [3] |
刘清宇. 海洋中尺度现象下的声传播研究[D]. 哈尔滨: 哈尔滨工程大学, 2006. LIU Qingyu. The research of wave propagation in ocean environment with mesoscale phenomena[D]. Harbin: Harbin Engineering University, 2006. (  0) 0)
|
| [4] |
ZHANG Zhengguang, WANG Wei, QIU Bo. Oceanic mass transport by mesoscale eddies[J]. Science, 2014, 345(6194): 322-324. DOI:10.1126/science.1252418 (  0) 0)
|
| [5] |
TSUCHIYA T, OKUYAMA T, ENDOH N, et al. Numerical analysis of acoustical propagation in ocean with warm and cold water mass used by the three-dimensional wide-angle parabolic equation method[J]. Japanese journal of applied physics, 1999, 38(5S): 3351-3355. (  0) 0)
|
| [6] |
卢晓亭, 胡均川, 李玉阳. 海洋涡中的三维声传播分析[C]//中国声学学会1999年青年学术会议[CYCA'99] 论文集. 武汉, 1999: 54-55. LU Xiaoting, HU Junchuan, LI Yuyang. 3-Dimensional analysis of sound transmission in ocean eddy[C]//Proceedings of China Acoustics Society 1999 Youth Conference[CYCA'99]. Wuhan, 1999: 54-55. (  0) 0)
|
| [7] |
MUNK W H. Horizontal deflection of acoustic paths by mesoscale eddies[J]. Journal of physical oceanography, 1980, 10(4): 596-604. DOI:10.1175/1520-0485(1980)010<0596:HDOAPB>2.0.CO;2 (  0) 0)
|
| [8] |
张旭, 张健雪, 张永刚, 等. 南海西部中尺度暖涡环境下汇聚区声传播效应分析[J]. 海洋工程, 2011, 29(2): 83-91. ZHANG Xu, ZHANG Jianxue, ZHANG Yonggang, et al. Effect of acoustic propagation in convergence zone under a warm eddy environment in the western South China Sea[J]. The ocean engineering, 2011, 29(2): 83-91. DOI:10.3969/j.issn.1005-9865.2011.02.012 (  0) 0)
|
| [9] |
张旭, 程琛, 邱仁贵. 一个西太平洋冷涡影响下的会聚区声传播变异特征分析[J]. 海洋通报, 2015, 34(2): 130-137. ZHANG Xu, CHENG Chen, QIU Rengui. Abnormal features of the convergence zone caused by the cold eddy in Western Pacific[J]. Marine science bulletin, 2015, 34(2): 130-137. (  0) 0)
|
| [10] |
WATSON J G, SIEGMANN W L, JACOBSON M J. Deep-ocean dynamics for environmental acoustics models[J]. The journal of the acoustical society of America, 1976, 60(2): 355-364. DOI:10.1121/1.381090 (  0) 0)
|
| [11] |
HENRICK R F, SIEGMANN W L, JACOBSON M J. General analysis of ocean eddy effects for sound transmission applications[J]. The journal of the acoustical society of America, 1977, 62(4): 860-870. DOI:10.1121/1.381606 (  0) 0)
|
| [12] |
HENRICK R F, JACOBSON M J, SIEGMANN W L. General effects of currents and sound-speed variations on short-range acoustic transmission in cyclonic eddies[J]. The journal of the acoustical society of America, 1980, 67(1): 121-134. DOI:10.1121/1.384471 (  0) 0)
|
| [13] |
BAER R N. Calculations of sound propagation through an eddy[J]. The journal of the acoustical society of America, 1980, 67(4): 1180-1185. DOI:10.1121/1.384178 (  0) 0)
|
| [14] |
BAER R N. Propagation through a three-dimensional eddy including effects on an array[J]. The journal of the acoustical society of America, 1981, 69(1): 70-75. DOI:10.1121/1.385253 (  0) 0)
|
| [15] |
JIAN Yongjun, ZHANG J, LIU Q S, et al. Effect of Mesoscale eddies on underwater sound propagation[J]. Applied acoustics, 2009, 70(3): 432-440. DOI:10.1016/j.apacoust.2008.05.007 (  0) 0)
|
| [16] |
姬莉莉, 林缅. 中尺度涡影响下目的层地震成像的畸变与影响因素分析[J]. 地球物理学报, 2013, 56(1): 195-203. JI Lili, LIN Mian. The distortion of seismic imaging in the presence of mesoscale eddies and analysis of influencing factors[J]. Chinese journal of geophysics, 2013, 56(1): 195-203. (  0) 0)
|
| [17] |
李立. 南海中尺度海洋现象研究概述[J]. 台湾海峡, 2002, 21(2): 265-274. LI Li. A review on mesoscale oceanographical phenomena in the South China Sea[J]. Journal of oceanography in Taiwan Strait, 2002, 21(2): 265-274. DOI:10.3969/j.issn.1000-8160.2002.02.021 (  0) 0)
|
| [18] |
LI Li, NOWLIN JR W D, SU Jilan. Anticyclonic rings from the Kuroshio in the South China Sea[J]. Deep sea research part I: oceanographic research papers, 1998, 45(9): 1469-1482. DOI:10.1016/S0967-0637(98)00026-0 (  0) 0)
|
| [19] |
LIU Changjian, DU Yan, ZHUANG Wei, et al. Evolution and propagation of a mesoscale eddy in the northern South China Sea during winter[J]. Acta oceanologica sinica, 2013, 32(7): 1-7. DOI:10.1007/s13131-013-0325-1 (  0) 0)
|
| [20] |
YANG G, WANG F, LI Y, et al. Mesoscale eddies in the northwestern subtropical Pacific Ocean: Statistical characteristics and three-dimensional structures[J]. Journal of geophysical research: oceans, 2013, 118(4): 1906-1925. DOI:10.1002/jgrc.20164 (  0) 0)
|
| [21] |
林夏艳, 董昌明, 陈大可. 台湾岛西南部一个暖涡的跨海盆粒子输运[J]. 热带海洋学报, 2018, 37(3): 9-18. LIN Xiayan, DONG Changming, CHEN Dake. Cross-basin particle transport by a warm eddy southwest of Taiwan Island[J]. Journal of tropical oceanography, 2018, 37(3): 9-18. (  0) 0)
|
| [22] |
郑瑞玺, 经志友, 罗士浩. 南海北部反气旋涡旋边缘的次中尺度动力过程分析[J]. 热带海洋学报, 2018, 37(3): 19-25. ZHENG Ruixi, JING Zhiyou, LUO Shihao. Analysis of sub-mesoscale dynamic processes in the periphery of anticyclonic eddy in the northern South China Sea[J]. Journal of tropical oceanography, 2018, 37(3): 19-25. (  0) 0)
|
| [23] |
韩玉康, 周林, 吴炎成. 基于HYCOM的南海中尺度涡数值模拟[J]. 海洋通报, 2016, 35(3): 299-316. Han Yukang, Zhou Lin, Wu Yancheng. Numerical simulation of the mesoscale eddy in the South China Sea based on HYCOM[J]. Marine science bulletin, 2016, 35(3): 299-316. (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


