2. 杭州应用声学研究所, 浙江 杭州 310023
2. Hangzhou Applied Acoustics Research Institute, Hangzhou 310023, China
深海声源深度估计一直是国际声学界研究的热点与难点。得益于可靠声路径模式下的声场特征,国内外最近的研究重心在于利用布放在深海临界深度(该深度的声速等于海面处的声速)以下的垂直线阵,来检测和定位表层水体(海面300 m内)的声源。Mccargar等[1-4]考虑到可靠声路径下声场劳埃德镜干涉-直达声与海面反射声的相干叠加,其在距离和深度平面上呈现与声源深度相关的干涉条纹,对于窄带信号,信号波束强度作为距离和时间的函数是随声源深度的调制而变化的,提出了基于广义傅里叶变换的声源深度估计方法,并分析了信噪比、距离-角度跨度等条件变换下的深度估计性能。对于宽带信号,Yang等[5]指出相对于频率的声强条纹会由声源深度调制(对于接收器低于临界深度的情况),并且可以通过匹配声场干涉结构用于声源深度估计。Duan等[6]使用扩展卡尔曼滤波器跟踪随距离和时间变化的测量频率条纹,将其与建模的干涉结构进行比较,以估计声源深度。王梦圆等[7]利用座底单水听器自相关函数提取的直达波与海面反射波时延差结合双水听器的距离估计结果估计声源深度。杨刚等[8]基于可靠声路径,根据目标仰角的变化进行深度估计。刘炎堃等[9]基于深海运动目标在深海中的直达波与海面发射波的到达时延与位置之间的关系用座底单水听器进行目标深度估计。
不难发现,国内外学者针对利用座底水听器或垂直阵检测和定位深海近海面目标已取得显著的研究成果,然而未见基于近海面水平拖曳阵的近海面(300 m以浅)目标声源深度估计研究。考虑到拖曳阵为现今水面舰船反潜的主战声呐,因此亟需突破基于水平阵的深海声源深度估计问题,为水面水下目标分辨提供判据[10-13]。
本文针对水平阵估计深海近海面声源深度的难题,基于虚源理论推导了深海海底反射区声信号到达结构。分析了海底反射区声波到达结构与声源-接收器深度的调制关系,进而提出了用于声源深度估计的匹配到达结构方法。针对拷贝场构建问题,提出了基于水平阵的垂直波数估计构建拷贝场声波到达结构的方法。最后基于仿真数据验证了本文深度估计方法的可行性,并分析了在不同距离、信噪比、基阵孔径、处理带宽等条件下的性能。
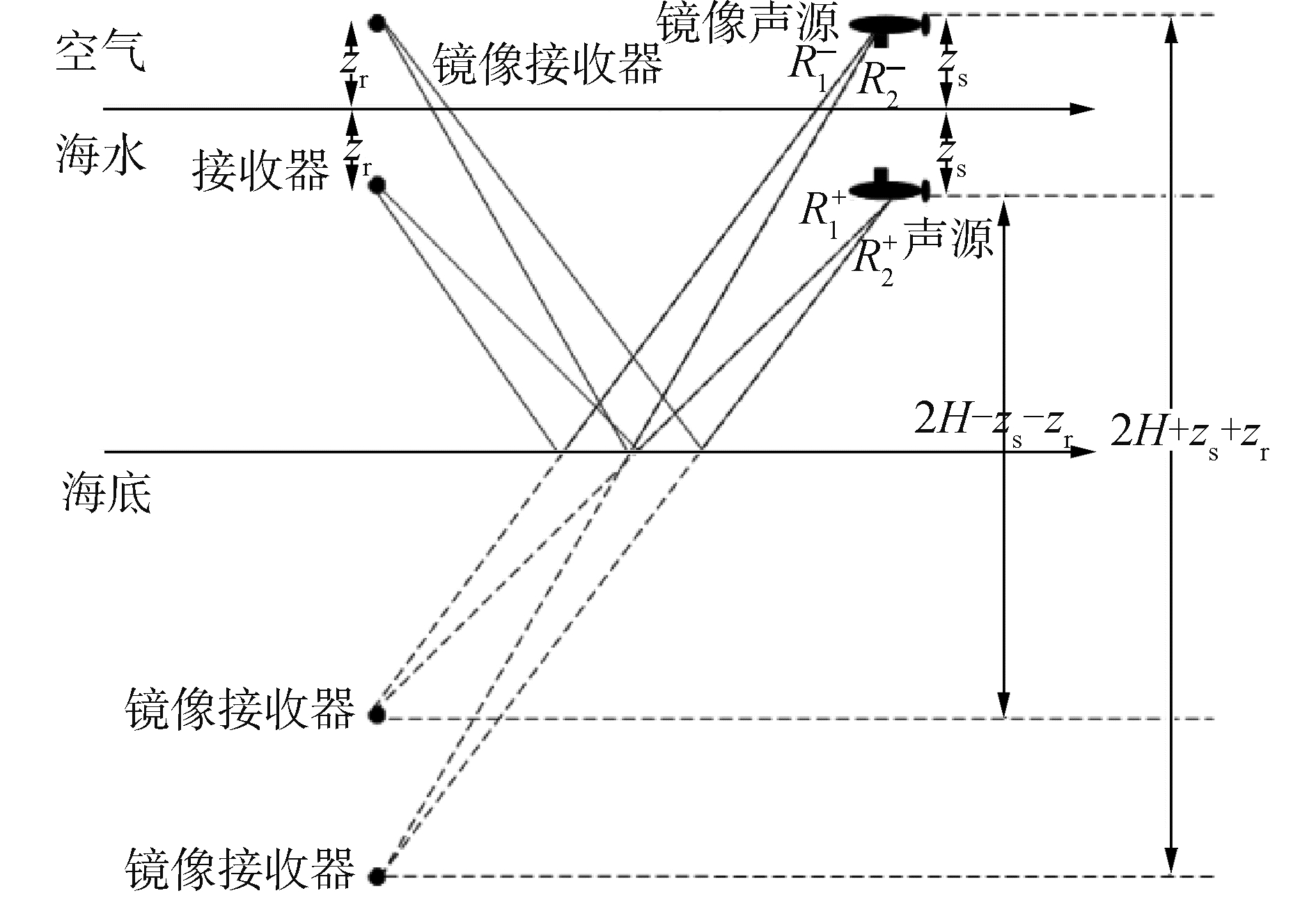
1 匹配到达结构处理基本原理 1.1 四元虚源理论本文讨论当声源和接收器都接近海面的情况,考虑到深海环境下,近海面声源辐射的声能量会向下折射,声源与接收器间直达波能量弱,所以忽略声源与接收器之间的直达波,如图 1所示,考虑一次海底反射形成的4条声线路径分别为:1)声源-海底-接收器(S-B-R)路径用R1+表示;2)声源-海面-海底-接收器(S-Sur-B-R)路径用R1-表示;3)声源-海底-海面-接收器(S-B-Sur-R)路径用R2+表示;4)声源-海面-海底-海面-接收器(S-Sur-B-Sur-R)路径用R2-表示。
|
Download:
|
| 图 1 深海海底反射路径下的虚源 Fig. 1 Schematic diagram of image theory in deep ocean bottom bounce area | |
因此到达接收器的声信号可近似表示为这4条路径声信号之和:
| $ \begin{gathered} P\left(z_{s}, z_{r}, R ; \omega\right)=S(\omega) V_{b}\left[\frac{\mathrm{e}^{\mathrm{i} k R_{1}^{+}}}{R_{1}^{+}}-\frac{\mathrm{e}^{\mathrm{i} k R_{1}^{-}}}{R_{1}^{-}}+\frac{\mathrm{e}^{\mathrm{i} k R_{2}^{+}}}{R_{2}^{+}}-\frac{\mathrm{e}^{\mathrm{i} k R_{2}^{-}}}{R_{2}^{-}}\right]= \\ S(\omega) V_{b}\left[\frac{\mathrm{e}^{\mathrm{i} k R_{1}^{+}}}{R_{1}^{+}}-\frac{\mathrm{e}^{\mathrm{i} k R_{1}^{-}}}{R_{1}^{-}}\right]+S(\omega) V_{b}\left[\frac{\mathrm{e}^{\mathrm{i} k R_{2}^{+}}}{R_{2}^{+}}-\frac{\mathrm{e}^{\mathrm{i} k R_{2}^{-}}}{R_{2}^{-}}\right]= \\ P^{1}\left(z_{s}, z_{r}, R ; \omega\right)+P^{2}\left(z_{s}, z_{r}, R ; \omega\right) \end{gathered} $ | (1) |
式中:ω为声源的角频率,k=ω/c为波数;S(ω)为声源强度;Vb为海底的反射系数;zs为声源深度;zr为接收器深度;R为声源到接收器的水平距离。4条主要路径长度分别为:
| $ \left\{\begin{array}{l} R_{1}^{+}=\sqrt{R^{2}+\left(2 H-z_{s}-z_{r}\right)^{2}} \\ R_{1}^{-}=\sqrt{R^{2}+\left(2 H+z_{s}-z_{r}\right)^{2}} \\ R_{2}^{+}=\sqrt{R^{2}+\left(2 H-z_{s}+z_{r}\right)^{2}} \\ R_{2}^{-}=\sqrt{R^{2}+\left(2 H+z_{s}+z_{r}\right)^{2}} \end{array}\right. $ | (2) |
式中:H为海深;P1(zs, zr, R; ω)部分为未到达接收器海面镜像源的声能量(S-B-R和S-Sur-B-R);P2(zs, zr, R; ω)部分为到达接收器海面镜像源的能量(S-B-Sur-R和S-Sur-B-Sur-R),分别近似可得:
| $ \begin{gathered} P^{1}\left(z_{s}, z_{r}, r ; \omega\right)=S(\omega) V_{b}\left[\frac{\mathrm{e}^{\mathrm{i} k R_{1}^{+}}}{R_{1}^{+}}-\frac{\mathrm{e}^{\mathrm{i} k R_{1}^{-}}}{R_{1}^{-}}\right] \approx \\ \quad-2 i V_{b} S(\omega) \frac{\mathrm{e}^{\mathrm{i} k R_{1}}}{R_{1}} \sin \left(k z_{s} \sin \theta_{1}\right) \end{gathered} $ | (3) |
| $ \begin{gathered} P^{2}\left(z_{s}, z_{r}, R ; \omega\right)=S(\omega) V_{b}\left[\frac{\mathrm{e}^{\mathrm{i} k R_{2}^{+}}}{R_{2}^{+}}-\frac{\mathrm{e}^{\mathrm{i} k R_{2}^{-}}}{R_{2}^{-}}\right] \approx \\ -2 i V_{b} S(\omega) \frac{\mathrm{e}^{\mathrm{i} k R_{2}}}{R_{2}} \sin \left(k z_{s} \sin \theta_{2}\right) \end{gathered} $ | (4) |
式中:θ1为到达接收器的到达角;θ2为到达接收器海面镜像的到达角,且
| $ \left\{\begin{array}{l} R_{1}=\sqrt{R^{2}+\left(2 H-z_{r}\right)^{2}} \\ R_{2}=\sqrt{R^{2}+\left(2 H+z_{r}\right)^{2}} \end{array}\right. $ | (5) |
当声源和接收器距离海面较近时,一般认为300 m以上时,有θ1≈θ2≈θ,θ为声线到达方向与水平方向的夹角,并将式(3)、(4)代入式(1)可得:
| $ \begin{gathered} P\left(z_{s}, z_{r}, R ; \omega\right)=P^{1}\left(z_{s}, z_{r}, R ; \omega\right)+P^{2}\left(z_{s}, z_{r}, R ; \omega\right) \approx \\ -2 i V_{b} S(\omega) \frac{\mathrm{e}^{\mathrm{i} k R_{1}}}{R_{1}} \sin \left(k z_{s} \sin \theta\right)- \\ 2 i V_{b} S(\omega) \frac{\mathrm{e}^{\mathrm{i} k R_{2}}}{R_{2}} \sin \left(k z_{s} \sin \theta\right)= \\ -2 i V_{b} S(\omega) \sin \left(k z_{s} \sin \theta\right)\left(\frac{\mathrm{e}^{\mathrm{i} k R_{1}}}{R_{1}}+\frac{\mathrm{e}^{\mathrm{i} k R_{2}}}{R_{2}}\right) \approx \\ -4 V_{b} S(\omega) \frac{\mathrm{e}^{\mathrm{i} k R_{s}}}{R_{s}} \sin \left(k z_{r} \sin \theta\right) \sin \left(k z_{s} \sin \theta\right) \end{gathered} $ | (6) |
式中
忽略强度系数-2iVbS(ω)后,有到达结构:
| $ \left|P_{a}\left(z_{s}, z_{r}, R ; \omega\right)\right|=\left|\sin \left(k z_{r} \sin \theta\right) \sin \left(k z_{s} \sin \theta\right)\right| $ | (7) |
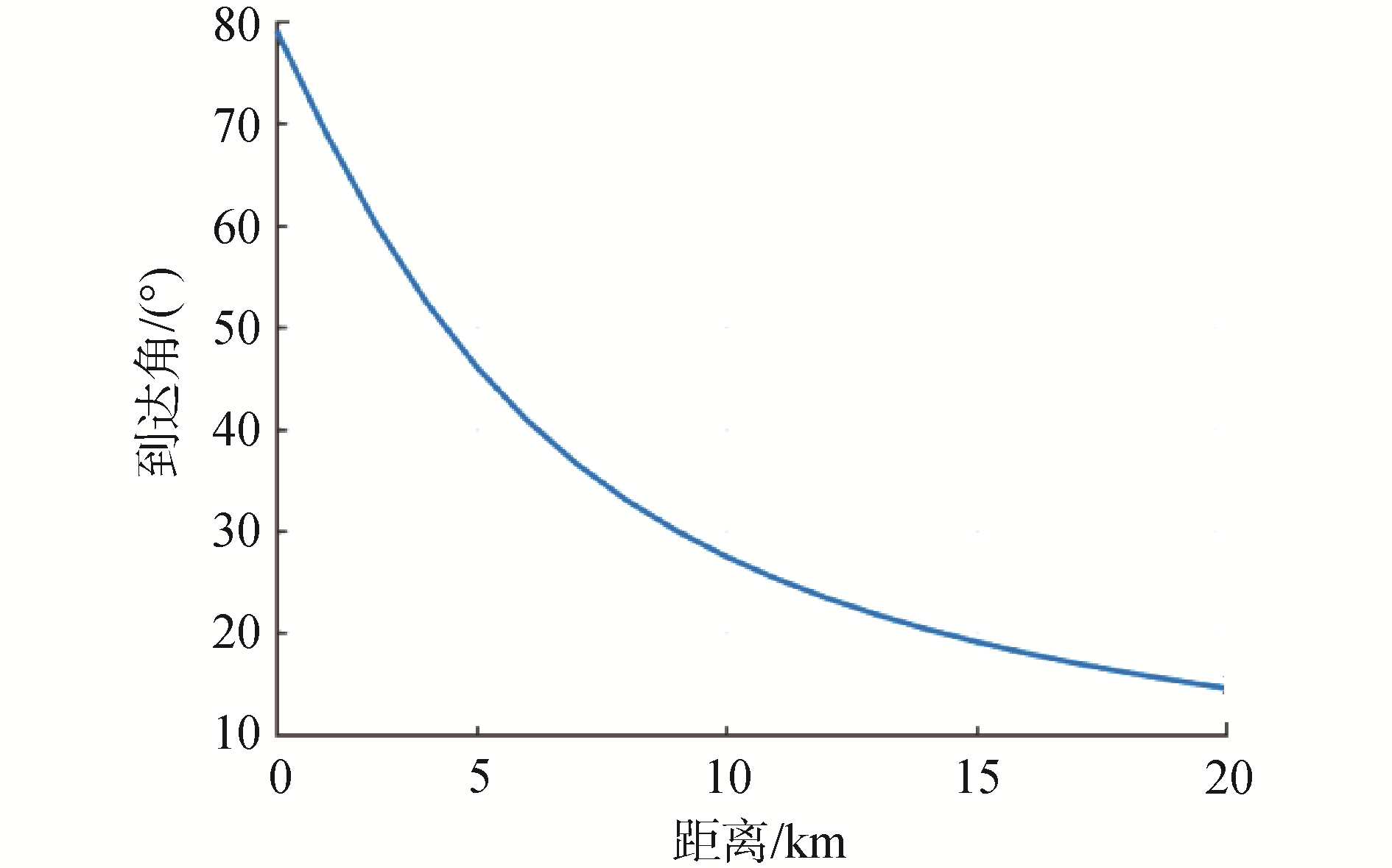
从式(7)可以看出,正弦调制函数中包含了垂直波数ksin θ、声源深度zs和接收深度zr,其中波数k可用k(f)表示代表不同频率下的波数,可以使用宽带信号进行处理,而到达角θ=arctan(2H/R)与距离相关,进而可知接收的声信号幅度会随着声源深度、接收器深度、频率以及距离等要素呈现干涉起伏。如图 2所示,不同的距离对应不同的到达角,基于此可以估计出声源与接收器之间的距离,但仅利用海底反射区声波到达角无法实现深度估计。而到达结构的干涉起伏隐含声源深度的信息,可用于声源深度估计,下文将在此基础上进一步推导。
|
Download:
|
| 图 2 距离-到达角关系(海深2 600 m) Fig. 2 Range-angle of arrival diagram(the sea depth is 2 600 m) | |
理论推导与数值分析指出了可以利用宽带信号的频谱起伏,实现声源深度的估计。然而从式(7)可以看出,实现声源深度估计的前提是可以获知不同频率下的ksin θ,即获知主要到达能量下近似的垂直波数kz(f),用kz(f)=k(f)sin θ表示,代表了此时不同频率下的垂直波数。
因此可以利用一条水平长阵实现不同频率下水平波数谱的估计:
| $ \tilde{s}\left(k_{r}, f ; z_{s}\right)=\int_{0}^{L} P\left(z_{s}, z_{r}, R ; \omega\right) \mathrm{e}^{-\mathrm{i} k_{r} r} \mathrm{~d} r $ | (8) |
式中:L为基阵的长度;kr为水平波数;r对应了各阵元与声源的水平距离,但这在现实中往往也是未知的。事实上实现波数谱的估计并不需要已知各阵元与声源的绝对距离,而是需要已知各阵元与声源的相对距离。不失一般性,假设基阵沿着声传播的方向放置,忽略水平方位角的情况下,可选取:
| $ r=(0, d, 2 d, \cdots, L) $ | (9) |
式中:d为阵元间距,L=(N-1)d为阵长;N为水平阵的阵元个数。
海底反射路径下主要能量到达的水平波数估计可以通过寻找不同频率下水平波数谱的峰值实现:
| $ \tilde{k}_{r}(f)=\operatorname{argmax}\left(\tilde{s}\left(k_{r}, f\right)\right) $ | (10) |
式中波浪线代表估计的波数。
则需要的垂直波数kz为:
| $ \tilde{k}_{z}(f)=\sqrt{k^{2}(f)-\tilde{k}_{r}^{2}(f)} $ | (11) |
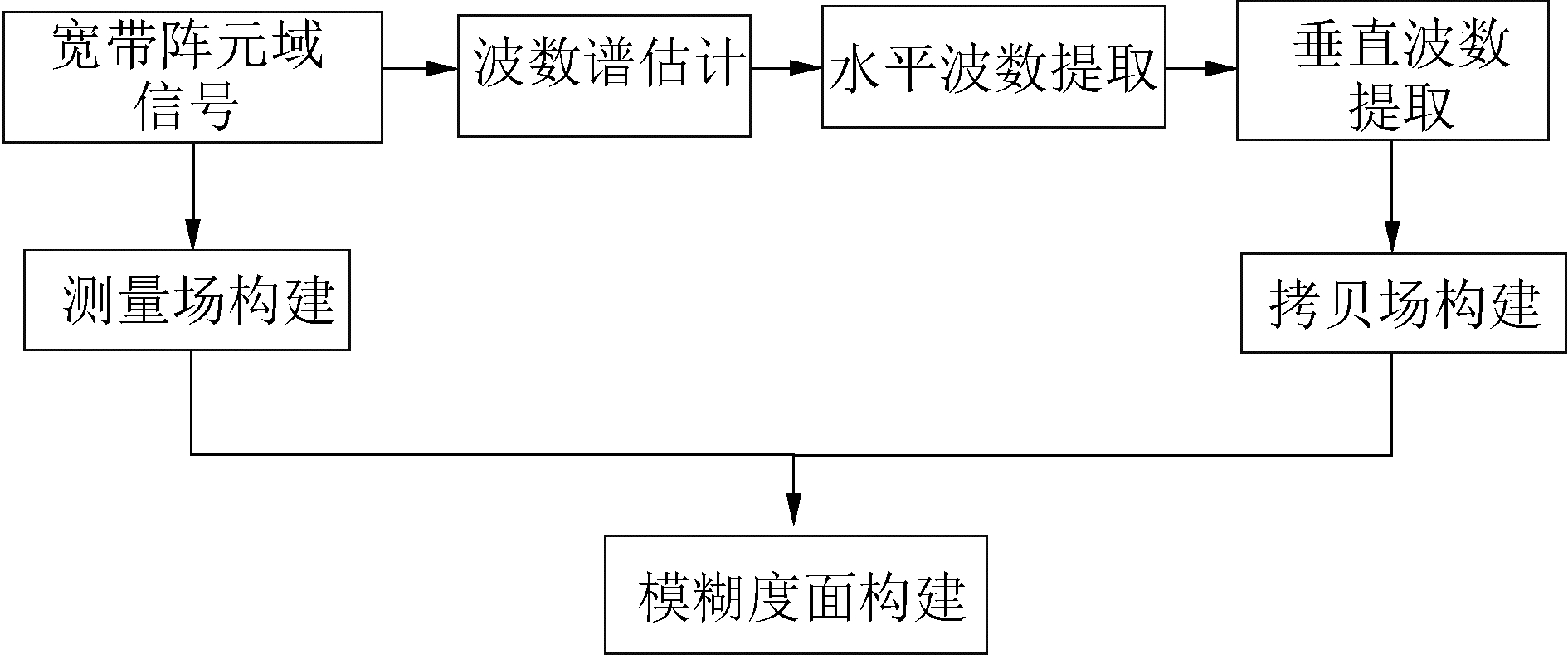
鉴于到达结构频谱上会呈现随声源深度和接收深度变化的起伏特征,因此在已知接收深度的情况下,可以利用到达结构频谱起伏特征提取声源的深度。这里提出匹配到达结构处理(matched arrival pattern processing,MAPP)用于声源深度的提取,如图 3所示。
|
Download:
|
| 图 3 匹配到达结构处理流程 Fig. 3 MAPP processing flow chart | |
将接收的宽带声信号的到达结构用|Pmeasured(zs; f)|表示,在利用水平阵估计出主要能量到达的垂直波数的情况下,利用虚源理论构建拷贝场的到达结构为:
| $ \left|P_{\text {replica }}(z ; f)\right|=\left|\sin \left(k_{z} z_{r}\right) \sin \left(k_{z} z\right)\right| $ | (12) |
定义匹配到达结构的模糊度面:
| $ M(z)=\frac{\int_{f_{l}}^{f_{h}}\left|P_{\text {replica }}(z ; f)\right|\left|P_{\text {measured }}\left(z_{s} ; f\right)\right| \mathrm{d} f}{\sqrt{\int_{f_{l}}^{f_{h}}\left|P_{\text {replica }}(z ; f)\right|^{2} \mathrm{~d} f \int_{f_{l}}^{f_{h}}\left|P_{\text {measured }}\left(z_{s} ; f\right)\right|^{2} \mathrm{~d} f}} $ | (13) |
式中fh和fl分别为处理频带的上下界。
匹配到达结构的模糊度面代表了测量场|Pmeasured(zs; f)|与拷贝场|Preplica(z; f)|起伏特征的非相干匹配程度。
根据处理数据量的不同,式(13)中测量场|Pmeasured(zs; f)|可以通过3种不同的方法计算得到:
方法1:选取单个阵元的接收信号幅度:
| $ \left|P_{\text {measured }}\left(z_{s} ; f\right)\right|=\left|P\left(z_{s}, z_{r}, R_{0} ; f\right)\right| $ | (14) |
方法2:通过水平阵多阵元幅度的叠加得到:
| $ \left|P_{\text {measured }}\left(z_{s} ; f\right)\right|=\sum\limits_{i=1}^{N}\left|P\left(z_{s}, z_{r}, R_{i} ; f\right)\right| $ | (15) |
方法3:通过水平阵多阵元相移补偿后的叠加得到:
| $ \left|P_{\text {measured }}\left(z_{s} ; f\right)\right|=\int_{0}^{L} P\left(z_{s}, z_{r}, R ; f\right) \mathrm{e}^{-\mathrm{j} \tilde{k}_{r}(f) r} \mathrm{~d} r $ | (16) |
理论上多路阵元信号的叠加,可提升抗干扰能力,进而提升匹配算法的稳定性。
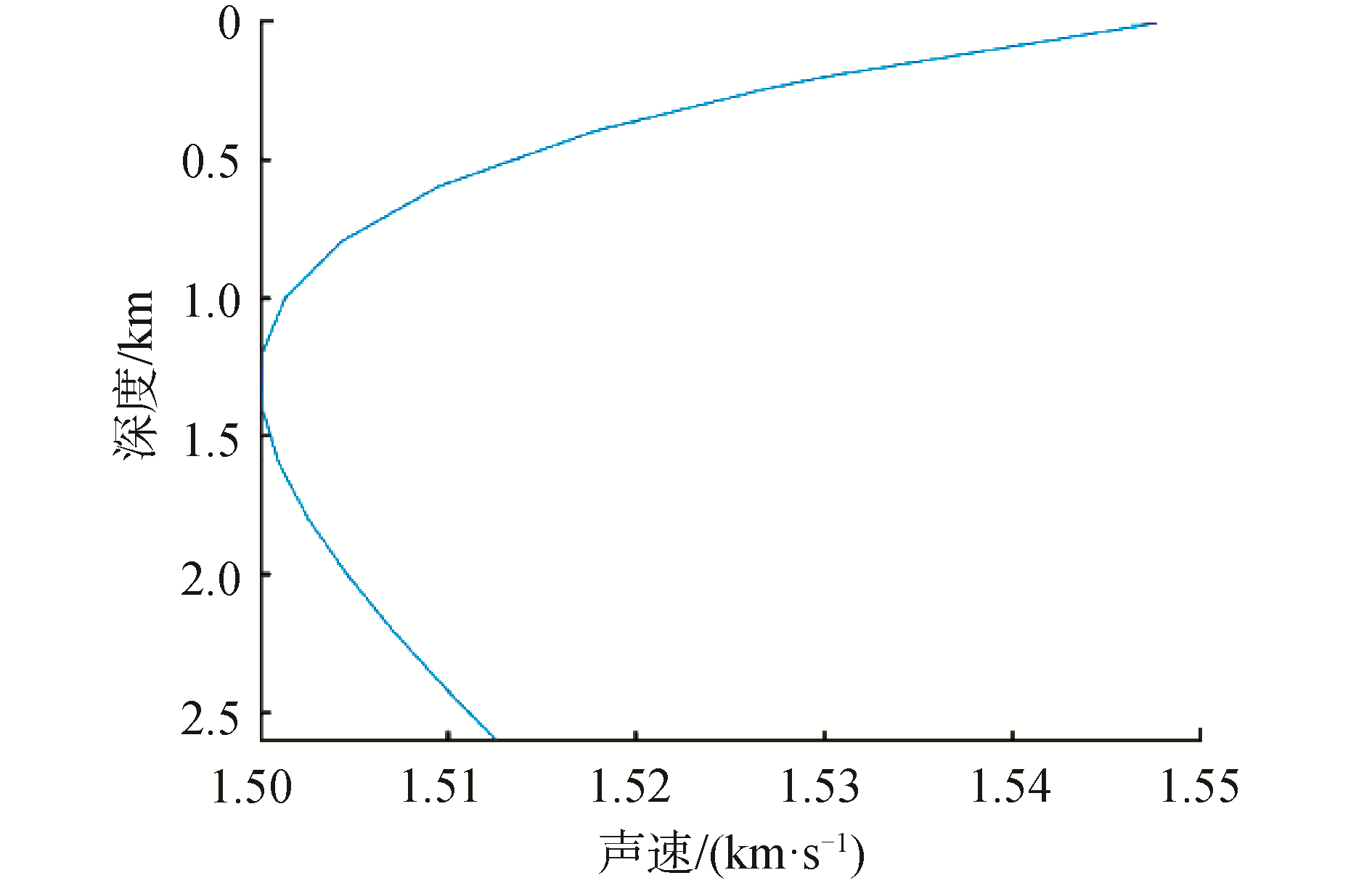
2 仿真试验 2.1 声源深度估计仿真仿真环境2 600 m深海,深海声速剖面如图 4所示,声道轴深度1 200 m,距离6 km处接收器接收的声信号。水平阵孔径1 000 m,阵元间距2 m,共501个阵元,阵元与目标声源距离范围设置为5.5~6.5 km。
|
Download:
|
| 图 4 仿真的声速剖面 Fig. 4 Simulated sound speed profile | |
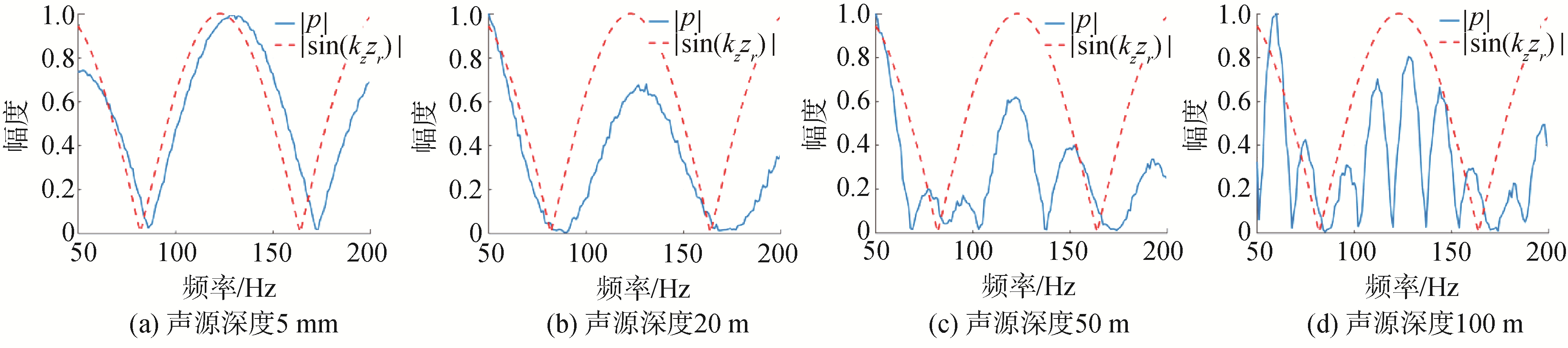
通过Kraken进行不同声源深度情况下的声场仿真建模得到接收信号的声压数据,从图 5可以看出,接收信号在频谱上呈现正弦变化的起伏特性,并且当声源深度大于接收深度时,频谱起伏的包络是由接收深度决定的。因此可利用宽带信号的频谱起伏,实现声源深度的估计。
|
Download:
|
| 图 5 接收信号归一化幅度随频率的起伏特性(接收深度固定20 m) Fig. 5 Fluctuation characteristics of normalized amplitude with frequency of received signal (receiving depth is 20 m) | |
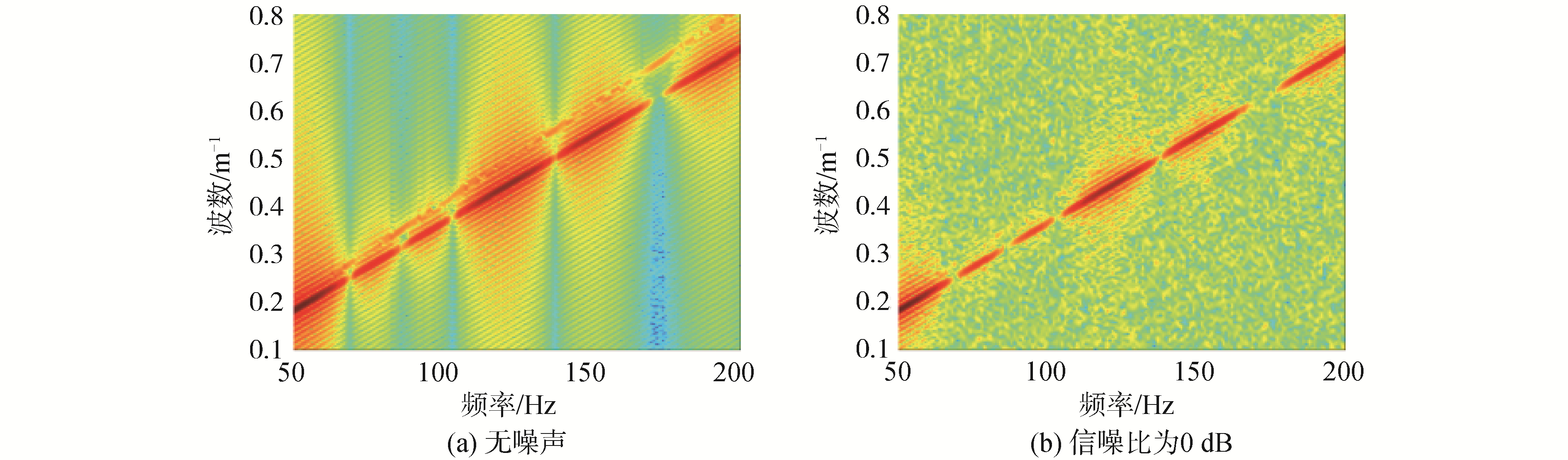
利用式(8)估计出水平波数谱,并通过寻找不同频率下水平波数谱的峰值估计出水平波数,如图 6所示。
|
Download:
|
| 图 6 波数能量-频率分布(距离6 km处不同频率下的水平波数谱) Fig. 6 Wavenumber energy-frequency distribution diagram (horizontal wavenumber spectrum at different frequencies from 6 km) | |
图中不同频率下波数能量的最大值就是估计得到的水平波数,从图中可以看出,水平波数与频率呈线性关系。
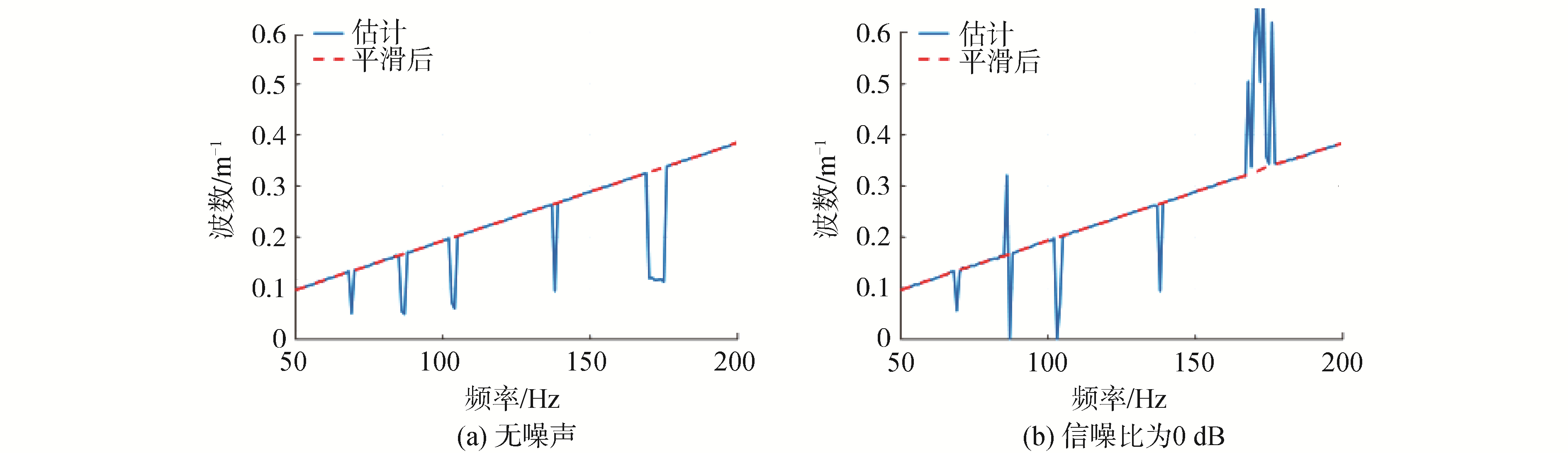
利用式(11)由估计的水平波数计算得到垂直波数。垂直波数的估计结果,如图 7所示,从波数谱中估计的波数有毛刺,通过数据平滑的方法去掉毛刺,结果用虚线画出,可以看出其与频率呈线性关系,这是符合物理规律的。
|
Download:
|
| 图 7 估计的垂直波数(距离6 km处) Fig. 7 Estimated vertical wavenumber (distance is 6 km) | |
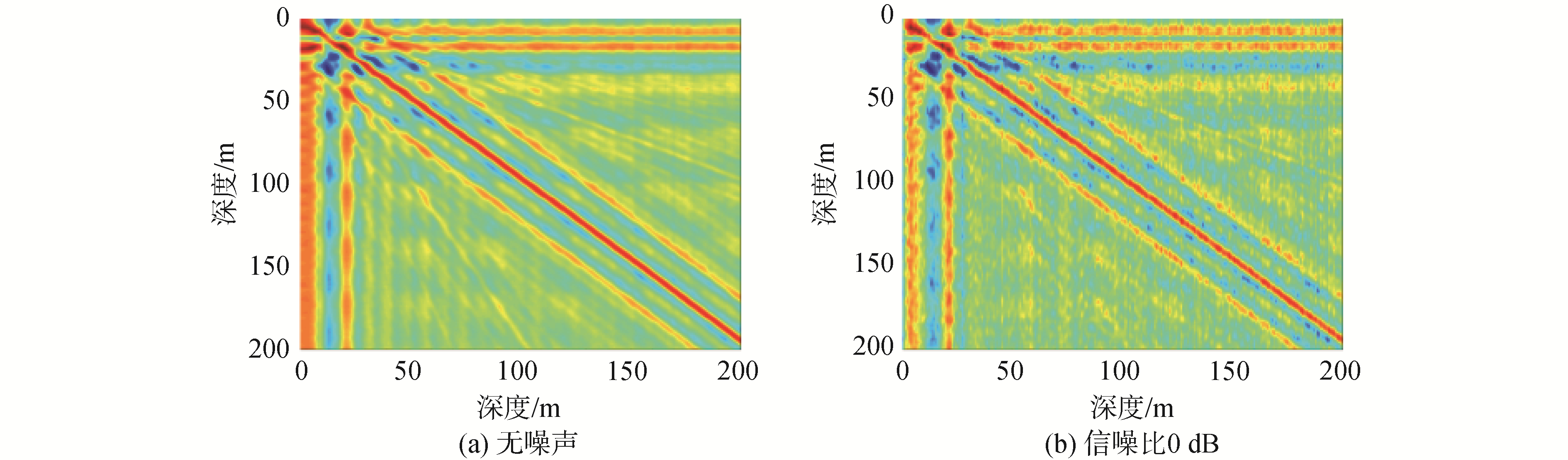
仿真处理频带50~200 Hz,水平阵中心与声源相距6 km处,设置输入声源真实深度1~200 m,通过估计出的垂直波数构建拷贝场到达结构,再匹配拷贝场与测量场的到达结构估计声源深度200次,得到声源真实深度与估计深度的模糊度面,如图 8所示,其横坐标为输入的真实深度,纵坐标为估计深度。
|
Download:
|
| 图 8 模糊度面(距离6 km处) Fig. 8 Schematic diagram of ambiguity surface (distance is 6 km) | |
其中对角线为深度估计的主瓣,其宽度与处理带宽成反比,从图中可以看出,估计深度与真实深度吻合程度较高。
2.2 匹配到达结构适用距离论证事实上,匹配到达结构的适用距离与四元虚源理论的近似适用距离有关。当声源距离远时,海底多次反射路径的能量及反转声线的能量则不能忽略。
考虑多次海底反射,声压场可近似表示为:
| $ \begin{gathered} P\left(z_{s}, z_{r}, R ; \omega\right)=-4 S(\omega) \cdot \\ \sum\limits_{n=1}^{\infty} V_{b}^{n} \frac{\mathrm{e}^{\mathrm{i} k R_{s}^{(n)}} \sin \left(k z_{r} \sin \theta^{(n)}\right) \sin \left(k z_{s} \sin \theta^{(n)}\right)}{R_{s}^{(n)}} \end{gathered} $ | (17) |
| $ R_{s}^{(n)} \approx \sqrt{(2 n H)^{2}+R^{2}} $ | (18) |
式(18)为声源和目标都处于近海面区的假设,注意到n=1时则为四元虚源理论的近似结果。
事实上,匹配到达结构深度估计失效的距离应是求和项中n=2的分量不可忽略或占主要作用的时刻。这与海深以及海底的反射能力有关,但一般情况下海深是起主要作用的。然而往往难以用解析形式获得匹配到达结构的适用距离,下面考虑利用仿真来寻找匹配到达结构的最大适用距离与海深的关系。
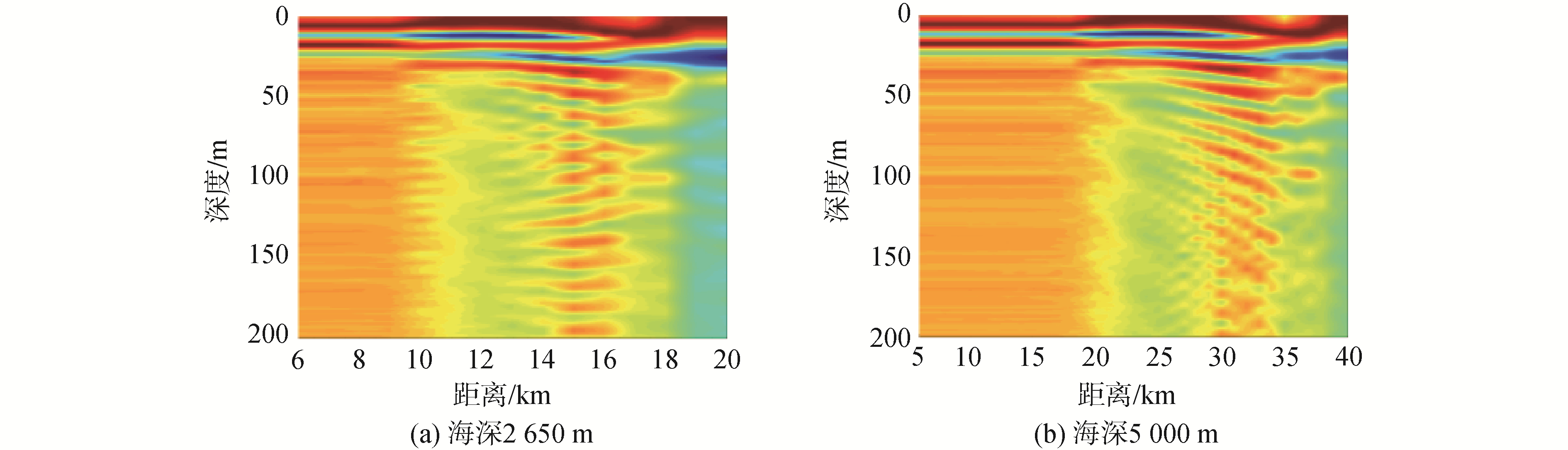
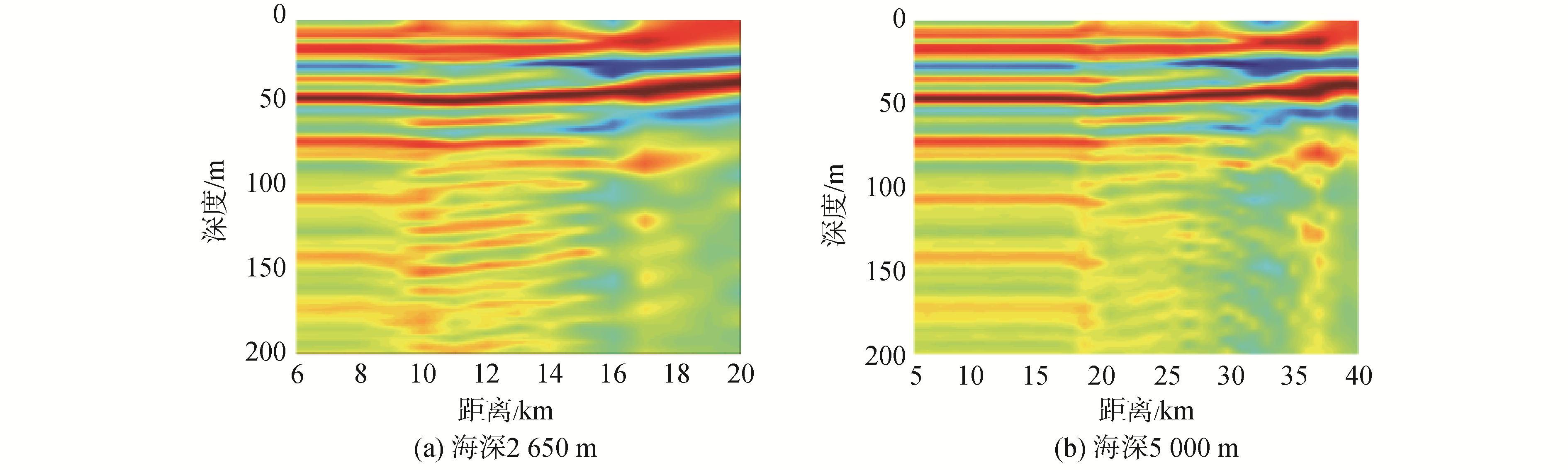
图 9、10分别仿真海深2 650 m与海深5 000 m,声源深度5 m的水面声源与声源深度50 m的水下声源,水平阵中心与声源距离仿真处于6~40 km变化,选择在第1影区(海底反射区),计算不同水平距离下声源深度估计的模糊度面。从下面4幅图的结果可以看出,深度估计结果的距离维变化与海深的倍数具有明显的相关性(深度估计结果的距离维变化受到海深的影响),当距离小于6倍海深时,声源深度估计的结果相对稳定;距离大于6倍海深时,声源深度估计的结果发生明显变化,且所有深度上的匹配系数明显减小,原因是距离远时由于小掠射角声线的不可忽略,导致难以估计一次海底反射声线的水平波数与垂直波数,且仅利用一次海底反射的声能量构建的拷贝场与测量场的匹配程度差,结果不可信(50 m声源在距离大于6倍海深时,存在较高的海面旁瓣)。
|
Download:
|
| 图 9 深度估计随水平阵中心与目标距离的变化(真实声源深度5 m) Fig. 9 The variation of depth estimation with the distance between the center of the horizontal array and the target (the real source depth is 5 m) | |
|
Download:
|
| 图 10 深度估计随水平阵中心与目标距离的变化(真实声源深度50 m) Fig. 10 The variation of depth estimation with the distance between the center of the horizontal array and the target(the real source depth is 50 m) | |
由此可以得出,匹配到达结构方法的距离限制为:
| $ R \leqslant 6 H $ | (19) |
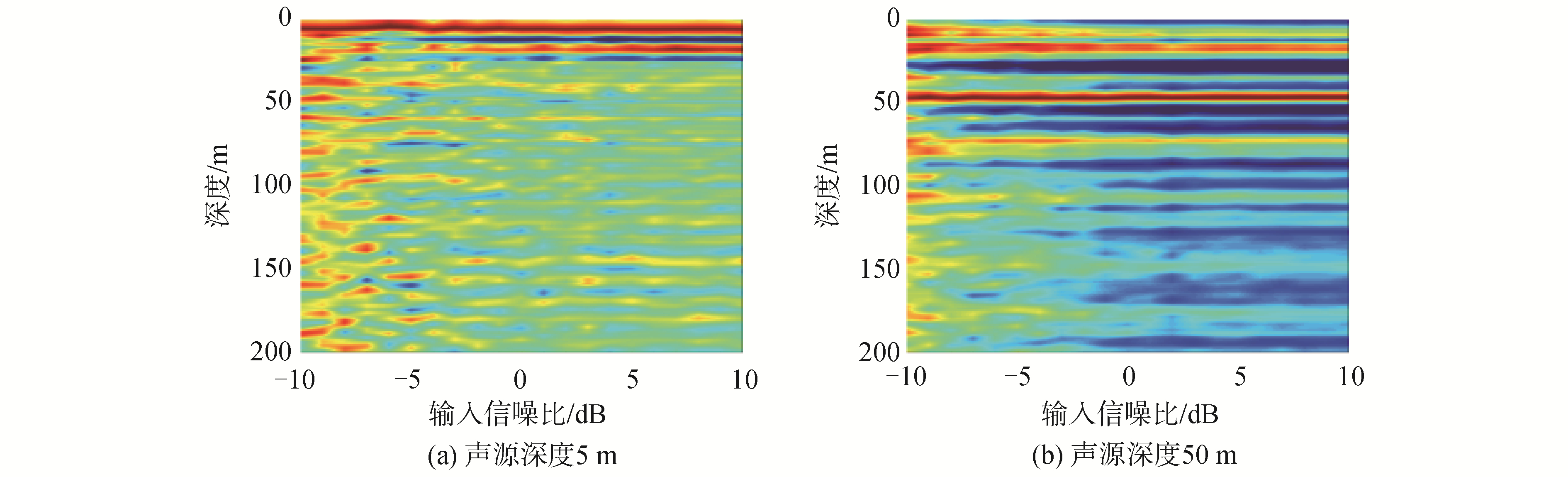
为了探究信噪比变化对匹配到达结构深度估计性能的影响,分别仿真研究了声源深度分别为5 m和50 m,不同信噪比条件下匹配到达结构的声源深度估计结果,如图 11所示。可以看出当信噪比低于-5 dB时,拷贝场与测量场的匹配程度较差,难以区分出深度信息,深度估计结果不可信。
|
Download:
|
| 图 11 深度估计性能随信噪比的变化 Fig. 11 Variation of depth estimation performance with signal-to-noise ratio | |
基阵孔径对匹配到达结构深度估计算法的影响体现在经过一次海底反射的水平波数与垂直波数提取,基阵孔径减小会影响波数提取的精度(当然这与输入信噪比的情况也是相关的)进而影响拷贝场的构建,影响深度估计的结果。
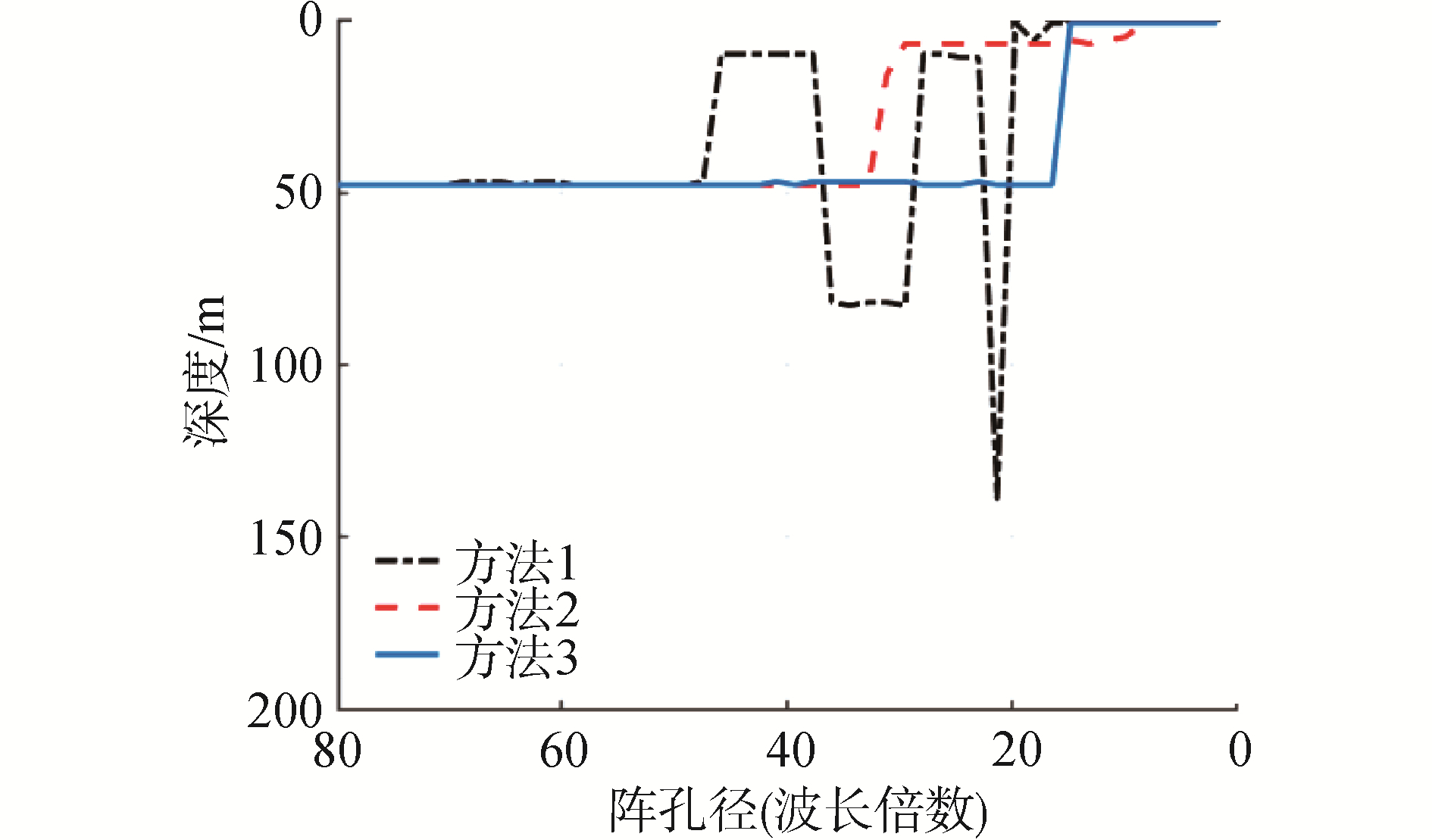
因此,为了探究基阵孔径的影响(限制),在阵元间距不变的情况下,逐渐减小用于波数谱处理的阵元数,开展深度估计性能的仿真研究。首先为了寻找基阵孔径减小下的最优处理方法,分别利用理论提出的3种测量场表示,计算深度估计结果,如图 11所示。可以看出,在输入信噪比为10 dB的情况下,随着基阵孔径的减小,3种方法的深度估计性能逐渐降低,方法1实现深度估计的要求是基阵孔径大于600 m,方法2实现深度估计的要求是基阵孔径大于400 m,方法3实现深度估计的要求是基阵孔径大于200 m,可以得出结论,相移后的阵元信号叠加,可以最大程度拾取声场信息,深度估计算法性能最高。
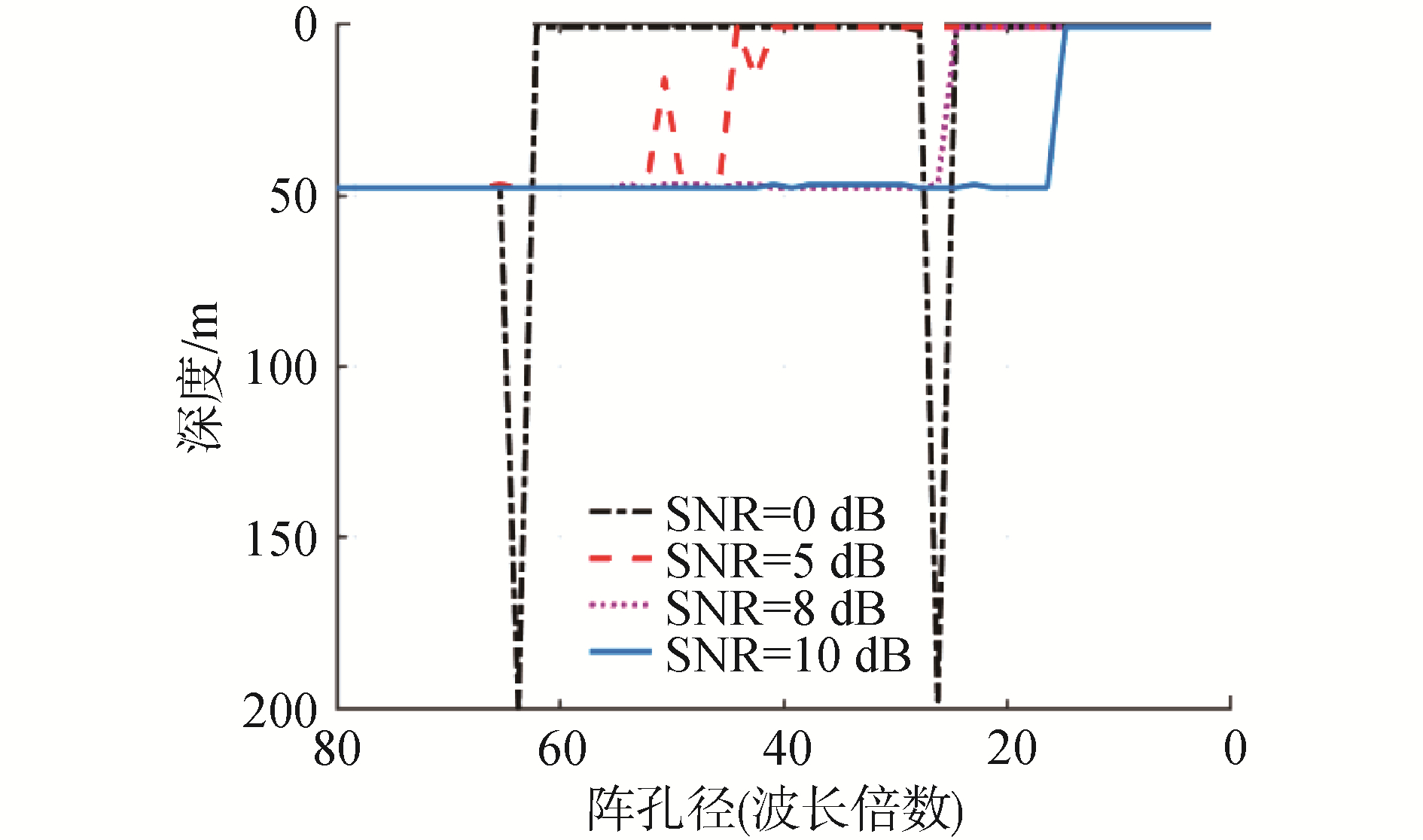
下面利用方法3,计算不同信噪比条件下的深度估计性能,由图 12可以看出信噪比越低,深度估计所需的基阵孔径越大,这与上文的预想是吻合的。且深度估计失效的信噪比区域与波数估计失效的信噪比区域是吻合的,这便验证了本文的论述,基阵孔径对匹配到达结构深度估计影响的根本在于波数谱的估计问题。
|
Download:
|
| 图 12 3种测量场表示下深度估计性能(输入信噪比10 dB) Fig. 12 Performance of depth estimation under three kinds of measurement field representation (input signal-to-noise is 10 dB) | |
|
Download:
|
| 图 13 不同信噪比下深度估计性能 Fig. 13 Performance of depth estimation under different signal-to-noise ratio | |
表 1依据图中信息,整理了不同信噪比下所需要的基阵孔径下限(取中心频率125 Hz,波长12.24 m),事实上探究信噪比与深度估计孔径与波长比下限的关系是有意义的,可以明确针对不同目标所需要的基阵孔径,减少布放成本。
| 表 1 不同信噪比下实现深度估计所需基阵孔径下限 Table 1 The lower limit of array aperture needed to realize depth estimation under different signal-to-noise ratio |
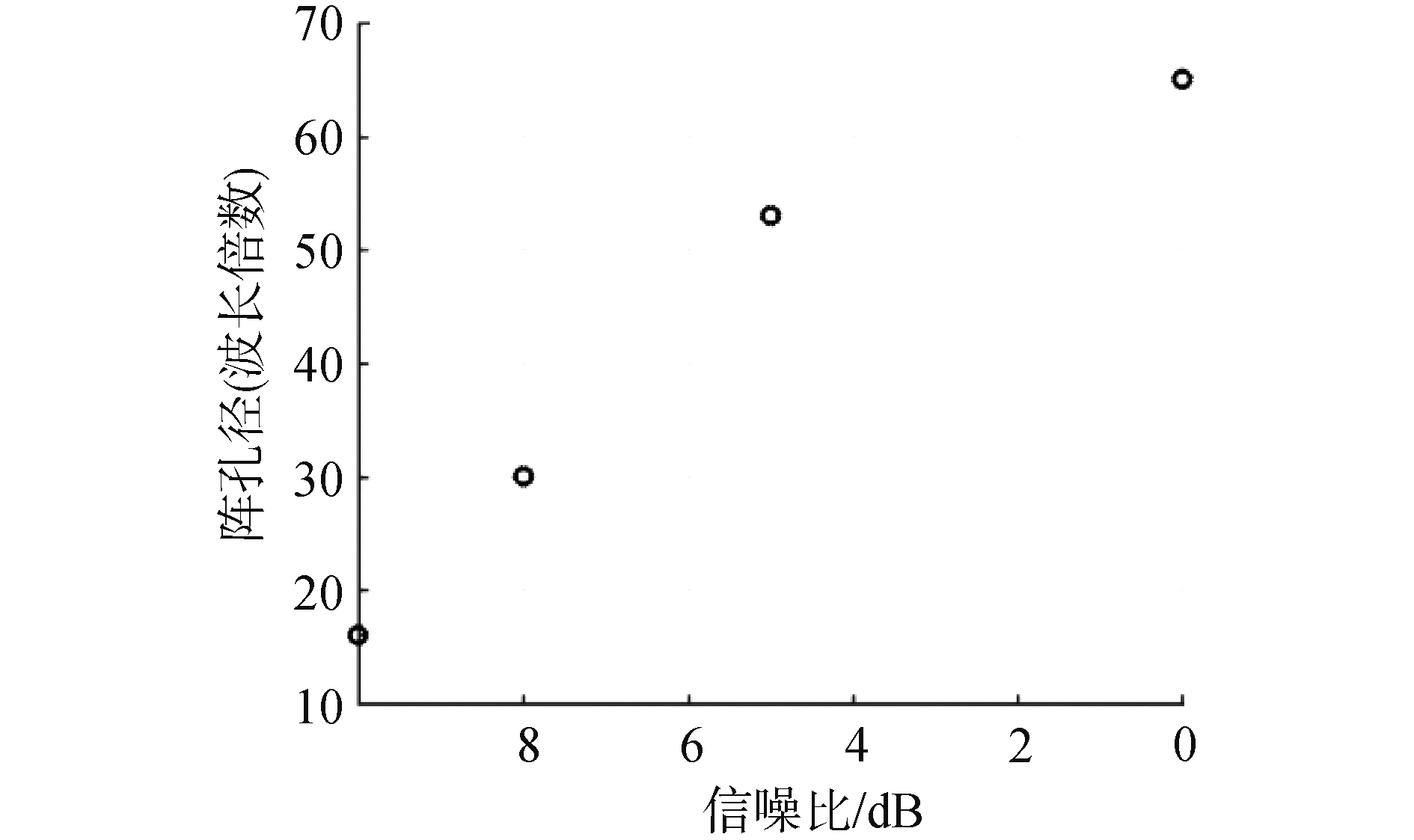
从信噪比降低所需要的基阵孔径散点图(图 14)可以看出,满足深度估计所需时基阵孔径越大,信噪比越小,但并不是简单的线性或是对数线性的关系。
|
Download:
|
| 图 14 信噪比降低所需要的基阵孔径散点 Fig. 14 Array aperture scatter diagram needed for signal-to-noise ratio reduction | |
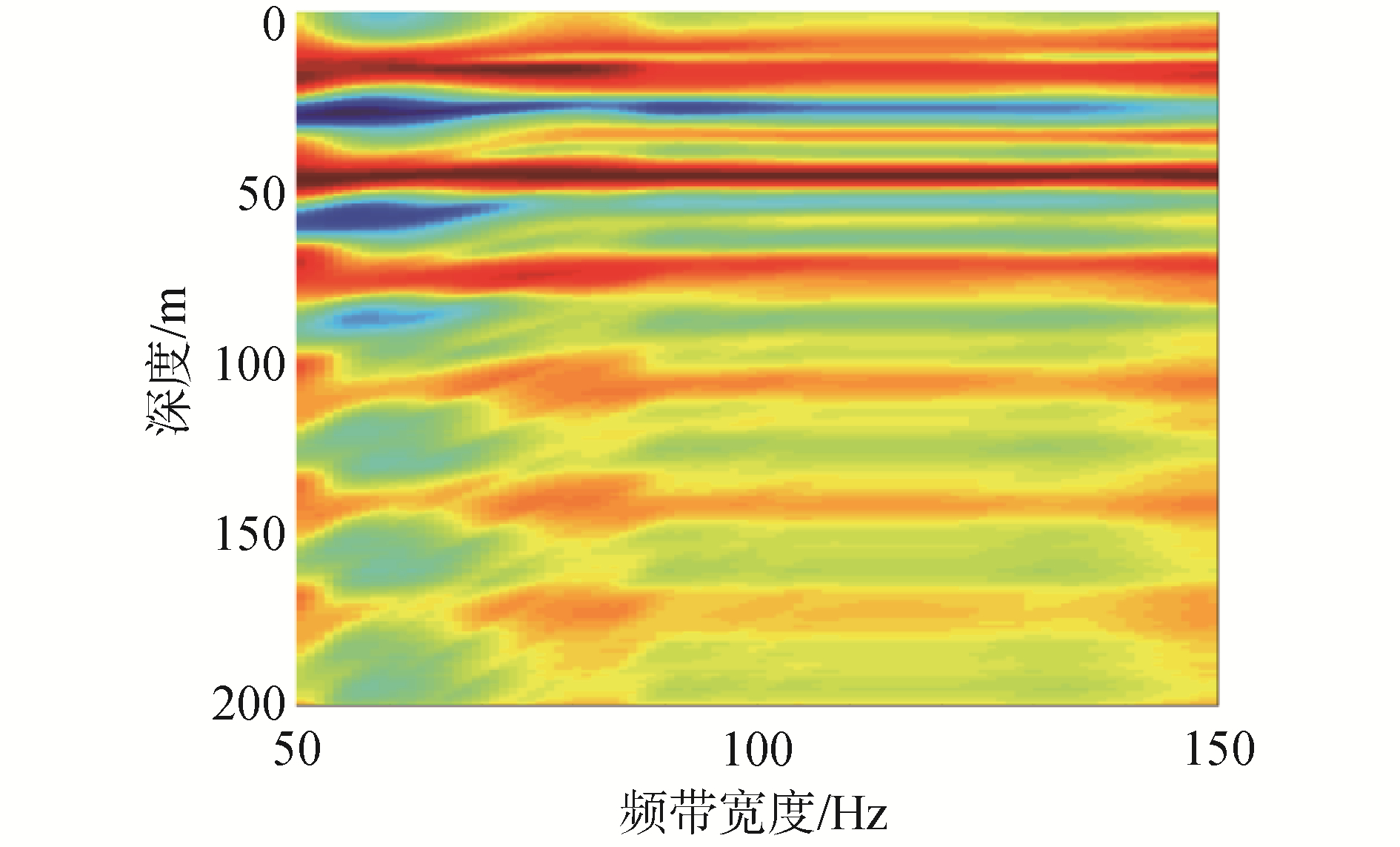
下限频率50 Hz,改变带宽,仿真了不同带宽下的深度估计模糊度面,如图 15所示,此时声源真实深度50 m,水平阵距离6 km,输入信噪比0 dB,采用方法三构建测量场的到达结构,可以看出,当处理带宽小于90 Hz时,深度估计受海面处旁瓣的干扰严重,难以准确估计真实的声源深度;处理带宽大于90 Hz时,可以从深度估计模糊度面提取出真实的声源深度。
|
Download:
|
| 图 15 不同带宽下的深度估计模糊度面 Fig. 15 Ambiguity surface of depth estimation under different bandwidth | |
1) 基于水平阵估计深海海底反射区声源深度的匹配到达结构方法的适用距离为6倍海深;
2) 当信噪比高于-5dB时,拷贝场与测量场的匹配程度较好;信噪比越低,深度估计所需的基阵孔径越大;
3) 当处理带宽过小时,深度估计模糊度面受到海面处旁瓣的干扰严重,难以准确估计真实的声源深度。
| [1] |
MCCARGAR R K, ZURK L M. Depth-based suppression of moving interference with vertical line arrays in the deep ocean[J]. The journal of the acoustical society of America, 2012, 132(3): 2081. (  0) 0)
|
| [2] |
MCCARGAR R K, ZURK L M. Depth-based signal separation with vertical line arrays in the deep ocean[J]. The journal of the acoustical society of America, 2013, 133(4): EL320-EL325. DOI:10.1121/1.4795241 (  0) 0)
|
| [3] |
ZURK L M, BOYLE J K, SHIBLEY J. Depth-based passive tracking of submerged sources in the deep ocean using a vertical line array[C]//2013 Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, USA, 2013: 2130-2132.
(  0) 0)
|
| [4] |
KNIFFIN G P, BOYLE J K, ZURK L M, et al. Performance metrics for depth-based signal separation using deep vertical line arrays[J]. The journal of the acoustical society of America, 2016, 139(1): 418-425. DOI:10.1121/1.4939740 (  0) 0)
|
| [5] |
YANG Kunde, XU Liya, YANG Qiulong, et al. Striation-based source depth estimation with a vertical line array in the deep ocean[J]. The journal of the acoustical society of America, 2018, 143(1): EL8-EL12. DOI:10.1121/1.5020267 (  0) 0)
|
| [6] |
DUAN Rui, YANG Kunde, LI Hui, et al. A performance study of acoustic interference structure applications on source depth estimation in deep water[J]. The journal of the acoustical society of America, 2019, 145(2): 903-916. DOI:10.1121/1.5091100 (  0) 0)
|
| [7] |
王梦圆, 李整林, 秦继兴, 等. 深海直达声区水下声源距离深度联合估计[J]. 信号处理, 2019, 35(9): 1535-1543. WANG Mengyuan, LI Zhenglin, QIN Jixing, et al. Combined estimation of range and depth for underwater source in the direct zone in deep water[J]. Journal of signal processing, 2019, 35(9): 1535-1543. (  0) 0)
|
| [8] |
杨刚, 韩树平. 一种深海垂直阵目标深度估计方法[C]//2015中国西部声学学术交流会论文集. 雅安, 中国, 2015: 42-44. YANG Gang, HAN Shuping. A target depth estimation method with VLA in the deep ocean[C]//2015 Western Acoustic Academic Exchange Meeting. Yaan, China, 2015: 42-44. (  0) 0)
|
| [9] |
刘炎堃, 郭永刚, 李整林, 等. 基于路径选择的深海水下运动目标被动深度估计[J]. 应用声学, 2020, 39(5): 647-655. LIU Yankun, GUO Yonggang, LI Zhenglin, et al. Depth estimation of moving underwater source based on routes choosing[J]. Applied acoustics, 2020, 39(5): 647-655. (  0) 0)
|
| [10] |
BREKHOVSKIKH L M, LYSANOV Y P. Fundamentals of ocean acoustics[M]. New York: Springer-Verlag, 1991.
(  0) 0)
|
| [11] |
JENSEN F B, KUPERMAN W A, PORTER M B, et al. Computational ocean acoustics[M]. New York: American Institute of Physics Press, 1994.
(  0) 0)
|
| [12] |
CREAMER D B. Scintillating shallow-water waveguides[J]. The journal of the acoustical society of America, 1996, 99(5): 2825-2838. DOI:10.1121/1.414817 (  0) 0)
|
| [13] |
PREMUS V. Modal scintillation index: a physics-based statistic for acoustic source depth discrimination[J]. The journal of the acoustical society of America, 1999, 105(4): 2170-2180. DOI:10.1121/1.426821 (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


