2. 中国航天科技工业集团南京晨光集团, 江苏 南京 210001
2. China Aerospace Science & Industry Nanjing Chenguang Group, Nanjing 210001, China
随着世界对自然资源的逐渐开发以及陆地资源的逐渐匮乏,海洋石油和天然气资源的开采比例不断增加, 海底管道运输是当前海洋油气运输的主要方式,这种运输方式在效率,经济性和可靠性方面具有明显的优势[1-2]。与刚性管道相比,柔性管道具有显著的优点,因此也越来越广泛地应用在钻井立管、生产立管、出口立管和修井立管方面[3]。随着油田的开发正在进入更深的水域,柔性管道铺设的主要应用场合将转变为深海领域,亦将面临更大的挑战[4]。
由于柔性管道的广泛应用,出现了专门铺设柔性管道的Flex-lay铺设方式,将柔性管道储存在船舶的卷筒当中,并在施工海域将管道下放到海水中[5-6]。软管铺设法相比于其他管道铺设方法,铺设水深范围更广泛,铺设效率更高。作为铺设系统设计的重要指标,管道的动态张力直接决定了管道铺设系统工作载荷的大小。在进行管道铺设的过程中,管道的动态张力会受到海洋环境载荷、船舶运动等因素的影响[7]。
在以往针对管道铺设过程的研究中主要包括静态和动态分析。静态分析是对一些极限环境条件下的铺管作业的特定状态进行管道曲率、形状、应力/应变的计算分析。Konuk[8]以弹性杆理论为基础,利用摄动法推导了海底管道的静力平衡公式,以求解海底管道的非线性问题。Lenci[9]对J-lay铺设的问题进行了简化,并与经典的悬链线算法进行了比对证明了其算法在深水和超深水安装的适用性。Brownn[10]应用悬链线理论并忽略管道的刚度对S-Lay铺设的管道形态和受力进行求解。
动态分析是在静态分析的基础上,引进波浪载荷和环境载荷对于铺管船产生的运动响应,分析柔性管道在动态下的应力变化。Brewer等[11]分析了深海铺设状态下的管道张力敏感性,通过对管道的铺设系统进行分析实现了恒张力铺设。Santillan等[12]考虑了立管平台运动对于管道的影响,引入柔性管道的振动敏感性问题,建立了平衡方程并进行解析求解,得到提高立管浮力可减小管道的轴向力的结果,并通过模拟实验验证了这一结论。Hong[13]基于质量流动原理提出了建立细长型海洋装备物模型的方法,使用绝对节点公式分析海底管道这种大位移,大转角结构,建立了基于达朗贝尔原理的系统控制方程。Gong等[14-15]利用Orcaflex软件建立了深水S-lay系统铺设过程的耦合模型,并分别对耦合模型中船舶的运动以及管道的动态张力进行了研究。Wang[16]等以小变形理论为基础,建立了海底管汇安装的理论模型,研究了海底管汇安装过程中不同安装阶段管汇的动态张力。
在以往海底管道铺设问题的研究中,大多数都是针对铺设刚性管道的S型铺设方法和J型铺设方法,而少有针对柔性管道的铺设过程进行动态张力分析的研究。因此本文以柔性管道作为研究对象,评估深水软管铺设作业中柔性管道的动态张力响应。本文建立了考虑船舶运动、海洋环境载荷以及管道动态模型等因素的柔性管道铺设的耦合模型。采用悬链线理论结合管道受到的莫里森水动力方程确定管道的静态张力及水下形态,利用ANSYS-AQWA软件以“海洋工程201”为分析对象确定了铺管船的相关参数,应用Orcaflex软件对四级海况下25.4 cm柔性管道在3 000 m水深条件下的铺设过程中管道的动态张力进行了分析,最后对海洋环境各因素对管道动态张力的影响进行了讨论。
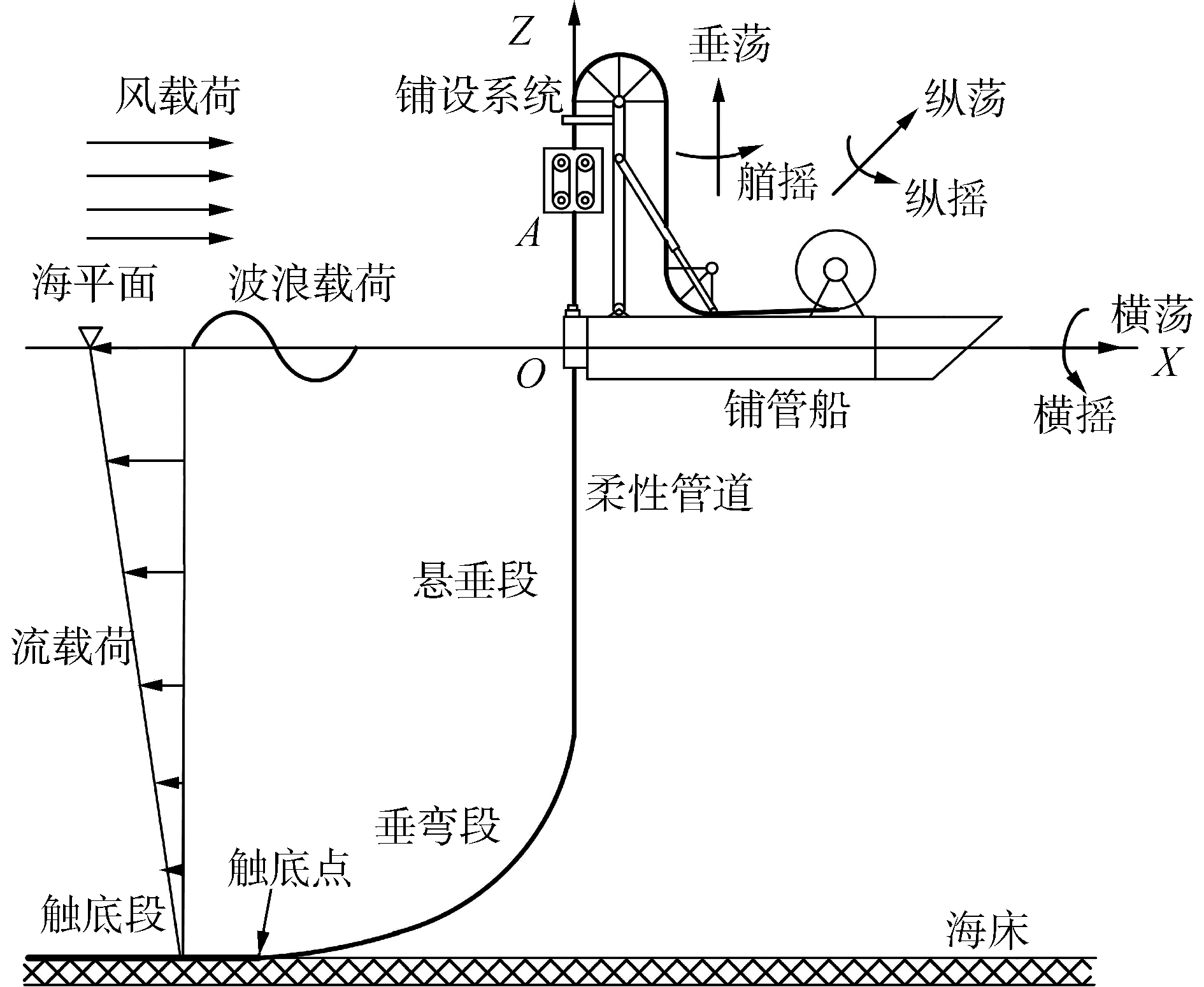
1 耦合模型的建立在柔性管道铺设过程中,柔性管道、作业船、铺设系统及海洋之间会构成一个广义的铺设系统,如图 1所示。柔性管道从滚筒释放经过软管铺设系统调整管道的入水方向,并由铺设系统中的张紧器夹持进入水中。在海洋环境载荷和铺管船运动的共同作用下,柔性软管离开张紧器至海底的曲线形态如图 1所示,从水面至海底可分为悬垂段、垂弯段以及触底段3个部分,此时管道形态由张紧力、管道线密度和入水角度决定。作为铺设装备设计的重要指标,图中管道在A点处的张力大小直接决定了管道铺设系统工作载荷的大小。因此对海洋环境载荷作用下A点处管道张力的变化情况及其影响因素进行研究,对软管铺设系统以及柔性管道的设计具有重大的意义。
|
Download:
|
| 图 1 柔性管道铺设 Fig. 1 Schematic diagram of flex-lay pipeline installation | |
在实际的工程中,将管道安全放置在海底的铺设过程十分复杂,管道受水深、水流、波浪等多种因素影响,加之在海洋环境下船舶不规则运动的影响,难以对管道动态张力准确估计,因此,考虑工程应用,为简化柔性管道铺设分析的模型,提出如下假设:
1) 假设模型中的海洋环境载荷为理想载荷,并将海床简化为具有一定刚度的水平海床,海流在船舶中纵剖面上线性分布,海床流速为0,海面流速为最大值;
2) 柔性管道在随机环境载荷作用下的扭转变形很小,因此在动力学分析过程中忽略柔性管道的扭转形变,同时忽略软管铺设塔系统与柔性管道接触位置对管道弯曲刚度的影响;
3) 将多层结构的柔性管道假定为材料均匀,各向同性的连续管道,管道铺设过程中柔性管道内部中空。
1.2 海洋环境载荷 1.2.1 风载荷海洋环境中海风主要作用在水面上的船舶以及各种浮式建筑之上,船舶所受的风载荷可以按照国际石油公司海洋论坛在超大型船舶的风和流载荷预测:
| $ \left\{\begin{array}{l} X_{\text {wind }}=0.5 \rho_{a} A_{f} U_{R}^{2} C_{w x} \\ Y_{\text {wind }}=0.5 \rho_{a} A_{s} U_{R}^{2} C_{w y} \\ N_{\text {wind }}=0.5 \rho_{a} A_{s} L_{B P} U_{R}{ }^{2} C_{u n} \end{array}\right. $ | (1) |
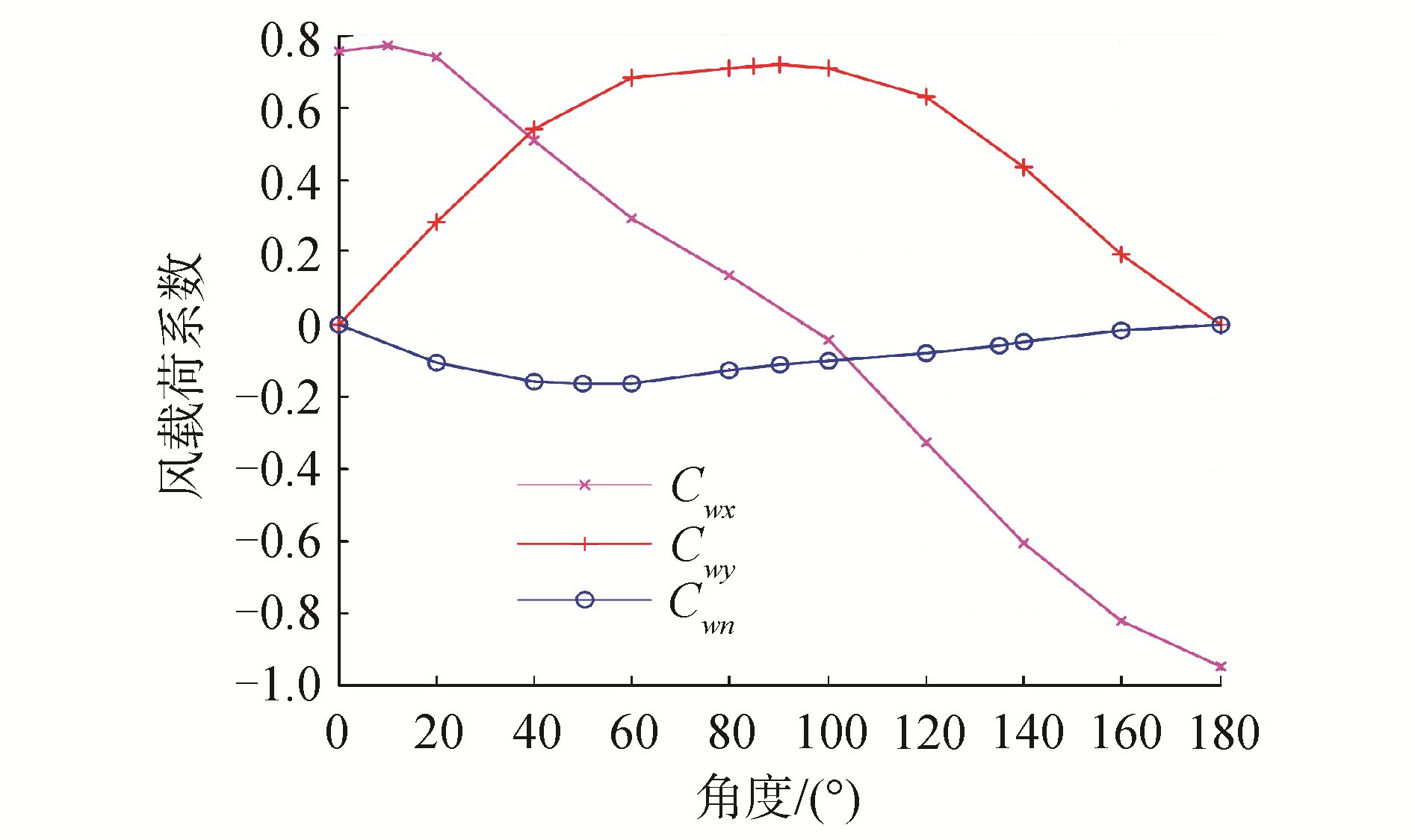
式中:Xwind、Ywind分别表示沿X、Y方向的风载荷;Nwind表示OZ轴的风载荷力矩;ρa空气密度;Af水面以上船舶侧投影面积;As水面以上船舶正投影面积;UR表示平均风速;LBP船舶垂线间长,Cwx、Cwy、Cwn分别表示沿X、Y、Z方向的风压力系数。其中风压力系数来源于1960年在密歇根大学进行的船体模型风洞试验。在满载情况下,船舶风压力系数的图谱如图 2所示。
|
Download:
|
| 图 2 风压力系数 Fig. 2 Wind pressure coefficient | |
因此,铺管船受到的风力载荷可以表示为
| $ \boldsymbol{f}_{w}(t)=\left[\begin{array}{llllll} X_{\text {wind }} & Y_{\text {wind }} & 0 & 0 & 0 & N_{\text {wind }} \end{array}\right]^{\mathrm{T}} $ | (2) |
在流载荷的作用下,船体以及管道将会承受流曳力和力矩,对管道铺设作业有十分重要的影响。船舶流载荷的计算同样可以按照国际石油公司海洋论坛中给出的公式计算:
| $ \left\{\begin{array}{l} X_{c}=0.5 \rho_{c} L_{B P} D U_{c}^{2} C_{c x} \\ Y_{c}=0.5 \rho_{c} L_{B P} D U_{c}^{2} C_{c y} \\ N_{c}=0.5 \rho_{c} L_{B P}^{2} D U_{c}^{2} C_{c n} \end{array}\right. $ | (3) |
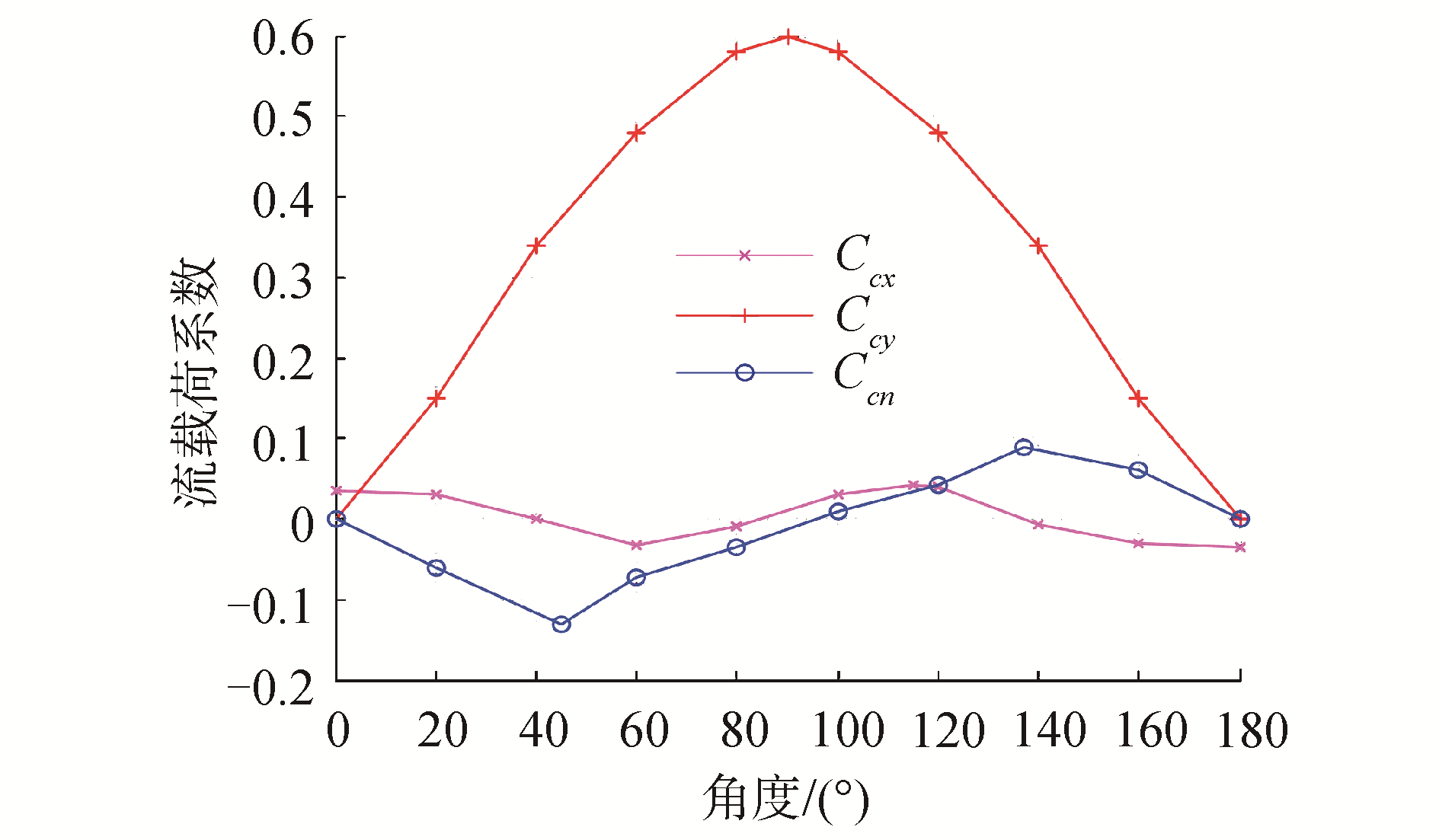
式中:Xc、Yc分别为X、Y方向的流载荷;Nc为OZ轴的流载荷力矩;ρc为海水密度;D为船舶吃水深度;Uc为平均流速;Ccx、Ccy、Ccn分别为沿X、Y、OZ方向的流曳力系数。船舶的流曳力系数可以根据OCIMF给出的图谱数据读谱得到,流曳力系数图谱如图 3所示。
|
Download:
|
| 图 3 流曳力系数 Fig. 3 Flow drag coefficient | |
因此,铺管船受到的流载荷可以表示为
| $ \boldsymbol{f}_{c}(t)=\left[\begin{array}{llllll} X_{c} & Y_{c} & 0 & 0 & 0 & N_{c} \end{array}\right]^{\mathrm{T}} $ | (4) |
一般来说,海浪的特征是统计数字,包括海浪的高度、周期和功率谱。在管道铺设过程中,由于波浪载荷的数学模型很难被建立,因此在工程中通常采用采用JONSWAP波浪谱来计算波浪载荷[17]。JONSWAP谱是由美国、荷兰、英国、德国等在1965年~1970年于“北海联合波浪项目”[18]中测量分析提出的,波浪谱公式由波浪有义高和波浪谱峰周期表示:
| $ S_{\varsigma}(\omega)=319.34 \frac{\bar{\varsigma}_{W / 3}^{2}}{T_{p}^{4} \omega^{5}}\left\{-\frac{1\ 948}{\left(T_{p} \omega\right)^{4}}\right\} 3.3^{\exp \left[-\frac{\left(0.159 \omega T_{p}-1\right)^{2}}{2 \sigma^{2}}\right]} $ | (5) |
式中Tp为谱峰周期,即海浪谱中最大谱值所对应的周期。
1.3 铺管船运动铺管船在进行海底管道铺设的过程中,会产生6个自由度的运动,包括3个平动横荡、纵荡、垂荡,和3个转动横摇、纵摇、艏摇。通常而言,铺管船的运动可由上述6个自由度对应的幅值响应算子(RAOs)确定[19]。每个位移的RAO由一组数字组成,这些数字定义了船舶在一个特定的波方向和周期内对一个特定自由度的响应。因此得到了铺管船的RAOs值,既可以求得船舶在不同波浪作用下对应的运动。
“海洋石油201”号是我国首艘可以在3 000 m深进行作业的深水管道铺设作业起重船,主要用于“S”型管道铺设作业,在改装后也可完成柔性管道铺设作业任务[20]。在本文研究中使用此船作为母型船进行分析,船舶参数如表 1所示。
| 表 1 船舶参数 Table 1 Vessel parameters |
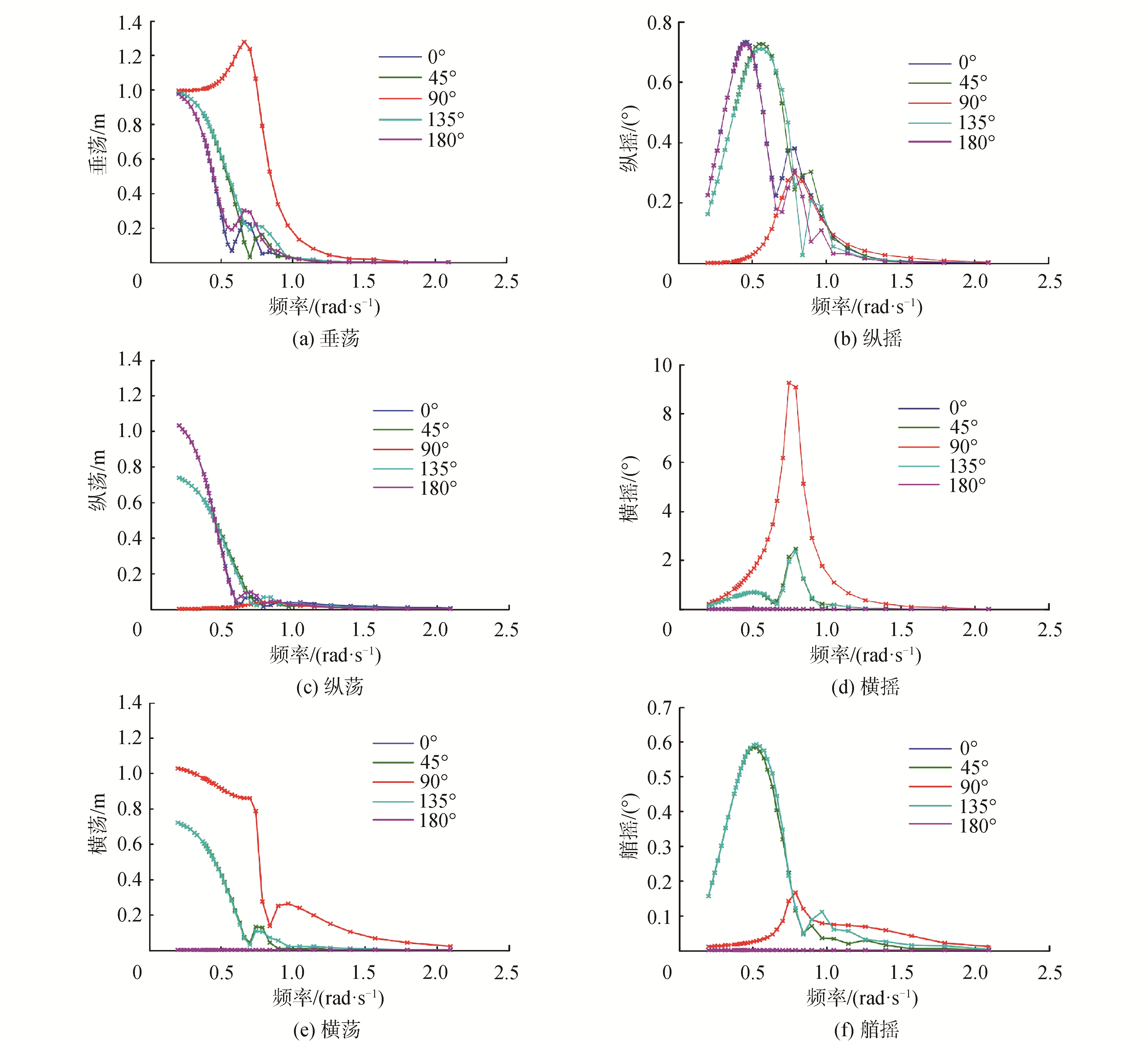
通过有限元软件AQWA建立“海洋工程201”的水动力模型,并对模型进行计算即得到了响应振幅算子(RAOs)的响应谱,在波浪条件下,船舶几乎所有响应都非常显著,尤其横摇最为剧烈。由图 4中可以看出,波浪角度0°与180°、45°与135°时,船舶的运动响应曲线基本重合,说明母型船沿剖面的对称性比较好,纵摇与纵荡在0°与180°浪角时响应较大,而在3个方向90°浪角的影响比较巨大。
|
Download:
|
| 图 4 船舶RAOs响应 Fig. 4 Vessel RAOs response | |
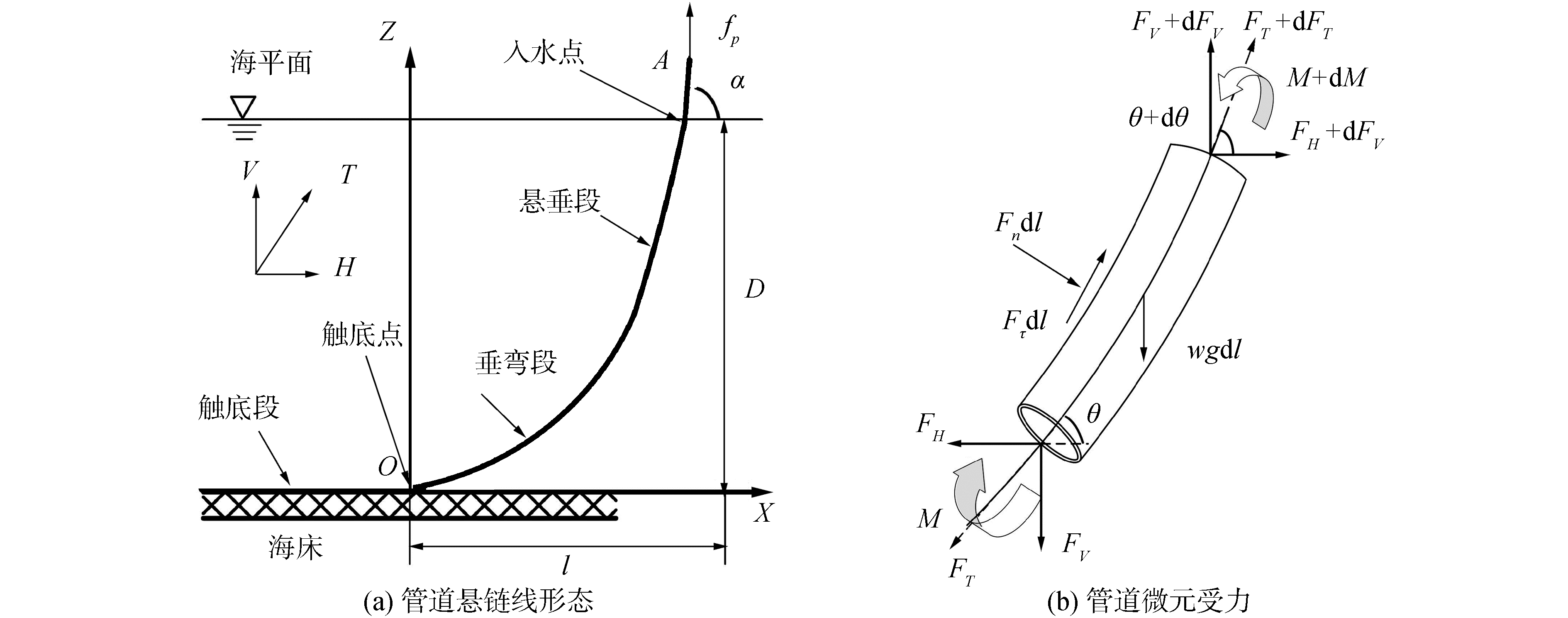
柔性管道相比于传统的刚性管道相比,具有更加复杂的结构,柔性管道制造时一般采用层状结构,由数层结构和功能都各异的材料组成[21]。在进行动态分析的过程中将柔性管道假设为均匀、连续、各向同性的单层管道。当铺管进行一段时间后,位于海洋中的管道状态可以表示为图 5(a)所示的悬链线状态。模型原点O建立在管道的触地点,x轴表示水平方向,z轴表示竖直方向,α代表管道铺设入水角度。
|
Download:
|
| 图 5 管道分析模型 Fig. 5 Pipeline analysis model | |
在忽略管道与船舶相互作用的情况下,此时管道的张力主要2部分组城,一部分为水下管道的湿重,由于柔性管道的抗弯刚度较小,选用悬链线模型计算的结果与真实结果较为接近,因此可以通过静态自然悬链线算法求得,悬链线理论基本控制方程为:
| $ z^{\prime \prime}(x)=\delta \sqrt{1+\left[z^{\prime}(x)\right]^{2}} $ | (6) |
式中:δ=w/H,其中w表示管道的湿重,H表示管道张力恒定的水平分量。由悬链线理论可以求得任意位置的管道微元张力:
| $ F_{T}(x)=\frac{w}{\delta} \operatorname{ch}(\delta x) $ | (7) |
另一部分为管道所受的水动力载荷,来自作用于管道上的流体动力学内线力,适用于使管道保持垂直和静止的加速流体环境可通过半经验的Morison方程获得:
| $ F_{\text {morison }}=0.5 \rho_{w} C_{d} D \boldsymbol{u}|\boldsymbol{u}|+\rho_{w} C_{w} A \dot{\boldsymbol{u}}+\rho_{w} A \dot{\boldsymbol{u}} $ | (8) |
式中:ρw表示水的密度;D为管道外径;A表示管道横截面积;u表示水流速度;Cd表示阻力系数;Cw表示表面粗糙度比。当进行管道铺设时,海洋环境载荷作用在单位长度的管道上时,可将上式分解成为海洋中单位管道在法向和切向受海流的拖曳力Fn和Fτ:
| $ F_{n}=0.5 \rho_{w} C_{n} D_{1}(v \sin \theta)^{2} $ | (9) |
| $ F_{\tau}=0.5 \rho_{w} C_{\tau} D_{1}(v \cos \theta)^{2} $ | (10) |
式中:Cn为法向拖曳力系数;v表示微分管道单元所在水平面的海流速度;θ表示微分管道单元与水平方向的夹角;Cτ切向拖曳力系数。因此管道任意段管道的微分单元受力可以表示为如图 5(b)所示,由此应用迭代法即可求得A点处的管道在受到海洋环境载荷作用下的实时张力。
综上所述,管道的动态张力fp(t)可以表示为:
| $ \boldsymbol{f}_{p}(t)=\boldsymbol{F}_{T}+\boldsymbol{F}_{\text {morison }} $ | (11) |
基于柔性管道铺设系统的坐标系,应用牛顿第二定律,可得到柔性管道铺设过程中,考虑铺管船运动,海洋环境以及柔性管道的动态耦合方程,其表达式可以表示为:
| $ \boldsymbol{M} \ddot{\boldsymbol{X}}(t)+\boldsymbol{C X}(t)=\boldsymbol{f}_{\mathrm{rad}}(t)+\boldsymbol{f}_{\text {wave }}(t)+\boldsymbol{f}_{c}(t)+\boldsymbol{f}_{p}(t) $ | (12) |
式中:M代表船舶惯性矩阵;C代表船舶静水刚度矩阵;X(t)代表船舶运动的位移矩阵。frad(t)代表由船舶运动引起的流体动量变化产生的辐射力;fwave(t)和fc(t)分别表示作用在铺管船上的波浪载荷和流载荷;fp(t)表示管道脱离张紧器位置的张力。
与此同时,由于船舶的运动将引起周边流体动量的变化,因而将产生流体的辐射力。应用势能理论可以得到[22]:
| $ \boldsymbol{f}_{\mathrm{rad}}(t)=-\boldsymbol{A}(\infty) \ddot{\boldsymbol{x}}(t)-\int_{0}^{t} \boldsymbol{K}(t-\tau) \dot{\boldsymbol{x}}(\tau) \mathrm{d} \tau $ | (13) |
式中:A(∞)表示无穷频率的船舶附加质量,等式右边的第2项表示流体记忆,它以自由表面辐射波的形式捕捉由船舶运动产生的流体能量的传递。卷积项K(t)表示延迟或记忆功能的矩阵,它代表了流体记忆效应,它包含了由船舶运动产生的辐射波引起的能量耗散。
当船舶在频域内不考虑其他载荷时,其运动形式可以表示为:
| $ \left\{-\omega^{2}[\boldsymbol{M}+\boldsymbol{A}(\omega)]+\mathrm{j} \omega \boldsymbol{B}(\omega)+\boldsymbol{C}\right\} \boldsymbol{X}(\mathrm{j} \omega)=\boldsymbol{F}_{\text {wave }}(\mathrm{j} \omega) $ | (14) |
式中:A(ω)和B(ω)分别表示阻尼矩阵的频率和附加质量;X(jω)表示船舶在波激励下的运动幅值和相位;Fwave(jω)表示由波浪引起的线性力。用傅里叶变换定义将A(ω)和B(ω)定义为:
| $ \boldsymbol{A}(\boldsymbol{\omega})=\boldsymbol{A}(\infty)-\frac{1}{\omega} \int_{0}^{\infty} \boldsymbol{K}(t) \sin (\omega t) \mathrm{d} t $ | (15) |
| $ \boldsymbol{B}({\omega})=\int_{0}^{\infty} \boldsymbol{K}(t) \cos (\omega t) \mathrm{d} t $ | (16) |
通过傅里叶变换可以将K(t)和K(jω)用A(ω)和B(ω)的形式表示:
| $ \boldsymbol{K}(t)=\frac{2}{{\rm{ \mathsf{ π} }}} \int_{0}^{\infty} \boldsymbol{B}(\omega) \cos (\omega t) \mathrm{d} \omega $ | (17) |
| $ \boldsymbol{K}(\mathrm{j} \omega)=\int_{0}^{\infty} \boldsymbol{K}(t) \mathrm{e}^{-\mathrm{j} \omega t} \mathrm{~d} t=\boldsymbol{B}(\omega)+\mathrm{j} \omega[\boldsymbol{A}(\omega)-\boldsymbol{A}(\infty)] $ | (18) |
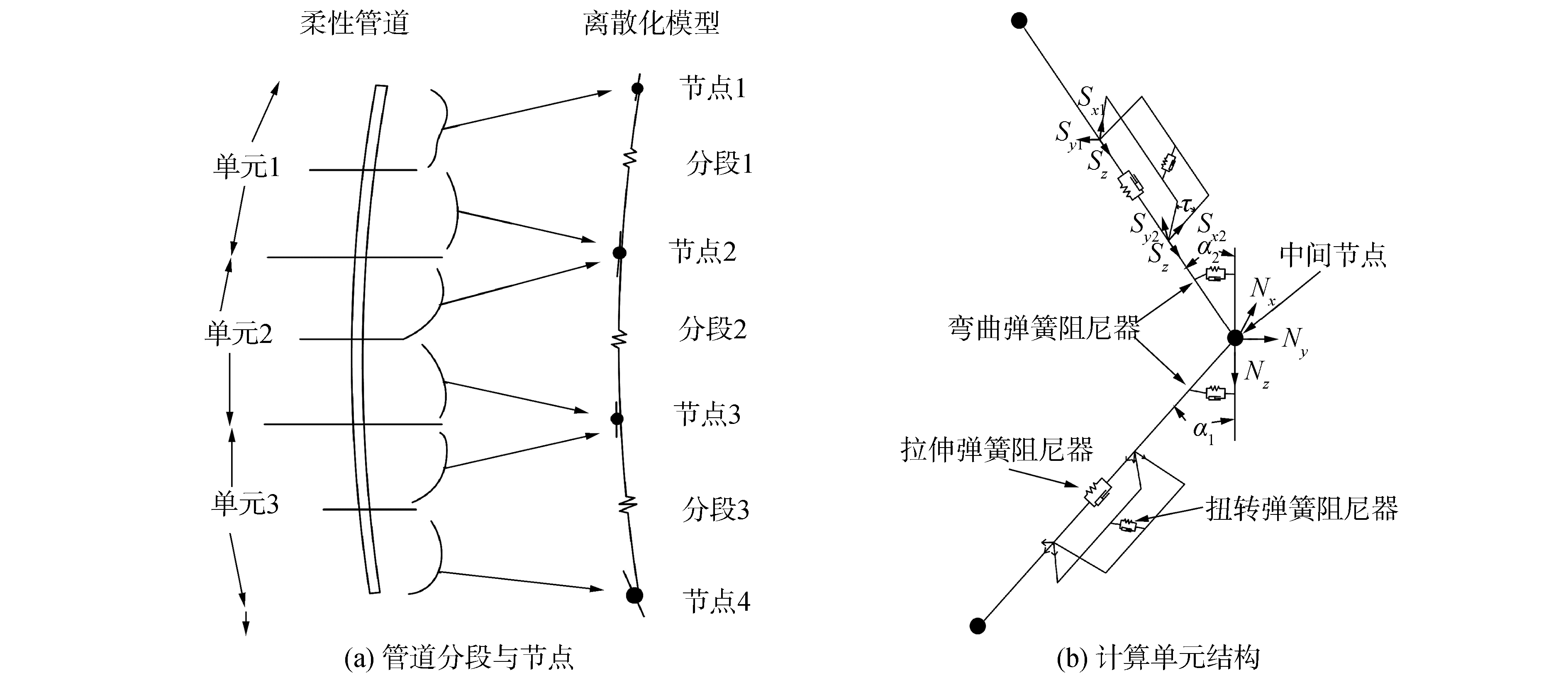
在动态计算的过程中需要对对柔性管道进行离散化处理,如图 6所示,将连续的柔性管道离散为管道微元,将管道的质量均匀分布到每个节点上,并通过管道单元中的拉伸弹簧+阻尼器和扭转弹簧+阻尼器模拟柔性管的轴向拉伸和扭转特性。因此在进行有限元计算时,只需将管道参数进行赋值即可得到所需的响应。
|
Download:
|
| 图 6 管道计算模型 Fig. 6 Pipeline calculation model | |
目前世界上主要的管道制造厂家是Technip、Wellstream以及Flexibles等公司,因此便是选取的Technip公司的管道作为预设对象,选取25.4 cm柔性管道。表 2是所选Technip公司生产的25.4 cm管道的性能参数,并且假定柔性管道铺设作业过程中柔性管内不注入填充物。
| 表 2 管道参数 Table 2 Pipeline parameters |
通常意义上,海底管道铺设作业的作业环境可以由海况来表示,按照国际标准可将海况区分为9个等级,海底管道铺设作业最少应能够满足在四级海况的条件下进行作业,因此假定此次分析的海况条件为四级海况,设定铺设水深为3 000 m,将管线铺设位置设置在船艉,设定铺设角度为90°,分析中不考虑船舶的航速,默认航速为0。除此之外,铺设中的柔性管道在接触到海床后会受到海床的反作用力,柔性管道所受的穿透阻力与管道沉入海床的深度成线性关系[22],线性比例系数为海床刚度Kn,因此设定数值模拟的海洋环境参数如表 3所示。
| 表 3 环境参数 Table 3 Environment parameters |
动态分析是对模型在指定时间段内的运动进行时间模拟,充分考虑各种复杂的非线性问题以及海洋环境、柔性管道以及铺管船之间的相互作用。为了给动态模拟提供一个启动配置,采用前文所述的管道模型进行静态分析,确定了深水柔性铺管系统的初始平衡位置。随后,并通过大量的试验分析选择了适当的时间步长。然后在每个时间步计算管道上的轴向张力变化以研究柔性管道铺设过程中管道的动态张力。
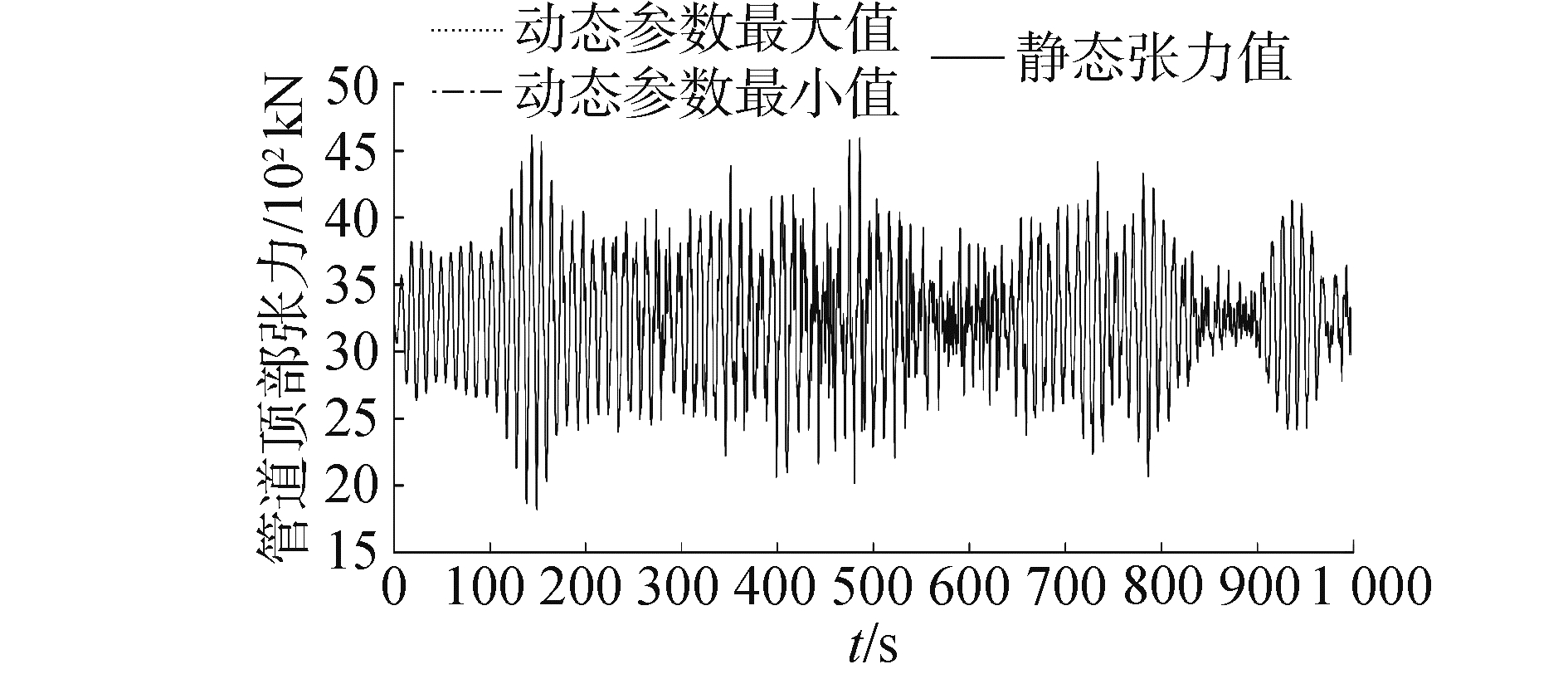
在上述条件下,应用Orcaflex软件对柔性管道的铺设过程进行数值分析,A点处管道拉力的时间历程如图 6所示,在145 s时,管道的动态最大张力为4 627 kN,比静态张力3 242 kN高42.7%,管道的最小动态张力为1 823 kN,比静态张力低43.7%。由此可以看出在进行柔性管道铺设的过程中,在海洋环境载荷以及船舶运动的共同作用下对管道的影响十分显著,因此,在设计的张紧力必须显著高于静态结果,在软管铺设系统的设计时需要充分考虑动态张力的变化情况。
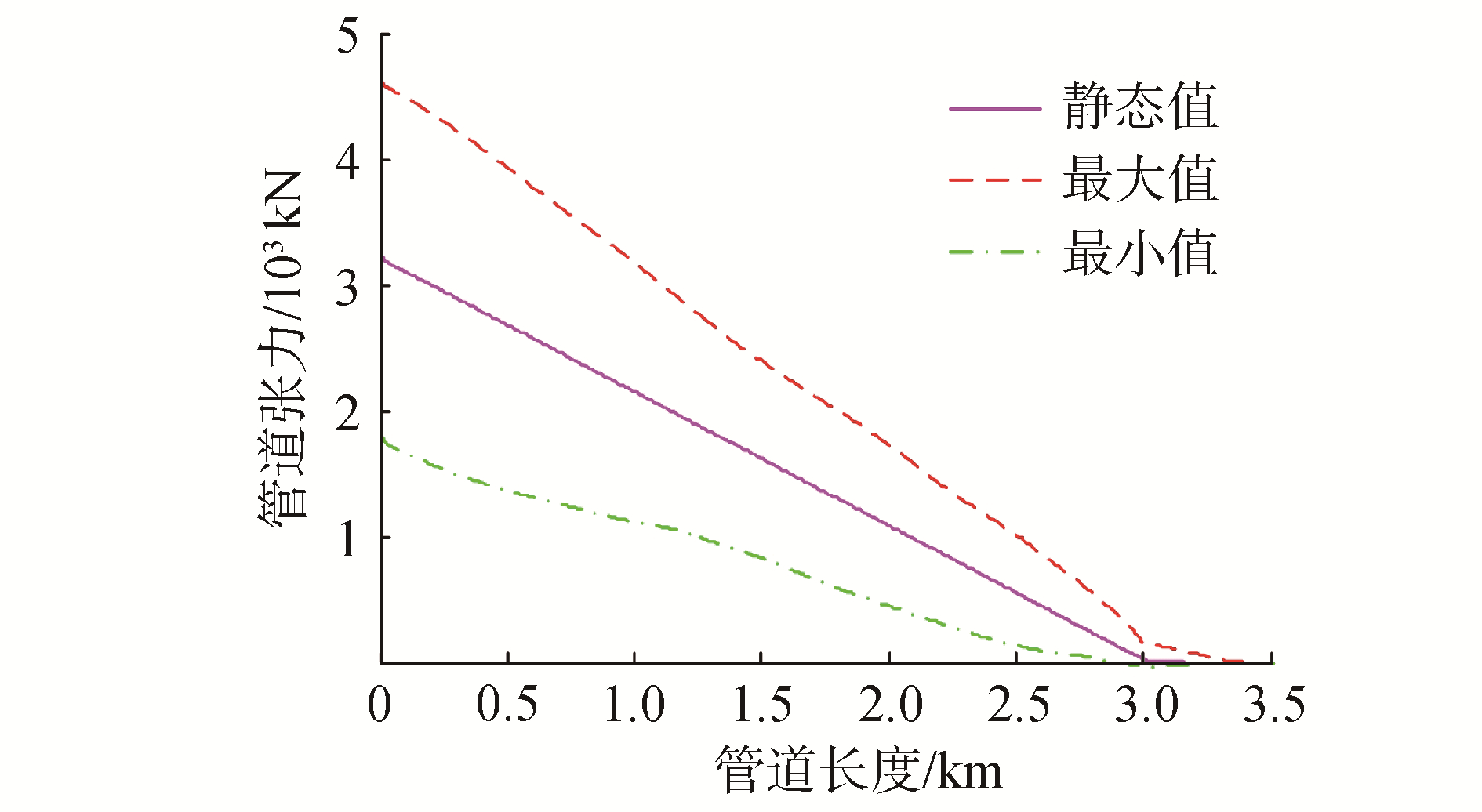
图 7为管道的轴向拉力的动态曲线,从图 7中可以看出,静轴向拉力与管道的最大和最小拉力存在显著差异,在管道与张紧器分离处管道的最大张力与最小张力差距最大,随着管道长度的不断增加,最大轴向拉力与最小轴向拉力的差值逐渐减小,直至触底点(touch down point, TDP)最大值、最小值和静态值重合。上述的结果表明,海洋环境以及船舶运动对管道动态张力存在明显的影响。
|
Download:
|
| 图 7 管线顶端张力与仿真时间的关系 Fig. 7 The relationship between the top tension of the pipeline and the time | |
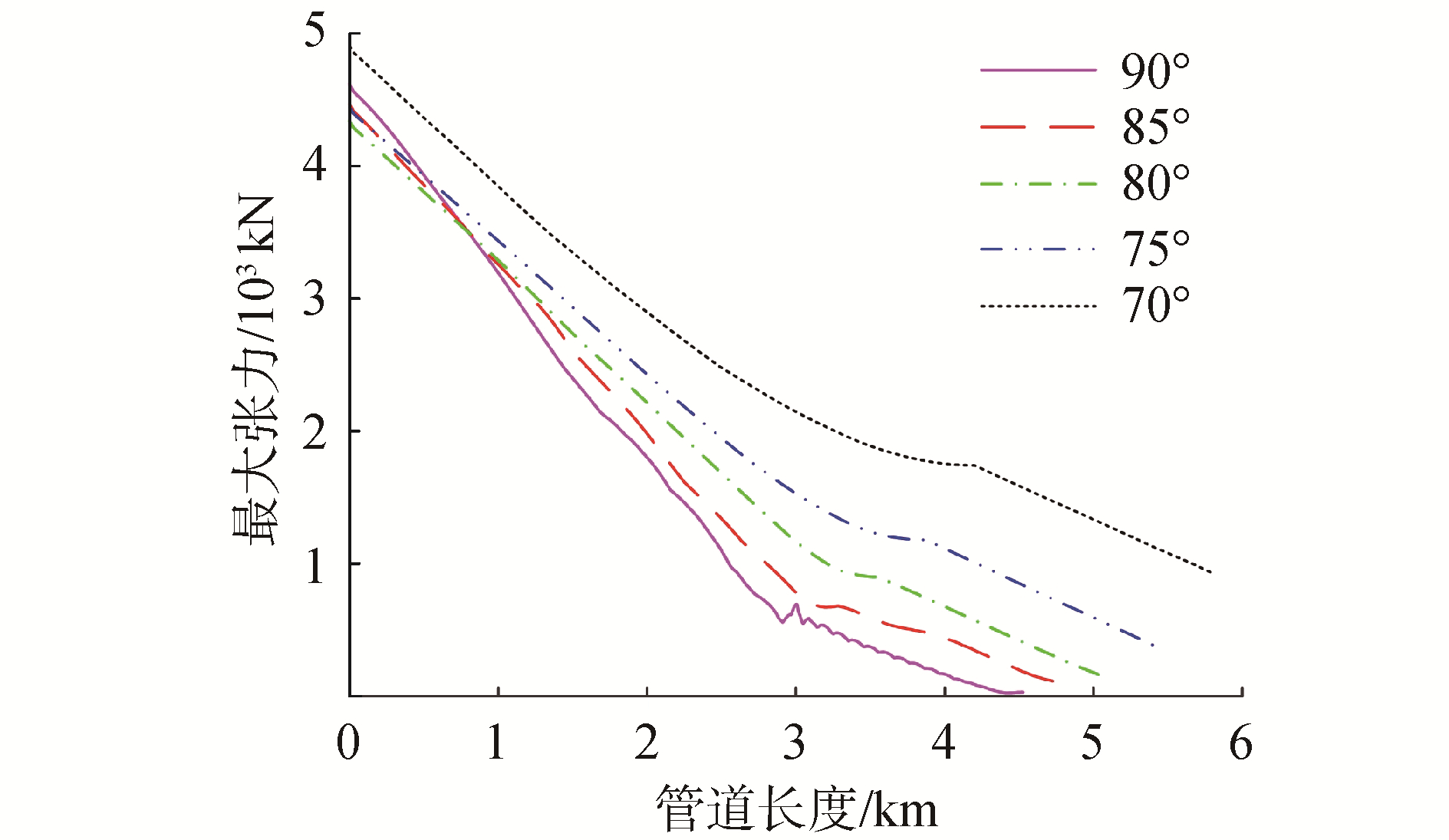
能够根据水深以及需求对铺设角度进行调整,是柔性管道铺设方式的一大优势。因此本文选取前文所述的条件下,对铺设角度分别为70°、75°、80°、85°、90°的情况了进行动态仿真,得到了不同角度条件下管线动态张力如图 8所示,相应的顶部最大张力以及放大系数数值如表 4所示。
|
Download:
|
| 图 8 管道动态张力 Fig. 8 Pipeline dynamic tension | |
| 表 4 不同铺设角度的管道动态张力 Table 4 Dynamic tension of pipes with different laying angles |
图 8可以看出,随着铺设角度的增大,管道弧长逐渐减小,管道触底段的最大张力随着铺设角度的增大逐渐减小,但管道顶端最大动态张力的数值并不能由铺设角度的变化决定。由表 4中数据可以看出,随着铺设角度的增大,柔性管道末端的静态张力逐渐减小,放大系数逐渐增加,说明随着铺设角度的增加,柔性管道的动态张力变化将逐渐增大。因此进行柔性管道铺设作业时,应根据实际情况选择对动态张力影响最小的铺设角度进行铺设。
3.2 铺设水深对动态张力的影响铺设水深也是进行管道铺设过程中一个重要的参考因素。因此选用前文的环境参数,分别设置1 000、1 500、2 000、2 500、3 000 m水深条件进行动态仿真,得到各水深下管道的动态最大张力如图 9所示,以及相应的顶部最大张力以及放大系数数值如表 5所示。
|
Download:
|
| 图 9 铺设角度对管道动力响应的影响 Fig. 9 Effect of laying angle on pipeline dynamic tension | |
| 表 5 不同水深的管道动态张力 Table 5 Dynamic tension of pipelines with different water depths |
由图 9可知,随着铺设作业水深增加,各曲线呈现出一致的趋势,但触底点附近的张力随着水深的增加出现了明显的扰动。由表 5中可以看出管道顶部最大张力,静态张力以及放大系数皆随着水深的增加而增大。这说明随着铺设水深的增加,波浪对于柔性管道的扰动程度越来越大。
3.3 波浪角度对动态张力的影响为了说明波浪方面对深水柔性管道铺设过程中管道的影响,特别规定了有效波高2.5 m,峰值周期为8 s的海况,并将波浪方向划分为0°、45°、90°、135°、180°这5个方向。分别对应船艉、1/4船艉、船宽、1/4船头、船头。利用Orcaflex软件对柔性管道在上述情况下的动态张力进行时域分析,得到管道的有效拉力结果如图 10所示,由图可知不同波浪方向,管道的轴向张力存在明显的差异。

|
Download:
|
| 图 10 水深对管道动力响应的影响 Fig. 10 Effect of water depth on pipeline dynamic tension | |
由图 10中可以看出,在波浪方向为90°的条件下,管道脱离张紧器处的最大轴向张力为4 826 kN,而在波浪方向为180°的条件下,管道脱离张紧器处的最大轴向张力为3 594 kN,2种海况下的差异为34.3%。仿真结果充分说明了波浪走向对管道动力响应有十分明显的影响, 其中90°波浪方向即船宽方向对管道影响最大,180°波浪方向即船首对管道铺设最为有利。
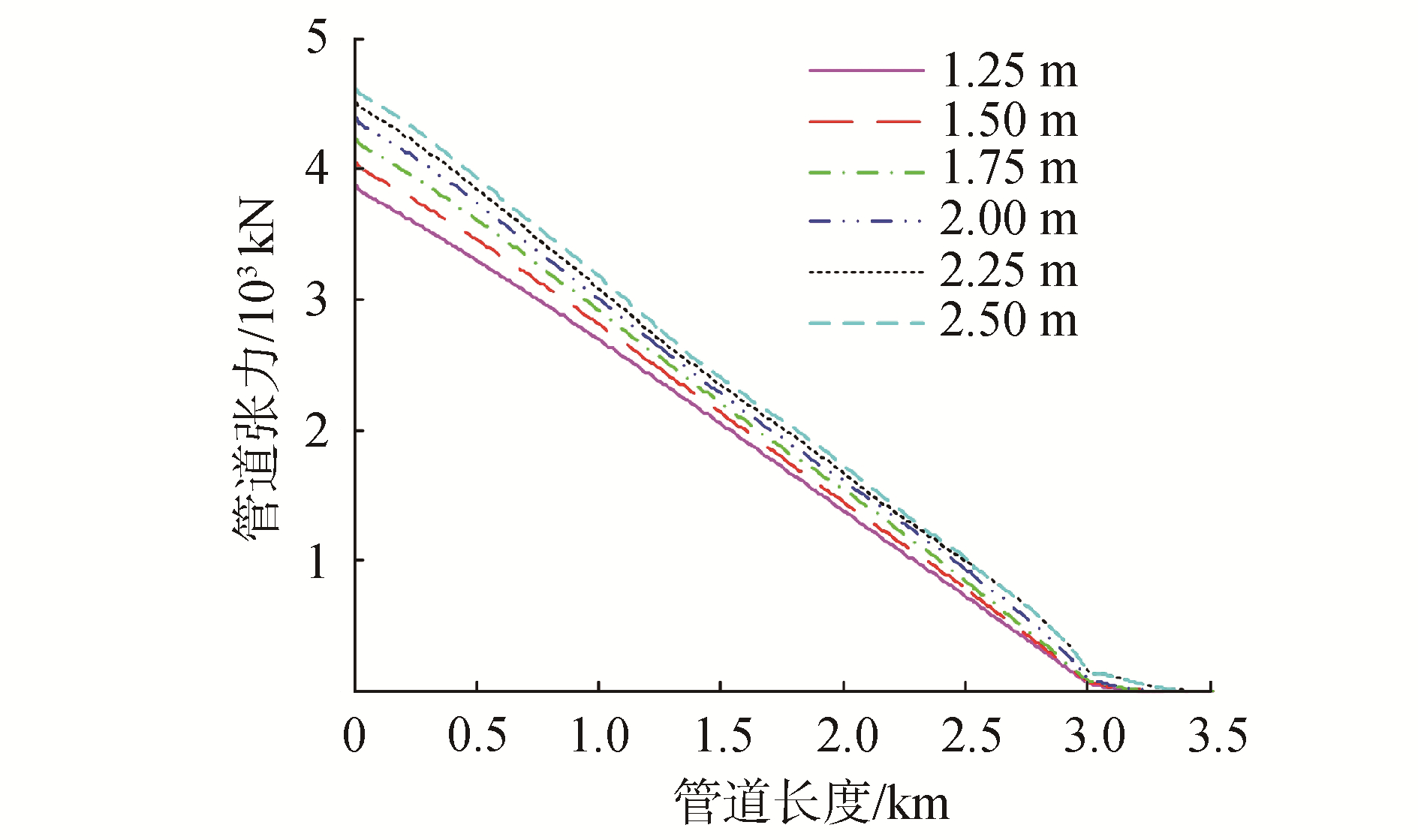
3.4 有义波高对动态张力的影响波高被认为是海底管道铺设过程中管道动态张力响应的另一个十分重要的因素,在波浪方向为0°,峰值周期为8 s的海况下,分别模拟1.25、1.50、1.75、2.00、2.25、2.50 m 6个波浪高度,对柔性管道在上述情况下的动态张力进行时域分析,得到管道的最大动态张力结果如图 11所示,由图可知在不同波浪高度下,管道的动态张力存在明显的差异。由图中可以看出,在波浪高度2.5 m的条件下,管道的最大轴向张力4 624 kN而在波浪高度为1.25 m的条件下,管道的最大轴向张力为3 883 kN,2种海况下的差异为19.1%此外,因此可以看出,管道的响应曲线随着波浪高度的增加而增大,且管道的响应曲线趋势几乎完全一致,由图 11中可以看出当有义波高不超过2 m时,弯矩,应力及应变的动态张力变化并不明显,而当波浪有义波高超过2 m后,对管道的动态张力则十分明显,因此当进行软管铺设作业的时候,应尽量避免波高高于2 m时的海况。

|
Download:
|
| 图 11 波浪方向对管道动力响应的影响 Fig. 11 Effect of wave heading on pipeline dynamic tension | |
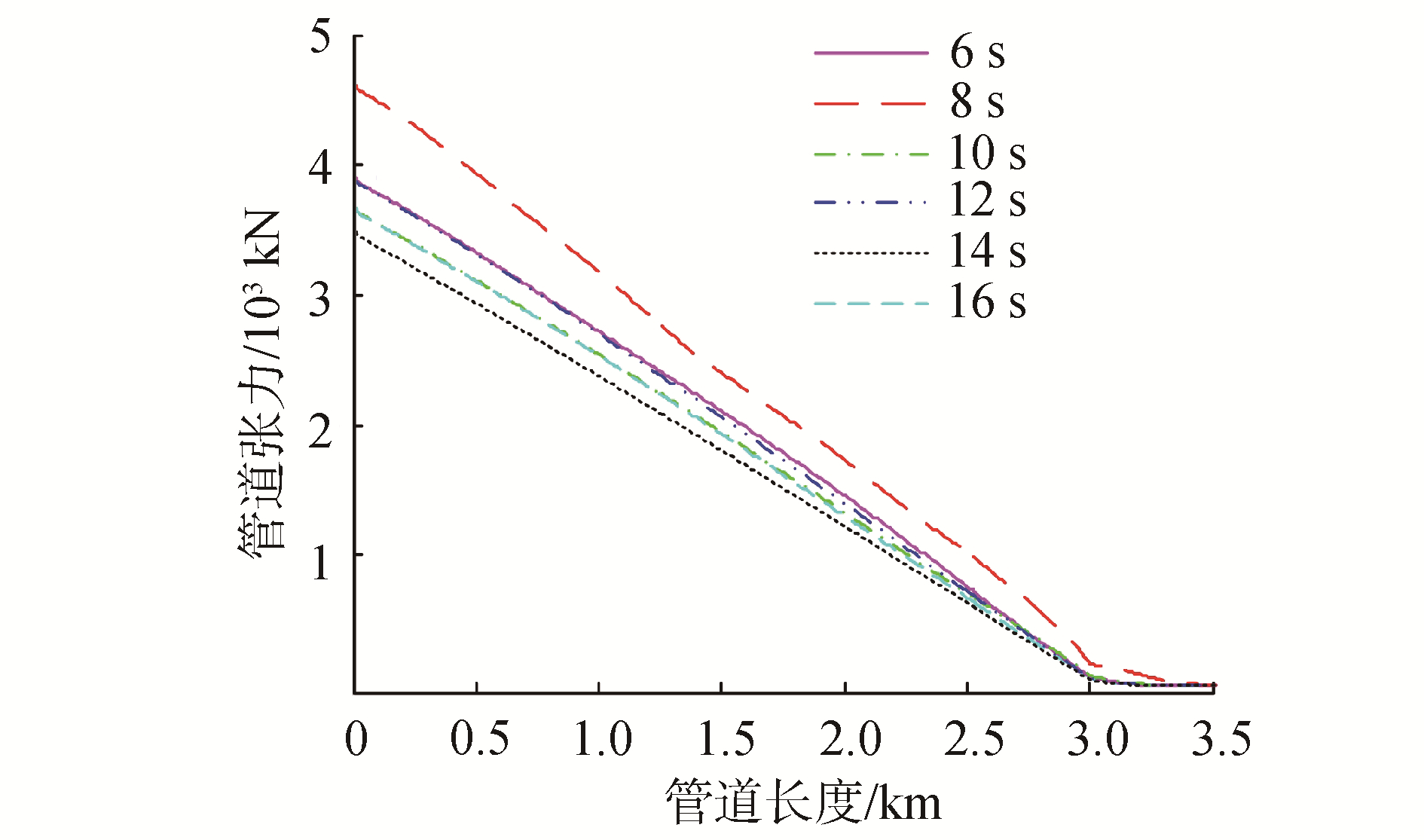
谱峰周期作为波浪载荷的一个十分重要的参数,将对深水柔性管道铺设过程中管道动态张力产生明显的影响,在波浪方向为0°,波高为2.5 m的海况下,分别选取6、8、10、12、14、16 s 6个周期进行时域分析,得到管道相关参数如图 12所示。由图 12可知,当谱峰周期为8 s时,对管道的动态张力影响最大。图 12(a)显示了不同谱峰周期下管道的最大轴向拉力,在管道与张紧器脱离位置,最大值为4 627 kN出现在8 s谱峰周期,最小值为3 502 kN出现在14 s谱峰周期,2种海况下的差异为32.1%。仿真结果说明了波浪谱峰周期对管道动态张力的影响,其中当谱峰周期为8 s时,对管道影响最大,除此之外,从图中可以得知,10 s和16 s与6 s和12 s谱峰周期的海浪对管道动态张力的影响几乎一致。
|
Download:
|
| 图 12 有义波高对管道动力响应的影响 Fig. 12 Effect of wave height on pipeline dynamic tension | |
|
Download:
|
| 图 13 谱峰周期对管道动力响应的影响 Fig. 13 Effect of peak spectral period on pipeline dynamic tension | |
1) 铺设水深与铺设角度对管道的动态张力有十分明显的影响,随着铺设水深以及铺设角度的增加,管道的动态张力将被逐渐放大,但由于铺设角度的改变将改变水下管道的形态以及湿重,因此在实际的铺设过程中应选择合理的铺设角度。
2) 波浪方向对管道动态张力存在很大的影响,最不利的波浪方向出现在船宽方向,对管道响应影响最大,而最有利的波浪方向是头浪,对管道的影响最小,因此在进行管道铺设过程中合理选择船舶的前进方向,可以有效降低管道的动态张力。
3) 管道的动态张力与波浪有义波高成正相关,当波高低于2 m时,有义波高对管道的动态张力变化影响较小,当波高超过2 m后其影响变的尤为明显,因此应尽量选在波高低于2 m的条件下进行管道铺设作业。谱峰周期也是管道动态张力十分明显的影响因素,当谱峰周期为8 s的时候对管道的动态张力影响最大,应避免在此种周期下进行作业。
| [1] |
赵政璋, 赵贤正, 李景明, 等. 国外海洋深水油气勘探发展趋势及启示[J]. 中国石油勘探, 2005, 10(6): 71-76. ZHAO Zhengzhang, ZHAO Xianzheng, LI Jingming, et al. Development trends and their inspiration of oversea deep offshore oil and gas exploration[J]. China petroleum exploration, 2005, 10(6): 71-76. DOI:10.3969/j.issn.1672-7703.2005.06.014 (  0) 0)
|
| [2] |
WANG Facheng, LANG Yiming, LI Jiannan, et al. Innovations in a submarine piggyback pipeline project in the East China Sea[J]. Proceedings of the institution of civil engineers, 2019, 172(2): 69-75. (  0) 0)
|
| [3] |
PUNJARAT O A, CHUCHEEPSAKUL S. Post-buckling analysis of a uniform self-weight beam with application to catenary riser[J]. International journal of structural stability and dynamics, 2019, 19(4): 1950047. DOI:10.1142/S0219455419500470 (  0) 0)
|
| [4] |
马昌峰, 王宝毅, 张光华. 中国石油海洋油气业务发展的机遇与挑战[J]. 国际石油经济, 2016, 24(3): 17-24. MA Changfeng, WANG Baoyi, ZHANG Guanghua. Opportunities and challenges of offshore oil and gas business for CNPC[J]. International petroleum economics, 2016, 24(3): 17-24. DOI:10.3969/j.issn.1004-7298.2016.03.003 (  0) 0)
|
| [5] |
龚海潮, 陈伟, 宫蕊, 等. 适用于渤海海底复合软管的铺设系统研制和应用[J]. 海洋工程装备与技术, 2017, 4(1): 43-47. GONG Haichao, CHEN Wei, GONG Rui, et al. Development and application of pipe laying system suitable for flexible pipe in Bohai bay[J]. Ocean engineering equipment and technology, 2017, 4(1): 43-47. DOI:10.3969/j.issn.2095-7297.2017.01.009 (  0) 0)
|
| [6] |
YUAN Yuchao, XUE Hongxiang, TANG Wenyong. Added mass variation effect on vortex-induced vibration for flexible risers based on force-decomposition model[J]. Ships and offshore structures, 2018, 13(S1): 1-12. (  0) 0)
|
| [7] |
WANG Liquan, JU Ming, XING Xiaodong, et al. Dynamic behavior of the deepwater flexible pipeline during pipe laying process[J]. Journal of marine science and engineering, 2020, 8(4): 286. DOI:10.3390/jmse8040286 (  0) 0)
|
| [8] |
KONUK I. Higher order approximations in stress analysis of submarine pipelines[J]. Journal of energy resources technology, 1980, 102(4): 190-196. DOI:10.1115/1.3227872 (  0) 0)
|
| [9] |
LENCI S, CALLEGARI M. Simple analytical models for the J-lay problem[J]. Acta mechanica, 2005, 178(1/2): 23-39. (  0) 0)
|
| [10] |
BROWN R J, PALMER A. Developing innovative deep water pipeline construction techniques with physical models[J]. Journal of offshore mechanics and arctic engineering, 2007, 129(1): 56-60. DOI:10.1115/1.2426982 (  0) 0)
|
| [11] |
BREWER W V, DIXON D A. Influence of lay barge motions on a deepwater pipeline laid under tension[J]. Journal of engineering for industry, 1970, 92(3): 595-604. DOI:10.1115/1.3427821 (  0) 0)
|
| [12] |
SANTILLAN S T, VIRGIN L N. Numerical and experimental analysis of the static behavior of highly deformed risers[J]. Ocean engineering, 2011, 38(13): 1397-1402. DOI:10.1016/j.oceaneng.2011.06.009 (  0) 0)
|
| [13] |
HONG Difeng, TANG Jiali, REN Gexue. Dynamic modeling of mass-flowing linear medium with large amplitude displacement and rotation[J]. Journal of fluids and structures, 2011, 27(8): 1137-1148. DOI:10.1016/j.jfluidstructs.2011.06.006 (  0) 0)
|
| [14] |
GONG Shunfeng, XU Pu. The influence of sea state on dynamic behaviour of offshore pipelines for deepwater S-lay[J]. Ocean engineering, 2016, 111: 398-413. DOI:10.1016/j.oceaneng.2015.11.013 (  0) 0)
|
| [15] |
ZAN Yingfei, YUAN Lihao, HUANG Kuo, et al. Numerical simulations of dynamic pipeline-vessel response on a deepwater S-laying vessel[J]. Processes, 2018, 6(12): 261. DOI:10.3390/pr6120261 (  0) 0)
|
| [16] |
WANG Yingying, TUO Haohu, LI Liwei, et al. Dynamic simulation of installation of the subsea cluster manifold by drilling pipe in deep water based on OrcaFlex[J]. Journal of petroleum science and engineering, 2018, 163: 67-78. DOI:10.1016/j.petrol.2017.12.049 (  0) 0)
|
| [17] |
蔡文山. 船舶风载荷研究现状及计算方法比较[J]. 上海船舶运输科学研究所学报, 2013, 36(4): 1-6, 19. CAI Wenshan. A review of researches on ship's wind load with comparison of the calculation methods[J]. Journal of Shanghai ship and shipping research institute, 2013, 36(4): 1-6, 19. DOI:10.3969/j.issn.1674-5949.2013.04.001 (  0) 0)
|
| [18] |
HASSELMANN K, BARNETT T P, BOUWS E, et al. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP)[R]. Hamburg: Deutches Hydrographisches Institut, 1973.
(  0) 0)
|
| [19] |
陈小邹. 船舶在波浪中频域分析[J]. 舰船科学技术, 2011, 33(2): 24-27. CHEN Xiaozou. Motions simulation of a tank moving in regular wave[J]. Ship science and technology, 2011, 33(2): 24-27. DOI:10.3404/j.issn.1672-7649.2011.02.005 (  0) 0)
|
| [20] |
DUAN Menglan, WANG Yi, ESTEFEN S, et al. An installation system of deepwater risers by an S-lay vessel[J]. China ocean engineering, 2011, 25(1): 139-148. DOI:10.1007/s13344-011-0012-y (  0) 0)
|
| [21] |
赵冬岩. 挠性软管在渤海海底管道的应用[J]. 中国海上油气(工程), 1994(4): 24-17. ZHAO Dongyan. Application of flexible pipe in Bohai submarine pipelines[J]. China offshore oil and gas (engineering), 1994(4): 24-17. (  0) 0)
|
| [22] |
TAGHIPOUR R, PEREZ T, MOAN T. Hybrid frequency-time domain models for dynamic response analysis of marine structures[J]. Ocean engineering, 2008, 35(7): 685-705. DOI:10.1016/j.oceaneng.2007.11.002 (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


