2. 海洋信息获取与安全工业和信息化部重点实验室(哈尔滨工程大学), 黑龙江 哈尔滨 150001;
3. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001;
4. 西北工业大学 航海学院, 陕西 西安 710072
2. Key Laboratory of Marine Information Acquisition and Security(Harbin Engineering University), Ministry of Industry and Information Technology, Harbin 150001, China;
3. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China;
4. School of Marine Science and Technology, Northwestern Polytechnical University, Xi'an 710072, China
水下目标跟踪技术是对特定海域进行实时监测的必要前提,对水下目标进行准确可靠的跟踪是对其进行后续操作的基础。然而传统的水下目标跟踪技术常常受制于目标运动模型不准确、水下环境干扰而导致的目标观测信息失效以及跟踪算法缺少容错性等缺陷而不能提供良好的水下目标跟踪精度。因此,研究高精度、高鲁棒性的水下目标跟踪算法已然成为水下目标跟踪领域研究的热点与难点问题[1-2]。
在复杂的水下环境中,水下目标可能进行多种机动,建立准确的水下机动目标运动学与动力学模型是对其进行跟踪算法设计的基础。在水下目标跟踪领域,目前研究多集中在基于质点模型的水下目标运动学与动力学建模,即将水下目标视为质点,从而对其运动学与动力学过程进行数学描述。通常,采用不同的数学模型对水下目标的加速度进行表达,从而建立不同的水下目标运动学与动力学模型。这一类基于质点的模型主要有:匀速模型(CV模型)[3-4]、匀速转弯模型(CT模型)以及变加速模型(Singer模型[5-7]、“当前”统计模型[8]、匀加速模型(CA模型)[9]、自适应高斯模型[10]等)等。对水下机动目标而言,为了将多种运动学与动力学模型统一描述,克服目标模型表述的不确定性,文献[16]提出了交互式多模型对水下目标的运动学与动力学过程进行了统一描述,从而对水下机动目标进行有效跟踪。然而,随着目前水下机动目标运动复杂性的增强以及水下观测精度的提升,将水下目标视为质点而对其进行描述的方法已经不能满足对水下目标运动学与动力学准确建模的需求,将其视为质点进行建模将会忽略其质心与观测位置之间的位移,同时也会忽略由水下环境干扰等因素引起的水下目标平动转动耦合作用,当干扰较大时,可能会引起跟踪发散的情况。因此,为了满足当下对水下机动目标准确可靠跟踪的需求,需要研究将水下目标视为刚体,同时将水下目标的加速度与角加速度作为待定跟踪量的新型水下目标运动学与动力学建模方法。
由于水下环境复杂以及水下目标的运动学动力学模型与观测模型具有较强的非线性,一般设计非线性滤波跟踪算法对水下目标进行跟踪。其中,扩展卡尔曼滤波(EKF)[11]是最为广泛使用的非线性滤波方法。然而,由于EKF采用一阶泰勒级数展开对非线性观测模型进行线性化处理,可能会带来较大线性化误差。针对此不足,诸多采用不同线性化方法的贝叶斯滤波技术被提出并应用于目标跟踪过程中,其中具有代表性的有无迹卡尔曼滤波(UKF)[12]、容积卡尔曼(CKF)滤波[13]和粒子滤波(PF)[14-15]。但不论是UKF、CKF,还是PF,理论上越强的线性化能力带来的后果就是急剧增加的运算量与随之而来的计算不确定性。尤其在水下环境复杂,干扰众多的条件下,滤波算法的稳定性与可靠性需对跟踪结果至关重要。因此,为了对水下机动目标进行准确可靠的跟踪,设计具有自适应抗干扰能力的滤波跟踪算法十分必要。
本文将水下机动目标视为刚体,考虑水下目标的平动转动耦合效应,采用矢量对偶四元数对水下刚体目标进行六自由度一体化建模,避免传统基于质点的模型对水下目标建模的局限性; 同时将水下机动目标的加速度与角加速度作为状态估计量进行跟踪估计,从而突破IMM算法要求完备模型集的限制。利用水下三维距离观测信息,建立目标观测点与跟踪平台之间的距离观测模型,并考虑水下复杂环境对观测量的干扰,结合新息信息,提出用于水下刚体机动目标跟踪的基于矢量对偶四元数的扩展卡尔曼滤波算法(DVQ-EKF)以及自适应扩展卡尔曼滤波算法(DVQ-AEKF),以实现复杂水下环境情况下,对水下机动目标的准确可靠跟踪。
1 基于矢量对偶四元数的水下机动目标运动学与动力学模型 1.1 矢量对偶四元数(DVQ)四元数具有如下形式:
| $ \mathit{\boldsymbol{q}} = ({q_0},{q_1},{q_2},{q_3}) = {q_0} + {q_1}\mathit{\boldsymbol{i}} + {q_2}\mathit{\boldsymbol{j}} + {q_3}\mathit{\boldsymbol{k}} $ | (1) |
式中:q0是标量部分; q1i+q2j+q3k是矢量部分。其共轭表示为:(q0, -q1, -q2, -q3)。
同时,四元数与实数域的映射关系表示为:[·]:Q4→R4。在这种映射定义下,四元数叉乘可以定义在实数域内:
| $ [\mathit{\boldsymbol{a}} \times \mathit{\boldsymbol{b}}] = [\mathit{\boldsymbol{a}} \times ][\mathit{\boldsymbol{b}}] $ | (2) |
类似地,四元数内积可以定义为:
| $ [\mathit{\boldsymbol{ab}}] = {[\mathit{\boldsymbol{a}}]^\mathit{\boldsymbol{L}}}[\mathit{\boldsymbol{b}}] $ | (3) |
其中:
| $ [\mathit{\boldsymbol{a}} \times ] = \left[ {\begin{array}{*{20}{c}} 0&{{{\bf{0}}_{1 \times 3}}}\\ {{{\bf{0}}_{3 \times 1}}}&{[\mathit{\boldsymbol{\bar a}} \times ]} \end{array}} \right], $ |
| $ [\mathit{\boldsymbol{\bar a}} \times ] = \left[ {\begin{array}{*{20}{c}} 0&{ - {a_3}}&{{a_2}}\\ {{a_3}}&0&{ - {a_1}}\\ { - {a_2}}&{{a_1}}&0 \end{array}} \right]。$ |
并且:
| $ {{{[\mathit{\boldsymbol{a}}]}^\mathit{\boldsymbol{L}}} = [\begin{array}{*{20}{l}} {[\mathit{\boldsymbol{a}}]_{4 \times 1}^\mathit{\boldsymbol{L}}}&{[\mathit{\boldsymbol{a}}]_{4 \times 3}^\mathit{\boldsymbol{L}}} \end{array}],} $ |
| $ {[\mathit{\boldsymbol{a}}]_{4 \times 1}^\mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{l}} {{a_0}}&{\mathit{\boldsymbol{\bar a}}} \end{array}} \right],} $ |
| $ [\mathit{\boldsymbol{a}}]_{4 \times 3}^\mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} { - {\mathit{\boldsymbol{a}}^{\rm{T}}}}\\ {{a_0}{\mathit{\boldsymbol{I}}_{3 \times 3}} + [\mathit{\boldsymbol{\bar a}} \times ]} \end{array}} \right] $ |
由于四元数仅仅描述了目标的转动过程,而忽略了对目标平动过程的表达,因此,单纯采用四元数对目标的运动进行建模将忽略其平动过程,从而不能完成对目标的转动平动一体化建模。为了解决这一问题,文献[17]提出对偶四元数的概念,文献[18]将对偶四元数用于空间目标的转动平动耦合一体化运动学与动力学建模中。
对偶四元数有:
| $ \mathit{\boldsymbol{\hat q}} = \mathit{\boldsymbol{q}} + \varepsilon {\mathit{\boldsymbol{q}}^\prime } $ | (4) |
式中q、q′均为四元数,并且对偶运算符ε2=0,ε≠0。
矢量对偶四元数有:
| $ \mathit{\boldsymbol{\bar {\hat q} }}= \mathit{\boldsymbol{\bar q}} + \varepsilon {\mathit{\boldsymbol{\bar q}}^\prime } $ | (5) |
式中:q、q′是四元数q和q′的矢量部分。
假设有2个矢量对偶四元数:
1) 矢量对偶四元数加法:
| $ {{\mathit{\boldsymbol{\bar {\hat q}}}}_1} + {{\mathit{\boldsymbol{\bar {\hat q}}}}_2} = \overline {{{\mathit{\boldsymbol{\hat q}}}_1} + {{\mathit{\boldsymbol{\hat q}}}_2}} $ | (6) |
2) 矢量对偶四元数乘法:
| $ \overline {{{\mathit{\boldsymbol{\hat q}}}_1}{{\mathit{\boldsymbol{\hat q}}}_2}} = \overline {{{\mathit{\boldsymbol{\hat q}}}_1}{{\mathit{\boldsymbol{\hat q}}}_2}} $ | (7) |
3) 矢量对偶四元数共轭:
| $ \bar{{\mathit{\boldsymbol{ {\hat q}}}}^ * } = \overline {{{\mathit{\boldsymbol{\hat q}}}^ * }} $ | (8) |
4) 矢量对偶四元数交换:
| $ \bar{{\mathit{\boldsymbol{ {\hat q}}}}^s} = \overline {{{\mathit{\boldsymbol{\hat q}}}^s}} $ | (9) |
其余有关矢量对偶四元数的运算可以参考文献[18]。
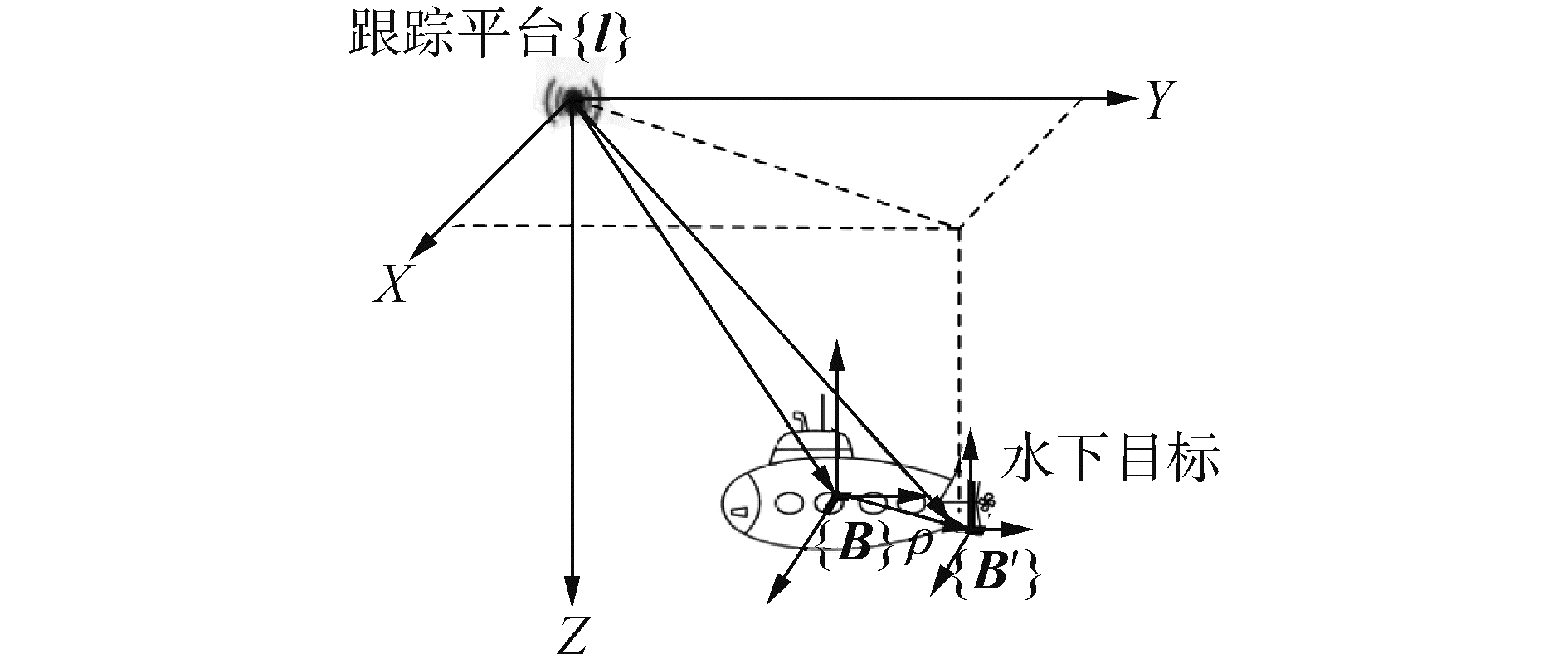
1.2 水下机动目标模型综述图 1展示了水下机动目标的运动模型。{I}为惯性系,{B}为水下目标的本体系,坐标原点为目标质心。{B′}为水下目标观测点坐标系,假设与{B}平行,之间有位移ρ。
|
Download:
|
| 图 1 水下机动目标模型 Fig. 1 Model of underwater maneuvering target | |
{B}相对于{I}的姿态四元数为:qB/I,{B}与{I}相对距离为rB/I,{B′}与{I}的距离为rm。同时,本文假设水下机动目标的线速度为v,角速度为ω。
1.3 基于矢量对偶四元数的水下机动目标运动学与动力学模型由文献[18],描述水下机动目标的位置和姿态的矢量对偶四元数为:
| $ {\overline {\mathit{\boldsymbol{\hat q}}} _{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}} = {{\mathit{\boldsymbol{\bar q}}}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}} + \overline {\varepsilon \mathit{\boldsymbol{q}}} {\kern 1pt} _{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}^\prime = {\mathit{\boldsymbol{\overline q}} _{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}} + \varepsilon \frac{1}{2}\overline {\mathit{\boldsymbol{r}}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}^\mathit{\boldsymbol{I}}{\mathit{\boldsymbol{q}}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}}} $ | (10) |
式中rB/II是水下机动目标的质心距离在{I}中的表达。
描述水下机动目标的速度和角速度的矢量对偶四元数为:
| $ \overline {\mathit{\boldsymbol{\hat \omega }}} {\kern 1pt} _{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}^\mathit{\boldsymbol{B}} = \overline {\mathit{\boldsymbol{\hat \omega }}} {\kern 1pt} _{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}^\mathit{\boldsymbol{B}} + \varepsilon \mathit{\boldsymbol{\overline \omega }} {{\kern 1pt} ^\prime }_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}^\mathit{\boldsymbol{B}} = \mathit{\boldsymbol{\bar \omega }}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}^\mathit{\boldsymbol{B}} + \varepsilon \mathit{\boldsymbol{\bar v}}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}^\mathit{\boldsymbol{B}} = \mathit{\boldsymbol{\omega }} + \varepsilon \mathit{\boldsymbol{v}} $ | (11) |
式中:ωB/IB是水下机动目标的角速度在{B}中的表达; vB/IB是水下机动目标的线速度在{B}中的表达。
基于式(10)、(11),由文献[18],得到基于矢量对偶四元数的水下机动目标运动学方程为:
| $ 2{{\mathit{\boldsymbol{\dot {\bar {\hat q}}}}}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}} = \overline {{{\mathit{\boldsymbol{\hat q}}}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}}\mathit{\boldsymbol{\hat \omega }}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}^\mathit{\boldsymbol{B}}} $ | (12) |
为了避免奇异,利用误差四元数将式(12)改写为:
| $ \frac{{{\rm{d}}\mathit{\boldsymbol{\delta {\bar {\hat q}}}}}}{{{\rm{d}}t}} = - \frac{1}{2}\bar{{ {\hat {\tilde {\boldsymbol{\omega}}}}}}\delta \mathit{\boldsymbol{\bar {\hat q}}} + \frac{1}{2}\delta \mathit{\boldsymbol{\bar {\hat q}{\bar {\hat \omega }}}} $ | (13) |
式中:
当水下机动目标受控做机动运动时,基于矢量对偶四元数的水下机动目标的动力学方程为:
| $ \frac{{{\rm{d}}{{(\mathit{\boldsymbol{\bar {\hat \omega} }}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}^\mathit{\boldsymbol{B}})}^\mathit{\boldsymbol{s}}}}}{{{\rm{d}}t}} = \left[ {\begin{array}{*{20}{c}} {\bf{0}}\\ {\mathit{\boldsymbol{v}} \times \mathit{\boldsymbol{\omega }}} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{a}}_\mathit{\boldsymbol{\omega }}}}\\ {{\mathit{\boldsymbol{a}}_\mathit{\boldsymbol{v}}}} \end{array}} \right] $ | (14) |
| $ \frac{{{\rm{d}}\mathit{\boldsymbol{\bar {\hat a}}}}}{{{\rm{d}}t}} = 0 $ | (15) |
式中:
由图 1可知,观测点(比如潜艇壳体)与目标质心具有位移ρ,因此,观测方程为:
| $ \mathit{\boldsymbol{Z}} = {\mathit{\boldsymbol{r}}_\mathit{\boldsymbol{m}}} + \mathit{\boldsymbol{v}} = \mathit{\boldsymbol{\bar r}}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}^\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{A}}({\mathit{\boldsymbol{q}}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}})\mathit{\boldsymbol{\rho }} + \mathit{\boldsymbol{v}} $ | (16) |
式中:A(qB/I)为水下目标质心与跟踪平台之间的姿态转移矩阵; v为观测噪声,满足:
| $ {{\rm{E}}(\mathit{\boldsymbol{v}}) = 0} $ | (17) |
| $ {{\rm{D}}(\mathit{\boldsymbol{v}}) = \mathit{\boldsymbol{R}} = \mathit{\boldsymbol{\sigma }}_v^2} $ | (18) |
式中σv2为水下未知干扰对观测模型扰动的强度。
2.2 DVQ-EKF设计水下机动目标跟踪系统的状态为:
| $ \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\bar {\hat q}}}}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}}}&{\mathit{\boldsymbol{\bar {\hat \omega }}}}&{\mathit{\boldsymbol{\bar {\hat a}}}}&{\mathit{\boldsymbol{\bar {\hat \rho }}}} \end{array}} \right] $ | (19) |
式中:
由于水下复杂环境所带来的干扰,假设水下机动目标在运动过程中,所受干扰力矩对其加速度产的干扰为w,由水下复杂环境带来的观测干扰为v,并且假设w满足:
| $ {{\rm{E}}(\mathit{\boldsymbol{w}}) = 0} $ | (20) |
| $ {{\rm{D}}(\mathit{\boldsymbol{w}}) = \mathit{\boldsymbol{\sigma }}_\mathit{\boldsymbol{w}}^2} $ | (21) |
式中:σw2为水下未知干扰对运动学动力学模型扰动的强度。结合式(19)~(21)以及式(12)~(14),基于矢量对偶四元数的水下机动目标线性化状态方程为:
| $ {\mathit{\boldsymbol{X}}_{\mathit{\boldsymbol{k}} + 1}} {\bf{ = }} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_\mathit{\boldsymbol{k}}}{\mathit{\boldsymbol{X}}_\mathit{\boldsymbol{k}}} + {\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{k}}} $ | (22) |
式中
F为状态方程的雅可比矩阵,并且:
| $ {\mathit{\boldsymbol{F}}_{24 \times 24}} {\bf{ = }} \frac{{\partial \mathit{\boldsymbol{f}}}}{{\partial \mathit{\boldsymbol{X}}}} {\bf{ = }} \left[ {\begin{array}{*{20}{c}} { - (\mathit{\boldsymbol{\bar {\hat \omega }}} \times )}&{\frac{1}{2}{\mathit{\boldsymbol{I}}_{6 \times 6}}}&{{{\bf{0}}_{6 \times 6}}}&{{{\bf{0}}_{6 \times 6}}}\\ {{{\bf{0}}_{6 \times 6}}}&\mathit{\boldsymbol{A}}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}} \end{array}}\\ {\begin{array}{*{20}{c}} {{{\bf{0}}_{3 \times 3}}}&{{\mathit{\boldsymbol{I}}_{3 \times 3}}} \end{array}} \end{array}}&{{{\bf{0}}_{6 \times 6}}}\\ {{{\bf{0}}_{6 \times 6}}}&{{{\bf{0}}_{6 \times 6}}}&{{{\bf{0}}_{6 \times 6}}}&{{{\bf{0}}_{6 \times 6}}}\\ {{{\bf{0}}_{6 \times 6}}}&{{{\bf{0}}_{6 \times 6}}}&{{{\bf{0}}_{6 \times 6}}}&{{{\bf{0}}_{6 \times 6}}} \end{array}} \right] $ | (23) |
| $ \mathit{\boldsymbol{A}} {\bf{ = }} \left[ {\begin{array}{*{20}{c}} {{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}\\ {(\mathit{\boldsymbol{v}} \times )}&{ - (\mathit{\boldsymbol{\omega }} \times )} \end{array}} \right] $ | (24) |
| $ {\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{k}}} {\bf{ = }} \left[ {\begin{array}{*{20}{l}} {{{\bf{0}}_{6 \times 1}}}\\ {{{\bf{0}}_{6 \times 1}}}\\ {{\mathit{\boldsymbol{w}}_{6 \times 1}}}\\ {{{\bf{0}}_{6 \times 1}}} \end{array}} \right] $ | (25) |
由式(16),观测方程的雅可比矩阵为:
| $ \mathit{\boldsymbol{H}}(\mathit{\boldsymbol{X}}) {\bf{ = }} \frac{{\partial \mathit{\boldsymbol{h}}}}{{\partial \mathit{\boldsymbol{X}}}} {\bf{ = }} [ - 2\mathit{\boldsymbol{A}}({\mathit{\boldsymbol{\tilde q}}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}})[\mathit{\boldsymbol{\rho }} \times ]\quad \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}({\mathit{\boldsymbol{\tilde q}}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}})\quad {{\bf{0}}_{3 \times 15}}\quad 2\mathit{\boldsymbol{A}}({\mathit{\boldsymbol{\tilde q}}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}})(\mathit{\boldsymbol{\delta }}{\mathit{\boldsymbol{\bar q}}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}} \times )] $ | (26) |
其中:
| $ \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}({\mathit{\boldsymbol{\tilde q}}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}}) {\bf{ = }} 2({\mathit{\boldsymbol{\bar {\hat q}}}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}})\mathit{\boldsymbol{\delta }}{\mathit{\boldsymbol{\bar {\tilde q}}}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}}\mathit{\boldsymbol{\bar {\tilde q}}}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}^* = 2\mathit{\boldsymbol{A}}({\mathit{\boldsymbol{\tilde q}}_{\mathit{\boldsymbol{B}}/\mathit{\boldsymbol{I}}}}) $ | (27) |
结合式(17)、(18)、(20)~(27),基于扩展卡尔曼滤波(EKF)的框架[19],得到基于矢量对偶四元数的水下机动目标跟踪算法(DVQ-EKF)。
2.3 水下机动目标跟踪算法设计考虑水下复杂环境可能对观测信息造成干扰,从而影响DVQ-EKF中的测量更新精度,进一步导致跟踪精度下降甚至发散的问题,需要设计具有自适应调节能力的水下机动目标跟踪算法。
定义新息量为:
| $ {\mathit{\boldsymbol{n}}_\mathit{\boldsymbol{k}}} {\bf{ = }} {\mathit{\boldsymbol{Z}}_\mathit{\boldsymbol{k}}} - \mathit{\boldsymbol{h}}({\mathit{\boldsymbol{X}}_{\mathit{\boldsymbol{k}}/\mathit{\boldsymbol{k}} - 1}}) $ | (28) |
由式(28),可得新息量的方差为:
| $ \mathit{\boldsymbol{E}}[{\mathit{\boldsymbol{n}}_\mathit{\boldsymbol{k}}}\mathit{\boldsymbol{n}}_\mathit{\boldsymbol{k}}^{\bf{T}}]{\bf{ = }}{\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{e}}}{\bf{ = }}{\mathit{\boldsymbol{H}}_\mathit{\boldsymbol{k}}}{\mathit{\boldsymbol{P}}_{\mathit{\boldsymbol{k}}/\mathit{\boldsymbol{k}} - 1}}\mathit{\boldsymbol{H}}_\mathit{\boldsymbol{k}}^{\bf{T}}{\bf{ + }}{\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{k}}} $ | (29) |
当水下机动目标跟踪系统正常工作,即跟踪量满足最优估计时,DVQ-EKF的滤波增益为:
| $ {\mathit{\boldsymbol{K}}_\mathit{\boldsymbol{k}}}{\bf{ = }}{\mathit{\boldsymbol{P}}_{\mathit{\boldsymbol{k}}/\mathit{\boldsymbol{k}} - 1}}\mathit{\boldsymbol{H}}_\mathit{\boldsymbol{k}}^{\bf{T}}{({\mathit{\boldsymbol{H}}_\mathit{\boldsymbol{k}}}{\mathit{\boldsymbol{P}}_{\mathit{\boldsymbol{k}}/\mathit{\boldsymbol{k}} - 1}}\mathit{\boldsymbol{H}}_\mathit{\boldsymbol{k}}^{\bf{T}}\mathit{\boldsymbol{ + }}{\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{k}}})^{ - 1}}{\bf{ = }}{\mathit{\boldsymbol{P}}_{\mathit{\boldsymbol{k}}/\mathit{\boldsymbol{k}} - 1}}\mathit{\boldsymbol{H}}_\mathit{\boldsymbol{k}}^{\bf{T}}\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{e}}^{ - 1} $ | (30) |
为了对受扰观测进行处理,需要通过计算nk,从而调节Kk对水下机动目标进行准确跟踪。将系统观测受扰的影响反映在观测噪声Rk上,由式(29)可得:
| $ {\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{e}}}{\bf{ = }}{\mathit{\boldsymbol{H}}_\mathit{\boldsymbol{k}}}{\mathit{\boldsymbol{P}}_{\mathit{\boldsymbol{k}}/\mathit{\boldsymbol{k}} - 1}}\mathit{\boldsymbol{H}}_\mathit{\boldsymbol{k}}^{\bf{T}}\mathit{\boldsymbol{ + }}{\mathit{\boldsymbol{\gamma }}_\mathit{\boldsymbol{k}}}{\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{k}}} $ | (31) |
其中γk为观测噪声的比例因子矩阵,可表示为:
| $ {\mathit{\boldsymbol{\gamma }}_\mathit{\boldsymbol{k}}}{\bf{ = }}({\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{e}}}{\bf{ - }}{\mathit{\boldsymbol{H}}_\mathit{\boldsymbol{k}}}{\mathit{\boldsymbol{P}}_{\mathit{\boldsymbol{k}}/\mathit{\boldsymbol{k}} - 1}}\mathit{\boldsymbol{H}}_\mathit{\boldsymbol{k}}^{\bf{T}})\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{k}}^{ - 1} $ | (32) |
在[0, k]时刻中,有:
| $ {\mathit{\boldsymbol{V}}_\mathit{\boldsymbol{e}}} \buildrel\textstyle.\over= {\mathit{\boldsymbol{\eta }}_\mathit{\boldsymbol{k}}}{\bf{ = }}\frac{1}{\mathit{\boldsymbol{k}}}\sum\limits_{i = 1}^\mathit{\boldsymbol{k}} {{\mathit{\boldsymbol{n}}_{\mathit{\boldsymbol{k,i}}}}} \mathit{\boldsymbol{n}}_{\mathit{\boldsymbol{k,i}}}^{\bf{T}} $ | (33) |
将式(33)代入式(32)可得:
| $ {\mathit{\boldsymbol{\gamma }}_\mathit{\boldsymbol{k}}}{\bf{ = }}({\mathit{\boldsymbol{\eta }}_\mathit{\boldsymbol{k}}}{\bf{ - }}{\mathit{\boldsymbol{H}}_\mathit{\boldsymbol{k}}}{\mathit{\boldsymbol{P}}_{\mathit{\boldsymbol{k}}/\mathit{\boldsymbol{k}} - 1}}\mathit{\boldsymbol{H}}_\mathit{\boldsymbol{k}}^{\bf{T}})\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{k}}^{ - 1} $ | (34) |
假设观测干扰均由水下环境波动导致,为了使γk的对角元素均大于等于1,定义修正的比例因子矩阵的第ii个对角元素为:
| $ \gamma _{k,ii}^* = \max \{ 1,{\gamma _{k,ii}}\} $ | (35) |
由式(35)可得,修正的观测噪声矩阵为:
| $ \mathit{\boldsymbol{R}}_\mathit{\boldsymbol{k}}^* = \mathit{\boldsymbol{\gamma }}_\mathit{\boldsymbol{k}}^*{\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{k}}} $ | (36) |
修正后的卡尔曼滤波增益为:
| $ \mathit{\boldsymbol{K}}_\mathit{\boldsymbol{k}}^* = {\mathit{\boldsymbol{P}}_{\mathit{\boldsymbol{k}}/\mathit{\boldsymbol{k}} - 1}}\mathit{\boldsymbol{H}}_\mathit{\boldsymbol{k}}^{\bf{T}}{({\mathit{\boldsymbol{H}}_\mathit{\boldsymbol{k}}}{\mathit{\boldsymbol{P}}_{\mathit{\boldsymbol{k}}/\mathit{\boldsymbol{k}} - 1}}\mathit{\boldsymbol{H}}_\mathit{\boldsymbol{k}}^{\bf{T}}{\bf{ + }}\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{k}}^*)^{ - 1}} $ | (37) |
可见,通过式(37)对DVQ-EKF的滤波增益进行修正,可以得到在干扰下较为准确的跟踪量。基于扩展卡尔曼滤波(EKF)的框架[19],将其中的卡尔曼增益与观测噪声矩阵替换为式(36)与式(37),即可得到基于矢量对偶四元数的水下机动目标自适应跟踪算法(DVQ-AEKF)。
2.4 观测干扰分析为了节约计算资源,提升跟踪系统的跟踪效率,对水下机动目标进行跟踪时,需要在DVQ-EKF以及DVQ-AEKF两者间进行合理切换。
定义系统的观测失效判别量为:
| $ {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_k} = \mathit{\boldsymbol{\eta }}_\mathit{\boldsymbol{k}}^\mathit{\boldsymbol{T}}{[{\mathit{\boldsymbol{H}}_\mathit{\boldsymbol{k}}}{\mathit{\boldsymbol{P}}_{\mathit{\boldsymbol{k}}/\mathit{\boldsymbol{k}} - 1}}\mathit{\boldsymbol{H}}_\mathit{\boldsymbol{k}}^{\bf{T}}{\bf{ + }}{\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{k}}}]^{ - 1}}{\mathit{\boldsymbol{\eta }}_\mathit{\boldsymbol{k}}} $ |
采用假设检验的思想,设定2个假设条件如下:
H0:跟踪系统不存在观测受强干扰扰情况,跟踪过程正常;
H1:跟踪系统存在观测受强干扰扰情况,跟踪过程异常;
基于上述2个条件,观测干扰分析步骤为:
1) 给定临界概率ξ(0 < ξ < 1),即满足:
| $ P\{ {\chi ^2} > \chi _{\xi ,n}^2\} = \xi $ |
2) 若Δk≤χξ, n2,则满足假设H0; 若Δk>χξ, n2,则满足假设H1。
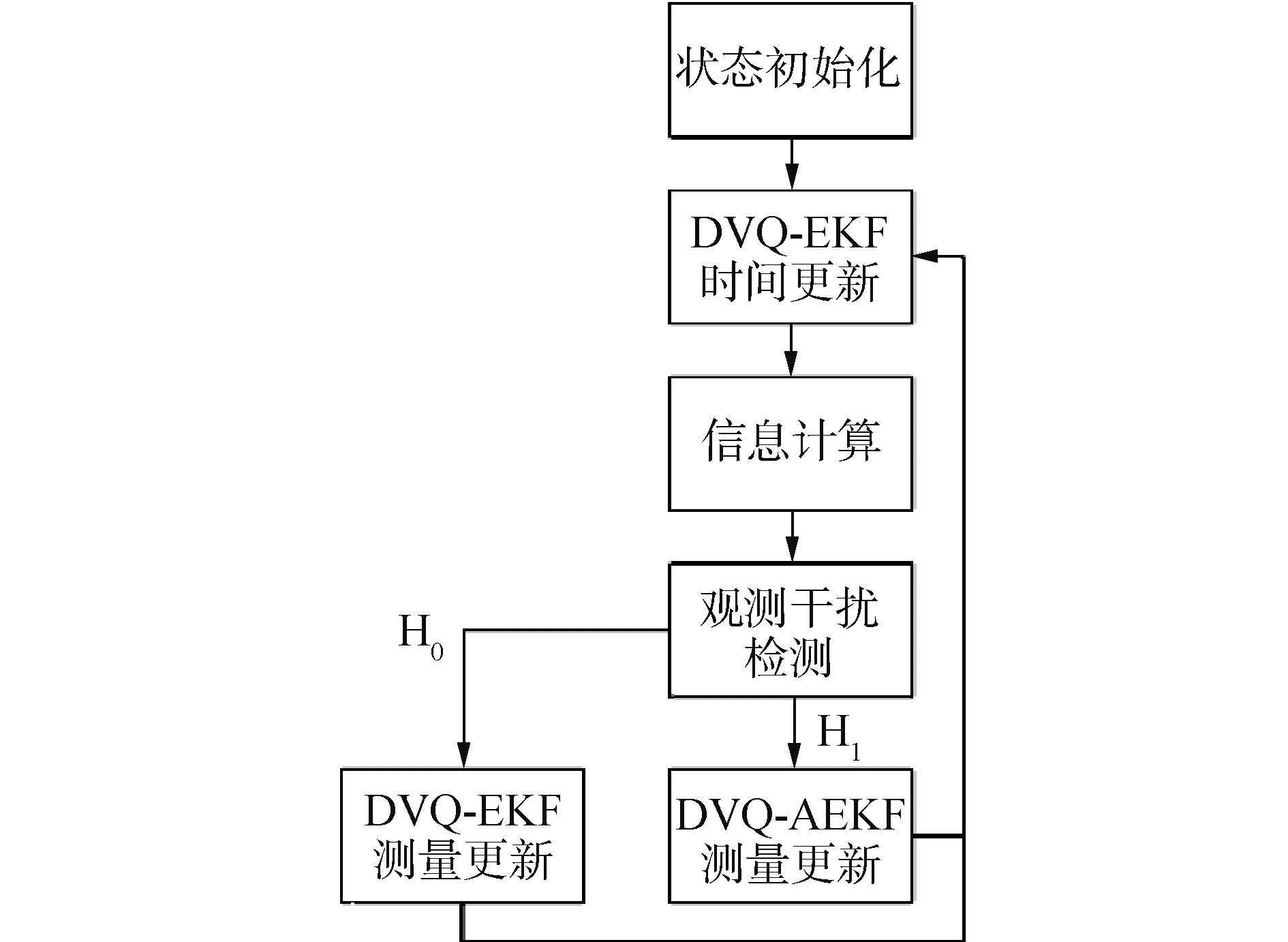
为了更直观的说明本文所设计的水下机动目标跟踪算法的工作过程,其算法流程图如图 2所示。
|
Download:
|
| 图 2 水下机动目标跟踪系统算法流程 Fig. 2 Flow chart of the proposed tracking algorithm | |
仿真案例为跟踪某三维运动的水下机动目标,采用蒙特卡洛仿真方法,仿真次数为1 000次。仿真时间设定为350 s,仿真步长ΔT=1 s。假定在水下三维空间内布置观测节点,测量节点通过主动探测的方式获得水下机动目标相对于跟踪平台的距离信息。假定在350 s仿真时间内,水下机动目标进行CV、CA,再到CV 3种模型的运动,并且在[0, 100] s内进行CV运动,[100,110] s内进行加速度为aω=[0.001 0.001 0.001]rad/s2,av=[0 0 0]m/s2的CA运动,在[110,120] s内进行加速度为aω=[0 0 0]rad/s2,av=[0.01 0.01 0.01]m/s2的CA运动,在[120,350] s进行CV运动。在仿真过程中,假设水下环境干扰导致的加速度噪声与距离观测噪声的强度为:
| $ {\sigma _\omega ^2 = 5 \times {{10}^{ - 4}}{{({\rm{rad/}}{{\rm{s}}^2})}^2}} $ |
| $ {\sigma _v^2 = 1 \times {{10}^{ - 3}}{{({\rm{m/}}{{\rm{s}}^2})}^2}} $ |
| $ {\sigma _r^2 = 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {{\rm{m}}^2}} $ |
并假设在[200,225] s,水下复杂环境对距离观测量有随机附加扰动,其强度为:
| $ \sigma _{r,{\rm{ RANDOM }}}^2 = 5{\kern 1pt} {\kern 1pt} {\kern 1pt} {{\rm{m}}^2} $ |
假设水下机动目进行三维运动,目标的质心位置为ρ=[40 5 5]m,从而反应其刚体形态。在仿真开始时刻目标的初始参数与仿真初始参数如下表所示:
基于上述条件,对DVQ-EKF于DVQ-AEKF的性能进行仿真测试,对水下机动目标的质心位移,质心速度和质心位置的跟踪结果如图 3~8所示。
| 表 1 水下机动目标初始参数 Table 1 Initial values of the target |

|
Download:
|
| 图 3 DVQ-EKF与DVQ-AEKF跟踪下的质心位移误差 Fig. 3 Error of tracking distance by DVQ-EKF and DVQ-AEKF | |
|
Download:
|
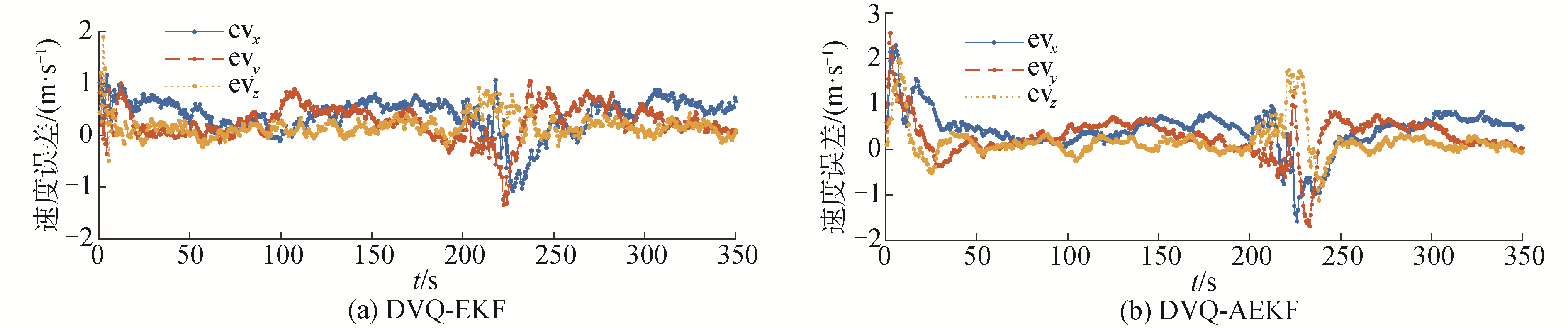
| 图 4 DVQ-EKF和DVQ-AEKF跟踪下的线速度误差 Fig. 4 Error of tracking velocity by DVQ-AEKF and DVQ-EKF | |
|
Download:
|
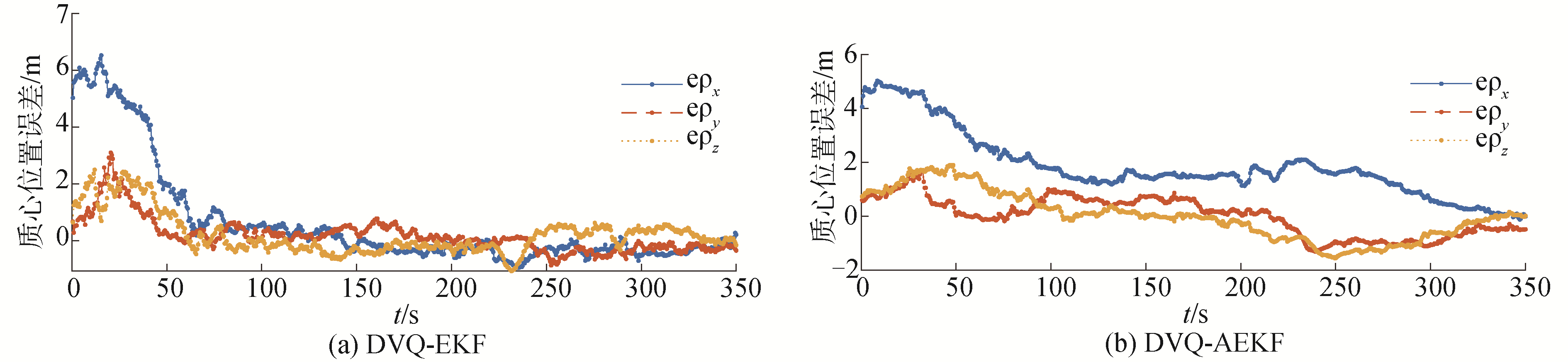
| 图 5 DVQ-EKF和DVQ-AEKF跟踪下的质心位置误差 Fig. 5 Error of tracking location of the mass point by DVQ-EKF and DVQ-AEKF | |
通过图 3~8,可以看到采用DVQ-EKF或DVQ-AEKF均能在设定仿真环境下对水下机动目标进行跟踪。在水下目标进行机动,并在观测收到一定强度的扰动时,DVQ-EKF的质心位移的跟踪精度小于25 m,DVQ-AEKF的质心位移的跟踪精度小于10 m; DVQ-EKF的线速度估计误差小于0.7 m/s,DVQ-AEKF的线速度估计误差小于0.4 m/s。并且,通过本文提出的基于DVQ的建模方法,能够对水下目标的相关尺寸(即目标质心与观测点之间的位移,本文称为质心位置)做出估计,从而弥补了传统质点建模方法对该参数估计的盲区。通过仿真发现,DVQ-EKF的目标质心位置估计误差在3 m左右; DVQ-AEKF的目标质心位置估计误差在1 m左右。
4 结论1) 本文将用于航空航天领域的矢量对偶四元数建模方法用于水下机动目标建模过程,克服了传统水下目标跟踪过程中采用质点模型描述目标运动学动力学过程的误差,并将CV与CA模型进行了一体化描述。
2) 结合了自适应滤波的技术手段,通过对受扰观测进行更新权重调整,从而对水下机动目标进行了有效跟踪。
3) 由于DVQ-AEKF采用了自适应调整跟踪滤波算法增益的技术手段,使其能够应对距离观测量受扰较大的情况,从而具有更高的跟踪精度与跟踪稳定性。
| [1] |
严卫生, 高磊, 张礴, 等. 水下目标跟踪技术[J]. 火力与指挥控制, 2000, 25(2): 2-7. YAN Weisheng, GAO Lei, ZHANG Bo, et al. Underwater Target Tracking[J]. Fire control & command control, 2000, 25(2): 2-7. (  0) 0)
|
| [2] |
LUO Junhai, HAN Ying, FAN Liying. Underwater acoustic target tracking:a review[J]. Sensors, 2018, 18(1): 112. (  0) 0)
|
| [3] |
李晓花.基于信息融合的水下多目标跟踪技术研究[D].西安: 西北工业大学, 2016: 18-19. LI Xiaohua. Research on the underwater multiple target tracking based on information fusion[D]. Xi'an: Northwestern Polytechnical University, 2016: 18-19. (  0) 0)
|
| [4] |
李闻白, 刘明雍, 雷小康, 等. 未知洋流干扰下基于单领航者的多自主水下航行器协同导航[J]. 兵工学报, 2011, 32(3): 292-297. LI Wenbai, LIU Mingyong, LEI Xiaokang, et al. Cooperative navigation for multiple autonomous underwater vehicles with single leader in unknown ocean current[J]. Acta armamentarii, 2011, 32(3): 292-297. (  0) 0)
|
| [5] |
SINGER R A. Estimating optimal tracking filter performance for manned maneuvering targets[J]. IEEE transactions on aerospace and electronic systems, 1970, AES-6(4): 473-483. DOI:10.1109/TAES.1970.310128 (  0) 0)
|
| [6] |
陈小龙, 庞永杰, 李晔, 等. 基于STF-Singer模型的AUV传感器故障诊断[J]. 仪器仪表学报, 2010, 31(7): 1502-1508. CHEN Xiaolong, PANG Yongjie, LI Ye, et al. AUV sensor fault diagnosis based on STF-Singer model[J]. Chinese journal of scientific instrument, 2010, 31(7): 1502-1508. (  0) 0)
|
| [7] |
谭顺成, 王国宏, 王娜. IMM-Singer模型的机动目标跟踪算法[J]. 火力与指挥控制, 2012, 37(2): 32-34. TAN Shuncheng, WANG Guohong, WANG Na. Maneuvering target tracking algorithm based on IMM-Singer model[J]. Fire control & command control, 2012, 37(2): 32-34. (  0) 0)
|
| [8] |
ZHOU Hongren, KUMAR K S P. A "current" statistical model and adaptive algorithm for estimating maneuvering targets[J]. Journal of guidance, control, and dynamics, 1984, 7(5): 596-602. DOI:10.2514/3.19900 (  0) 0)
|
| [9] |
苏骏, 李亚安, 陈晓, 等. 双观测站水下纯方位多目标跟踪的数据关联算法[J]. 水下无人系统学报, 2018, 26(2): 115-121, 128. SU Jun, LI Yaan, CHEN Xiao, et al. Data association algorithm for multi-target tracking of underwater bearings-only systems with double observation stations[J]. Journal of unmanned undersea systems, 2018, 26(2): 115-121, 128. (  0) 0)
|
| [10] |
党建武. 水下多目标跟踪理论[M]. 西安: 西北工业大学出版社, 2009: 38-44.
(  0) 0)
|
| [11] |
AIDALA V, HAMMEL S. Utilization of modified polar coordinates for bearings-only tracking[J]. IEEE transactions on automatic control, 1983, 28(3): 283-294. DOI:10.1109/TAC.1983.1103230 (  0) 0)
|
| [12] |
LI Xiaohua, ZHAO Chenxu, YU Jing, et al. Underwater bearing-only and Bearing-Doppler target tracking based on square root unscented Kalman filter[J]. Entropy, 2019, 21(8): 740. DOI:10.3390/e21080740 (  0) 0)
|
| [13] |
石桂欣, 鄢社锋, 郝程鹏, 等. 不完全量测下长基线系统的水下目标跟踪算法[J]. 声学学报, 2019, 44(4): 480-490. SHI Guixin, YAN Shefeng, HAO Chengpeng, et al. Target tracking algorithm for underwater ranges-only long baseline system with incomplete measurements[J]. Acta acustica, 2019, 44(4): 480-490. (  0) 0)
|
| [14] |
GORDON N J. Non-linear/non-Gaussian filtering and the bootstrap filter[C]//IEE Colloquium on Non-linear Filters. London, 1994.
(  0) 0)
|
| [15] |
GORDON N J, SALMOND D J, SMITH A F M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation[J]. IEE proceedings F (radar and signal processing), 1993, 140(2): 107-113. DOI:10.1049/ip-f-2.1993.0015 (  0) 0)
|
| [16] |
BLOM H A P, BAR-SHALOM Y. The interacting multiple model algorithm for systems with Markovian switching coefficients[J]. IEEE transactions on automatic control, 1988, 33(8): 780-783. DOI:10.1109/9.1299 (  0) 0)
|
| [17] |
GODDARD J S, ABIDI M A. Pose and motion estimation using dual quaternion-based extended Kalman filtering[C]//Proceedings of SPIE, Three-Dimensional Image Capture and Applications. San Jose, 1998: 189-200.
(  0) 0)
|
| [18] |
FILIPE N, TSIOTRAS P. Adaptive position and attitude-tracking controller for satellite proximity operations using dual quaternions[J]. Journal of guidance, control, and dynamics, 2015, 38(4): 566-577. DOI:10.2514/1.G000054 (  0) 0)
|
| [19] |
LEFFENS E J, MARKLEY F L, SHUSTER M D. Kalman filtering for spacecraft attitude estimation[J]. Journal of guidance, control, and dynamics, 1982, 5(5): 417-429. DOI:10.2514/3.56190 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


