2. 海洋信息获取及安全工业和信息化部重点实验室(哈尔滨工程大学), 哈尔滨 150001;
3. 哈尔滨工程大学 水声工程学院, 哈尔滨 150001
2. Key Laboratory of Marine Information Acquisition & Security(Harbin Engineering University), Minister Industry & Information Technology, Harbin 150001, China;
3. College Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
在浅海环境下,由于受海底及海面的影响,准确测量水下目标的噪声是很困难的,混响水池提供了测量水下声源的新思路且具有效率高、费用低等优点。
在空气声学中测量声源的辐射声功率经常使用混响室,与混响室测量相关的测量方法也有相应的国际标准。混响室理论发展较成熟[1-6],混响室中的声场只有近似满足扩散场条件才能够进行声源的辐射声功率测量。Kuttruff等[7]、Pierce等[8]提出了扩散场的特性如下:在扩散场中的某测量点,声波由所有方向的入射声波构成且每个方向的声波具有随机的相位和相同的强度; 在扩散场中的某测点,声波的声能密度都相等[9-10]。
混响室理论及测量方法已广泛应用于不规则复杂结构的辐射声功率测量。在混响室中,Mailing等[11]、Morse等[12]及House[13]研究了有关单极子源的辐射声功率测量并得出如下结论:频率较高时,单极子源可以激励起很多交叠的模态,因此能保证输出的声功率足够准确,此输出的声功率等于自由场输出的声功率。在截止频率以下的低频激励起的模态很少,此时的输出声功率低于自由场输出的声功率。Waterhouse校正可对截止频率以下测量的声功率进行校正[14],Schaffner更进一步提出了弹性边界的低频校正方法[15]。
根据混响室测量方法,Maidanik[16]测量了加肋板的辐射声功率,Ludwig[17]测量了流激薄钢板的辐射声功率。在机器所在环境,Schultz[18]测量了某大型机器的辐射声功率。Hubner[19-20]研究了具体环境条件下机器辐射声功率的测量及误差修正方法。加拿大NRC-IAR公司采用混响法对飞机部件进行测试,印度Holisol planet公司采用混响法测量了汽车的辐射声功率并指导汽车的设计。
为了提高混响室的测量精度,Kuttruff[2]通过提高房间壁面的反射及在房间中添加散射体而改善混响室的扩散性。Sabine[21]最早提出了采用移动反射体改善声场扩散性的方法,很明显足够尺度的移动反射体将对混响室的模态产生平均效果。Lubman等[22]开展了新型散射体的研究,该散射体与传统反射体相比有诸多优点,实验结果已表明该新型散射体可以提高测量的精度。Sepmeyer[23]开展了最佳形状及比例的混响室研究。Schroeder[24]及Mailing[25]通过研究给出了混响室测量的Schroeder截止频率。Nutter等[26]认为:通过测量总能量密度比基于势能密度的测量更能减少测量的误差,尤其是在低频段。
由于构成混响水池和混响室介质特性的巨大差异,使得混响水池的声场特性与空气中的混响室完全不同,主要表现为:混响水池壁面的反射系数远远低于空气中的混响室。由于一般混响水池壁面的反射系数较低,同时由于水池的边界存在着干涉模式,导致混响水池中混响声场的声能分布极不均匀,所以水下较难建立理想扩散场,这是水下无法直接采用混响室法的主要原因。
文献[27]的测试结果表明:在水池内某固定点的测量结果最大误差将近20 dB。Blake等[28]采用同长宽高分别为10 m、13 m及13 m的同一混响室分别充空气和水采用混响法测量声源的辐射声功率。其测得的混响室充水情况下测得的50 Hz带宽内声压级的脉动为10 dB左右。国内已开始在混响水池中测量高频小目标的辐射声功率,俞孟萨等[29]在半混响水池中测量了加肋圆柱壳的辐射噪声,王春旭等[30]在小型水池中测量了湍射流的辐噪声。但得到的结果不确定度都较大,究其原因在于混响水池中混响声场能量密度的不均匀性。
本文为解决混响水池在实际阻抗边界且不满足扩散场条件下的测量问题,提出了基于空间平均的混响水池方法,并建立了声源声功率与水池混响控制区空间平均声压级的关系,形成混响水池法测量理论,不再要求混响水池声场满足扩散场条件。采用混响水池法实现水下声源辐射声功率、管路噪声、材料吸声系数的测量及水听器的校准。
1 混响水池基本理论及混响水池法 1.1 混响水池基本理论以长、宽、高分别为Lx、Ly、Lz的矩形混响水池为例,如图 1所示。水池池壁的相对声导纳为β=ξ-iσ=ρ0c0/Z(ρ0、c0、Z为水的密度、水的声速及阻抗),水池的上表面为空气,以绝对软边界近似。

|
Download:
|
| 图 1 矩形水池示意 Fig. 1 The diagram of the rectangular pool | |
以速度势函数表示水池内某点的声波方程为:
| $ {\nabla ^2}\phi (r) + {k^2}\phi (r) = - 4{\rm{ \mathsf{ π} }}{Q_0}\delta (r - {r_0}) $ | (1) |
及边界条件:
| $ {\frac{{\partial \phi }}{{\partial n}}{|_\varSigma } = ik\beta \phi } $ | (2) |
与
| $ {\phi {|_{z = {L_z}}} = 0} $ | (3) |
式中:4πQ0为声源的容积速度; r为测点的坐标; r0为源点的坐标; Σ为不包括水池上表面z=Lz的其余表面; k=ω/c0。将ϕ(r)及δ(r-r0)按简正波展开,代入式(1)可得:
| $ \phi (r,{r_0}) = - 4{\rm{ \mathsf{ π} }}{Q_0}\sum\limits_n {\frac{{{\phi _n}({r_0}){\phi _n}(r)}}{{({k^2} - k_n^2)V{\varLambda _n}}}} $ | (4) |
式中: ϕn(r)和kn为水池中第n阶简正波的本征函数和本征值; V为该矩形水池的体积; Λn为本征函数ϕn(r)的空间平均值。
| $ {\varLambda _n} = \frac{1}{V} {\iiint_V | } {\phi _n}(r){|^2}{\rm{d}}V $ | (5) |
参考文献[31],可求得声压的均分值P2(r, r0)(有效值)为:
| $ \begin{align} & {{P}^{2}}\left( r,{{r}_{0}} \right)=\frac{1}{2}{{\left| {{P}^{2}}\left( r,{{r}_{0}} \right) \right|}^{2}}=\frac{{{\left( 4\text{ }\!\!{\rm{ \mathsf{ π} }}\!\!\text{ }{{\rho }_{0}}{{Q}_{0}}c_{0}^{2} \right)}^{2}}}{2{{V}^{2}}} \\ & \left\{ \sum\limits_{n}{\frac{{{\omega }^{2}}}{\varLambda _{n}^{2}}}\frac{\phi _{n}^{2}\left( {{r}_{0}} \right)\phi _{n}^{2}(r)}{{{\left( 2{{\omega }_{n}}{{\delta }_{n}} \right)}^{2}}+{{\left( {{\omega }^{2}}-\omega _{n}^{2} \right)}^{2}}}+\sum\limits_{n}{\sum\limits_{\begin{smallmatrix} m \\ m\ne n \end{smallmatrix}}{\frac{{{\omega }^{2}}}{\varLambda _{n}^{2}}}\cdot } \right. \\ & \left. \frac{{{\phi }_{n}}\left( {{r}_{0}} \right){{\phi }_{n}}(r)\phi _{m}^{*}\left( {{r}_{0}} \right)\phi _{m}^{*}(r)}{\left[ 2{{\omega }_{n}}{{\delta }_{n}}+i\left( {{\omega }^{2}}-\omega _{n}^{2} \right) \right]\left[ 2{{\omega }_{m}}{{\delta }_{m}}+i\left( {{\omega }^{2}}-\omega _{m}^{2} \right) \right]} \right\} \\ \end{align} $ | (6) |
式(6)中大括号内第1项表示声源所激起的各阶简正波在观察点处对声能贡献之独立相加,第2项表示各阶简正波在观察点处的干涉相加。
根据简正波的正交性可得到:
| $ {\frac{1}{V} {\iiint_V {{\phi _n}} } (r)\phi _m^*(r){\rm{d}}V = \left\{ {\begin{array}{*{20}{l}} {0,n \ne m}\\ {{\varLambda _n},n = m} \end{array}} \right.} $ | (7) |
| $ {\frac{1}{V} {\iiint_V {{\phi _n}} } ({r_0})\phi _m^*({r_0}){\rm{d}}V = \left\{ {\begin{array}{*{20}{l}} {0,n \ne m}\\ {{\varLambda _n},n = m} \end{array}} \right.} $ | (8) |
若只是对观察点进行时间平均消除不掉式(6)大括号中的第2项的影响,因此无法消除简正波干涉的影响,而通过空间平均可完全消除式(6)大括号中的第2项。对式(6)中测量点的均方声压进行空间平均并利用简正波的正交性可得:
| $ \begin{array}{*{20}{l}} { \langle {P^2}({r_0})\rangle = \frac{1}{V} {\iiint_V {{P^2}} } (r,{r_0}){\rm{d}}V = }\\ {\frac{{{{(4{\rm{ \mathsf{ π} }}{\rho _0}{Q_0}c_0^2)}^2}}}{{2{V^2}}}\frac{{{\omega ^2}}}{{{\varLambda _n}}}\frac{{\phi _n^2({r_0})}}{{{{(2{\omega _n}{\delta _n})}^2} + {{({\omega ^2} - \omega _n^2)}^2}}}} \end{array} $ | (9) |
再对声源进行空间平均可得:
| $ \langle {P^2}\rangle = \frac{{4{\rho _0}{c_0}{W_0}}}{{{R_0}}} $ | (10) |
式中: R0称为混响水池常数,m2;
式(10)就是混响水池中混响控制区测量的空间平均均方声压与声源的辐射声功率之间的关系,式(10)形式上与混响室理论的结果一致。
式(10)也可以表示为对数形式:
| $ \langle {\rm{SPL}}\rangle = {\rm{SWL}} + 10{\rm{lg}}\left( {\frac{4}{{{R_0}}}} \right) $ | (11) |
式中:〈SPL〉(dB re 1μPa)表示混响水池混响控制区所测空间平均声压级; SWL(dB re 0.67×10-18 W)表示声源的声功率级。
式(11)就是混响水池中声源的辐射声功率级与混响控制区测量的空间平均声压级之间的关系。
在空气中的混响室中,认为混响场为扩散场[31]:
| $ {\rm{SPL}} = {\rm{SWL}} + 10\lg \left( {\frac{1}{{4{\rm{ \mathsf{ π} }}{r^2}}} + \frac{4}{{{R_0}}}} \right) $ | (12) |
式中:SPL(dB re 2×10-5Pa)为空气中混响室扩散场中某点声压级,SWL(dB re 1×10-12W)为空气中混响室中声源的辐射声功率级。
当r>2rh(rh为混响半径),式(12)可表示为:
| $ {\rm{SPL}} = {\rm{SWL}} + 10\lg \left( {\frac{4}{{{R_0}}}} \right) $ | (13) |
式(13)就是空气中的混响室理论。
若把式(11)中空间平均声压级〈SPL〉看作空气中的混响室理论的场点声压级SPL,则式(11)接近于空气中的混响室理论,说明混响水池中空间平均声压级与声功率级间存在类似空间中混响室理论的关系。
1.2 混响水池测量方法混响水池法是通过在混响水池离声源较远处的混响控制区通过空间平均测量出空间平均声压级,再经过混响水池的校准,从而得到声源的辐射声功率。
混响水池测量方法不再要求混响水池满足扩散场条件,混响水池法测量声源辐射声功率的表达式为:
| $ {\rm{SWL}} = \langle {\rm{SPL}}\rangle - 10\lg (R) $ | (14) |
式中:SWL(dB re0.67×10-18 W)表示声源的声功率级,〈SPL〉(dB re1 μPa)表示混响水池混响控制区所测空间平均声压级,10lg(R)为混响场至自由场的修正量,也可以表示为:
| $ 10\lg (R) = 10\lg \left( {\frac{4}{{{R_0}}}} \right) $ | (15) |
式(15)中的修正量10lg(R)的结果为混响水池中混响控制区所测空间平均声压级与声源辐射声功率级之差。该量反映的是混响水池本身的特性,其值与声源无关,可通过比较法校准得到。
采用混响水池法根据式(14)可测得声源的辐射声功率。
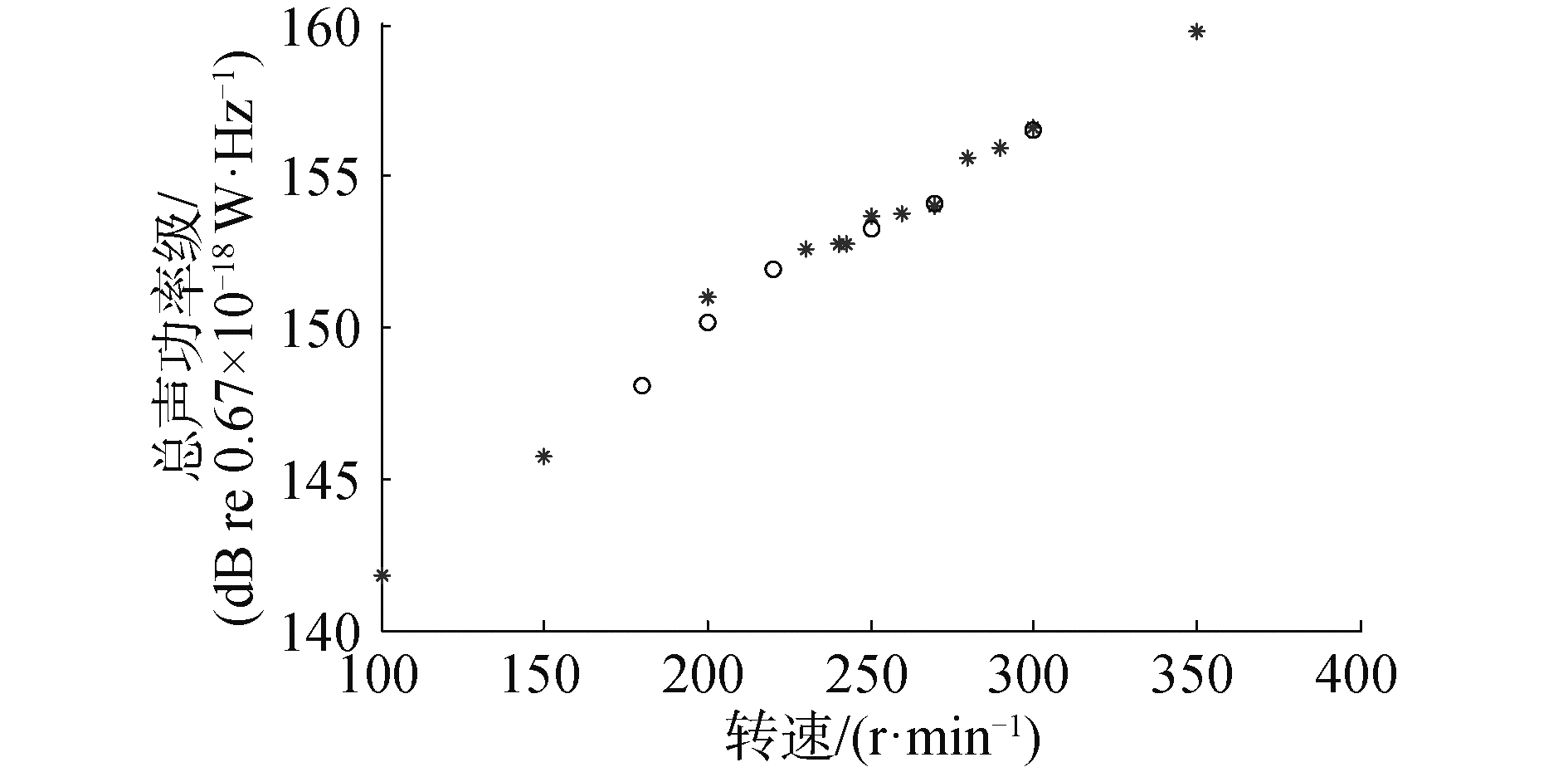
1.3 混响水池测量方法准确性验证在海上采用包面法测量不同转速下的某水下推进器电机的辐射声功率,同时在混响水池中采用基于空间平均的混响水池法测量该水下推进器电机的辐射声功率,测量结果如图 2,可见:采用混响水池法测量的水下推进器电机的总声功率级与海上采用包面法测得的总声功率级基本一致,两者在1/3倍频程频带相差不超过1.5 dB,由此验证了混响水池法测量的准确性。
|
Download:
|
| 图 2 水下推进器总辐射声功率级的海上测量与混响水池测量结果对比 Fig. 2 Comparison of the results of the marine measurement of the total radiated sound power level of the underwater propulsion and the measurement of the reverberation pool | |
由于混响水池中简正波的干涉,导致混响水池混响控制区声场声能密度分布极不均匀,因此需要对测点进行空间平均,或通过对声源空间平均来实现混响水池法的准确测量。若混响水池中独立测点或声源的个数为N,则测量的标准差为[32]:
| $ \sigma = 5.57{N^{ - \frac{1}{2}}}{\rm{dB}} $ | (16) |
若同时对频率进行平均,假设频率的带宽为B,则式(16)变为[32]:
| $ \sigma = 5.57{[N(1 + 0.238{T_{60}}B)]^{ - \frac{1}{2}}}{\rm{dB}} $ | (17) |
如声源或测点空间平均是通过沿直线扫描声场中的距离X,则:
| $ \sigma = 5.57{[N(1 + 0.238{T_{60}}B)(1 + 3.3X/\lambda )]^{ - \frac{1}{2}}}{\rm{dB}} $ | (18) |
因此,欲使混响水池中声源的辐射声功率达到预订的精度(标准差小于指定值),可以通过空间平均、频率平均,或同时采用以上2种平均方式。
2 基于混响水池法的应用 2.1 在水下声源辐射声功率测量中的应用采用混响水池法可测量水下声源的辐射声功率,从而对水下声源的噪声水平进行评价。
为测量某推进器电机的辐射噪声以评估推进器电机的减振降噪效果。某推进器实物图如图 3。

|
Download:
|
| 图 3 固定于混响水池中的某推进器电机 Fig. 3 A propulsion motor fixed in the reverberation pool | |
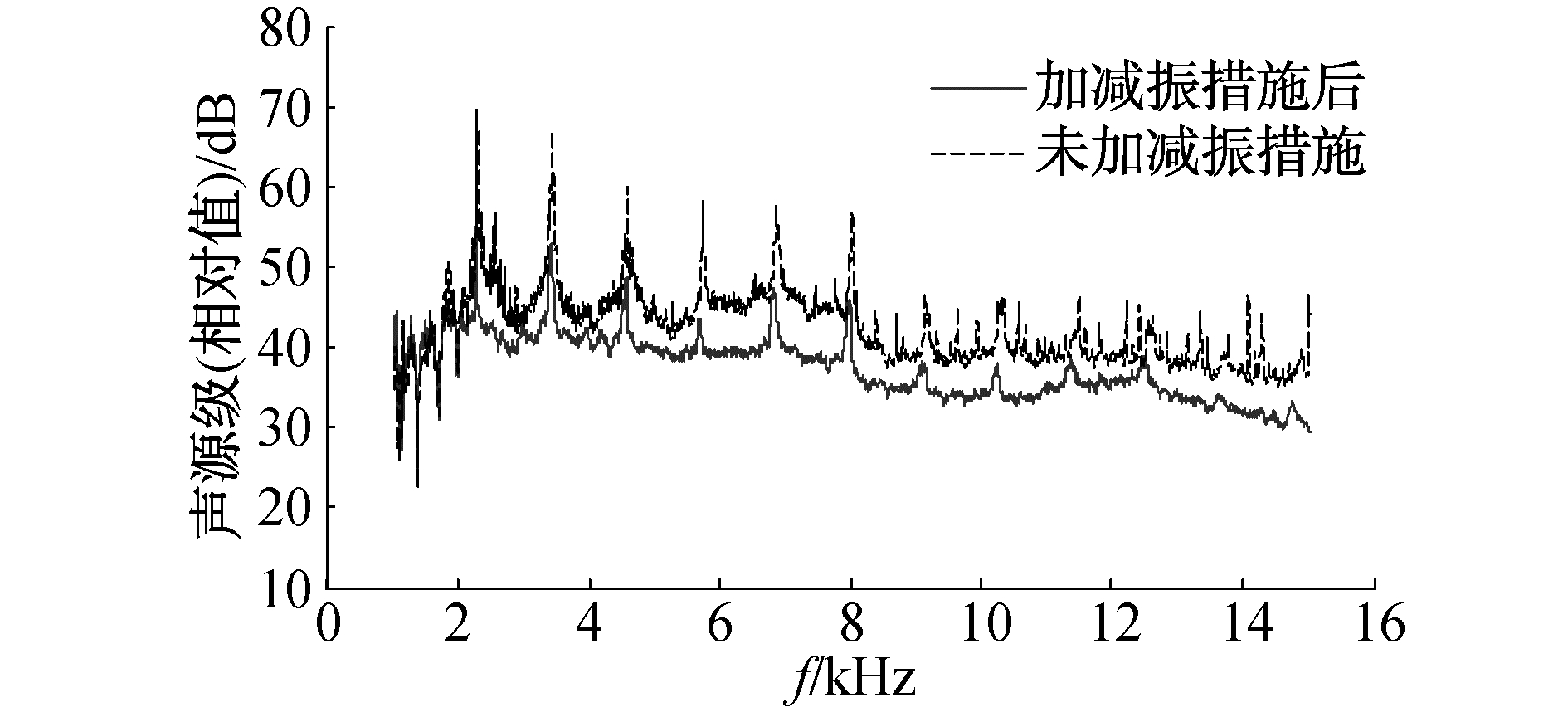
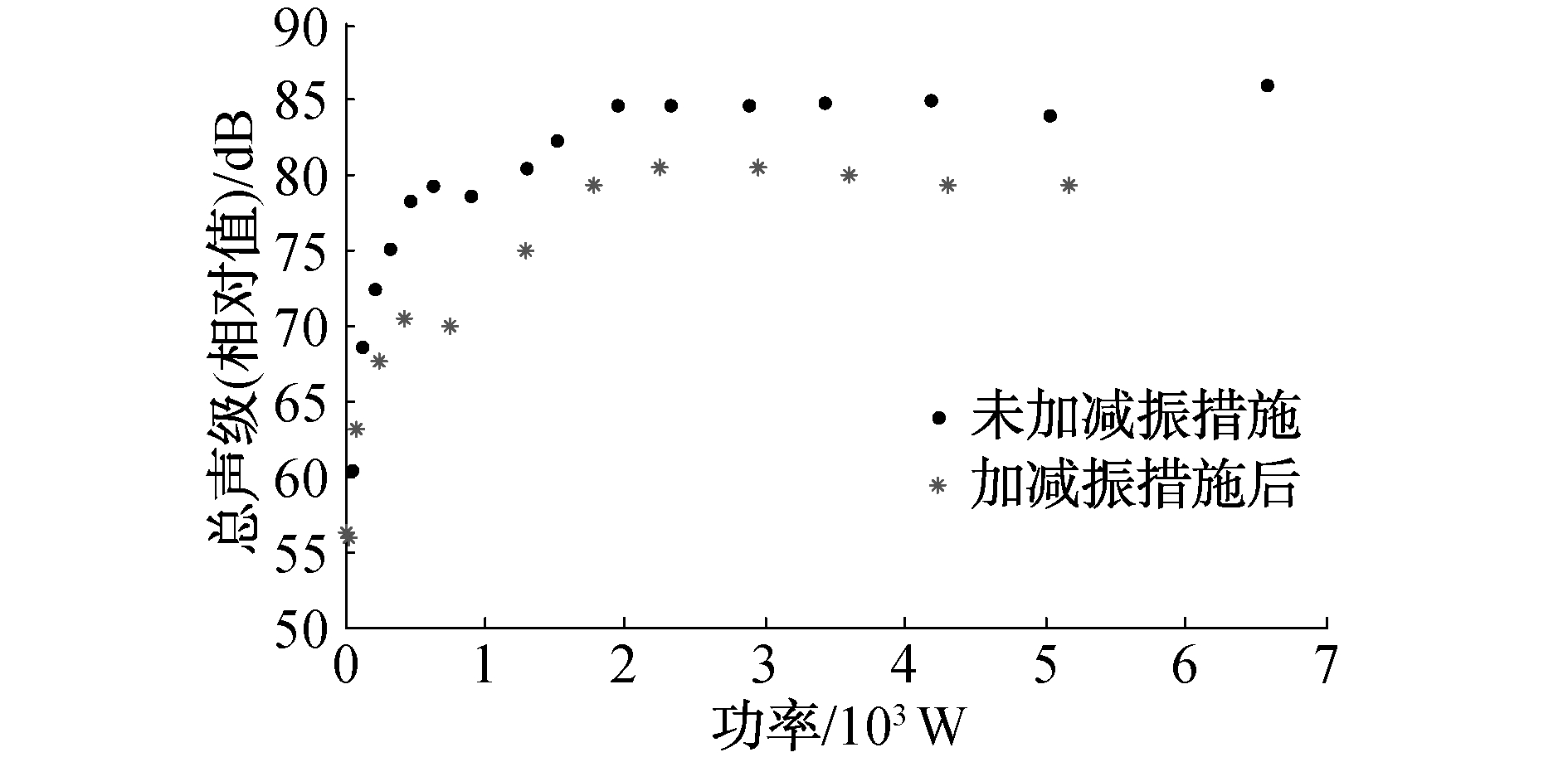
在混响水池中,测量了加减振装置前后的推进器电机的辐射噪声,推进器电机的辐射声功率测量结果如图 4及图 5所示。由此可见:加减振装置后,推进器电机的总声级平均降低5 dB,主要峰值频率噪声降低超过10 dB。因此,通过混响水池法测量加减振装置前后推进器电机的辐射噪声,就可以对不同状态下推进器电机的辐射噪声水平进行评价。
|
Download:
|
| 图 4 加减振装置前后推进器电机噪声比较 Fig. 4 Noise comparison of a propulsion motor before and after adding vibration reduction device | |
|
Download:
|
| 图 5 加减振装置前后推进器电机总声级比较 Fig. 5 Comparison of total sound level of a propulsion motor before and after adding vibration reduction device | |
针对在管路中直接测量管路噪声传感器受流冲击导致测量结果畸变问题,提出了混响水池测量方法。通过把管路系统的管口引入到混响水池中,针对不同频段,分别采用近场直接测量法与远场空间平均法相结合测得管路系统的管口辐射噪声,并通过各噪声源单独工作的方式,采用以上测量方法将不同噪声源对管路系统的噪声作用进行评价。
若把管路系统的管口引入到混响水池中,设管口在自由场中辐射声功率为W,当测量频率大于混响场的截止频率fs时,可按式(14)测量管口的声辐射; 当测量频率低于Schroeder截止频率fs时,管口的辐射声功率级可通过近处直接测量得到:
| $ {\rm{SPL}} = {\rm{SWL}} - 20\lg r - 10\lg (4{\rm{ \mathsf{ π} }}) $ | (19) |
式中:SWL(dBre0.67×10-18W)表示声源的声功率级,SPL(dBre1μPa)表示表示在近场测量的声压级; 测量直达声需满足远场条件,即r>a2/λ,其中a为通海口管口截面外径,λ为波长,由测量频率所决定,此条件在低于fs的低频段较容易满足。
由于直接法测量距管口较近,管口流体冲击对测量结果有一定影响,因此,只在低频段(f<fs)采用此方法,当f>fs时采用远场的空间平均法进行测量,避免了管口流体冲击对测量结果的影响。
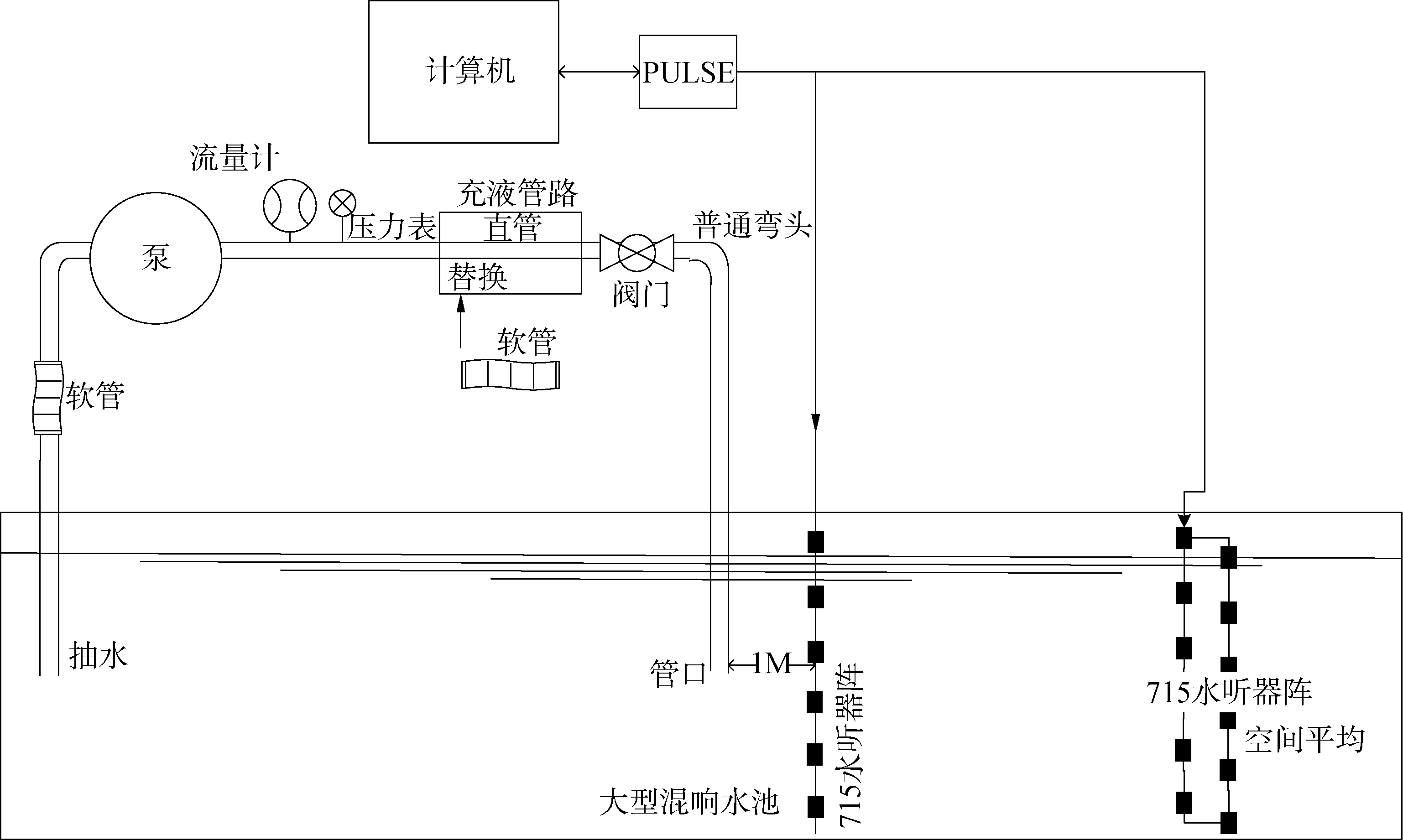
基于混响水池的管口声辐射分频段测量方法,建立了管路系统管口声辐射测量系统,如图 6所示。图 6左侧为一管路系统,系统中包含泵、金属直管、阀门、弯头等设备。离心泵工作时会产生与转速成倍频的机械噪声; 离心泵周期性改变管内液体压力,这些压力通过通海管路管口释放,形成脉动压力,影响管路系统管口处的辐射噪声; 机械振动与流体脉动压力会激励管壁,产生结构振动噪声。这些噪声相互耦合叠加,与流体在管口喷射产生的流噪声一起在管口处辐射。
|
Download:
|
| 图 6 管路系统管口辐射声功率测量系统 Fig. 6 The radiated sound power measurement system of the nozzle from the pipeline system | |
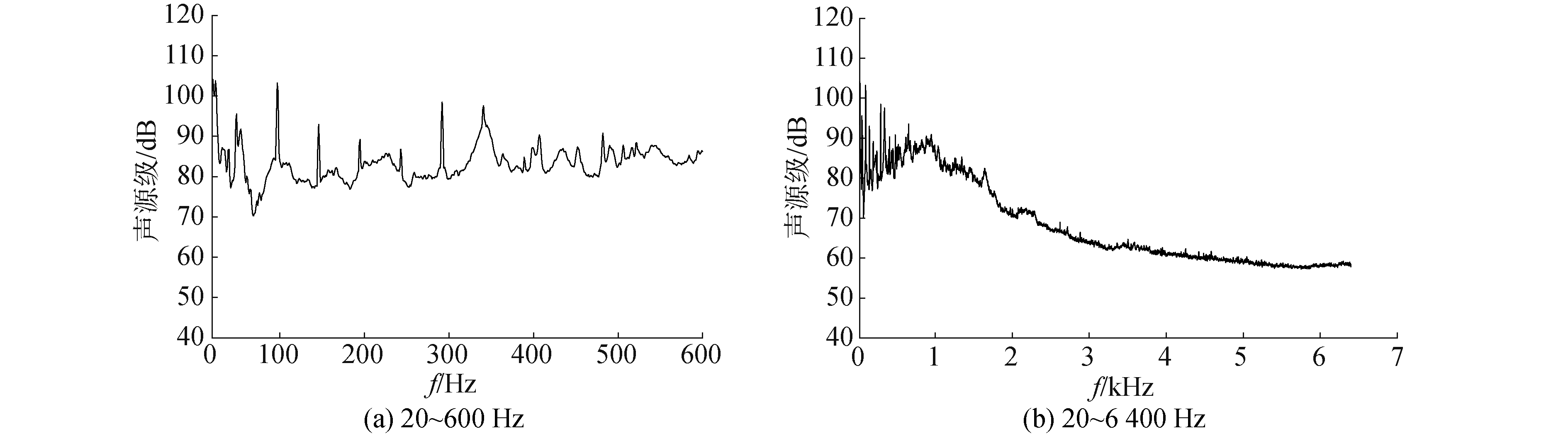
管口声辐射的测量结果如图 7所示,工况为:泵+直管+正常弯头; 流量:37.6 m3/h, 得到声源级为118.77 dB,管路系统的管口辐射噪声主要集中在2 000 Hz以下的低频段,其中500 Hz以下主要以50 Hz及其倍频线谱为主,主要为离心泵引入的结构振动。500~2 000 Hz以连续谱为主,主要为流噪声及流体脉动压力在管口处产生的声辐射。
|
Download:
|
| 图 7 整体管路系统管口辐射声功率测量结果 Fig. 7 The radiated sound power measurement results of the nozzle of the overall pipeline system | |
混响水池(箱)法测量材料的吸声系数是通过分别测量布放吸声材料前后混响水池(箱)内的混响时间,再计算材料的吸声系数。由于混响水池(箱)不满足扩散性场条件,此时在混响水池(箱)中设置多个测量点,并在每个测量点进行多次重复,通过多点的空间平均及每个点的时间平均,即时空平均以减少声场不均匀性对吸声系数测量结果的影响。根据每个频段的混响时间可以计算吸声系数:
| $ {\alpha _s} = \frac{{55.3V}}{{c \cdot S}}\left( {\frac{1}{{\langle {T_{60\_2}}\rangle }} - \frac{1}{{\langle {T_{60\_1}}\rangle }}} \right) $ | (20) |
式中:αs为吸声材料的混响水池(箱)法吸声系数测量结果; S为试件面积; 〈T60_1〉和〈T60_2〉为布放试件前后混响水池(箱)内时空平均混响时间; c为介质中声速。
在保持试件面积相同的情况下,通过分割试件为不同块数并按一定方式进行布放,来比较试件不同布放方式对吸声系数测量结果的影响。在保持试件面积为6 m2的情况下,分别进行集中式布放; 试件分为2块,每块尺寸为2 m×1.5 m; 试件平均分为3块,每块尺寸为2 m×1 m。试件在混响水箱长度方向上平行布放,在布放过程中应保持试件与声源距离不少于1 m,距宽度方向壁面距离不少于0.5 m,距长度方向壁面距离不少于1.5 m。实验试件现场布置见图 8。

|
Download:
|
| 图 8 试件实验布置 Fig. 8 The layout of the test specimens | |
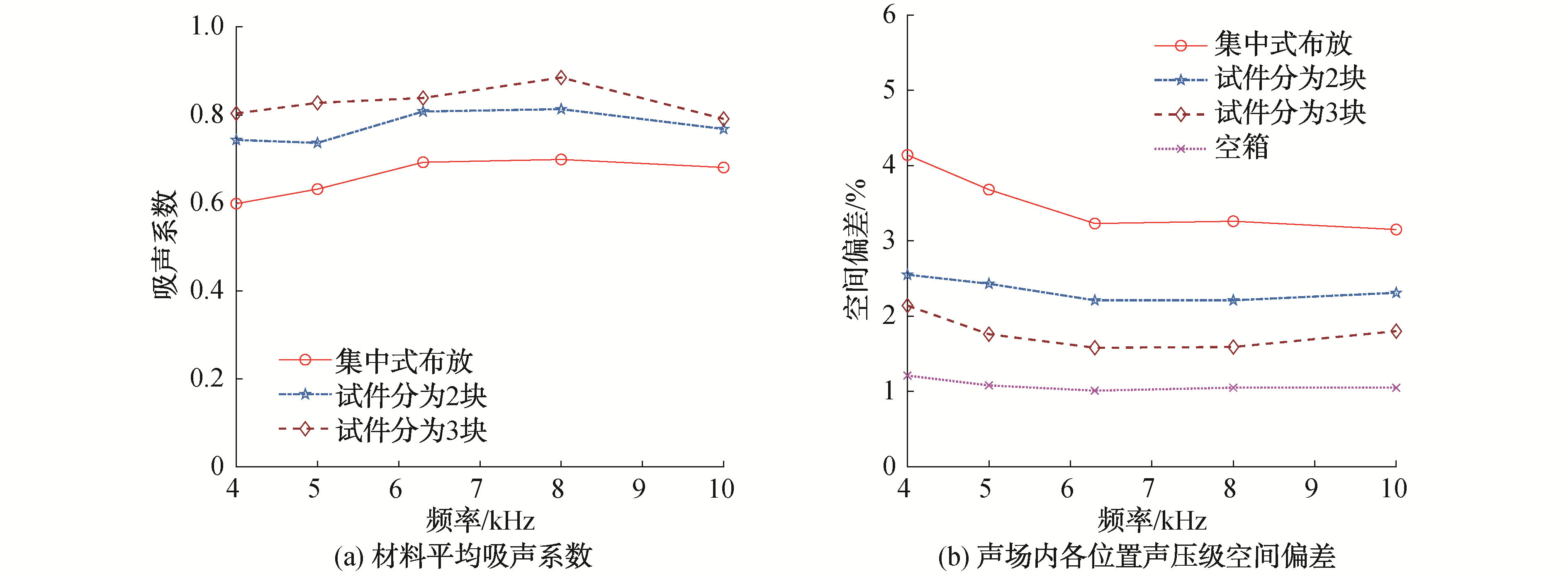
图 9为试件集中式布放、分为2块以及3块分布式布放情况下,各1/3倍频程频带试件吸声系数测量结果以及3种不同布放方式和混响水箱空箱状态时混响水箱内声压级的空间偏差。通过图 6(a)可以看出,分布式布放吸声系数测量结果优于集中式布放; 试件分为3块时材料吸声系数测量值最大。图 6(b)为不同布放方式的声压级空间偏差,采用集中式布放时声压级空间偏差最大,吸声材料试件对声场扩散性影响较大,吸声系数测量结果偏小; 试件分为3块布放时声压级空间偏差与空箱最接近,声场扩散性最好,吸声系数测量结果最准确。因此,采用分布式布放方式时吸声材料试件吸声系数测量结果优于集中式布放方式; 对于分布式布放方式,在满足试件间距d>2λ及声源与试件间距r>2rh,试件总面积一定的情况下,试件块数越多,声场扩散性越好,吸声系数测量越准确。
|
Download:
|
| 图 9 试件面积为6 m2时分布式布放测量结果 Fig. 9 Distributed deployment measurement results when the specimen area is 6 m2 | |
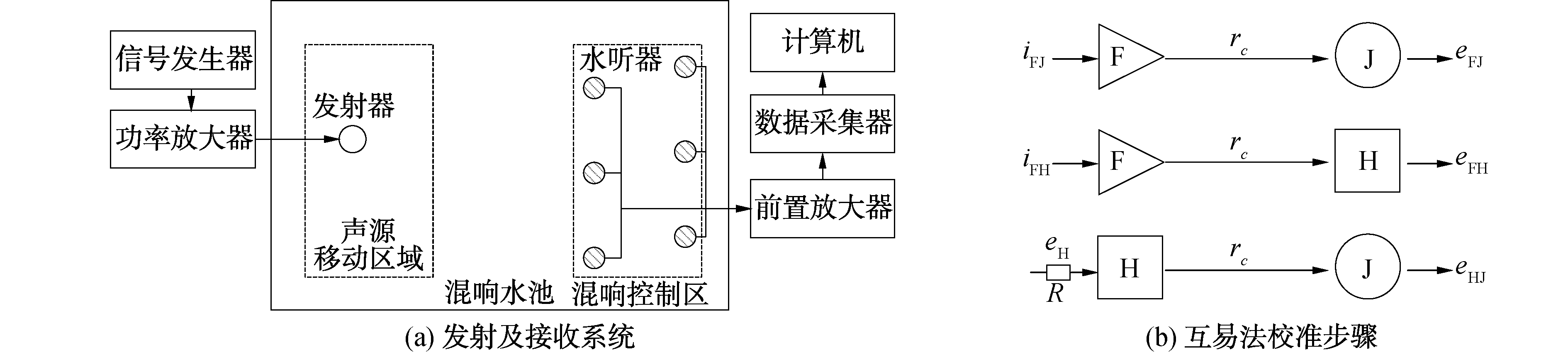
混响水池法的又一重要应用在于进行水听器的校准,根据混响水池声场的互易原理和水声换能器机电互易原理,借助空间平均测量技术,完成了混响水池的水听器互易校准。校准在一个尺度为长9 m、宽3 m、水深1.8 m的混响水箱中进行,校准试验系统如图 10所示。
|
Download:
|
| 图 10 混响水箱互易法水听器校准系统 Fig. 10 Reverberation tank reciprocity hydrophone calibration system | |
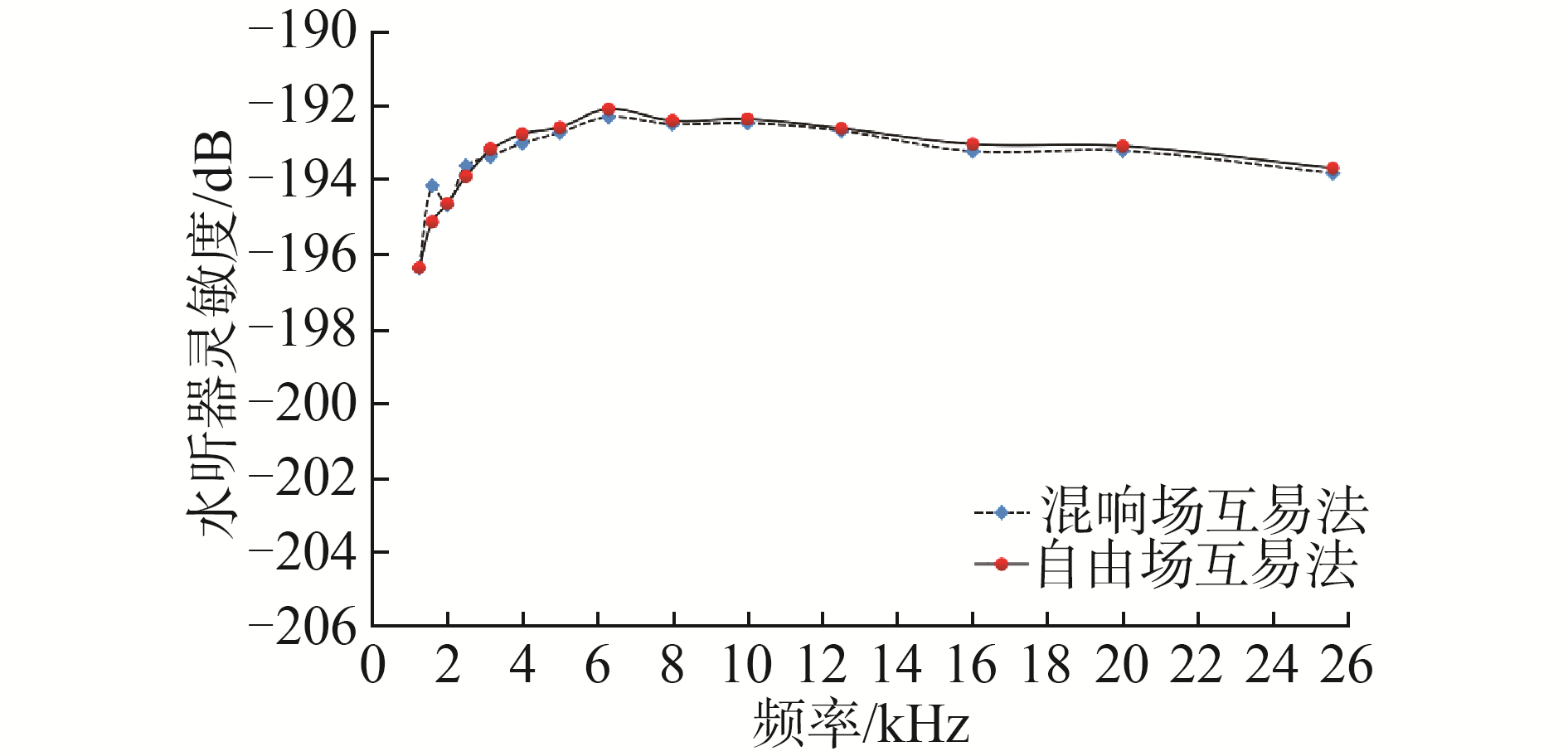
混响水箱水听器互易校准过程如下:1)将发射换能器F作为发射器向水箱中辐射单频正弦信号,互易水听器H和接收换能器J作为接收器,接收器采用空间扫描方法,在水箱中做往复S型扫描移动,移动过程中数据采集器测量接收器末端的开路输出电压,经过功率的空间平均计算得到互易换能器开路电压〈eFH〉和接收换能器的开路输出电压〈eFJ〉; 2)将互易换能器H作为发射器,接收换能器J作为接收器,同样采用空间扫描方法和空间平均,得到接收换能器开路输出电压〈eHJ〉,同时测量测量标准电阻两端电压〈eH〉。根据以上两步测量数据,按式(21)得到待测水听器J的自由场电压灵敏度MJ,如图 11所示。
|
Download:
|
| 图 11 混响水箱中互易法校准得到的水听器灵敏度 Fig. 11 Sensitivity of hydrophone obtained by reciprocity calibration in the reverberation tank | |
| $ {M_J} = {\left( {\frac{{\langle {e_{{\rm{FJ}}}}\rangle \langle {e_{{\rm{HJ}}}}\rangle }}{{\langle {e_{{\rm{FH}}}}\rangle \langle {e_{\rm{H}}}\rangle }}R{J_r}} \right)^{1/2}} $ | (21) |
对同一个水听器在消声水池中采用自由场互易法测量灵敏度,结果证明:采用混响场互易校准结果与自由场互易校准结果基本一致,接收水听器在低频段混响水池法与自由场测量结果相差不超过0.8 dB,在高频段内相差不超过0.3 dB。
3 结论1) 基于简正波理论及实际水池阻抗边界,推导了声源作用下离声源较远处的混响控制区内空间平均声压级与声源辐射声功率级之间的关系,建立了混响水池理论,根据混响水池理论建立的混响水池测量方法,不再要求声场满足扩散条件,这就给混响室声学测量带来很大方便,拓展了测量范围,提高了测量精度;
2) 采用混响水池法在混响水池中测量的水下推进器电机的辐射声功率级与海上采用包面法测得的辐射声功率级的1/3倍频程频带结果相差不超过1.5 dB,由此验证了混响水池法测量的准确性;
3) 混响水池测量方法可应用于水下声源的辐射声功率测量、管路噪声测量评价、材料吸声系数测量及水听器的校准;
4) 若条件允许此测量方法也可用于小型水下航行体辐射声功率的测量及评价研究。
| [1] |
MORSE P M, UNO INGARD K. Theoretical acoustics[M]. New York: McGraw-Hill Inc, 1967.
(  0) 0)
|
| [2] |
KUTTRUFF H. Room acoustics[M]. 4th ed. London, UK: Spon Press, 2000.
(  0) 0)
|
| [3] |
马大猷. 论室内声场[J]. 声学学报, 2003, 28(2): 97-101. MA Dayou. Theory of sound field in a room[J]. Acta acustica, 2003, 28(2): 97-101. (  0) 0)
|
| [4] |
马大猷. 室内声场公式[J]. 声学学报, 1989, 14(5): 383-385. MA Dayou. Formulae of sound field in enclosures[J]. Acta acustica, 1989, 14(5): 383-385. (  0) 0)
|
| [5] |
马大猷. 室内稳态声场[J]. 声学学报, 1994, 19(1): 13-21. MA Dayou. Steady-state sound field in enclosures[J]. Acta acustica, 1994, 19(1): 13-21. (  0) 0)
|
| [6] |
马大猷. 复议室内稳态声场公式[J]. 声学学报, 2002, 27(5): 385-388. MA Dayou. The formula of sound field in a room, re-examination[J]. Acta acustica, 2002, 27(5): 385-388. (  0) 0)
|
| [7] |
KUTTRUFF H. Room acoustics[M]. 3rd ed. New York: Elsevier Applied Science, 1991.
(  0) 0)
|
| [8] |
PIERCE A D. Acoustics[M]. New York: Acoustical Society of America, 1989.
(  0) 0)
|
| [9] |
CREMER L, MVLLER H A. Principles and applications of room acoustics[M]. New York: Applied Science Publishers, Ltd, 1978.
(  0) 0)
|
| [10] |
KINSLER L E. Fundamentals of acoustics[M]. 3rd ed. New York: John Wiley and Sons, 1982.
(  0) 0)
|
| [11] |
MORSE P M, UNO INGARD K. Theoretical acoustics[M]. New York: McGraw-Hill Inc, 1967.
(  0) 0)
|
| [12] |
MAILING JR C G. Calculation of the acoustic power radiated by a monopole in a reverberation chamber[J]. The journal of the acoustical society of America, 1967, 42(4): 859-865. DOI:10.1121/1.1910658 (  0) 0)
|
| [13] |
WATERHOUSE R V. Noise measurement in reverberant rooms[J]. The journal of the acoustical society of America, 1973, 54(4): 931-934. DOI:10.1121/1.1914349 (  0) 0)
|
| [14] |
WATERHOUSE R V. Interference patterns in reverberant sound fields[J]. The journal of the acoustical society of America, 1955, 27(2): 247-258. DOI:10.1121/1.1907509 (  0) 0)
|
| [15] |
SCHAFFNER A. Accurate estimation of the mean sound pressure level in enclosures[J]. The journal of the acoustical society of America, 1999, 106(2): 823-827. DOI:10.1121/1.427099 (  0) 0)
|
| [16] |
MAIDANIK G. Response of ribbed panels to reverberant acoustic fields[J]. The journal of the acoustical society of America, 1962, 34(6): 809-826. DOI:10.1121/1.1918200 (  0) 0)
|
| [17] |
LUDWIG G R. An experimental investigation of the sound generated by thin steel panels excited by turbulent flow (boundary layer noise)[R]. Toronto: University of Toronto, 1987.
(  0) 0)
|
| [18] |
SCHULTZ T J. Outlook for in-situ measurement of noise from machines[J]. The journal of the acoustical society of America, 1973, 54(4): 982-984. DOI:10.1121/1.1914356 (  0) 0)
|
| [19] |
HVBNER G. Analysis of errors in measuring machine noise under free-field conditions[J]. The journal of the acoustical society of America, 1973, 54(4): 965-975. (  0) 0)
|
| [20] |
HVBNER G. Qualification procedures for free-field conditions for sound-power determination of sound sources and methods for the determination of the appropriate environmental correction[J]. The journal of the acoustical society of America, 1977, 61(2): 456-464. DOI:10.1121/1.381285 (  0) 0)
|
| [21] |
SABINE W C. Collected papers on acoustics[M]. New York: Harvard University Press, 1964.
(  0) 0)
|
| [22] |
LUBMAN D. Spatial averaging in sound power measurements[J]. Journal of sound and vibration, 1971, 16(1): 43-58. DOI:10.1016/0022-460X(71)90394-4 (  0) 0)
|
| [23] |
SEPMEYER L W. Computed frequency and angular distribution of the normal modes of vibration in rectangular rooms[J]. The journal of the acoustical society of America, 1965, 37(3): 413-423. DOI:10.1121/1.1909344 (  0) 0)
|
| [24] |
SCHROEDER M R. Frequency-correlation functions of frequency responses in rooms[J]. The journal of the acoustical society of America, 1962, 34(12): 1819-1823. DOI:10.1121/1.1909136 (  0) 0)
|
| [25] |
MALING JR G C. Computer studies of mode-spacing statistics in reverberation rooms[J]. Journal of sound and vibration, 1971, 16(1): 79-87. DOI:10.1016/0022-460X(71)90397-X (  0) 0)
|
| [26] |
NUTTER D B, LEISHMAN T W, SOMMERFELDT S D, et al. Measurement of sound power and absorption in reverberation chambers using energy density[J]. The journal of the acoustical society of America, 2007, 121(5): 2700-2710. DOI:10.1121/1.2713667 (  0) 0)
|
| [27] |
尚大晶, 李琪, 商德江, 等. 水下声源辐射声功率测量实验研究[J]. 哈尔滨工程大学学报, 2010, 31(7): 938-944. SHANG Dajing, LI Qi, SHANG Dejiang, et al. Measurement of the radiated power of sound sources in a reverberation pool[J]. Journal of Harbin Engineering University, 2010, 31(7): 938-944. (  0) 0)
|
| [28] |
BLAKE W K, MAGA L J. Chamber for reverberant acoustic power measurements in air and in water[J]. The journal of the acoustical society of America, 1975, 57(2): 380-384. DOI:10.1121/1.380452 (  0) 0)
|
| [29] |
俞孟萨, 吕世金, 吴永兴. 半混响环境中水下结构辐射声功率测量[J]. 应用声学, 2001, 20(6): 23-27. YU Mengsa, LYU Shijin, WU Yongxing. The determination of radiated sound power from underwater structures in a semi-reverberant environment[J]. Applied acoustics, 2001, 20(6): 23-27. (  0) 0)
|
| [30] |
王春旭, 邹建, 张涛, 等. 水下湍射流噪声试验研究[J]. 船舶力学, 2010, 14(1/2): 172-180. WANG Chunxu, ZOU Jian, ZHANG Tao, et al. Experimental measurements of submerged free jet noise[J]. Journal of ship mechanics, 2010, 14(1/2): 172-180. (  0) 0)
|
| [31] |
杜功焕, 朱哲民, 龚秀芬. 声学基础[M]. 3版. 南京: 南京大学出版社, 2012. DU Gonghuan, ZHU Zhemin, GONG Xiufen. Acoustic basis[M]. 3rd ed. Nanjing: Nanjing University Publishing Press, 2012. (  0) 0)
|
| [32] |
SCHROEDER M R. Effect of frequency and space averaging on the transmission responses of multimode media[J]. The journal of the acoustical society of America, 1969, 46(2A): 277-283. DOI:10.1121/1.1911685 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


