2. 海洋信息获取与安全工业和信息化部重点实验室(哈尔滨工程大学), 黑龙江 哈尔滨 150001;
3. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001;
4. 中国船舶重工集团公司 第七一九研究所, 湖北 武汉 430064
2. Key Laboratory of Marine Information Acquisition and Security(Harbin Engineering University), Ministry of Industry and Information Technology, Harbin 150001, China;
3. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China;
4. No. 719 Research Institute of China Shipbuilding Industry Corporation, Wuhan 430064, China
近年来,三维前视声呐作为一种重要的水下探测系统,在海底地形测绘、石油管道检测、沉船打捞、水下航行器避障、水下机器视觉等领域具有广泛的应用[1-3]。目前,国外多个公司已研制出实用化的三维前视声呐设备。其中典型代表如TriTech公司Eclipse[4]、CodaOctopus公司的Echoscope4G[5],Reson公司SeaBat 7130[6]等。Eclipse声呐采用“T”型阵列结构,以水平向波束形成、垂直向扫描的方式完成三维探测,然而垂直扫描方式对于三维探测来说仍然效率偏低;Echoscope4G声呐则采用了二维接收面阵设计,采用二维方位搜索技术完成三维探测,其阵元总数为M2=482,系统复杂度可近似描述为O(M2)。显然地,该声呐虽然具备目标三维探测能力,但系统实现复杂度非常高。相比之下,SeaBat 7130声呐采用二维稀疏矩形面阵设计,其阵元总数为MN, 系统复杂度可近似描述为O(MN)。因而,相比Echoscope声呐,SeaBat 7130声呐系统具有更低的系统复杂度。
现阶段公开报道国内三维前视声呐研制工作中,文献[7]采用“T”型阵列结构,文献[8]采用覆盖不同探测区域的多条水平线阵结构,垂直向均采用相控扫描的方式完成垂直向目标方位估计,也即多次发射接收探测信号,进行多Ping联合三维目标探测,探测效率较低。本文对比分析国内外前视声呐系统方案的局限性,在文献[6, 9]基础上,提出具备单Ping高效率三维探测能力的前视声呐系统解决方案,并进行了理论推导、计算机仿真和工程实现验证。该系统方案涉及了一种二维稀疏阵布阵方案以及基于此基阵模型的一维和Vernier联合方位估计(one-dimensional and Vernier combined DOA estimation, ODVCDE)算法;仿真实验,验证了所提出方法在估计精度和计算复杂度方面优于2D波束形成算法;通过水池主被动目标探测实验和外场试验,验证了声呐系统和相关算法的工程实用性。
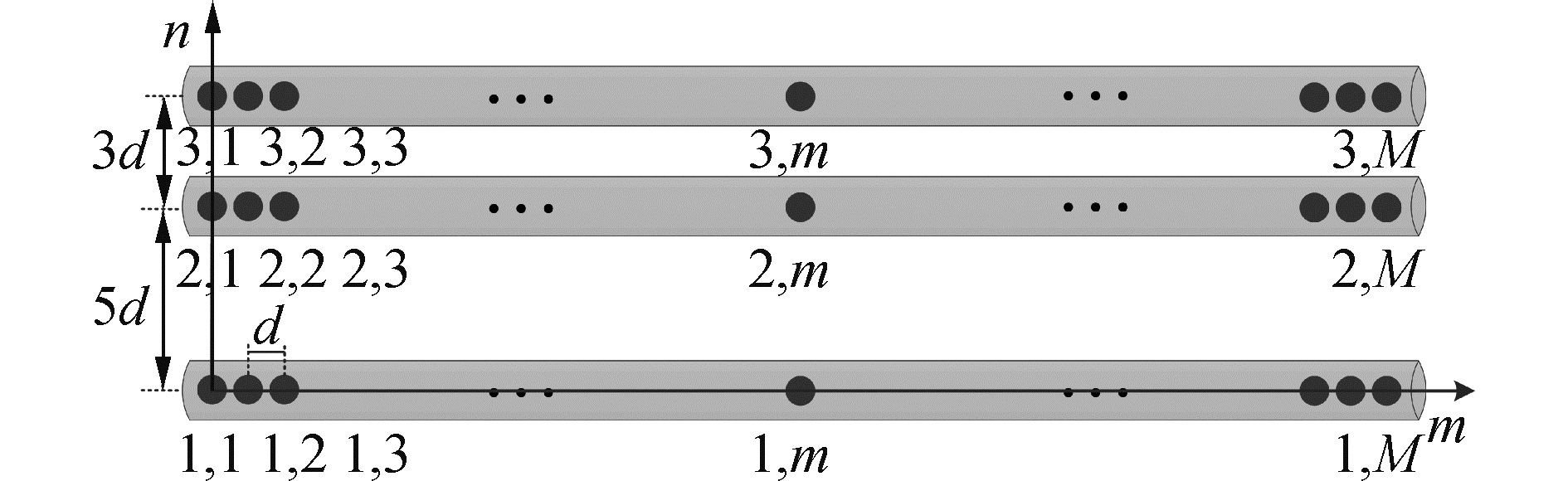
1 稀疏阵列模型本文设计的前视声呐接收阵列结构如图 1所示。该阵列为二维面阵设计,由3个均匀线性子阵构成,3个子阵之间阵元间距由一对互质的整数(5和3)构成,其中每一个子阵由M个阵元构成,为了避免相位模糊阵元间距为半波长d=λ/2[10-11]。因此,该阵列由MN个阵元组成,其中,M=48、N=3。
|
Download:
|
| 图 1 前视声呐接收阵列结构 Fig. 1 Receiving array configuration in forward-looking sonar | |
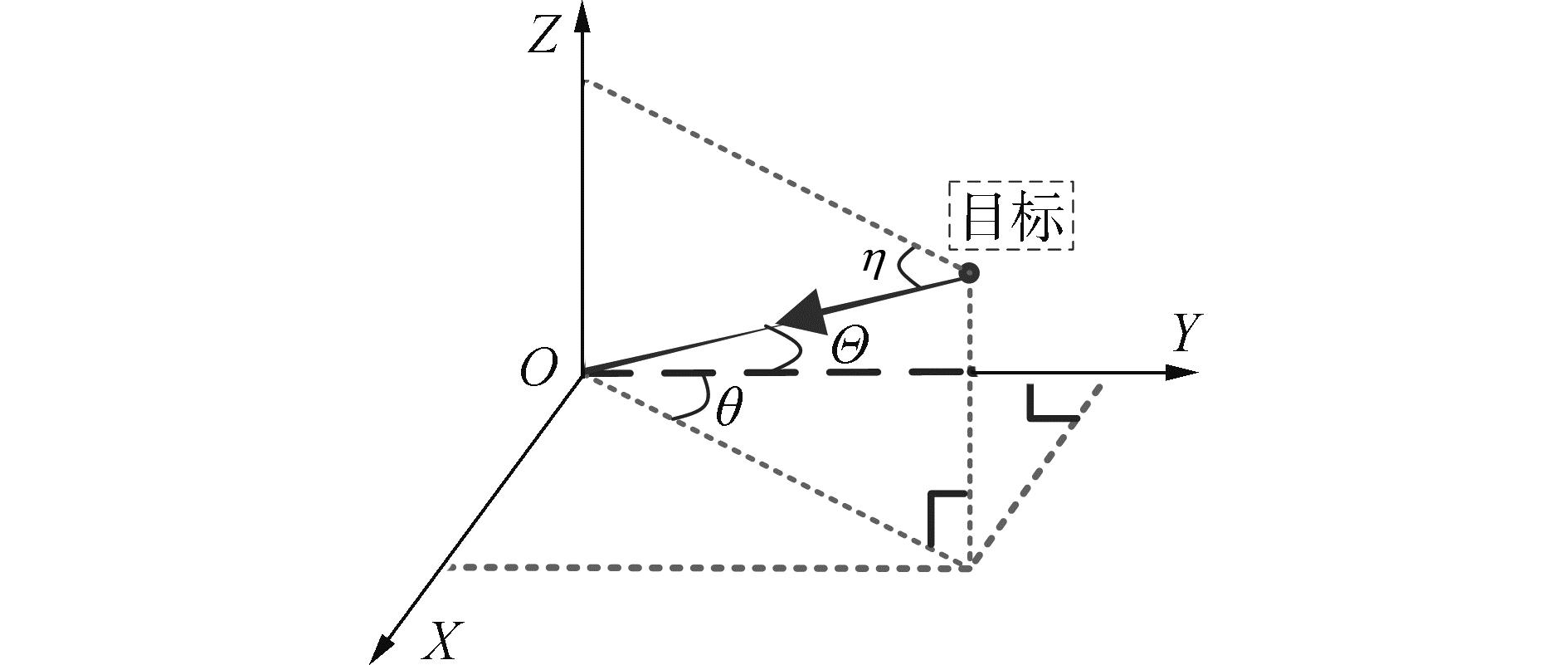
信号模型如图 2所示,在快拍号t,考虑K个远场窄带相干回波信号同时入射二维接收阵列,第n行第m列阵元接收回波信号模型可表述为:
|
Download:
|
| 图 2 三维笛卡尔坐标系下的目标方位 Fig. 2 Orientation representation of the target in three-dimensional Cartesian coordinates | |
| $ \begin{array}{*{20}{l}} {{{\langle x\rangle }_{m,n}}(t) = \sum\limits_{k = 1}^K {\langle s(} t){\rangle _{m,n}}\exp ({\rm{j}}{{\langle {\tau _k}\rangle }_{m,n}}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\langle n(t)\rangle }_{m,n}},t = 1,2, \cdots ,L} \end{array} $ | (1) |
| $ \begin{array}{l} {\langle {\tau _k}\rangle _{m,n}} = 2{\rm{ \mathsf{ π} }}d\sqrt {{{(m\cos {\eta _k}\cos {\theta _k})}^2} + {{({S_n}\sin {\eta _k})}^2}} /\lambda \approx \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2{\rm{ \mathsf{ π} }}d(m\cos {\eta _k}\cos {\theta _k} + {S_n}\sin {\eta _k})/\lambda \end{array} $ | (2) |
式中:s(t)=exp(j2πft/fs)为主动探测信号;f和fs分别为工作频率和采样频率;n(t)为加性复高斯白噪声且与探测信号s(t)统计独立;θk和ηk分别为方位角和俯仰角;λ=c/f为波长;d为阵元间距。本文中,第1行第1列阵元设置为相位参考点。
| $ {S_n} = \left\{ {\begin{array}{*{20}{l}} {0,}&{n = 1}\\ {5,}&{n = 2}\\ {8,}&{n = 3} \end{array}} \right. $ | (3) |
将式(1)改写为矩阵形式:
| $ \mathit{\boldsymbol{X}}(t) = \sum\limits_{k = 1}^K {{\mathit{\boldsymbol{A}}_k}} \odot \mathit{\boldsymbol{S}}(t) + \mathit{\boldsymbol{N}}(t),t = 1,2, \cdots ,L $ | (4) |
式中⊙为Hadamard乘积。其中,Ak∈CN×M,
| $ {\mathit{\boldsymbol{A}}_k} = \left[ {\begin{array}{*{20}{c}} {\exp ({\rm{j}}{{\langle {\tau _k}\rangle }_{1,1}})}& \cdots &{\exp ({\rm{j}}{{\langle {\tau _k}\rangle }_{1,M}})}\\ {\exp ({\rm{j}}{{\langle {\tau _k}\rangle }_{2,1}})}& \cdots &{\exp ({\rm{j}}{{\langle {\tau _k}\rangle }_{2,M}})}\\ {\exp ({\rm{j}}{{\langle {\tau _k}\rangle }_{3,1}})}& \cdots &{\exp ({\rm{j}}{{\langle {\tau _k}\rangle }_{3,M}})} \end{array}} \right] $ | (5) |
X(t)∈CN×M,S(t)∈CN×M,N(t)∈CN×M与导向矩阵Ak结构类似,这里不再赘述。
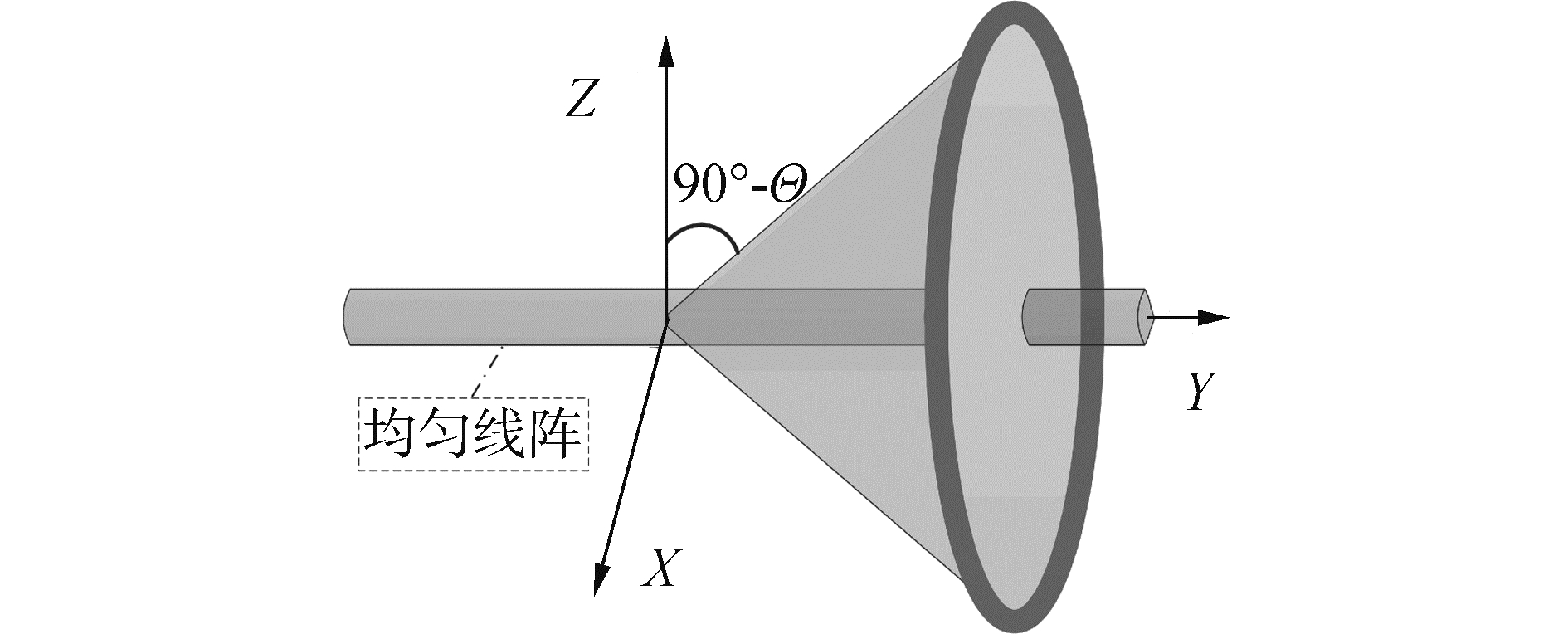
2 空间方位估计算法 2.1 空间角Θ估计根据线阵几何性质,空间域的导向波束具有锥形形状[12],也即沿同一锥面入射的信号具有相同的空间角,如图 3所示。
|
Download:
|
| 图 3 导向波束的三维波束 Fig. 3 Three-dimensional beam pattern of steered beams | |
对于空间角Θ估计问题,基于每一个均匀线性子阵,本文分别设置第1号阵元为相位参考点,进而本文有Sn=0,也即各子阵在空间角估计问题上的信号模型是一致的。第m号阵元相对参考阵元延迟可写作:
| $ {\langle {\tau _k}\rangle _{m,n}} = {\rm{ \mathsf{ π} }}md\cos {\varTheta_k}/\lambda $ | (6) |
进而,可直接使用一维方法完成空间方位估计。
依据空间角分析俯仰角可行解范围。根据如图 3所示的三维锥形波束图案,有:
| $ {{R_Y} = R\cos \varTheta} $ | (7) |
| $ {{R_Z} = R\sin \eta } $ | (8) |
式中:R表示阵列参考点与目标的距离;RY和RZ为R投影到Y轴和Z轴方向的距离,满足:
| $ {R^2} = {(R\cos \varTheta)^2} + {(R\sin \eta )^2} + R_X^2 $ | (9) |
显然RX2≥0,得到下面不等式:
| $ {\sin ^2}\varTheta \ge {\sin ^2}\eta $ | (10) |
由于Θ∈[0, π],η∈[-π/2, π/2],进而有:
| $ \left\{ {\begin{array}{*{20}{l}} {|\eta | \le \varTheta,}&{({\rm{ \mathsf{ π} }}/2 - \varTheta) \le 0}\\ {|\eta | \le {\rm{ \mathsf{ π} }} - \varTheta,}&{({\rm{ \mathsf{ π} }}/2 - \varTheta) > 0} \end{array}} \right. $ | (11) |
显然,俯仰角估计范围受空间角约束。例如,当Θ=140°时,|η|≤50°,此为下一节Vernier法解俯仰角的约束条件。
2.2 Vernier法[13-14]俯仰角估计由于子阵间阵元间距大于半波长,目标回波相位差可以在[-π, π]范围内展开:
| $ {\sin {\eta _p} = (2{\rm{ \mathsf{ π} }}p + \Delta {\varphi _{12}})/[{\rm{ \mathsf{ π} }}({S_1} - {S_2})]} $ | (12) |
| $ {\sin {\eta _q} = (2{\rm{ \mathsf{ π} }}q + \Delta {\varphi _{23}})/[{\rm{ \mathsf{ π} }}({S_2} - {S_3})]} $ | (13) |
式中:
| $ {\Delta {\varphi _{12}} = {\rm{angle}} (\langle X\rangle _1^*{{\langle X\rangle }_2})} $ | (14) |
| $ {\Delta {\varphi _{23}} = {\rm{angle}} (\langle X\rangle _2^*{{\langle X\rangle }_3})} $ | (15) |
式中:angle(·)为计算复数相位角的函数; 〈·〉*为取复数共轭的函数,〈X〉n表示取矩阵X中的第n行。进而由式(12)和式(13)得到目标回波方位的候选子集为:
| $ {\varLambda _p} = \{ {\eta _{12}}|p \in [\left\lfloor { - ({S_2} - {S_1})/2} \right\rfloor ,\left\lfloor {({S_2} - {S_1})/2} \right\rfloor ]\} $ | (16) |
| $ {\varLambda _q} = \{ {\eta _{23}}|q \in [\left\lfloor { - ({S_3} - {S_2})/2} \right\rfloor ,\left\lfloor {({S_3} - {S_2})/2} \right\rfloor ]\} $ | (17) |
根据互质特性,由候选子集S12和S23可得到目标回波方位估计:
| $ \eta = {S_{12}} \cap {S_{23}} $ | (18) |
然而,上述等式成立建立在相位差Δφ12和Δφ23估计无偏的前提下,为了提高对于估计误差的宽容性,本文定义下面Vernier法估计的正则化表达式:
| $ \eta = \mathop {{\rm{ argmin }}}\limits_{|\eta | \le |{{90}^\circ } - \varTheta|} |{\eta _{12}} - {\eta _{23}}| $ | (19) |
根据式(19)可得到俯仰角η估计。
2.3 基于最小角定理的方位角估计根据式(9),目标距离基阵参考点沿X轴分量为:
| $ {R_X} = \sqrt {{R^2} - {{(R\cos \varTheta)}^2} - {{(R\sin \eta )}^2}} $ | (20) |
进而,方位角可写作:
| $ \theta = \arctan ({R_X}/{R_Y}) = \arctan (\sqrt {{{\cos }^2}\eta - {{\cos }^2}\varTheta} /\cos \varTheta) $ | (21) |
简化后:
| $ {\sec ^2}\theta = {\cos ^2}\eta /{\cos ^2}\varTheta $ | (22) |
由于声呐功能定位为前视声呐,目标位于一、四、五、八卦限,有:
| $ \left\{ {\begin{array}{*{20}{l}} {\cos \varTheta = \cos \theta \cos \eta ,}&{一、五卦限}\\ { - \cos \varTheta = - \cos \theta \cos \eta ,}&{{\rm{四、八卦限}}} \end{array}} \right. $ | (23) |
整理得cos Θ=cos θcos η,也即最小角定理。对于方位角θk估计,由2.1节得到空间角估计Θk,由2.2节得到俯仰角估计ηk,再由最小角定理可得到方位角估计:
| $ {\theta _k} = \arccos (\cos {\varTheta_k}/\cos {\eta _k}) $ | (24) |
至此,完成目标二维方位估计(包括方位角θk和俯仰角ηk)的相关算法,总结相关算法流程如下:1)对MN个通道进行一维空间角搜索,得到Θ;2)由式(14)、(15)计算子阵间相位差Δφ12和Δφ23;3)由式(12)、(13)展开得到俯仰角候选子集Λp和Λq;4)由式(19)解算得到俯仰角估计η;5)结合步骤1)和步骤4)结果,由式(24)解算目标方位角θ。
系统复杂度分析:1)硬件复杂度。本文所述声呐硬件复杂度为MN个阵元,而Echoscope4G二维面阵声呐硬件复杂度为M2个阵元,这里N≪M,因而本文所述声呐基阵构型具有更低的硬件复杂度;2)计算复杂度。忽略算法中的俯仰角、方位角解算计算复杂度(相比空间角搜索计算复杂度可忽略不计),所提出算法计算复杂为O(MNB),而二维目标搜索方案计算复杂为O(M2B2),相比之下,所提出的算法计算复杂度仅为二维方法的N/MB,这里B为波束数,N≪M,N≪B,因而该方法具有更低的计算复杂度。
3 仿真及分析国外单Ping三维前视探测方案中,Echoscope4G声吶采用二维波束形成算法[5, 7],本节拟将所提出的算法与波束形成算法进行仿真比较,定量分析方位估计精度和算法计算复杂度。定义均方根误差(root mean square error,RMSE)为:
| $ {\rm{RMSE}} = \sqrt {\frac{1}{{K \cdot MC}}\sum\limits_{i = 1}^{MC} {\sum\limits_{k = 1}^K {{{({\xi _k} - {{\hat \xi }_{k,i}})}^2}} } } $ | (25) |
式中:
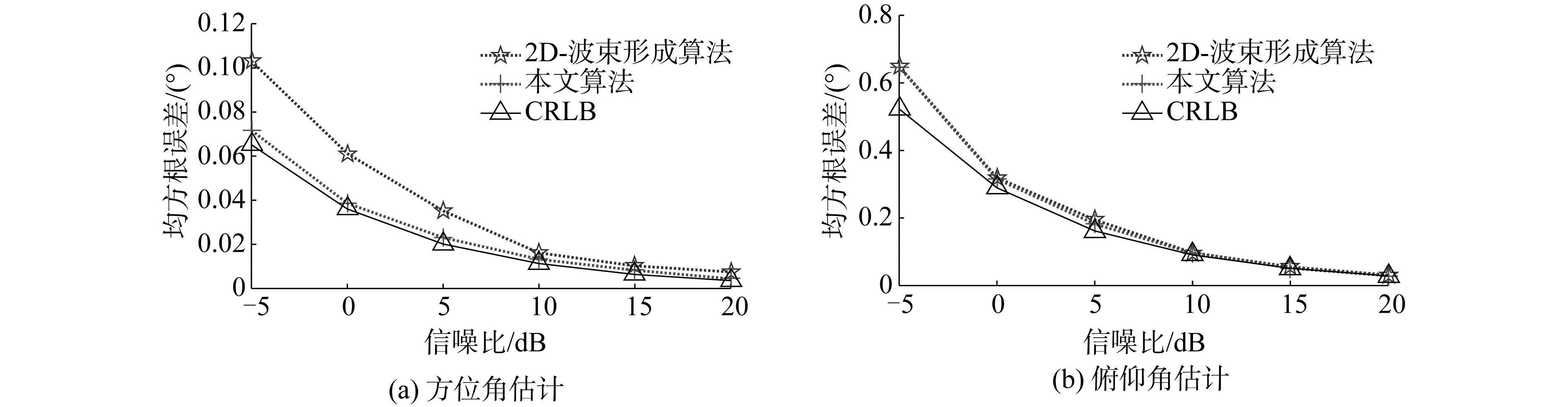
考虑一个方位角85°,俯仰角7°的回波信号,信噪比以5 dB为步长从-5 dB变化到20 dB,采用2D波束形成算法和本文提出的算法对回波空间方位进行估计,B=1 024,MC=1 000次蒙特卡洛仿真实验结果如图 4所示。计算机配置为Intel(R) Core(TM) i5-8250 u CPU,16 GB RAM。
|
Download:
|
| 图 4 仿真结果对比信噪比 Fig. 4 Simulated results versus SNR | |
如图 4所示为2种算法估计方差随信噪比变化曲线,2种算法估计均方根误差均随信噪比增加而单调递减,然而低信噪比条件下2种算法估计均方根误差稍差于CRLB,且随着信噪比的增加2种方法逐渐接近CRLB[15],所提出的方法估计性能方面优于2D波束形成算法。此外,本文统计2D波束形成算法和所提出的方法的平均计算时间分别为32.864 1 s和0.009 8 s,显然,所提出算法计算复杂度方面更优,这与2.2节的理论分析一致。
4 试验及结果分析为进一步检验上述算法的有效性,本文依托哈尔滨工程大学研制的三维前视声呐分别于哈尔滨工程大学信道水池、吉林市松花湖地区开展试验研究,以下试验中三维空间原点均设为接收基阵第1行第1列阵元。三维前视声呐关键参数如表 1所示。
| 表 1 三维前视声呐关键参数 Table 1 The key parameters of three-dimensional forward-looking sonar |
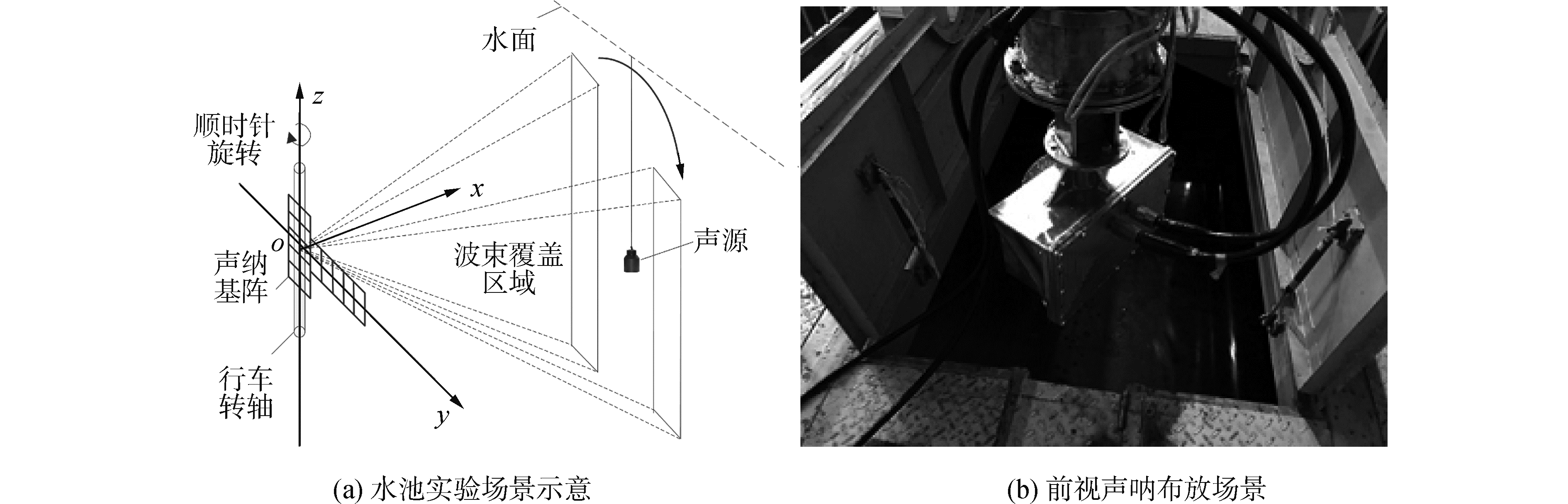
本节实验于哈尔滨工程大学水声技术重点实验室信道水池中开展,信道水池宽6 m,水深5 m,距离声呐基阵10 m处放置一个工作频率为150 kHz的声源,声呐基阵和声源均置于水面以下2.5 m,声源发射和声呐基阵接收机使用同步触发,声呐基阵分别竖直安装从-37°旋转至43°、水平安装从-71°旋转至72°,每隔1°旋转一次并采集声源发射信号,依托二维波束形成算法和所提出的算法进行实验数据处理。水池实验场景和三维前视声呐安装布放实景如图 5所示。
|
Download:
|
| 图 5 水池实验场景和前视声呐布放示意 Fig. 5 Deployment and rotating of the forward-looking sonar | |
如图 6所示为旋转至14°时各通道相位输出曲线,由图可见,随着阵元编号增加,相位连续变化。为了更清晰地描述相位差曲线,基阵从-37°旋转至43°,子阵间相位差曲线在图 7中给出。由图 7可见,子阵间相位差随基阵旋转角度连续变化,基本符合理论上的线性关系。

|
Download:
|
| 图 6 子阵输出相位箱线 Fig. 6 Phase boxplot of subarray output | |

|
Download:
|
| 图 7 子阵相位差箱线 Fig. 7 Phase differences boxplot between two subarrays | |
解析声源方位后的DOA估计如图 8所示。由图可见,估计的DOA随基阵旋转角度连续变化,基本符合理论上的线性关系。水池实验验证了第2节相关算法的有效性。值得注意的是,由于接收阵元存在幅度、相位等误差,估计结果与理论值存在一定误差。

|
Download:
|
| 图 8 方位估计结果 Fig. 8 Estimated results of DOA | |
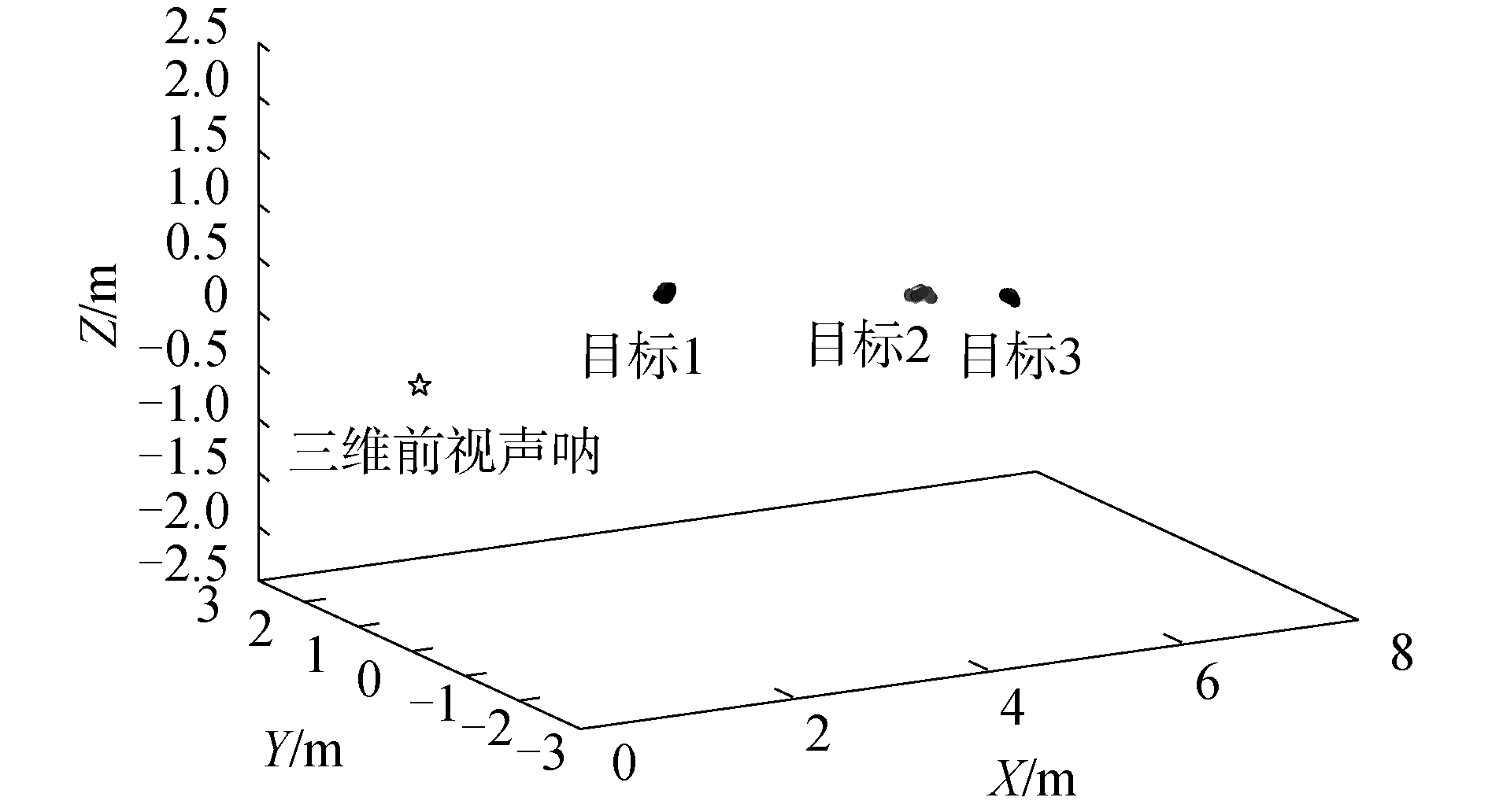
本实验同样于信道水池中开展,声呐基阵置于水面以下2.5 m,距离声呐基阵2.5、5.2、6.1 m处分别放置3个直径280 mm的塑料球目标,各目标距离水面深度分别为2.0、2.3、2.5 m。如图 9所示为应用波束形成技术形成的声呐图像。以声呐基阵原点所在位置为参考原点,目标估计结果图如图 10所示。

|
Download:
|
| 图 9 水池实验场景声图像 Fig. 9 Acoustic image of tank experiment scene | |
|
Download:
|
| 图 10 水池实验估计结果 Fig. 10 Estimated results in tank experiment | |
由图 10可见,依据本文所提出的算法能够对水池中目标方位角、俯仰角进行估计,联系回波到达时间,可完成目标的三维定位。
4.3 外场试验外场试验于2019年8月在吉林市松花湖进行。3个目标分别呈三角形布放,每个目标悬浮于水中;水面悬挂一个浮标;水底设置一个重物用于定位目标。3个目标均置于水面以下5 m位置处,声呐系统固定安装在舷侧并置于水面以下1 m位置处,采用光学激光测距仪测量3个目标距离声呐分别为157.1、160.7、165.7 m。通过声呐发射探测信号、接收回波数据可对目标方位进行估计。外场湖试场景及前视声呐、目标安装布放实景如图 11所示。

|
Download:
|
| 图 11 外场湖试场景及三维前视声呐、目标安装布放实景 Fig. 11 The scene of field lake experiment and deployment of the three-dimensional forward-looking sonar and targets | |
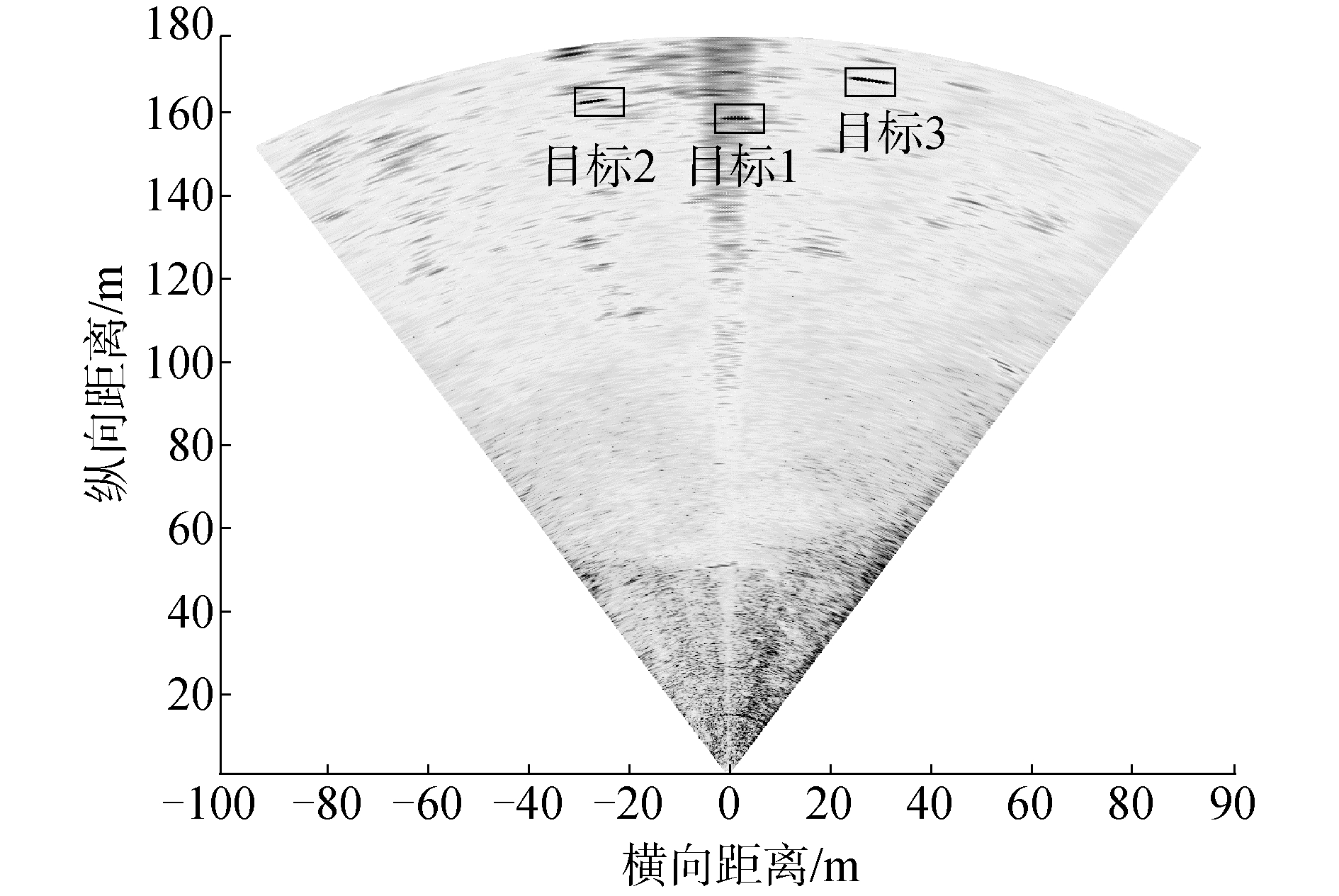
如图 12为应用波束形成技术形成声呐图像,可以显著地看出有3个目标。以声呐基阵原点所在位置为参考原点,应用本文中所提方法,目标三维空间位置估计结果如图 13所示。
|
Download:
|
| 图 12 外场试验场景声图像 Fig. 12 Acoustic image of field experiment scene | |

|
Download:
|
| 图 13 外场湖试估计结果 Fig. 13 Estimated results in field lake experiment | |
由图 13可见,依据本文所提出的算法能够对外场湖试布放的目标进行方位角、俯仰角估计,依据回波到达时间,可完成目标的三维定位。
5 结论1) 相比Echoscope4G三维前视声呐基于二维面阵的方案,所提出的方法具有更低的系统复杂度和实现成本,仅仅利用MN个阵元即可完成目标的三维探测,阵元数仅为二维方案的N/M,计算复杂度为二维方案的N/MB。
2) 仿真实验表明,相比2D波束形成算法,所提出的JSODVM算法具有更高的方位估计精度、更低的计算复杂度。结合三维前视声呐的水池、湖上试验进一步验证了上述算法能够准确估计目标在三维空间中的方位,工程实用性强。
本文更关注于相关算法的研究,在未来的研究中,将针对阵列校准这一问题开展深入研究。
| [1] |
HENLEY H, ZIMMERMAN M J. Performance of 3D forward looking sonar for bathymetric survey[C]//Proceedings of OCEANS 2017-Anchorage. Anchorage, AK, 2017: 1-9.
(  0) 0)
|
| [2] |
RUSSEL I, WRIGHT R G. Navigation SONAR: more than underwater radar realizing the full potential of navigation and obstacle avoidance sonar[J]. International Hydrographic Review, 2017: 41-60. (  0) 0)
|
| [3] |
ZIMMERMAN M J, HENLEY H. Applications of today's 3D forward looking sonar for real-time navigation and bathymetric survey[C]//Proceedings of OCEANS 2017-Anchorage. Anchorage, AK, 2017: 1-7.
(  0) 0)
|
| [4] |
Tritech International Ltd. Eclipse 3D imaging sonar product manual[EB/OL]. Aberdeen: Tritech International Ltd. [2020-05-20]. https://www.tritech.co.uk/media/support/manuals/eclipse-multibeam-sonar-operator-installation-manual0.pdf.
(  0) 0)
|
| [5] |
Coda Octopus Products Ltd. Echoscope 4G[EB/OL]. Scotland: Coda Octopus Products Ltd. [2020-05-20]. https://d1io3yog0oux5.cloudfront.net/_d5c808f4da6c3542e43d3cef98f952d3/codaoctopus/db/443/2846/brochure/Echoscope+4G+Datasheet+1.1.1.20.pdf.
(  0) 0)
|
| [6] |
Teledyne Reson. SeaBat F30[EB/OL]. Denmark: Teledyne Reson. [2020-05-20]. https://www.bluezonegroup.com.au/_literature_165599/SeaBat_F30_Product_Leaflet.
(  0) 0)
|
| [7] |
李婷婷.三维前视声纳的高分辨方位估计研究[D].哈尔滨: 哈尔滨工程大学, 2009: 10-12, 31-33. LI Tingting. The research of 3-D forward looking sonar on high resolution DOA estimation[D]. Harbin: Harbin Engineering University, 2009: 10-12, 31-33. (  0) 0)
|
| [8] |
王维.某型前视声纳信号处理系统的设计与实现[D].北京: 中国科学院大学, 2013: 15-20, 30-31. WANG Wei. Design and implementation of a forward-looking sonar signal processing system[D]. Beijing: University of Chinese Academy of Sciences, 2013: 15-20, 30-31. (  0) 0)
|
| [9] |
YUFIT G, MAILLARD E P. 3D forward looking sonar technology for surface ships and AUV: example of design and bathymetry application[C]//Proceedings of 2013 IEEE International Underwater Technology Symposium. Tokyo, Japan, 2013: 1-5.
(  0) 0)
|
| [10] |
张揽月, 杨德森. 矢量水听器扩展孔径线阵方位估计技术[J]. 哈尔滨工程大学学报, 2004, 25(6): 714-718. ZHANG Lanyue, YANG Desen. DOA estimation using extended-aperture uniformly linear vector-hydrophone array[J]. Journal of Harbin Engineering University, 2004, 25(6): 714-718. (  0) 0)
|
| [11] |
李海森, 陈宝伟, 周天, 等. 一种噪声环境中的多波束相位差估计新方法[J]. 哈尔滨工程大学学报, 2011, 32(5): 632-636. LI Haisen, CHEN Baowei, ZHOU Tian, et al. A new approach to multibeam phase difference estimation in noise circumstances[J]. Journal of Harbin Engineering University, 2011, 32(5): 632-636. (  0) 0)
|
| [12] |
BURDIC W S. Underwater acoustic system analysis[M]. 2nd ed. Englewood Cliffs: Prentice-Hall, 1991: 317-320.
(  0) 0)
|
| [13] |
LLORT-PUJOL G, SINTES C, Gueriot D. Analysis of Vernier interferometers for sonar bathymetry[C]//Proceedings of OCEANS 2008. Quebec City, QC, 2008: 1-5.
(  0) 0)
|
| [14] |
LLORT-PUJOL G, SINTES C. Vernier interferometer performance analysis[C]//Proceedings of OCEANS'11 MTS/IEEE KONA. Waikoloa, HI, 2011: 1-6.
(  0) 0)
|
| [15] |
LLORT-PUJOL G, SINTES C. Interferometric angle estimation for bathymetry performance analysis[C]//Proceedings of OCEANS 2011 IEEE-Spain. Santander, Spain, 2011: 1-8.
(  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


