2. 海军研究院 北京 100161;
3. 海洋信息获取与安全工业和信息化部重点实验室(哈尔滨工程大学), 黑龙江 哈尔滨 150001;
4. 哈尔滨工程大学 水声技术重点实验室, 黑龙江 哈尔滨 150001
2. Naval Research Institute, Beijing 100161, China;
3. Key Laboratory of Marine Information Acquisition and Security(Harbin Engineering University), Ministry of Industry and Information Technology, Harbin 150001, China;
4. Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001, China
了解水中声传播特性是进行水声调查、声呐系统设计的基础。本文中甚低频特指10~100 Hz的频率带宽。近20年来,国内外进行了一系列深海低频(100~1 000 Hz)/甚低频声传播实验,声场的低频声散射问题[1]、模态耦合效应[2]、声场时空相关性[3-4]以及深海远程声传播的稳定性及可靠性[5]均得到了进一步的研究与认知。
以往关于甚低频声传播问题的研究主要集中在浅海界面波的研究上[6-7],深海甚低频条件下,声场的空间分布特性与频率有关,到目前为止这方面的研究内容相对较少。Guthrie等[8]最先通过实验观察到会聚区位置对频率依赖性,但并没有给出系统性的解释。本文从射线-简正波的角度出发,分析了深海甚低频声场的空间分布特性,包括2种声传播模式:深海声道模式和会聚区模式。
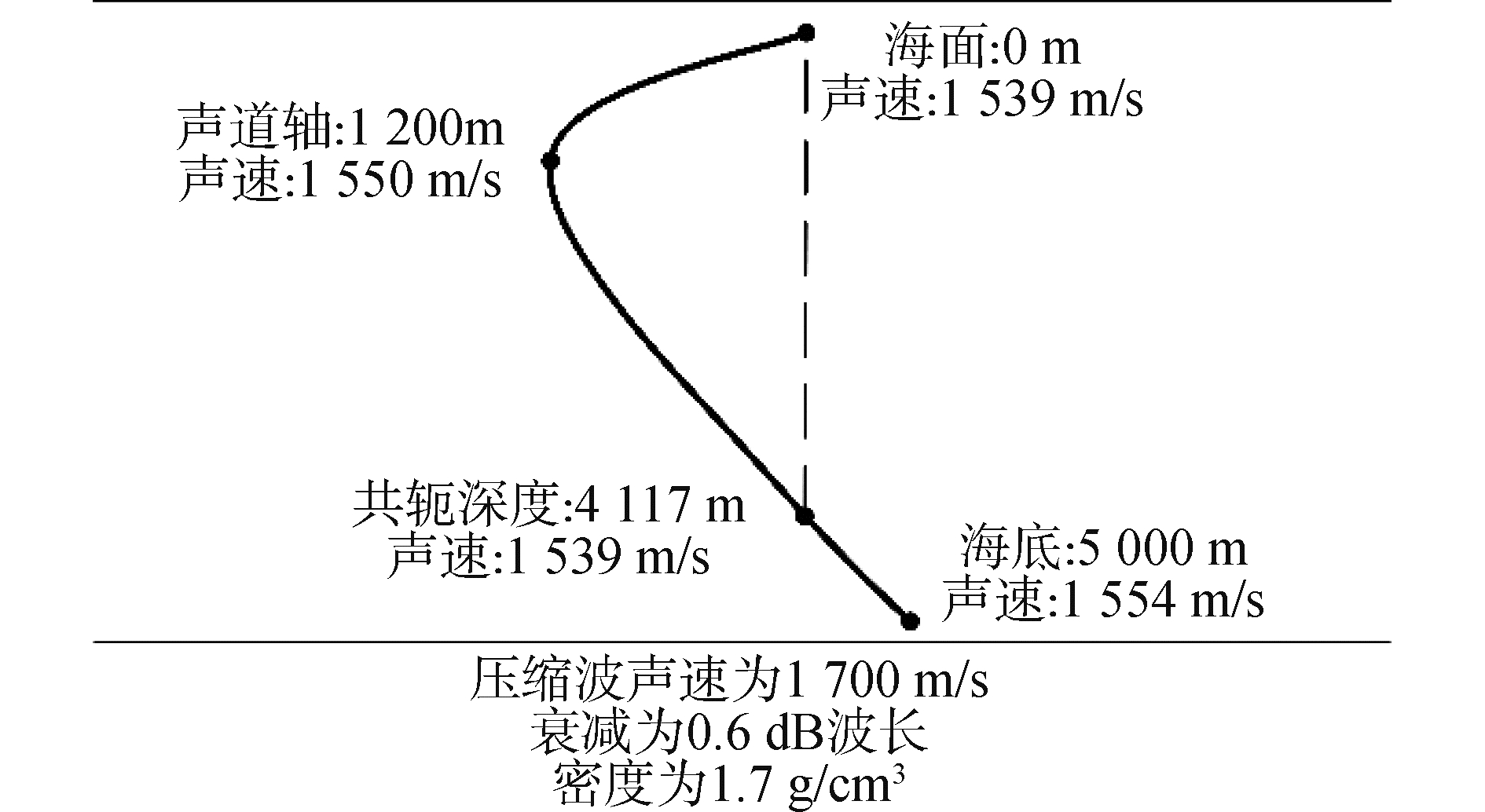
1 深海波导中简正模态的几何特征考虑图 1所示的环境模型,海深5 000 m,典型Munk[9]声速剖面,声道轴深度1 200 m,声速1 500 m/s,海面声速1 539 m/s,海底处水中声速1 554 m/s,海底为液态半无限空间,海底声速1 700 m/s,衰减系数0.6 dB/波长,海底密度1.7 g/cm3。若无特殊说明,全文仿真环境均如图 1所示。
|
Download:
|
| 图 1 环境模型 Fig. 1 Environment model | |
根据简正波理论,远场条件下,波导中任意点的声压p是各阶简正模态的叠加,考虑距离非相关环境,在柱坐标系下,时间因子取e-jωt有[10]:
| $ p(r, z) \simeq \frac{j}{{4\rho \left( {{z_s}} \right)}}{\psi _m}\sum\limits_m^\infty {\left( {{z_s}} \right)} {\psi _m}(z){\rm{H}}_0^{(1)}\left( {{k_{rm}}r} \right) $ | (1) |
式中:zs是声源深度;ρ是介质密度;krm是水平波数;ψm是本征函数;H0(1)是零阶第一类Hankel函数。
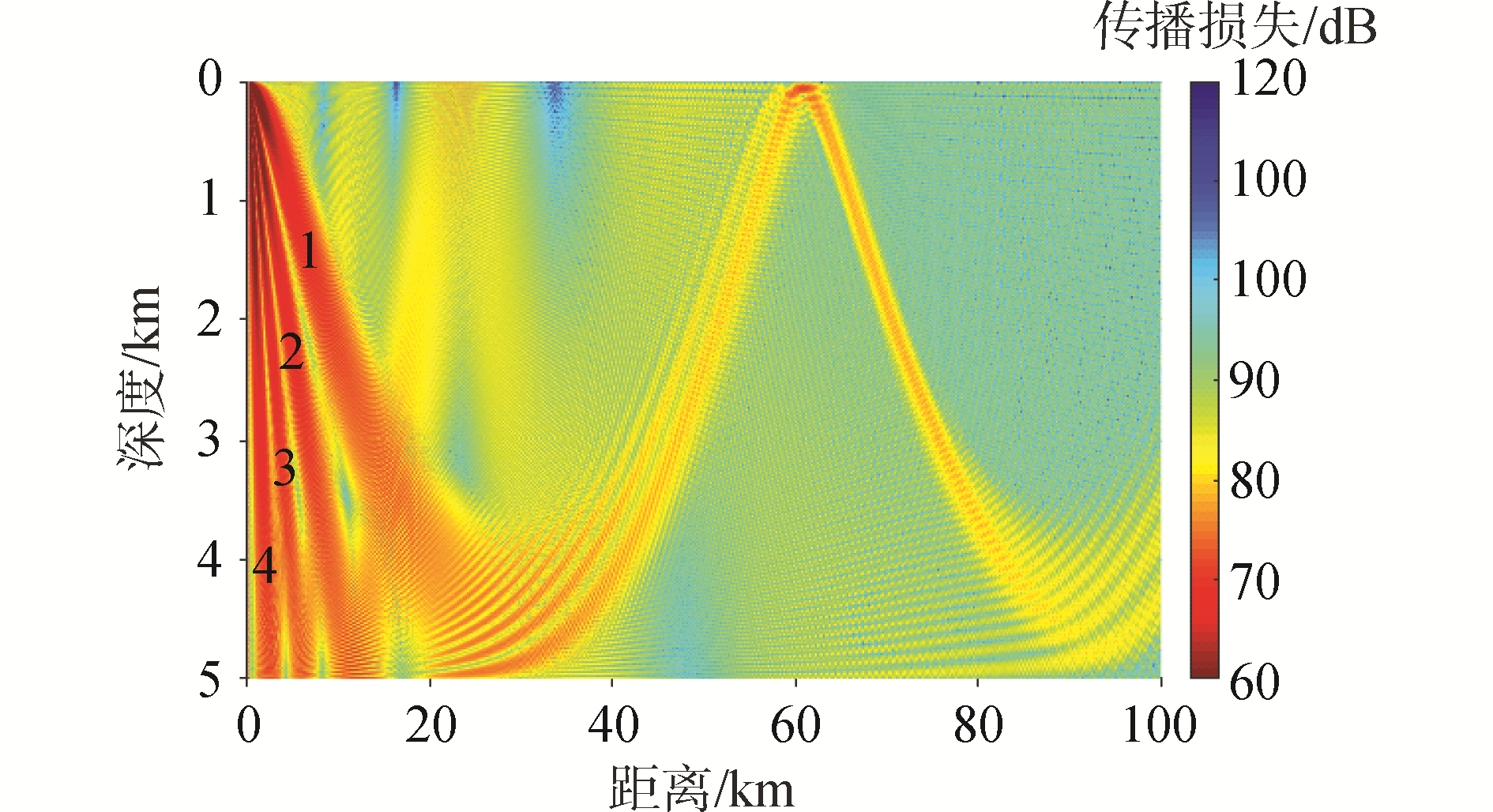
声源为单频点源(如果无特殊说明,全文仿真均为无指向性的单频点源),声源深度zs=50 m,频率f=60 Hz时的传播损失如图 2所示。从图 2中可以看出,有4条波束从声源发出,按照掠射角大小对波束排序,掠射角最小的波束为第1号波束,其主要形成会聚区,其余3条波束会经过波导的上下界面反射。
|
Download:
|
| 图 2 传播损失伪彩图(zs=50 m,f=60 Hz) Fig. 2 Transmission loss (zs=50 m, f=60 Hz) | |
广义相积分理论(WKBZ)[11]为波导中简正波和射线之间的转换搭建了“桥梁”,波导中第m阶模态对应于以掠射角±θm从声源发出的2条本征声线,根据介质波数和水平波数间的几何关系[12]:
| $ \theta_{m}=\left|\arccos \left(k_{r m} / k_{s}\right)\right| $ | (2) |
式中ks为声源处的介质波数。将第m阶模态对应的θm作为自变量,模态幅值作为因变量可以得到波导中各阶模态在声源处的掠射角度谱分布[13]。
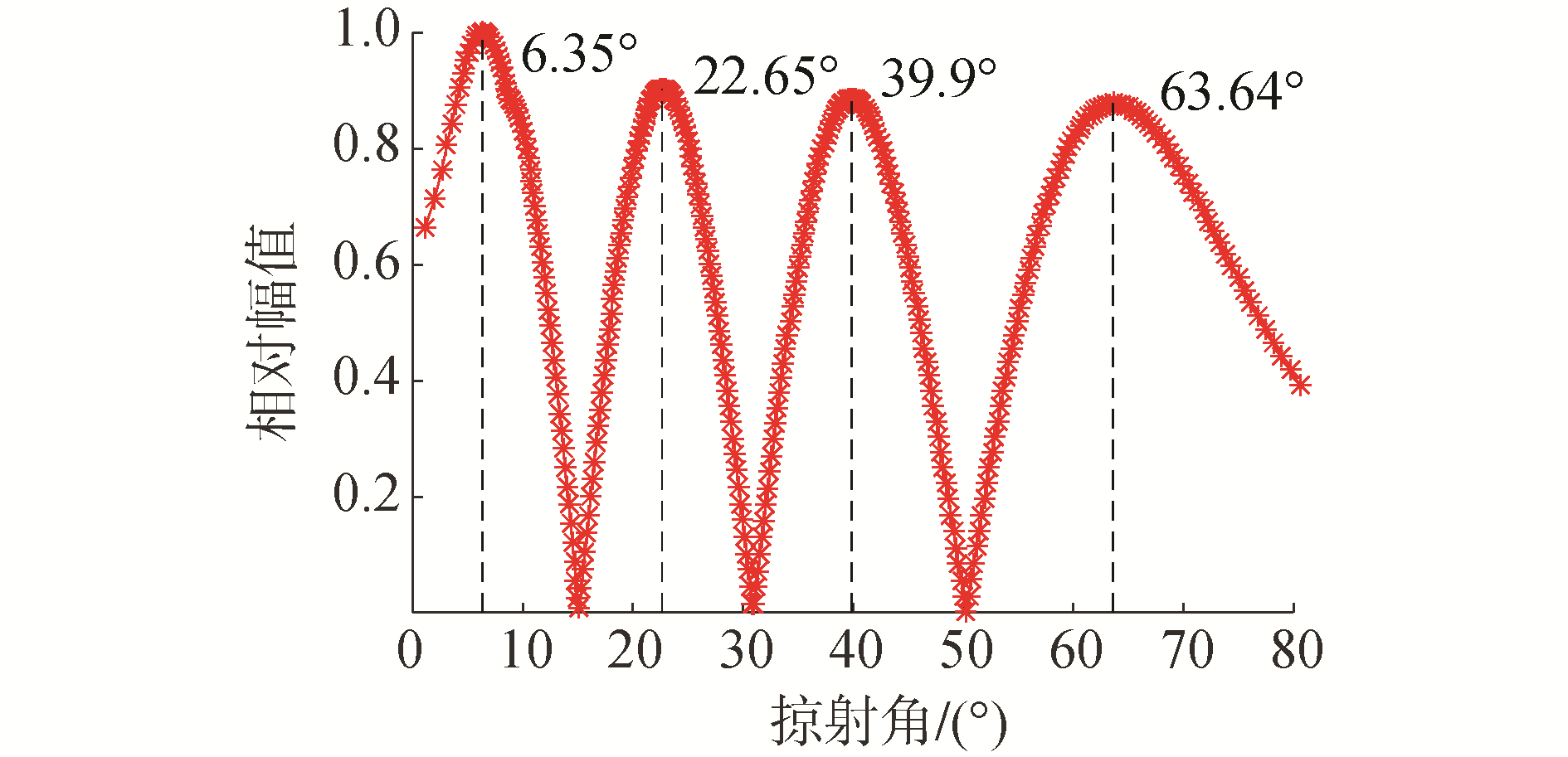
根据式(2)计算了各阶模态在声源处的掠射角分布,如图 3所示,图 3中2个相邻波谷之间的模态被定义为一组声线簇[13]。按照从左到右的顺序,从图中可以看出4个波峰,也就是有4组声线簇,这4组声线簇对应于图 2中从声源发出的4条波束,其中第1组声线簇(模态)是会聚区的主要贡献者,对应于图 2中第1号波束。本文重点关注水中翻转声线(包括在声道轴上下翻转不与波导界面相互作用的声线和海面反射到达海底前完成翻转的声线),具体做法是:将相速度上边界取水中声速最大值,将相速度下边界取水中声速最小值,根据Snell折射定律[10]可知,相速度取值满足该条件的模态会被限制在波导中传播,不与海底相互作用。
|
Download:
|
| 图 3 声场角度谱分布(zs=50 m,z=50 m,f=60 Hz) Fig. 3 Acoustic field distribution of grazing angle dimension (zs=50 m, z=50 m, f=60 Hz) | |
波动声学中模态的水平干涉周期和射线声学中声线的“跨距”是等效的[10, 12],模态水平干涉周期Lm的计算公式为[10]:
| $ L_{m}=\frac{2 \pi}{k_{r m}-k_{r(m+1)}} $ | (3) |
根据式(3)就可以计算第m阶模态所对应的射线在深海声道轴上下完成一次循环所经过的水平距离。
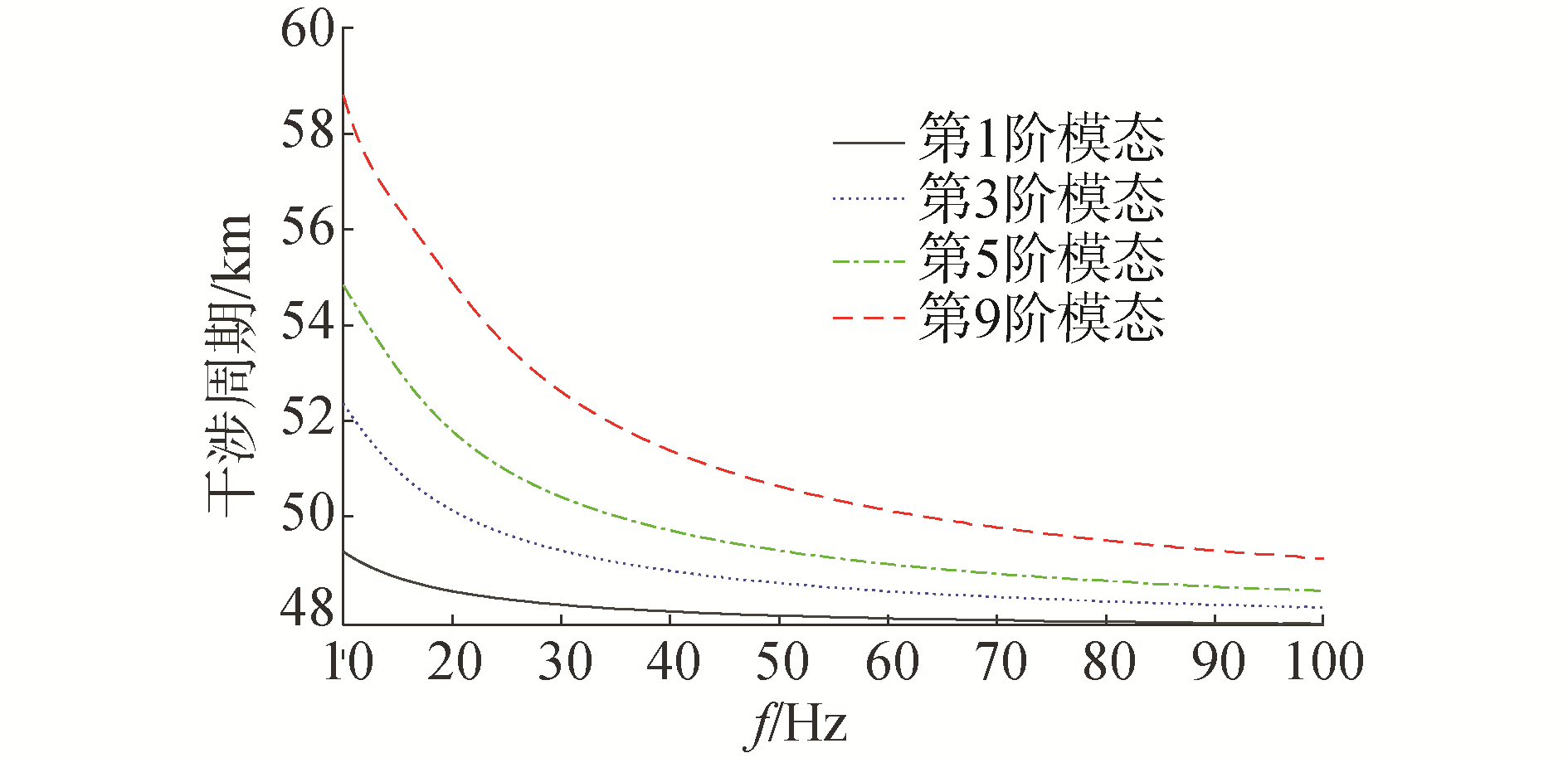
图 4给出了第1、3、5、9阶模态的干涉周期随频率的变化曲线,可以看出,模态阶数越低,干涉周期越小,随着频率增大,模态干涉周期单调递减,并且频率越高曲线越趋于水平。
|
Download:
|
| 图 4 模态干涉周期随频率的变化曲线 Fig. 4 Curves of modes interference periods with frequency | |
模式区分主要依据是声源位置的不同,其中会聚区模式特指声源位于海面附近的情况,深海声道模式特指声源位于声道轴附近的情况。
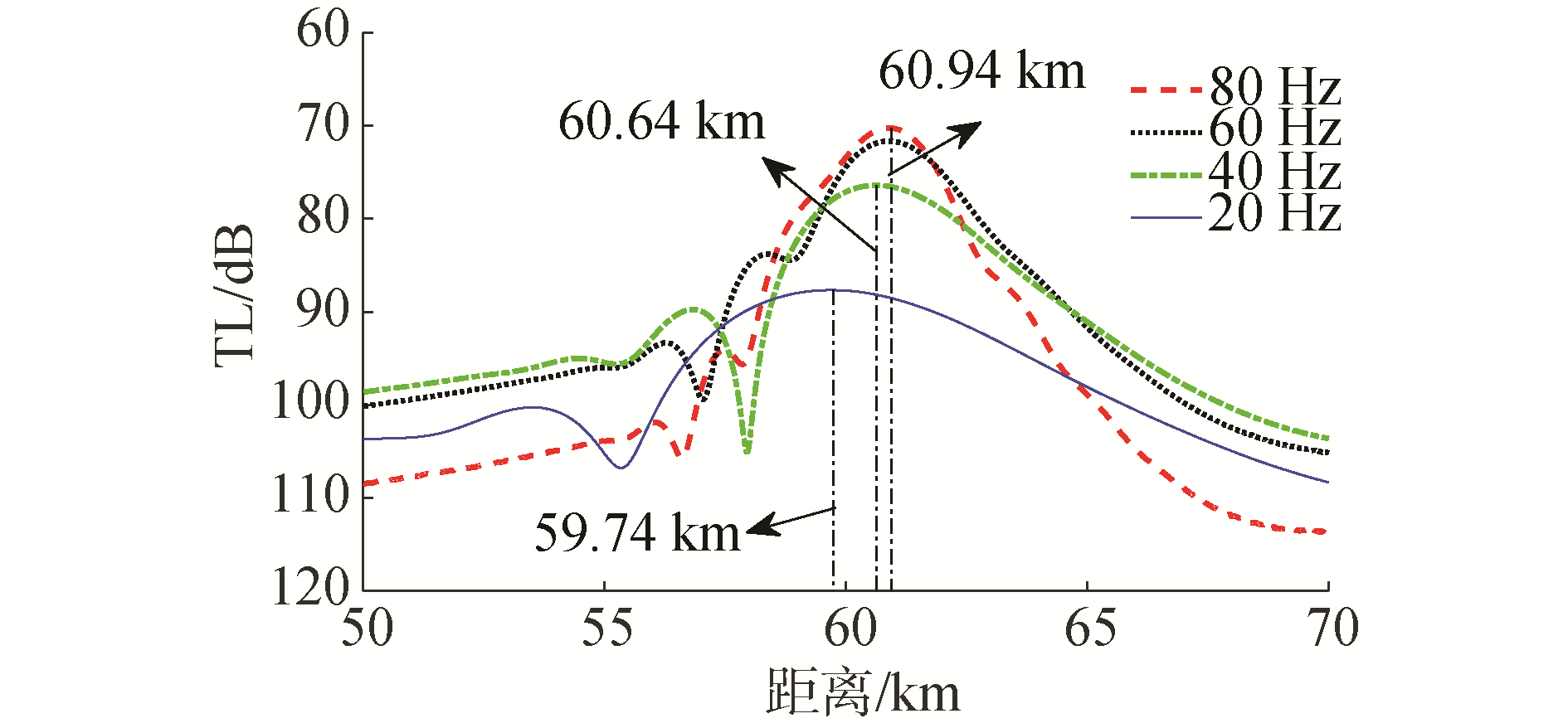
2.1 会聚区模式图 5给出了会聚区模式下,不同声源频率下的传播损失曲线,声源深度zs=50 m,接收深度z=50 m,横坐标表示距离声源的水平距离。对比20 Hz和40 Hz 2条传播损失曲线会发现:会聚区的位置以及其传播损失大小均与频率有关,20 Hz时会聚区传播损失极小值位置距离声源的水平距离为59.74 km,而40 Hz时变为了60.64 km,声源频率从20 Hz增大到40 Hz时,会聚区传播损失减小约11.2 dB。对比图 5中80 Hz和60 Hz 2条传播损失曲线可以发现:当声源频率从60 Hz增加到80 Hz时,会聚区距离声源的水平距离几乎无变化,传播损失减小约1.4 dB。
|
Download:
|
| 图 5 不同频率下传播损失曲线对比(zs=50 m,z=50 m) Fig. 5 Comparison of transmission loss curves at different frequencies (zs=50 m, z=50 m) | |
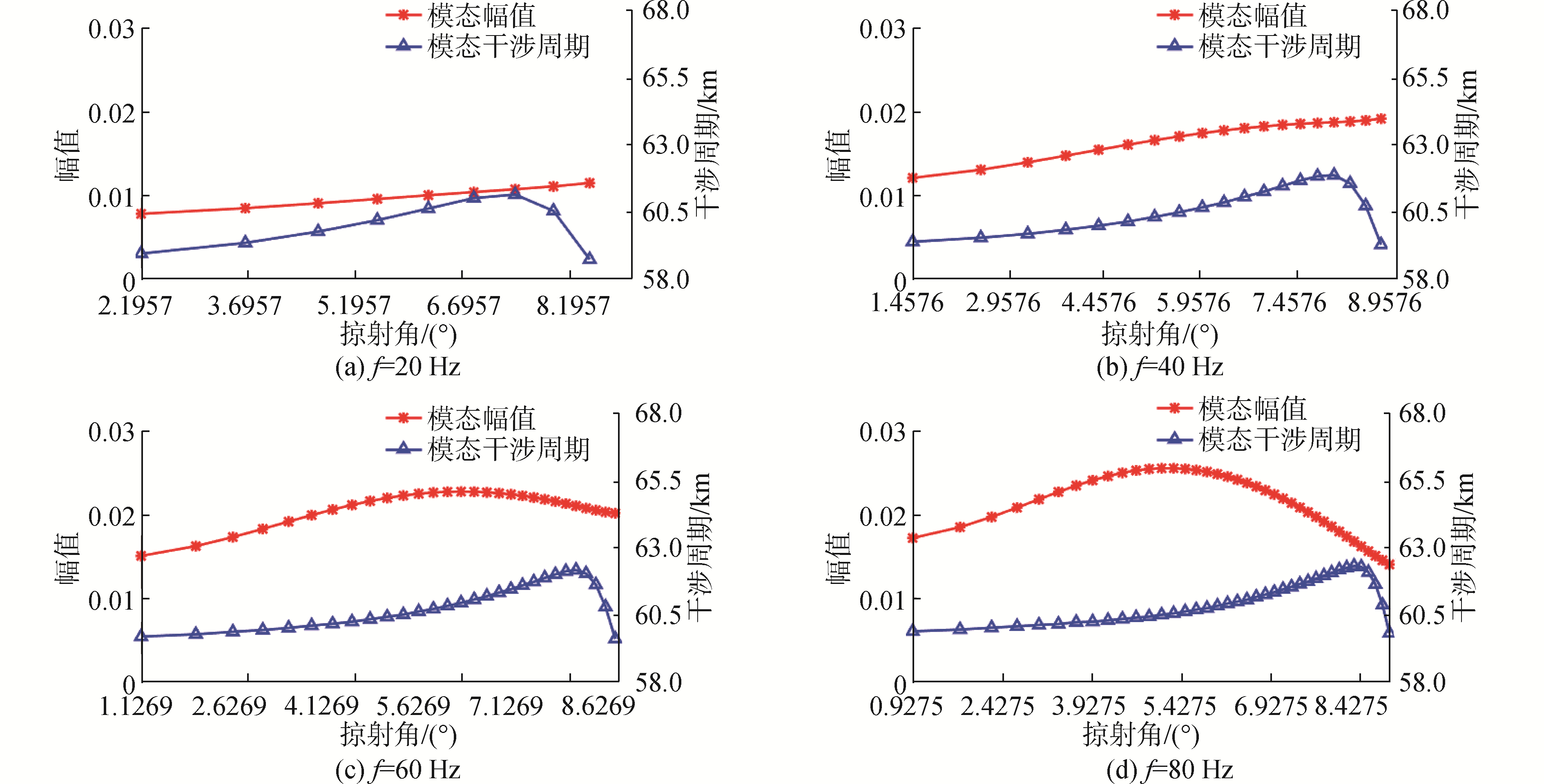
依据式(2)和式(3)分别计算构成会聚区模态的角度谱和水平干涉周期,如图 6所示,可以看出,整体上,模态掠射角随着频率的增大而减小,所有折射模态的水平干涉周期随阶数增大近似单调增大,在局部波动起伏,频率升高时,被激发出的模态个数也在增加。
|
Download:
|
| 图 6 不同频率下模态水平干涉周期、角度谱和本征模态幅值对比(zs=50 m,z=50 m) Fig. 6 Comparison of mode interference period, grazing angle spectrum and mode amplitude at different frequencies (zs=50 m, z=50 m) | |
幅值最大的模态在波导中占据主导地位,从图 6(a)中的模态幅值曲线可以看出,声源频率升高时,模态幅值的最大值是单调增大的,但增幅逐渐变小,当频率达到或超过60 Hz时,模态幅值出现波峰,也就是说20 Hz时,第1组声线簇只有不到1/2的声线可以通过会聚区模式传播,从声源发出的第1号波束并不全部构成会聚区,当频率升高时,第1组声线簇中通过会聚区传播的声线个数比例增大,如图 6(b)和图 6(d)所示。
声源深度zs=50 m时,不同频率下的传播损失伪彩图如图 7所示,实线1表示不经过海面和海底反射,对应于图 6中掠射角最小的模态的声线轨迹;虚线2只经过海面反射,对应于图 6中掠射角最大的模态的声线轨迹。掠射角小于图中实线1声线掠射角的模态,因声源位置在其本征函数的震荡区域外,无法被有效激发,掠射角大于图中虚线2声线掠射角的模态,会经过海面海底反射无法形成会聚区。根据上文分析,声源频率不同,模态掠射角也不同,所以图 7中4幅图的声线轨迹存在微小差异。20 Hz时,第1号波束能量峰值对应的掠射角大于图中虚线2声线的掠射角,所以第1号波束主要能量经海面海底反射向前传播,如图 7(a)所示,当频率增大时,第1号波束能量峰值掠射角越来越小,当小于图中虚线2声线的掠射角时,由海面海底反射传播逐渐变为会聚区传播,会聚区的能量逐渐增加,如图 7(b)至图 7(d)所示。

|
Download:
|
| 图 7 不同频率下传播损失(zs=50 m) Fig. 7 Transmission loss at different frequencies (zs=50 m) | |
通过总结图 6和图 7所揭示的现象得出如下规律:声源频率不同时,模态幅值的最大值也不同,只有当第1组声线簇中幅值最大的声线也能形成会聚区时(图 6中模态幅值出现波峰),会聚区传播损失大小才是比较稳定的,因为此时占主导地位的模态能量不随频率增加而发生明显变化。
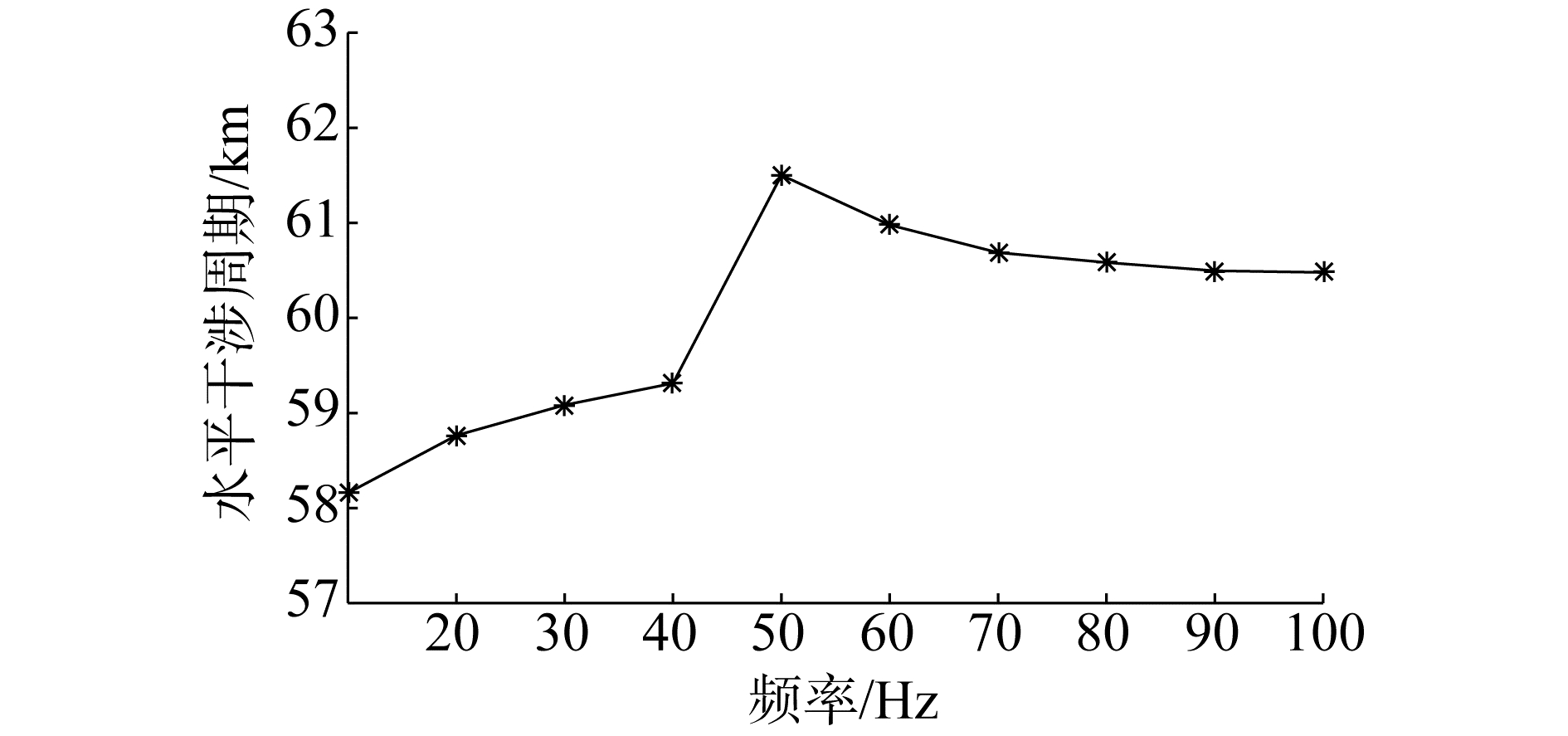
图 4显示的规律表明:第m阶模态的水平干涉周期是随着频率增大单调递减的,但对会聚区起主导作用的是图 6中相对幅值最大的声线(模态)。图 8给出了相对幅值最大的模态对应的干涉周期随频率的变化关系,可以看出,频率在10~50 Hz时,幅值取最大值的模态,其干涉周期随频率增大单调增大;在50~70 Hz内,其干涉周期随频率增大单调减小,在70~100 Hz内,其干涉周期随频率增大变化不明显,曲线趋于水平。这就很好解释了图 5中频率发生变化时,会聚区位置发生变化的现象。
|
Download:
|
| 图 8 幅值取最大值的模态干涉周期随频率的变化曲线 Fig. 8 Curve of modes (with maximum amplitude) interference periods with frequency | |
对上述现象的分析探讨近在甚低频段成立,当频率变化步长较小,涉及到中高频问题时,需要另行分析。
2.2 深海声道模式声源置于声道轴附近时,声场主要能量集中在声道轴附近。根据式(2)以及Snell折射定律[10]可知,模态相速度等于介质中某一深度处的声速时,模态对应的本征声线会在该深度完成翻转,或者说在该深度声线的掠射角为0。
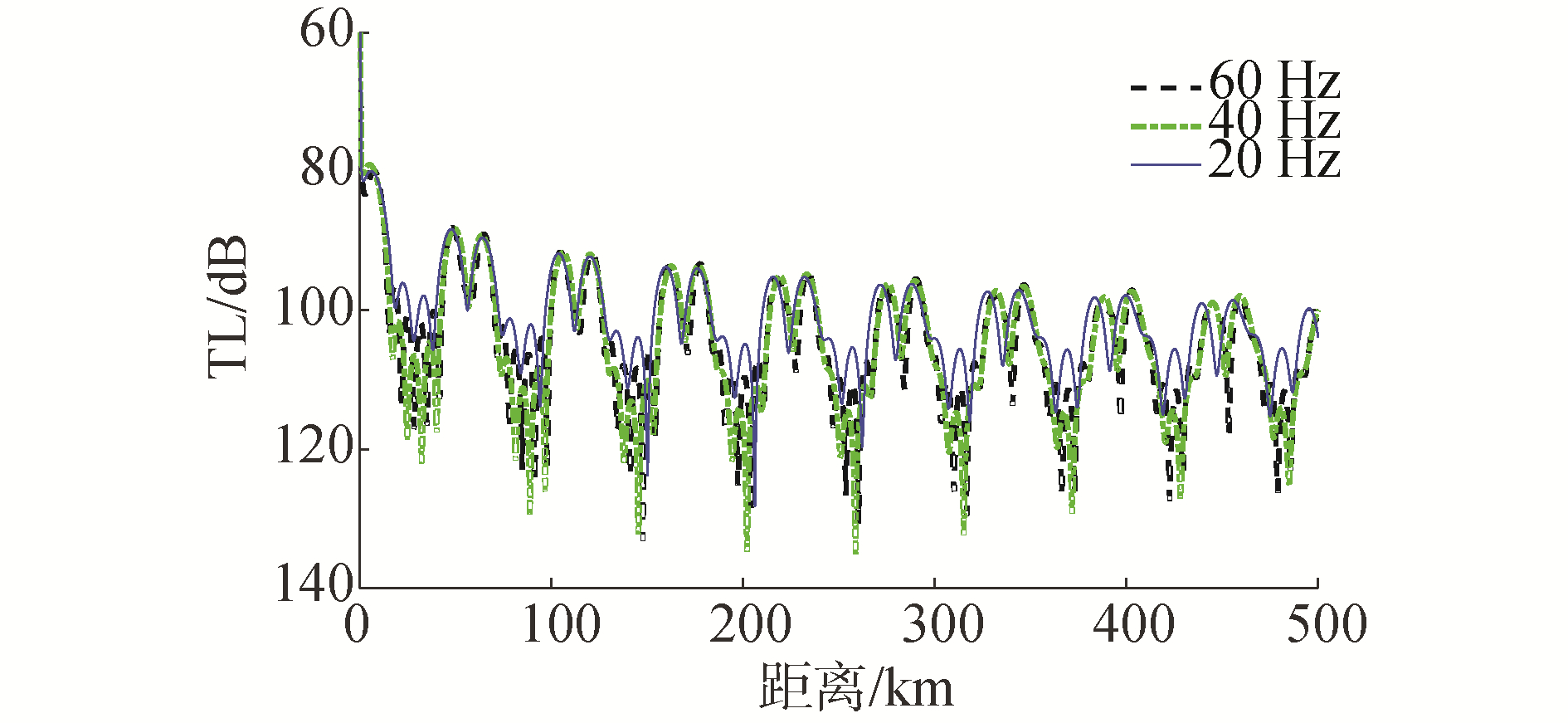
声源深度zs=1 200 m,海深200 m处介质声速为1 523.5 m/s,相速度等于或接近1 523.5 m/s的模态相长干涉对应的本征声线将会在200 m深度附近完成翻转。图 9给出了接收深度z=200 m处不同频率下的传播损失曲线,声源频率为20 Hz时相速度限制区间为1 518.5~1 528.5 m/s,因为要观察在200 m处翻转的模态,所以相速度限制区间选择的原则是:在保证区间内存在二到三阶模态的前提下,相速度区间的选择要尽可能窄,使得区间内的模态相速度近似等于区间中值1 523.5 m/s,在该原则下,声源频率变大时,则相速度限制区间应该适当减小。声源频率为40 Hz时相速度限制区间为1 519.5~1 527.5 m/s,而声源频率为60 Hz时相速度限制区间为1 520.5~1 526.5 m/s。
|
Download:
|
| 图 9 不同频率下传播损失曲线对比(zs=1 200 m,z=200 m) Fig. 9 Comparison of transmission loss curves at different frequencies (zs=1 200 m, z=200 m) | |
通过图 9可以看出,图中所有曲线均有18个波峰,根据WKBZ理论,本征模态可以看做一组上行波和下行波的组合。这些峰值来自于模态相速度接近1 523 m/s的上行波和下行波在翻转深度(200 m)附近的贡献,其中40 Hz和60 Hz所对应的曲线峰值几乎重叠,而与20 Hz对应的曲线峰值错位明显,并且距离越远错位现象越明显。
根据模态水平波数和声源处介质波数的几何关系,模态簇相长干涉所对应的本征声线掠射角与模态簇的相速度有关。频率为20 Hz时,区间内相邻模态簇的相速度均值为1 523.3 m/s,这些模态簇近似以掠射角10.03°向前传播;频率40 Hz和60 Hz时,区间内相邻模态簇的相速度均值为1 523.5 m/s,模态簇则近似以掠射角10.08°向前传播,声线轨迹如图 10所示,图中虚线在声源处掠射角为10.08°,实线在声源处掠射角为10.03°,距离越大,2种声线错位越明显,这与图 9显示的规律一致。
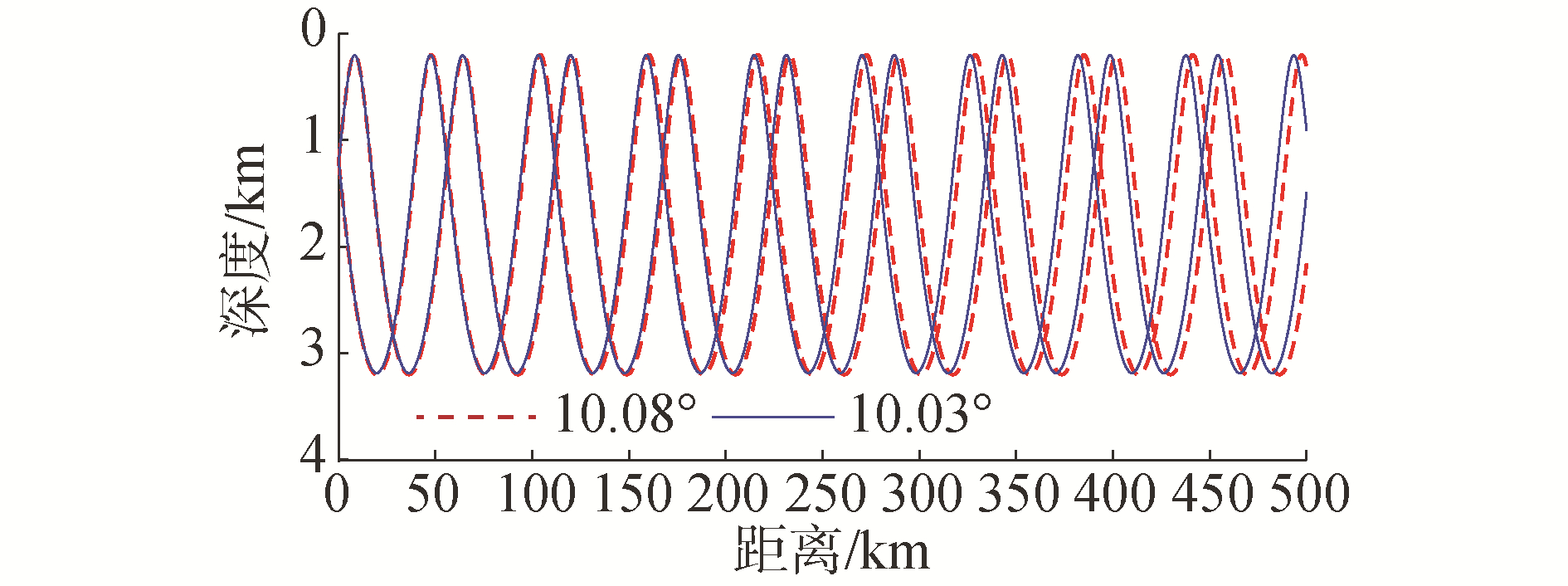
|
Download:
|
| 图 10 声线轨迹 Fig. 10 Ray trace | |
当波导环境确定时,波导中简正波的个数以及本征模态的空间分布规律都是确定的。根据式(1)可知,声源深度会影响到模态的激发强度,同时根据深海Lloyd镜理论[10]可知,从声源发出的波束个数M和声源深度zs以及波长λ关系表示为:
| $ M=\operatorname{int}\left(\frac{2 z_{s}}{\lambda}+0.5\right) $ | (4) |
所以,声源离海面越近,相同频率下波束个数越少。
图 11给出了不同声源深度下,频率f=50 Hz时的传播损失伪彩图和模态角度谱。声源深度zs=20 m时,从声源发出2条波束,如图 11(a)所示。
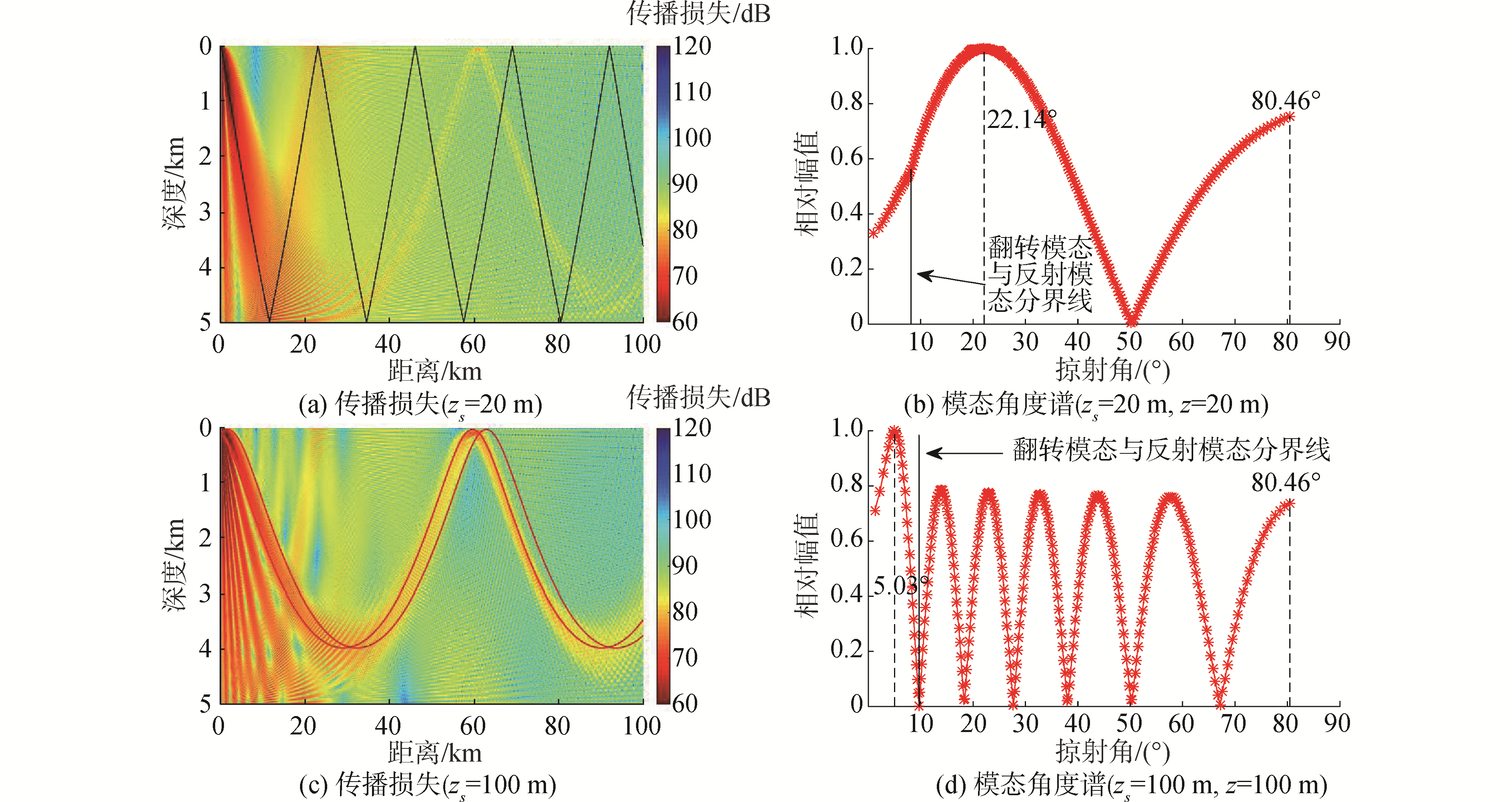
|
Download:
|
| 图 11 不同声源深度下的传播损失以及模态角度谱 Fig. 11 Transmission loss and grazing angle spectrum at different sources depth | |
图 11(b)给出了对应的模态在声源处的掠射角分布,图中实线是翻转模态与反射模态分界线,实线左侧的模态通过会聚区模式传播,实线右侧的模态经海面海底反射传播,可以看出第1组声线簇中幅值最大的声线(模态)在翻转模态与反射模态分界线的右侧,所以第1号波束主要能量通过海面海底反射传播,声线轨迹如图 11(a)中折线所示。
声源深度zs=100 m时,从声源发出7条波束,如图 11(c)所示,图 11(d)给出了对应模态在声源处的掠射角分布,此时第1组声线簇全部在翻转模态与反射模态分界线左侧,第1号波束的能量全部通过会聚区模式传播,波束能量峰值的传播轨迹如图 11(c)中实线所示。
根据2.1节的分析,zs=20 m,频率50 Hz时第1号波束(第1簇声线)中能量最强的声线无法形成会聚区,此时声场是不稳定的,声源频率变化时,会聚区位置和传播损失大小也会发生明显变化。图 12(a)给出了声源频率为50、70和90 Hz,zs=20 m,z=20 m时的传播损失曲线对比图,可以发现会聚区传播损失大小和位置均随频率变化而变化。
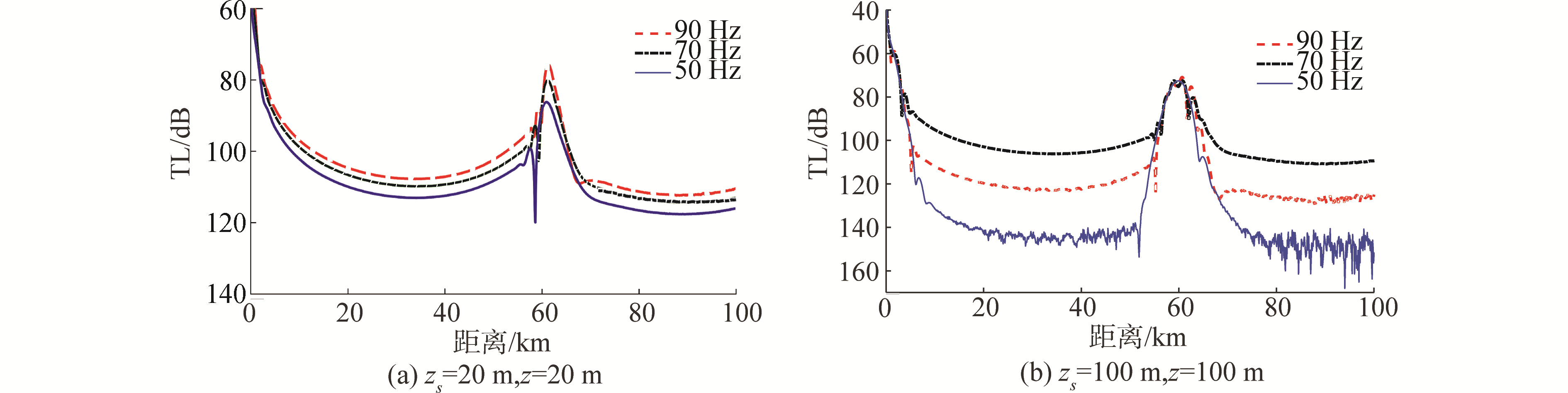
|
Download:
|
| 图 12 不同频率下的传播损失曲线对比 Fig. 12 Comparison of transmission loss curves at different frequencies | |
从对图 11(c)和(d)的分析中可知,zs=100 m,频率50 Hz时第1号波束(第1簇声线)全部可以形成会聚区,所以声源频率大于50 Hz时,会聚区位置和传播损失大小不会随频率升高而发生明显改变。图 12(b)给出了声源频率为50、70和90 Hz条件下,zs=100 m时的传播损失曲线对比图,图中会聚区传播损失大小及距离声源的水平位置均不随频率改变发生明显变化。
4 结论1) 不同频率下,深海波导中占主导地位的模态(声线)能量大小不同,这会导致声传播损失大小随频率变化而变化。
2) 不同频率下,深海波导中占主导地位的模态干涉周期(声线水平跨距)不同,这会导致声场的空间分布规律随频率变化而变化。
3) 不同频率下,声源深度不同,声场的空间分布特性也不同。
本文研究结论仅在深海甚低频条件下成立,对于更高频段的声场特性,需要进一步研究。
| [1] |
MERCER J A, COLOSI J A, HOWE B M, et al. LOAPEX:the long-range ocean acoustic propagation EXperiment[J]. IEEE journal of oceanic engineering, 2009, 34(1): 1-11. DOI:10.1109/JOE.2008.2010656 (  0) 0)
|
| [2] |
UDOVYDCHENKOV I A, STEPHEN R A, DUDA T F, et al. Bottom interacting sound at 50 km range in a deep ocean environment[J]. The journal of the acoustical society of America, 2012, 132(4): 2224-2231. DOI:10.1121/1.4747617 (  0) 0)
|
| [3] |
CHANDRAYADULA T K, COLOSI J A, WORCESTER P F, et al. Observations and transport theory analysis of low frequency, acoustic mode propagation in the Eastern North Pacific Ocean[J]. The journal of the acoustical society of America, 2013, 134(4): 3144-3160. DOI:10.1121/1.4818883 (  0) 0)
|
| [4] |
李整林, 董凡辰, 胡治国, 等. 深海大深度声场垂直相关特性[J]. 物理学报, 2019, 68(13): 134305. LI Zhenglin, DONG Fanchen, HU Zhiguo, et al. Vertical correlations of sound field at large depths in deep water[J]. Acta physica sinica, 2019, 68(13): 134305. (  0) 0)
|
| [5] |
BLACKMAN D K, DE GROOT-HEDLIN C, HARBEN P, et al. Testing low/very low frequency acoustic sources for basin-wide propagation in the Indian ocean[J]. The journal of the acoustical society of America, 2004, 116(4): 2057-2066. DOI:10.1121/1.1786711 (  0) 0)
|
| [6] |
张海刚.浅海甚低频声传播建模与规律研究[D].哈尔滨: 哈尔滨工程大学, 2010. ZHANG Haigang. Research on modeling and rule of infrasound propagation in shallow sea[D]. Harbin: Harbin Engineering University, 2010. (  0) 0)
|
| [7] |
张海刚, 朴胜春, 杨士莪. 水中甚低频声源激发海底地震波的传播[J]. 哈尔滨工程大学学报, 2010, 31(7): 879-887. ZHANG Haigang, PIAO Shengchun, YANG Shie. Propagation of seismic waves caused by underwater infrasound[J]. Journal of Harbin Engineering University, 2010, 31(7): 879-887. (  0) 0)
|
| [8] |
GUTHRIE A N, FITZGERALD R M, NUTILE D A, et al. Long-range low-frequency CW propagation in the deep ocean:Antigua-Newfoundland[J]. The journal of the acoustical society of America, 1974, 56(1): 58-69. DOI:10.1121/1.1903233 (  0) 0)
|
| [9] |
MUNK W H. Sound channel in an exponentially stratified ocean, with application to SOFAR[J]. The journal of the acoustical society of America, 1974, 55(2): 220-226. DOI:10.1121/1.1914492 (  0) 0)
|
| [10] |
JENSEN F B, KUPERMAN W A, PORTER M B, et al. Computational ocean acoustics[J]. Computers in physics, 1995, 9(1): 55-56. (  0) 0)
|
| [11] |
张仁和, 何怡, 刘红. 水平不变海洋声道中的WKBZ简正波方法[J]. 声学学报, 1994, 19(1): 1-12. ZAHNG Renhe, HE Yi, LIU Hong. WKBZ mode approach to sound propagation in horizontally stratified oceans[J]. Acta acustica, 1994, 19(1): 1-12. (  0) 0)
|
| [12] |
林巨, 赵越, 王欢, 等. 基于射线稳定性参数的声传播特性分析[J]. 南京大学学报(自然科学), 2015, 51(6): 1223-1233. LIN Ju, ZHAO Yue, WANG Huan, et al. Analysis of deep sea acoustic propagation based on ray stability parameter[J]. Journal of Nanjing University (natural sciences), 2015, 51(6): 1223-1233. (  0) 0)
|
| [13] |
韩志斌, 彭朝晖, 刘雄厚. 深海海底反射区声场角谱域分布结构分析及在声呐波束俯仰上的应用[J]. 物理学报, 2020, 69(11): 201-212. HAN Zhibin, PENG Zhaohui, LIU Xionghou. Analysis of sound field distribution of angle dimension in deep ocean bottom bounce area and its application to active sonar vertical beam pitch[J]. Acta physica sinica, 2020, 69(11): 201-212. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


