2. 海洋信息获取与安全工业和信息化部重点实验室(哈尔滨工程大学), 黑龙江 哈尔滨 150001;
3. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001
2. Key Laboratory of Marine Information Acquisition and Security(Harbin Engineering University), Ministry of Industry and Information Technology, Harbin 150001, China;
3. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
深海复杂海底山地形环境对水下声传播有着重要影响,研究深海海底山周围声传播的三维效应对水下探测有着重要的指导意义。近些年来,国内外学者,针对深海海底山地形已经开发了很多声传播模型,但大多数集中在利用二维模型来解决深度和距离上的声场分布问题,忽略了方位角及非轴对称地形等三维因素的影响, 由于海底山会产生复杂的三维效应,二维(2D)或伪三维(N×2D)模型不再适用; 而目前三维数值模型均为基于一些近似条件进行的数值模拟,因此对于复杂的海底山地形的影响仍有很多问题尚不明确[1-2]。另一方面,近年来声呐逐渐向低频发展,信号具有了更高的平稳性和更好的可预测性,使得对海洋波导进行时域信号分析成为重要研究课题[3]。近年来计算机技术发展迅速,大规模超级计算机的实现和高性能并行算法的开发,使得基于有限元的复杂海洋环境下的声传播数值模拟得以实现[4-5]。因此,本文利用三维谱元法[6]对理想高斯型海底山环境下的声传播问题进行时域特性分析。
Harrison[7]实验发现海底山后产生明显的影区,影区内能量损失约12 dB。此后,为分析海底山环境下的声传播规律,国内外学者开发了很多三维数值模型,如三维射线模型、抛物模型等[8-11]。但抛物模型采用单向散射近似,无法计算海底山环境中的反向散射能量,一部分学者致力于三维海底山波导简正波模型,距离有关波导耦合简正波理论复杂,通常对海底地形进行简化[12-16],从而实现声场的数值表示。Burns等[17]利用2016年中国南海深海海底山环境下的声传播实验数据,分析了海底山引起的水平折射现象,并利用三维射线模型对海底山三维声传播机理进行了解释。然而,上述工作均为在频域内的能量上的分析,而对海底山环境下的时域声场研究工作较少[18-19],无法完整分析信号的到达结构、时延等重要信息。
此外,近年的实验表明海底山环境下的时域声场以及其形成机制仍需进一步数值分析,尤其在声信号到达结构方面。Stephen等[1]利用实验数据分析了小海底山周围的海底衍射-海面反射(BDSR)信号,虽然BDSR存在于整个水体中,但在共轭深度以下最为明显,且多来源于声源-接收点所在平面外,为三维衍射现象,并指出能够激发BDSR的三维海底结构需进一步建模分析。国外学者在一次深海远距离传播实验中发现海底OBS接收到一系列通过二维仿真无法解释的到达信号[2],而海水中的垂直阵没有接收到,同时实验海域地形复杂且包括海底山地形,因此分析OBS接收到的信号需进行三维仿真分析。
为了更进一步的研究深海三维海底山对声传播时域声场的影响等问题,以有限元为基础的三维谱元法(SPECFEM3D)将作为本文进行模拟的主要方法。谱元法在近几年被应用于水声传播建模仿真[20-21],谱元法具有有限元方法的几何灵活性适用于任意地形变化的环境模拟;此外,计算积分时通过选取不均匀的配置节点,可以得到声场显式的时间表示,适用于大型计算机的并行计算。文献[22]中利用楔形海域的仿真结果完成了三维谱元法数值模型的验证。
本文谱元法对深海海底山地形条件下进行三维声传播数值模拟,从多途结构、界面波传播特性和三维效应等方面分析了该复杂海洋环境下的声场时空分布。
1 谱元法与SPECFEM3D模型建立 1.1 谱元法理论基础谱元法[23]是基于有限元理论的一种数值方法,是波动方程的弱形式解。首先将计算区域进行单元划分,在每个单元上采用伪谱法,利用不均匀的配置节点,把单元内的声场表示成高阶拉格朗日多项式的叠加,然后采用Galerkin方法求解得到全局的声场解,从而完成对计算域内波传播过程的数值模拟。流体部分忽略声源项,波动方程为:
| $ \frac{1}{\kappa }\partial _t^2P = \mathit{\boldsymbol{\nabla}} \cdot \left( {\frac{1}{\rho }\mathit{\boldsymbol{\nabla}} P} \right) $ | (1) |
式中κ为流体体积弹性模量,根据欧拉方程位移可表示为
| $ \partial _t^2\chi = - P $ | (2) |
在xs处增加点压力源,流体中波动方程变为:
| $ \frac{1}{\kappa }\ddot \chi = \mathit{\boldsymbol{\nabla}} \cdot \left( {\frac{1}{\rho }\mathit{\boldsymbol{\nabla}} \chi } \right) + \frac{1}{\kappa }f(t){\delta _{{x_s}}} $ | (3) |
将方程(3)两端乘以任意一个测试函数w,并对空间求解区域进行积分,然后利用分部积分可以得到波动方程的弱形式:
| $ \begin{array}{*{20}{l}} {\int_{{\Omega _f}} w \frac{1}{\kappa }\ddot \chi {{\rm{d}}^3}x = - \int_{{\Omega _f}} {\frac{1}{\rho }} \mathit{\boldsymbol{\nabla}} w \cdot \mathit{\boldsymbol{\nabla}} \chi {{\rm{d}}^3}x + }\\ {\int_{{\Omega _{f - s}}} {\frac{1}{\rho }} w\mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{\dot u}}{\rm{d}}s + \frac{1}{{\kappa ({x_s})}}w({x_s})f(t)} \end{array} $ | (4) |
式中:d3x=dxdydz;Ωf为流体区域;Ωf-s为流体弹性体界面,海面自由边界已经计入其中。由于海面为自由边界,边界条件在任意时刻都满足P(x, t)=-
弹性体内的矢量位移u的运动方程为:
| $ \rho (x)\mathit{\boldsymbol{\ddot u}}(x,t) - \mathit{\boldsymbol{\nabla}} \cdot \mathit{\boldsymbol{\sigma }}(x,t) = f(x,t) $ | (5) |
式中应力张量σ(x, t)可以通过胡克定律由位移表示为:
| $ \mathit{\boldsymbol{\sigma }}(x,t) = C(x):\mathit{\boldsymbol{\nabla}} \mathit{\boldsymbol{u}}(x,t) $ | (6) |
介质的弹性性质由四阶弹性张量C(x)描述。将式(5)乘一个任意的可微地与时间无关的检验函数w,并在空间对其积分并利用高斯定理得到其弱形式:
| $ \int\limits_G \rho w \cdot \mathit{\boldsymbol{\ddot u}}{{\rm{d}}^3}\mathit{\boldsymbol{x}} - \int\limits_G w \cdot \sigma \cdot n{{\rm{d}}^2}\mathit{\boldsymbol{x}} + \int\limits_G \mathit{\boldsymbol{\nabla}} w:\sigma {{\rm{d}}^3}\mathit{\boldsymbol{x}} = \int\limits_G w \cdot f{{\rm{d}}^3}\mathit{\boldsymbol{x}} $ | (7) |
同样得到式(6)的弱形式:
| $ \int\limits_G w \cdot \sigma {{\rm{d}}^3}\mathit{\boldsymbol{x}} = \int\limits_G w \cdot C:\mathit{\boldsymbol{\nabla}} \mathit{\boldsymbol{u}}{{\rm{d}}^3}\mathit{\boldsymbol{x}} $ | (8) |
得到波动方程的弱形式解意味着分别找到满足积分(4)、(7)和(8)的标量势χ和位移场u。SPECFEM3D模型利用谱元法求解上述积分方程的开源代码,由普林斯顿大学和法国国家科学研究中心联合开发,用于区域性及全球性的地震波数值模拟。
1.2 模型及参数设置本文主要研究理想的高斯型海底山环境下的三维声传播特性,主要模拟分析甚低频声波的传播过程及地形剧烈变化环境下的三维声场结构变化。为横向对比非对称平面内地形变化带来的传播过程中的三维效果,模型计算域必须足够大,但考虑到计算时间合理性,计算域的大小必须受到限制。
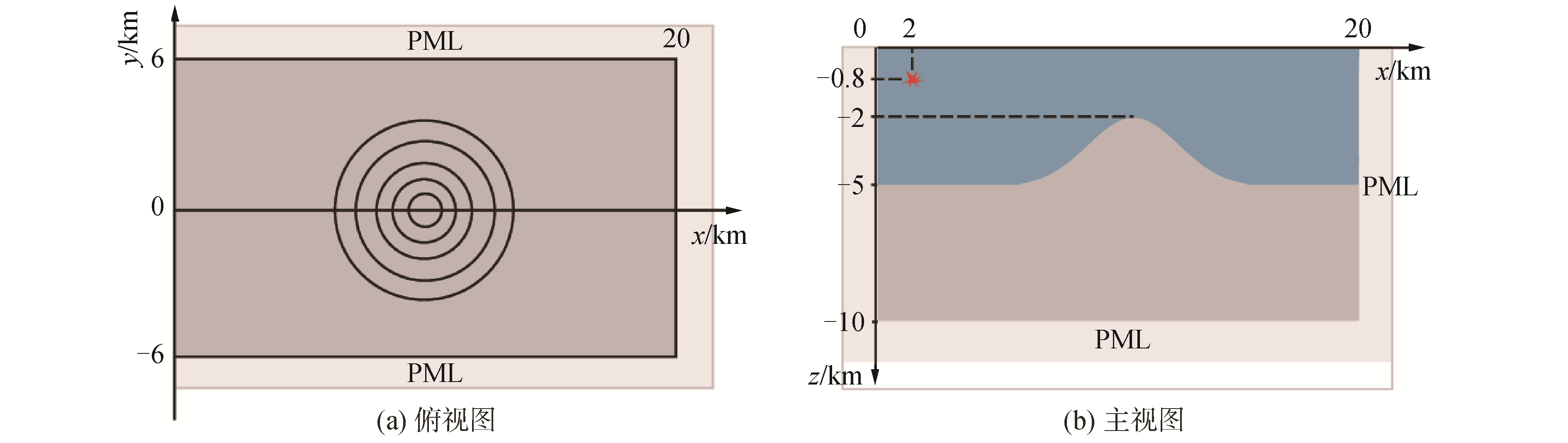
因此模型参数设置如图 1所示,水平计算区域宽度为20 km×12 km,深度方向为10 km,包含5 km厚的流体介质(海水)和5 km厚的固体介质(海底)。为了避免不必要的边界反射波影响,除了海面(z=0 km), 其他3个边界均设置为完美匹配层(PML)[24],可视作均匀半无限海底。海底设置为均匀岩石层,其压缩波速度和剪切波速度分别设置为3 000 m/s和1 700 m/s,密度为2 000 kg/m3。海水同样设为均匀介质,密度为1 000 kg/m3,声速为1 500 m/s。高斯山地形中心位置位于水平距离x=10 km处,高度为h=3 km, 底部最大宽度10 km。声源位于海水中的甚低频点压力源,为中心频率fs=5 Hz的Ricker子波,位置距海面hs=800 m,水平距离ds=2 km。本文只关注地形的影响,在固体和流体介质中都没有声吸收衰减。
|
Download:
|
| 图 1 计算区域地形示意 Fig. 1 Views of the calculation domain with a Gaussian seamount | |
采用谱元法进行数值计算时,计算域中划分的网格大小取决于声波在2种介质中的传播速度和声源频率, 为了保证计算结果所需精度,要求在每个波长内至少包含5个控制节点,也就是划分的网格尺寸d、Lagrange多项式阶数n和信号的波长λ之间需满足d≤n/5λ。本文所使用模型采用4阶Lagrange多项式,网格选择为边长大小约100 m的六面体,利用开源软件Gmesh[25]将计算域划分为4 009 335个非结构化六面体网格, 保证计算模型在有效的时间内提供相对精确的模拟结果。
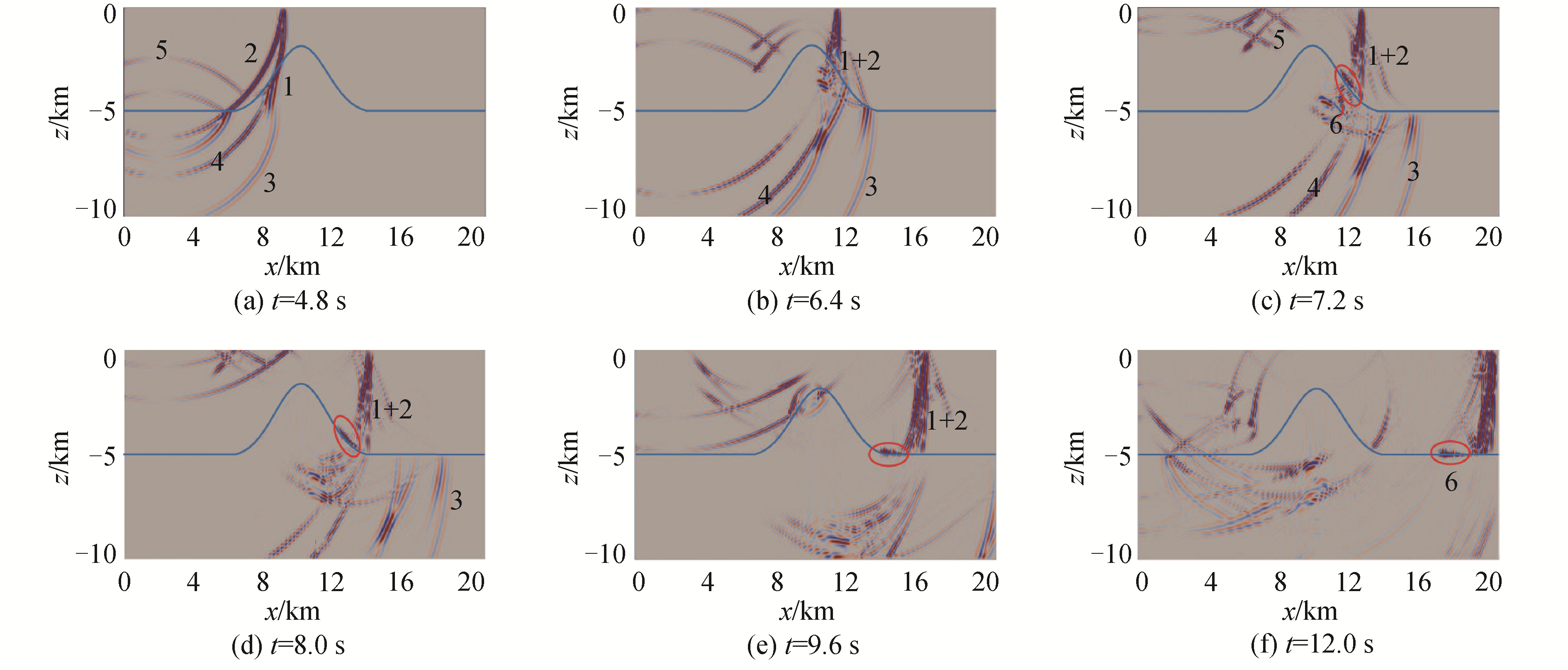
2 数值结果分析 2.1 声场多途结构及传播过程分析图 2显示了在不同时刻(t=4.8,6.4,7.2,8.0,9.6,12 s)水中点声源发出声波在y=0平面内海水及海底中传播情况的声场快照。图中符号1代表直达波,2为海面反射波,3为海底透射压缩波,4为海底透射剪切波以及5为海底反射波;与海底反射波5相对的,还存在部分能量经山前折射耦合进海底山,转变为海底山内的压缩波和剪切波,这部分能量继续传播又经山后折射回到海水中,最终能量变得较为微弱。此外,在7.2 s以后的声场快照中,图 2(c)~(f),海底山界面上出现较强能量传播6,且沿海底山界面传播到水平海底,研究发现该声波信号的传播规律符合Scholte界面波特性。
|
Download:
|
| 图 2 垂向位移分量在y=0平面内不同时刻声场快照 Fig. 2 The sound field snapshots of vertical displacement at different times in y=0 plane 注:1. 直达波,2. 海面反射波,3. 海底射透压缩波,4. 海底透射剪切波,5. 海底反射波,6. 界面波。 | |
Scholte界面波的激发与Rayleigh波相似,与声源和界面间的距离有着很强的依赖关系,当声源靠近海底时(~λ),可以激发很强的Scholte波,而在深海声源距海底较远,通常无法激发界面波。然而,已有仿真结果表明Scholte波有另外一种有效的激发机制——海底地形变化[26]。
水平海底界面下,Scholte波特性已有大量研究。海水声速cp0,密度ρ0,海底压缩波速度cp1,剪切波速度cs1,密度ρ1时,Scholte波满足频散方程:
| $ 4\frac{{{\alpha _{{p_1}}}{\alpha _{{s_1}}}}}{{{k^2}}} - {\left( {2 - \frac{{{\omega ^2}}}{{{k^2}c_{{s_1}}^2}}} \right)^2} = \frac{{{\rho _0}}}{{{\rho _1}}}{\left( {\frac{\omega }{{k{c_{{s_1}}}}}} \right)^4}\frac{{{\alpha _{{p_1}}}}}{{{\alpha _{{p_0}}}}} $ | (9) |
式中:αp0, p1, s1=-iγp0, p1, s1=
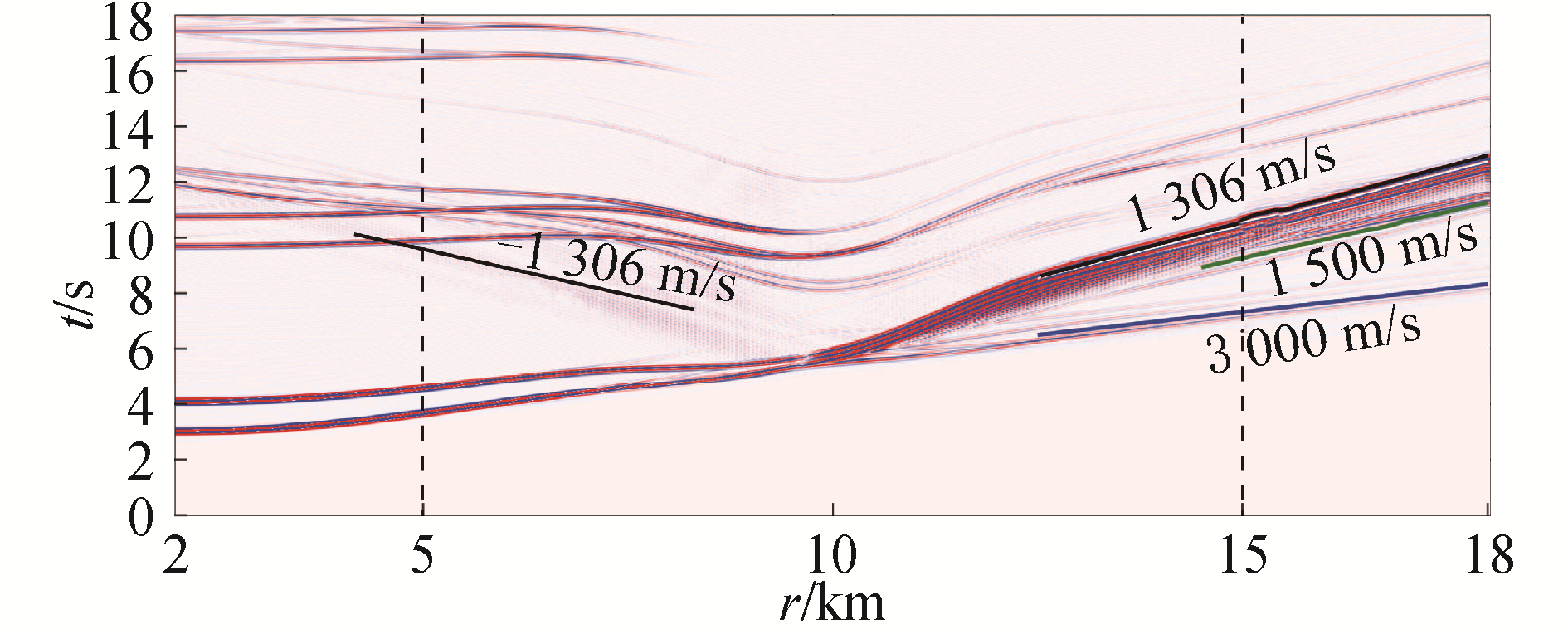
海底山附近以不同速度传播的声信号可在时程图中区分出来,由时域声压信号构成的时程图如图 3所示,其中接收点沿着海底界面布放,位于距海底界面垂直距离为10 m的水中,间隔为50 m。在距离-时间域内,到达信号的斜率可视为其传播速度。在海底山后水平海底区域(15~18 km)处,最早到达信号为头波,以海底压缩波速度3 000 m/s传播;随后到达的是以速度1 500 m/s由海水中传播而来的信号,由于接收点位于海底山掩蔽效应产生的影区内,水中多途信号能量较弱;图中显示,在该区域能量强度最大的为存在于海底界面的Scholte界面波,其传播速度最慢为1 306 m/s;同时,图中还存在沿海底山左侧以速度1 306 m/s反向传播的Scholte波,但由于入射波场向右传播的幅度更高,其反向传播能量十分微弱。由于海底山附近耦合激发的Scholte界面波的强度较强,且传播损失也相对较小,对于海洋探测开发提供了新的方式也将具有新的意义。
|
Download:
|
| 图 3 y=0平面内海底界面附近接收声压信号时程 Fig. 3 Distance-time diagram of the acoustic pressure near seafloor | |
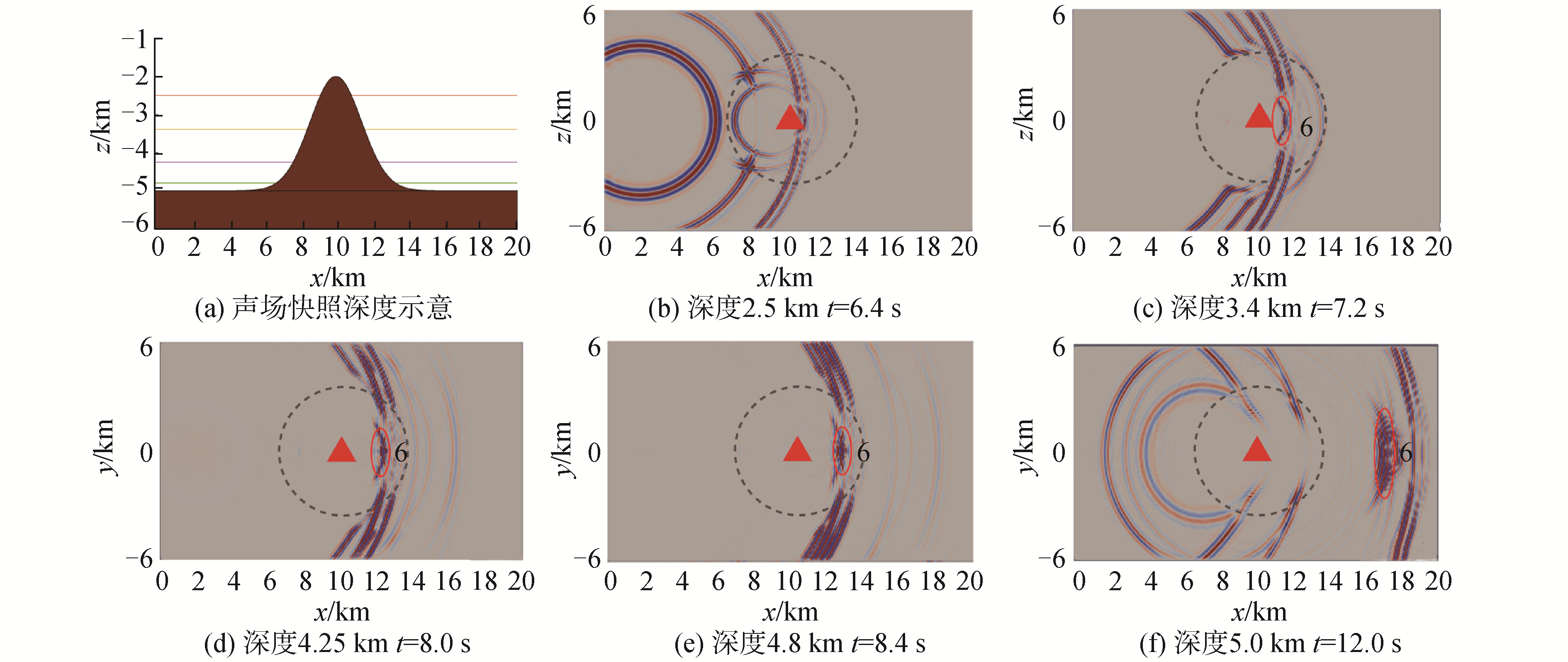
界面波产生于海底山顶部,其绕海底山传播方式可由水平截面声场快照中区分。随着时间推移,Scholte波沿着海底山界面由上向下传播,图 4给出不同时刻Scholte波所在深度处的垂直分量位移声场快照,图中三角形和虚线分别对应海底山山顶和山脚所在位置。Scholte波由6.4 s海底山顶部随着地形变化逐渐扩展,直到水平海底。由于波场快照显示各到达结构相对能量,反向传播的Scholte波无法在图 4内区分。
|
Download:
|
| 图 4 垂向位移分量声场快照 Fig. 4 The sound field snapshots of vertical displacement | |
为方便讨论地形变化激发界面波的强度,将脉冲波形的相对能量定义为:
| $ E(r,z,t) = - 20\log \left| {\frac{{p(r,z,t)}}{{{p_{\max }}}}} \right| $ | (10) |
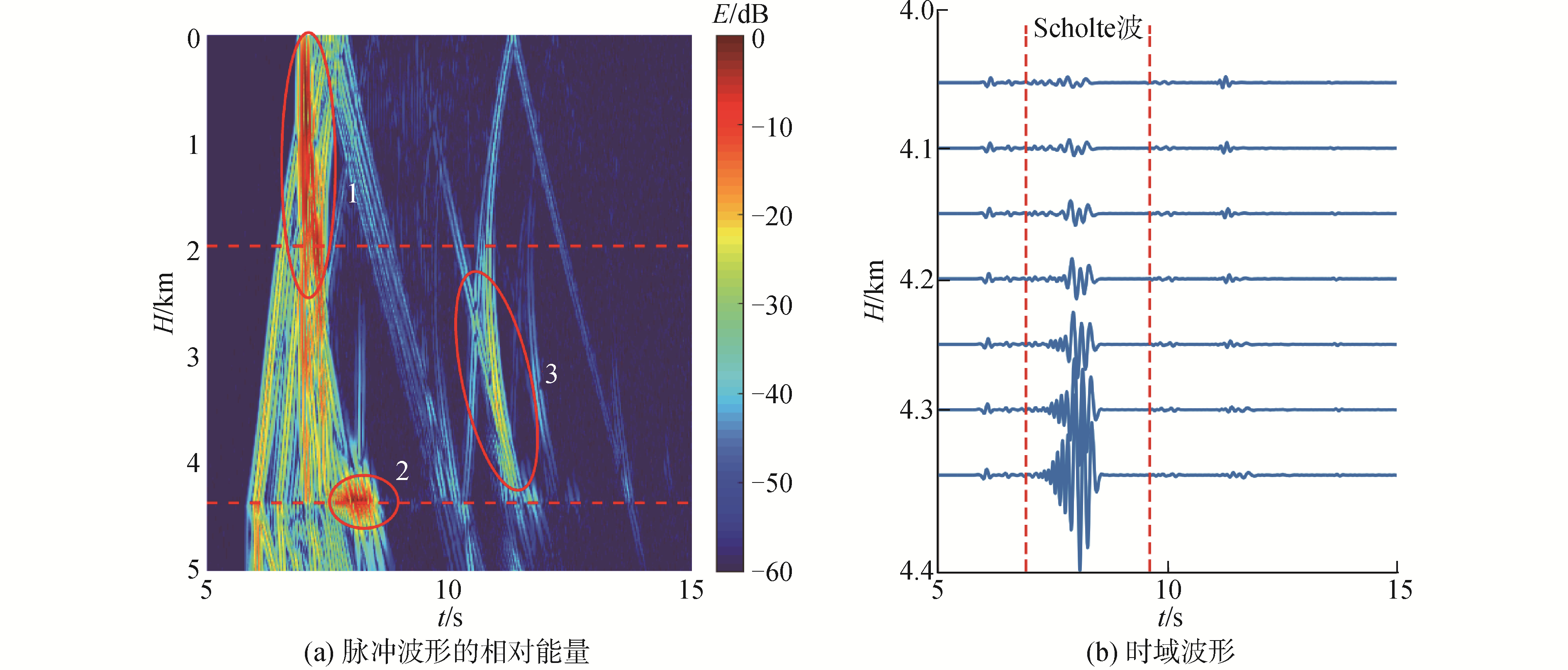
式中:p(r, z, t)为接收到的信号,pmax是接收波形的幅度的最大值。图 5(a)为y=0截面内12.5 km处的垂直接收点脉冲波形的相对能量,此处水深4 371 m,红线标注为海底山所在深度,图中1为直达波与海面反射波叠加;2为界面波;3为衍射波。其中衍射波部分为海底山掩蔽效应造成的影区内能量的主要来源,这与Stephen等[1]实验中观察到的BDSR信号相同。由于本文模型内仅包含一座海底山,地形变化带来的衍射现象仅存在于二维对称平面内,不存在三维衍射现象,因此本文不再对此做更多讨论。图 5(a)中可以看出,由于山的遮挡2 000 m以下直达波和海面反射波能量迅速下降。海水与弹性体界面处接收到很强的界面波。图 5(b)为距界面300 m内深度间隔50 m的7个接收点的声压时域信号,随着与界面距离的增加,界面波幅度呈指数衰减,而其他类型的到达信号在一个波长内(300 m)幅度几乎没有变化。
|
Download:
|
| 图 5 脉冲波形的相对能量与时域波形随深度变化 Fig. 5 The relative energy of the received signal and the time domain waveform vary with the depth | |
Stephen等[2]在一次深海远距离传播实验中发现海底OBS接收到一系列无法解释的到达波,而海水中的垂直阵没有接收到,同时实验海域声源附近有一海底山,因此实验中OBS接收到的很可能是海底地形变化激发的Scholte波。实验与仿真结果均证明了深海海底界面波的存在且可由海底OBS接收,这为深海及声影区的定位、探测等应用提供新的手段。
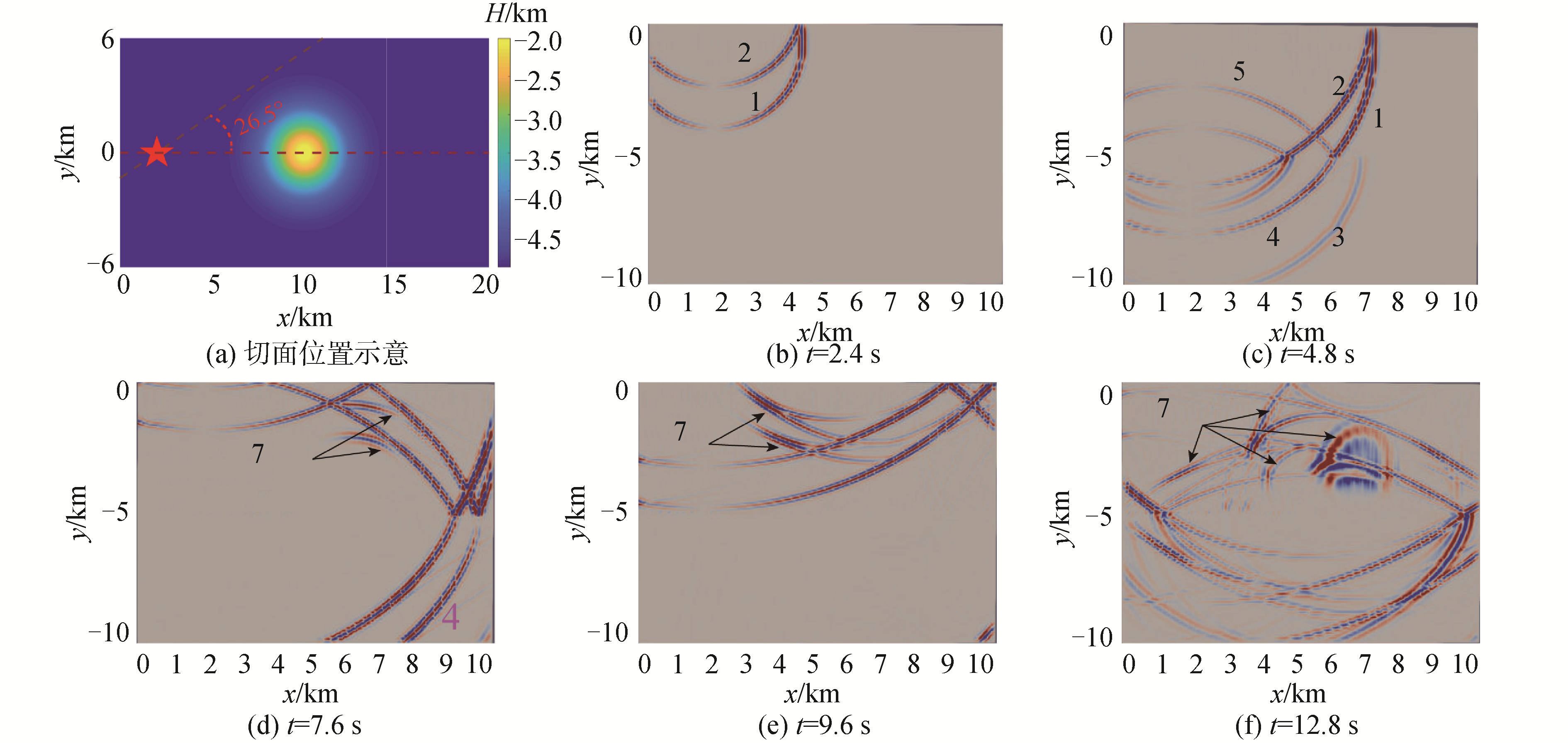
2.3 三维效应分析已有研究表明,声波在倾斜海底界面与水平海面之间进行多次反射后,会改变其水平传播方向,即呈现水平折射效应。为分析这一现象选取与海底山夹角26.5°的截面声场快照如图 6所示,对应时刻分别为2.4、4.8、7.6、9.6、12.8 s,其中多途结构字母标注与图 2相同。该截面未经过海底山,在利用2D或N×2D模拟时不会有海底山的反射波。但实际上,经海底海面多次反射后于7.6 s开始出现其他平面的水平折射波7,且随着时间的增加反射次数增多,该平面内水平折射波的到达越来越多。这与Badiey等[26]在实验中观察到的由内波引起的水平多途现象是相似的。
|
Download:
|
| 图 6 与海底山夹角26.5°的截面声场快照 Fig. 6 The sound field snapshots of line 26.5° from the symmetry plane 注:1. 直达波,2. 海面反射波,3. 海底射透压缩波,4. 海底透射剪切波,5. 海底反射波,6. 界面波,7. 水平折射波。 | |
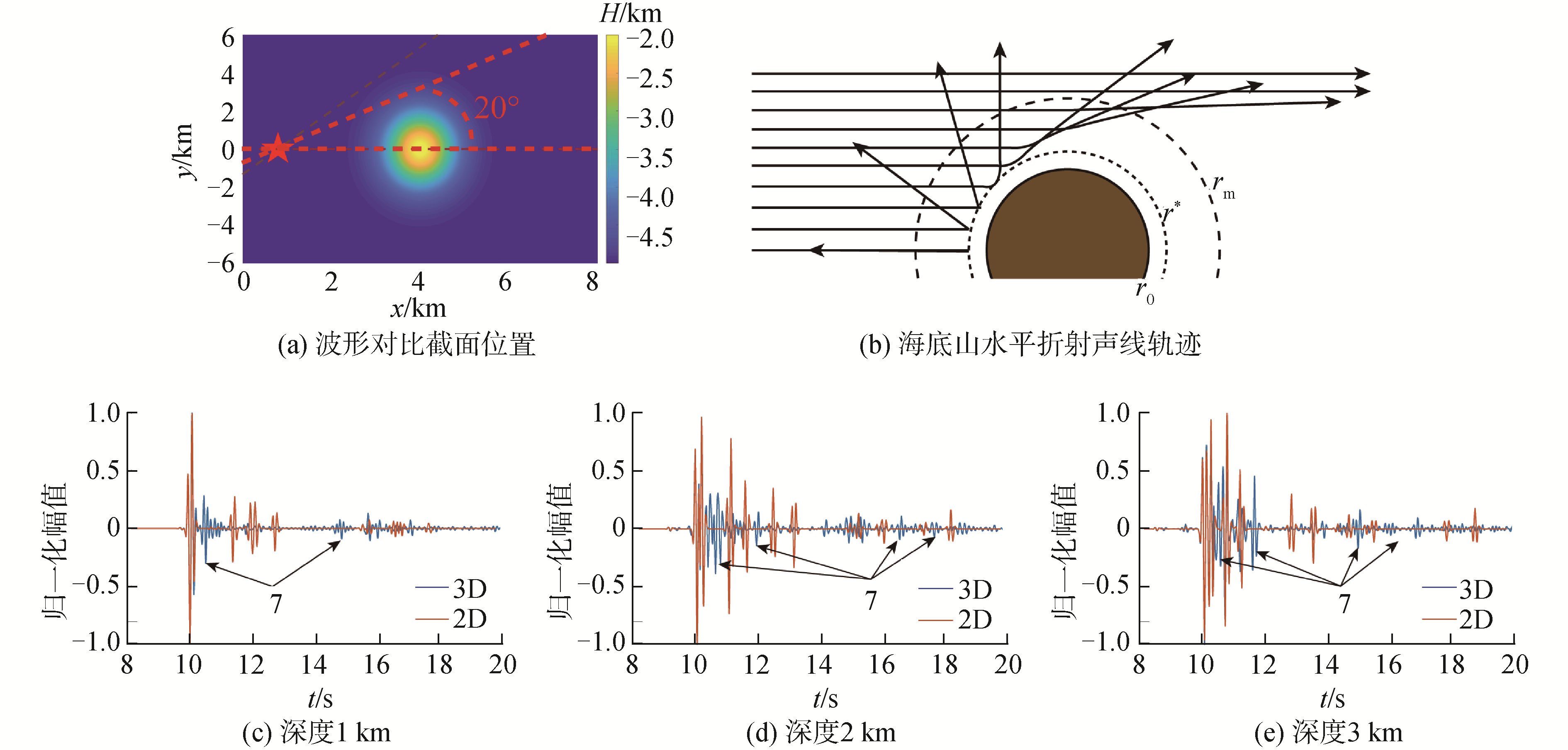
为突出海底山地形变化带来的三维效应对时域信号的影响,将与海底山对称平面夹角20°的垂面内声场与二维模型计算结果对比,如图 7所示。图 7(b)为基于射线理论给出的海底山水平折射声线轨迹的水平投影,很好的解释了水平折射多途信号的来源。图 7(c)(d)、(e)分别为距声源15 km处不同深度下二维与三维模型仿真的声压波形对比,3个深度分别对应海底山上方、海底山顶所在深度和深度大于海底山顶,随着深度的增加水平折射信号7增多。此外,两模型海面、海底多次反射波强度相差很大,这是由于二维计算选择轴对称坐标,与三维模型仍有差别。
|
Download:
|
| 图 7 与海底山夹角20°声压波形与二维模型对比 Fig. 7 The time domain waveform of line 20° from the symmetry plane compared with SPECFEM2D | |
1) 谱元法不仅能模拟出不同到达结构的传播过程,还能较好地反映出地形变化对水下声传播的影响。
2) 海底山环境下的声传播会产生复杂的三维水平折射与散射现象。
3) 海底山地形变化会引起声信号在传播过程中与海底的耦合从而激发Scholte波,沿海底山表面传播。
4) 海底界面附近Scholte波能量最强可由海底OBS接收,可成为为深海及声影区定位、探测新手段。
本文仿真采用的是理想地形和均匀介质,实际海洋中海底山地形会起上升流导致声速变化,海底分层结构及地质特征复杂。仍需进一步考虑水文条件、结合地质构造背景建立更加精确的计算模型,在对三维效应、声会聚效应、海底地震波传播等进行研究的过程中,采用谱元法进行数值模拟分析是可行的。
| [1] |
STEPHEN R A, BOLMER S T, WORCESTER P F, et al. Three-dimensional bottom diffraction in the North Pacific[J]. The journal of the acoustical society of America, 2019, 146(3): 1913-1922. DOI:10.1121/1.5125427 (  0) 0)
|
| [2] |
JENSEN F B, KUPERMAN W A, PORTER M B, et al. Computational ocean acoustics[M]. 2nd ed. New York: Springer, 2011: 611-660.
(  0) 0)
|
| [3] |
KOMATITSCH D, ERLEBACHER G, GÖDDEKE D, et al. High-order finite-element seismic wave propagation modeling with MPI on a large GPU cluster[J]. Journal of computational physics, 2010, 229(20): 7692-7714. DOI:10.1016/j.jcp.2010.06.024 (  0) 0)
|
| [4] |
ISAKSON M J, GOLDSBERRY B, CHOTIROS N P. A three-dimensional, longitudinally-invariant finite element model for acoustic propagation in shallow water waveguides[J]. The journal of the acoustical society of America, 2014, 136(3): EL206-EL211. DOI:10.1121/1.4890195 (  0) 0)
|
| [5] |
TROMP J, KOMATITSCH D, LIU Qinya. Spectral-element and adjoint methods in seismology[J]. Communications in computational physics, 2008, 3(1): 1-32. (  0) 0)
|
| [6] |
NORTHROP J. Underwater sound propagation across the Hawaiian Arch[J]. The journal of the acoustical society of America, 1970, 48(1B): 417-418. DOI:10.1121/1.1912145 (  0) 0)
|
| [7] |
HARRISON C H. Three-dimensional ray paths in basins, troughs, and near seamounts by use of ray invariants[J]. The journal of the acoustical society of America, 1977, 62(6): 1382-1388. DOI:10.1121/1.381670 (  0) 0)
|
| [8] |
BAER R N. Calculations of sound propagation through an eddy[J]. The journal of the acoustical society of America, 1980, 67(4): 1180-1185. DOI:10.1121/1.384178 (  0) 0)
|
| [9] |
PERKINS J S, BAER R N. An approximation to the three-dimensional parabolic-equation method for acoustic propagation[J]. The journal of the acoustical society of America, 1982, 72(2): 515-522. DOI:10.1121/1.388032 (  0) 0)
|
| [10] |
徐传秀, 朴胜春, 杨士莪, 等. 采用能量守恒和高阶Padé近似的三维水声抛物方程模型[J]. 声学学报, 2016, 41(4): 477-484. XU Chuanxiu, PIAO Shengchun, YANG Shi'e, et al. A three-dimensional parabolic equation model using energy-conserving and higher-order Padé approximant in underwater acoustics[J]. Acta acustica, 2016, 41(4): 477-484. (  0) 0)
|
| [11] |
BUCKINGHAM M J. Theory of acoustic propagation around a conical seamount[J]. The journal of the acoustical society of America, 1986, 80(1): 265-277. DOI:10.1121/1.394183 (  0) 0)
|
| [12] |
TAROUDAKIS M I. A coupled-mode formulation for the solution of the Helmholtz equation in water in the presence of a conical sea-mount[J]. Journal of computational acoustics, 1996, 4(1): 101-121. DOI:10.1142/S0218396X96000246 (  0) 0)
|
| [13] |
LUO Wenyu, SCHMIDT H. Three-dimensional propagation and scattering around a conical seamount[J]. The journal of the acoustical society of America, 2009, 125(1): 52-65. DOI:10.1121/1.3025903 (  0) 0)
|
| [14] |
ATHANASSOULIS G A, BELIBASSAKIS K A. All-frequency normal-mode solution of the three-dimensional acoustic scattering from a vertical cylinder in a plane-horizontal waveguide[J]. The journal of the acoustical society of America, 1997, 101(6): 3371-3384. DOI:10.1121/1.418295 (  0) 0)
|
| [15] |
ATHANASSOULIS G A, PROSPATHOPOULOS A M. Three-dimensional acoustic scattering from a penetrable layered cylindrical obstacle in a horizontally stratified ocean waveguide[J]. The journal of the acoustical society of America, 2000, 107(5): 2406-2417. DOI:10.1121/1.428627 (  0) 0)
|
| [16] |
李晟昊, 李整林, 李文, 等. 深海海底山环境下声传播水平折射效应研究[J]. 物理学报, 2018, 67(22): 224302. LI Shenghao, LI Zhenglin, LI Wen, et al. Horizontal refraction effects of seamounts on sound propagation in deep water[J]. Acta physica sinica, 2018, 67(22): 224302. (  0) 0)
|
| [17] |
BURNS D R. Acoustic and elastic scattering from seamounts in three dimensions-a numerical modeling study[J]. The journal of the acoustical society of America, 1992, 92(5): 2784-2791. DOI:10.1121/1.405293 (  0) 0)
|
| [18] |
STURM F. Numerical study of broadband sound pulse propagation in three-dimensional oceanic waveguides[J]. The journal of the acoustical society of America, 2005, 117(3): 1058-1079. DOI:10.1121/1.1855791 (  0) 0)
|
| [19] |
CRISTINI P, KOMATITSCH D. Some illustrative examples of the use of a spectral-element method in ocean acoustics[J]. The journal of the acoustical society of America, 2012, 131(3): EL229-EL235. DOI:10.1121/1.3682459 (  0) 0)
|
| [20] |
BOTTERO A, CRISTINI P, KOMATITSCH D, et al. An axisymmetric time-domain spectral-element method for full-wave simulations:application to ocean acoustics[J]. The journal of the acoustical society of America, 2016, 140(5): 3520-3530. DOI:10.1121/1.4965964 (  0) 0)
|
| [21] |
董阳, 朴胜春.三维楔形波导谱元法声场分析[C]//2018年全国声学大会论文集B水声物理.北京: 中国声学学会, 2018. DONG Yang, PIAO Shengchun. Acoustic field analysis using three-dimensional wedge-shaped Waveguide Spectral element method[C]//Proceedings of 2018 National Acoustical Academic Conference of Acoustical Society of China. Beijing: Acoustical Society of China, 2018. (  0) 0)
|
| [22] |
FICHTNER A. Full seismic waveform modelling and inversion[M]. Berlin, Heidelberg: Springer, 2011.
(  0) 0)
|
| [23] |
XIE Zhinan, MATZEN R, CRISTINI P, et al. A perfectly matched layer for fluid-solid problems:application to ocean-acoustics simulations with solid ocean bottoms[J]. The journal of the acoustical society of America, 2016, 140(1): 165-175. DOI:10.1121/1.4954736 (  0) 0)
|
| [24] |
GEUZAINE C, REMACLE J F. Gmsh:a 3-D finite element mesh generator with built-in pre-and post-processing facilities[J]. International journal for numerical methods in engineering, 2009, 79(11): 1309-1331. DOI:10.1002/nme.2579 (  0) 0)
|
| [25] |
ZHENG Yingcai, FANG Xinding, LIU Jing, et al. Scholte waves generated by seafloor topography[J]. arXiv preprint arXiv: 1306.4383, 2013.
(  0) 0)
|
| [26] |
BADIEY M, KATSNELSON B G, LIN Y T, et al. Acoustic multipath arrivals in the horizontal plane due to approaching nonlinear internal waves[J]. The journal of the acoustical society of America, 2011, 129(4): EL141-EL147. DOI:10.1121/1.3553374 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


