2. 西藏大学 信息科学技术学院, 西藏 拉萨 850000;
3. 海洋信息获取与安全工业和信息化部重点实验室(哈尔滨工程大学), 黑龙江 哈尔滨 150001;
4. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001;
5. 中国船舶工业系统工程研究院 水声对抗技术实验室, 北京 100036
2. College of Information Science and Technology, Tibet University, Lhasa 850000, China;
3. Key Laboratory of Marine Information Acquisition and Security(Harbin Engineering University), Ministry of Industry and Information Technology, Harbin 150001, China;
4. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China;
5. National Key Laboratory of Science and Technology on Underwater Acoustic Antagonizing, China State Shipbuilding Corporation Systems Engineering Research Institute, Beijing 100036, China
高分辨方位谱估计技术提出以来便得到迅速发展,如今已广泛应用于通信、声呐、雷达等领域。水声阵列信号处理中波达方估计(direction of arrival,DOA)始终是研究热点。传统的常规波束形成(conventional beamforming,CBF)算法因瑞利限问题使得分辨率受阵列孔径限制。高分辨方位谱估计算法的分辨率则不受瑞利限影响,方位估计性能更好。
高分辨方位谱估计算法中Schmidt[1]的多重信号分类(multiple signal classification,MUSIC)算法和Paulraj[2]提出的旋转不变子空间(estimation of signal parameters via rotational invariance technique, ESPRIT)算法较为经典。MUSIC算法通过分离信号子空间和噪声子空间,利用子空间正交性估计目标波达角度[3]。ESPRIT算法利用阵列子阵间的旋转不变性估计目标方位角[4]。Hoffman提出了利用相关矩阵的特征结构进行方位估计的特征子空间(Eigenspace)算法[5]。Eigenspace算法较经典的MUSIC等算法具有更低的旁瓣和更高的方位估计精度,却如诸多的高分辨方位谱估计算法一样,在水声等低信噪比环境下方位估计效果并不理想。
传统的水声信号处理大多基于声压水听器阵列。Nehorai[6]建立了声矢量水听器阵列方位测量模型。声矢量水听器阵列可以同时获得声场中的声压和振速信息,相比于相等阵元数的声压阵具有更高的处理增益和抗干扰能力,更加有利于水声低信噪比条件下的信号处理[7]。惠俊英等[8]提出声压振速联合信息处理方法,提高了声矢量阵抑制各项同性干扰噪声的能力;孙大军等[9]将反卷积波束形成技术应用于声矢量阵列。
常规的特征空间谱估计算法无法对相干源信号解相干,因此对相干源目标进行方位估计时性能较差[10]。一些学者进行了相干源方位估计的研究,梁国龙等[11]利用声矢量线阵进行相干信号源的方位估计,提高了方位估计精度。姚直象等[12]对矢量阵空间平滑算法进行研究,提高MUSIC算法对相干源的分辨能力。
水声低信噪比环境下方位估计效果较差,声矢量阵相对于相等阵元数的声压阵具有更高的处理增益。因此,本文将常规Eigenspace算法推广到矢量水听器阵列并结合声压振速信息联合处理方法抑制各向同性噪声并且提高方位估计能力。本文提出了基于声压振速联合处理的Eigenspace-wiener算法,在较低信噪比下获得良好方位估计效果;针对常规算法对相干源方位估计性能下降的问题,本文进一步研究了空间平滑Eigenspace算法,结合维纳后置滤波Eigenspace技术,使算法的性能进一步提高。
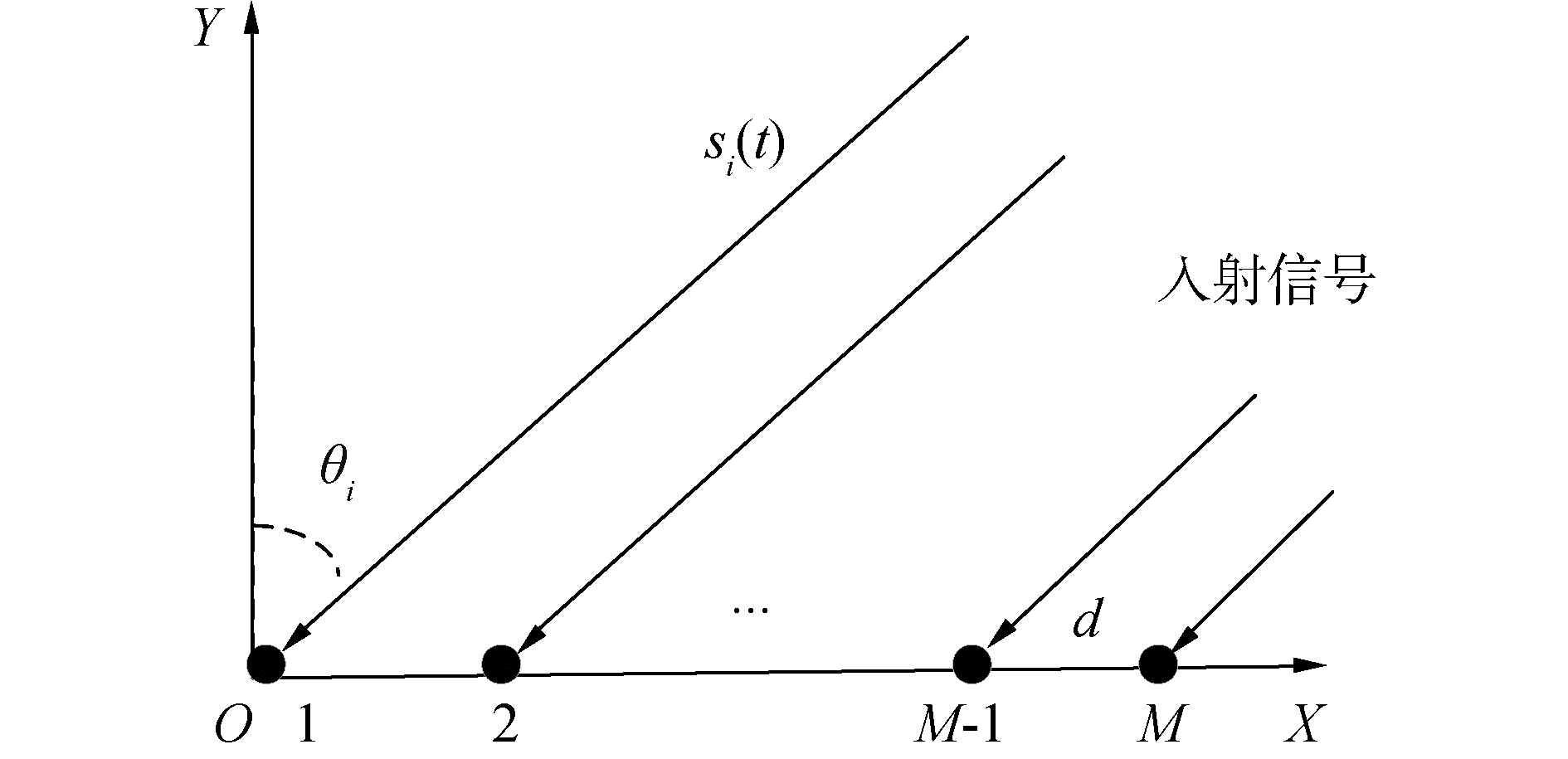
1 Eigenspace算法失量陈列理论分析 1.1 声矢量阵接收信号模型如图 1所示,以二维声矢量水听器阵为例,假设存在具有M个矢量水听器的声矢量阵列,第m个矢量水听器的空间位置矢量为km,m=1,2,…,M,K个空间信号入射到该矢量阵列上,第k个空间信号的二维空间到达角为θi,定义第m个阵元声压通道和振速通道输出为:
|
Download:
|
| 图 1 M元声矢量水听器均匀线阵示意 Fig. 1 M element acoustic vector sensor uniform linear array | |
| $ \left\{ {\begin{array}{*{20}{l}} {{p_m}(t) = \sum\limits_{i = 1}^K {{a_m}} \left( {{\theta _i}} \right){s_i}(t) + {n_{{p_m}}}(t)}\\ {{v_{xm}}(t) = \sum\limits_{i = 1}^K {{a_m}} \left( {{\theta _i}} \right)\sin {\theta _i}{s_i}(t) + {n_{{v_{xm}}}}(t)}\\ {{v_{ym}}(t) = \sum\limits_{i = 1}^K {{a_m}} \left( {{\theta _i}} \right)\cos {\theta _i}{s_i}(t) + {n_{{v_{ym}}}}(t)} \end{array}} \right. $ | (1) |
式中:pm(t)、vxm(t)、vym(t)分别是第m个阵元声压通道输出分量、振速x通道的输出分量、振速y通道的输出分量;npm(t)、nvxm(t)、nvym(t)分别对应第m个阵元声压通道、振速x通道、振速y通道的噪声。a(θi)为均匀直线阵的导向矢量:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{a}}\left( {{\theta _i}} \right) = {{\left[ {{a_1}\left( {{\theta _i}} \right),{a_2}\left( {{\theta _i}} \right), \cdots ,{a_M}\left( {{\theta _i}} \right)} \right]}^{\rm{T}}} = }\\ {\left[ {1,\exp \left( { - {\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}d\sin {\theta _i}}}{\lambda }} \right), \cdots ,} \right.}\\ {{{\left. {\exp \left\{ { - {\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}(M - 1)d\sin {\theta _i}}}{\lambda }} \right\}} \right]}^{\rm{T}}}(i = 1,2, \cdots ,K)} \end{array} $ | (2) |
将各个阵元输出分量排列组合,得到M元声矢量水听器均匀线阵声压通道P(t)、振速x通道Vx(t)、振速y通道Vy(t)的输出:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{P}}(t) = {{[{p_1}(t),{p_2}(t), \cdots ,{p_M}(t)]}^{\rm{T}}}}\\ \begin{array}{l} {\mathit{\boldsymbol{V}}_x}(t) = {[{v_{x1}}(t),{v_{x2}}(t), \cdots ,{v_{xM}}(t)]^{\rm{T}}}\\ {\mathit{\boldsymbol{V}}_y}(t) = {[{v_{x1}}(t),{v_{x2}}(t), \cdots ,{v_{xM}}(t)]^{\rm{T}}} \end{array} \end{array}} \right. $ | (3) |
根据文献[7]所述,声压通道与振速通道噪声互不相关,可利用声压振速联合处理的方法抑制噪声,提高增益。将Vx和Vy通道组合,获得组合通道Vc:
| $ {\mathit{\boldsymbol{V}}_c}(t) = {\mathit{\boldsymbol{V}}_x}(t)\sin \varphi + {\mathit{\boldsymbol{V}}_y}(t)\cos \varphi $ | (4) |
式中:φ是引导方位角,调整φ的角度可改变Vc的指向性,实现波束空间的全方位覆盖。将声压与振速通道进一步组合后可获得PVc、(P+Vc)Vc、(P+Vc)(P+Vc)等组合指向性。
由图 2可知,声压与振速通道的不同组合可获得不同指向性以实现不同的工程需求,相对于其他2种组合方法,(P+Vc)Vc联合处理主瓣较窄并且没有左右舷模糊,本文采用(P+Vc)Vc的组合形式。

|
Download:
|
| 图 2 矢量水听器的组合指向性 Fig. 2 Vector hydrophone combined directivity | |
在(P+Vc)Vc联合处理下该阵列对应的协方差矩阵为:
| $ {\mathit{\boldsymbol{R}}_{(P + {V_c}){V_c}}} = {\rm{E}}\{ [\mathit{\boldsymbol{P}}(t) + {\mathit{\boldsymbol{V}}_c}(t)]{\mathit{\boldsymbol{V}}_c}{(t)^{\rm{H}}}\} $ | (5) |
Eigenspace算法是将最小方差无失真响应(minimum variance distortionless response, MVDR)算法的权向量投影到信号子空间得到该算法的权向量,通过投影变换使得权向量范数减小,提升了算法的收敛性和稳健性;同时该算法充分利用了信号子空间,空间分辨性能更好。
MVDR算法的最优权为:
| $ {\mathit{\boldsymbol{w}}_{{\rm{MVDR}}}} = \frac{{{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{a}}(\mathit{\boldsymbol{\theta }})}}{{{\mathit{\boldsymbol{a}}^{\rm{H}}}(\mathit{\boldsymbol{\theta }}){\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{a}}(\mathit{\boldsymbol{\theta }})}} $ | (6) |
将(P+Vc)Vc联合处理构成互协方差矩阵R(P+Vc)Vc,使用特征分解。将声压振速联合处理构成协方差矩阵特征分解为信号子空间和噪声子空间:
| $ {\mathit{\boldsymbol{R}}_{(\mathit{\boldsymbol{P}} + {\mathit{\boldsymbol{V}}_c}){\mathit{\boldsymbol{V}}_c}}} = {\mathit{\boldsymbol{R}}_s} + {\mathit{\boldsymbol{R}}_n} = {\mathit{\boldsymbol{U}}_s}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_s}\mathit{\boldsymbol{U}}_s^{\rm{H}} + {\mathit{\boldsymbol{U}}_n}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_n}\mathit{\boldsymbol{U}}_n^{\rm{H}} $ | (7) |
其中Rs=UsΣsUsH,Rn=UnΣnUnH,US和UN分别代表了协方差矩阵R(P+Vc)Vc张成的信号子空间和噪声子空间,可定义ΣS和ΣN为:
| $ {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_S} = {\rm{diag}} ({\alpha _1},{\alpha _2}, \cdots ,{\alpha _Q})} $ | (8) |
| $ {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_N} = {\rm{diag}} ({\alpha _{Q + 1}},{\alpha _{Q + 2}}, \cdots ,{\alpha _M})} $ | (9) |
其中ΣS中α1,α2,…,αQ为R(P+Vc)Vc较大的特征值,对应信号项,ΣN中αQ+1,αQ+2,…,αM为R(P+Vc)Vc较小的特征值,对应噪声项。
定义
| $ {\mathit{\boldsymbol{w}}_{{\rm{MVDR}}}} = \lambda \mathit{\boldsymbol{R}}_{(\mathit{\boldsymbol{P}} + {\mathit{\boldsymbol{V}}_c}){\mathit{\boldsymbol{V}}_c}}^{ - 1}\mathit{\boldsymbol{a}}(\mathit{\boldsymbol{\theta }}) = \lambda {\varGamma _S}\mathit{\boldsymbol{a}}(\mathit{\boldsymbol{\theta }}) + \lambda {\varGamma _N}\mathit{\boldsymbol{a}}(\mathit{\boldsymbol{\theta }}) $ | (10) |
其中ΓS=USΣs-1UST,ΓN=UNΣN-1UNT。
由此得到Eigenspace算法的最优权为:
| $ {\mathit{\boldsymbol{w}}_{{\rm{ Eigenspace }}}}(\theta ) = \frac{{{\varGamma _S}\mathit{\boldsymbol{a}}(\mathit{\boldsymbol{\theta }})}}{{{\mathit{\boldsymbol{a}}^{\rm{H}}}(\mathit{\boldsymbol{\theta }})\mathit{\boldsymbol{Ra}}(\mathit{\boldsymbol{\theta }})}} $ | (11) |
Eigenspace算法使用了阵列输出协方差矩阵中信号子空间分量,保证期望方向和干扰方向的输出能量基本不变,并使得阵列噪声输出功率减小,提高了输出信噪比,改善谱估计输出旁瓣。
1.3 维纳后置滤波Eigenspace算法在最小均方误差准则条件下维纳波束形成器权矢量利用约束波束输入信号和期望信号得到,约束条件可表示为[13]:
| $ {\mathit{\boldsymbol{w}}_{{\rm{ Wiener }}}} = \arg\mathop {\min}\limits_w {\rm{E}}\{ |\mathit{\boldsymbol{S}} - {\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{X}}{|^2}\} $ | (12) |
式中w代表任意无失真波束形成器的权矢量,对式(10)进行求解,可得到维纳后置滤波系数为:
| $ {\mathit{\boldsymbol{H}}_{{\rm{Wiener}}}} = \frac{{|s{|^2}}}{{|s{|^2} + {\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{R}}_p}\mathit{\boldsymbol{w}}}} $ | (13) |
结合式(12)、(13),最终得到维纳滤波的Eigenspace算法的权矢量:
| $ \begin{array}{l} {\mathit{\boldsymbol{w}}_{{\rm{ Eigenspace - Wiener }}}} = {\mathit{\boldsymbol{H}}_{{\rm{ Wiener }}}}{\mathit{\boldsymbol{w}}_{{\rm{ Eigenspace }}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{|s{|^2}}}{{|s{|^2} + {\mathit{\boldsymbol{w}}_{{\rm{ Eigenspace }}}}{\mathit{\boldsymbol{R}}_n}{\mathit{\boldsymbol{w}}_{{\rm{ Eigenspace }}}}}}{\mathit{\boldsymbol{w}}_{{\rm{ Eigenspace }}}} \end{array} $ | (14) |
式中|s|2=wEigenspaceHRswEigenspace。
1.4 空间平滑处理的Eigenspace算法复杂的传播环境会使水声阵列接收到不同方向的相干信号,导致相应信源下的协方差矩阵出现“秩亏”现象。空间平滑技术的基本思想是:将均匀线阵分成若干个相重叠的子阵,若各子阵列的阵列流形相同,则子阵对应的协方差矩阵相加取平均可取代原阵列的协方差矩阵。通过这种降维处理的方法在谱估计之前进行预处理,将协方差矩阵的秩恢复到与信源数相同,在牺牲部分阵列有效孔径条件下实现信号源去相干,提高相干源分辨能力[14-15]。
针对基于空间平滑的Eigenspace算法,将M元均匀线阵利用滑动方式分成N个子阵,每个子阵由J个阵元构成,则有:
| $ M = N + J - 1 $ | (15) |
定义第n个子阵(P+Vc)Vc联合处理构成互协方差矩阵为Rn,将子阵结果加权得到:
| $ \mathit{\boldsymbol{\bar R}} = \frac{1}{N}\sum\limits_{n = 1}^N {{\mathit{\boldsymbol{R}}_n}} $ | (16) |
对该矩阵特征分解为噪声子空间和信号子空间有:
| $ \mathit{\boldsymbol{\bar R}} = {\mathit{\boldsymbol{E}}_s}{\varLambda _s}\mathit{\boldsymbol{E}}_s^{\rm{H}} + {\mathit{\boldsymbol{E}}_n}{\varLambda _n}\mathit{\boldsymbol{E}}_n^{\rm{H}} $ | (17) |
按上述常规Eigenspace算法推导有:
| $ {\mathit{\boldsymbol{w}}_{{\rm{ Eigenspace }}}}(\theta ) = \frac{{{\varGamma _S}\mathit{\boldsymbol{a}}(\theta )}}{{{\mathit{\boldsymbol{a}}^{\rm{H}}}(\theta )\mathit{\boldsymbol{\bar Ra}}(\theta )}} $ | (18) |
| $ {P_{{\rm{ Eigenspace }}}}(\theta ) = \mathit{\boldsymbol{w}}_{{\rm{ Eigenspace }}}^{\rm{H}}(\theta )\mathit{\boldsymbol{\bar R}}{\mathit{\boldsymbol{w}}_{{\rm{ Eigenspace }}}}(\theta ) $ | (19) |
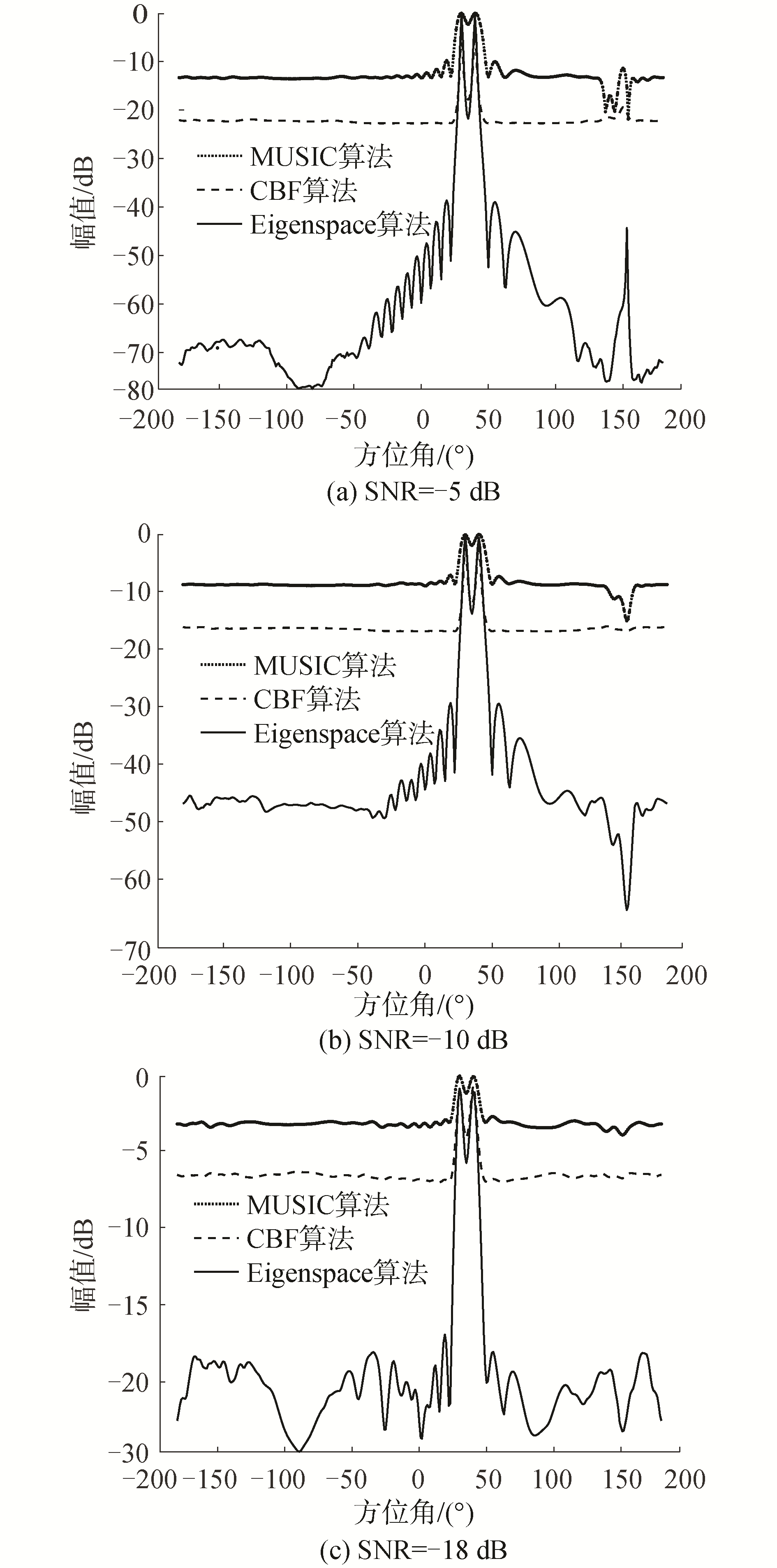
仿真实例1:仿真阵列为16元矢量均匀线阵,阵元间距为半波长,采样频率为10 kHz,快拍数为40M(M为阵元个数),接收机带宽为400~1 200 Hz,海水声速取1 500 m/s,假设目标是远场单频信源,频率分别为600 Hz和800 Hz,以阵的法线方向为0°,入射角度分别为30°和40°,所加噪声为带限白噪声,采用声矢量阵(P+Vc)Vc联合处理的方法,得到不同信噪比下Eigenspace算法方位谱图,如图 3所示。
|
Download:
|
| 图 3 不同信噪比下对2个独立目标方位估计谱 Fig. 3 Estimating the spectra of two independent target azimuths under different signal-to-noise ratios | |
对比图 3中的3种算法可知,相比于CBF算法,MUSIC算法和Eigenspace算法对双目标均具有较好的分辨能力,分辨率高。在较低信噪比下,Eigenspace算法相对于其他2种算法可较好抑制噪声,并且具有旁瓣较低的优势。
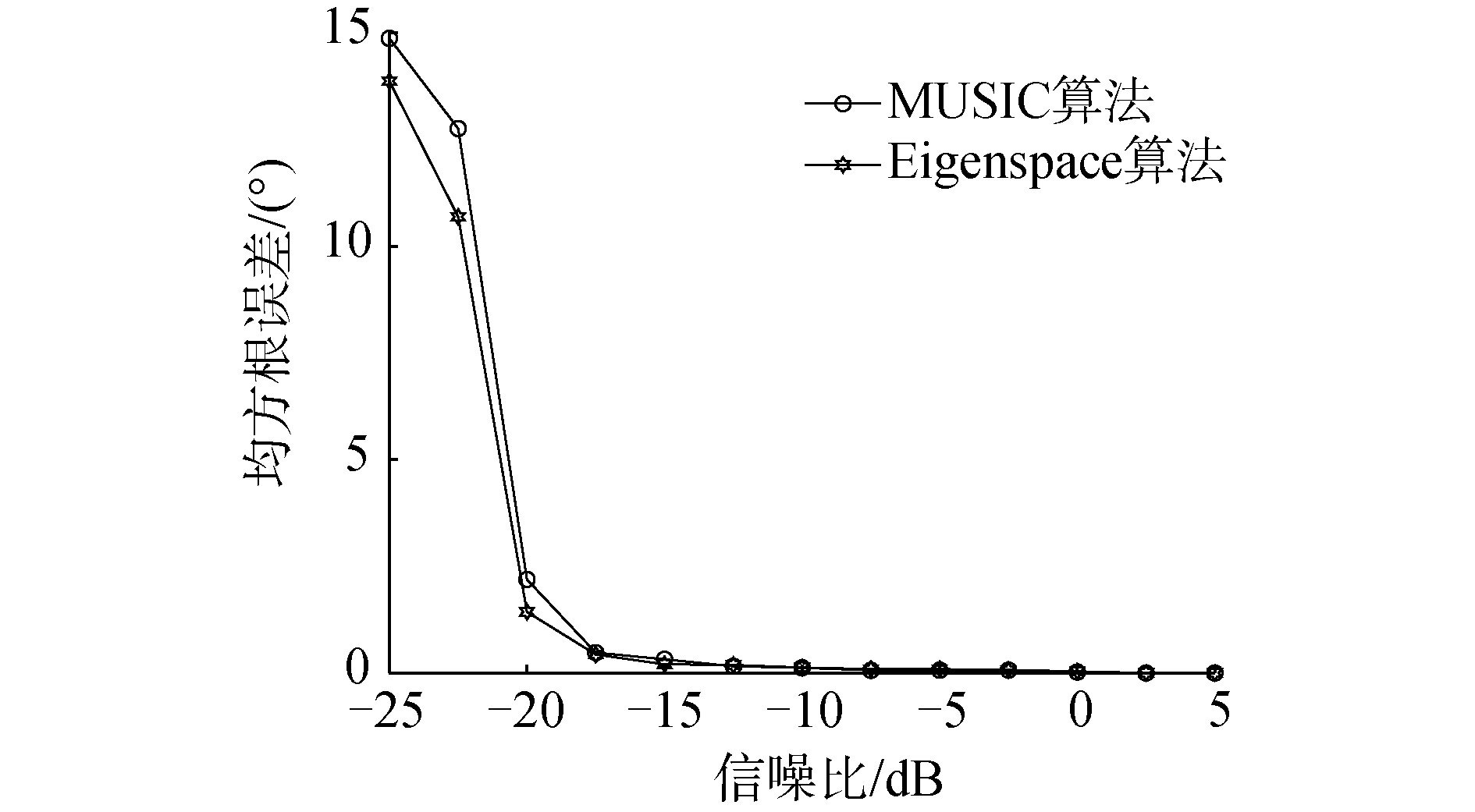
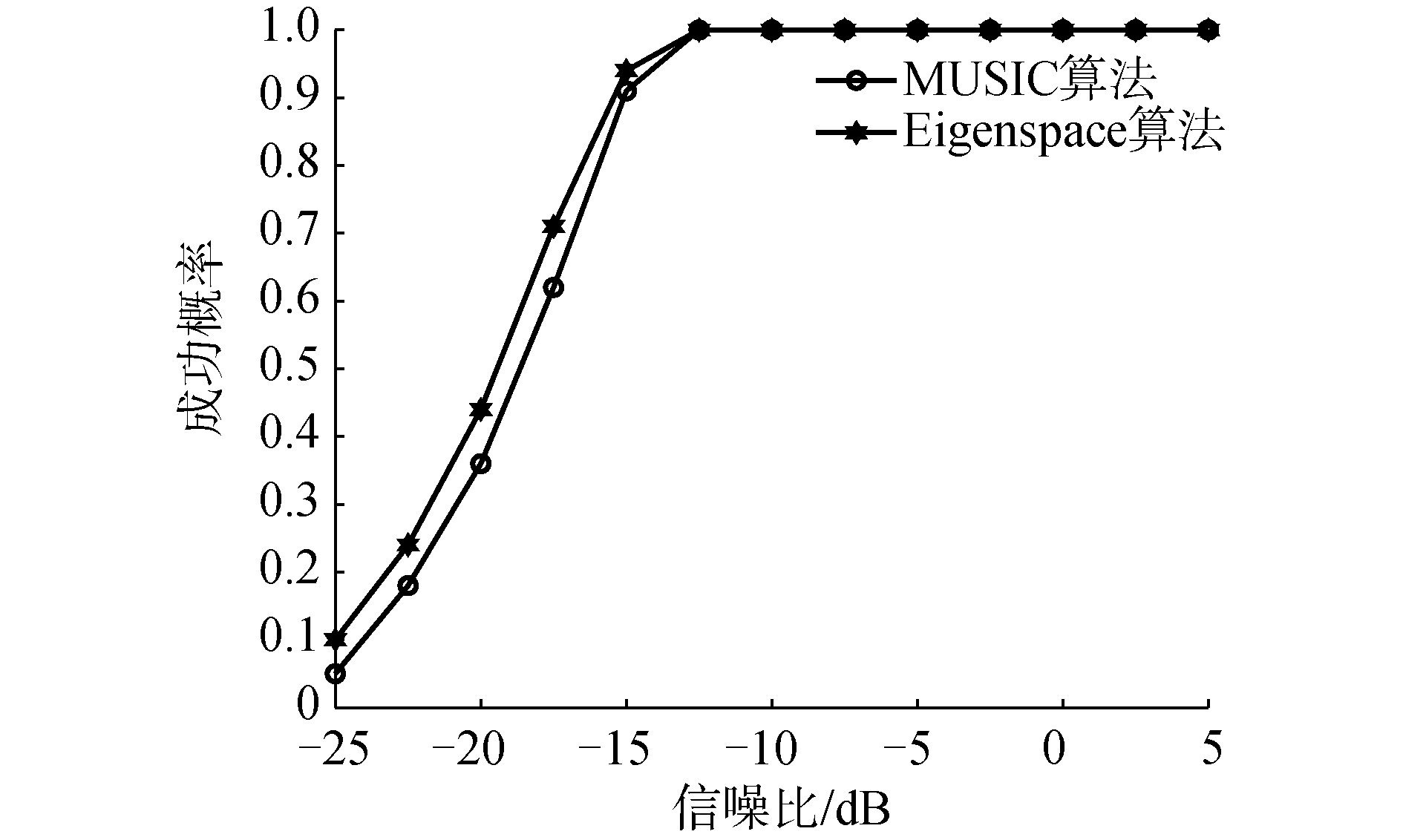
仿真实例2:假设目标为频率600 Hz的远场单频信源,入射角度为30°,其他条件同仿真实例1。信噪比变化范围从-25~5 dB,蒙特卡罗仿真实验次数为200次,得到Eigenspace算法的均方根误差和DOA估计成功概率(阈值±1°),如图 4和图 5所示。
|
Download:
|
| 图 4 测向均方根误差 Fig. 4 RMSE of azimuth estimation | |
|
Download:
|
| 图 5 测向成功概率 Fig. 5 Direction finding success probability | |
由图 4和图 5可知,高信噪比下MUSIC算法和Eigenspace算法均具有良好性能,信噪比低于-18 dB时Eigenspace算法估计精度和成功概率均优于MUSIC算法。仿真结果表明Eigenspace算法较MUSIC算法更适合水声等低信噪比环境。信噪比大于-18 dB时阵列采用2种算法均方根误差小于1°,为满足后续仿真准确测向的要求,后文中方位估计信噪比均在-18 dB以上。
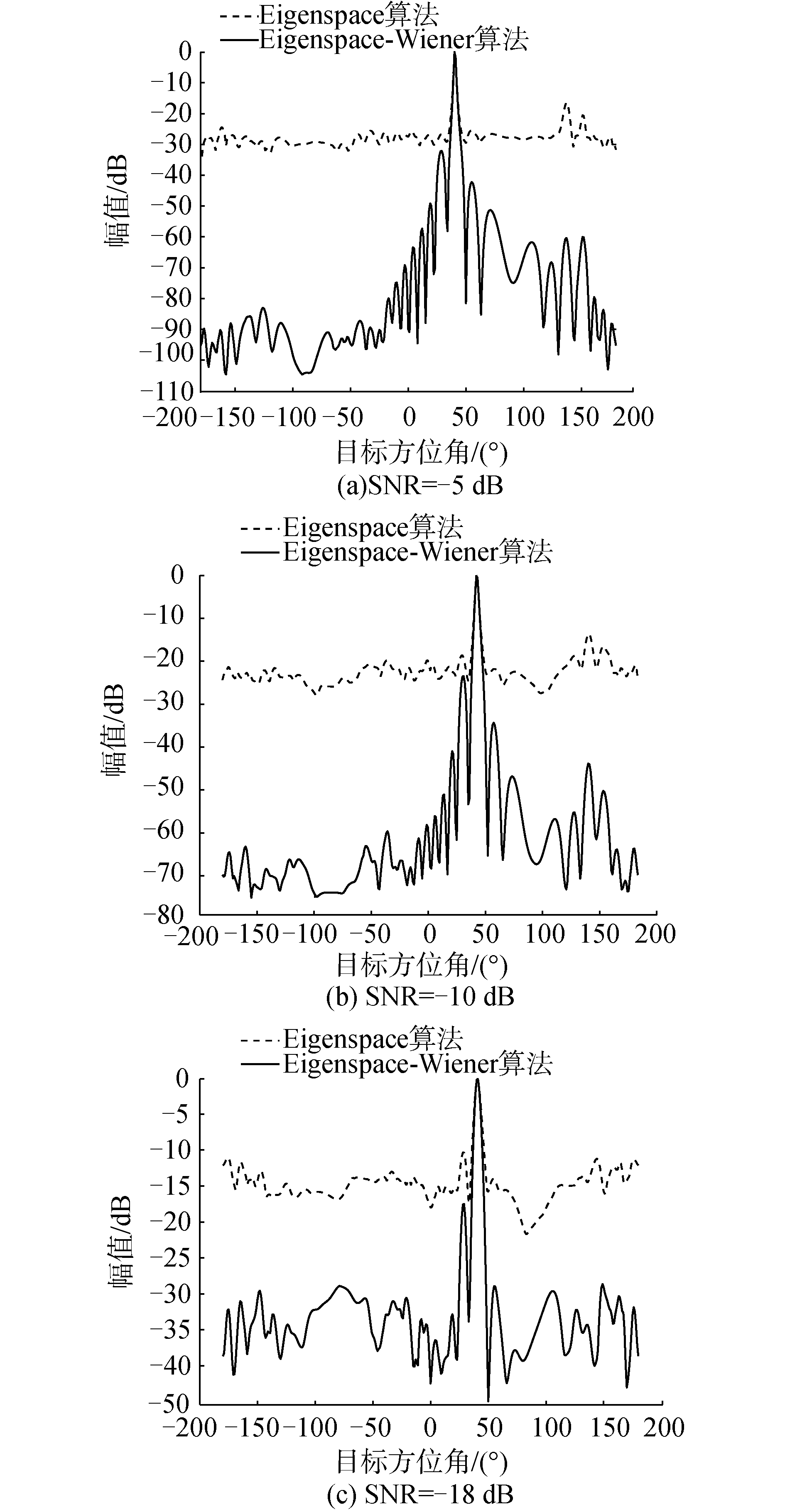
2.2 Eigenspace-Wiener算法仿真分析仿真实例3:假设信号为频率600 Hz的远场单频信源,入射角度40°,其他条件同仿真实例1,采用声矢量阵(P+Vc)Vc联合处理的方法,得到不同信噪比下Eigenspace-Wiener算法方位谱图,如图 6所示;改变信噪比变化范围,蒙特卡罗仿真实验次数为200次,得到Eigenspace-Wiener算法的均方根误差随信噪比变化曲线,如图 7所示。
|
Download:
|
| 图 6 Eigenspace算法与Eigenspace-Wiener算法方位估计对比 Fig. 6 Eigenspace algorithm and Eigenspace-Wiener algorithm position estimation comparison | |

|
Download:
|
| 图 7 Eigenspace-Wiener算法均方根误差随信噪比变化曲线 Fig. 7 RMSE of Eigenspace-Wiener algorithm | |
由图 6可知,对比2种算法,Eigenspace-Wiener算法能较大程度抑制旁瓣,降低旁瓣干扰;由图 7可知,2种算法的方位谱和均方误差根曲线,2种算法均方根误差几乎一致,估计精度相近。Eigenspace-Wiener算法在抑制旁瓣,降低旁瓣干扰,提高对目标信号方位的分辨能力的同时,没有降低方位估计精度,性能更优。
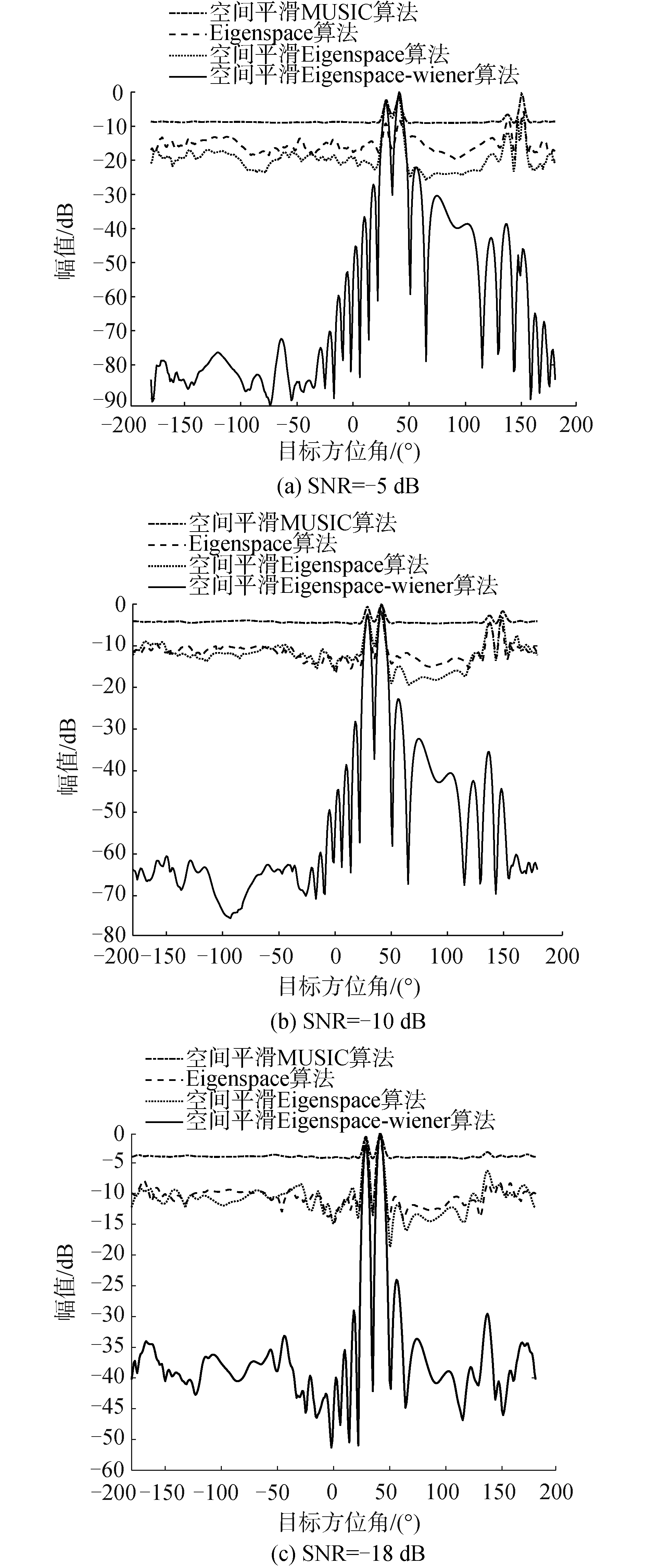
2.3 空间平滑Eigenspace-Wiener算法仿真分析仿真实例4:假设目标为频率600 Hz的远场单频信源,入射角度分别为30°和40°(仿真目标角度间隔小于瑞利限),其余条件同仿真实例3,采用声矢量阵(P+Vc)Vc联合处理的方法,得到不同信噪比下空间平滑Eigenspace-Wiener算法方位谱图,如图 8所示。
|
Download:
|
| 图 8 相干源方位估计算法性能对比 Fig. 8 Performance comparison of coherent source position estimation algorithms | |
通过对图 8中不同算法的方位谱进行对比,可知空间平滑技术可有效解决常规算法相干源方位估计性能下降的问题。结合维纳后置滤波技术,使得方位谱旁瓣进一步降低,算法性能进一步提高。
3 结论1) 本文对Eigenspace算法进行理论分析并改进,提出基于声矢量阵声压振速联合处理的Eigenspace-Wiener算法和空间平滑的Eigenspace-Wiener算法。相对于声压阵对声压信息单独处理,声矢量阵(P+Vc)Vc声压振速联合处理可获得更高阵列增益并抑制左右舷模糊现象。
2) 针对常规Eigenspace算法在低信噪比下部分旁瓣过高的问题,本文提出的Eigenspace-Wiener算法可以有效的降低旁瓣干扰。
3) 针对常规Eigenspace算法无法分辨相干源问题,本文采用空间平滑处理,得到空间平滑Eigenspace-Wiener算法,可以有效地对相干源目标进行区分,同时结合后置维纳滤波技术,进一步提高算法性能。计算机仿真结果与理论分析相一致,验证了算法的正确性。
本文针对Eigenspace算法提出的改进均具有一定理论意义的工程应用价值。
| [1] |
SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE transactions on antennas and propagation, 1986, 34(3): 276-280. DOI:10.1109/TAP.1986.1143830 (  0) 0)
|
| [2] |
ROY R, PAULRAJ A, KAILATH T. ESPRIT——A subspace rotation approach to estimation of parameters of cisoids in noise[J]. IEEE transactions on acoustics, speech, and signal processing, 1986, 34(5): 1340-1342. DOI:10.1109/TASSP.1986.1164935 (  0) 0)
|
| [3] |
张揽月, 杨德森. 基于MUSIC算法的矢量水听器阵源方位估计[J]. 哈尔滨工程大学学报, 2004, 25(1): 30-33. ZHANG Lanyue, YANG Desen. DOA estimation based on MUSIC algorithm using an array of vector hydrophones[J]. Journal of Harbin Engineering University, 2004, 25(1): 30-33. (  0) 0)
|
| [4] |
范文泉, 肖文书. 基于MUSIC和ESPRIT算法的DOA动态布站[J]. 电子测量技术, 2019, 42(2): 142-148. FAN Wenquan, XIAO Wenwen. Sea-based DOA dynamic deployment based on MUSIC and ESPRIT algorithms[J]. Electronic measurement technology, 2019, 42(2): 142-148. (  0) 0)
|
| [5] |
HOSSAIN M D, MOHAN A S. Eigenspace time-reversal robust capon beamforming for target localization in continuous random media[J]. IEEE antennas and wireless propagation letters, 2017, 16: 1605-1608. DOI:10.1109/LAWP.2017.2653809 (  0) 0)
|
| [6] |
NEHORAI A, PALDI E. Acoustic vector-sensor array processing[J]. IEEE transactions on signal processing, 1994, 42(9): 2481-2491. DOI:10.1109/78.317869 (  0) 0)
|
| [7] |
惠俊英, 惠娟. 矢量声信号处理基础[M]. 北京: 国防工业出版社, 2009: 6-7. HUI Junying, HUI Juan. Basis of vector acoustic signal processing[M]. Beijing: National Defense Industry Press, 2009: 6-7. (  0) 0)
|
| [8] |
惠俊英, 刘宏, 余华兵, 等. 声压振速联合信息处理及其物理基础初探[J]. 声学学报, 2000, 25(4): 303-307. HUI Junying, LIU Hong, YU Huabing, et al. Study on the physical basis of pressure and particle velocity combined processing[J]. Acta acustica, 2000, 25(4): 303-307. (  0) 0)
|
| [9] |
孙大军, 马超, 梅继丹, 等. 反卷积波束形成技术在水声阵列中的应用[J]. 哈尔滨工程大学学报, 2020, 41(6): 860-869. SUN Dajun, MA Chao, MEI Jidan, et al. Application of deconvolved beamforming technology in underwater acoustic array signal processing[J]. Journal of Harbin Engineering University, 2020, 41(6): 860-869. (  0) 0)
|
| [10] |
林彬. 基于改进空间平滑算法的复杂多信号测向技术研究[J]. 舰船电子工程, 2018, 38(10): 49-52, 141. LIN Bin. Research on direction-finding technique for complicated multiple-signal based on improved spatial smoothing algorithm[J]. Ship electronic engineering, 2018, 38(10): 49-52, 141. (  0) 0)
|
| [11] |
梁国龙, 张柯, 王逸林, 等. 声矢量阵相干源方位估计算法[J]. 声学技术, 2013, 32(6): 464-468. LIANG Guolong, ZHANG Ke, WANG Yilin, et al. DOA estimation of coherent signals based on acoustic vector array[J]. Technical acoustics, 2013, 32(6): 464-468. (  0) 0)
|
| [12] |
姚直象, 胡金华. 矢量阵前向平滑MUSIC方位估计算法性能分析[J]. 声学技术, 2013, 32(4): 142-144. YAO Zhixiang, HU Jinhua. Performance of forward smoothing MUSIC bearing estimation using an acoustic vector sensor array[J]. Technical acoustics, 2013, 32(4): 142-144. (  0) 0)
|
| [13] |
NILSEN C I C, HOLM S. Wiener beamforming and the coherence factor in ultrasound imaging[J]. IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 2010, 57(6): 1329-1346. DOI:10.1109/TUFFC.2010.1553 (  0) 0)
|
| [14] |
王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004: 99-104. WANG Yongliang, CHEN Hui, PENG Yingning, et al. Spatial spectrum estimation theory and algorithm[M]. Beijing: Tsinghua University Press, 2004: 99-104. (  0) 0)
|
| [15] |
任全会, 陈享成. 低信噪比下相干信号DOA估计算法研究[J]. 电子技术应用, 2018, 44(11): 53-56. REN Quanhui, CHEN Xiangcheng. Research on DOA estimation algorithm for coherent signal under low signal to noise ratio[J]. Application of electronic technique, 2018, 44(11): 53-56. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


