随着声隐身技术的发展,潜艇等水下航行器的噪声越来越小,并且主要集中在低频,因此对水下安静型目标的探测成为水声领域迫切需要解决的问题[1-2]。传统的阵列信号处理通常采用加大阵列孔径的做法来保证低频的波束宽度和阵增益,但是大孔径往往会降低工程实用性。如何利用小孔径阵列实现高增益是长久以来的难题,可以同时从单个阵元的选择和阵列波束形成方法2个方面入手:高阶声场传感器和超指向性波束形成方法,两者结合将为解决这类难题提供一种思路。高阶声场传感器阵列在消除栅瓣、降低旁瓣、抑制左右舷模糊等方面有很大的潜力,而超指向性波束形成方法则为进一步提高阵列探测性能奠定基础[3-6]。
高阶声场传感器的概念最早于1994年由D’Spain[7]提出,他将声场通过泰勒级数展开,指出了各阶项与声压以及质点振速之间的关系,并提出利用声压二阶导数提高阵列的指向性。Cray[8]通过泰勒级数展开的各分量之间的关系,引入了二阶声传感器,可以提供65°的波束宽度和9.5 dB的最大阵增益,而一般的矢量传感器只能同时提供105°的波束宽度和6 dB的最大阵增益。可见,高阶量的获取对提高信号处理的能力至关重要。二阶矢量传感器能同步共点测量声压、振速以及振速梯度3种声场分量[9-11],但矢量传感器的研究最高停留在二阶的振速梯度分量上,并且二阶分量对非声学噪声尤其敏感,稳健性很差,在实际中暂时难以应用。
利用泰勒级数展开并利用有限差分来估算高阶量的方法,在理论上是一种近似的求解过程,并不是一个解析解。本文从另一个全新的角度—高阶超指向性波束来阐释高阶传感器以及高阶分量的物理含义。Ma等[3, 5]提出了圆环阵特征波束分解与综合(eigen-beam decomposition and synthesis, EBDS)超指向性模型,能够提供超指向性的精确闭合解,将最优波束图表示成了有限阶子分量的叠加和形式,并且阶数越高,能提供的指向性因子也越大。圆环阵能够提供圆周360°较为均匀的波束,且没有左右舷模糊的影响,通过EBDS模型实现高阶波束分量的空间指向性,因此可选取圆环阵作为高阶传感器阵元,各阶波束分别代表了高阶传感器的各阶分量。相比于矢量传感器目前能提供的二阶分量,圆环阵能够提供更高的有效阶数,并且观测方向灵活可调,而将EBDS各阶分量合成后的波束将具有更窄的波束和更高的指向性因子,这相当于是高阶传感器多通道的联合处理。
在高阶传感器阵列的波束形成研究方面,以往的研究主要针对常规波束形成(conventional beamforming,CBF)分析阵列性能,而对超指向性方法研究较少,仍然停留在传统的最小方差无失真响应[12](minimum variance distortionless response,MVDR)波束形成。Wang等[13]提出的Gram-Schmidt(GS)模态波束分解与综合超指向性波束形成适用于任意声压阵,但无法处理矢量传感器或高阶声场传感器阵列,这是因为GS方法是基于噪声互谱矩阵全部为实数的假设下求解的,而高阶传感器的噪声空间相关性往往存在虚部,是一个复数,因此GS方法不再适用。
本文选取圆环阵作为高阶传感器阵元,从特征波束分解与综合的角度阐释其高阶分量的物理意义;通过将各阶分量相加进行的联合处理,得到高阶传感器的空间接收响应,求解了空间均匀噪声场中高阶传感器的噪声空间相关性;最后利用改进的GS(improved gram-schmidt,IGS)模型得到了高阶传感器阵列的超指向性波束、指向性因子以及稳健性水平等,而IGS模型成为真正的适用于带任意指向性的阵元组成的任意阵型的超指向性方法,填补了具有空间指向性的阵元组成的阵列没有稳健超指向性方法的空白。
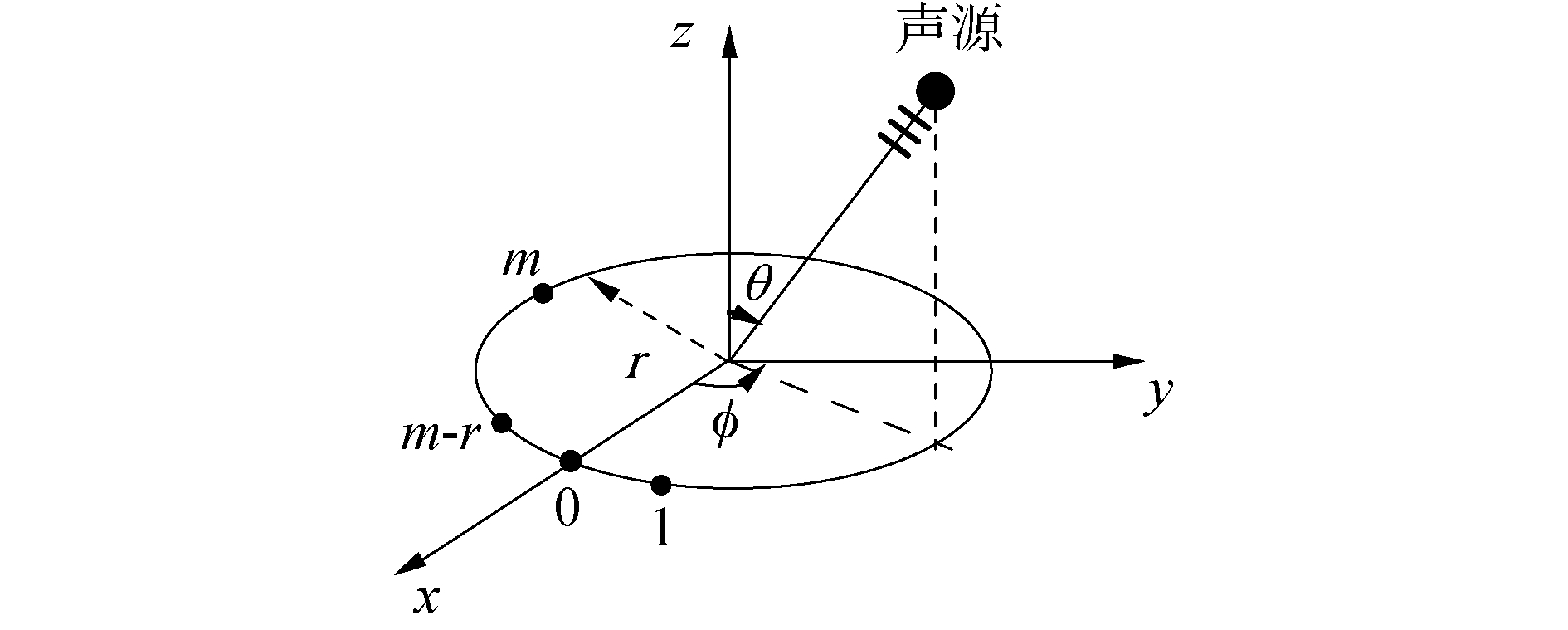
1 高阶声场传感器 1.1 高阶声场传感器的构成传统的高阶声场传感器一般指矢量传感器,其阶数最高到2阶。本文采用多个无指向性声压传感器组成一个阵列来体现高阶传感器。为方便能够灵活在周向360°范围内都能有相对均匀的空间接收响应,可以设计一个圆环形的高阶传感器,见图 1。相对于矢量水听器中的振速分量的观测方向固定的缺点,采用圆环阵作为高阶传感器阵元具有观测方向灵活可控、稳健性可调的优点,并且各阶分量在观测方向上的到达信号都具有无失真的空间接收响应。
|
Download:
|
| 图 1 圆环形高阶声场传感器坐标示意 Fig. 1 Coordinates of high-order circular array | |
圆环阵EBDS超指向性模型[3]能够提供超指向性的精确闭合解,将最优波束图表示成了有限阶子分量的叠加和形式,在较宽的频带内具有恒定束宽的特性。基于圆环阵的以上特点,在本文中定义:圆环阵为高阶传感器阵元,EBDS子分量波束分别为高阶传感器的各阶分量。对于高阶声场传感器而言,所采用的阶数越高,能提供的指向性因子越大,但同时对误差也越敏感,稳健性越差;如果阶数较低,其指向性因子也会降低,因此一个稳健的超指向性波束需要在阶数和指向性之间进行权衡。
下面用EBDS超指向性模型具体分析高阶声场传感器。假设圆环阵均匀分布有M个阵元,如图 2所示,θ和ϕ分别表示入射平面波的俯仰角和水平方位角,EBDS最优加权向量可表示关于特征值和特征向量的叠加和的形式[3],有:
|
Download:
|
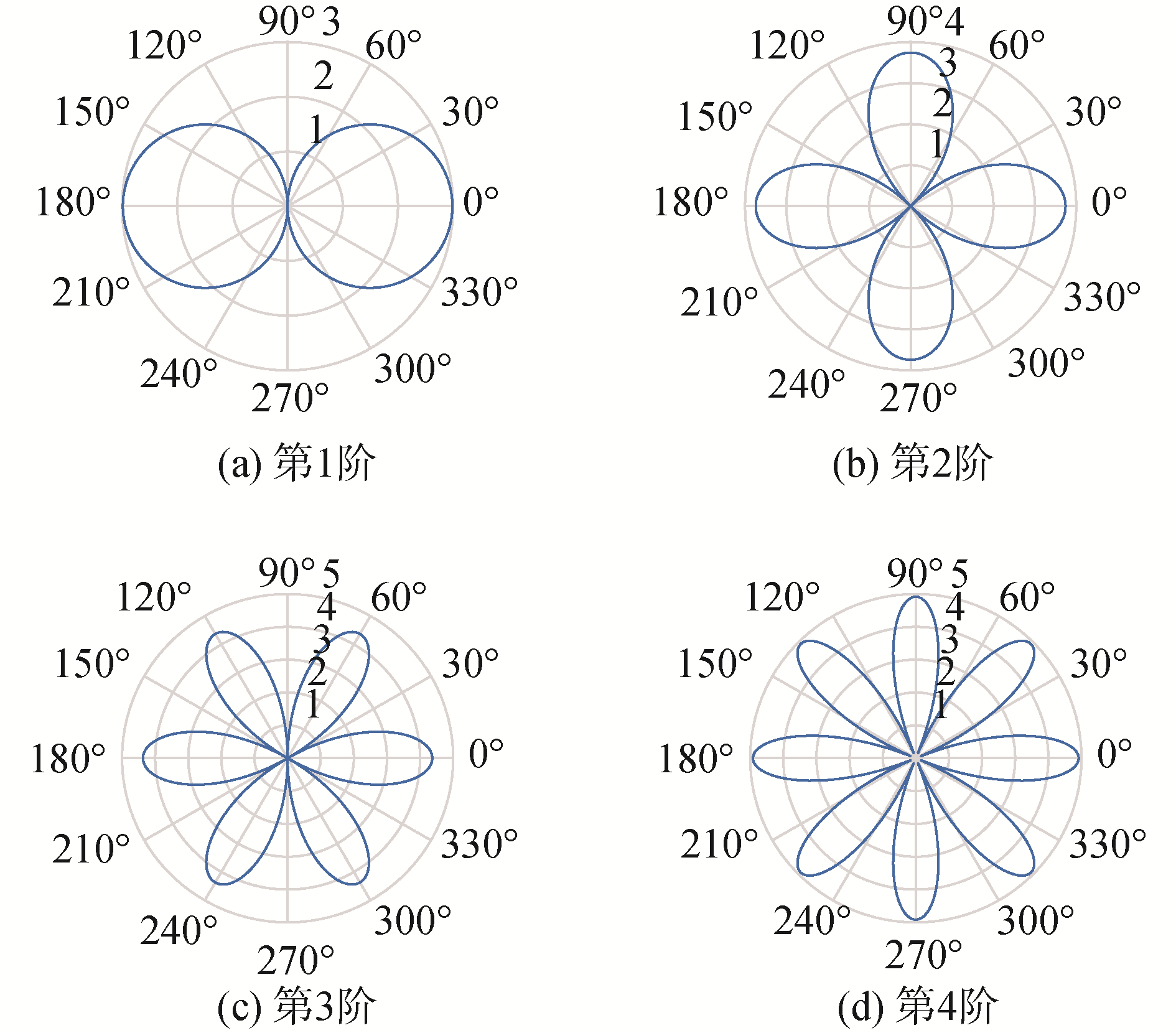
| 图 2 高阶传感器第1~4阶分量的空间指向性(即第1~4阶EBDS波束),(θ0, ϕ0)=(90°, 180°) Fig. 2 The 1st-4th components of the high-order sensor, (θ0, ϕ0)=(90°, 180°) | |
| $ {\mathit{\boldsymbol{w}}_{{\rm{opt}}}} = \alpha \left[ {\sum\limits_{m = 0}^{M - 1} {\frac{1}{{{\lambda _m}}}} {\mathit{\boldsymbol{v}}_m}\mathit{\boldsymbol{v}}_m^{\rm{H}}} \right]\mathit{\boldsymbol{P}}({\theta _0},{\phi _0}) $ | (1) |
式中:P为阵列流形向量;α=1/[P(θ0, ϕ0)Hρc-1P(θ0, ϕ0)]是用来保证期望方向波束输出不失真的参数;ρc为圆环阵在空间均匀噪声场中的噪声互谱矩阵;vm和λm分别为空间均匀噪声场中的噪声互谱矩阵的第m个特征向量和特征值,且:
| $ {\mathit{\boldsymbol{v}}_m} = {M^{ - 1/2}}{[1,\exp ({\rm{i}}m\beta ), \cdots ,\exp ({\rm{i}}(M - 1)m\beta )]^{\rm{T}}} $ | (2) |
| $ {\lambda _m} = \sum\limits_{s = 0}^{M - 1} {{\rho _s}} \exp ({\rm{i}}sm\beta ) $ | (3) |
式中:β=2π/M是相邻阵元之间的夹角;ρs=sinc(k·Δds);波数k=2π/λ;λ为波长。Δds是第m个阵元和第m′个阵元之间的距离,s=|m-m′|。
圆环阵的最优波束响应为[3]:
| $ \begin{array}{*{20}{c}} {B(\theta ,\phi ,{\theta _0},{\phi _0}) = \mathit{\boldsymbol{w}}_{{\rm{ opt }}}^{\rm{H}}\mathit{\boldsymbol{P}}(\theta ,\phi ) = }\\ {\sum\limits_{m = 0}^{M - 1} {\frac{\alpha }{{{\lambda _m}}}} {{[\mathit{\boldsymbol{v}}_m^{\rm{H}}\mathit{\boldsymbol{P}}({\theta _0},{\phi _0})]}^*}\mathit{\boldsymbol{v}}_m^{\rm{H}}\mathit{\boldsymbol{P}}(\theta ,\phi ) = \sum\limits_{m = 0}^{M - 1} {{{\hat B}_m}} } \end{array} $ | (4) |
式中:
| $ {B_m} = \left\{ {\begin{array}{*{20}{l}} {{{\hat B}_m},}&{m = 0,M/2}\\ {{{\hat B}_m} + {{\hat B}_{M - m}},}&{m = 1,2, \cdots ,M/2 - 1} \end{array}} \right. $ | (5) |
式中:M为偶数,而Bm在本文中是高阶传感器的第m阶分量。假设高阶传感器(圆环阵)由12个无指向性声压传感器组成,半径为1.5 m,信号频率为50 Hz。当观测方向为(θ0, ϕ0)=(90°, 180°)时,图 2给出了第1~4阶分量(理论上最高阶为第6阶)的空间指向性(或空间接收响应)图,可见第m阶分量与第m阶的柱面贝塞尔函数具有类似的几何形状,而与矢量传感器cosmθ是不一样的。
最优波束响应可以由所有特征波束来合成,即:
| $ B(\theta ,\phi ,{\theta _0},{\phi _0}) = \sum\limits_{m = 0}^{M/2} {{B_m}} $ | (6) |
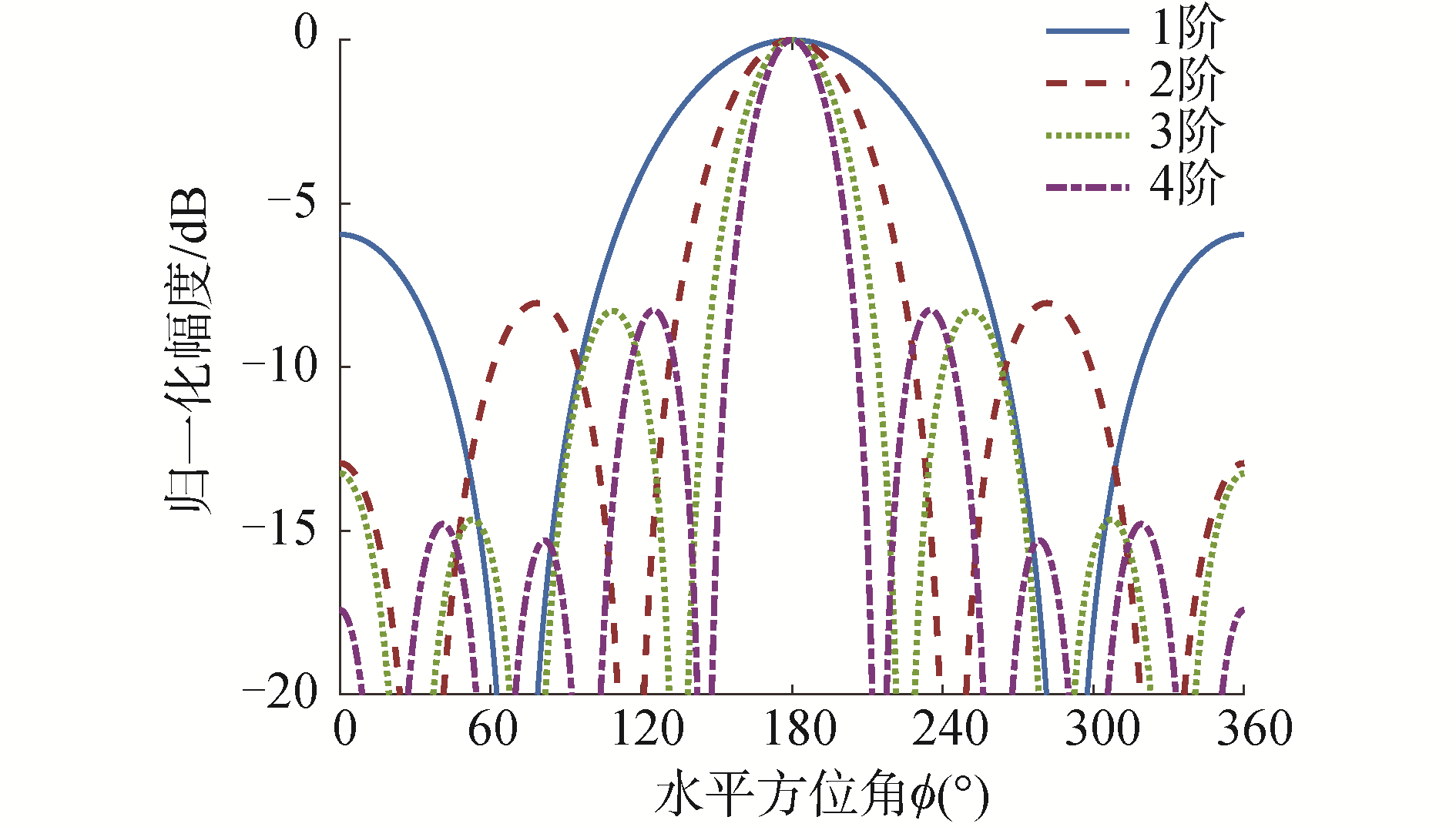
这可以看作是高阶传感器的空间响应是各阶分量空间响应的叠加和表示。在实际应用中,由于高阶波束在低频时不稳健,因此可以使用降秩技术,舍弃不稳健的高阶项而保留低阶项来保持稳健性,第0~m阶的合成波束可表示为:
| $ {\tilde B_m}(\theta ,\phi ,{\theta _0},{\phi _0}) = \sum\limits_{n = 0}^m {{B_n}} $ | (7) |
定义:圆环阵第m阶合成波束
|
Download:
|
| 图 3 高阶传感器第1~4阶合成分量的空间指向性(即第1~4阶EBDS合成波束),(θ0, ϕ0)=(90°, 180°) Fig. 3 Synthesized parts of the 1st-4th components of the high-order sensor | |
高阶声场传感器具有空间指向性,其组阵后第l个阵元的空间接收响应可表示为:
| $ {\hat p_l}(\theta ,\phi ) = {\tilde B_l}(\theta ,\phi ,{\theta _0},{\phi _0}){p_l}(\theta ,\phi ) $ | (8) |
式中:
三维各向同性空间均匀噪声场可认为是从空间所有方向到达的具有均匀谱密度的独立平面波的叠加,根据此原理,第l个和第l′个高阶传感器间的噪声相关性可表示为:
| $ \begin{array}{*{20}{l}} {{{\hat \rho }_{l,{l^\prime }}} = \frac{1}{{4{\rm{ \mathsf{ π} }}}}\int_0^{2{\rm{ \mathsf{ π} }}} {\int_0^{\rm{ \mathsf{ π} }} {{N_A}} } (\theta ,\phi ) \cdot {{\hat p}_l}(\theta ,\phi ) \cdot \hat p_{{l^\prime }}^*(\theta ,\phi )\sin \theta {\rm{d}}\theta {\rm{d}}\phi = }\\ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{{4{\rm{ \mathsf{ π} }}}}\int_0^{2{\rm{ \mathsf{ π} }}} {\int_0^{\rm{ \mathsf{ π} }} {{N_A}} } (\theta ,\phi ) \cdot {{\tilde B}_l}(\theta ,\phi ,{\theta _0},{\phi _0}){p_l}(\theta ,\phi ) \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {p_{{l^\prime }}}{(\theta ,\phi )^*}{{\tilde B}_{{l^\prime }}}{(\theta ,\phi ,{\theta _0},{\phi _0})^*}\sin \theta {\rm{d}}\theta {\rm{d}}\phi \end{array} \end{array} $ | (9) |
式中:NA(θ, ϕ)是噪声场的角谱密度函数;NA(θ, ϕ)=1是球面各向同性均匀噪声场的角谱密度函数。一般情况下,假定各阵元的空间接收响应和观测方向都相同,有
| $ \begin{array}{*{20}{l}} {{{\hat \rho }_{l,{l^\prime }}} = \frac{1}{{4{\rm{ \mathsf{ π} }}}}\int_0^{2{\rm{ \mathsf{ π} }}} {\int_0^{\rm{ \mathsf{ π} }} {{N_A}} } (\theta ,\phi ) \cdot |{{\tilde B}_l}(\theta ,\phi ,{\theta _0},{\phi _0}){|^2} \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {p_l}(\theta ,\phi ){p_{{l^\prime }}}{{(\theta ,\phi )}^*}\sin \theta {\rm{d}}\theta {\rm{d}}\phi } \end{array} $ | (10) |
式(10)较难求解得到解析表达式,但是可以通过数值积分得到一个近似值。
2 IGS超指向性波束形成方法高阶声场传感器的空间接收响应具有明显的指向性,这导致其组阵后的噪声互谱矩阵的元素(阵元间的噪声空间相关性)在某些观测方向上存在虚部。Wang等[13]提出的超指向性方法值适用于噪声互谱矩阵中的元素全部为实数的阵列,并不适用于矩阵元素存在虚部的情况。针对这一问题,需要对GS超指向性方法的正交变换矩阵重新推导以改进波束形成的性能,以便对有指向性的阵元组成阵列的稳健超指向性波束形成奠定基础。
对于由Q个阵元组成的具有任意阵型的声压阵,基于GS模态分解与综合的超指向性方法中的噪声互谱矩阵ρ的逆矩阵可表示为[13]:
| $ {\mathit{\boldsymbol{\rho }}^{ - 1}} = {\mathit{\boldsymbol{C}}^{\rm{T}}}{\mathit{\boldsymbol{D}}^{ - 2}}C $ | (11) |
式中:D为一个Q×Q对角矩阵;D-2用来对输入噪声进行归一化;C是一个正交变换矩阵,为:
| $ \mathit{\boldsymbol{C}} = {\left[ {\begin{array}{*{20}{l}} {{c_0}}&{{c_1}}& \cdots &{{c_q}}& \cdots &{{c_{Q - 1}}} \end{array}} \right]^{\rm{T}}} $ | (12) |
式中:cq=[cq0cq1…cqq0 … 0]T,当噪声互谱矩阵ρ中的元素全部是实数时,cqi为:
| $ {c_{qi}} = \left\{ {\begin{array}{*{20}{l}} {1,}&{i = q}\\ { - \sum\limits_{j = i}^{q - 1} {\frac{{{c_{ji}}}}{{{\chi _j}}}} \sum\limits_{h = 0}^j {{c_{jh}}} {\rho _{qh}},}&\begin{array}{l} 1 \le q \le Q - 1{\rm{ 且}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} h,i,j \le q - 1 \end{array}\\ {0,}&{{\rm{其他}}} \end{array}} \right. $ | (13) |
式中χj=
| $ {c_{qi}} = \left\{ {\begin{array}{*{20}{l}} {1,}&{i = q}\\ { - \sum\limits_{j = i}^{q - 1} {\frac{{{c_{ji}}}}{{{\chi _j}}}} {{(\sum\limits_{h = 0}^j {{c_{jh}}} {\rho _{qh}})}^*},}&\begin{array}{l} 1 \le q \le Q - 1{\rm{ 且}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} h,i,j \le q - 1 \end{array}\\ {0,}&{{\rm{其他}}} \end{array}} \right. $ | (14) |
式(14)与式(13)在表达上略有区别,但式(14)也适用于噪声互谱矩阵中元素全部为实数的情形。IGS方法最优加权向量为:
| $ {\mathit{\boldsymbol{w}}_{{\rm{opt}}}} = \alpha {\mathit{\boldsymbol{C}}^{\rm{T}}}{\mathit{\boldsymbol{D}}^{ - 2}}\mathit{\boldsymbol{C}} \cdot \mathit{\boldsymbol{P}}({\theta _0},{\phi _0}) $ | (15) |
IGS超指向性波束响应可进一步写为:
| $ \begin{array}{*{20}{c}} {B(\theta ,\phi ) = \mathit{\boldsymbol{w}}_{{\rm{opt}}}^{\rm{H}}\mathit{\boldsymbol{P}}(\theta ,\phi ) = }\\ {\alpha {{[\mathit{\boldsymbol{C}} \cdot \mathit{\boldsymbol{P}}({\theta _0},{\phi _0})]}^{\rm{H}}}{\mathit{\boldsymbol{D}}^{ - 2}}[\mathit{\boldsymbol{C}} \cdot \mathit{\boldsymbol{P}}(\theta ,\phi )] = }\\ {\sum\limits_{q = 0}^{M - 1} {{B_q}} (\theta ,\phi )} \end{array} $ | (16) |
式中:Bq为第q(q=0, 1, …, Q-1)阶IGS模态波束,即:
| $ {B_q}(\theta ,\phi ) = \frac{\alpha }{{{\eta _q}}} \cdot E_q^*({\theta _0},{\phi _0}){E_q}(\theta ,\phi ) $ | (17) |
式中:Eq(θ, ϕ)=cqTP(θ, ϕ);ηq=cqTρcq;ηq表示正交变换之后的第q号阵元所在通道的噪声功率。基于超指向性方法的最大指向性因子(空间均匀噪声场中等于阵增益)可表示为:
| $ \begin{array}{*{20}{c}} {{\rm{DF}} = \mathit{\boldsymbol{P}}{{({\theta _0},{\phi _0})}^{\rm{H}}}{\mathit{\boldsymbol{\rho }}^{ - 1}}\mathit{\boldsymbol{P}}({\theta _0},{\phi _0}) = }\\ {{{[\mathit{\boldsymbol{C}} \cdot \mathit{\boldsymbol{P}}({\theta _0},{\phi _0})]}^{\rm{H}}}{\mathit{\boldsymbol{D}}^{ - 2}}[\mathit{\boldsymbol{C}} \cdot \mathit{\boldsymbol{P}}({\theta _0},{\phi _0})] = }\\ {\sum\limits_{q = 0}^{Q - 1} | {E_q}({\theta _0},{\phi _0}){|^2}/{\eta _q} = \sum\limits_{q = 0}^{Q - 1} {{D_q}} } \end{array} $ | (18) |
式中:
| $ {D_q} = |{E_q}({\theta _0},{\phi _0}){|^2}/{\eta _q} $ | (19) |
是第q阶IGS模态波束的指向性因子。由于式(17)~(19)中的分母均有ηq,并且与误差敏感度函数有关,是误差敏感度函数中的分母[13],因此其值的大小对波束形成稳健性有直接的影响,ηq值越大代表第q阶波束越稳健,可以将ηq作为对稳健性表征的因子。指向性指数(directivity index, DI)是指向性因子(directivity factors, DF)的分贝表示,有
| $ {\rm{DI}} = 10\lg ({\rm{DF}}) $ | (20) |
本文中单个高阶传感器是基于EBDS超指向性模型得到的,而高阶传感器所组成阵列的超指向性波束形成是基于IGS模型进行计算的。下面以高阶传感器组成直线阵为例,分析超指向性波束形成具体实施步骤。
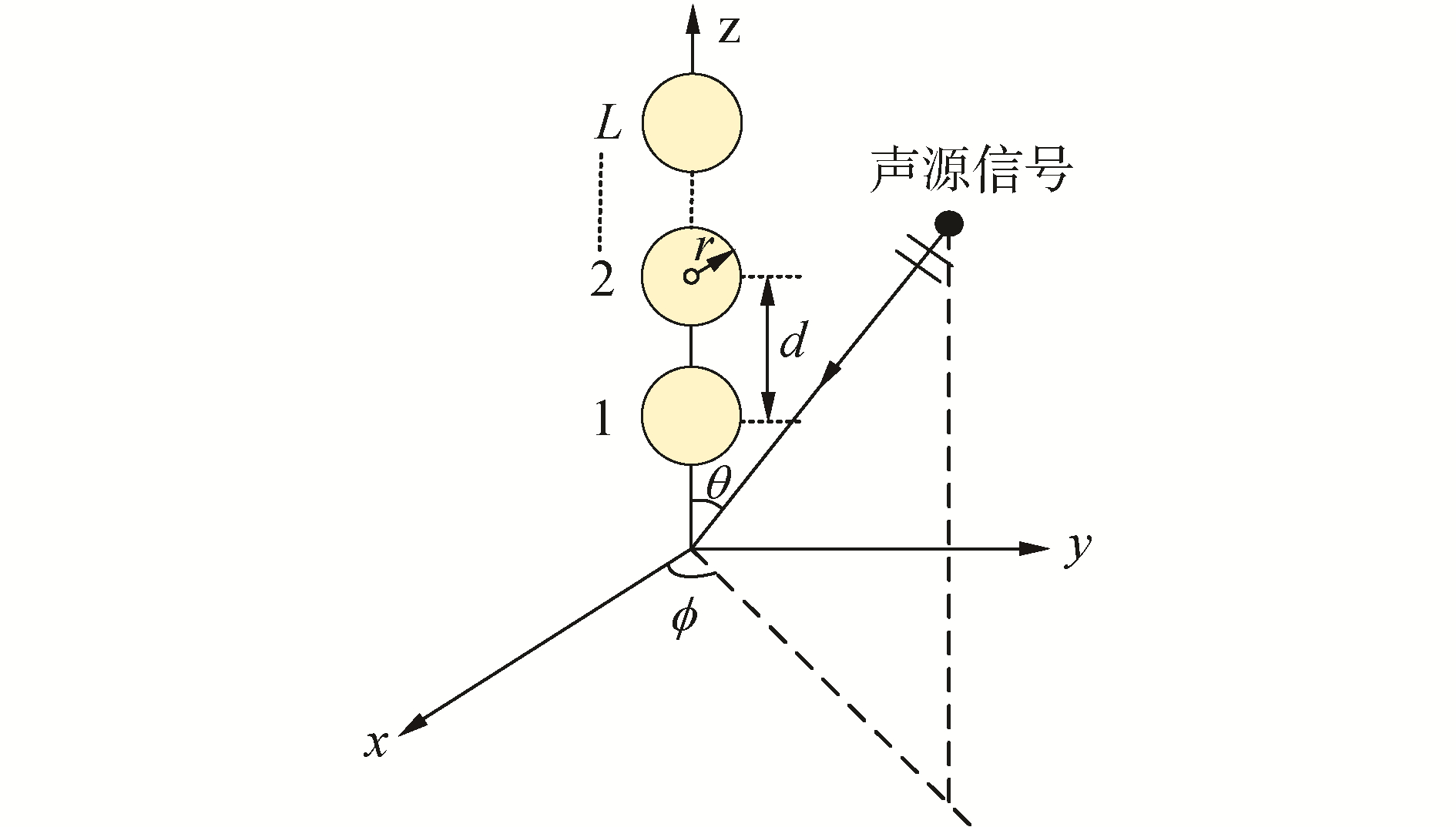
假设直线阵由均匀分布在z轴的L个高阶传感器组成,阵元间距为d,如图 4所示;每个高阶传感器半径为r,由M个无指向性声压传感器组成。高阶传感器阵列波束形成主要分为以下几步:
|
Download:
|
| 图 4 高阶声场传感器直线阵坐标示意 Fig. 4 High-order sensor line array | |
1) 得到单个高阶传感器的接收空间响应。
现有一远场窄带平面波信号从角度(θ, ϕ)入射到该直线阵,其中θ为垂直俯仰角,ϕ为水平方位角,那么该信号传播方向的单位向量可定义为:
| $ \mathit{\boldsymbol{u}} = - {[\sin \theta \cos \phi \quad \sin \theta \sin \phi \quad \cos \theta ]^{\rm{T}}} $ | (21) |
如果高阶传感器阵列在y-z坐标平面上,第1个高阶传感器(圆环阵)的中心位于原点,那么其第m个阵元的位置坐标为:
| $ {\mathit{\boldsymbol{L}}_m} = {\left[ {\begin{array}{*{20}{l}} 0&{r\cos {\theta _m}}&{r\sin {\theta _m}} \end{array}} \right]^{\rm{T}}} $ | (22) |
式中:θm=2π(m-1)/M。第m个阵元的接收响应可表示为:
| $ \begin{array}{*{20}{c}} {{p_m}(\theta ,\phi ) = \exp ( - {\rm{i}}k{\mathit{\boldsymbol{u}}^{\rm{T}}}{L_m}) = }\\ {\exp [{\rm{i}}kr(\sin \theta \sin \phi \cos {\theta _m} - \cos \theta \sin {\theta _m})]} \end{array} $ | (23) |
那么,单个高阶传感器的阵列流形向量为:
| $ {\mathit{\boldsymbol{P}}_c}(\theta ,\phi ) = {[{p_0}(\theta ,\phi )\quad {p_1}(\theta ,\phi )\quad \cdots \quad {p_{M - 1}}(\theta ,\phi )]^{\rm{T}}} $ | (24) |
令w为加权向量,那么其波束响应为:
| $ {B_c}(\theta ,\phi ,{\theta _0},{\phi _0}) = {\mathit{\boldsymbol{w}}_c}{({\theta _0},{\phi _0})^{\rm{H}}}{\mathit{\boldsymbol{P}}_c}(\theta ,\phi ) $ | (25) |
此波束响应具体可由将式(4)和式(7)得到EBDS第m阶合成波束,即得到高阶传感器第m阶合成分量,从而得到其空间接收响应。
2) 确定直线阵阵列流形向量。
假设一个具有L个阵元的直线阵位于z轴上,如图 4所示,相邻阵元间距为d,如果第1个阵元位于原点,那么第l个阵元的位置坐标:
| $ {\mathit{\boldsymbol{L}}_l} = {\left[ {\begin{array}{*{20}{l}} 0&0&{(l - 1)d} \end{array}} \right]^{\rm{T}}} $ | (26) |
对于由无指向性阵元组成的声压直线阵,第l个阵元的接收响应可表示:
| $ {p_l}(\theta ,\phi ) = \exp ( - {\rm{i}}k{\mathit{\boldsymbol{u}}^{\rm{T}}}{\mathit{\boldsymbol{L}}_l}) = \exp [{\rm{i}}k(l - 1)d\cos \theta ] $ | (27) |
当直线阵的阵元为高阶声场传感器时,每个阵元都有指向性,当观测方向为(θ0, ϕ0)时,第l个阵元(圆环阵)的接收响应变:
| $ {\hat p_l}(\theta ,\phi ) = {\tilde B_l}(\theta ,\phi ) \cdot {p_l}(\theta ,\phi ) $ | (28) |
这相当于波束图乘积定理。此时,高阶传感器直线阵的阵列流形向量为:
| $ \mathit{\boldsymbol{\hat P}}(\theta ,\phi ) = {[{\hat p_1}(\theta ,\phi )\quad {\hat p_2}(\theta ,\phi )\quad \cdots \quad {\hat p_L}(\theta ,\phi )]^{\rm{T}}} $ | (29) |
3) 求高阶传感器阵列噪声互谱矩阵。
高阶传感器直线阵归一化的噪声互谱矩阵为
| $ {\mathit{\boldsymbol{\rho }}_L} = \frac{1}{{4{\rm{ \mathsf{ π} }}}}\int_0^{2{\rm{ \mathsf{ π} }}} {\int_0^{\rm{ \mathsf{ π} }} {{N_A}} } (\theta ,\phi ) \cdot \mathit{\boldsymbol{P}}(\theta ,\phi ) \cdot {\mathit{\boldsymbol{P}}^{\rm{H}}}(\theta ,\phi )\sin \theta {\rm{d}}\theta {\rm{d}}\phi $ | (30) |
式中:矩阵ρL中第l行、第l′列的元素代表了第l个和第l′个阵元间的空间相关性,可由式(10)计算。
4) 高阶传感器直线阵波束形成。
得到阵列噪声互谱矩阵后,依据IGS超指向性方法进行波束形成,通过式(17)、(19)等得到阵列超指向性波束图、指向性指数(阵增益)、稳健性因子等性能指标。
4 仿真分析当圆环阵的阵元数较少时,其无法在周向360°范围内提供均匀的波束;阵元数过多会增加经济成本,因此应选择适当的阵元数目以使利益最大化。仿真中选择由M=12个无指向性声压传感器组成一个高阶声场传感器。为了使阵列在可探测低频目标的同时保持较小的孔径,选取高阶传感器的半径为r=1.5 m,直线阵由L=7个阵元组成,如图 4所示,阵元间距为d=10 m,水下声速设为1 500 m/s,在d/λ=0.1时,理论上可探测的目标信号频率低至15 Hz。仿真中选取直线阵端射和舷侧2个典型方向为例进行分析。
4.1 高阶声场传感器的噪声空间相关性噪声的空间相关性是组成噪声互谱矩阵的元素,当观测方向沿z轴的端射方向(即θ0=0°)时,图 5给出了直线阵第1个和第2个高阶传感器阵元间的第1~4阶合成分量随d/λ变化的噪声相关性曲线。从图 5(a)中可以看到,阶数越高,噪声相关性的实部在d/λ→0时越小;由于在低频时高阶波束对计算误差较为敏感的原因,第4阶在d/λ→0时出现了偏差。噪声相关性的虚部(见图 5(b))在d/λ→0时接近于0,同时阶数越高,曲线初始的起伏振荡的幅度越小,但随着频率的升高,收敛速度也越慢。

|
Download:
|
| 图 5 端射方向高阶声场传感器的噪声空间相关性 Fig. 5 Spatial correlation of the noise in the endfire look direction | |
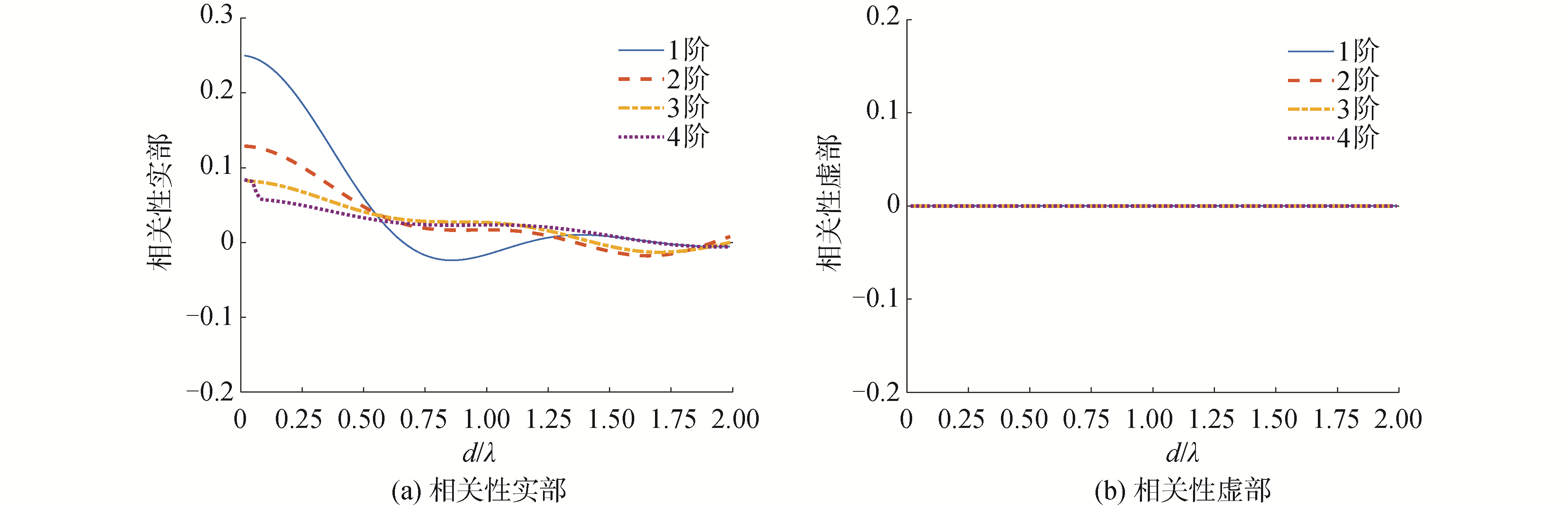
当观测方向为舷侧方向(即(θ0, ϕ0)=(90°, 90°))时,图 6给出了直线阵第1个和第2个高阶传感器阵元间的第1~4阶合成分量随d/λ变化的噪声相关性曲线。舷侧方向的噪声相关性实部的曲线(见图 6(a))变化规律与端射方向(见图 5(a))明显不同,各阶曲线的振荡起伏更加平缓,相关性实部第1次到达0点的d/λ值远高于0.5,这提醒我们若使用常规波束形成方法,阵元间距的设置应大于半波长,以使阵元间的噪声相关性尽量趋于0。
|
Download:
|
| 图 6 舷侧方向高阶声场传感器的噪声空间相关性 Fig. 6 Spatial correlation of the noise in the broadside look direction | |
高阶声场传感器由M=12个无指向性声压传感器组成,理论上其最高阶分量可取到第6阶,但由于波束在不同频率对误差的敏感程度不同,可选取适当的阶数调整稳健性,这样既能在低频时提供稳健的恒定束宽波束,也能在高频是提供较高的指向性指数,根据图 5和图 6的噪声相关性曲线,本文中高阶传感器EBDS模型合成分量中的最高阶数选取到第4阶。
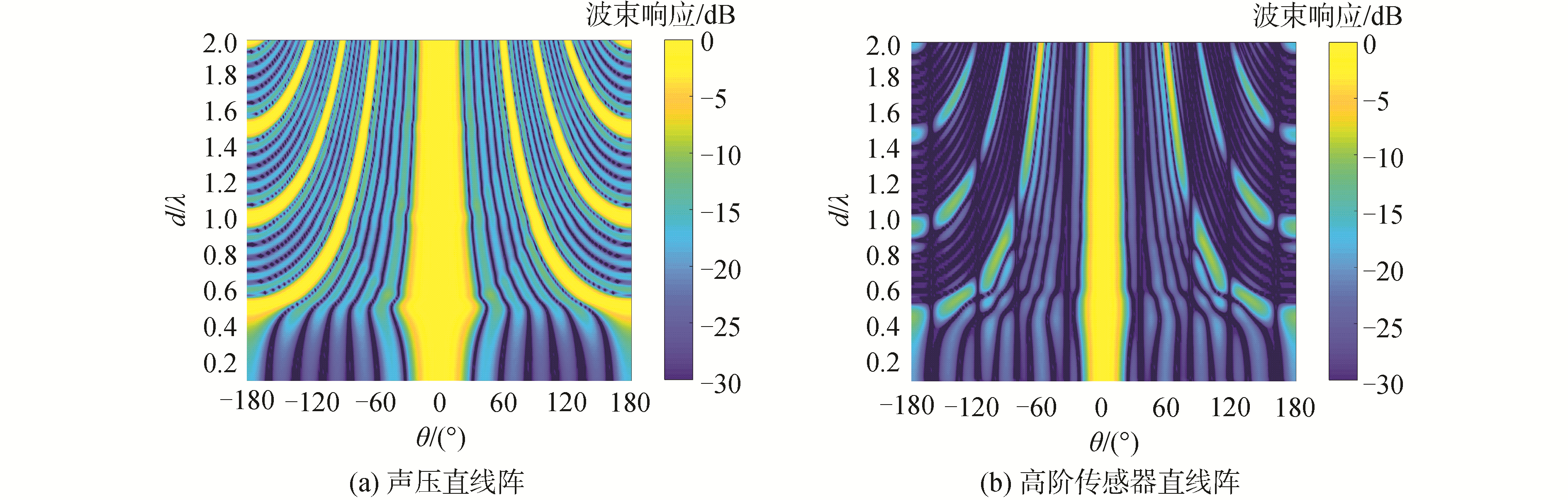
直线阵采用IGS超指向性模型,7元阵的IGS最高阶数为第6阶。根据式(16)、(17),图 7给出了传统声压直线阵和高阶传感器直线阵在端射方向随d/λ值变化的IGS方法的波束图,为节省篇幅,仿真中的波束响应直接采用第0~6阶的合成波束,不再分析单阶波束响应。从图 7(a)中可以看到,声压阵在d/λ约为0.5处会出现栅瓣;而高阶传感器阵(见图 7(b))在较宽的d/λ值范围内没有出现栅瓣,表现出较强的抑制栅瓣的能力,同时高阶传感器阵的波束主瓣更窄、旁瓣更低,说明高阶传感器阵能有效抑制来自非观测方向的干扰和噪声。
|
Download:
|
| 图 7 观测方向为端射方向时随d/λ变化的IGS波束图 Fig. 7 Beampatterns vs d/λ in the endfire look direction | |
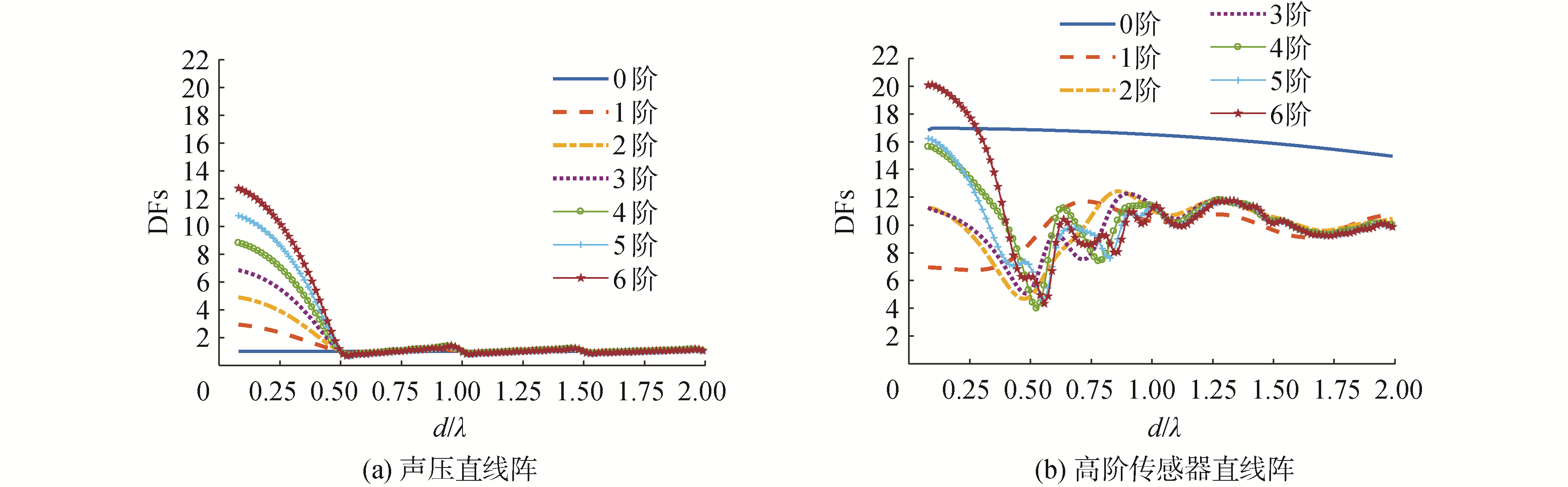
根据式(19),图 8给出了随d/λ值变化的IGS第0~6阶波束的指向性因子。从图 8(a)中可以看出,在d/λ < 0.5时,声压阵阶数越高,指向性因子越大;高阶传感器阵则无此规律,反而第0阶在较大的频率范围内的指向性因子保持最大,而且各阶的变化没有明显的规律;除第0阶外,第1~6阶指向性因子随着频率的升高逐渐接近。
|
Download:
|
| 图 8 端射方向随d/λ变化的IGS各阶指向性因子 Fig. 8 Different-order directivity factors vs d/λ in the endfire look direction | |
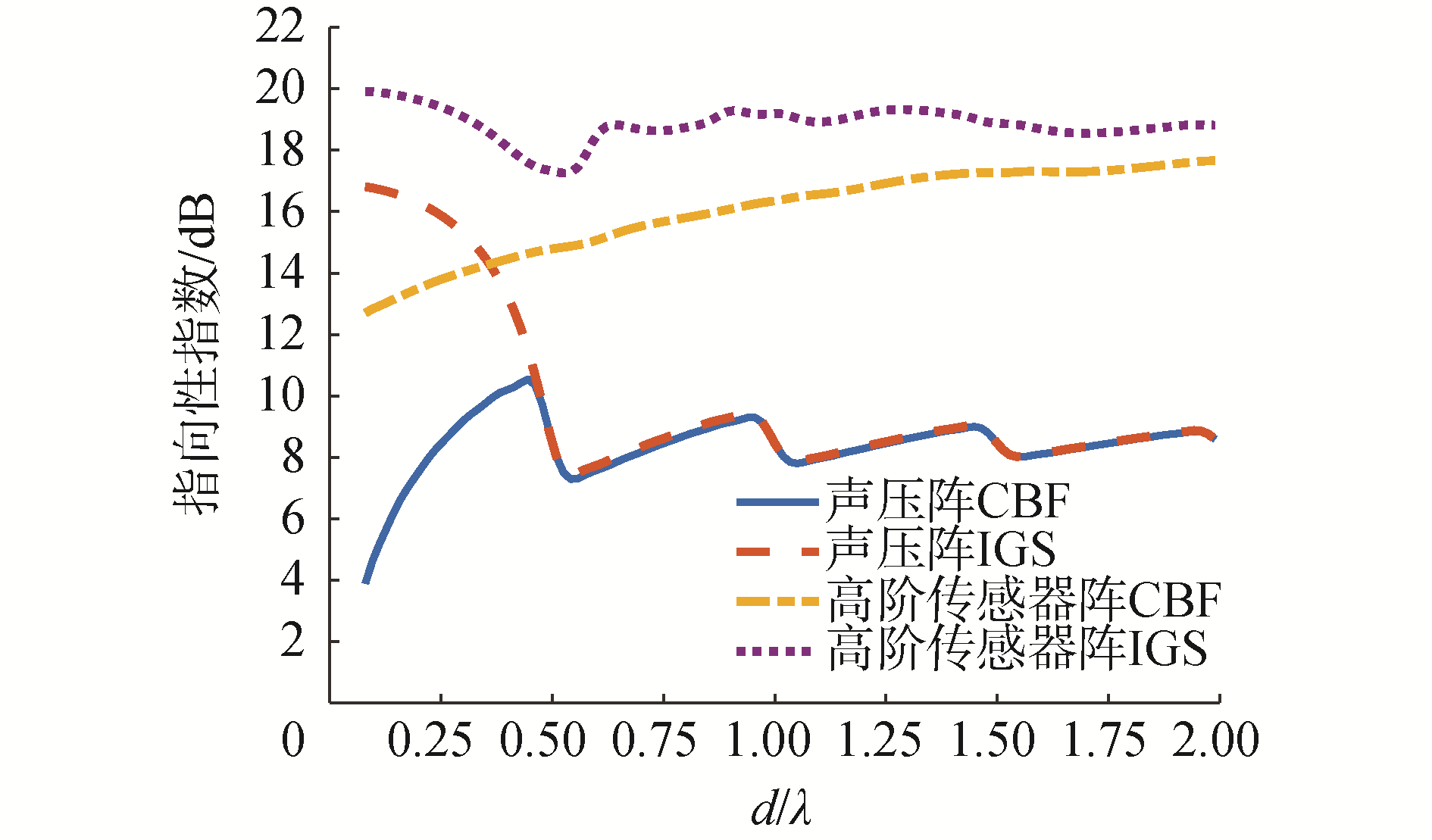
图 9中IGS的指向性指数是图 8中IGS第0~6阶波束的指向性因子相加后的分贝表示,并与CBF进行了对比。作为超指向性方法,2种阵列的IGS的指向性指数在d/λ < 0.5时远远大于CBF方法。当d/λ→0时,高阶传感器阵的IGS指向性指数比声压阵高约3 dB;当d/λ>0.5时,高阶传感器阵在较宽的频带内比声压阵高约10 dB。声压阵在d/λ为0.5时,CBF和IGS方法的指向性指数的曲线基本已经重合;在图 9所示的频带内,高阶传感器阵IGS方法的指向性指数始终大于CBF。可见,对于分析高阶传感器阵列的性能不能照搬声压阵的规律。
|
Download:
|
| 图 9 端射方向随d/λ变化的CBF和IGS方法的指向性指数 Fig. 9 Directivity index of CBF and IGS vs d/λ in the endfire look direction | |
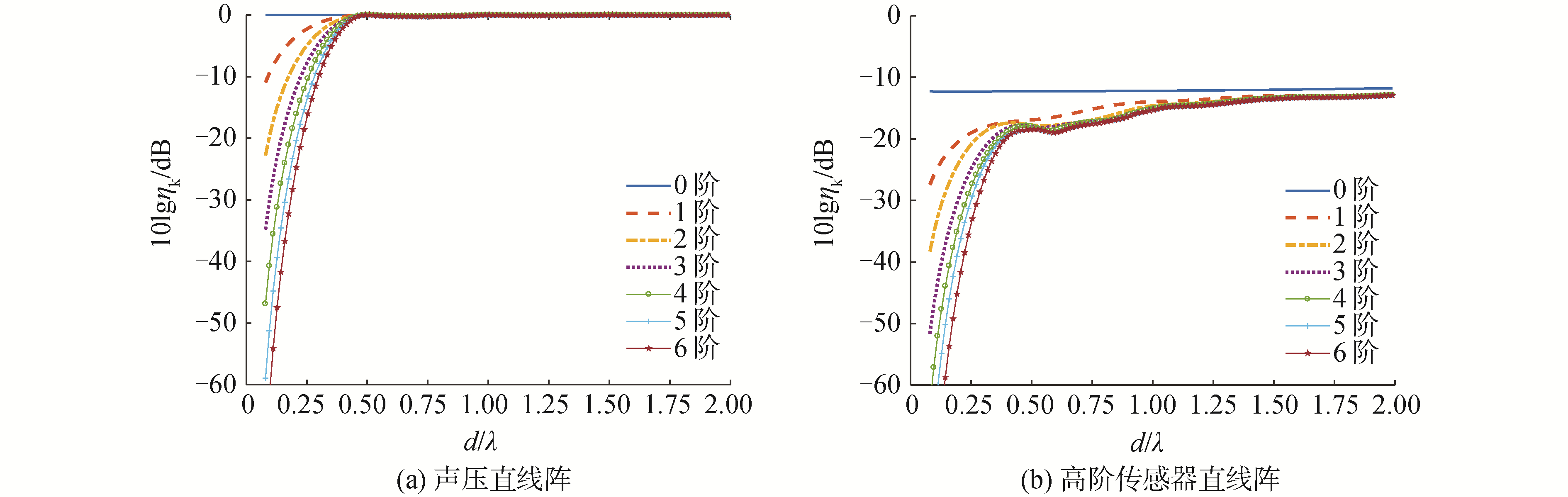
由于ηm与各阶IGS模态波束的稳健性有关,可以表征IGS方法的稳健性水平,其值越大,代表第m阶波束的稳健性越好。图 10给出了2种阵列随d/λ值变化的IGS第0~6阶波束的稳健性水平。对比图 10(a)和(b),高阶传感器阵的各阶稳健性水平均比声压阵要低,对误差更敏感,因此稳健的超指向性波束形成对高阶传感器阵列尤为重要。与EBDS模型类似,在有位置误差、相位误差等存在的情况下,可以舍弃不稳健的高阶波束,只选取较为稳健的低阶波束合成所需的稳健超指向性波束。
|
Download:
|
| 图 10 端射方向随d/λ变化的IGS稳健性水平 Fig. 10 Robustness levels vs d/λ in the endfire look direction | |
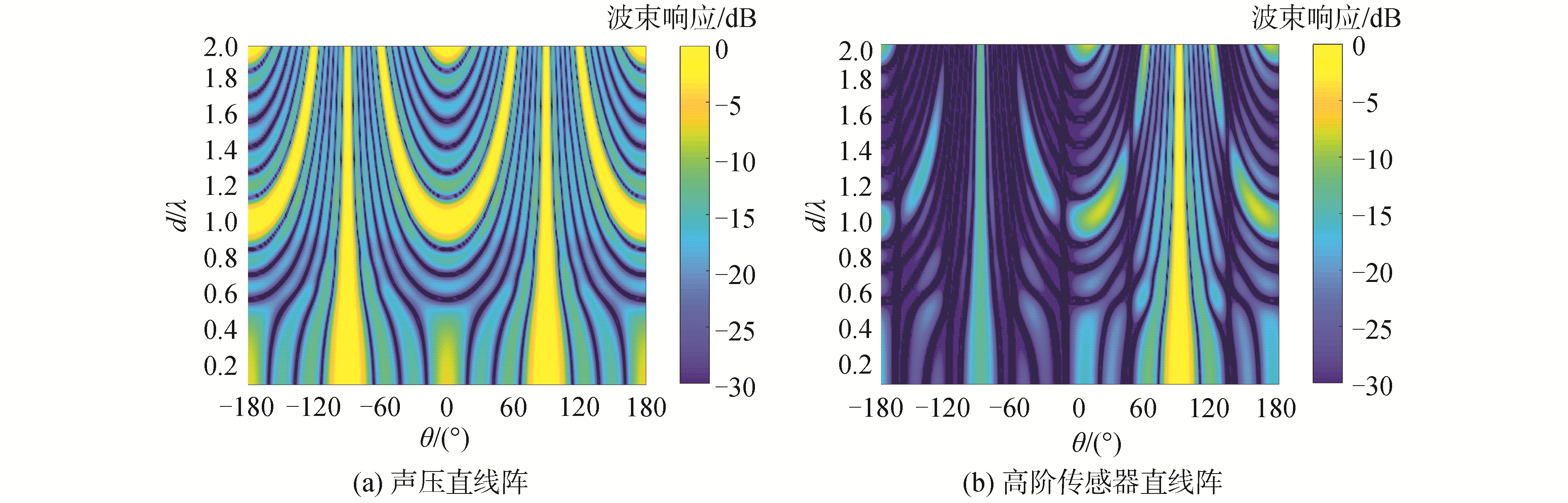
根据式(16)和(17),图 11给出了传统声压直线阵和高阶传感器直线阵在舷侧方向(θ0, ϕ0)=(90°, 90°)随d/λ值变化的IGS方法的第0~6阶波束的合成图。从图 11(a)中可以看到,声压阵在舷侧方向会出现左右舷模糊的现象,并且在d/λ约为1处会出现栅瓣;而高阶传感器阵(见图 11(b))不仅成功消除了左右舷模糊,并且在较宽的频率范围内没有栅瓣。
|
Download:
|
| 图 11 舷侧方向随d/λ变化的IGS波束图 Fig. 11 Beampatterns vs d/λ in the broadside look direction | |
根据式(19),图 12给出了舷侧方向随d/λ值变化的IGS第0~6阶波束的指向性因子。与图 8(a)对比可以发现,声压阵在d/λ < 0.5时并没有出现阶数越高,指向性因子越大的现象,除了第0阶外,其他阶数的指向性因子在整个频带内都很接近;高阶传感器阵偶数阶(第0,2,4,6阶)比奇数阶(第1,3,5阶)的指向性因子要大,奇数阶的指向性因子在低频时比较接近。除第0阶外,第1~6阶指向性因子的数值随着频率的升高逐渐趋于一致。

|
Download:
|
| 图 12 舷侧方向随d/λ变化的IGS各阶指向性因子 Fig. 12 Different-order directivity factors vs d/λ in the broadside look direction | |
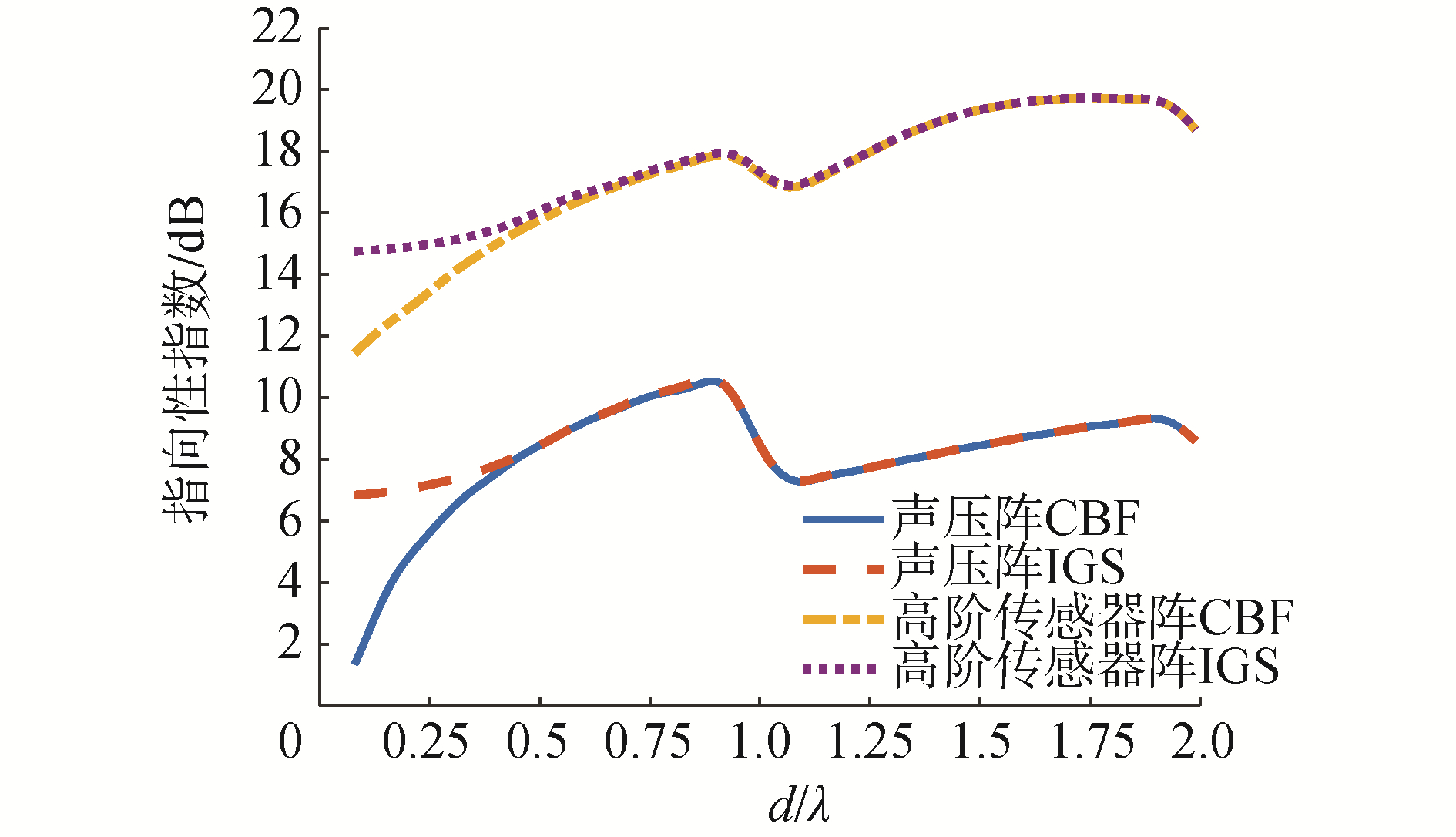
图 13中IGS的指向性指数是图 12中IGS第0~6阶波束的指向性因子相加后的分贝表示。通过图 9与图 13对比可以发现,直线阵在端射方向的超指向性比舷侧方向更加明显,这符合以往的理论常识。2种阵列在d/λ> 0.5后,IGS方法的性能都迅速退化为CBF,从而失去了超指向性的效果。总体而言,高阶传感器阵在舷侧方向的指向性指数仍然高于声压阵约8 dB。
|
Download:
|
| 图 13 端射方向随d/λ变化的CBF和IGS方法的指向性指数 Fig. 13 Directivity index of CBF and IGS vs d/λ in the endfire look direction | |
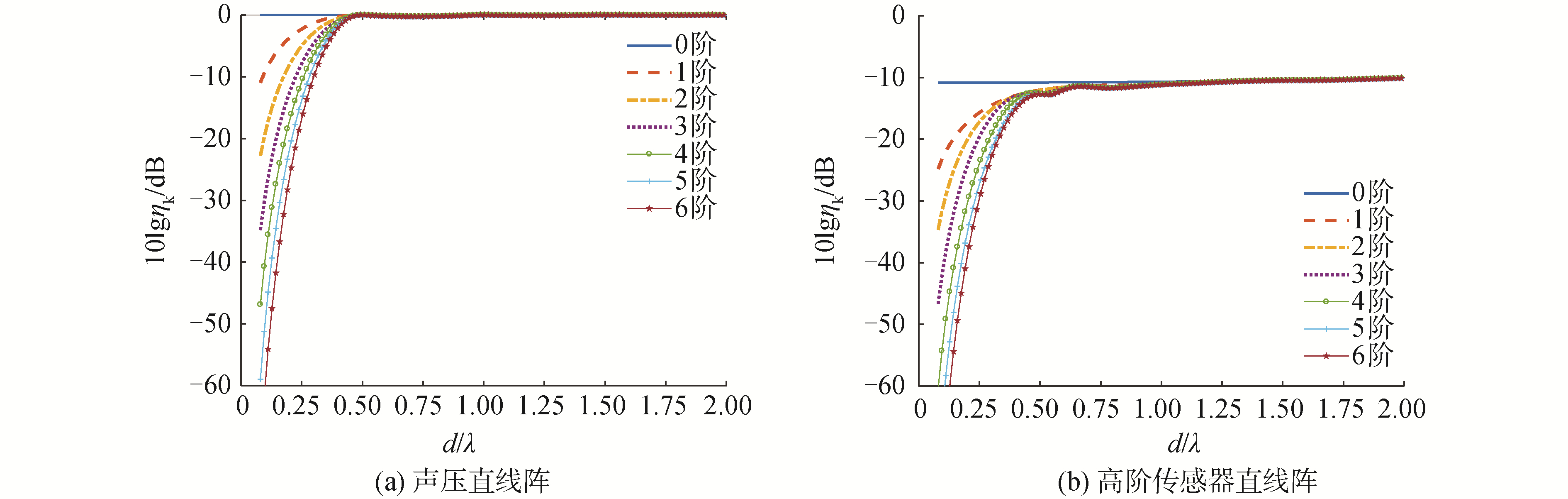
图 14给出了舷侧方向2种阵列随d/λ值变化的IGS第0~6阶波束的稳健性水平。与图 10(a)相比,声压阵的稳健性水平变化较小(见图 14(a)); 与图 10(b)相比,高阶传感器阵的各阶稳健性水平(见图 14(b))有所提高,说明高阶传感器阵在舷侧方向的超指向性波束更稳健。
|
Download:
|
| 图 14 舷侧方向随d/λ变化的IGS稳健性水平 Fig. 14 Robustness levels vs d/λ in the broadside look direction | |
1) 本文通过EBDS高阶超指向性模型给出了以圆环阵作为高阶声场传感器的物理意义,然后研究了高阶传感器阵元的噪声空间相关性及其阵列IGS超指向性波束形成方法,并举例给出了波束形成具体实施步骤。
2) 仿真中采用了12元均匀圆环阵作为高阶传感器阵元,并选取EBDS第0~4阶的合成分量给出了高阶传感器阵元的空间接收响应以及噪声相关性,然后将高阶传感器阵元组成直线阵采用IGS超指向性模型进行性能分析。仿真结果表明,具有空间指向的高阶传感器阵列具有较强的消除栅瓣和抑制左右舷模糊的能力,7个4阶传感器组成的直线阵比传统声压阵的指向性指数在较宽的频带内高约8 dB以上。
3) 高阶声场传感器在水声应用中可组成端射阵和拖曳线列阵等,这对于探测水下低频安静型潜艇等目标具有重要的实际意义。
| [1] |
CLARK J A. High-order angular response beamformer for vector sensors[J]. Journal of sound and vibration, 2008, 318(3): 417-422. DOI:10.1016/j.jsv.2008.04.030 (  0) 0)
|
| [2] |
王笑.高阶矢量水听器阵列信号处理[D].哈尔滨: 哈尔滨工程大学, 2018. WANG Xiao. High-Order hydrophone array signal processing[D]. Harbin: Harbin Engineering University, 2018. (  0) 0)
|
| [3] |
MA Yuanliang, YANG Yixin, HE Zhengyao, et al. Theoretical and practical solutions for high-order superdirectivity of circular sensor arrays[J]. IEEE transactions on industrial electronics, 2013, 60(1): 203-209. DOI:10.1109/TIE.2012.2185020 (  0) 0)
|
| [4] |
朱少豪, 汪勇, 杨益新. 圆柱阵子阵分级处理的稳健超指向性波束形成方法[J]. 声学学报, 2018, 43(4): 600-611. ZHU Shaohao, WANG Yong, YANG Yixin. Robust Superdirective Beamforming for cylindrical arrays based on subarray processing[J]. Acta acustica, 2018, 43(4): 600-611. (  0) 0)
|
| [5] |
汪勇, 杨益新, 马远良. 圆环形声学传感器阵列超指向性理论及方法[J]. 水下无人系统学报, 2017, 25(4): 297-309. WANG Yong, YANG Yixin, MA Yuanliang. Discussion about the Superdirective Beamforming theory and methods of circular acoustic sensor arrays[J]. Journal of unmanned undersea systems, 2017, 25(4): 297-309. (  0) 0)
|
| [6] |
汪勇.传感器阵列超指向性原理及方法研究[D].西安: 西北工业大学, 2015. WANG Yong. Study of superdirectivity principles and methods for sensor arrays[D]. Xi'an: Northwestern Polytechnical University, 2015. (  0) 0)
|
| [7] |
D'SPAIN G L. Relationship of underwater acoustic intensity measurements to beamforming[J]. Canadian acoustics, 1994, 22(3): 157-158. (  0) 0)
|
| [8] |
CRAY B A, EVORA V M, NUTTALL A H. Highly directional acoustic receivers[J]. The journal of the acoustical society of America, 2003, 113(3): 1526-1532. DOI:10.1121/1.1543851 (  0) 0)
|
| [9] |
HAWKES M, NEHORAI A. Acoustic vector-sensor beamforming and capon direction estimation[J]. IEEE transactions on signal processing, 1998, 46(9): 2291-2304. DOI:10.1109/78.709509 (  0) 0)
|
| [10] |
杨德森, 朱中锐, 时胜国, 等. 声矢量圆阵相位模态域目标方位估计[J]. 声学学报, 2014, 39(1): 19-26. YANG Desen, ZHU Zhongrui, SHI Shengguo, et al. Direction-of-arrival estimation based on phase modal space for a uniform circular acoustic vector-sensor array[J]. Acta acustica, 2014, 39(1): 19-26. (  0) 0)
|
| [11] |
孙贵青, 李启虎. 声矢量传感器信号处理[J]. 声学学报, 2004, 29(6): 491-498. SUN Guiqing, LI Qihu. Acoustic vector sensor signal processing[J]. Acta acustica, 2004, 29(6): 491-498. (  0) 0)
|
| [12] |
CAPON J. High-resolution frequency-wavenumber spectrum analysis[J]. Proceedings of the IEEE, 1969, 57(8): 1408-1418. DOI:10.1109/PROC.1969.7278 (  0) 0)
|
| [13] |
WANG Yong, YANG Yixin, HE Zhengyao, et al. A general superdirectivity model for arbitrary sensor arrays[J]. EURASIP journal on advances in signal processing, 2015, 2015(1): 68. (  0) 0)
|
| [14] |
HARRY L, TREES V. Optimum array processing: part IV of detection, estimation, and modulation theory[M]. New York: John Wiley & Sons, Inc., 2002.
(  0) 0)
|
| [15] |
SAHALOS J N. Orthogonal methods for array synthesis:theory and the ORAMA computer tool[M]. London: Wiley, 2006.
(  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


