2. 水声对抗技术重点实验室, 上海 201108
2. National key Laboratory of Science and Technology on Underwater Acoustic Antagonizing, Shanghai 201108, China
层析成像是一项用于推演物体断层剖面的方法[1],其通过获得目标各个角度的散射信息完成对目标外形的反演计算,从而获得目标的截面成像信息,得益于在医学计算机化断层显像(computerized tomography,CT)领域的成功应用[2],层析成像方法已经渗透到工程科学中的多个领域,如地震层析[3]、计算机断层成像[4]、海洋参数反演层析[5]和合成孔径雷达层析[6-11]等。层析成像方法本质上属于谱分析法[1],其圆形测量几何能够形成圆合成孔径,从而获取目标的多角度观测信息,同时拓展了波数域的有效带宽,使得成像理论分辨率可达1/4波长,且层析成像技术能够获得目标的三维信息,可以有效的减小甚至消除目标叠掩、透视缩短和阴影等现象[12]。水下目标三维图像对于目标探测识别具有重要意义,现有条带合成孔径声呐只能够获得目标的二维斜距图像[13-15],干涉合成孔径声呐只能形成斜距面2.5维图像[16-17]。层析成像技术能够获得目标精确二维图像,且具备三维图像能力,Friedman等[18]通过圆合成孔径声呐层析试验得到了目标的精确二维外形轮廓图像。Ferguson等[19-20]理论分析和比较了不同层析重建方法的特点,并通过仿真和试验验证了层析成像技术在声呐成像中应用的可行性。范威等[21]对单圈圆合成孔径声呐进行了层析成像仿真和试验,得到了Benchmark目标模型的精确二维外形轮廓。单圈层析数据具有圆柱对称性,波数支撑域在高度向具有一定带宽,因此具有三维成像能力[22]。然而单圈层析数据信号波数谱支撑域是中空的,因此,单圈层析三维成像存在高度向高旁瓣效应。为了增加三维层析图像高度向的分辨率和抑制旁瓣,可以沿着高度向进行多圈层析测量[20]。Marston等[23]通过无人水下航行器(unmanned underwater vehicle, UUV)在9个不同高度对目标形成多圈测量,形成垂直方向的稀疏孔径,通过对多圈回波数据相干处理得到了多个水下目标的三维图像。
通过水下航行器绕观测目标进行多圈层析测量,会导致测绘时间较长,而且由于运动载体受到环境的影响,多圈测量时会形成运动平台累积误差,这会对对声呐层析成像时的运动补偿形成巨大挑战。本文提出利用垂直短阵的水下目标三维层析方法,通过垂直短阵在一定高度绕着目标做圆周运动,一次性获得多个高度向的回波测量信息,有效提升了测绘效率。对采用垂直短阵进行水下目标三维层析成像方法的成像能力进行了分析,并进行了典型参数下仿真试验和水池试验。
1 基于垂直短阵的水下小目标三维层析成像模型 1.1 基本信号模型图 1为简化的声呐层析成像工作原理图,图 1中的O为待测场景中的被观测目标,S为收发合置圆合成孔径声呐,H为声呐离待测目标平面的高度,Rs为声呐运动半径,R0为声呐到被测目标之间的斜距,θ为声呐波束俯仰角。

|
Download:
|
| 图 1 层析成像系统模型 Fig. 1 Tomography system model | |
为了增加观测效率,利用垂直短阵作为接收阵,通过垂直阵一次圆轨迹观测,获得观测场景不同高度向的回波。采取单发模式,发射阵位于垂直接收阵中心。为简化回波模型,采用“等效相位中心”理论,取发射阵和接收阵的中点为等效相位中心,声波被认为是从等效相位中心发射,并由等效相位中心接收。对观测场景中的点
| $ \left\{ {\begin{array}{*{20}{l}} {{x_m} = \frac{{{x_{r,n}} + {x_{{\rm{tr}}}}}}{2}}\\ {{y_m} = \frac{{{y_{r,n}} + {y_{{\rm{tr}}}}}}{2}}\\ {{z_m} = \frac{{{z_{r,n}} + {z_{{\rm{tr}}}}}}{2}} \end{array}} \right. $ | (1) |
等效相位中心与观测场景中的点之间的距离Rm以及时延τm可以表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {{R_m} = \sqrt {{{({x_m} - {x_0})}^2} + {{({y_m} - {y_0})}^2} + {{({z_m} - {z_0})}^2}} }\\ {{\tau _m} = \frac{{2{R_m}}}{c}} \end{array}} \right. $ | (2) |
式中c为介质中的声速。
发射阵元发射线性调频信号,原始回波经过解调得到第m个接收阵元的基带时域信号
| $ \begin{array}{l} {s_{{\rm{base }},m}}(t) = \sigma \cdot {\mathop{\rm rect}\nolimits} \left( {\frac{{t - {\tau _m}}}{{{T_r}}}} \right) \cdot \exp \left\{ {{\rm{j}}\left[ {2{\rm{ \mathsf{ π} }}{f_0}{\tau _m} + } \right.} \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\left. {{\rm{ \mathsf{ π} }}{K_r}{{\left( {t - {\tau _m}} \right)}^2}} \right]} \right\} + N(t) \end{array} $ | (3) |
式中:rect(·)表示矩形波; f0为发射信号中心频率; Tr为发射信号脉冲宽度; Kr为调频率; N(t)为信号传播过程的干扰和噪声; σ为目标反射系数。对圆轨迹各个观察角度的阵元回波信号经过同样处理,即得到第m阵元接收阵信号
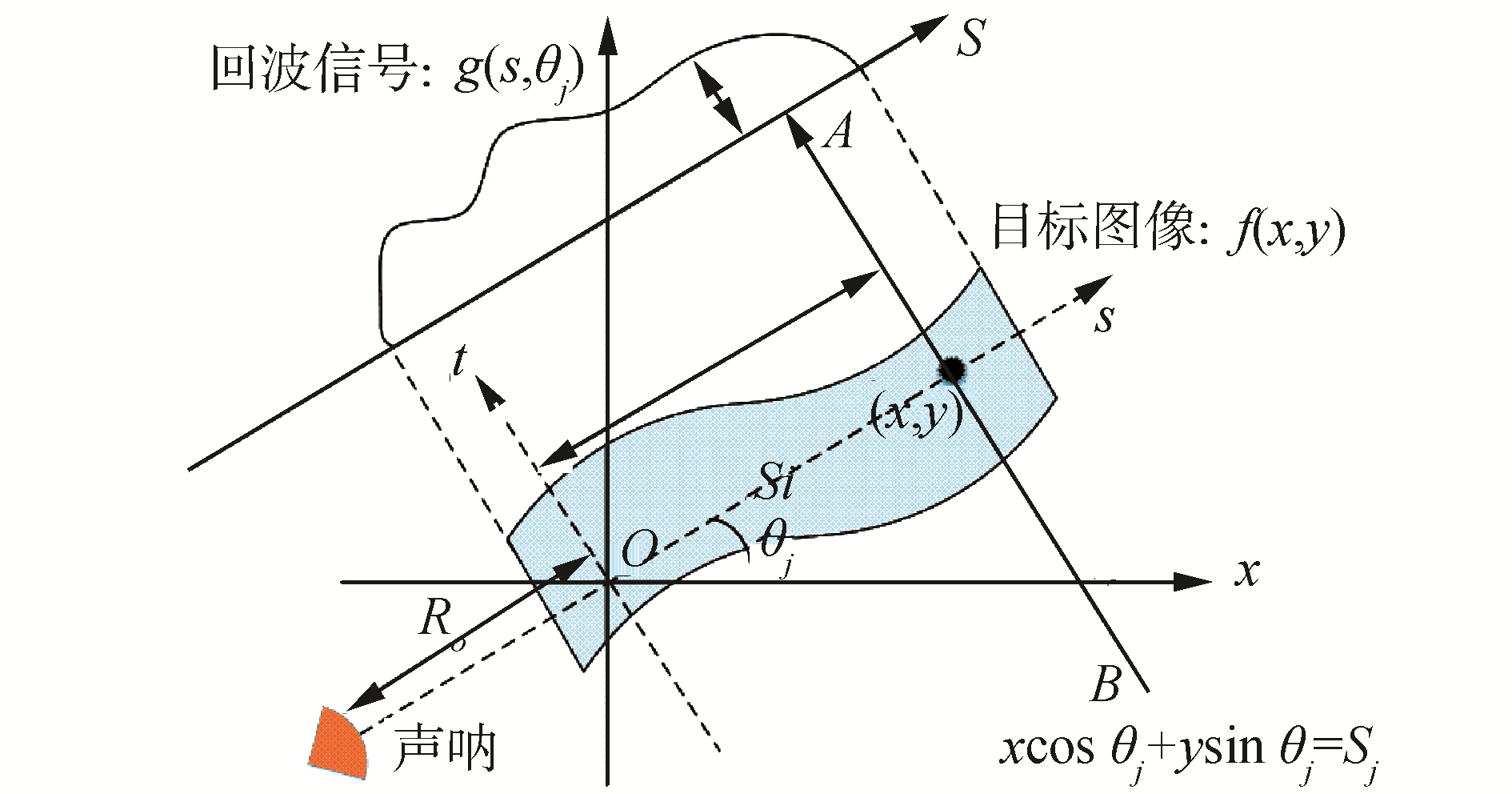
方位-距离向层析成像观测几何如图 2所示。记声呐声波的传播方向与x轴夹角为θj。投影线记为
| $ g({s_i},{\theta _j}) = \int f (x,y){\rm{d}}{s_ \bot } $ | (4) |
|
Download:
|
| 图 2 层析成像的基本原理 Fig. 2 Basic principles of tomography | |
对获得的投影数据g(s, θ)进行傅里叶变换F1(s→ξ)将信号变换到波数域,通过波数域插值将极坐标波数数据变为笛卡尔系下波数域数据,通过傅里叶逆变换即得到重建一维图像。目标的外形轮廓能够通过二维逆傅里叶变换得到[18]:
| $ \begin{array}{*{20}{l}} {f(x,y) = F_2^{ - 1}[F({\xi _x},{\xi _y})] = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} F_2^{ - 1}[F(\xi \cos \theta ,\xi \sin \theta )] = F_2^{ - 1}[G(\xi ,\theta )] = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} F_2^{ - 1}[{F_1}g(s,\theta )]} \end{array} $ | (5) |
式中:如果
| $ f(x,y) = \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty F } ({\xi _x},{\xi _y})\exp [{\rm{j}}2{\rm{ \mathsf{ π} }}({\xi _x}x + {\xi _y}y)]{\rm{d}}{\xi _x}{\rm{d}}{\xi _y} $ | (6) |
垂直短阵测量几何如图 3所示,在roz笛卡尔坐标系下,将成像场景离散为各像素点。垂直短阵发射阵元在阵中心,记发射阵元到观测场景中心的距离记为Ra,对于场景中某像素点(ri, zj), 接收阵元n到该像素点距离为:
| $ R_n^{ij} = \sqrt {{{({r_i} + {r_a})}^2} + {{({z_j} - {z_n})}^2}} $ | (7) |

|
Download:
|
| 图 3 垂直短阵测量几何示意 Fig. 3 Geometric diagram of vertical short array measurement | |
对式(7)进行泰勒展开,像素点距离为:
| $ R_n^{ij} \approx ({z_j} - {z_n}) + \frac{{{{({r_i} + {r_a})}^2}}}{{2({z_j} - {z_n})}} $ | (8) |
接收阵元n到(0, zj)距离为:
| $ R_n^j = \sqrt {r_a^2 + {{({z_j} - {z_n})}^2}} $ | (9) |
对式(9)进行泰勒展开,距离为:
| $ R_n^{ij} \approx ({z_j} - {z_n}) + \frac{{{{({r_a})}^2}}}{{2({z_j} - {z_n})}} $ | (10) |
对于小的成像场景,ri是高阶小量,因此Rnij≈Rnj。通过此近似,可以减小逐像素聚焦MVDR波束形成的计算时间。
N元等间距d布置的垂直接收阵阵元时延记为
| $ \mathit{\boldsymbol{z}}(m) = {\mathit{\boldsymbol{w}}^{\rm{H}}}(m)\mathit{\boldsymbol{x}}(m) = {\left[ {\begin{array}{*{20}{c}} {{w_1}(m)}\\ {{w_2}(m)}\\ \vdots \\ {{w_N}(m)} \end{array}} \right]^{\rm{H}}}\left[ {\begin{array}{*{20}{c}} {{x_1}(m)}\\ {{x_2}(m)}\\ \vdots \\ {{x_N}(m)} \end{array}} \right] $ | (11) |
| $ \mathit{\boldsymbol{w}}(m) = \frac{{\mathit{\boldsymbol{R}}{{(m)}^{ - 1}}{I_N}}}{{{\bf{1}}_N^{\rm{H}}\mathit{\boldsymbol{R}}{{(m)}^{ - 1}}{I_N}}} $ | (12) |
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{R}}(m) = \frac{1}{{(2K + 1)(N - L + 1)}} \cdot }\\ {\quad \sum\limits_{k = - K}^K {\sum\limits_{l = 0}^{N - L} {{\mathit{\boldsymbol{x}}_l}} } (m - k)\mathit{\boldsymbol{x}}_l^{\rm{H}}(m - k)} \end{array} $ | (13) |
式中:N为垂直短阵阵元数;L为子阵长度;K为时间平均长度;xl表示l子阵时延测量值。
式(13)为利用子阵平均和时间平均估计得到的空间协方差矩阵,其具有更好的鲁棒性[24]。
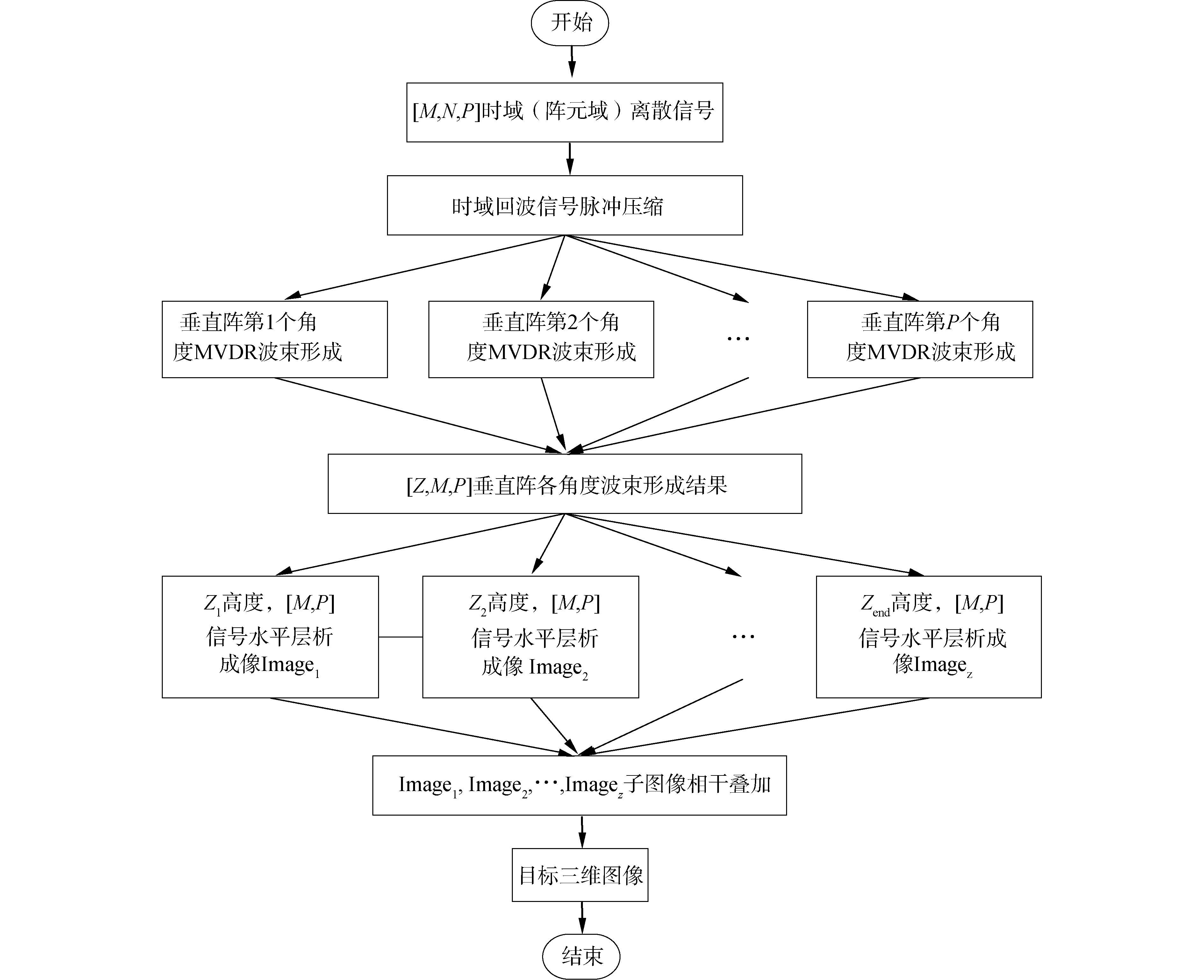
1.4 三维层析波束形成传统的水下三维声成像技术包括波束形成方法、声透镜法和声全息方法[18],波束形成方法是应用最为广泛的三维成像方法。本文提出一种垂直短阵三维层析方法,该方法利用垂直短阵绕目标一次圆周运动替代单发单收合成孔径声呐绕目标在不同高度做多圈层析,实现对观测场景声信号快速获取。利用垂直短阵形成的垂直孔径进行高分辨波束形成成像处理,提升高度向分辨率,然后对波束形成得到的高度向数据进行水平-距离向层析成像处理,通过对所有层析成像结果相干处理得到最终的三维图像结果。图 4为垂直短阵三维层析成像方法的基本流程,其中,P为角度采样点数,M为距离向采样点数。
|
Download:
|
| 图 4 三维层析算法流程 Fig. 4 3D tomography algorithm | |
点扩散函数能够表征声呐系统的成像能力,点扩散函数波数谱支撑域决定了声呐图像的分辨率。从分辨率角度来看,在水平方位-距离向,单圈层析与垂直短阵层析具有相同的合成孔径大小,因此水平方位-距离分辨率一致;在高度向,由于垂直短阵孔径大于单圈层析孔径。因此,垂直短阵的高度向分辨率优于单圈层析的垂直分辨率。从抑制旁瓣的角度来看,由于方位向采样率不满足香农采样定理,使得单圈层析成像存在水平向高旁瓣缺陷[25],垂直短阵形成的多圈层析成像能够抑制水平向旁瓣。
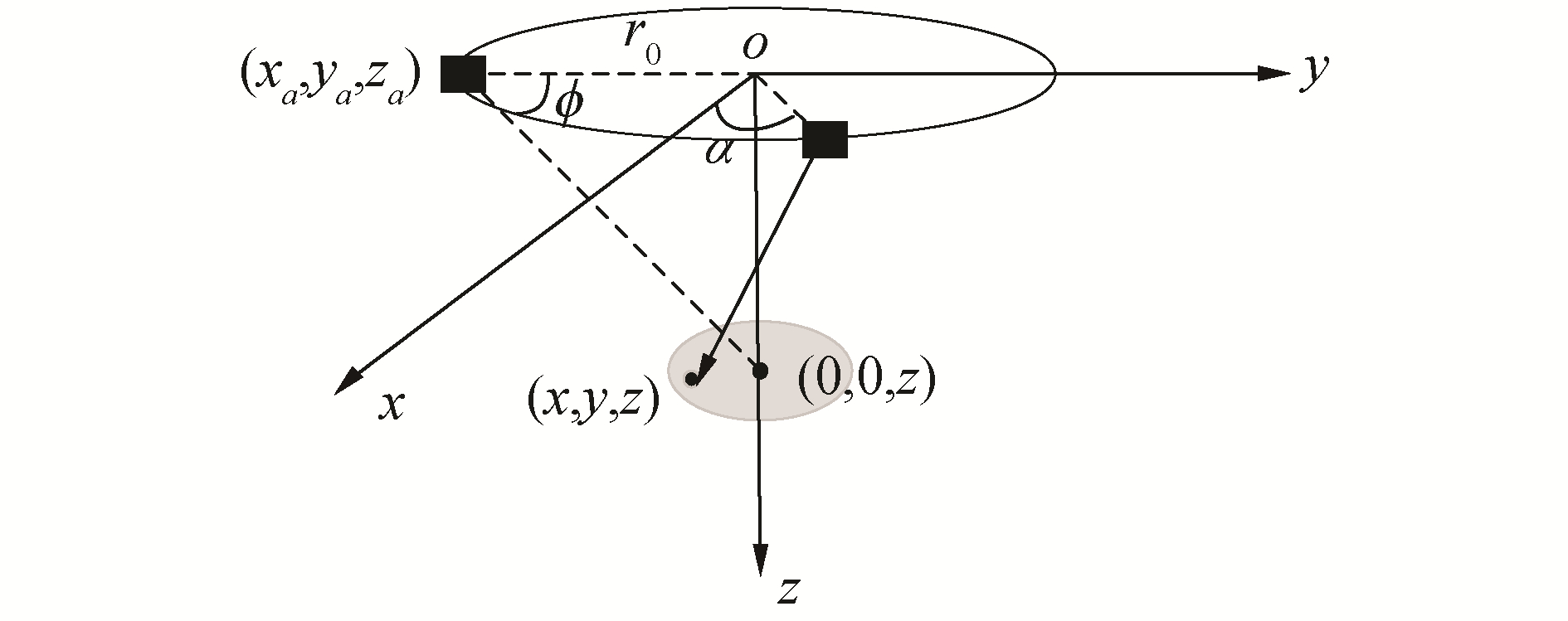
2.1 单圈点扩散函数分析单圈层析成像的观测几何如图 5所示。设声呐阵元所在空间为Ω,单圈时发射接收阵元等效相位中心为
| $ \left\{ {\begin{array}{*{20}{l}} {{K_x} = K\frac{{{r_0}\cos \alpha - x}}{{\sqrt {{{(x - {r_0}\cos \alpha )}^2} + {{(y - {r_0}\sin \alpha )}^2} + {z^2}} }}}\\ {{K_y} = K\frac{{{r_0}\sin \alpha - y}}{{\sqrt {{{(x - {r_0}\cos \alpha )}^2} + {{(y - {r_0}\sin \alpha )}^2} + {z^2}} }}}\\ {{K_z} = K\frac{{ - z}}{{\sqrt {{{(x - {r_0}\cos \alpha )}^2} + {{(y - {r_0}\sin \alpha )}^2} + {z^2}} }}} \end{array}} \right. $ | (14) |
|
Download:
|
| 图 5 单圈层析成像观测几何 Fig. 5 Single circle tomography observation geometry | |
式中
| $ {\rm{ROS}}(x,y,z) = \left\{ {({K_x},{K_y},{K_z})\left| {\begin{array}{*{20}{c}} {\frac{{4{\rm{ }}\pi {f_{\min }}}}{c} \le K \le \frac{{4\pi {f_{\max }}}}{c}}\\ {x_a^2 + y_a^2 = r_0^2,{z_a} = 0} \end{array}} \right.} \right\} $ | (15) |
通过对支撑域模糊度函数分析,可以得到单圈层析成像模型对于观测场景中心(0, 0, 0)点扩散函数为[26-27]:
| $ {F_{{\rm{psf}}}}(\varphi ) \approx {r_0} \cdot {J_0}\left( {\frac{{4{\rm{ \mathsf{ π} }}{r_0}\tan \varphi }}{\lambda }} \right) $ | (16) |
式中φ=arctan(r0/z)。非中心目标的点扩散函数没有解析解,只能通过数值计算模拟。通过式(14)可知,单圈层析成像中心点扩散函数为0阶贝塞尔函数形式。0阶贝塞尔函数的峰值旁瓣比为-8 dB, 而sinc函数峰值旁瓣比约为-13 dB, 可见单圈层析成像模型具有较高的旁瓣。
2.2 垂直短阵点扩散函数分析垂直短阵层析成像观测几何如图 6所示。记不同单圈层析的等效相位中心为
| $ \left\{ {\begin{array}{*{20}{l}} {{K_x} = K\frac{{{r_0}\cos \alpha - x}}{{\sqrt {{{\left( {x - {r_0}\cos \alpha } \right)}^2} + {{\left( {y - {r_0}\sin \alpha } \right)}^2} + {{\left( {z - {z_i}} \right)}^2}} }}}\\ {{K_y} = K\frac{{{r_0}\sin \alpha - y}}{{\sqrt {{{\left( {x - {r_0}\cos \alpha } \right)}^2} + {{\left( {y - {r_0}\sin \alpha } \right)}^2} + {{\left( {z - {z_i}} \right)}^2}} }}}\\ {{K_z} = K\frac{{z - {z_i}}}{{\sqrt {{{\left( {x - {r_0}\cos \alpha } \right)}^2} + {{\left( {y - {r_0}\sin \alpha } \right)}^2} + {{\left( {z - {z_i}} \right)}^2}} }}} \end{array}} \right. $ | (17) |

|
Download:
|
| 图 6 垂直阵层析模型 Fig. 6 Vertical array tomography model | |
垂直短阵层析成像点扩散函数波数谱支撑域为:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{ROS}} (x,y,z) = \\ \left\{ {({K_x},{K_y},{K_z})\left| \begin{array}{l} \frac{{4{\rm{ \mathsf{ π} }}{f_{\min }}}}{c} \le K \le \frac{{4{\rm{ \mathsf{ π} }}{f_{\max }}}}{c}\\ x_i^2 + y_i^2 = r_0^2,{z_a} \in [0,{z_{\max }}] \end{array} \right.} \right\} \end{array} $ | (18) |
垂直短阵的图像可以通过单圈等效相位中心信号相干叠加重建。其成像场景中心点(0, 0, 0)的扩散函数可以表示为单圈点扩散函数的积分形式:
| $ {F_{{\rm{psf}}}}(\varphi ) = \sum\limits_{i = 1}^N {{r_0}} \cdot {J_0}\left( {\frac{{4{\rm{ \mathsf{ π} }}{r_0}\tan {\varphi _i}}}{\lambda }} \right) $ | (19) |
其中不同高度阵元对观测场景中心的掠射角φi记为:
| $ {\varphi _i} = \arctan ({r_0}/{z_{\rm{i}}}) $ | (20) |
式(19)表明,垂直短阵层析成像模型在水平向的分辨率是对称的,信号波长以及布阵形式影响最终的分辨率。
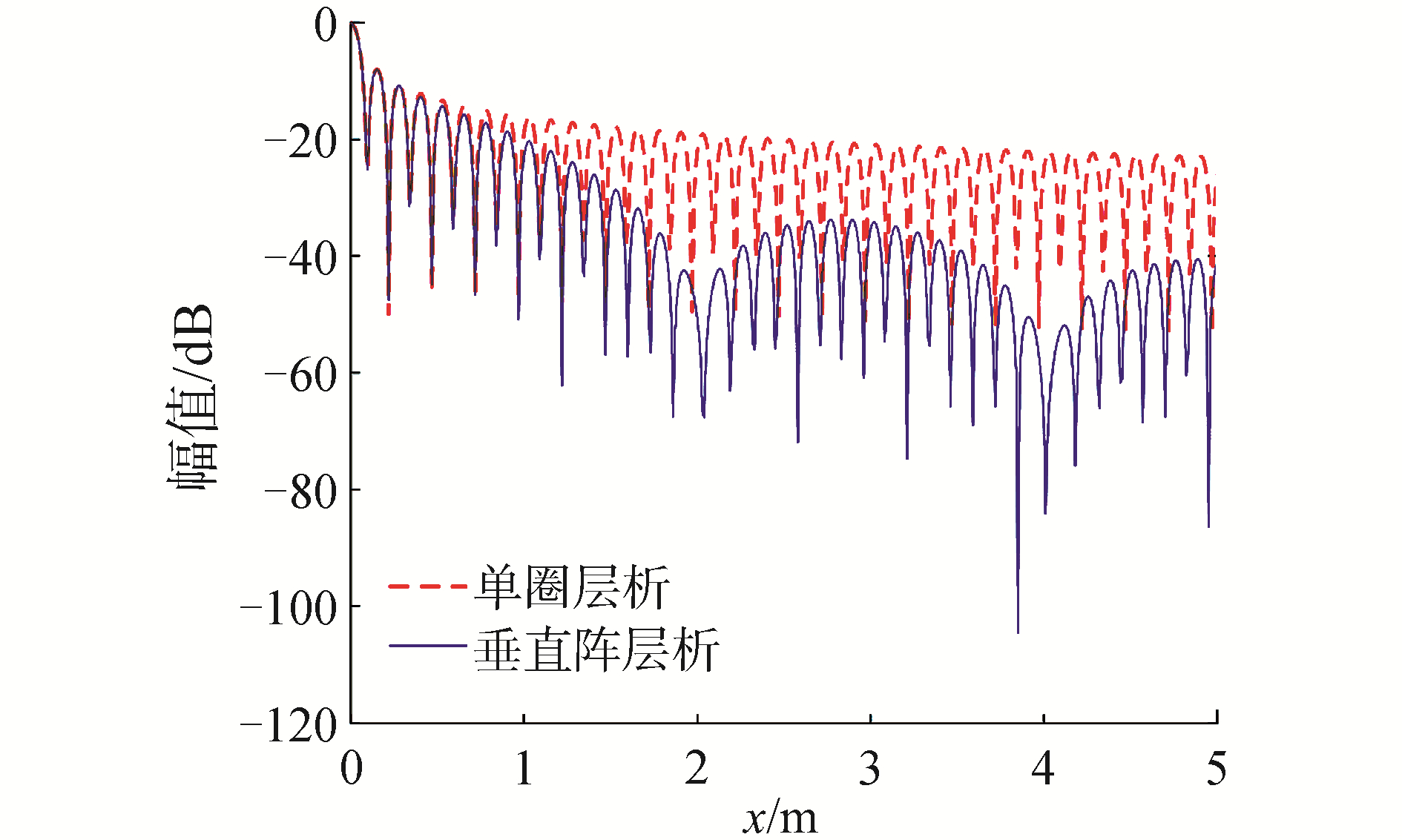
2.3 点扩散函数仿真分析为直观反应单圈层析与垂直阵层析模型分辨率和旁瓣的差异,通过仿真单圈和垂直短阵层析模型对成像场景中心点目标的点扩散函数,利用后向投影(back projection, BP)成像算法对成像结果进行对比。仿真参数如表 1所示,仿真得到的点扩散函数图像切航迹向剖面图如图 7所示,点扩散函数图像切航迹向3 dB带宽、峰值旁瓣比(peak side lobe ratio, PSLR)和积分旁瓣比(integral side lobe ratio, ISLR)结果如表 2所示。由图 7和表 2可以看出,单圈层析和垂直阵层析具有相当的分辨率,而垂直阵层析具有更低的峰值旁瓣比,即目标整体的旁瓣得到了抑制。
|
Download:
|
| 图 7 点扩散函数图像切航迹向剖面 Fig. 7 Point spread function image cut path | |
| 表 1 仿真参数设置 Table 1 Simulation parameter settings |
| 表 2 点扩散函数性能比较 Table 2 Cross-track performance comparison |
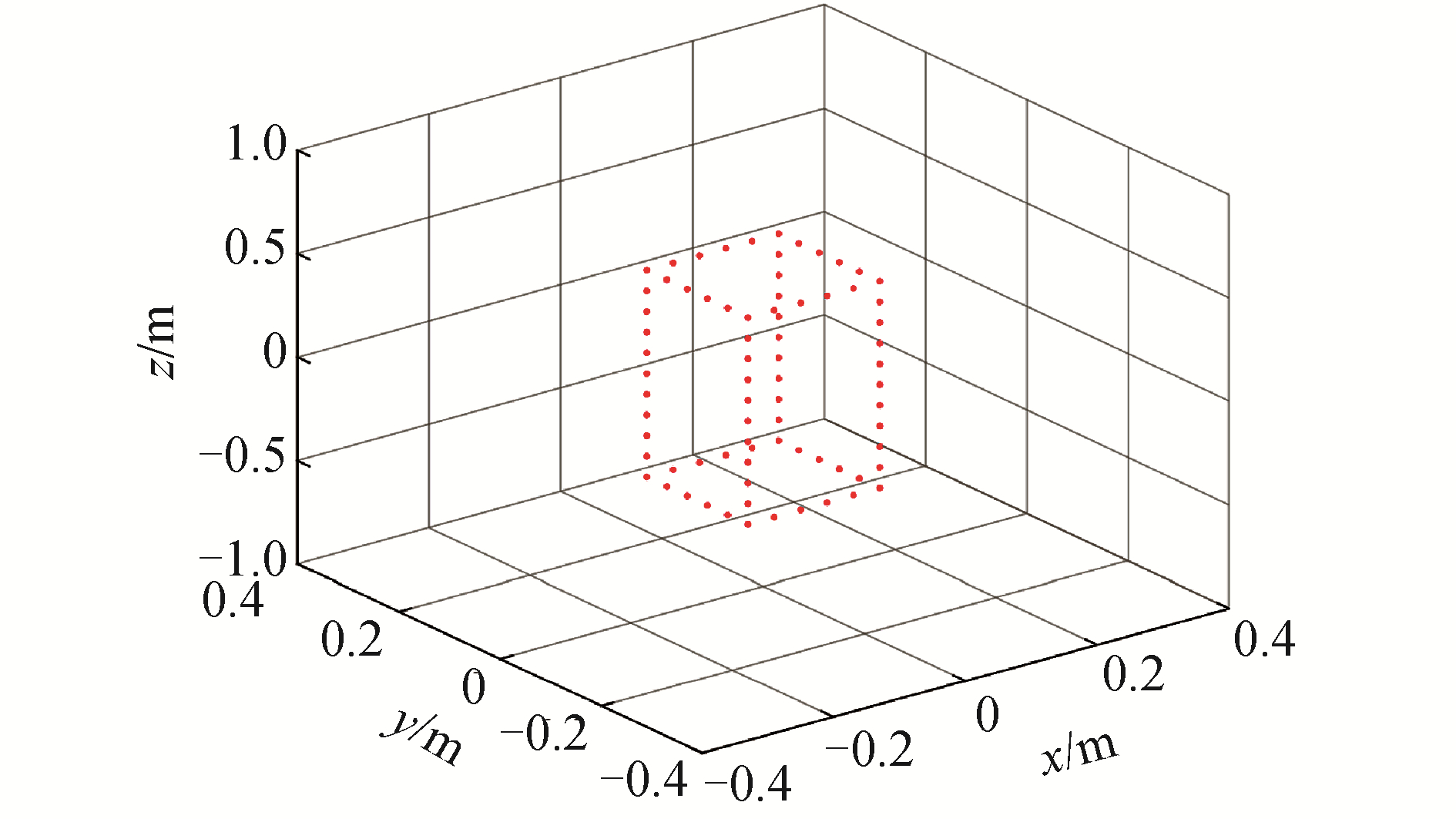
为验证垂直短阵三维层析成像方法的有效性,进行体目标计算机仿真试验,仿真参数设置为:声速1 500 m/s,信号为线性调频信号,中心频率为100 kHz, 带宽为30 kHz, 发射脉宽为10 ms, 接收阵元数为32阵元间距为0.037 5 m, 声呐安装平台做圆周运动速度为0.175 m/s,运动半径为10 m,声呐平台高度为10 m。仿真试验的体目标如图 8所示,由68个点目标组成。
|
Download:
|
| 图 8 仿真体目标 Fig. 8 Simulation target | |
图 9为仿真试验时垂直短阵的测量几何示意图,通过垂直短阵绕目标运动一次性获得多圈层析数据。图 10为利用本方法得到的仿真体目标三维图像,三维成像结果与图 8中的目标完全一致。

|
Download:
|
| 图 9 垂直短阵测量几何示意 Fig. 9 Geometric diagram of vertical short array measurement | |

|
Download:
|
| 图 10 仿真目标三维层析成像结果 Fig. 10 Simulation target 3D tomography results | |
通过水池试验进一步验证提出的垂直短阵三维层析成像算法的有效性。试验用垂直短阵长1.2 m,其中接收阵由32个阵元组成,发射阵布置在接收阵的中间。试验目标为利用高散射强度小球搭建的三维立体目标。小球直径为8 cm,小球间距为15 cm,小球横穿在直径为0.5 cm的铁杆上,铁杆长为1 m,每个铁杆上横穿4个目标球。3个铁杆相互垂直布置。试验目标如图 11所示。

|
Download:
|
| 图 11 试验用的三维目标 Fig. 11 Three-dimensional target for experiment | |
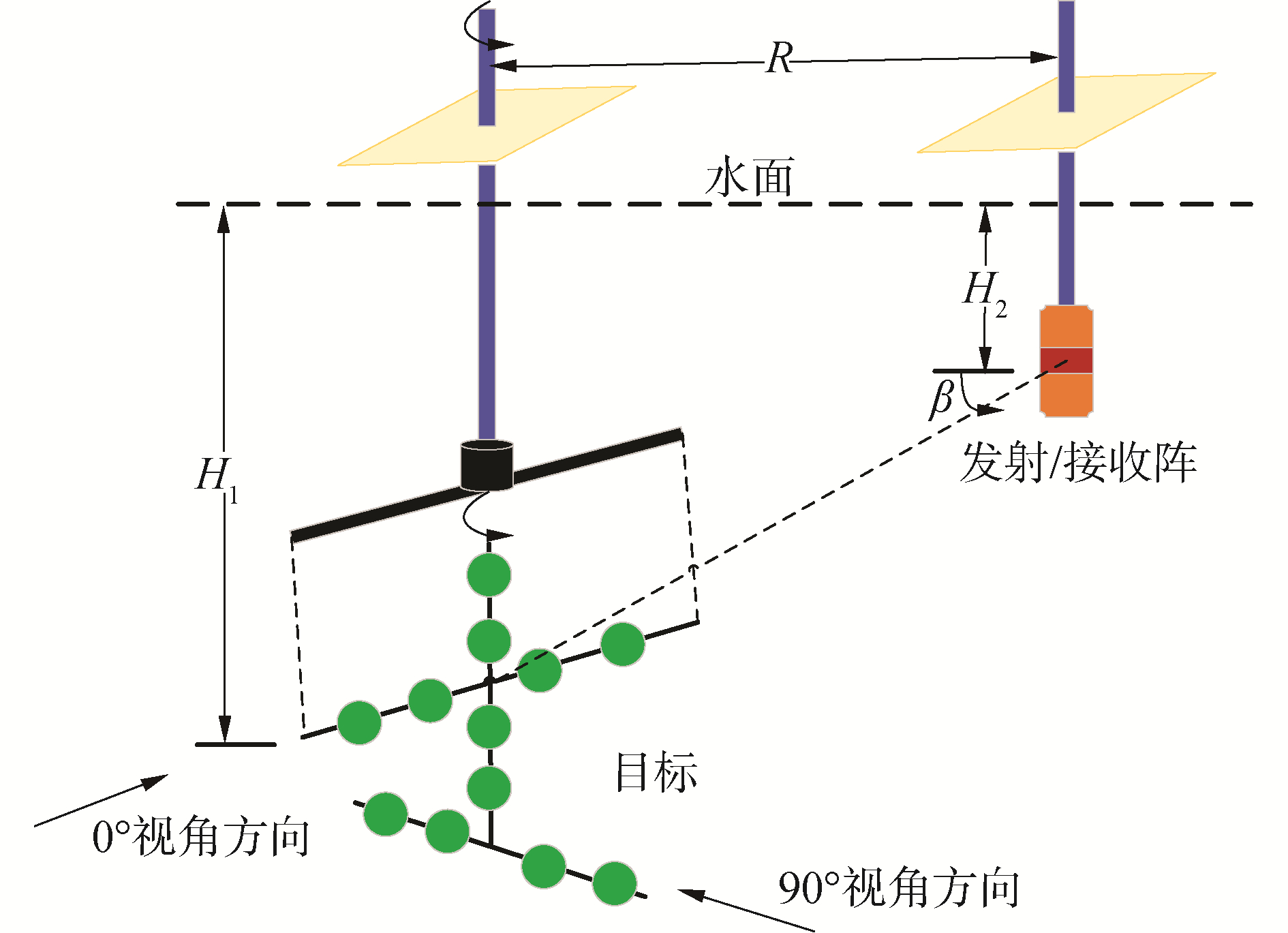
水池试验目标与垂直短阵测试距离R为10 m,待测目标与声呐湿端分别置于2个旋转台下端, 试验测量态势如图 12所示。发射阵离水面距离H2=3 m,试验目标中心离水面距离H1=3.55,试验目标通过吊放绳系在转台两端。在测试过程中,目标匀速旋转,速度为0.129°/s。在目标匀速旋转过程中,声呐系统不断发射和接收目标回波信号,其中发射阵发射信号形式为CW脉冲,中心频率为100 kHz,信号脉宽为20 μs。
|
Download:
|
| 图 12 试验测量几何 Fig. 12 Test measurement geometry | |
图 13为试验目标回波信号,从中可以看出,随着目标的旋转,目标回波信号呈现类似正弦曲线的结构。图 14为垂直短阵在30°视角方向逐像素点MVDR波束形成结果。图 14为试验目标在不同视角下的三维图像结果,从中可以看出,组成三维立体目标的12个小球均在三维图像中得到显示,且12个小球的空间分布与实际情况相符合,在0°视角下,目标三维图像呈现倒“T”字形;在45°视角下,三维图像完全反应目标空间分布;在90°视角下,目标图像呈现“十”字形。图 15中第2层目标旁边的亮点和上方的亮点为吊放绳。

|
Download:
|
| 图 13 目标回波结构 Fig. 13 Target echo structure | |

|
Download:
|
| 图 14 垂直短阵30°视角方向波束形成结果 Fig. 14 Schematic diagram of vertical short array 30-degree viewing angle direction beamforming | |

|
Download:
|
| 图 15 试验目标三维成像结果 Fig. 15 Test target 3D imaging results | |
1) 采用水下无人航行器搭载合成孔径声呐在不同高度上绕目标进行多圈圆周测量会导致测绘时间变长,随着时间的积累,无人航行器的运动误差会累积,对成像时的运动补偿带来困难。
2) 本文提出的采用垂直短阵的水下小目标三维层析成像方法提升了测绘效率。垂直短阵阵列高分辨处理提升三维图像高度向分辨率,通过水平层析成像处理获得不同高度二维图像,对各高度向二维图像进行相干融合处理获得水下目标三维图像。
3) 仿真试验提升了三维图像的成像质量,水池试验验证了本文方法的有效性。本文提出的基于垂直短阵的水下小目标三维层析成像方法,能够获得水下小目标的三维图像,对于水下小目标的探测和识别具有重要意义。
仿真试验和水池试验均是在理想运动轨迹下进行的,后续将优化现有三维成像算法,开展非理想运动轨迹的运动误差补偿研究,进一步提升三维图像的垂直向成像精度。
| [1] |
林珲, 马培峰, 陈旻, 等. SAR层析成像的基本原理、关键技术和应用领域[J]. 测绘地理信息, 2015, 40(3): 1-5. LIN Hui, MA Peifeng, CHEN Min, et al. Basic principles, Key techniques and applications of tomographic SAR imaging[J]. Journal of geomatics, 2015, 40(3): 1-5. (  0) 0)
|
| [2] |
GOLDMAN L W. Principles of CT:multislice CT[J]. Journal of nuclear medicine technology, 2008, 36(2): 57-68. (  0) 0)
|
| [3] |
CAROLLO A, CAPIZZI P, MARTORANA R. Joint interpretation of seismic refraction tomography and electrical resistivity tomography by cluster analysis to detect buried cavities[J]. Journal of applied geophysics, 2020, 178: 104069. DOI:10.1016/j.jappgeo.2020.104069 (  0) 0)
|
| [4] |
PAN Yaling, SHI Dejun, WANG Hanqi, et al. Automatic opportunistic osteoporosis screening using low-dose chest computed tomography scans obtained for lung cancer screening[J]. European radiology, 2020, 30(7): 4107-4116. DOI:10.1007/s00330-020-06679-y (  0) 0)
|
| [5] |
DORADOR J, RODRÍGUEZ-TOVAR F J, TITSCHACK J. Exploring computed tomography in ichnological analysis of cores from modern marine sediments[J]. Scientific reports, 2020, 10(1): 201. DOI:10.1038/s41598-019-57028-z (  0) 0)
|
| [6] |
YU Y H, D'ALESSANDRO M M, TEBALDINI S, et al. Signal processing options for high resolution SAR tomography of natural scenarios[J]. Remote sensing, 2020, 12(10): 1638. DOI:10.3390/rs12101638 (  0) 0)
|
| [7] |
LIAO Zhanmang, HE Binbin, QUAN Xingwen. Potential of texture from SAR tomographic images for forest aboveground biomass estimation[J]. International journal of applied earth observation and geoinformation, 2020, 88: 102049. DOI:10.1016/j.jag.2020.102049 (  0) 0)
|
| [8] |
RAMBOUR C, DENIS L, TUPIN F, et al. Urban surface reconstruction in SAR tomography by graph-cuts[J]. Computer vision and image understanding, 2019, 188: 102791. DOI:10.1016/j.cviu.2019.07.011 (  0) 0)
|
| [9] |
NANNINI M, MARTONE M, RIZZOLI P, et al. Coherence-based SAR tomography for spaceborne applications[J]. Remote sensing of environment, 2019, 225: 107-114. DOI:10.1016/j.rse.2019.01.040 (  0) 0)
|
| [10] |
BI Hui, ZHANG Bingchen, HONG Wen. Matrix completion-based distributed compressive sensing for polarimetric SAR tomography[J]. Science China information sciences, 2015, 58(11): 1-3. (  0) 0)
|
| [11] |
PINHEIRO M, PRATS P, SCHEIBER R, et al. Tomographic 3D reconstruction from airborne circular SAR[C]//Proceedings of 2009 IEEE International Geoscience and Remote Sensing Symposium. Cape Town, South Africa, 2009.
(  0) 0)
|
| [12] |
张冰尘, 洪文, 吴一戎. 稀疏微波成像导论[M]. 北京: 科学出版社, 2018: 70-71.
(  0) 0)
|
| [13] |
HAWKINS D W. Synthetic aperture imaging algorithms: with application to wide band sonar[D]. Christchurch, New Zealand: University of Canterbury, 1996: 20-63.
(  0) 0)
|
| [14] |
孙大军, 田坦. 合成孔径声呐技术研究(综述)[J]. 哈尔滨工程大学学报, 2000, 21(1): 51-56. SUN Dajun, TIAN Tan. The study of synthetic aperture sonar (SAS) technique (review)[J]. Journal of Harbin Engineering University, 2000, 21(1): 51-56. (  0) 0)
|
| [15] |
汪海涛, 唐劲松, 苑秉成. 多子阵SAS逐线成像算法研究[J]. 哈尔滨工程大学学报, 2009, 30(7): 820-823. WANG Haitao, TANG Jinsong, YUAN Bingcheng. Research on a multi-receiver synthetic aperture sonar imaging algorithm based on FFT[J]. Journal of Harbin Engineering University, 2009, 30(7): 820-823. (  0) 0)
|
| [16] |
HAYES M P, GOUGH P T. Synthetic aperture sonar:a review of current status[J]. IEEE journal of oceanic engineering, 2009, 34(3): 207-224. DOI:10.1109/JOE.2009.2020853 (  0) 0)
|
| [17] |
HANSEN R E, CALLOW H J, SABO T O, et al. Challenges in seafloor imaging and mapping with synthetic aperture sonar[J]. IEEE transactions on geoscience and remote sensing, 2011, 49(10): 3677-3687. DOI:10.1109/TGRS.2011.2155071 (  0) 0)
|
| [18] |
FRIEDMAN A D, MITCHELL S K, KOOIJ T L, et al. Circular synthetic aperture sonar design[C]//Proceedings of Europe Oceans 2005. Brest, France, 2005: 1038-1045.
(  0) 0)
|
| [19] |
FERGUSON B G, WYBER R J. Application of acoustic reflection tomography to sonar imaging[J]. The journal of the acoustical society of America, 2005, 117(5): 2915-2928. DOI:10.1121/1.1848071 (  0) 0)
|
| [20] |
FERGUSON B G, WYBER R J. Generalized Framework for Real Aperture, Synthetic aperture, and Tomographic Sonar Imaging[J]. IEEE journal of oceanic engineering, 2009, 34(3): 225-238. DOI:10.1109/JOE.2009.2017801 (  0) 0)
|
| [21] |
FAN Wei, KONG Hui, ZHANG Xuebo. Simulation of circular synthetic aperture sonar imaging using TriKirch scattering model and experimental validation[C]//OCEANS 2017. Aberdeen, UK, 2017: 1-5.
(  0) 0)
|
| [22] |
BRYANT M L, GOSTIN L L, SOUMEKH M. 3-D E-CSAR imaging of a T-72 tank and synthesis of its SAR reconstructions[J]. IEEE transactions on aerospace and electronic systems, 2003, 39(1): 211-227. DOI:10.1109/TAES.2003.1188905 (  0) 0)
|
| [23] |
MARSTON T M, KENNEDY J L. Volumetric acoustic imaging via circular multipass aperture synthesis[J]. IEEE journal of oceanic engineering, 2016, 41(4): 852-867. DOI:10.1109/JOE.2015.2502664 (  0) 0)
|
| [24] |
BLOMBERG A E A, AUSTENG A, HANSEN R E, et al. Improving Sonar performance in shallow water using adaptive beamforming[J]. IEEE journal of oceanic engineering, 2013, 38(2): 297-307. DOI:10.1109/JOE.2012.2226643 (  0) 0)
|
| [25] |
SOUMEKH M. Synthetic aperture radar signal processing with MATLAB algorithms[M]. New York: John Wiley & Sons, 1999: 327-352.
(  0) 0)
|
| [26] |
明婧, 张晓玲, 蒲羚, 等. 一种新型圆迹阵列三维SAR系统的点扩散函数分析与地面实验结果[J]. 雷达学报, 2018, 7(6): 770-776. MING Jing, ZHANG Xiaoling, PU Ling, et al. PSF analysis and ground test results of a novel circular array 3-D SAR system[J]. Journal of radars, 2018, 7(6): 770-776. (  0) 0)
|
| [27] |
AXELSSON S R J. Beam characteristics of three-dimensional SAR in curved or random paths[J]. IEEE transactions on geoscience and remote sensing, 2004, 42(10): 2324-2334. DOI:10.1109/TGRS.2004.834802 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


