为了描述水下声源并研究其辐射的声场，经常使用全向点辐射器模型，称其为单极子模型。但实际上声源在一定程度上都具有指向性，即声源在介质中产生的声压幅度和相位与观测点的位置有关。在同一水平面内，沿船一周测得的辐射噪声分布曲线，明显是不均匀的，船艏和船艉方向上要小一些，前者是因为船体对螺旋桨噪声的屏蔽，后者则因为尾流的屏蔽所造成^[1]。因此，采用单极子模型难以对声场特性准确描述。近年来，研究者提出了一些辐射噪声模型和声场计算方法。Бреховских等^[2]利用简正波展开研究了不同波导和不同边界条件下单极子辐射器的声场。Хауга等^[3]研究了平行分层波导中有限尺寸的指向性声源的简正波理论。Кулакова等^[4-6]的工作中研究了含有指向性和无指向性声源的波导中各种局部情况下利用简正波展开的特点。被积函数在积分区域内不仅有极点还有分支点，在近场除了考虑简正波离散谱外，还必须考虑旁侧波形式的连续谱^[7-8]。Кузнецов等^[9-10]对水下指向性声源声场特性进行了持续的研究，对指向性声源声场特性的数学物理问题进行了细致阐述。孟春霞^[11]研究了在船舶的艏部、舯后部和艉部，用不同权系数的多极子来描述船舶的水下辐射噪声场，并利用渔政船水下辐射噪声数据对多极子模型的有效性进行了验证。罗建^[12]把舰船作为具有主机、辅机和螺旋桨3个辐射噪声亮点的体积目标，研究了其辐射噪声的空间指向性的重构方法。

本文推导出多极子声源声场势函数，并针对能够远距离传输的低频段，深入探讨波导中不同阶次多极子声特性的衰减规律。

1 多极子声场势函数的数学表示

令有限尺寸并且具有任意形状的单频声源位于均匀无限空间中。在声源的内部选择任意一点O，这点是半径为r₀的球面S₀的中心，使得声源完全处于球面内，如图 1所示。

建立坐标中心与O点重合的球坐标系，单频声源在球面上某点产生的声压P由函数$ \tilde P$确定：

$ \tilde P({r_0},\theta ,\varphi ,t) = {\rm{i}}\omega {\rho _0}\tilde \psi ({r_0},\theta ,\varphi ){{\rm{e}}^{ - {\rm{i}}\omega t}} $

(1)

式中：(r₀, θ, φ)是观察点坐标；ω是振动频率；ρ₀是介质的密度；$\tilde \psi $是声场速度势函数。声压场的速度势函数$\tilde \psi ({r_0}, \theta , \varphi ) $存在二阶导数。在Ω区域内，得到满足齐次亥姆霍兹方程的函数：

$ \Delta \psi (M) + {k^2}\psi (M) = 0,M \in \varOmega $

(2)

在边界上具有确定的值：

$ \psi (M) = \tilde \psi (M),M \in {S_0} $

(3)

式中：Δ是拉普拉斯算子；k=ω/c是波数；c是介质的声速；M是研究的区域Ω或它的边界S₀上的点。在无穷远处所求的势函数ψ满足索莫菲尔德条件。

在利用指向性点状多极子辐射器模型时，省略时间因子${{\rm{e}}^{ - {\rm{i}}\mathit{\omega t}}} $，无界均匀空间中声场势函数为：

$ \psi (R,\theta ,\varphi ) = \sum\limits_{n = 0}^L {\sum\limits_{m = - n}^n {{C_{nm}}} } {\rm{h}}_n^{(1)}(kR){{\rm{P}}_n}^{\left| m \right|}\cos \theta {{\rm{e}}^{{\rm{i}}m\varphi }} $

(4)

式中：R、θ、φ球坐标系中的声压观察点; L是模型的多极子阶数；C_nm是系数，它的值不取决于球面半径r₀；h_n⁽¹⁾是n阶第1类球汉克尔函数；${\rm{P}}_n^{\left| m \right|} $是连带勒让德多项式。

式(4)是与有限尺寸的实际声源等效的指向性点状辐射器的声场势函数。在包含原始声源的任意球面以外，这种点状辐射器的声场与有限尺寸的原始声源的声场处处吻合。模型辐射器的方向特性完全由系数C_nm确定，C_nm为复数，－n≤m≤n，该参数的物理意义是构成展开式的初级球面多极子的力矩。对于式(4)来说，利用特殊函数的积分表达式，可以得到多极子声源声场的积分表达式为平面波之和的展开形式：

$ \psi (R,\theta ,\varphi ) = \frac{{\rm{i}}}{k}\sum\limits_{n = 0}^L {\sum\limits_{m = - n}^n {{D_{nm}}} } \int\limits_{ - \infty }^\infty {{\rm{H}}_m^{(1)}} (r\xi ){{\rm{e}}^{b|z|}}{\rm{P}}_n^{|m|}(b/{\rm{i}}k)\frac{{\xi {\rm{d}}\xi }}{b} $

(5)

式中$ {D_{nm}} = \frac{1}{2}{C_{nm}}{{\rm{e}}^{{\rm{i \mathsf{ π} }}\left( {m - n} \right)/2}};{\rm{H}}_m^{(1)}$是m阶第1类柱汉克尔函数；$r = R{\rm{sin}}\;\theta $是声源与接收器之间的水平距离；$ b = {\rm{i}}\sqrt {{k^2} - {\xi ^2}} $ 。

当L=0时，这个表达式实际上是无指向性单极子辐射器的势函数；当L=2时，相当于研究到四极子，其中单极子有1种形式，偶极子有3种形式，四极子有5种形式，这时，指向性点状辐射器是包含18个未知参数的模型。在声学正问题中，在研究各个多极子非相干分量的特性时，为简便起见假设它们的多极子矩等于1，即C_nm=1。求解声学逆问题，实际上就是根据实测的辐射声压值，对等效源模型中的各个多极子系数C_nm进行求解。

1.1 多极子势函数的简正波近似

考虑海底和海面的声学边界条件，经过推导，可得到Pekeris波导中多极子声源 声场势函数的简正波近似形式的表达式：

$ \psi (R,\theta ,\varphi ) = \frac{{4{\rm{ \mathsf{ π} }} }}{{kh}}\sum\limits_{l = 0}^\infty {\sum\limits_{n = 0}^L {\sum\limits_{m = - n}^n {{A_{nml}}} } } {\rm{H}}_m^{(1)}({\xi _l}r){{\rm{e}}^{{\rm{i}}m\varphi }} $

(6)

其中：$ {A_{nml}} = \frac{{{\mu _{nm}}{D_{nm}}{x_l}{\rm{sin}}\;{\alpha _{l0}}{\rm{sin}}\;{\alpha _l}{\rm{P}}_n^{\left| m \right|}({x_l}/kh)}}{{{\rm{si}}{{\rm{n}}^2}{x_l}{\rm{tan}}\;{x_l}/{{\tilde m}^2} + {\rm{sin}}\;{x_l}{\rm{cos}}\;{x_l} - {x_l}}}$是简正波激发系数${\mu _{nm}} = {\rm{exp}}({\rm{i \mathsf{ π} }}(1 - {\chi _{nm}})/4);{\chi _{nm}} = {\left( { - 1} \right)^{n + |m|}} $；x_l是Pekeris波导离散方程的根，${\alpha _{l0}} = \frac{{{\rm{ }}\pi }}{4}(1 - {\chi _{nm}}) + {x_l}\frac{{{z_0}}}{h};{\alpha _l} = {x_l}\frac{z}{h}$；ξ_l是水平波数；h为波导的厚度；z₀是声源的深度；z是接收器的深度，利用离散方程的近似解${x_l} \approx l{\rm{ \mathsf{ π} }}h/H $和简正波的水平波数$ {\xi _l} \approx k{\rm{cos}}({\rm{ \mathsf{ π} }}l/kH) + {\rm{i}}\delta {l^2}$，其中l为简正波的序号$ \delta = 2\beta {\rm{ }}{\pi ^2}n_0^2\tilde m/{(kH{v_0})^3}$，$H = h + \tilde m/(k{v_0}) $表示Pekeris波导的有效厚度，$ {v^2} = 1 - {n^2}, \tilde n = {n_0}(1 + {\rm{i}}\beta )$，$ {n_0} = {c_0}/{c_1}$为海水与海底声速的比值，β≥0为无量纲的海底吸收系数$ \tilde m = {\rho _1}/{\rho _0}$表示海底与海水密度的比值，c₀为水中声速，利用汉克尔函数的近似表达式：

$ {\rm{H}}_m^1(u) \approx \sqrt {2/{\rm{ \mathsf{ π} }} u} \exp ({\rm{i}}u + {\rm{i}}m{\rm{ \mathsf{ π} }} /2 - {\rm{i}}{\rm{ \mathsf{ π} }} /4) $

(7)

声场势函数可以表示成非相干分量和相干分量之和的形式，非相干分量确定声场的平均声级，相干分量确定声场在平均声级附近的振荡。多极子声场势函数幅度平方非相干分量的表达式为：

$ \begin{array}{*{20}{l}} {|{{\bar \psi }^2}| = \frac{{8{\rm{ \mathsf{ π} }} }}{{{{(kh)}^2}kr}} \times \sum\limits_{n = 0}^L {\sum\limits_{m = - n}^n {\sum\limits_{l = 1}^N ( } } |{C_{nm}}|\sin {\alpha _{l0}}\sin {\alpha _l} \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{P}}_n^{|m|}({x_l}/kh){)^2}\exp ( - \delta r{l^2})} \end{array} $

(8)

式中：$ N = {\rm{int}}(kh{v_0}/{\rm{ \mathsf{ π} }} + 1/2)$是在观测的波导中声源激发的简正波数量。为了简化分析，给出下列形式的表达式${\left| {\bar \psi } \right|^2} = \sum\limits_{n = 0}^L {\sum\limits_{m = - n}^n {{{\left| {{{\bar \psi }_{nm}}} \right|}^2}} } $，则有：

$ \begin{array}{*{20}{c}} {{{\left| {{{\bar \psi }_{nm}}} \right|}^2} = \frac{{8{\rm{ \mathsf{ π} }} \left| {{C_{nm}}} \right|}}{{{{(kh)}^2}kr}} \times \sum\limits_{l = 1}^N {\left( {\sin {\alpha _{l0}}\sin {\alpha _l}{\rm{P}}_n^{|m|} \cdot } \right.} }\\ {{{\left. {\left( {{x_l}/kh} \right)} \right)}^2}\exp \left( { - \delta r{l^2}} \right)} \end{array} $

(9)

式(9)是单个选取的多极子声场势函数的幅度平方的非相干分量。

近场$\delta r \ll 1 $时，所有号数为l的简正波，${\rm{exp}}( - \delta r{l^2}) \approx 1 $，在中等距离$ {\rm{exp}}( - \delta r{l^2})$不为1；在远距离δr>1时，声场中的指数项迅速衰减。利用不同的近似条件可以得到不同区域声场的近似表达式，针对实际需求，能够方便地对不同区域的声传播规律进行估计。

1.2 多极子势函数的围线积分表示

围线积分方法直接进行数值积分，能给出声场的精确解。利用围线积分的方法将式(1)表示为：

$ \begin{array}{l} \psi (R,\theta ,\varphi ) = {\psi _H}(R,\theta ,\varphi ) - {\psi _F}(R,\theta ,\varphi ) + \sum\limits_{n = 0}^L {\sum\limits_{m = - n}^n {{C_{nm}} \cdot } } \\ {{\rm{e}}^{\frac{{{\rm{i}}(m - n)}}{2}}}\int\limits_0^{{\rm{ \mathsf{ π} }}/2 - {\rm{i}}\infty } {{J_m}} (kR\sin \beta ){\rm{P}}_n^{|m|}(\cos \beta )F(\beta ){\rm{d}}\beta \end{array} $

(10)

式中：$ {\psi _H}\left( {R, \theta , \varphi } \right)$为无界空间中的声场势函数，由式(1)确定；$ {\psi _F}\left( {R, \theta , \varphi } \right)$为波导中来自绝对软上边界的声波对总声场的贡献。

$ \begin{array}{*{20}{l}} {{\psi _F}(R,\theta ,\varphi ) = }\\ {\sum\limits_{n = 0}^L {\sum\limits_{m = - n}^n {{\chi _{nm}}} } {C_{nm}}{{\rm{e}}^{{\rm{i}}m\varphi }}{\rm{h}}_n^{(1)}(k{R^\prime }){\rm{P}}_n^{|m|}(\cos {\theta ^\prime })} \end{array} $

(11)

式中：${R^\prime } = \sqrt {{R^2} + 4R{z_0}{\rm{cos}}\;\theta + 4z_0^2} $，由波导中虚源图像可知，宗量${\rm{cos}}\;{\theta ^\prime } = (R{\rm{cos}}\;\theta + 2{z_0})/{R^\prime };$ $ F\left( \beta \right) = 4{\rm{ }}V\left( \beta \right){{\rm{e}}^{2bh}}/(1 + V\left( \beta \right){{\rm{e}}^{2bh}}){\rm{sh}}b(z + {z_0}){f_1}, F\left( \beta \right)$为包含反射系数的项，当n+|m|为偶数时$ {f_1} = {\rm{sh}}(b{z_0})$；当n+|m|为奇数时${f_1} = {\rm{ch}}(b{z_0}) $。

2 声场近似解适用条件仿真

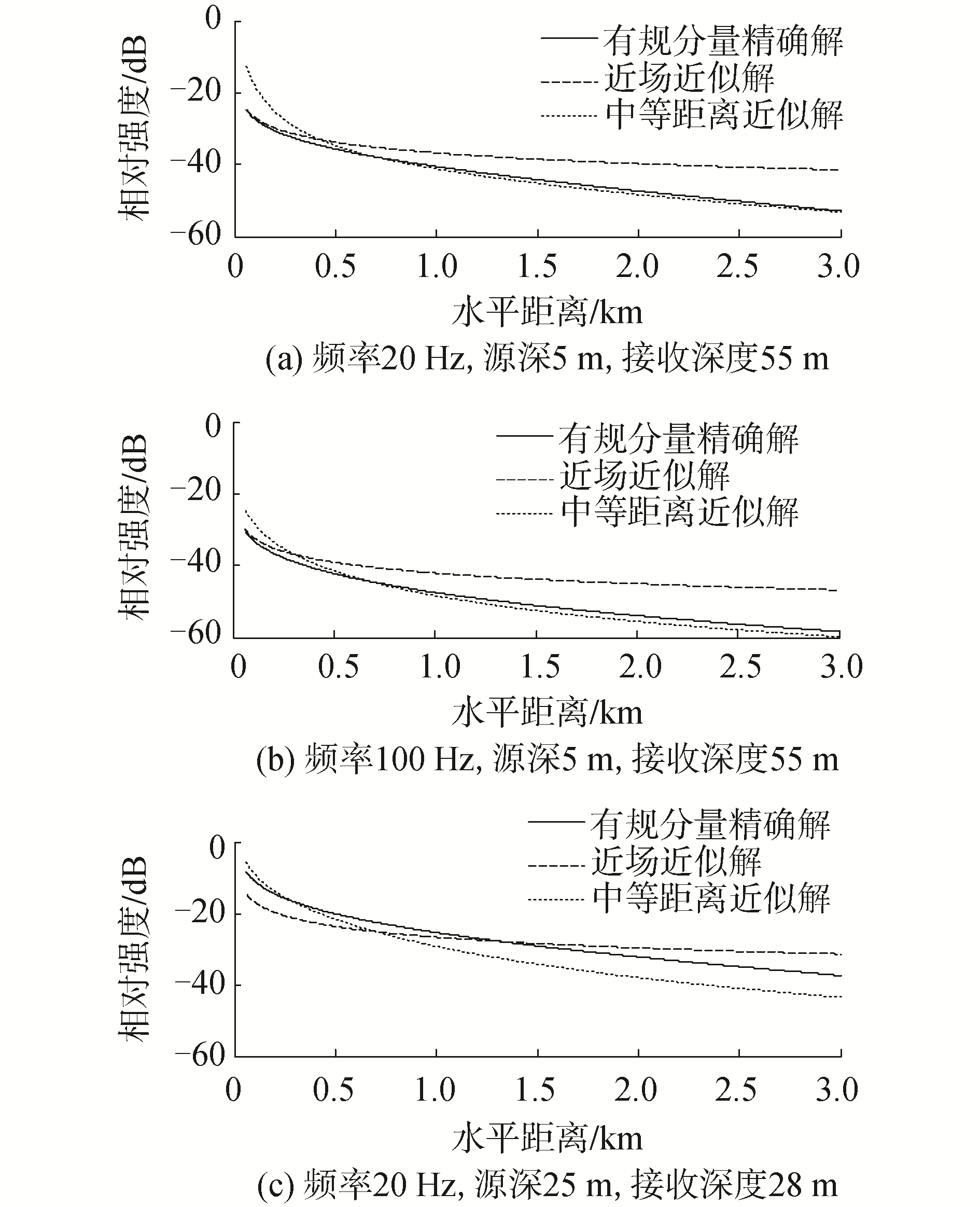
浅海波导通常可以看作是水平均匀波导，能够用Pekeris波导来描述。仿真计算条件如下：海水深度60 m，水中声速1 500 m/s，水体下方为液态半无限空间，海底声速1 800 m/s，海底密度2 700 kg/m³, 海底无量纲的吸收系数为0.1。图 2为对声源位于海面和接收器位于海底的情况，以及声源和接收器都位于海水中部的情况进行仿真。

图 2中，纵坐标表示$20{\rm{lg}}(\left| {{{\overline \psi }_{00}}\left( r \right)} \right|/{\overline \psi _{00}}({r_0})) $，从图 2可以看出：对于水深60 m的情况来说，势函数近场近似解适用的距离不超过750 m，声源频率越高，适用距离的范围越小。改变声源和接收器深度，如声源和接收器都位于近似水体中间深度时，势函数幅度增大，曲线抬高，近场近似解适用距离减小。

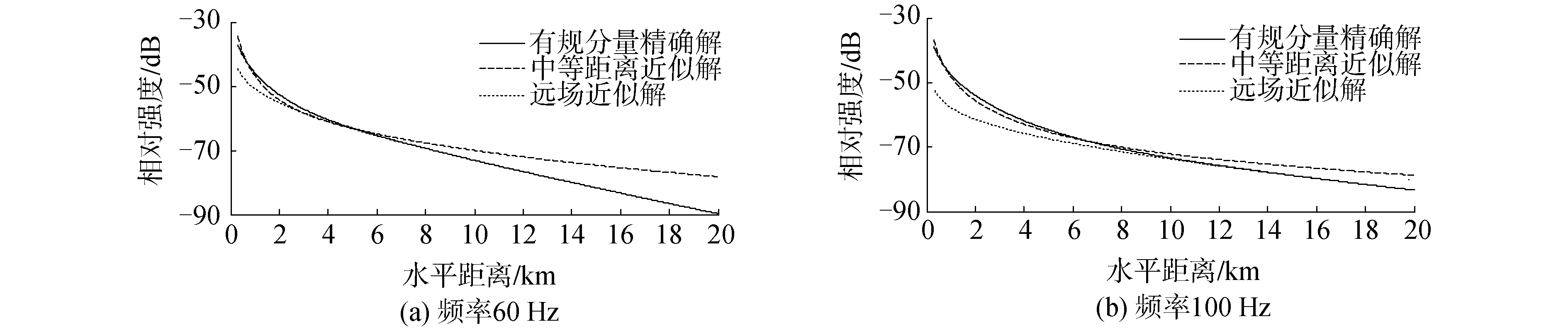
波导的声学参数不变，设声源深度5 m、接收器深度55 m，图 3给出单极子声源频率60 Hz和100 Hz时势函数非相干分量与中等距离近似解及远场近似解的对比。

从图 3可以看出：对于水深60 m的情况来说，势函数远场近似解适用距离大于5 km，而且频率越高，适用距离越大。可见中等距离近似解的适用条件很宽泛。

3 多极子衰减规律仿真 3.1 中远距离声场势函数衰减规律仿真

在中远距离上，与简正波相比旁侧波对声场的贡献可以忽略，声场表现为简正波叠加的形式。在式(1)中，n=1, m=－1为y偶极子；n=2，m=－2为有2个水平轴的yy四极子；n=1，m=1为有1个水平轴1个垂直轴的yz四极子，n=1，m=0为z偶极子；n=2，m=0为有2个垂直轴的zz四极子。其他类型的多极子在声信号观测角度上势函数为0。

在研究声学逆问题时，利用声场势函数与声压之间的关系：

$ p = - {\rho _0}\frac{{\partial \psi }}{{\partial t}} = {\rm{i}}\omega {\rho _0}\psi $

(12)

并进一步与实测的声压值进行比对。

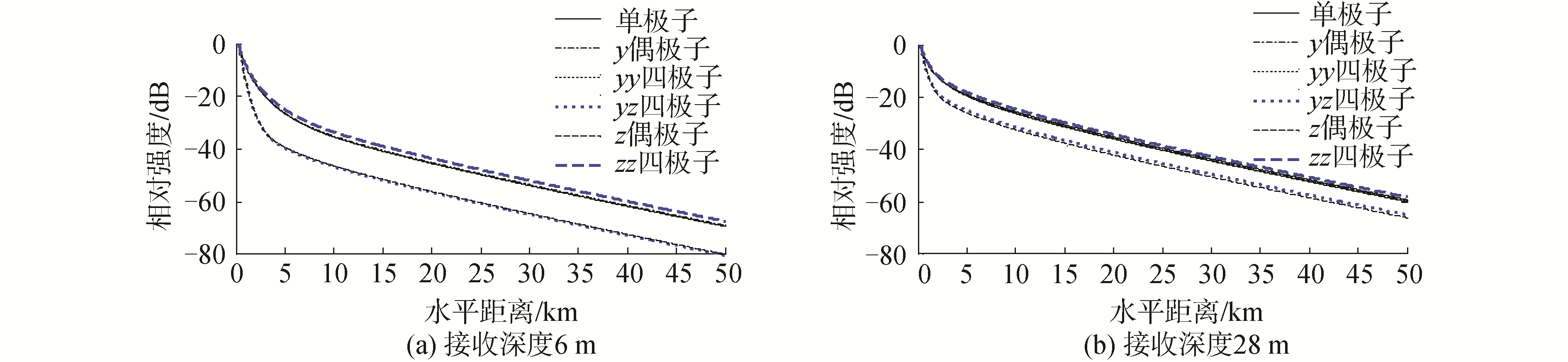
波导的声学参数不变，图 4(a)为声源深度5 m，接收器深度6 m频率100 Hz不同类型多极子声场势函数非相干分量衰减曲线。图 4(b)为声源深度5 m，接收器深度28 m，频率100 Hz时不同类型多极子势函数非相干分量衰减曲线。为了便于比较，将图中曲线沿着垂直轴进行了平移。

从图 4可以看出：在中远距离上，根据声场势函数衰减规律，多极子可以分为2组，第1组包括：单极子、水平偶极子、具有2个水平轴的四极子、具有2个垂直轴的四极子; 第2组包括：垂直偶极子与具有一个水平轴一个垂直轴的四极子。这样，在远场分析实际声源的指向性时，可以忽略垂直面上的指向性，并且远场条件下，实际水下声场的多极子模型可以简化。

3.2 近场衰减规律仿真

在声源特性精细研究和观测的近场，接收器与声源之间的距离在300~400 m到1~2 km。在这个距离上旁侧波对声场的作用不能忽视，此时简正波形式的声场近似解无法给出声场在空间上的细致结构，因此采用围线积分方法研究多极子的声场分布。声压接收方向为沿着x轴方向，此时y轴水平偶极子的声场为0，因此只研究x轴水平偶极子的声场衰减规律。

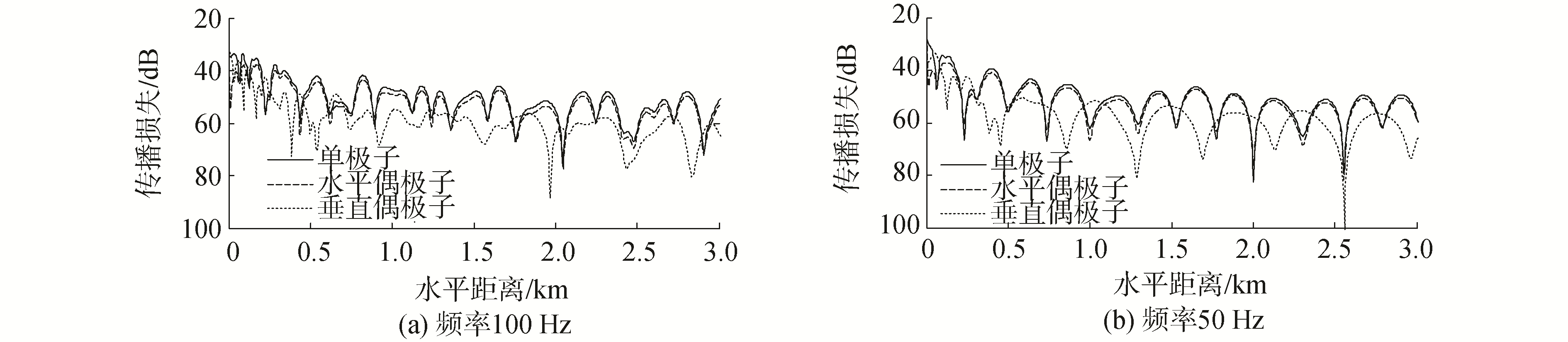
声源深度36 m，接收器深度98 m，波导厚度为100 m。海底声学参数与前述相同。图 5分别给出了声源频率100 Hz和50 Hz时单极子与水平偶极子和垂直偶极子声场特性的对比结果。

在图 5中，声信号观测方向为水平偶极子极大值方向，因此声场看不出方位的变化。从图 5可以看出：相同波导条件下，在近距离上，水平偶极子与单极子的衰减规律相同，垂直偶极子比单极子和水平偶极子都衰减的快，传播损失较大。对于同一种多极子来说，频率越高，声信号衰减速度越快。

水平偶极子声源是最常见的多极子声源，设波导的声学参数不变，水平偶极子声源沿着直线运动，研究声源与接收器之间正横距离分别为50、100和200 m时，不同频率水平偶极子声源声场衰减规律，仿真结果如图 6所示。

从图 6可以看出：水平偶极子的声场具有指向性，但是在海洋信道滤波器的作用下水平偶极子声场的8字型指向性发生了畸变。在水平距离较小的情况下，接收器与声源之间的正横距离对声场的指向性非常明显；随着水平距离的增大，接收器与声源之间正横距离对声场的影响减弱。相同频率不同接收深度的声场也存在差异，这是由于在波导中到达不同接收位置的声线能量不同。

4 结论

1) 在不同的传播距离上，可以采用不同的近似公式来描述多极子势函数非相干分量的衰减规律。

2) 在中远距离上，按照势函数衰减规律分类，多极子可以分为2类：单极子、水平偶极子、具有2个水平轴的四极子和具有2个垂直轴的四极子；垂直偶极子及具有1个水平轴和1个垂直轴的四极子。

3) 在近场水平方向上，单极子与水平偶极子传播规律相同，垂直偶极子比单极子衰减速度快。海洋波导中随着传播距离的增大，多极子的指向性减弱。

4) 本文的研究工作为描述水下声源的声场提供了精确的理论模型，利用该模型，能够有效地预报海洋波导中低频水下声源辐射声信号在不同区域的传输规律，具有重要的实用价值。