主动声呐工作在浅海中时,海底散射强度大,散射机理复杂,与目标回波极为类似的海底混响中的杂波干扰更是导致虚警概率升高,限制主动声呐探测性能的重要干扰。明确浅海海底杂波的形成机理是区分真假目标,抑制杂波干扰的重要理论基础。海底杂波已经成为浅海混响研究的热点问题,许多学者探讨了不同的浅海环境中杂波干扰的形成机制。浅海杂波散射源有以下几类:海底界面以及海底浅层底质中的离散的强散射体[1](如海底山、海底沉船)、非连续的海底底质结构[2]、水体中鱼群[3]、和特殊的海洋动力学现象[4](如非线性孤子内波)等。文献[5]通过仿真计算首次给出了孤子内波会导致类似目标回波的强杂波干扰。并从射线理论角度,分析了声波入射到孤子内波后产生强折射,从而以更大的入射角与海底发生散射,散射强度增大,因此孤子内波可能会产生10 dB左右的杂波干扰。文献[4]发现杂波干扰过后的平均混响强度会比产生杂波前的平均混响强度略高,而其机理并未给出。另外,浅海信道中可能产生杂波的机制繁杂,如何确定某个杂波是水体起伏引起的也是亟需解决的问题。浅海信道具有典型的时变空变特性,移动的非线性孤子内波引起的水体起伏对混响强度的影响是本文的重点关注内容。本文为了进一步揭示内波引起的水体起伏对浅海混响强度的影响,以非线性孤子内波为例,将孤子内波导致的声模态间的能量耦合嵌入到简正波混响理论,提出了一种考虑水体耦合效应的耦合简正波混响模型。
1 非线性内波引起的混响与杂波理论本文选取浅海Pekeris波导,平均海深为70 m,上层海水的平均声速为1 500 m/s,液态半无限海底声速为1 700 m/s。水体和液态海底密度比为1.6,海底声吸收系数为0.4 dB/λ,海水中的声速梯度是黄海夏季常见的典型孤子内波环境,在15~25 m处有强的温跃层,具体的海水中声速分布如图 1所示。声源接收器的配置形式为收发合置,布放深度为35 m,仿真所用信号为中心频率3 kHz的窄带信号。

|
Download:
|
| 图 1 内波结构和声速梯度 Fig. 1 The soliton wave structure and the sound speed profile | |
为了仿真需要,假设孤子内波的波包沿着声传播路径移动,且移动中孤子波的波形保持不变。孤子内波的描述采用经典的KdV方程解的形式:
| $ \eta = 15{\rm{sec}}{{\rm{h}}^2}\left( {\frac{{r - {r_x}}}{\mathit\Delta }} \right) $ | (1) |
式中:rx为内波的中心位置;Δ为内波的宽度。内波引起的强杂波主要是受声波遇到内波的第1个波包影响[4]。虽KdV方程解并非最优,但本文的主要目的是阐述在声波的传播路径上遇到孤子波包后,引起的声场各模态简的能量耦合现象。采用KdV方程解的形式刻画内波结构能够满足本文的需求。
1.1 引入内波耦合矩阵的简正波混响修正模型对于浅海收发合置的混响,包含传播和海底散射2个过程,为了刻画声波在传播过程中遇到强孤子内波导致的声场各模态间的能量耦合过程,本文在经典简正波混响模型基础上,借助耦合简正波理论刻画水体不均匀导致的模态耦合,表征孤子内波引起的简正波间的能量交换,揭示内波引起的强杂波的物理机制。
浅海混响的理论模型众多[6-11],利用经典的简正波混响理论,海底混响的声压ps(r, zr)为:
| $ {p_s}(r,{z_r}) = \sum\limits_m {{b_m}} (r,{z_b}){\phi _m}({z_r}){\rm{H}}_0^{(1)}({k_m}r) $ | (2) |
| $ {b_m}(r,{z_b}) = {\phi _m}(r,{z_b})\sum\limits_n {{T_{nm}}} \frac{{{A_n}\left( {r,\omega } \right)}}{{\sqrt {{k_n}r} }}{\phi _n}({z_b}) $ | (3) |
式中:zs、zr为收发合置配置形式下的声源和接收器深度。φ(zr)和φ(r, zb)分别为接收器深度和海底散射区域的简正波幅度。海底散射过程用经典的Lambert散射函数表征,则描述海底混响声压的式(2)中的Tmn为Lambert散射函数1/2次方,即
| $ \mathit{\boldsymbol{A}}\left( 0 \right) = \frac{{{\rm{iexp}}\left( { - {\rm{i}}\frac{{\rm{ \mathit{ π} }}}{4}} \right)}}{{\sqrt {8{\rm{ \mathit{ π} }}} }}{[{\phi _1}({z_s}){\rm{ }}{\phi _2}({z_s}){\rm{ }} \cdots {\rm{ }}{\phi _M}({z_s})]^{\rm{H}}} $ | (3) |
当声波的前向传播路径中遭遇孤子内波引起的水文跃变,在入射到海底发生海底散射前会产生强烈的模态间耦合效应。假设内波波包存在的水平距离范围是r1 < r < r2,当声波入射到内波后,简正波间的能量耦合使得声场幅值A(r)将随水平距离产生变化[5]:
| $ \mathit{\boldsymbol{A}}\left( r \right) = \mathit{\boldsymbol{E}}(r, {r_2})\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}({r_2}, {r_1})\mathit{\boldsymbol{E}}({r_1}, 0)A\left( 0 \right) $ | (4) |
式中:Λ(r2, r1)表征在距离r1 < r < r2上的内波引起模态间能量传递的耦合矩阵。
| $ \begin{array}{*{20}{l}} {{p_s}\left( {r,{z_s},{z_r}} \right) = \sum\limits_m {{\varphi _m}} \left( {0,{z_r}} \right){\varphi _m}\left( {{r_b},{z_b}} \right){\rm{H}}_0^{(1)}\left( {{k_m}r} \right) \cdot }\\ {\sum\limits_n {{T_{mn}}} \frac{{\mathit{\boldsymbol{E}}(r,{r_2})\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}({r_2},{r_1})\mathit{\boldsymbol{E}}({r_1},0)\mathit{\boldsymbol{A}}\left( 0 \right)}}{{\sqrt {{k_n}r} }}{\phi _n}({z_b})} \end{array} $ | (5) |
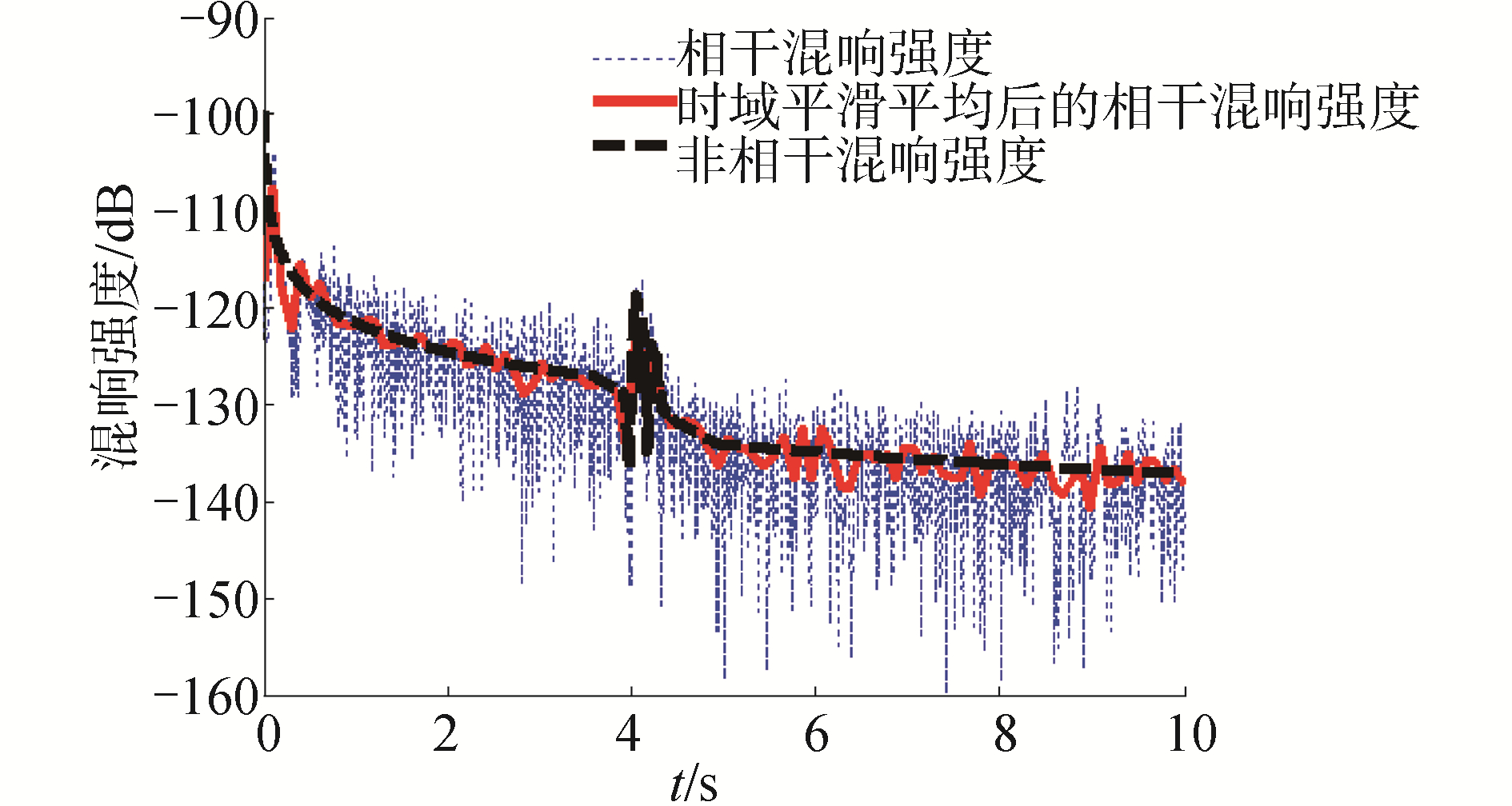
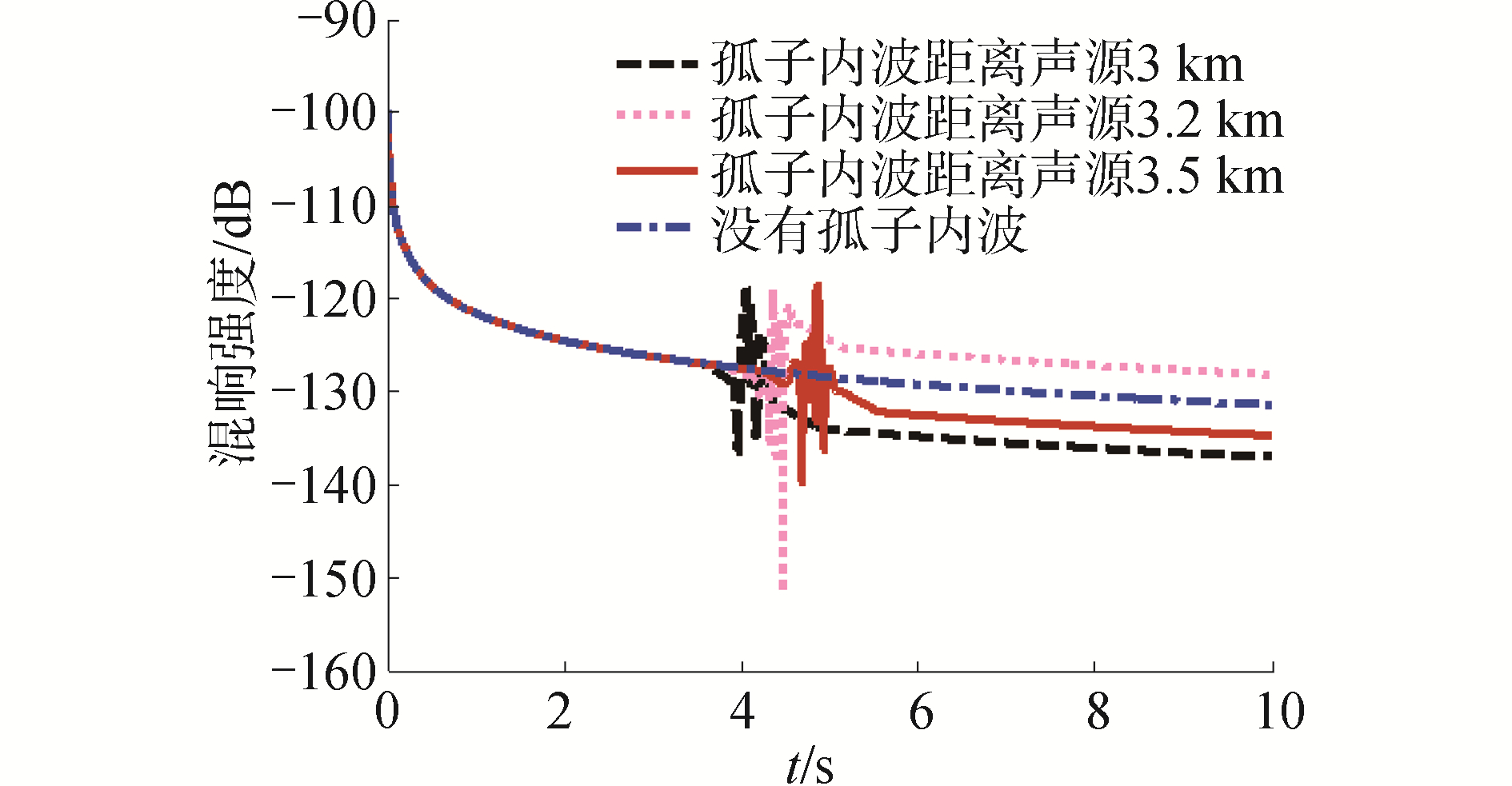
依据式(5)得到混响强度仿真结果如图 2所示。为了进一步验证基于水体耦合矩阵的简正波混响理论的准确性,探讨有无内波以及内波移动后引起的混响杂波和混响强度的畸变规律。本文分别仿真了无内波情况、有内波且内波移动到距声源不同水平位置的情况。结果如图 3所示。通过对比得出,当没有孤子内波引起的水文跃变时,海底混响强度正常衰减,不会产生海底杂波;而当孤子内波出现在不同位置时,与内波位置相对应的时间上会产生杂波。需注意:1)在仿真时假设内波在移动过程中保持波形不变,即内波导致的模态间的耦合能量交换的强度不变,因此产生海底杂波的声强也是一致的,出现的时间随着内波位置发生了相对应的变化;2)海底散射后的混响声场与前向传播声场相比为小量,故只需考虑前向传播过程中水体起伏引起的能量耦合过程,因此式(5)中只在前向传播的n阶模态水平因子中考虑了耦合矩阵影响,以此提高算法的运算效率。
|
Download:
|
| 图 2 距声源3 km处的孤子内波引起的海底杂波 Fig. 2 Simulated RL when the distance between a source and the NIW is 3 km | |
|
Download:
|
| 图 3 无孤子内波和有孤子内波其位于不同位置时的非相干混响强度 Fig. 3 Simulated incoherent RL when there is no soliton wave and when the soliton wave is existing at different position | |
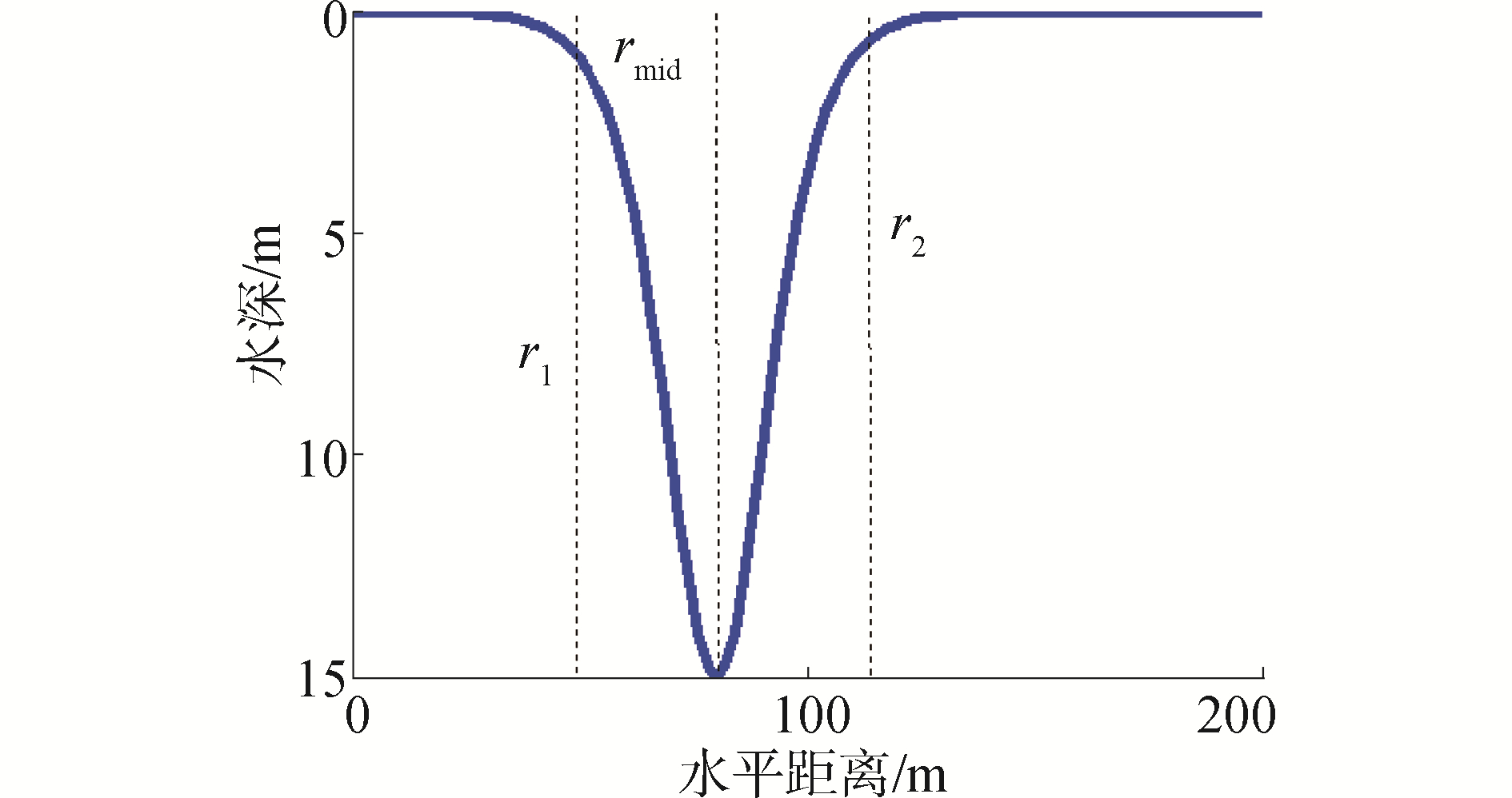
在声波传播路径上的非线性孤子内波会导致各模态间的能量耦合,耦合的强度由内波的垂向幅度η和水平宽度决定。为了表征该耦合过程,将孤子内波结构分为3段,如图 4中的r1、rmid、r2所示。其中r1为声波刚刚进入内波,rmid为声波进入到内波的中心位置,r2为声波基本经过了一个完整的内波波包。图 5则分别给出了与r1、rmid、r2位置处相对应的耦合矩阵,各仿真结果中只展示了前100阶模态间的能量转换。可以发现:1)声波刚进入内波的r1位置时,水文环境开始发生变化,相应的图 5(a)中可以看出能量开始向高号简正波转移,高号简正波能量出现增大的现象;2)当前向传播的声场进入到rmid位置时,即孤子内波波包的中心位置,此处的水文跃变最为剧烈,大量的能量转移到高号简正波(如图 6所示);3)等传播到r2位置,即将完全经过内波波包时,除了部分高号简正波的能量消逝掉,和入射内波前相比,仍出现了大量的高阶模态(如图 6所示)。在前向传播路径上有孤子内波出现时,水体变化引起强烈的耦合效应,大量能量转移到高号模态,海底混响的入射角增大,海底散射强度增加,从而产生类目标的强杂波。仿真结果表明,当内波中心位置在距离声源3 km处时,考虑了水体耦合效应后的相干混响强度和非相干混响强度的衰减规律均在混响时间为4 s处(对应于空间上的3 km处的内波位置)产生了类似目标回波的强杂波。
|
Download:
|
| 图 4 孤子内波的结构示意 Fig. 4 Geometry of the nonlinear internal wave structure | |

|
Download:
|
| 图 5 利用耦合矩阵表示处各模态间的能量耦合 Fig. 5 The energy redistributed at position by couple matrix | |

|
Download:
|
| 图 6 移动内波引起的混响强度震荡 Fig. 6 The fluctuation of RL induced by moving internal wave | |
用更精准的非线性方程刻画出更精细的内波结构,有助于得到更为准确的耦合矩阵和海底混响杂波结构,但本文重点关注的是利用模态耦合矩阵分析混响杂波的物理机制和过程。图 5的结果表明,本文提出的基于内波耦合矩阵的简正波混响模型可以详细的表征孤子内波引起的海底混响杂波的耦合机理和物理过程。
2 移动内波引起的混响强度起伏在图 3的算例中,由不同位置的孤子内波引起的不同时刻的混响杂波到达接收点之前,海底混响强度是一致的。而类目标的杂波出现后的平均混响强度是明显不同的。与没有内波的情况相比,不同位置的内波会引起杂波后的混响强度增加或减小。以第8 s的混响时间为例,即对应于距离声源6 km位置处的海底散射产生的混响。此时声波已经过内波的波包结构。图 3中所示内波距离声源3.2 km时,海底杂波结构后面的混响强度要高于没有内波时的情况。当内波距离声源3 km和3.5 km时,海底杂波结构到达接收点后的混响强度均不同程度的弱于没有内波时的混响强度。
为了进一步解释海底杂波结构后面的混响强度异常现象,进行了如下环境的仿真:假设声源在35 m深度处,每隔10 s发射一次中心频率为3 kHz脉宽为0.1 s的CW窄带脉冲。设2 000 s内发射200个信号,同时有图 1所示的孤子内波在2 000 s内以0.5 m/s的速度远离声源,即孤子内波开始出现的位置由距声源3 km移动至4 km。运动过程中,设孤子波的波包结构不变。则依据前文理论,类目标的海底杂波结构出现的初始时刻也从第4 s连续变化至5.33 s,如图 7所示。
|
Download:
|
| 图 7 随着移动内波第8 s时刻的混响强度震荡 Fig. 7 The fluctuation of RL at the moment of the 8 s | |
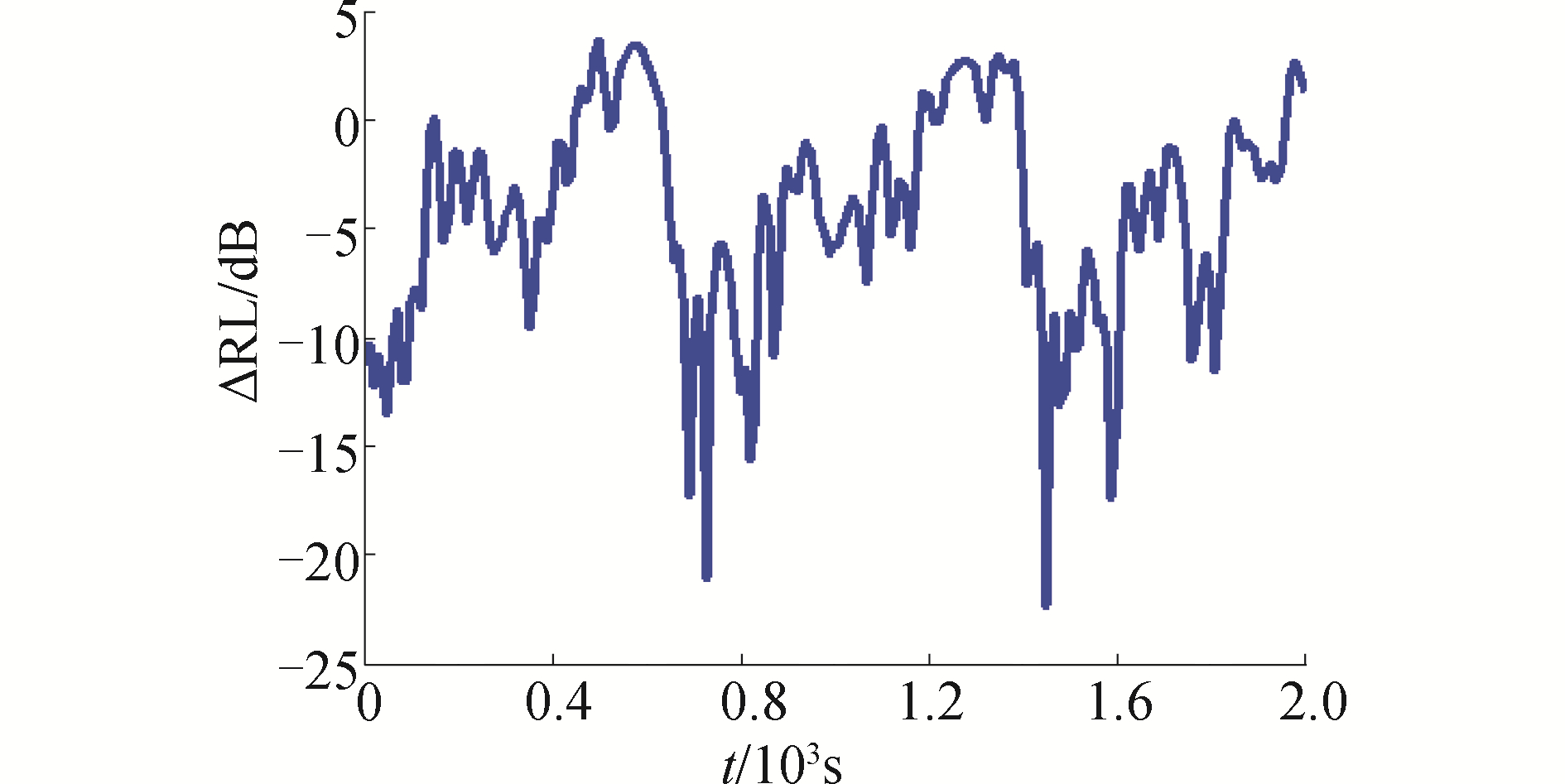
将图 7中第8 s固定为观测时间点,有移动内波时该观测时间点的非相干混响强度定义为RLs,无孤子内波时,定义该观测时间点的非相干混响强度为RL0,在内波移动的2 000 s内该观测时间点的混响强度变化量可以表述为:ΔRL=RLs-RL0。图 8为ΔRL的变化规律。
|
Download:
|
| 图 8 混响强度随时间起伏的频域谱 Fig. 8 Spectrum of the RL fluctuation shown | |
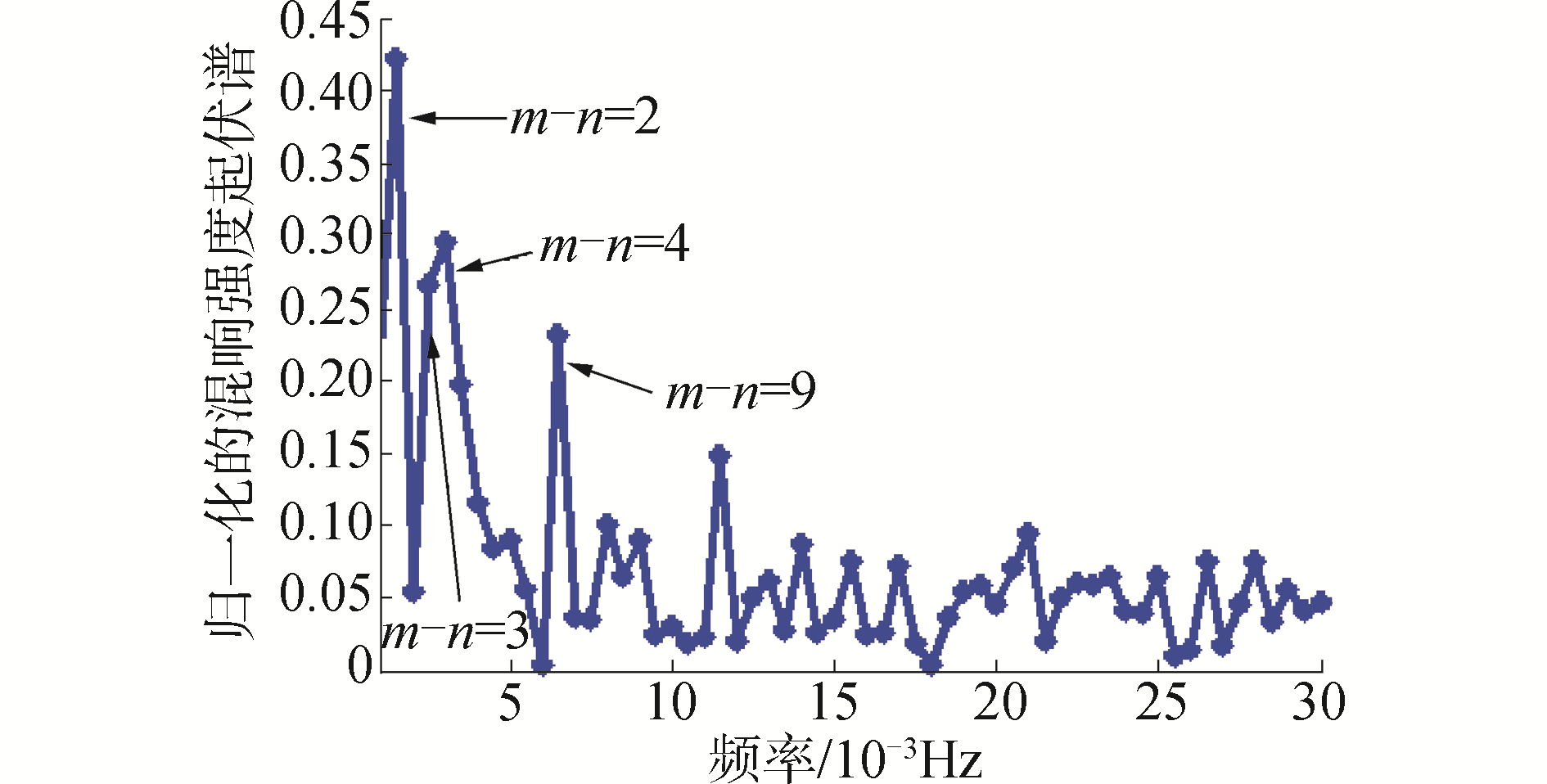
结合图 6和图 7可以发现,移动内波引起混响杂波结构到达之后的某固定时间点的混响强度起伏ΔPL呈现出一种不规则的准周期震荡结构。为了探究其物理机制,对该结构进行了傅里叶谱分析。图 8给出了其归一化的频谱结构,当前向传播的声波经过移动内波后,固定观测时间点的混响强度震荡ΔPL的主要频率分量与某对简正波间的干涉跨度有关,其关系式为fmn=vkmn/2π。其中,kmn=km-kn为第m阶和第n阶简正波的水平波数差,v表示内波的移动速度。
本文的仿真算例中,孤子波以0.5 m/s的速度运动,该移动内波导致了海底杂波到达后的混响强度产生不规则的准周期震荡,其震荡结构的前4阶频率分量,分别由波数差为2、3、4、9的简正波之间的干涉周期决定,如图 8所示。内波移动造成前向传播的声场与内波发生耦合的位置随时间变化,由此导致了不同模态之间相位差发生变化。孤子内波作为一个移动的散射体,引起的模态间的干涉也存在相应的起伏震荡,而起伏震荡的周期则和某对模态之间的干涉跨度相关,对应的时间周期等于干涉跨度除以内波速度。
移动孤子内波导致的混响强度在某个确定时刻产生不规则震荡现象,即观测的混响起伏是杂波结构到达后同一个混响时刻的非相干混响强度的起伏,这个物理过程相当于固定的水平位置观测内波移动带来的相位起伏。类似的现象在孤子内波环境下的声传播起伏研究中已有论述,相关理论结果和物理机制得到了SWARM实验数据的验证[12]。而内波的移动可以导致混响杂波和杂波后混响强度的异常震荡现象尚未有文献报道。而文献[4]中所提的杂波结构后混响强度增大,只是本文所述震荡现象中某个时刻的特例。杂波结构后紧跟的混响强度增加还是减小,取决于前向传播的声波与孤子内波发生耦合的位置。利用本文中所述的耦合简正波混响理论可以解释该现象的机理。
3 结论1) 浅海环境中非线性内波引起的模态间的能量耦合效应,是浅海混响杂波的一种形成机制。当声波进入内波至内波波包的中心位置处,能量由低号模态向高号模态转移,产生大量的高阶模态,海底散射强度增大,海底杂波强度也达到峰值。而声波完全穿过内波,高号简正波的能量又向低号转移,只有部分高号简正波得以存活,因此杂波结构也回落至正常的海底混响强度。
2) 移动非线性内波会使得海底杂波结构到达之后的混响强度发生不规则的准周期震荡现象。震荡频率与内波的速度,内波引起某对模态间的干涉跨度有关,具体的关系是为fnm=vkmn/2π。这种杂波后的混响强度震荡现象有望用来区分移动目标(孤子内波、AUV等)和固定目标(沉船、海底山、海底沉积层结构等)产生的杂波。
3) 由非线性内波对声场的耦合效应可知,孤子内波引起的海底混响杂波结构、到达时刻分别和内波的精细结构、位置有关。因此,移动孤子内波导致的混响杂波和混响起伏可以成为获取内波速度、距离的信息载体。
| [1] |
PRIOR M K. A scatterer map for the Malta Plateau[J]. IEEE journal of oceanic engineering, 2005, 30(4): 676-690. DOI:10.1109/JOE.2005.862129 (  0) 0)
|
| [2] |
HOLLAND C W, ELLIS D D. Clutter from non-discrete seabed structures[J]. The journal of the acoustical society of America, 2012, 131(6): 4442-4449. DOI:10.1121/1.4714791 (  0) 0)
|
| [3] |
WEBER T C. Observations of clustering inside oceanic bubble clouds and the effect on short-range acoustic propagation[J]. The journal of the acoustical society of America, 2008, 124(5): 2783-2792. DOI:10.1121/1.2990707 (  0) 0)
|
| [4] |
HENYEY F S, TANG Dajun. Reverberation clutter induced by nonlinear internal waves in shallow water[J]. The journal of the acoustical society of America, 2013, 134(4): EL289-EL293. DOI:10.1121/1.4818937 (  0) 0)
|
| [5] |
YANG T C. Acoustic mode coupling induced by nonlinear internal waves:evaluation of the mode coupling matrices and applications[J]. The journal of the acoustical society of America, 2014, 135(2): 610-625. DOI:10.1121/1.4861253 (  0) 0)
|
| [6] |
ELLIS D D. A shallow-water normal-mode reverberation model[J]. The journal of the acoustical society of America, 1995, 97(5): 2804-2814. DOI:10.1121/1.411910 (  0) 0)
|
| [7] |
GRIGOR'EV V A, KUZ'KIN V M, PETNIKOV B G. Low-frequency bottom reverberation in shallow-water ocean regions[J]. Acoustical physics, 2004, 50(1): 37-45. DOI:10.1134/1.1640723 (  0) 0)
|
| [8] |
GAO Bo, YANG Shie', PIAO Shengchun, et al. Method of coupled mode for long-range bottom reverberation[J]. Science China physics, mechanics and astronomy, 2010, 53(12): 2216-2222. DOI:10.1007/s11433-010-4162-3 (  0) 0)
|
| [9] |
TANG Dajun, JACKSON D R. Application of small-roughness perturbation theory to reverberation in range-dependent waveguides[J]. The journal of the acoustical society of America, 2012, 131(6): 4428-4441. DOI:10.1121/1.4707437 (  0) 0)
|
| [10] |
杨士莪. 利用逐次近似法对三维非规则弹性海底条件下声传播特点的分析[J]. 哈尔滨工程大学学报, 2020, 41(2): 161-165. YANG Shie'. Characteristics of sound propagation in sea with 3-dimensional irregular elastic bottom[J]. Journal of Harbin Engineering University, 2020, 41(2): 161-165. (  0) 0)
|
| [11] |
刘冰, 殷敬伟, 朱广平, 等. 基于随机算法的抗混响目标探测方法[J]. 哈尔滨工程大学学报, 2019, 41(2): 277-281. LIU Bing, YIN Jingwei, ZHU Guangping, et al. A target detection method in reverberation environment based on stochastic algorithm[J]. Journal of Harbin Engineering University, 2019, 41(2): 277-281. (  0) 0)
|
| [12] |
DUDA T F, PREISIG J C. A modeling study of acoustic propagation through moving shallow-water solitary wave packets[J]. IEEE journal of oceanic engineering, 1999, 24(1): 16-32. DOI:10.1109/48.740153 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


