2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
海洋中的声速剖面是影响水声装备性能的重要因素之一,决定了海洋中的声传播特性。海洋内波是广泛存在于近海大陆架的一种中尺度海洋现象,在夏季,由于海水沿重力方向的温度分布不均匀,海水中会形成一定的密度分层[1]。内波活动使海水的声速分布产生剧烈变化,严重影响水下声场分布[2-3],进而干扰水下声场预报效能[4],特别是夏季有温跃层时,若声速扰动改变了跃层的斜率,可使声波向下折射到海底进而影响探测作用距离[5],因此声速剖面的实时监测非常重要,为了预先了解区域声场分布,对声速剖面的预报更有实用价值。
海水声速与温度、盐度和静压力有关,随温度、盐度、压力的增加而增加,其中以温度的影响最为显著,同时,温度的变化也是最为显著的,通常可通过现场监测的温度数据和声速经验公式计算得到声速剖面分布。声速剖面具有明显的深度分布,常表示为深度和声速的矩阵数组,涉及参数量较大,即便在浅海环境也给声速剖面的预报带来很多困难,为简化表达,提出了经验正交函数(EOF)的方法[6],基函数确定后,用有限的几阶系数即可重构声速剖面,可以大大降低所需要的参数。Gaelle[7]在对意大利墨西拿海峡区域的内波分布研究中,指出可以利用2个EOF系数散点分布图的统计特性监测内波,利用该特征可以进一步的降低声速剖面预报所需参数,提升预报效率。
目前海温预报主要方式有经验预报方法、统计预报方法[8]和数值预报方法。其中经验预报方法与人的主观因素有很大关系;数值预报运算量极大,在要求预报时效性的基础上对计算环境要求较高,且在初始场构建及物理过程参数化等方面有待完善;统计方法则是利用以往历史数据或在线的实时、准实时数据,通过概率统计的方法计算预报未来海水温度的变化规律。卡尔曼滤波方法是以统计理论为基础的代表性同化方法,现在已逐渐应用到海洋数值模拟和预报中[9],但卡尔曼滤波方法在状态空间建模时仍需要较为准确的状态方程描述海洋变化过程。神经网络具有较好的自学习能力,可跳过复杂的海洋模型,直接从历史及在线数据中挖掘内在联系,尤其近年来海洋预报数据量骤增,积累了大量的潜浮标监测数据,均为神经网络在海洋预报中的应用[10-11]提供了有力支撑。长短时记忆循环神经网络(LSTM)[12]能有效利用时间序列数据中长距离依赖信息的能力,非常适合海洋温度、声速等时间序列的预测[13]。
本文深入挖掘了有无内波情形下时序声速剖面所呈现的不同统计特征,结合LSTM对长时间序列的记忆功能,通过深度学习中神经网络的方法学习历史水文数据的变化规律,对浅海典型水文现象影响下的声速剖面变化进行实时预测。
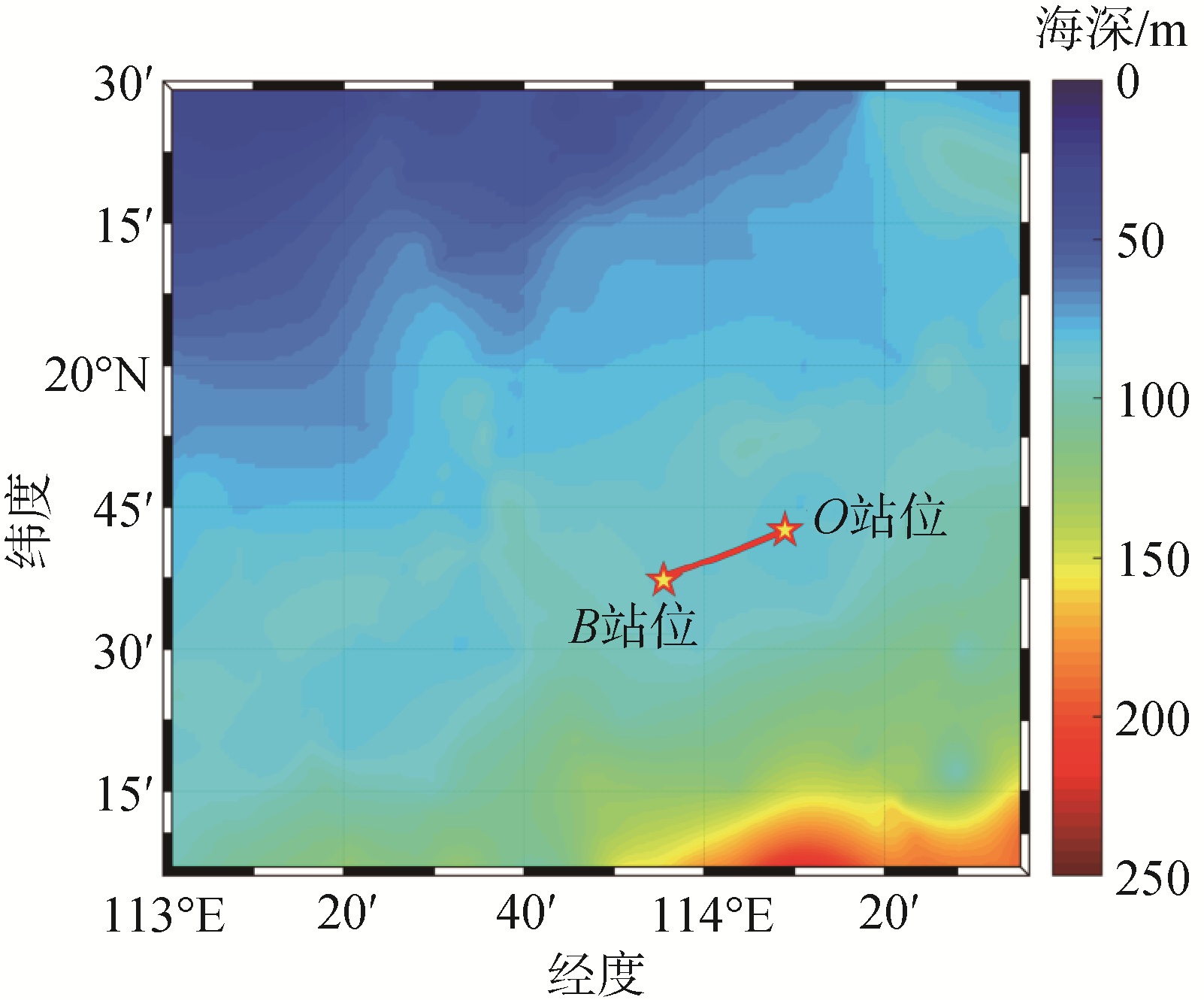
1 浅海内波环境下的声速剖面统计特征分析 1.1 南海试验概况2019年9月,中科院声学所水声环境特性重点实验室在中国南海海域组织了海洋调查试验,试验海区地形如图 1所示,海深约85 m,试验期间在沿等深线方向布放了2套温度链潜标,西侧站位记为B站位,东侧站位记为O站位。
|
Download:
|
| 图 1 南海试验地形 Fig. 1 Bathymetry of the experiment area in South China Sea | |
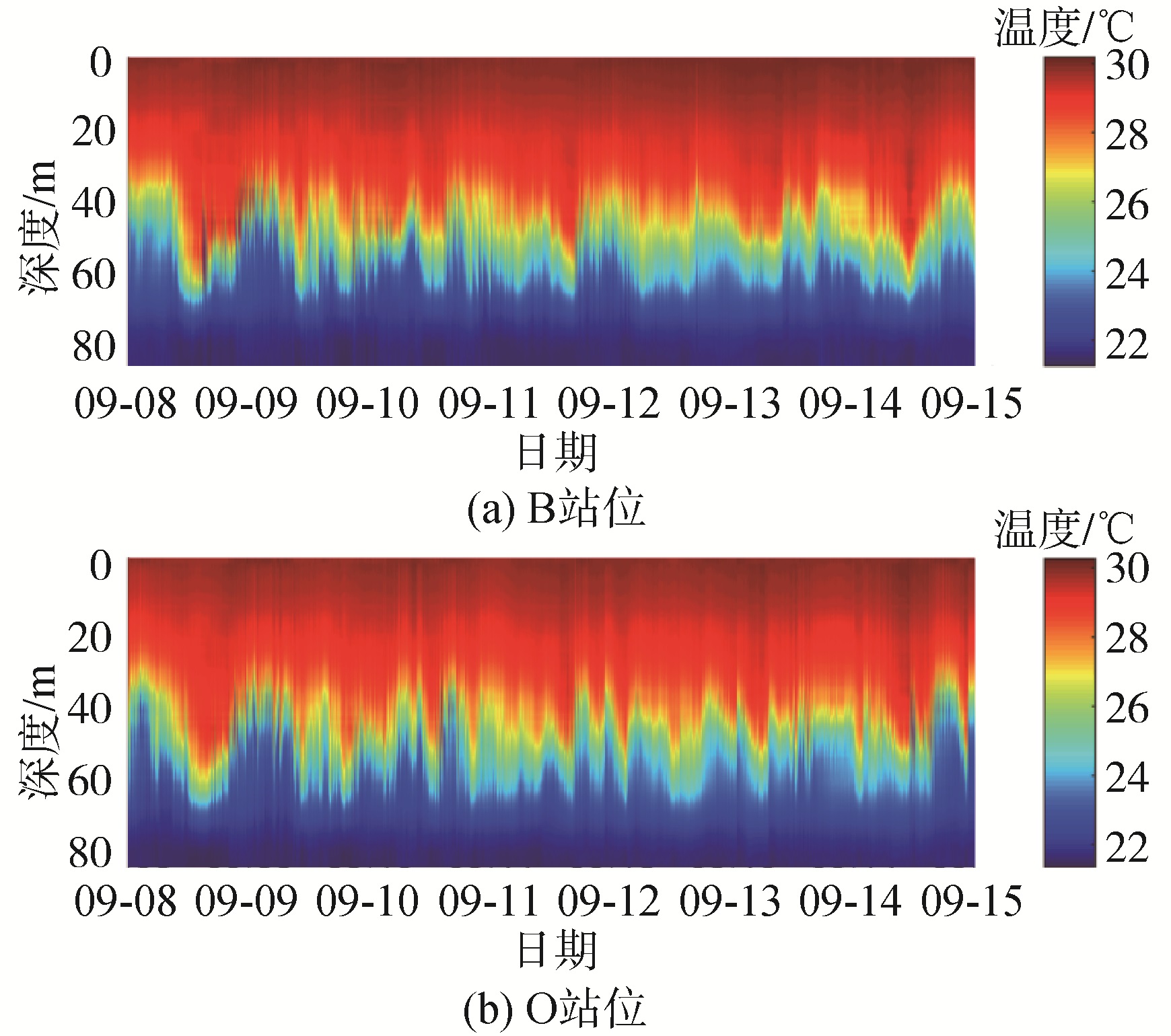
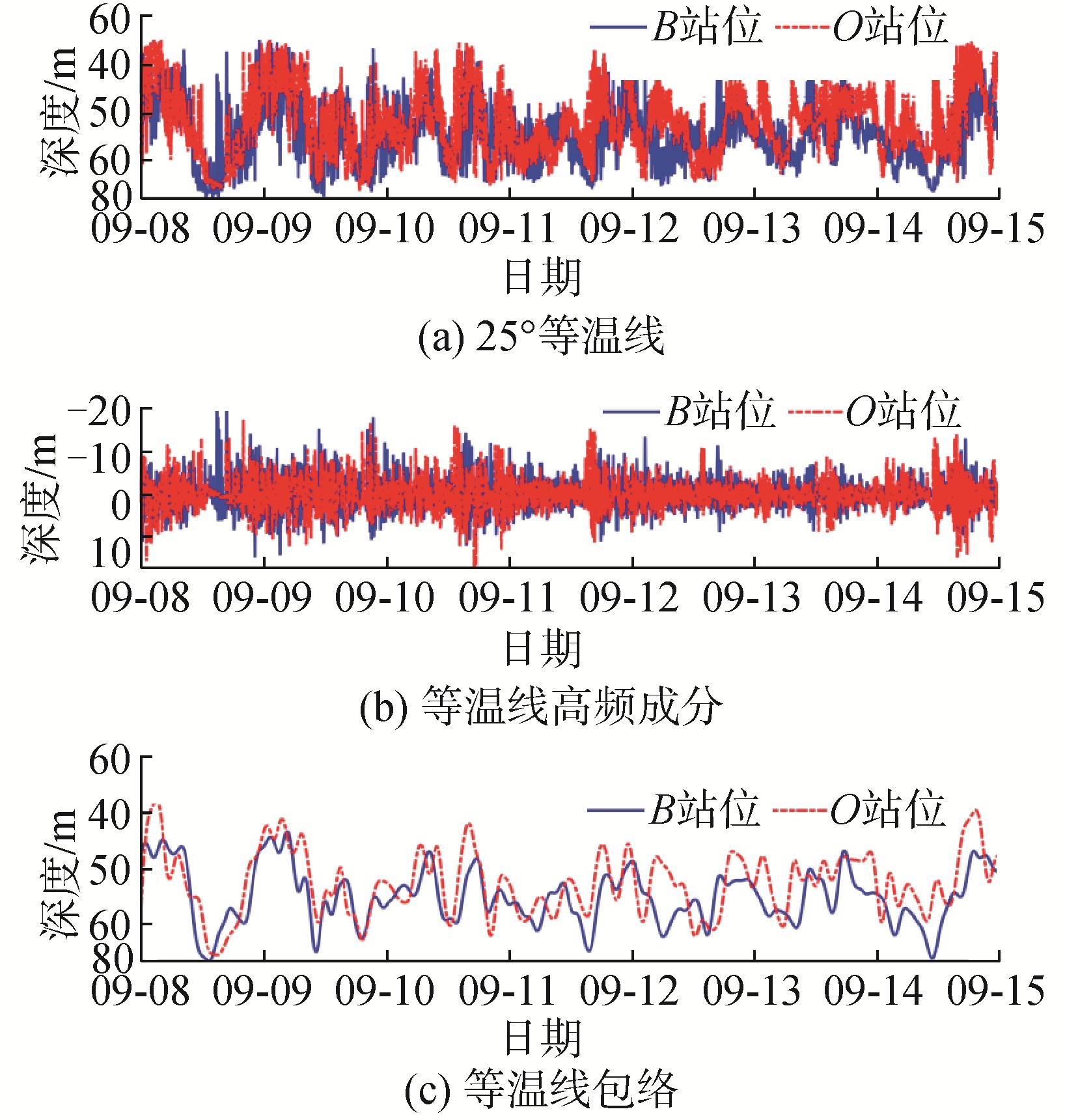
试验从9月8日持续到9月15日,共采集到约171 h的温度数据,如图 2所示,在整个试验周期内可以观测到丰富的内波活动,仅在8、9日2 d可观察到明显的半日潮,之后受到多源内波的影响,2个站位的温度数据均出现无规律起伏,甚至覆盖掉半日潮的大周期。提取2个站位的25 ℃等温线及其包络如图 3所示,从等温线包络线可以观察到,在试验初期2个站位的等温线变化趋势基本一致,之后出现较大差异,2个站位的25°等温线深度相差高达20 m,推测试验期间不仅存在B-O方向的内波,试验后期还在O站位出现了垂直等深线方向传播的内波,由于未观测到更大空间范围的温度变化情况,对于内波的运动方向和速度尚不能确定。
|
Download:
|
| 图 2 9月8日-9月15日连续水文监测数据 Fig. 2 Thermistor string measured temperature from Sep 8th to Sep 15th | |
|
Download:
|
| 图 3 B站位和O站位25 ℃等温线分布 Fig. 3 The 25 ℃ temperature contour of station B and station O | |
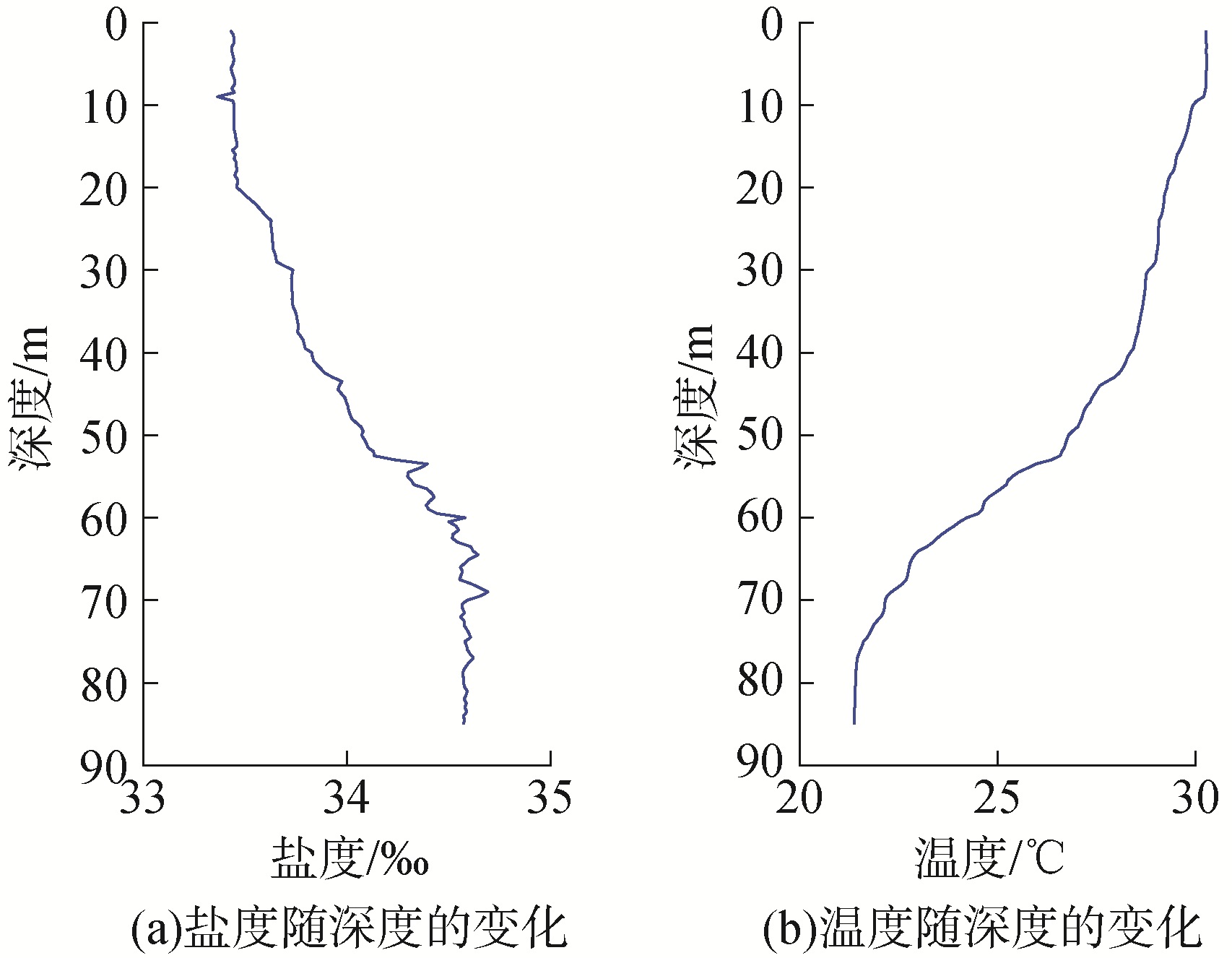
试验中采用CTD测量得到了全海深的温盐深数据,如图 4所示。目前已经建立了许多利用温度、盐度和深度来计算声速的经验公式,为方便,采用Mackenzie[14]给出的9项算法,利用现场CTD测量得到的盐度数据代入经验公式,可将图 2中的温度数据转化为声速数据,二者变化趋势基本一致:
| $ \begin{array}{c} c = 1\;448.96 + 4.591T - 5.304 \times {10^{ - 2}}{T^2} + \\ 2.374 \times {10^{ - 4}}{T^2} + 1.340\left( {S - 35} \right) + 1.630 \times \\ {10^{ - 2}}D + 1.675 \times {10^{ - 7}}{D^2} - 1.025 \times \\ {10^{ - 2}}T\left( {S - 35} \right) - 7.139 \times {10^{ - 13}}T{D^3} \end{array} $ | (1) |
|
Download:
|
| 图 4 CTD测量得到的温度和盐度随深度的变化 Fig. 4 The temperature and salinity data measured by CTD | |
利用EOF方法表示声速剖面可以大大降低声速剖面预报所需要的参数个数,基函数确定后,用有限的几阶系数即可进行重构。
根据一段时间内测量到的N条SSP数据,可通过求平均值的办法得到背景声速剖面:
| $ \bar c(z) = \frac{1}{N}\sum\limits_{i = 1}^N {{c_i}} (z) $ | (2) |
则声速起伏可表示为:
| $ \Delta {c_i}(z) = {c_i}(z) - \bar c(z), i = 1, 2, \cdots , N $ | (3) |
设每条剖面离散到M个深度上,则N个Δc1(z) 可以组成一个M×N的声速起伏矩阵:
| $ \boldsymbol{C} = \left[ {\begin{array}{*{20}{c}} {\Delta {c_1}\left( {{z_1}} \right)}&{\Delta {c_2}\left( {{z_1}} \right)}& \cdots &{\Delta {c_N}\left( {{z_1}} \right)}\\ {\Delta {c_1}\left( {{z_2}} \right)}&{\Delta {c_2}\left( {{z_2}} \right)}& \cdots &{\Delta {c_N}\left( {{z_2}} \right)}\\ \vdots & \vdots & \vdots & \vdots \\ {\Delta {c_1}\left( {{z_M}} \right)}&{\Delta {c_2}\left( {{z_M}} \right)}& \cdots &{\Delta {c_N}\left( {{z_M}} \right)} \end{array}} \right] $ | (4) |
求得C的协方差矩阵:
| $ \boldsymbol{R} = \frac{1}{N}\boldsymbol{C}{\boldsymbol{C}^{\rm{T}}} $ | (5) |
对矩阵R进行特征值分解:
| $ \boldsymbol{RU} = \boldsymbol{U\lambda} $ | (6) |
式中:U=[u1(z) u2(z) … uM(z)]T为特征函数矩阵,λ=diag(λ1,λ2,…,λM) 为特征值向量,即R可以表示为:
| $ \boldsymbol{R} = \sum\limits_{m = 1}^M {{\boldsymbol{\lambda} _m}} {\boldsymbol{u}_m}\boldsymbol{u}_m^{\rm{T}} $ | (7) |
式中:um为要提取的第m阶经验正交函数,将M个特征值λm降序排列,选取前d个特征值对应的特征向量用来表示声速剖面:
| $ c(z) \approx \bar c(z) + \sum\limits_{m = 1}^d {{\alpha _m}} {u_m}(z) $ | (8) |
式中αm为第m阶EOF系数。
通常情况下,在掌握了背景声速剖面数据并提取到EOF基函数后,式(8)就可以较为准确地描述声速剖面。同理,也可以由声速剖面、EOF基函数和背景声速剖面数据计算得到对应的EOF系数。
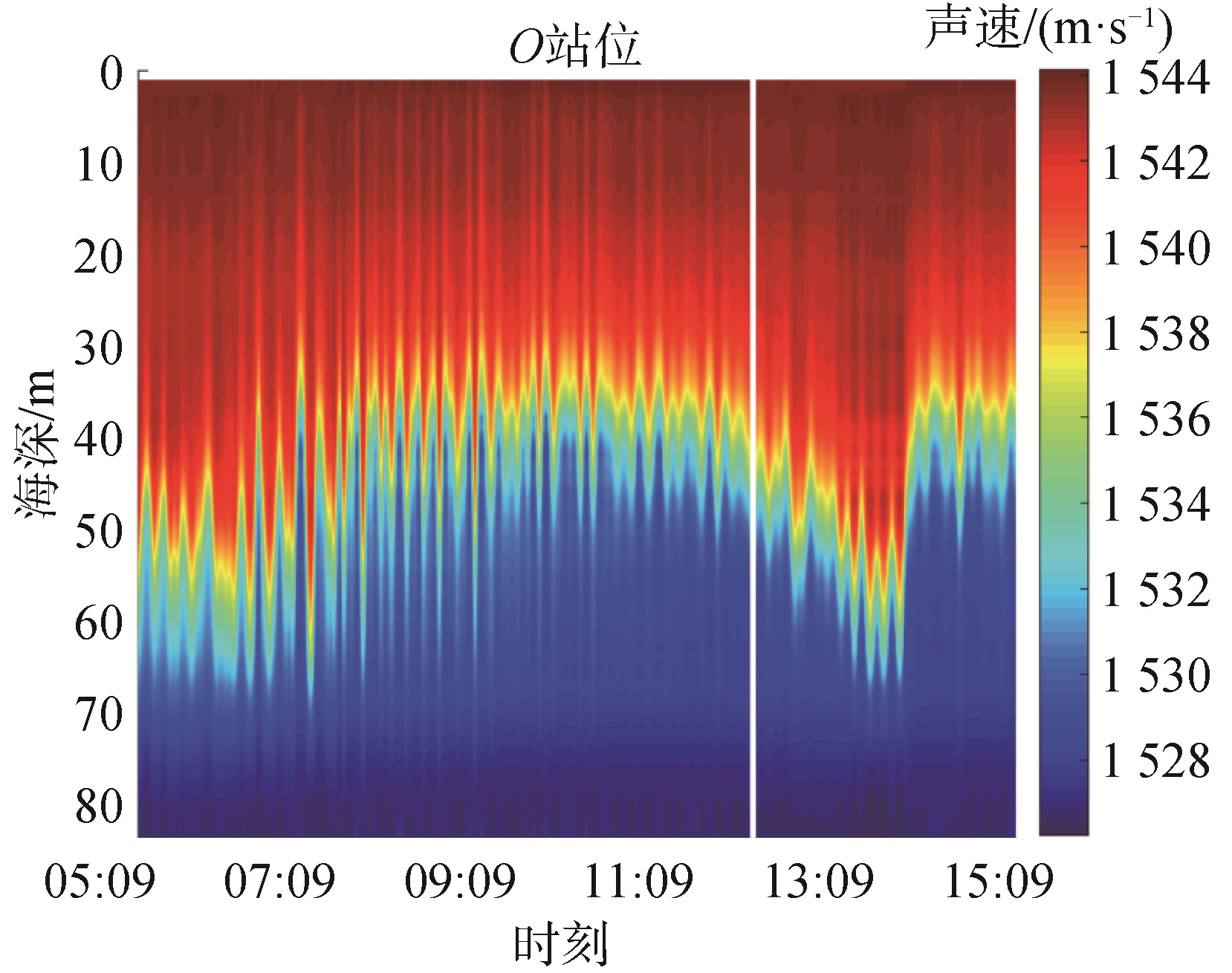
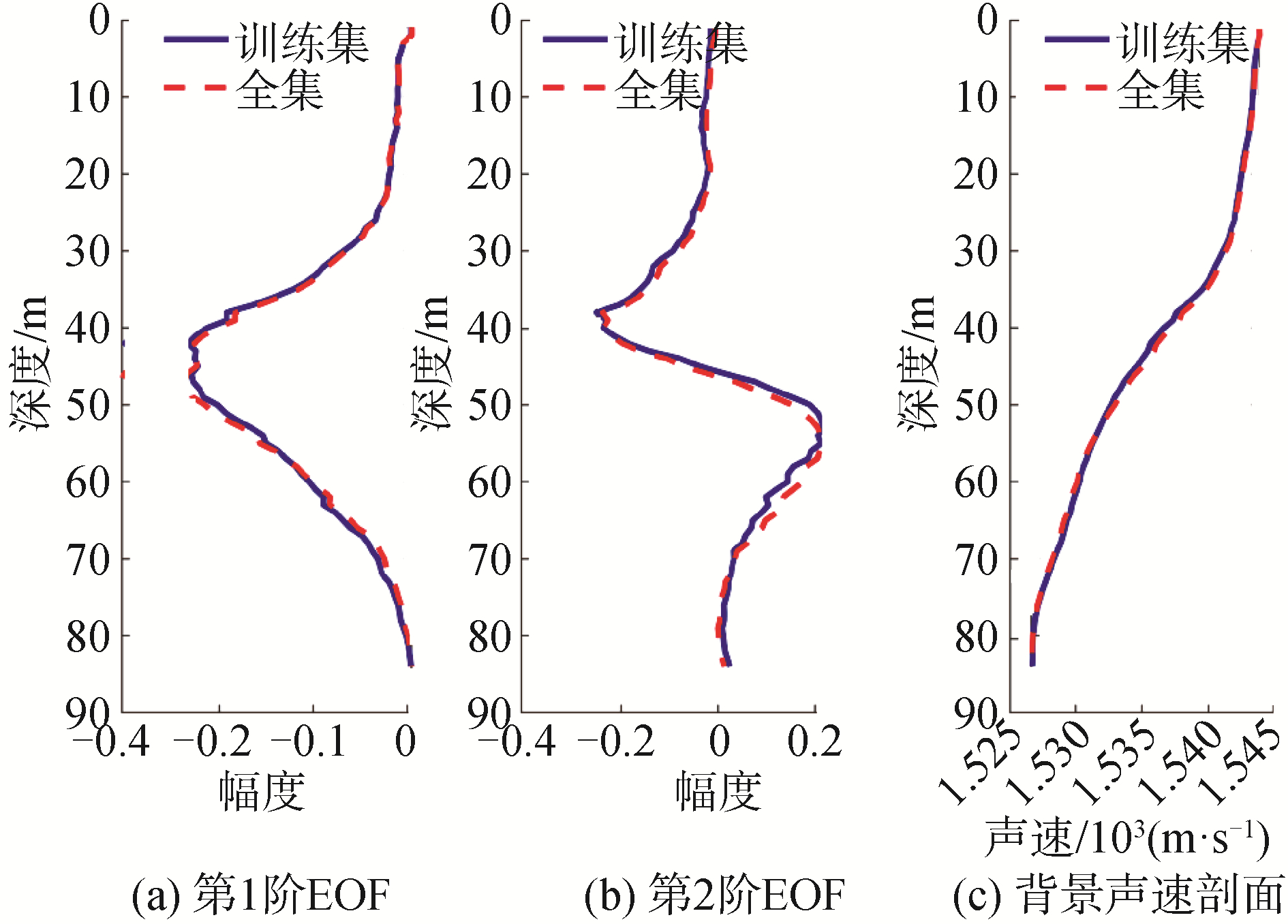
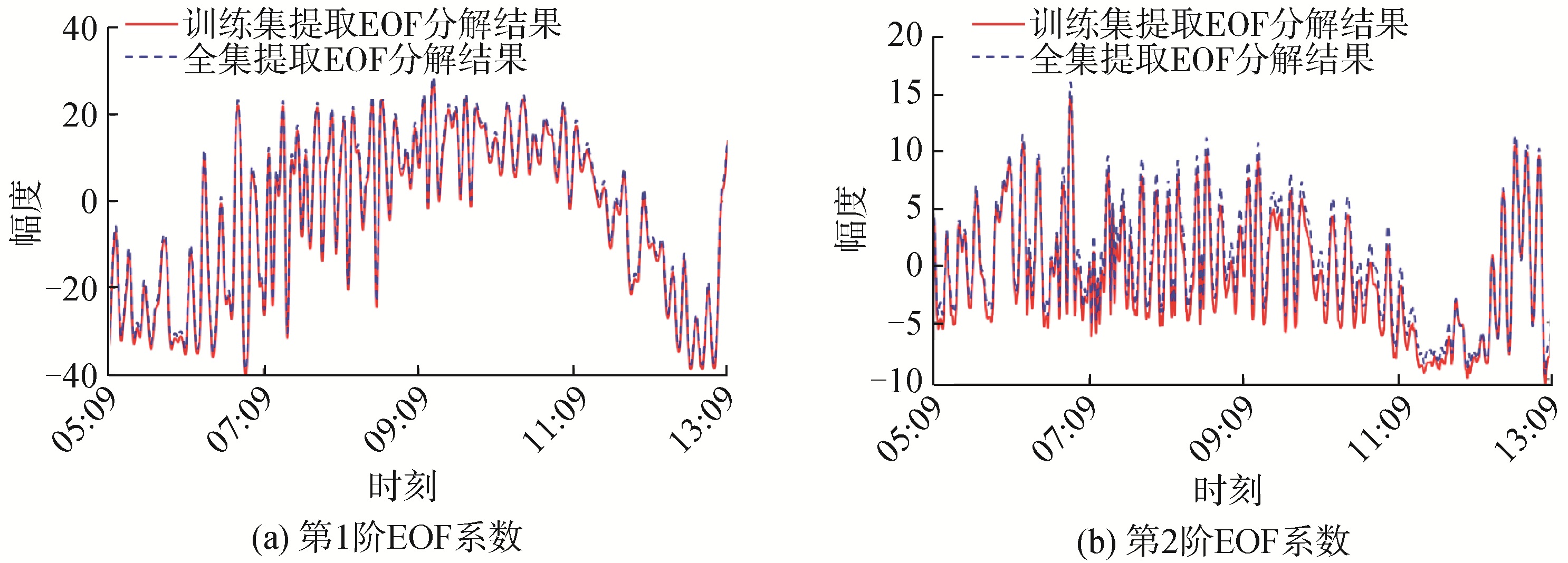
1.3 试验数据的统计特征分析由1.1节的试验数据初步分析可知,在试验最后一段时间监测到了内波活动,因此选取试验最后一天(9月15日)的声速数据进行EOF分析,截取时间段为15日5∶00-15∶00,该时间段的声速起伏变化如图 5所示,其中白色分割线划分出了训练集以及待预测的测试集,整个时间段内的声速剖面集称为全集。图 6为使用图 5中训练集声速数据和全集声速数据得到的前2阶EOF基函数和背景声速剖面,二者形状基本一致。分别利用2个站位分解得到的EOF基函数和背景声速剖面计算得到O站位声速剖面的EOF系数随时间变化如图 7所示,2种方法得到的系数变化趋势基本一致。从O站位剖面中任取一条进行重构,重构剖面与原始剖面吻合较好,说明在全集时间段内,声速剖面基函数未发生较大变化,可使用训练集提取的背景剖面和EOF基函数重构测试集声速剖面而不产生系统偏差。
|
Download:
|
| 图 5 参与统计分析的声速数据 Fig. 5 Sound speed data used for statistical analysis | |
|
Download:
|
| 图 6 分别利用训练集和全集声速数据得到的前两阶EOF基函数和背景声速 Fig. 6 The two first modes and the background sound speed profile extracted from training sets and complete sets respectively | |
|
Download:
|
| 图 7 训练集提取的EOF系数(9月15日) Fig. 7 EOF coefficient extracted from the training set (sep.15) | |
对比图 7中第1阶EOF系数与图 5中的温跃层深度的变化规律,可以发现,二者变化趋势基本一致,在温跃层深度变化较大的时刻,第2阶EOF系数较大,尤其在15日13∶00左右最为明显。Gaelle曾在研究中给出了EOF系数的物理解释[15],第1阶EOF系数α1表示了温跃层的垂直位移,即α1越大则代表温跃层越浅,跃层深度的变化周期也反映在α1的演化趋势中,第2阶EOF系数α2则表示了温度梯度的改变,在温跃层变化剧烈的时刻,α2取值也比较大。由此可推论,前两阶EOF系数之间并非完全独立,二者取值存在某种内在联系,即α2=f(α1)。
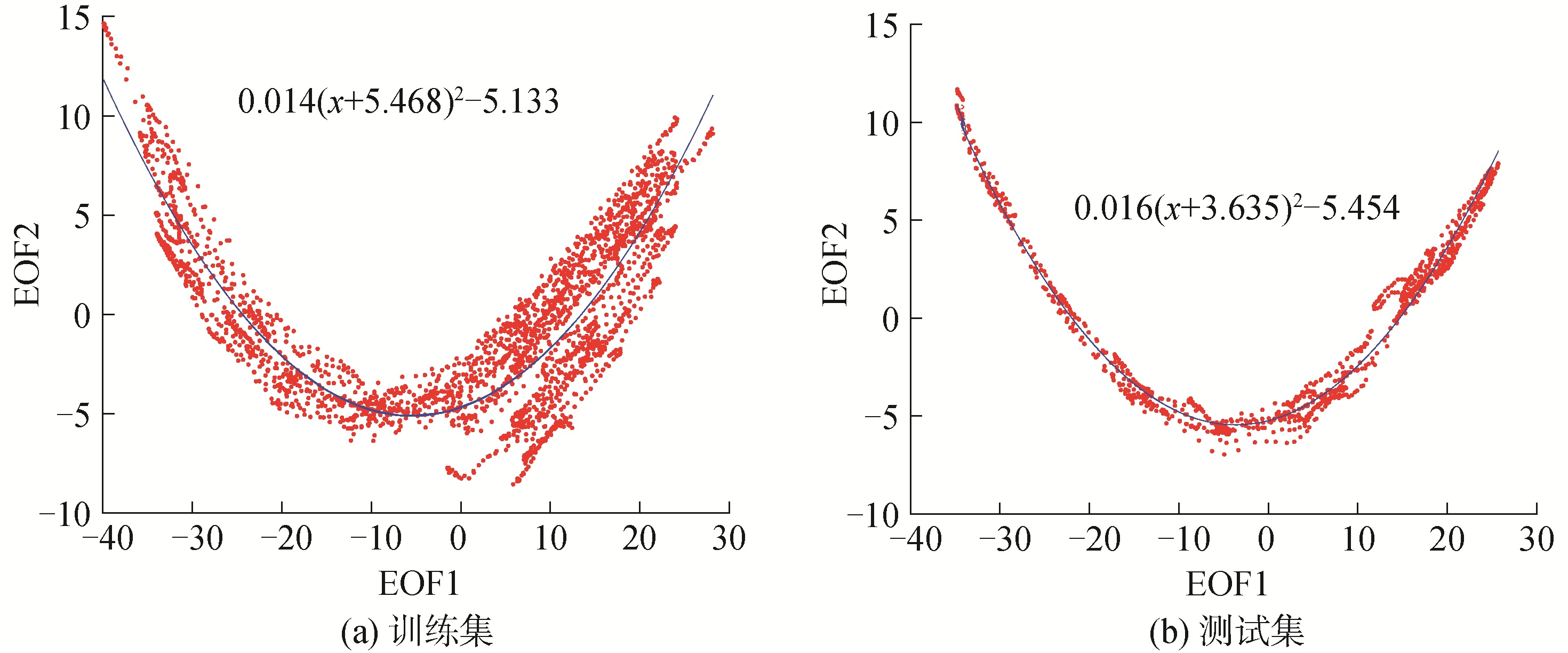
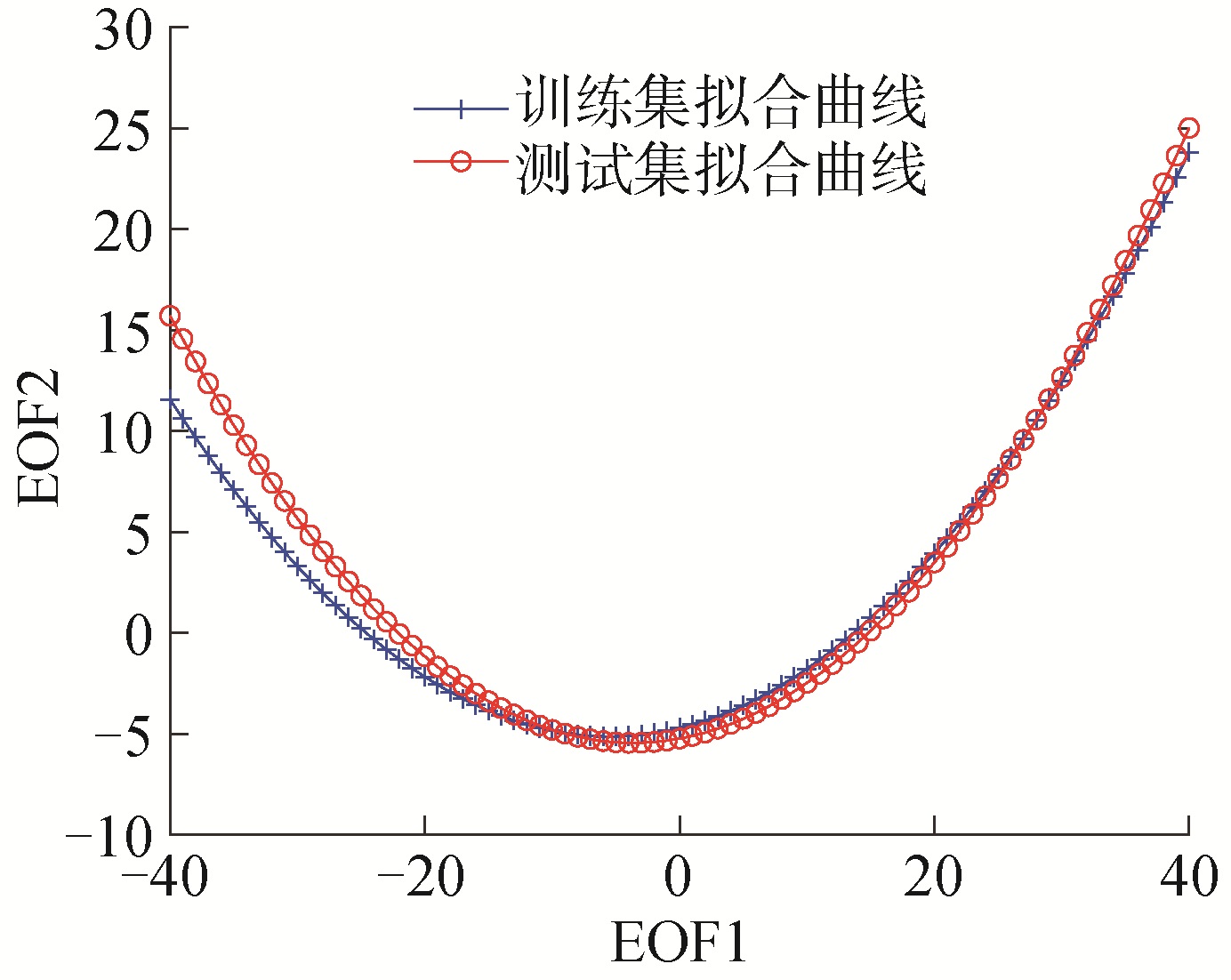
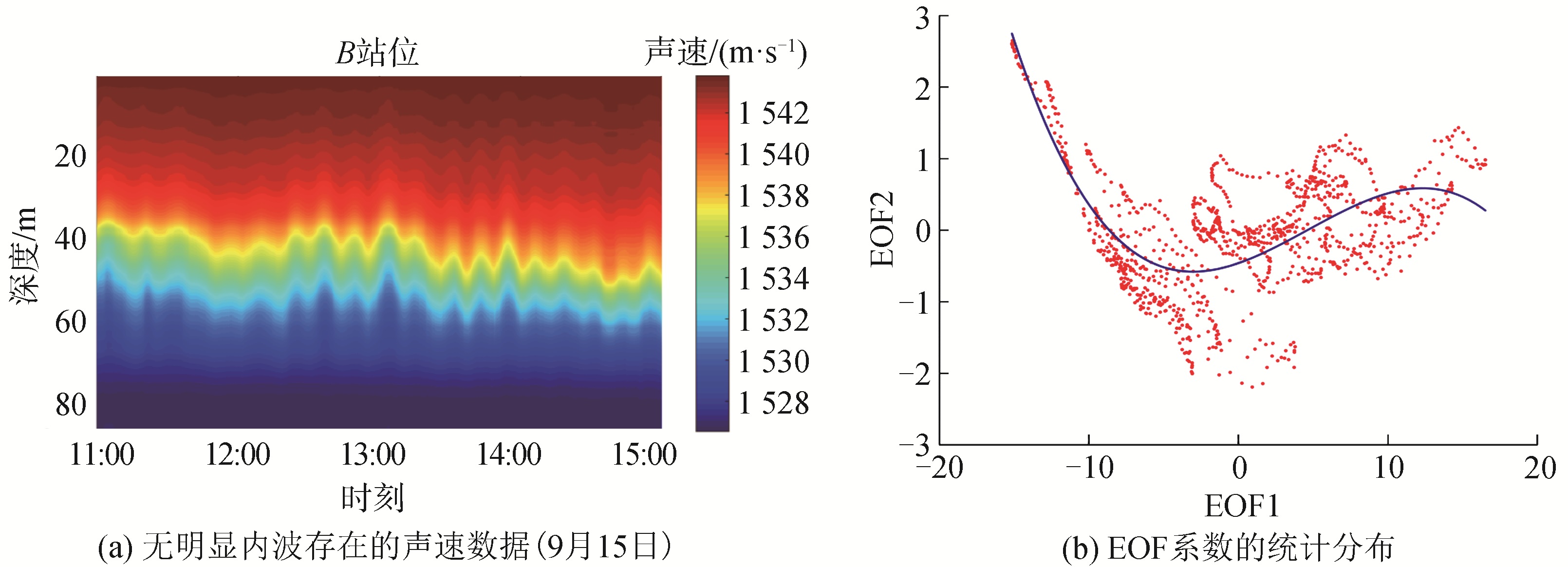
将训练集和测试集的前2阶EOF系数分别绘制成散点图如图 8所示,图中散点对应EOF系数分布,实线是通过多项式拟合得到的曲线,训练集和测试集数据均呈现出开口向上的抛物曲线分布,这与文献[15]中墨西拿海峡试验中得到的“新月形”分布是一致的。图 8中同时给出了曲线拟合的一元二次多项式,且开口大小基本一致。图 9给出了2条拟合曲线的比较,在第1阶EOF系数取值[-20, 40],二者基本吻合,只在[-40, 20]有偏差,最大偏差为4,由于第2阶EOF基函数贡献相对较小,认为这个偏差在可以容忍的范围。对于没有明显内波存在的同时刻B站位声速数据(见图 10),EOF系数之间的统计特征则显得杂乱无章,无法得到较精准的拟合曲线。这也进一步印证了可以从一段时间内EOF系数之间的统计特征来监测内波的存在。另一方面,可以将内波存在时的特殊统计模型作为先验输入,从而简化声速剖面的预测。
|
Download:
|
| 图 8 有内波存在时声速数据的统计特征 Fig. 8 Statistical characterization of SSP in the presence of interval waves | |
|
Download:
|
| 图 9 训练集和测试集拟合曲线比较 Fig. 9 Comparison of fitting curves of training and test sets | |
|
Download:
|
| 图 10 与图 5同时刻的B站位声速数据的统计特征 Fig. 10 Statistical characterization of SSP of station B at the same time of Fig. 5 | |
循环神经网络(RNN)是以序列数据为输入,在序列演进方向进行递归且所有节点链式连接的递归神经网络。因其具有记忆性、参数共享等特点,在对序列的非线性特征学习建模方面具有一定的优势,被用于各类时间序列预报。然而RNN在处理时间序列上距离较远的节点时会涉及到雅可比矩阵的多次相乘,带来梯度消失或者梯度膨胀的问题。
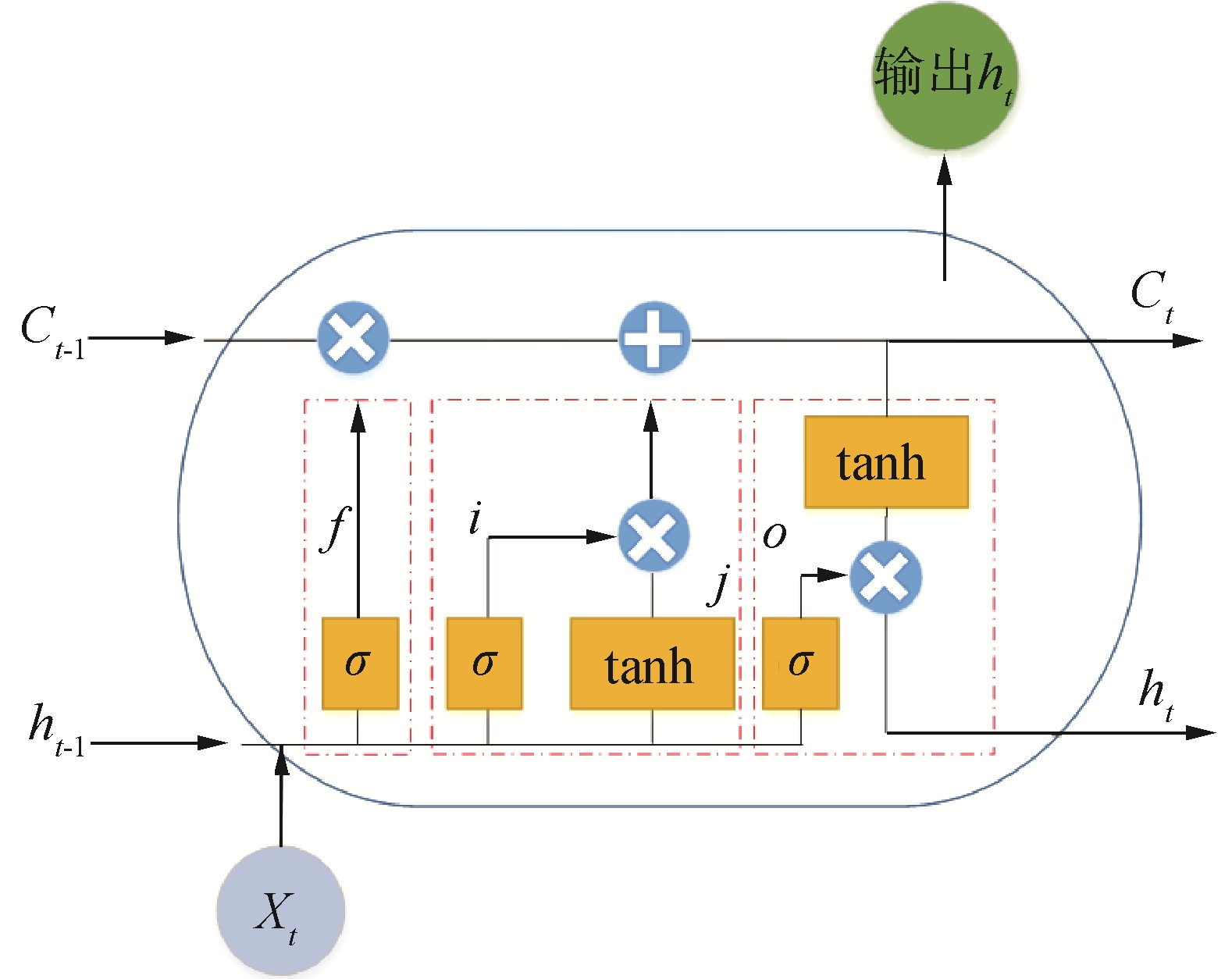
LSTM是基于RNN的一种完善,增加了记忆单元输入门、输出门和遗忘门等机制,网络结构示意图如图 11所示。各记忆单元内部运算机制为:
| $ \left\{ {\begin{array}{*{20}{l}} {{I_t} = \sigma \left( {{W_{i1}}{x_t} + {W_{i2}}{h_{t - 1}} + {b_i}} \right)}\\ {{F_t} = \sigma \left( {{W_{f1}}{x_t} + {W_{f2}}{h_{t - 1}} + {b_f}} \right)}\\ {{O_t} = \sigma \left( {{W_{o1}}{x_t} + {W_{o2}}{h_{t - 1}} + {b_o}} \right)} \end{array}} \right. $ | (9) |
|
Download:
|
| 图 11 LSTM模型结构 Fig. 11 The schematic diagram of LSTM | |
式中:It、Ft和Ot分别代表输入门、遗忘门和输出门向量值;W1、W2和b分别表示输入节点与隐藏节点、隐藏节点与输出节点的连接权值以及对应的偏置项;xt对应t时刻的输入;ht-1对应t-1时刻的输出,代表了LSTM的隐藏状态;σ为sigmoid激活函数,可将实数映射到[0, 1],1表示上一时刻单元的信息全部保留,0表示上一时刻单元的信息全部遗忘。这些“门”的结构实质上是使用sigmoid神经网络与按位相乘结合,使用sigmoid作为激活函数的全连接神经网络层会输出一个0~1的数值描述当前通过该门的信息量,使得自循环的权重是变化的,避免了梯度消失等问题,可以控制不同时刻信息的传递来提升整个网络对于长序列数据的处理能力。
2.2 试验数据分析考虑到内波统计特征,只将第1阶EOF系数作为预测值,同时从训练集提取的特征还包括EOF基函数、背景声速剖面及内波统计特征。训练集共包含7 h的声速数据,从中提取第1阶EOF系数并将数据预处理为具有零均值和单位方差的标准化数据,最终输入LSTM网络进行训练,最大迭代次数为200,学习率设置为0.005,在150次迭代以后学习率降低为0.000 1,训练在200代截至时已达到收敛,图 12为去标准化后的网络输出与实际测量值的比较,预测值变化趋势与实际测量值基本一致,均方误差为3.4,只在跃层深度剧烈变化的时刻,预测误差略有增加。

|
Download:
|
| 图 12 LSTM对第1阶EOF系数网络预测结果 Fig. 12 The first expansion coefficient predicted by LSTM model | |
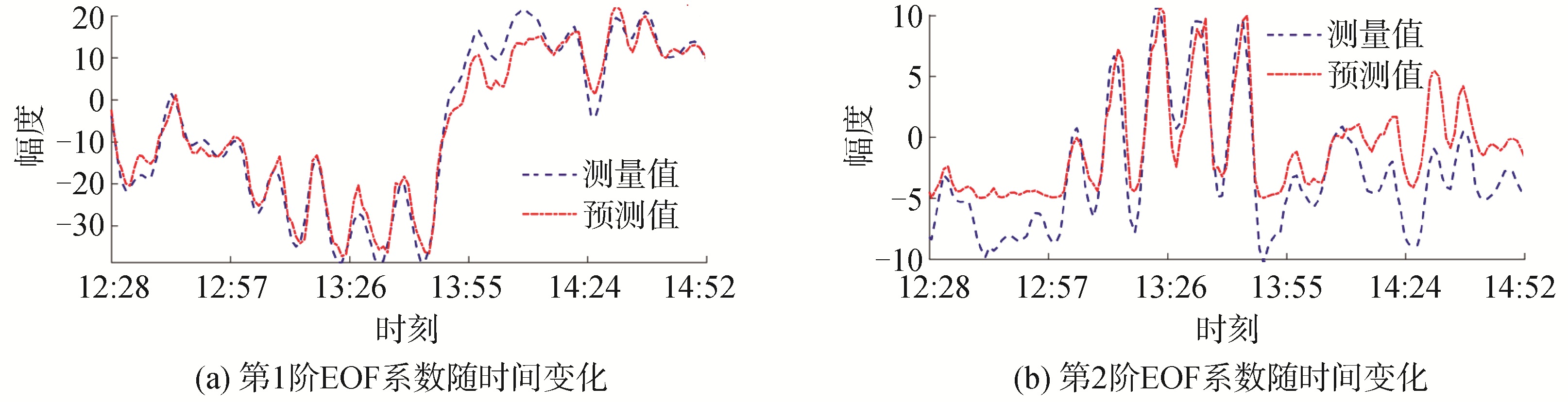
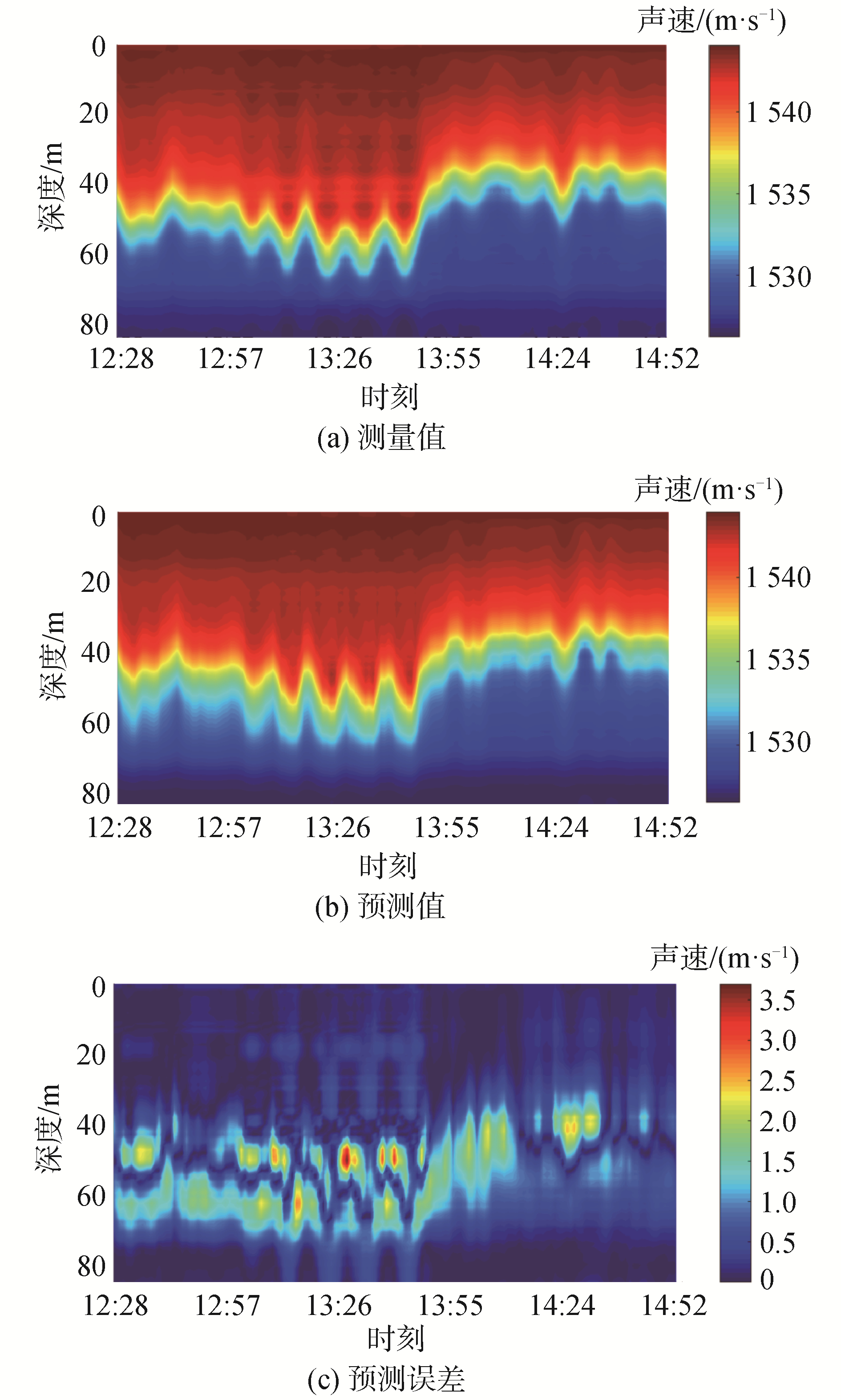
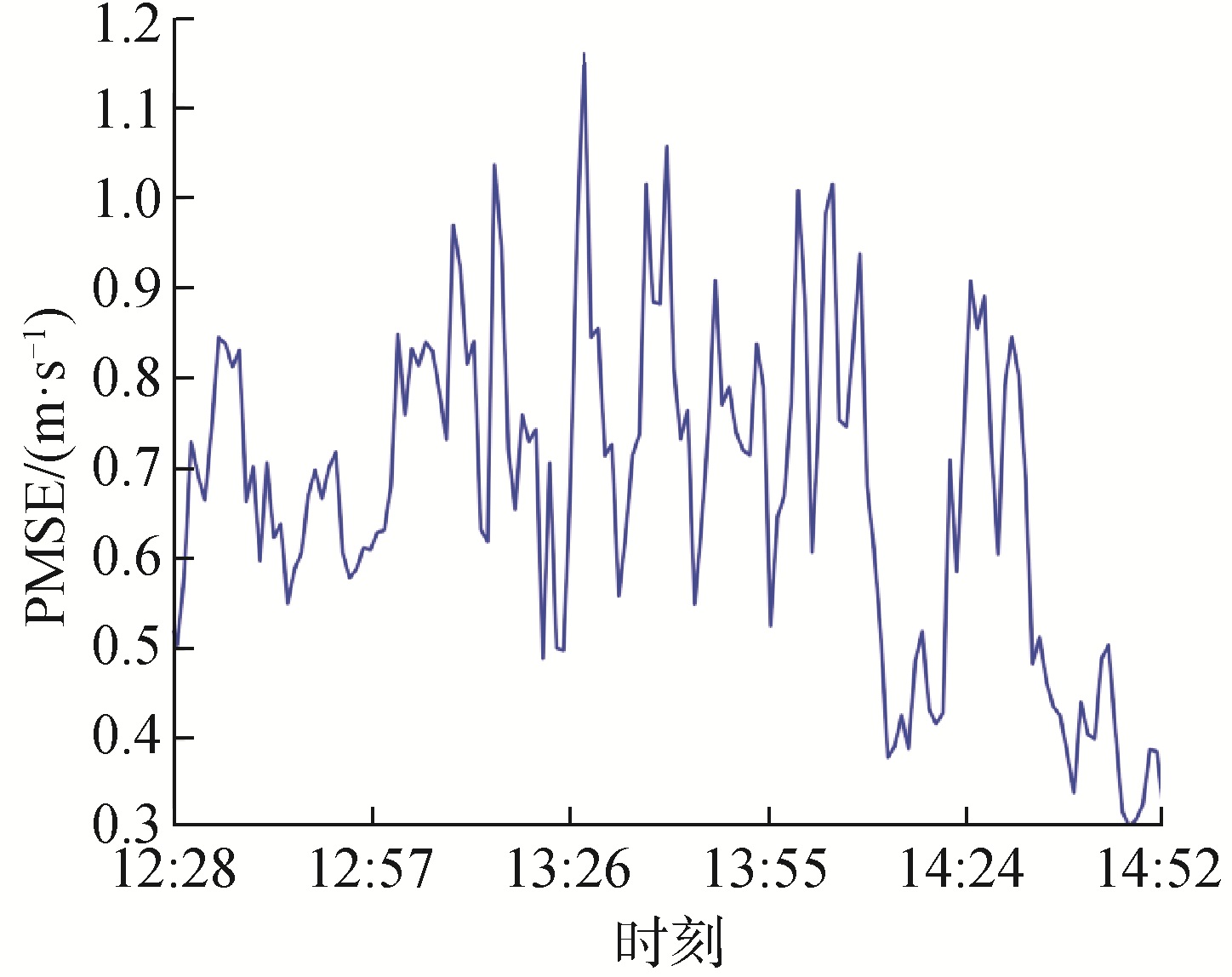
利用内波统计特征和预测得到的第1阶EOF系数即可计算得到第2阶EOF系数的变化规律,如图 13所示,与测量值基本符合。进一步利用先验EOF基函数和背景声速剖面重构得到测试集声速剖面如图 14所示,预测值与测量值基本一致,最大绝对误差为3.69 m/s, 图 15为时间序列预测的均方根误差(RMSE),最大误差为1.3 m/s。
|
Download:
|
| 图 13 基于声速剖面统计特征的LSTM网络时前两阶EOF系数预测结果 Fig. 13 The two first expansion coefficients predicted by LSTM model based on the statistical characterization of SSP | |
|
Download:
|
| 图 14 预测声速剖面与测量声速剖面对比 Fig. 14 Comparison of predicted SSP and measured SSP | |
|
Download:
|
| 图 15 预测声速剖面的均方误差 Fig. 15 Mean square error of predicted SSP | |
值得说明的是,本文算法为简化预测过程引入了内波统计模型,这同时也限制了其使用范围,只在可观测到明显内波存在的时间段可实现声速剖面快速实时预报。
3 结论1) 以南海实测声速数据为基础,深入挖掘了浅海环境中有无内波情形下的时序声速剖面内在统计特征,根据提取到的前2阶EOF系数α1、α2的变化趋势与温跃层深度变化规律,总结了有无内波情形下α1、α2的内在关联关系和分布特征。
2) 利用LSTM网络对长序列的记忆功能,通过设计深度神经网络对历史声速数据进行无监督特征学习,最后利用一段内波环境数据对训练网络进行验证,声速剖面预测结果与测量值符合较好。
综上所述,融合内波统计特性和LSTM网络模型的声速剖面实时预报方法可跳过复杂的海洋模型,预先估计感兴趣区域的声速场分布特征。然而在实际海洋环境中,声速剖面往往呈现出四维时空动态变化,水平非均匀变化也是影响声场分布的重要因素,下一步工作将结合卫星遥感数据等更多样的测量数据开展三维声速场预报研究。
致谢: 本文研究成果得益于丰富宝贵的海试数据,特别感谢组织2019年9月南海试验的胡涛、郭圣明老师以及参加试验的同事和“实验1”号全体船员。| [1] |
胡涛, 宋文华. 海洋内波对水下声场的影响[J]. 物理, 2014, 43(10): 667-672. HU Tao, SONG Wenhua. Effect of internal waves on sound propagation in the Ocean[J]. Physics, 2014, 43(10): 667-672. DOI:10.7693/wl20141004 (  0) 0)
|
| [2] |
APEL J R, BADIEY M, CHIU C S, et al. An overview of the 1995 SWARM shallow-water internal wave acoustic scattering experiment[J]. IEEE journal of oceanic engineering, 1997, 22(3): 465-500. DOI:10.1109/48.611138 (  0) 0)
|
| [3] |
RUBENSTEIN D. Observations of cnoidal internal waves and their effect on acoustic propagation in shallow water[J]. IEEE journal of oceanic engineering, 1999, 24(3): 346-357. DOI:10.1109/48.775296 (  0) 0)
|
| [4] |
张纪铃, 胡鹏涛. 浅海声速剖面对声呐作用距离的影响研究[J]. 电声技术, 2014, 38(10): 36-38. ZHANG Jiling, HU Pengtao. Shallow water sound speed effect research to the sonar affecting distance[J]. Audio engineering, 2014, 38(10): 36-38. DOI:10.3969/j.issn.1002-8684.2014.10.009 (  0) 0)
|
| [5] |
FEUILLADE C, DEL BALZO D R, ROWE M M. Environmental mismatch in shallow-water matched-field processing: geoacoustic parameter variability[J]. The journal of the acoustical society of America, 1989, 85(6): 2354-2364. DOI:10.1121/1.397781 (  0) 0)
|
| [6] |
LEBLANC L R, MIDDLETON F H. An underwater acoustic sound velocity data model[J]. The journal of the acoustical society of America, 1980, 67(6): 2055-2062. DOI:10.1121/1.384448 (  0) 0)
|
| [7] |
CASAGRANDE G, VARNAS A W, STÉPHAN Y, et al. Genesis of the coupling of internal wave modes in the Strait of Messina[J]. Journal of marine systems, 2009, 78(Suppl): S191-S204. (  0) 0)
|
| [8] |
方玥炜, 唐佑民, 李俊德, 等. 几种统计模型对热带印度洋海温异常的预报[J]. 海洋学研究, 2018, 36(1): 1-15. FANG Yuewei, TANG Youmin, LI Junde, et al. Several statistical models to predict tropical Indian Ocean Sea surface temperature anomaly[J]. Journal of marine sciences, 2018, 36(1): 1-15. DOI:10.3969/j.issn.1001-909X.2018.01.001 (  0) 0)
|
| [9] |
KURAPOV A L, EGBERT G D, MILLER R N, et al. Data assimilation in a Baroclinic Coastal ocean model: ensemble statistics and comparison of methods[J]. Monthly weather review, 2002, 130(4): 1009-1025. DOI:10.1175/1520-0493(2002)130<1009:DAIABC>2.0.CO;2 (  0) 0)
|
| [10] |
朱贵重, 胡松. 基于LSTM-RNN的海水表面温度模型研究[J]. 应用海洋学学报, 2019, 38(2): 191-197. ZHU Guizhong, HU Song. Study on sea surface temperature model based on LSTM-RNN[J]. Journal of applied oceanography, 2019, 38(2): 191-197. DOI:10.3969/J.ISSN.2095-4972.2019.02.005 (  0) 0)
|
| [11] |
顾兴健, 赵璐, 金明, 等. 基于LSTM神经网络的我国典型试航海域环境短期预报方法研究[J]. 中国造船, 2017, 58(4): 100-107. GU Xingjian, ZHAO Lu, JIN Ming, et al. Research on short-term prediction of typical trial sea environment in china based on LSTM neural network[J]. Shipbuilding of China, 2017, 58(4): 100-107. (  0) 0)
|
| [12] |
SUNDERMEYER M, NEY H, SCHLUTER R. From feedforward to recurrent LSTM neural networks for language modeling[J]. IEEE/ACM transactions on audio, speech, and language processing, 2015, 23(3): 517-529. DOI:10.1109/TASLP.2015.2400218 (  0) 0)
|
| [13] |
ZHANG Qin, WANG Hui, DONG Junyu, et al. Prediction of sea surface temperature using long short-term memory[J]. IEEE geoscience and remote sensing letters, 2017, 14(10): 1745-1749. DOI:10.1109/LGRS.2017.2733548 (  0) 0)
|
| [14] |
MACKENZIE K V. Nine-term equation for sound speed in the oceans[J]. The journal of the acoustical society of America, 1981, 70(3): 807-812. DOI:10.1121/1.386920 (  0) 0)
|
| [15] |
CASAGRANDE G, STEPHAN Y, WARN VARNAS A C, et al. A novel empirical orthogonal function (EOF)-based methodology to study the internal wave effects on acoustic propagation[J]. IEEE journal of oceanic engineering, 2011, 36(4): 745-759. DOI:10.1109/JOE.2011.2161158 (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


