2. 中国科学院声学研究所, 北京 100190;
3. 中国科学院大学, 北京 100049
2. Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
浅海水声环境往往呈现水平非均匀性,其中海底底质声学特性的水平变化是其主要表现之一。由于直接采样测量海底底质声学特性的方法过程繁琐、成本高昂,许多研究聚焦于利用声学信号反演沉积层声学参数的间接方法。一种典型间接方法是基于单波束测深仪的沉积层地声参数反演方法[1]。它基于海底高频反向散射的复合粗糙度模型[2],给出小入射角高频声波海底反向散射声信号包络时域建模方法[3],并通过海底反向散射信号包络进行地声参数反演[4]。
地声参数反演问题通常看成一个非线性优化问题,将各种全局优化算法(模拟退火、遗传算法等)应用于求代价函数最优解问题[5]。此类方法在寻优过程中需反复调用正演模型计算,普遍存在计算开销大、收敛速度慢,以及易陷入局部最优、超参数调优困难等问题。考虑到在实际的海洋测试中,海底底质特性在局部区域随距离变化的过程较为缓慢,这为地声参数的序贯估计提供了可行性。
卡尔曼滤波是一种典型序贯估计算法[7],可对线性或非线性系统中状态变量和参数进行动态估计[8],利用卡尔曼滤波框架进行序贯估计的方法已被有效应用于水声目标测距[9]、声速剖面反演[10]等领域。卡尔曼滤波过程分为预测和校正2个步骤,可根据正演模型预测与实测数据之间的误差反馈,自适应地更新对状态变量的激励,从而校正模型参数的预测值。
本文提出了一种利用卡尔曼滤波对海底反向散射回波进行沉积层参数序贯估计的方法,将模型应用于2018年8月采集的海试数据,获得测线上海底底质类型平均粒径分布,并与全局优化算法中性能较优的模拟退火算法进行了计算效率和反演精度的对比。
1 高频海底反向散射包络模型海底反向散射包络计算需要考虑发射声脉冲、声源级、接收灵敏度、指向性、换能器姿态、球面扩散、海底界面的反向散射和沉积物体积的不均匀性等大量物理特征。假设海底界面的粗糙度各向同性并且满足高斯分布,其功率谱可以写成Von Karman谱形式W(k)=w2kbγ,其中kb为波数,w2为谱强度,γ=3.5为本文中模型的谱指数。根据Jackson等[2]提出的散射模型,海底反向散射回波包络强度分为海底表层散射和海底体积散射2部分,单波束声呐接收到的随时间t变化的强度可表示为:
| $ I(t)=I_{i}(t)+I_{v}(t) $ | (1) |
式中:Ii为海底粗糙界面散射包络;Iv为海底介质体积散射包络,假设两者相互独立。Ii是一个亥姆霍兹衍射积分方程的Kirchhoff近似解,考虑了单波束声呐系统的安放位置、指向性、信号特征、水体扩展和吸收等,可以很好地描述沉积层界面反向散射的物理过程,特别是在小入射角条件下。体积散射信号包络Iv考虑了界面粗糙度对体积散射的影响。根据Sternlicht等[3]的模型,散射回波包络声压最终表示为:
| $ p_{a}\left(t, M_{z}\right)=\sqrt{\rho_{w} v_{w} I\left(t, M_{z}\right)} $ | (2) |
式中:ρw和vw分别为水层的密度和声速;Mz为海底底质平均粒径,其他参数根据经验公式[14]计算。
2 沉积层参数估计 2.1 全局优化方法地声参数反演问题通常看作是非线性数值优化问题,以待反演参数为决策变量,确立代价函数和优化的可行域,即决策变量的搜索区间,并给定其须满足的约束条件,通过全局优化方法进行迭代计算,最终得到模型参数的全局最优解。
利用包络反演海底声学和散射特性参数通常采用最小二乘均方误差函数作为优化问题中的代价函数[5]:
| $ \boldsymbol{E}_{k}(\hat{\boldsymbol{X}})=\frac{\sum\limits_{n}\left[p_{a}(n, \hat{\boldsymbol{X}})-p_{k}(n)\right]^{2}}{\sum\limits_{n}\left[p_{a}(n, \hat{\boldsymbol{X}})\right]^{2}} $ | (3) |
式中:k为测量的散射回波包络的索引值;
常用的非线性全局优化算法包括模拟退火算法[11]、遗传算法[12]、粒子群算法[13]等。利用此类算法对海底底质平均粒径Mz进行搜索,通过多次迭代使式(3)中的代价函数最小化。在与序贯估计进行对比分析时,本文采用模拟退火作为反演模型的优化算法。
2.2 无迹卡尔曼滤波无迹卡尔曼滤波(unscented Kalman filter,UKF)是通过无迹变换(unscented transform,UT)产生一系列确定样本来逼近状态的后验概率密度,既没有线性化忽略高阶项的过程,也不用求解雅可比矩阵[7]。综合考虑滤波性能和运算效率,UKF是3种方法中的首选。
基于隐马尔可夫模型[15],卡尔曼滤波首先建立状态空间方程。假设非平稳随机过程中Xk为系统状态,状态空间方程表示为:
| $ \boldsymbol{X}_{k}=\boldsymbol{f}_{k}\left(\boldsymbol{X}_{k-1}, \boldsymbol{V}_{k}\right) $ | (4) |
| $ \boldsymbol{Y}_{k}=\boldsymbol{h}_{k}\left(\boldsymbol{X}_{k-1}, \boldsymbol{W}_{k}\right) $ | (5) |
式中:Xk和Yk的方程表达式又分别称为系统的状态方程和观测方程;Vk和Wk分别为模型中状态噪声与观测噪声,两者之间互不相关。利用无迹变换选取2n+1个采样点作为Sigma点集:
| $ \boldsymbol{X}_{k-11 k-1}^{(i)}=\left[\hat{\boldsymbol{X}}_{k-1 \mid k-1} \quad \hat{\boldsymbol{X}}_{k-1 \mid k-1}+\sqrt{(n+\lambda) \boldsymbol{P}_{k-1 \mid k-1}} \quad \hat{\boldsymbol{X}}_{k-1 \mid k-1}-\sqrt{(n+\lambda) \boldsymbol{P}_{k-1 \mid k-1}}\right] $ | (6) |
采样点的权值ω(i)为:
| $ \left\{\begin{array}{l} \omega_{m}^{(0)}=\frac{\lambda}{n+\lambda} \\ \omega_{c}^{(0)}=\frac{\lambda}{n+\lambda}+\left(1-a^{2}+\beta\right) \\ \omega_{m}^{(i)}=\omega_{c}^{(i)}=\frac{\lambda}{2(n+\lambda)}, i=1,2, \cdots, 2 n \end{array}\right. $ | (7) |
UKF在此求出一组Sigma点的预测,并对他们加权求均值,得到系统状态和协方差的预测值:
| $ \boldsymbol{X}_{k | k-1}^{(i)}=\boldsymbol{f}_{k}\left(k, \boldsymbol{X}_{k-1| k-1}^{(i)}\right) $ | (8) |
| $ \hat{\boldsymbol{X}}_{k \mid k-1}=\sum\limits_{i=0}^{2 n} \omega^{(i)} \boldsymbol{X}_{k \mid k-1}^{(i)} $ | (9) |
| $ \boldsymbol{P}_{k \mid k-1}=\sum\limits_{i=0}^{2 n} \omega^{(i)}\left[\hat{\boldsymbol{X}}_{k \mid k-1}-\boldsymbol{X}_{k \mid k-1}^{(i)}\right]\left[\hat{\boldsymbol{X}}_{k \mid k-1}-\boldsymbol{X}_{k \mid k-1}^{(i)}\right]^{\mathrm{T}}+\boldsymbol{Q} $ | (10) |
根据预测值,再次利用UT变换产生新的Sigma点集,并代入观测方程得到预测的观测量:
| $ \boldsymbol{X}_{k \mid k-1}^{(i)}=\left[\hat{\boldsymbol{X}}_{k \mid k-1} \quad \hat{\boldsymbol{X}}_{k \mid k-1}+\sqrt{(n+\lambda) \boldsymbol{P}_{k \mid k-1}} \quad \hat{\boldsymbol{X}}_{k \mid k-1}-\sqrt{(n+\lambda) \boldsymbol{P}_{k \mid k-1}}\right] $ | (11) |
| $ \boldsymbol{Z}_{k \mid k-1}^{(i)}=h\left(\boldsymbol{X}_{k \mid k-1}^{(i)}\right) $ | (12) |
接着,通过加权求和得到系统预测的均值及协方差,并计算卡尔曼增益和系统状态的协方差更新:
| $ {\boldsymbol{\widehat Z}_{k\mid k - 1}} = \sum\limits_{i = 0}^{2n} {{\omega ^{(i)}}} \boldsymbol{Z}_{k\mid k - 1}^{(i)} $ | (13) |
| $ \boldsymbol{P}_{z_{k}{z}_k}=\sum\limits_{i=0}^{2 n} \omega^{(i)}\left[\boldsymbol{Z}_{k \mid k-1}^{(i)}-\hat{\boldsymbol{Z}}_{k \mid k-1}\right]\left[\boldsymbol{Z}_{k \mid k-1}^{(i)}-\hat{\boldsymbol{Z}}_{k \mid k-1}\right]^{\mathrm{T}}+\boldsymbol{R} $ | (14) |
| $ \boldsymbol{P}_{x_{k} z_{k}}=\sum\limits_{i=0}^{2 n} \omega^{(i)}\left[\boldsymbol{X}_{k \mid k-1}^{(i)}-\hat{\boldsymbol{X}}_{k \mid k-1}\right]\left[\boldsymbol{Z}_{k \mid k-1}^{(i)}-\hat{\boldsymbol{Z}}_{k \mid k-1}\right]^{\mathrm{T}} $ | (15) |
| $ \boldsymbol{K}_{k}=\boldsymbol{P}_{x_{k}{z}_k} \boldsymbol{P}_{x_{k}{z}_k}^{-1} $ | (16) |
| $ \boldsymbol{P}_{k \mid k}=\boldsymbol{P}_{k \mid k-1}-\boldsymbol{K}_{k} \boldsymbol{P}_{x_{k}{z}_k} \boldsymbol{K}_{k}^{\mathrm{T}} $ | (17) |
最后对系统状态量的预测值进行校正:
| $ \left\{\begin{array}{l} \hat{\boldsymbol{X}}_{k \mid k}=\hat{\boldsymbol{X}}_{k \mid k-1}+\Delta \hat{\boldsymbol{X}}_{k} \\ \Delta \hat{\boldsymbol{X}}_{k}=\boldsymbol{K}_{k} \cdot \boldsymbol{E}_{k}\left(\hat{\boldsymbol{Z}}_{k \mid k-1}\right) \end{array}\right. $ | (18) |
式中Ek为误差函数,这里采用式(3)定义的最小二乘均方误差。式(18)在预测值
本试验于2018年8月在黄海进行,通过走航式测量海底散射回波,主要目的是对沉积物声学特征遥测的可行性进行研究。走航试验开始于试验海区E1站位点(36°00.180 4′N 121°36.804 0′E),利用收发合置换能器发射25 kHz单频信号和线性调频信号,于次日到达E2站位点,全程约为130 km。
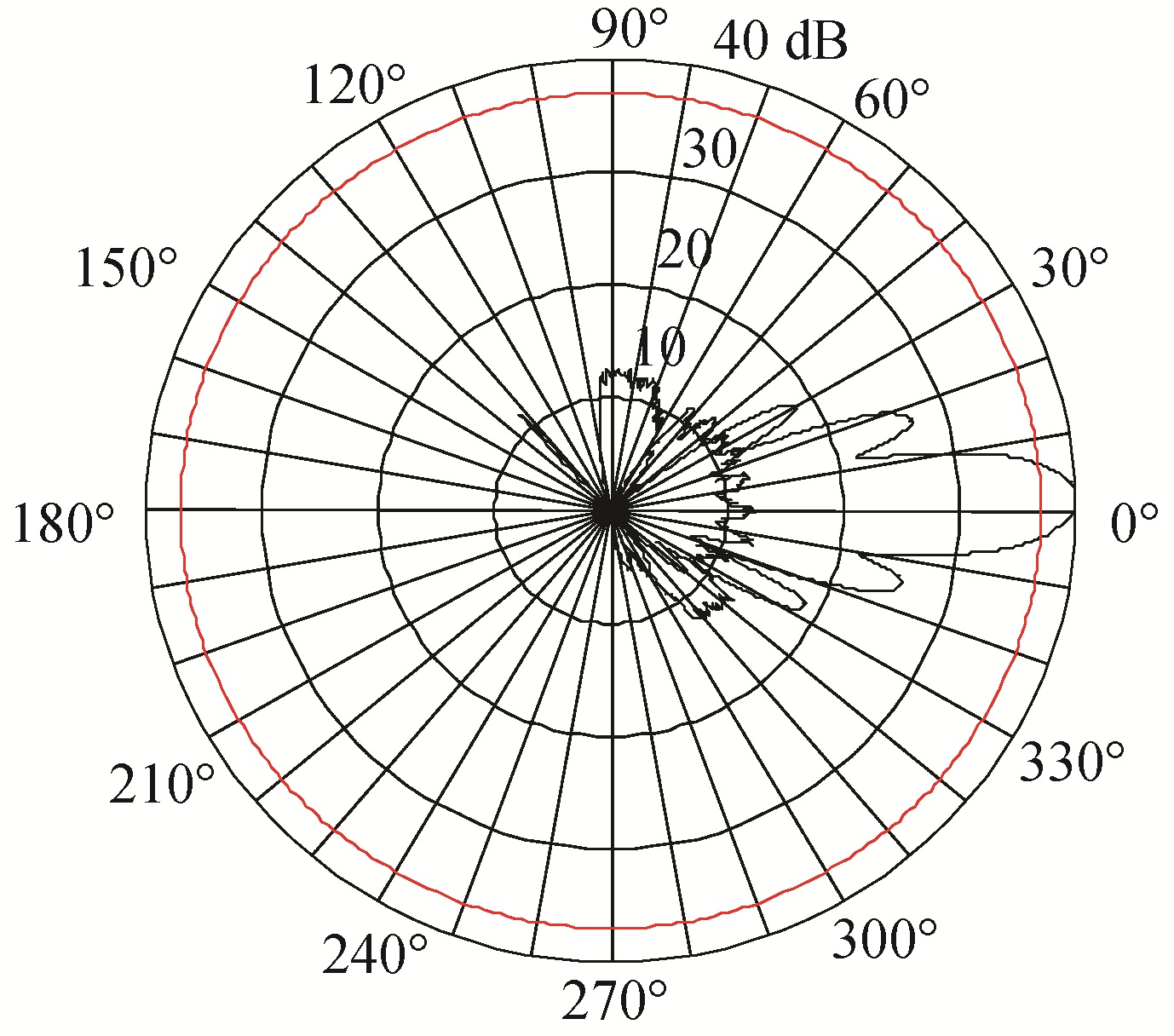
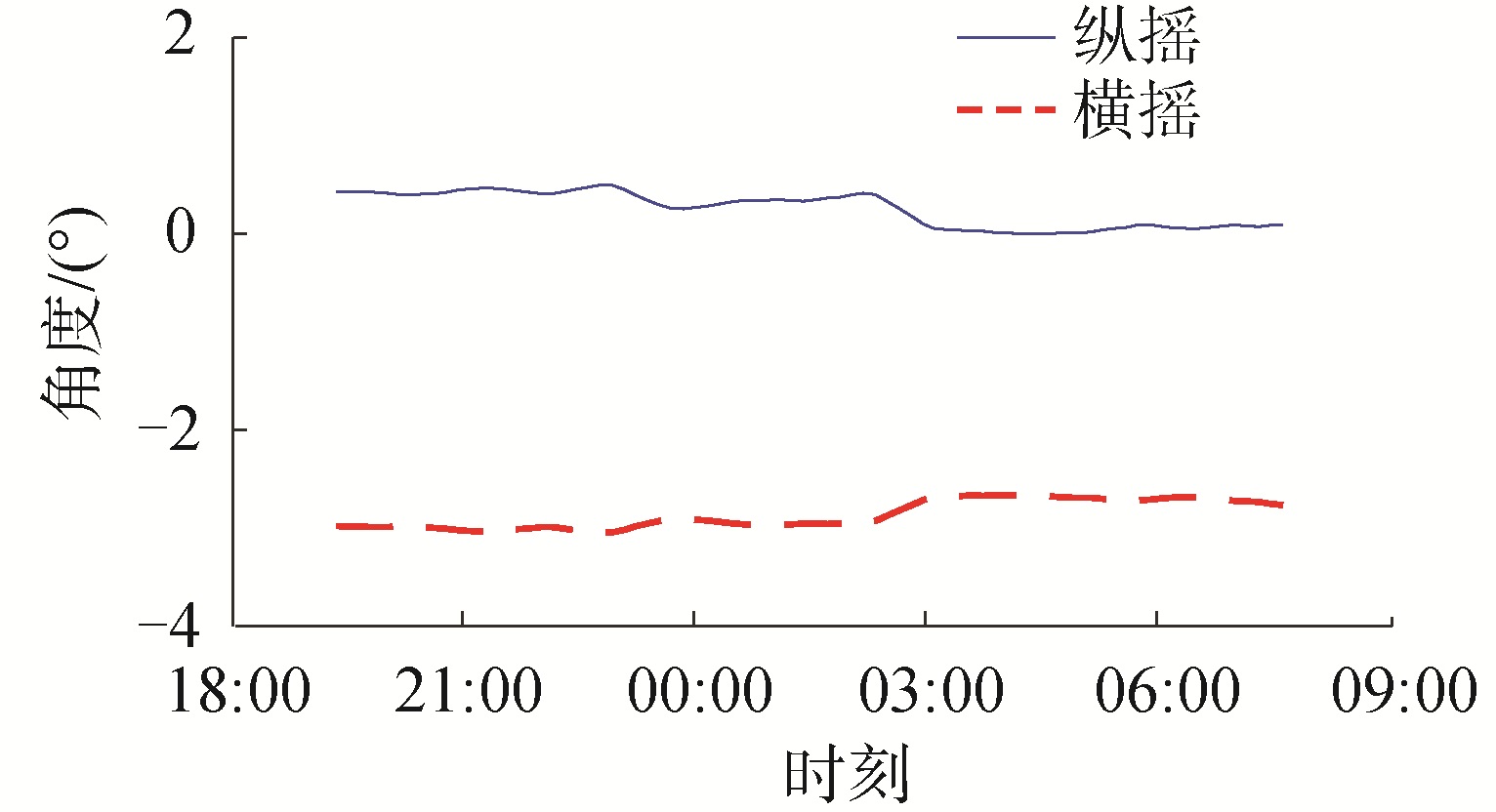
本次试验采用的换能器声源级和接收灵敏度较高,25 kHz声源级为212.72 dB,接收灵敏度为-186.1 dB,收发合置换能器具有较好的指向性,如图 1所示。图 2给出了收发合置换能器上罗经监测的换能器姿态,在实验的后半部分随海况恶化其姿态有所偏离,在反向散射包络的建模中引入了对指向性的纠正。
|
Download:
|
| 图 1 换能器指向性 Fig. 1 Directionality pattern of SBS | |
|
Download:
|
| 图 2 换能器姿态监视 Fig. 2 Pitch and roll angle of SBS along the track | |
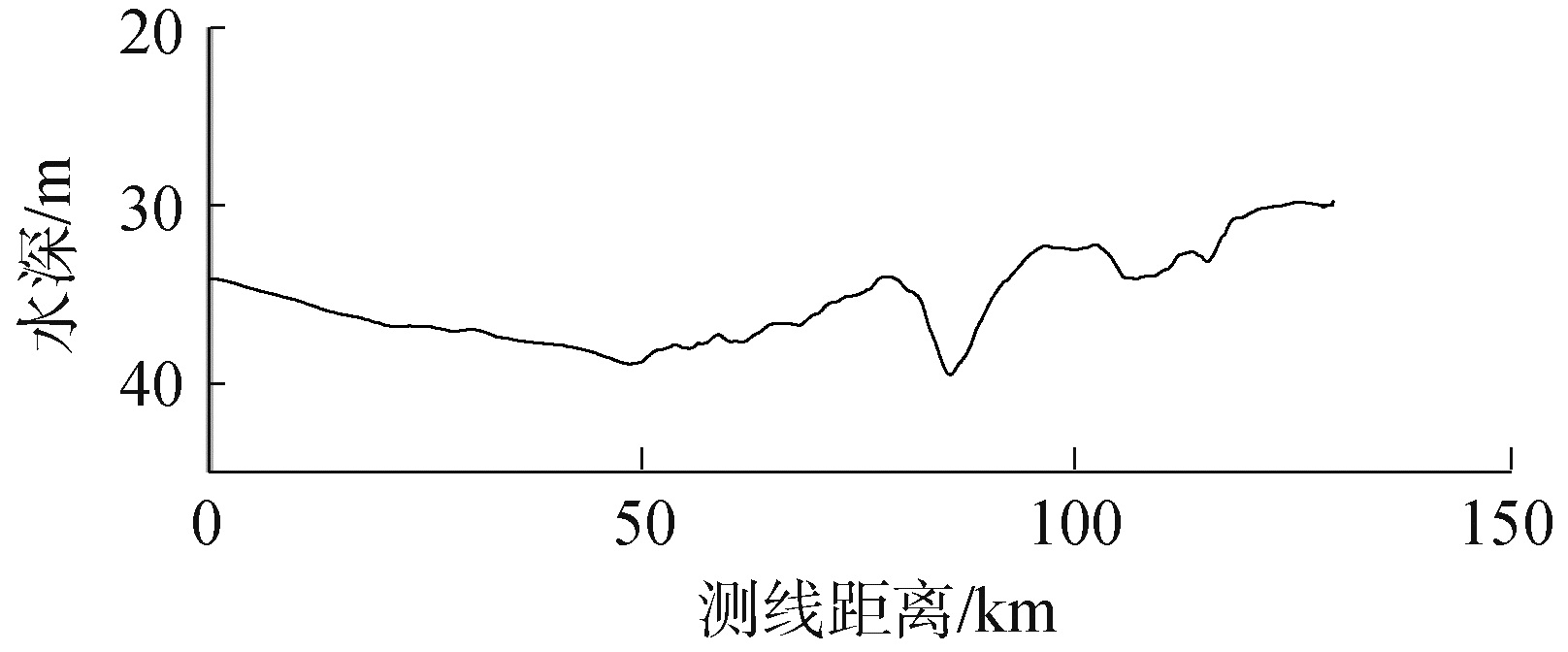
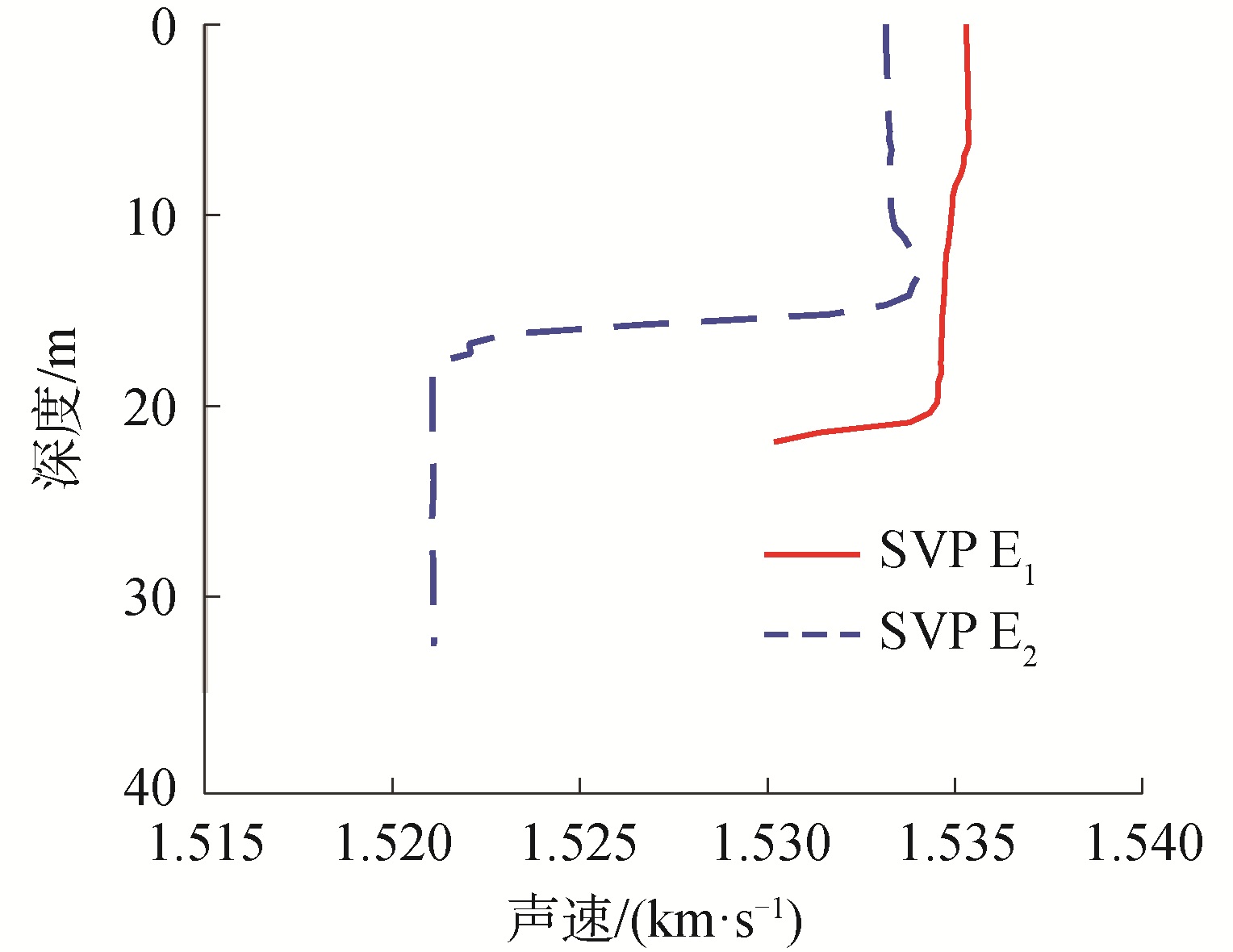
通过对发射的线性调频信号进行处理得到换能器距离海底深度,如图 3所示。水深在80 km处有相对较小的波动,其他较为平稳。图 4给出了E1和E2站位测量的水文声速剖面,在15~20 m海深处存在明显的跃变层,在此声速剖面基础上计算信号的传播时间。
|
Download:
|
| 图 3 测线海水深度 Fig. 3 Water depth along the track | |
|
Download:
|
| 图 4 声速剖面曲线 Fig. 4 Speed of sound profile | |
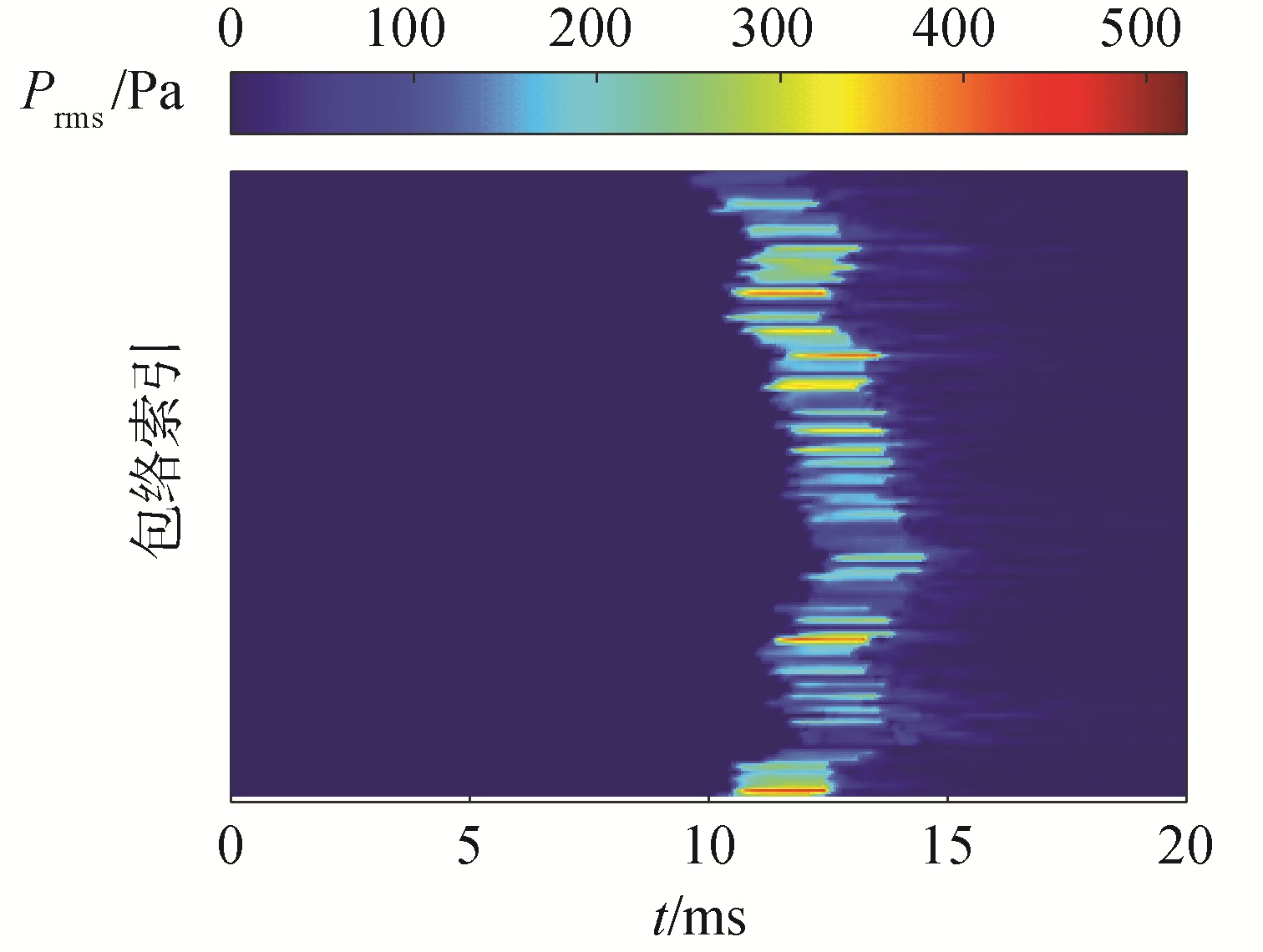
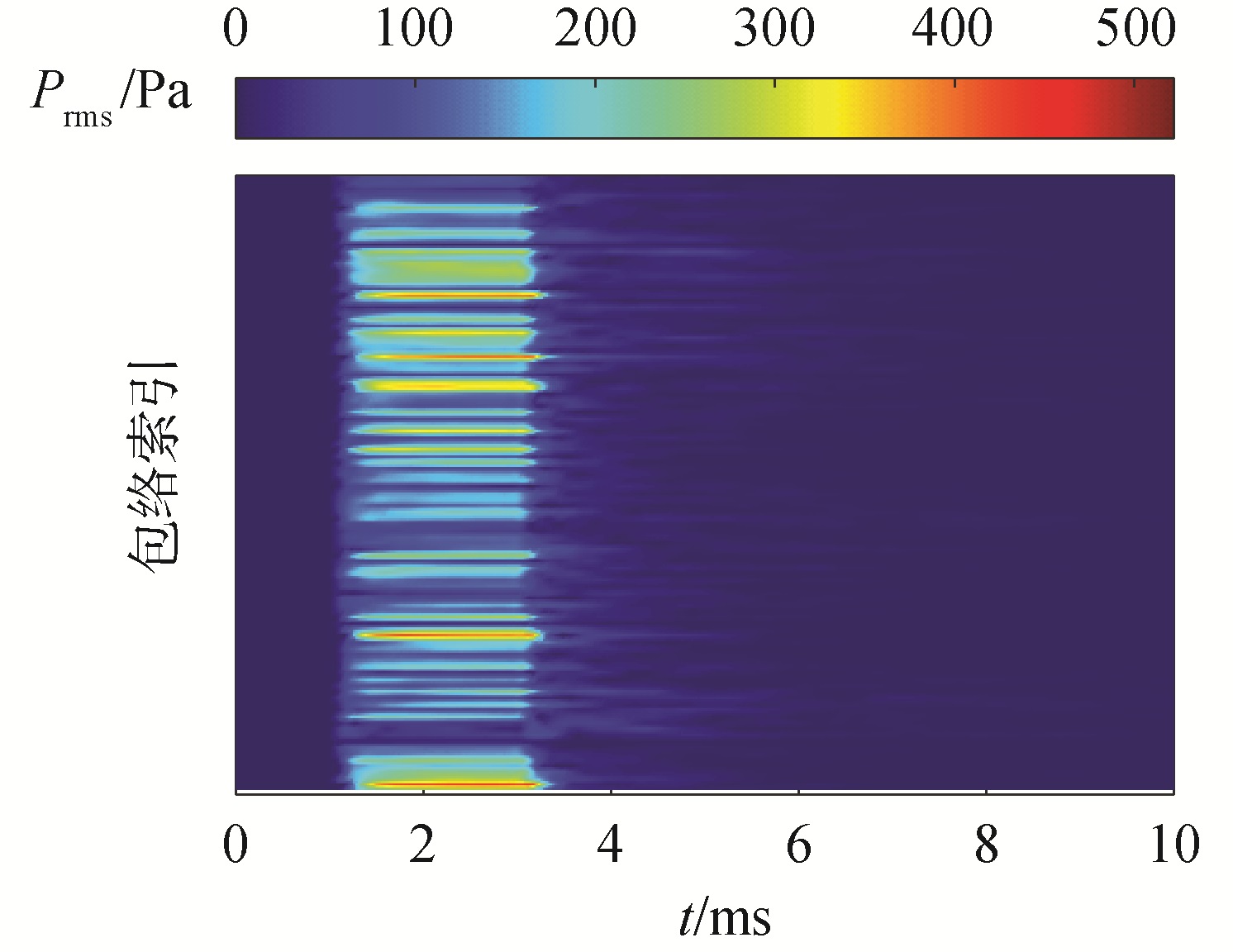
实验中发射了频率为25 kHz,时间脉冲长度为2 ms的单频信号。信号采样频率为500 kHz,同时记录了功率放大器监视信号和收发合置换能器信号。散射信号包络的获取是通过对滤波后的原始信号进行Hilbert变换并取绝对值获得。图 5给出了第40组100个信号的海底散射回波包络图,可以看出由于海底的深度变化和换能器的上下浮动等因素,接收信号的包络到达时刻变化很大。由于收发合置换能器具有较高的源级,接收信号信噪比较高,故对信号包络可采用最小门限法[5]进行对齐。图 6给出了信号的第40组包络对齐结果。在走航过程中海底的散射不同获得的信号包络差别较大,对获取的散射回波包络每100个样本进行平均,共得到80组信号包络。
|
Download:
|
| 图 5 第40组信号的海底散射回波包络 Fig. 5 Original backscatter envelopes of color plot for the 40th dataset | |
|
Download:
|
| 图 6 第40组海底散射回波包络对齐结果 Fig. 6 Aligned backscatter envelopes of color plot for the 40th dataset | |
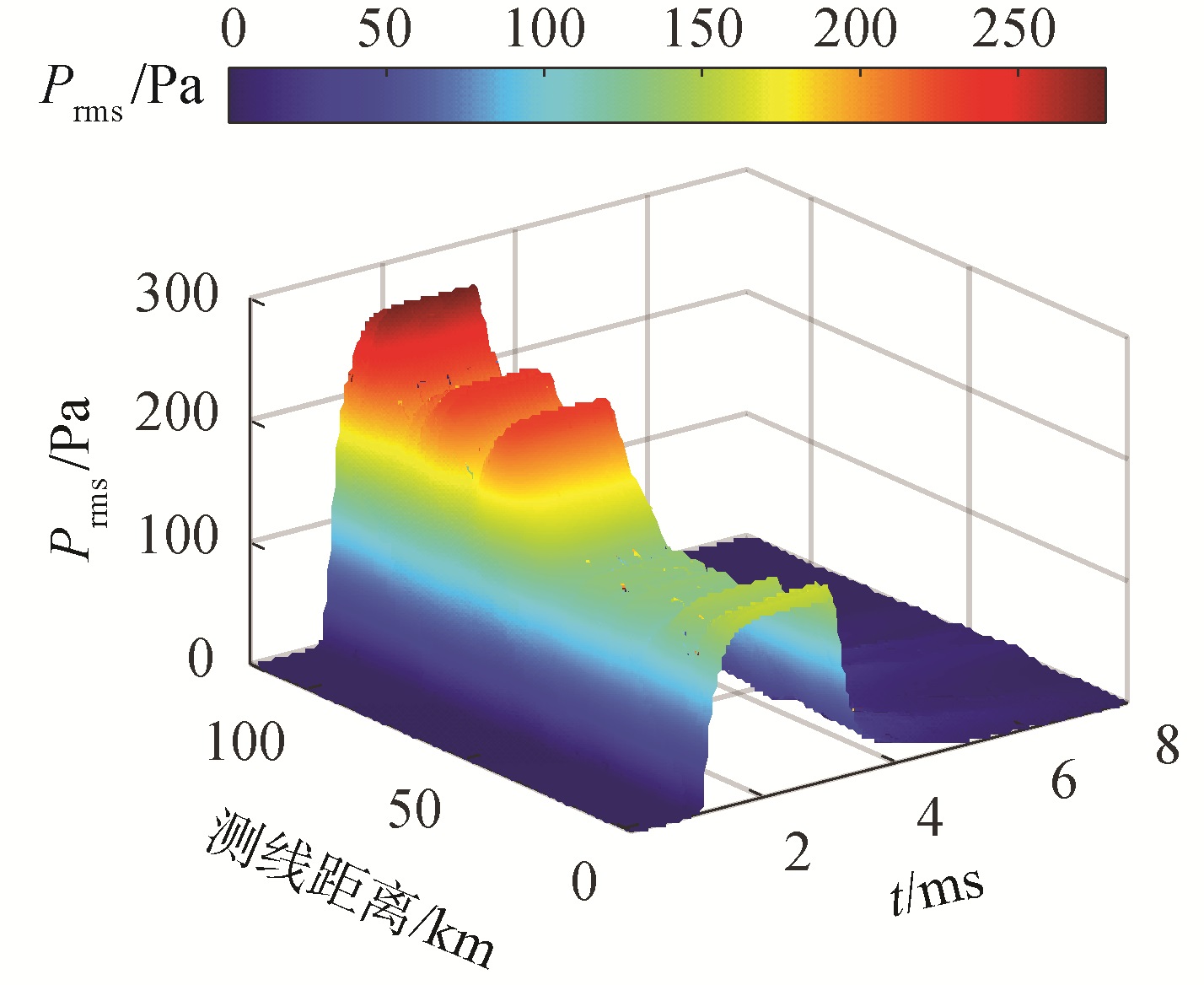
基于最小门限法对齐的信号,对获取的信号回波包络进行80%的重叠平均处理,获得整个E1-E2测线海底散射回波包络,如图 7所示。利用获得的信号的80组包络分别进行海底声学参数全局优化反演和序贯估计。
|
Download:
|
| 图 7 整个测线海底散射回波包络 Fig. 7 The experimental backscatter envelope on the track | |
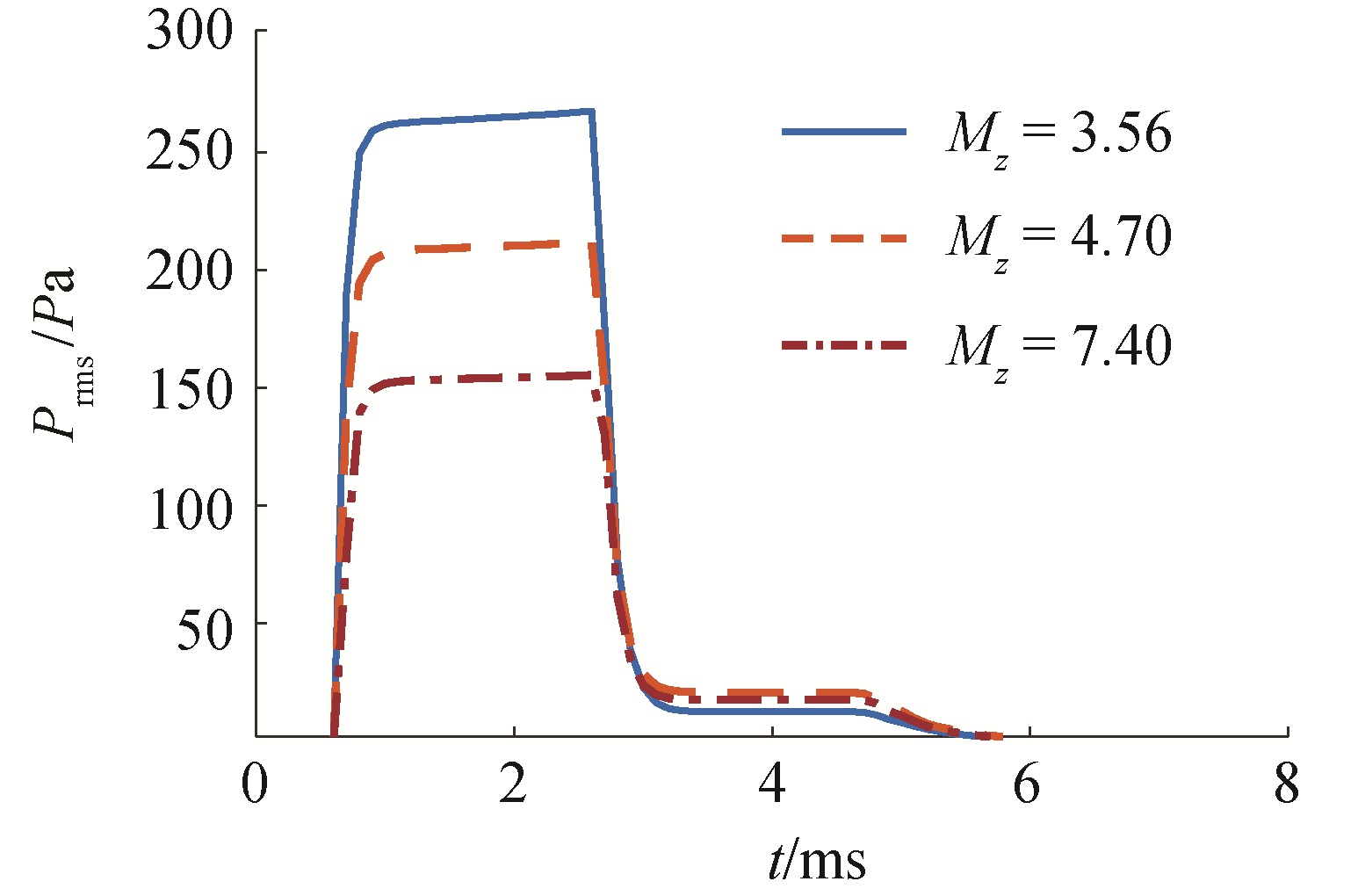
图 8给出了海底底质平均粒径值Mz分别取3.56、4.70、7.40时高频海底反向散射包络模型预报的散射包络。当Mz增大时,单波束声呐接收到的声强度增大,散射包络的面积增大。在该模型的基础上可利用预处理后的80组散射信号包络分别进行海底声学参数全局反演和序贯估计。
|
Download:
|
| 图 8 不同海底底质平均粒径值的预报包络 Fig. 8 Prediction envelope of different mean grain sizes | |
首先,利用全局优化法分别对80组散射包络进行地声参数反演,所用算法为SA,搜索区间为[0, 10],初始温度T0=100,温度变化率ΔT=0.98,设多个终止条件,当10次迭代内目标函数平均变化率δ < 10-3或代价函数值小于0.02时终止迭代,且最大迭代次数Nmax=50。其次,利用序贯估计法对80组散射包络依序进行地声参数估计,所用算法为UKF,为获取相对准确的初始状态值,将第1组包络的全局优化反演结果作为UKF初始状态,UKF初始状态协方差设为单位矩阵I。序列长度设为80,对应信号的80组散射包络。由于地声参数在短距离内的状态变化可视为缓变过程,令式(4)中状态方程为Xk=Xk-1+Vk。其中Vk表示k时刻过程中的随机扰动,服从均值为零、协方差矩阵为Q=qI的高斯分布;式(5)测量方程设为Yk=hk(Xk-1)+Wk,hk为式(3)给出的函数,Wk表示测量噪声,服从均值为零、方差为r的高斯分布。根据状态转移过程和测量特性将q设为0.01,r试设为1和2。
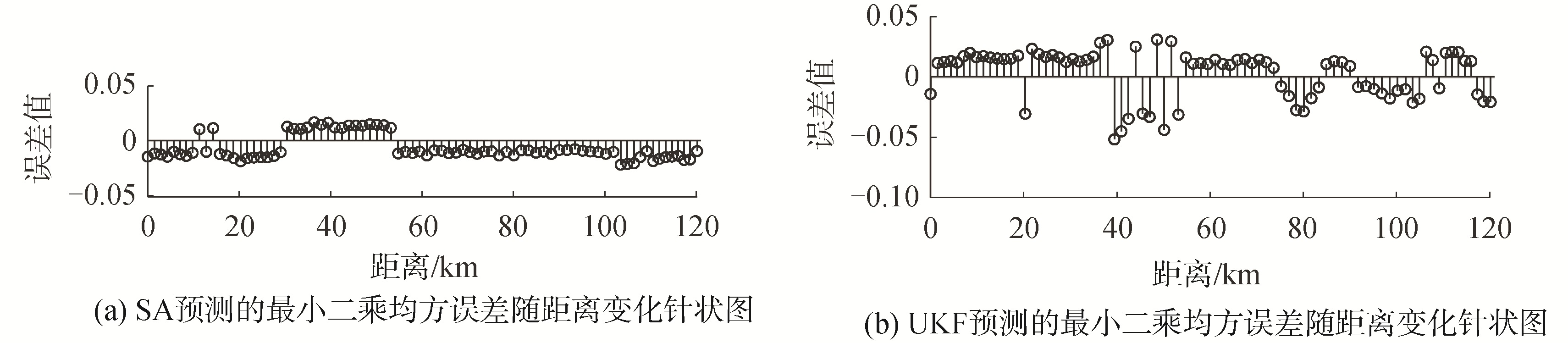
图 9(a)和图 9(b)分别给出了SA和UKF预测包络与实测包络的最小二乘均方误差随距离变化的针状图。由于SA在误差收敛到一定阈值时终止搜索,其预测精度较为稳定。UKF根据预测与实测数据之间的误差反馈,自适应地调整待估参数的激励,由图可见在拐点附近UKF可及时调整状态参数的更新量以减小预测误差,但在海底底质剧变区测量误差增大,这是因为状态转移方程假定动态模型为缓变过程。SA和UKF的最小二乘均方误差均控制在0.05以下,表明预测结果可信度尚好。
|
Download:
|
| 图 9 2种方法预测的最小二乘均方误差随距离变化针状图 Fig. 9 Stem figure of least square mean square error at different distance predicted by two methods | |
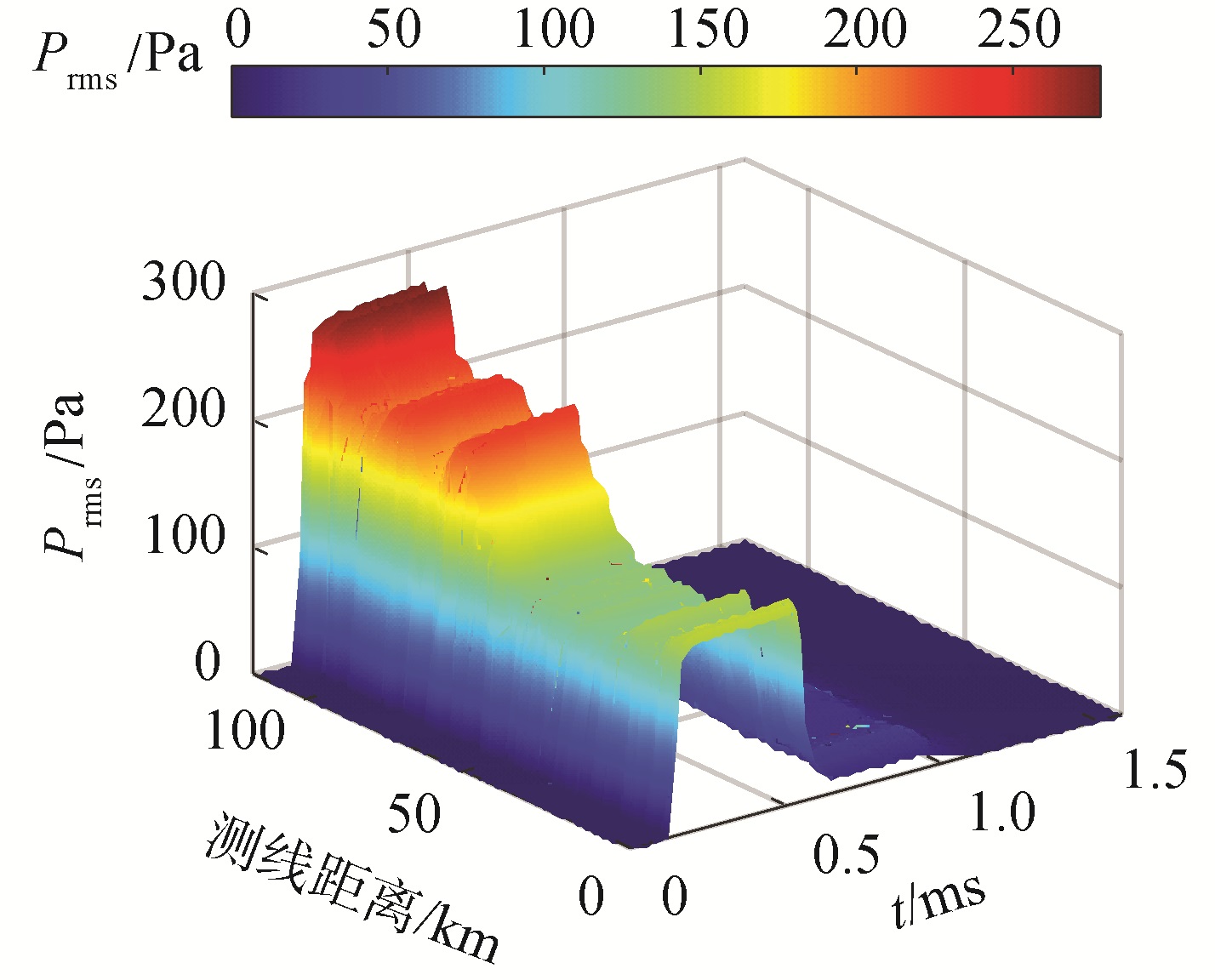
利用序贯估计的海底声学参数预测海底散射包络随距离如图 10所示。通过对比图 7可知预测的海底散射包络与实测结果对应较好。
|
Download:
|
| 图 10 利用序贯估计的海底声学参数预测海底散射包络 Fig. 10 The seafloor backscattering envelope predicted by sequential estimation | |
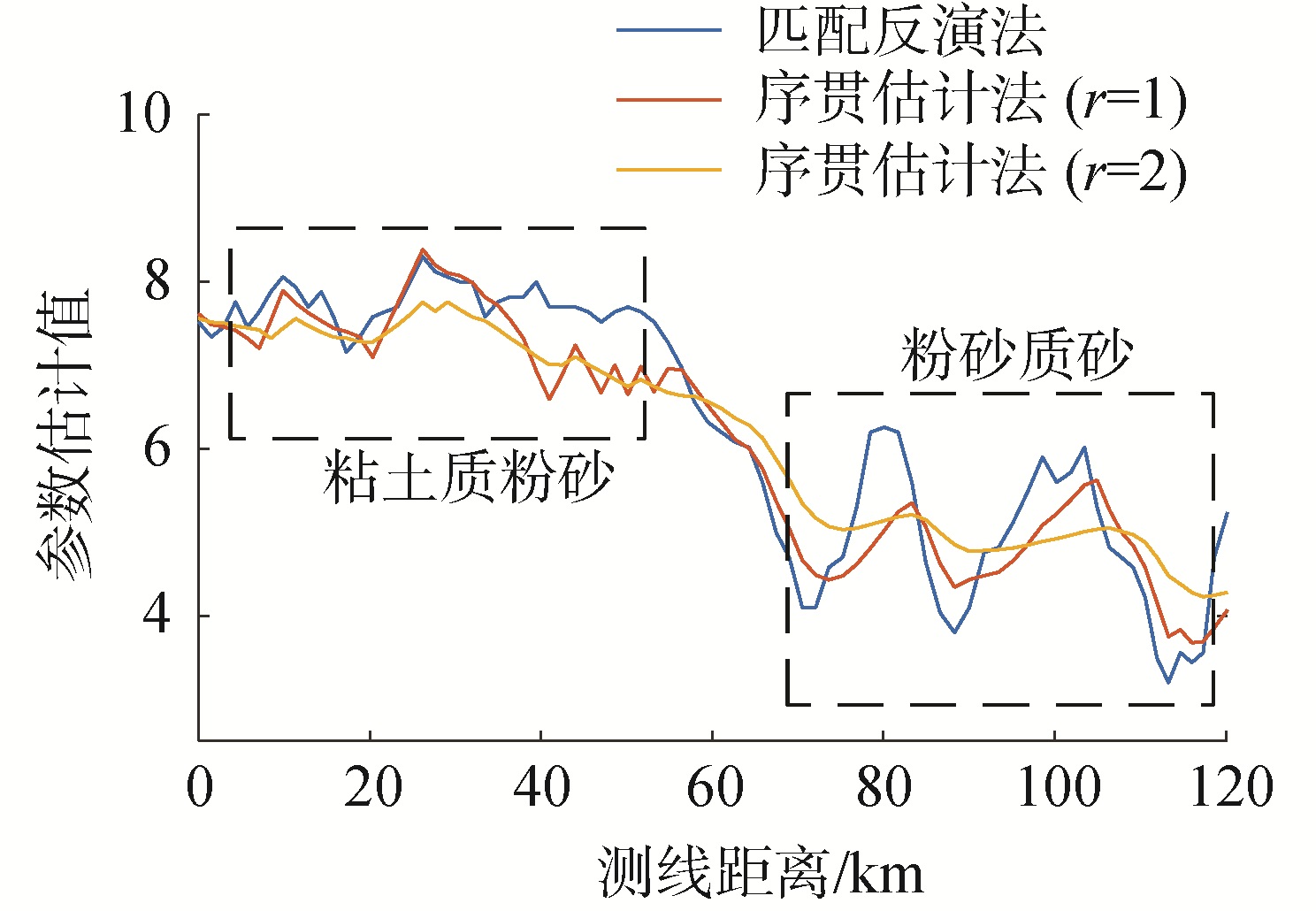
图 11给出了全局优化法和序贯估计法对海底底质平均粒径Mz的预测与海底底质分类结果。从图中可以看出UKF与SA的底质分类结果基本一致,从大约60 km处海底底质平均粒径变小,表明海底底质由软变硬。测量噪声方差r=2时相比r=1时测量结果曲线更加平滑,说明r的增大可使测量噪声对模型的影响增大,使卡尔曼增益Kk减小,从而减弱系统的校正权值,降低了系统的瞬态响应和稳态值。根据Wentworth分类标准,获得海底底质平均粒径为极细粉砂到中粉砂范围。
|
Download:
|
| 图 11 海底底质平均粒径 Fig. 11 Estimation results of mean grain size | |
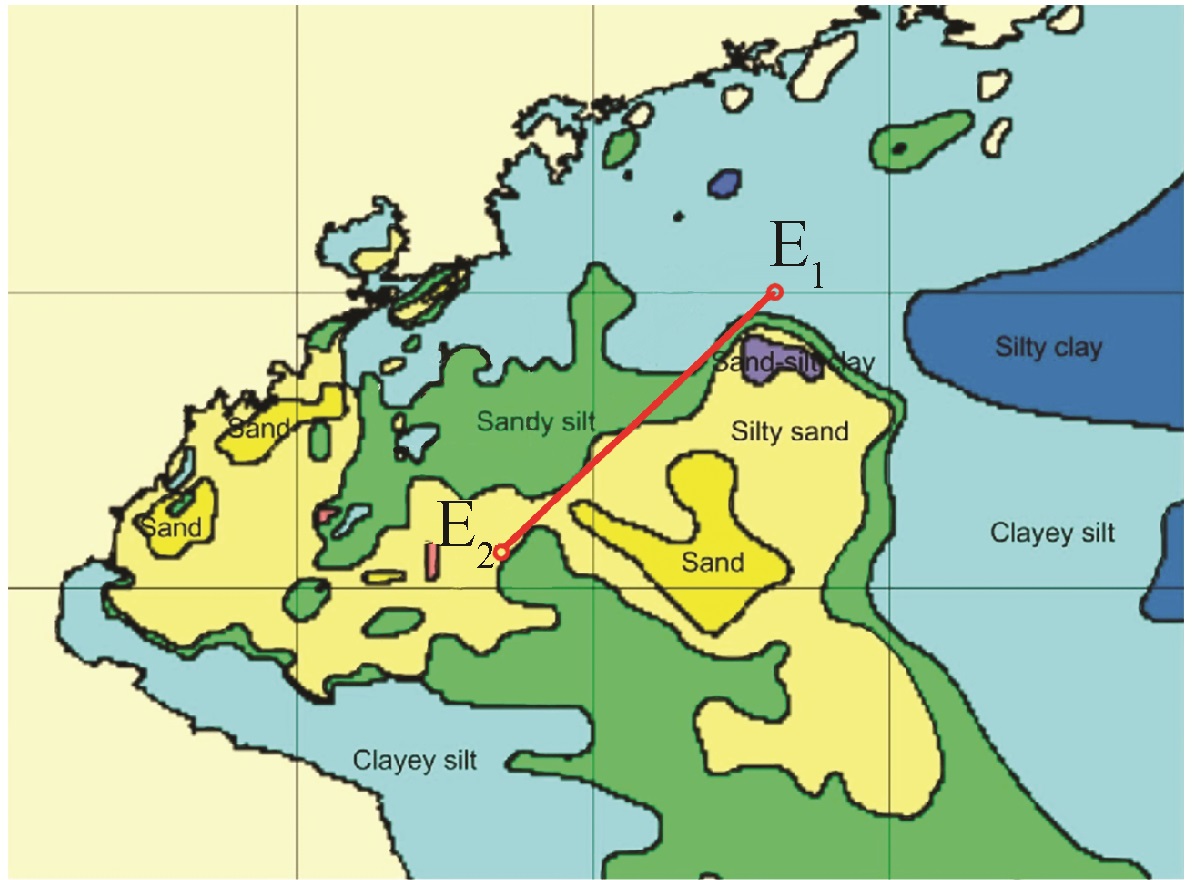
图 12给出了试验海区位置的海底底质类型分布,E1-E2测线为试验走航测线,在试验起始端底质类型为黏土质粉砂,与反演得到的平均粒径一致,如图 11中左侧方框所示;并很快过渡到砂质粉砂,后半段测线为粉砂质砂,与图 11中的右侧方框一致。序贯估计结果与试验预报结果符合很好。
|
Download:
|
| 图 12 海底底质类型分布 Fig. 12 Core sampler type distribution | |
利用UKF进行一步估计时,由于UKF无需同EKF一样计算非线性函数的雅可比矩阵,其计算复杂度仅来源于UT变换中产生Sigma点集时和预测校正时所调用的正演函数计算。因此,序贯估计法所需的时间代价同全局优化法一样由正演程序的计算次数决定。对于序贯估计法,每组包络固定执行2L+1次正演模型计算,L为待估参数个数;对于全局优化法,每组包络需执行的正演次数由寻优过程的迭代次数N决定,且根据预定的终止条件有所不同,每组反演所需的迭代次数根据具体收敛情况、伪峰和鞍点个数而不定,可达数十次到上百次不等。在Intel Core i5-9400F 2.90Ghz处理器的PC机环境下应用Matlab计算,二者所用计算时间对比如表 1所示。UKF在单次估计中平均计算时间相比SA法缩短83.4%,总体时间开销缩短79.6%。
| 表 1 SA与UKF的计算时间代价对比 Table 1 Calculating time cost comparison |
1) 序贯估计预测的海底散射回波包络与实测包络符合较好,全局优化反演和序贯估计法预测的最小二乘均方误差均可控制在0.05以下,预测精度尚好。
2) 海底底质平均粒径的预测值与海底底质分类分布对比具有较高的可信度。序贯估计的结果显示,海底底质类型在试验起始端为黏土质粉砂,并很快过渡到砂质粉砂,后半段测线为粉砂质砂,与试验预报结果符合很好。
3) 序贯估计法在保证和全局优化法精度相似的情况下有效提升算法效率,参数估计消耗的平均时间显著缩短,具有良好的研究和应用价值。
| [1] |
STERNLICHT D D, DE MOUSTIER C P. Remote sensing of sediment characteristics by optimized echo-envelope matching[J]. The journal of the acoustical society of America, 2003, 114(5): 2727-2743. DOI:10.1121/1.1608019 (  0) 0)
|
| [2] |
JACKSON D R, WINEBRENNER D P, ISHIMARU A. Application of the composite roughness model to high-frequency bottom backscattering[J]. The journal of the acoustical society of America, 1986, 79(5): 1410-1422. DOI:10.1121/1.393669 (  0) 0)
|
| [3] |
STERNLICHT D D, DE MOUSTIER C P. Time-dependent seafloor acoustic backscatter (10-100 kHz)[J]. The journal of the acoustical society of America, 2003, 114(5): 2709-2725. DOI:10.1121/1.1608018 (  0) 0)
|
| [4] |
鹿力成. 水平非均匀环境地声反演及海底散射测量[D]. 北京: 中国科学院大学, 2011.
(  0) 0)
|
| [5] |
WELCH G, BISHOP G. An introduction to the Kalman filter[R]. Chapel Hill: University of North Carolina, 1995.
(  0) 0)
|
| [6] |
WAN E A, VAN DER MERWE R. The unscented Kalman filter for nonlinear estimation[C]//Proceedings of IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium (Cat. No. 00EX373). Lake Louise, AB, Canada: IEEE, 2000: 153-158.
(  0) 0)
|
| [7] |
卢迪, 刘明基, 吴海涛. 永磁同步电动机系统参数和状态的推广卡尔曼滤波估计[J]. 电机与控制学报, 2003, 7(4): 281-284. LU Di, LIU Mingji, WU Haitao. Parameter and state estimation of PMSM system with extended Kalman filter[J]. Electric machines and control, 2003, 7(4): 281-284. DOI:10.3969/j.issn.1007-449X.2003.04.004 (  0) 0)
|
| [8] |
张雪冬, 牛海强, 吴立新. 一种基于序贯估计的直达声区水面舰船被动测距方法[J]. 应用声学, 2020, 39(4): 491-500. ZHANG Xuedong, NIU Haiqiang, WU Lixin. Passive tracking of a surface ship in the direct zone using sequential parameter estimation[J]. Applied acoustics, 2020, 39(4): 491-500. (  0) 0)
|
| [9] |
苏林, 任群言, 庞立臣, 等. 强非线性时间演化声速剖面的序贯反演[J]. 声学学报, 2019, 44(4): 452-462. SU Lin, REN Qunyan, PANG Lichen, et al. Sequential inversion of highly nonlinear time-evolving sound speed profiles[J]. Acta acustica, 2019, 44(4): 452-462. (  0) 0)
|
| [10] |
LINDSAY C E, CHAPMAN N R. Matched field inversion for geoacoustic model parameters using adaptive simulated annealing[J]. IEEE journal of oceanic engineering, 1993, 18(3): 224-231. DOI:10.1109/JOE.1993.236360 (  0) 0)
|
| [11] |
GERSTOFT P. Inversion of seismoacoustic data using genetic algorithms and a posteriori probability distributions[J]. The journal of the acoustical society of America, 1994, 95(2): 770-782. DOI:10.1121/1.408387 (  0) 0)
|
| [12] |
KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of 1995 International Conference on Neural Networks. Perth, WA, Australia: IEEE, 1995: 1942-1948.
(  0) 0)
|
| [13] |
University of Washington Seattle Applied Physics Lab. APL-UW High-frequency ocean environmental acoustic models handbook[R]. University of Washington Seattle Applied Physics Laboratory, 1994.
(  0) 0)
|
| [14] |
RABINER L R. A tutorial on hidden Markov models and selected applications in speech recognition[J]. Proceedings of the IEEE, 1989, 77(2): 257-286. DOI:10.1109/5.18626 (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


