2. 哈尔滨理工大学 自动化学院 黑龙江, 哈尔滨 150080
2. School of Automation, Harbin University of Science and Technology, Harbin 150080, China
气垫船作为一种特殊的高速水面船,具有独特的两栖性,能够在水面、地面以及沼泽等地带航行,因此被广泛应用于军事和民事中。全垫升气垫船是气垫船的一种,其工作原理是:依靠船体底部与航行表面之间的静升压力支撑船体脱离航行表面,同时利用安装于艉部的空气螺旋桨旋转产生推力,通过空气舵等装置进行控制操作,从而实现高速航行于航行表面的目的。全垫升气垫船垫态航行过程中,由于不具有横向推力,极易受到外界环境的干扰,从而极易产生较大的侧滑。而全高速回转与侧滑会导致全垫升气垫船处于危险的航行状态。如果侧滑与回转超过船的安全限界,可能造成翻船事故[1]。
导引系统是海洋运载器完成诸多控制任务的前提,例如:路径跟踪[2]、轨迹跟踪[3]、目标跟踪[4]、避障控制[5]、编队控制[6]等,都需要导引子系统给出精确的导引参考角度,作为控制子系统的参考输入,进而由控制子系统根据控制算法跟踪导引参考角度。因此,导引技术近年来成为了广大学者关注的热点[7-9]。然而,传统的导引方法中并没有考虑侧滑角的影响,难以实现高精度的路径跟踪效果。因此,提高气垫船的路径跟踪精度、侧滑角的估计和补偿技术成为设计导引方法的关键技术之一。
目前,对于导引算法的研究已经取得的一定的研究成果,主要集中于传统排水水面船以及水下无人潜器上的LOS导引算法研究上,例如无人水面艇[10-11]、水下无人潜器[12]等。值得说明的是,在现有的导引算法中,LOS导引算法、ILOS导引算法和ALOS导引算法是较为经典且实际运用效果较好的导引算法。Fossen等[13]将Line-of-sight(LOS)导引方法应用于自主水下潜器的路径导引上,取得了良好的三维路径跟踪效果。其侧滑角的补偿是假设侧滑角已知,并对导引进行了补偿。随后,Fossen等[14]又将LOS应用于三自由度水面船的路径跟踪上,并证明了LOS导引律的全局指数渐进稳定性。Borhaug等[15]针对欠驱动水面船在海流干扰下的路径跟踪问题,设计了积分LOS导引方法,以补偿海流产生的侧漂力对其路径跟踪效果以及精度的影响,但其仅对直线路径进行了仿真验证。Lekkas等[16]基于积分LOS导引方法提出了直接侧滑补偿和积分侧滑补偿2种方法,由于实际船舶上测量设备的准确度和造价高等问题,直接测量侧滑角不易实现,比较而知,侧滑补偿算法研究具有实际意义。而后,Fossen等[17]又针对Dubins路径,提出了基于自适应侧滑角补偿的LOS导引策略,这是通过对侧滑角的估计设计LOS导引策略,对于恒定小侧滑角的补偿,其效果较好。Liu等[18]提出一种基于预测器的侧滑角估计方法,并对恒定小侧滑角的估计进行了仿真验证。国内,对侧滑的研究比较少,王浩铎等[19]提出一种变增益导引策略,能够补偿外部环境干扰的引起的侧滑,但其只适用于直线路径,且并没有对侧滑角进行直接估计补偿。
以上研究都是基于侧滑角是小范围常量的假设基础上进行的,而针对全垫升气垫船极易产生大侧滑的特点,本文提出了一种基于自适应时变大侧滑角补偿的LOS导引策略。首先,采用三次样条插值法生成一般曲线路径,其优点是能够保证曲线在经过特定航路点时保证其二阶导数连续。其次,设计了一种基于预测器的侧滑角自适应估计方法,通过引入2个侧滑角参数,取缔了现有侧滑角的恒定小角度假设,实现时变大侧滑角的估计与补偿目的。最后,在设计的侧滑角参数估计的模型基础上设计基于时变大侧滑角估计和补偿自适应LOS导引方法,实现了气垫船在未知侧漂力下的路径跟踪收敛目标。
1 气垫船运动模型及LOS导引算法 1.1 气垫船运动数学模型为描述气垫船运动过程,分别引入北东坐标系(north east down, NED),船体坐标系以及Serret-Frenet (SF)坐标系,并建立气垫船三自由度运动学和动力学数学模型为[20]:
| $ \left\{\begin{array}{l} \dot{x}=u \cos \psi-v \sin \psi \\ \dot{y}=u \sin \psi+v \cos \psi \\ \dot{\psi}=r \\ m(\dot{u}-v r)=F_{x} \\ m(\dot{v}+u r)=F_{y} \\ I_{z} \dot{r}=M_{z} \end{array}\right. $ | (1) |
式中:x、y、ψ分别表示气垫船在北东坐标系下的北向位置,东向位置和艏向角度;u、v、r分别表示气垫船在船体坐标系下的纵荡速度、横荡速度和艏摇角速度;m、Iz分别表示气垫船的质量和转动惯量;Fx、Fy、Mz分别表示气垫船在x、y、z方向上受到的合力及力矩。
由于全垫升气垫船的物理垫升结构,其船体是脱离航行表面的,因而与传统水面船不同,空气阻力是气垫船的主要阻力,因而建模过程中首要考虑空气动力/力矩。
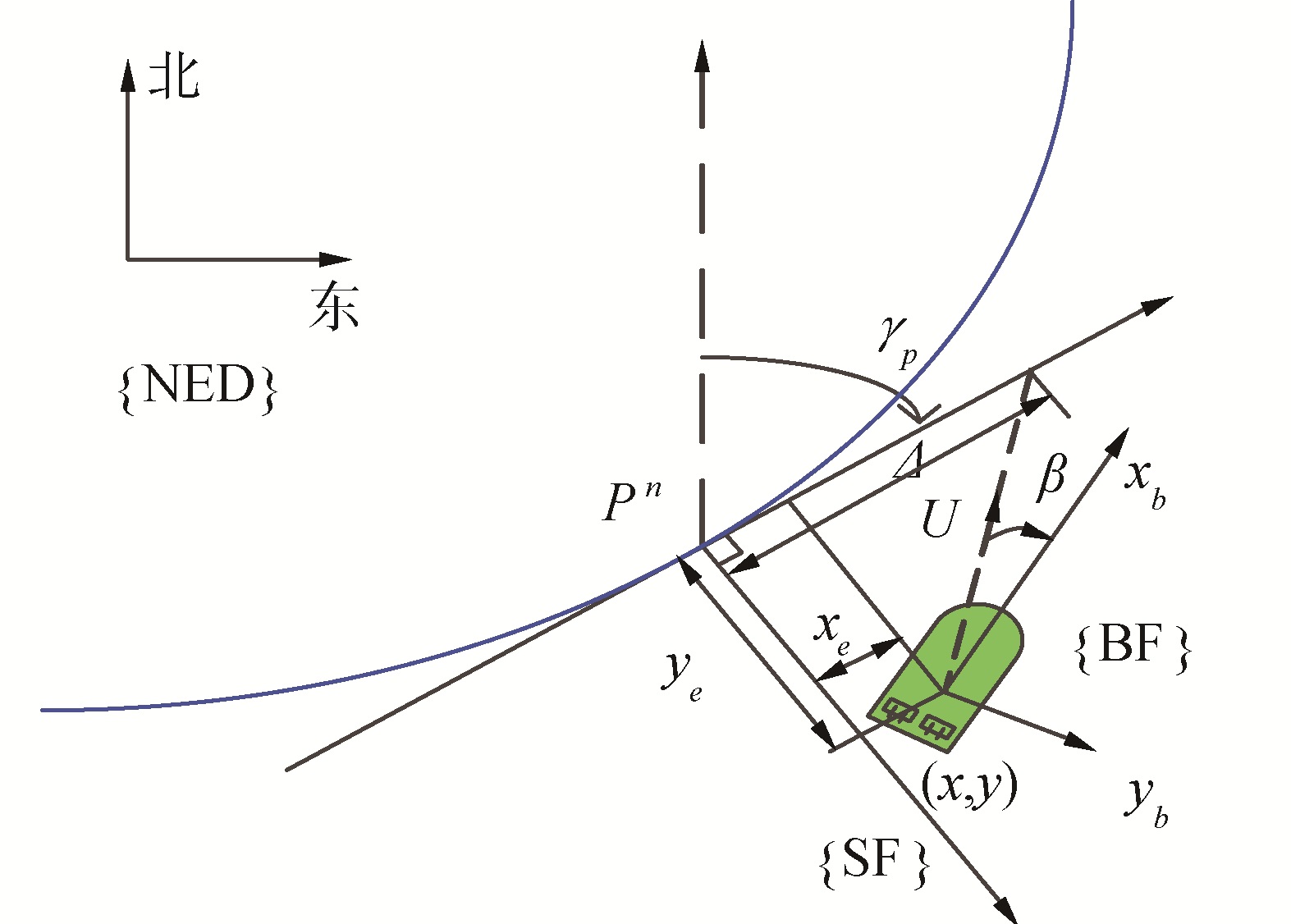
1.2 LOS导引基于LOS导引方法的气垫船路径跟踪原理图,如图 1所示。其中,β为侧滑角,是合速度U与船体坐标系xb轴的夹角;Δ为前视距离;ϑ代表大于零的路径参数化变量,任意ϑ都对应一个参考点位置(xp(ϑ), yp(ϑ))。为到达由参考点的切向向量和法向向量构成的SF坐标系、NED坐标系需要旋转角度:
| $ r_{p}({\vartheta})=\arctan \left(y_{p}^{\prime}({\vartheta}), x_{p}^{\prime}({\vartheta})\right) $ | (2) |
|
Download:
|
| 图 1 LOS曲线路径跟踪原理 Fig. 1 The geometrical illustration of LOS guidance | |
式中:
由式(2)可得:
| $ \dot{\gamma}_{p}=\frac{x_{p}^{\prime}(\vartheta) y_{p}^{\prime \prime}({\vartheta})-x_{p}^{\prime \prime}({\vartheta}) y_{p}^{\prime}({\vartheta})}{x_{p}^{\prime 2}({\vartheta})+y_{p}^{\prime 2}({\vartheta})} $ | (3) |
对于位于NED坐标下(x, y) 位置的气垫船,由模型(1)可得其路径跟踪的切向误差xe以及法向误差ye模型:
| $ \left\{\begin{aligned} \dot{x}_{e} &=U\left[\cos \left(\psi-\gamma_{p}\right) \cos \beta(t)-\right.\\ &\left.\sin \left(\psi-\gamma_{p}\right) \sin \beta(t)\right]+\dot{\gamma}_{p} y_{e}-u_{p} \\ \dot{y}_{e}&=U\left[\sin \left(\psi-\gamma_{p}\right) \cos \beta(t)+\right.\\ &\left.\cos \left(\psi-\gamma_{p}\right) \sin \beta(t)\right]-\dot{\gamma}_{p} x_{e} \end{aligned}\right. $ | (4) |
式中:
本文设计的路径跟踪控制系统采用基于侧滑识别补偿的LOS导引策略与PID航向控制器相结合。导引系统根据实际位置和参考路径位置计算出航向角度;控制系统根据导引系统给出的期望航向角以及当前气垫船的航向角度进行航向控制,本文假设速度可以控制到期望速度,对速度不进行控制设计。
1.3 参数化路径生成在许多领域中,多项式插值法是一种解决给定航路点的曲线路径生成问题的通用方法。然而,三次多项式插值法并不能保证曲线的二阶导数连续,鉴于本文的路径跟踪更新涉及到路径的二阶导数,本文设计了基于航路点式的三次样条插值曲线路径生成方法。有效地保证了曲线路径的二阶导数的在航路点处的连续,进而进一步提高了曲线路径的光滑度。
预设航路点集N,参考点(xp(ϑ), yp(ϑ)) 可采用三次多项式模型计算:
| $ \left\{\begin{array}{l} x_{p}({\vartheta})=a_{3} {\vartheta}^{3}+a_{2} {\vartheta}^{2}+a_{1} {\vartheta}+a_{0} \\ y_{p}({\vartheta})=b_{3} {\vartheta}^{3}+b_{2} {\vartheta}^{2}+b_{1} {\vartheta}+b_{0} \end{array}\right. $ | (5) |
式中参数aj、bj(j=0, 1, 2, 3) 为位置参数。参考点xp(ϑ) 和yp(ϑ) 对参数ϑ的导数为:
| $ \left\{\begin{array}{l} x_{p}^{\prime}({\vartheta})=\frac{\mathrm{d} x_{p}(\vartheta)}{\mathrm{d} \vartheta}=3 a_{3} \vartheta^{2}+2 a_{2} \vartheta+a_{1} \\ y_{p}^{\prime}({\vartheta})=\frac{\mathrm{d} y_{p}(\vartheta)}{\mathrm{d} \vartheta}=3 b_{3} \vartheta^{2}+2 b_{2} \vartheta+b_{1} \end{array}\right. $ | (6) |
所以,全垫升气垫船的参考速度up可计算为:
| $ u_{p}=\sqrt{\dot{x}_{p}^{2}(\vartheta)+\dot{y}_{p}^{2}(\vartheta)}=\dot{\vartheta} \sqrt{x_{p}^{\prime 2}(\vartheta)+y_{p}^{\prime 2}(\vartheta)} $ | (7) |
式中:
| $ \left\{\begin{array}{l} \dot{x}_{p}(\vartheta)=\frac{\mathrm{d} x_{p}(\vartheta)}{\mathrm{d} \vartheta} \dot{\vartheta}(t) \\ \dot{y}_{p}(\vartheta)=\frac{\mathrm{d} y_{p}(\vartheta)}{\mathrm{d} \vartheta} \dot{\vartheta}(t) \end{array}\right. $ | (8) |
对于式(6)中的未知参数,可采用三次样条法计算[20]。
在航路点集N中的任意2个相邻航路点(xk-1, yk-1) 与(xk, yk) 须满足:
| $ \left\{\begin{array}{l} x_{p}\left({\vartheta}_{k-1}\right)=x_{k-1}, x_{p}\left({\vartheta}_{k}\right)=x_{k} \\ y_{p}\left({\vartheta}_{k-1}\right)=y_{k-1}, y_{p}\left({\vartheta}_{k}\right)=y_{k} \end{array}\right. $ | (9) |
式中k=1, 2,…, n。
且为保证曲线的光滑性还须满足:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathop {\lim }\limits_{\vartheta \to \vartheta _k^ - } x_d^\prime \left( {{\vartheta _k}} \right) = \mathop {\lim }\limits_{\vartheta \to \vartheta _k^ + } x_d^\prime \left( {{\vartheta _k}} \right)}\\ {\mathop {\lim }\limits_{\vartheta \to \vartheta _k^ - } x_d^{\prime \prime }\left( {{\vartheta _k}} \right) = \mathop {\lim }\limits_{\vartheta \to \vartheta _k^ + } x_d^{\prime \prime }\left( {{\vartheta _k}} \right)} \end{array}} \right. $ | (10) |
为了满足上述约束,添加速度和加速度的上界条件,那么:
| $ \left\{\begin{array}{l} x_{p}^{\prime}\left({\vartheta}_{0}\right)=x_{0}^{\prime}, x_{p}^{\prime}\left({\vartheta}_{n}\right)=x_{n}^{\prime} \\ y_{p}^{\prime}\left({\vartheta}_{0}\right)=y_{0}^{\prime}, y_{p}^{\prime}\left({\vartheta}_{n}\right)=y_{n}^{\prime} \end{array}\right. $ | (11) |
| $ \left\{\begin{array}{l} x_{p}^{\prime \prime}\left(\vartheta_{0}\right)=x_{0}^{\prime \prime}, x_{p}^{\prime \prime}\left(\vartheta_{n}\right)=x_{n}^{\prime \prime} \\ y_{p}^{\prime \prime}\left(\vartheta_{0}\right)=y_{0}^{\prime \prime}, y_{p}^{\prime \prime}\left(\vartheta_{n}\right)=y_{n}^{\prime \prime} \end{array}\right. $ | (12) |
多项式xp(ϑk) 通过ak=[a3k a2k a1k a0k]T计算,将n个航路点的未知参数写成向量形式:
| $ \boldsymbol{x}=\left[\boldsymbol{a}_{k}^{\mathrm{T}}, \boldsymbol{a}_{k+1}^{\mathrm{T}}, \cdots, \boldsymbol{a}_{n-1}^{\mathrm{T}}\right]^{\mathrm{T}} $ | (13) |
从而,三次插值问题转化为线性等式:
| $ \boldsymbol{y}=\boldsymbol{A}\left({\vartheta}_{k-1}, \cdots, \vartheta_{k}\right) \boldsymbol{x}, \quad k=1,2, \cdots, n $ | (14) |
式中
| $ \boldsymbol{A} = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{c}_{{\rm{start }}}}}&{{{\bf{0}}_{1 \times 4}}}&{{{\bf{0}}_{1 \times 4}}}& \cdots &{{{\bf{0}}_{1 \times 4}}}\\ {\boldsymbol{p}\left( {{\vartheta _0}} \right)}&{{{\bf{0}}_{1 \times 4}}}&{{{\bf{0}}_{1 \times 4}}}& \cdots &{{{\bf{0}}_{1 \times 4}}}\\ {\boldsymbol{p}\left( {{\vartheta _1}} \right)}&{{{\bf{0}}_{1 \times 4}}}&{{{\bf{0}}_{1 \times 4}}}& \cdots &{{{\bf{0}}_{1 \times 4}}}\\ {{{\bf{0}}_{1 \times 4}}}&{\boldsymbol{p}\left( {{\vartheta _1}} \right)}&{{{\bf{0}}_{1 \times 4}}}& \cdots &{{{\bf{0}}_{1 \times 4}}}\\ { - \boldsymbol{v}\left( {{\vartheta _1}} \right)}&{\boldsymbol{v}\left( {{\vartheta _1}} \right)}&{{{\bf{0}}_{1 \times 4}}}& \cdots &{{{\bf{0}}_{1 \times 4}}}\\ { - \boldsymbol{a}\left( {{\vartheta _1}} \right)}&{\boldsymbol{a}\left( {{\vartheta _1}} \right)}&{{{\bf{0}}_{1 \times 4}}}& \cdots &{{{\bf{0}}_{1 \times 4}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {{{\bf{0}}_{1 \times 4}}}&{{{\bf{0}}_{1 \times 4}}}&{{{\bf{0}}_{1 \times 4}}}& \cdots &{\boldsymbol{p}\left( {{\vartheta _n}} \right)}\\ {{{\bf{0}}_{1 \times 4}}}&{{{\bf{0}}_{1 \times 4}}}&{{{\bf{0}}_{1 \times 4}}}& \cdots &{{\boldsymbol{c}_{{\rm{final }}}}} \end{array}} \right] $ | (15) |
式中:
根据x=A-1y可解得所有未知参数值。参数bk=[b3kb2kb1kb0k]T采用同样的方法计算。
2 基于预测模型的自适应大侧滑角估计器设计本节针对未知侧滑角参数, 设计基于预测器的自适应大侧滑角的估计。Fossen等[17]将侧滑角的范围假设为β∈(0°,5°),而气垫船的极易产生侧滑的特点导致侧滑角的范围有所扩大β∈(0°,15°),导致小侧滑的假设不再适用。本文设计的侧滑角估计有别于Fossen等小侧滑角估计,取缔其小侧滑角的假设,引入2个参数θ1与θ2,对大侧滑角进行了自适应估计。
设参数θ1=cosβ, θ2=sinβ,模型(4)可转化为:
| $ \left\{\begin{array}{l} \dot{x}_{e}=U\left[\cos \left(\psi-\gamma_{p}\right) \theta_{1}-\sin \left(\psi-\gamma_{p}\right) \theta_{2}\right]+\dot{\gamma}_{p} y_{e}-u_{p} \\ \dot{y}_{e}=U\left[\sin \left(\psi-\gamma_{p}\right) \theta_{1}+\cos \left(\psi-\gamma_{p}\right) \theta_{2}\right]-\dot{\gamma}_{p} x_{e} \end{array}\right. $ | (16) |
由于参数θi(i=1, 2) 为未知参数,设计预测器为:
| $ \left\{\begin{aligned} \hat{x}_{e}=& U\left[\cos \left(\psi-\gamma_{p}\right) \hat{\theta}_{1}-\sin \left(\psi-\gamma_{p}\right) \hat{\theta}_{2}\right]+\\ & \dot{\gamma}_{p} \hat{y}_{e}-u_{p}+k_{x}\left(x_{e}-\hat{x}_{e}\right) \\ \hat{y}_{e}=& U\left[\sin \left(\psi-\gamma_{p}\right) \hat{\theta}_{1}+\cos \left(\psi-\gamma_{p}\right) \hat{\theta}_{2}\right]-\\ & \dot{\gamma}_{p} \hat{x}_{e}+k_{y}\left(y_{e}-\hat{y}_{e}\right) \end{aligned}\right. $ | (17) |
式中:
设计基于预测误差的参数自适应估计律为:
| $ \left\{\begin{array}{c} \dot{\hat{\theta}}_{1}=\gamma_{1} U\left[\cos \left(\psi-\gamma_{p}\right) \tilde{x}_{e}+\sin \left(\psi-\gamma_{p}\right) \tilde{y}_{e}\right] \\ \dot{\hat{\theta}}_{2}=\gamma_{2} U\left[-\sin \left(\psi-\gamma_{p}\right) \tilde{x}_{e}+\cos \left(\psi-\gamma_{p}\right) \tilde{y}_{e}\right] \end{array}\right. $ | (18) |
得到预测误差动态系统为:
| $ \left\{\begin{aligned} \dot{\tilde{x}}_{e}=& U\left[\cos \left(\psi-\gamma_{p}\right) \tilde{\theta}_{1}-\sin \left(\psi-\gamma_{p}\right) \tilde{\theta}_{2}\right]+\\ & \dot{\gamma}_{p} \tilde{y}_{e}-k_{x} \tilde{x}_{e} \\ \dot{\tilde{y}}_{e}=&U\left[\sin \left(\psi-\gamma_{p}\right) \tilde{\theta}_{1}+\cos \left(\psi-\gamma_{p}\right) \tilde{\theta}_{2}\right]-\\ & \dot{\gamma}_{p} \tilde{x}_{e}-k_{y} \tilde{y}_{e} \end{aligned}\right. $ | (19) |
定理1 在状态预测器(17)以及参数自适应律(18)下,预测误差
假设:全垫升气垫船的侧滑角是缓慢变化的,即:
证明:取李雅普诺夫函数:
| $ V_{1}=\left(\tilde{x}_{e}^{2}+\tilde{y}_{e}^{2}+\tilde{\theta}_{1}^{2} / \gamma_{1}+\tilde{\theta}_{2}^{2} / \gamma_{2}\right) / 2 $ | (20) |
对其进行求导并根据假设,得:
| $ \begin{array}{c} \dot{V}_{1}=\tilde{x}_{e} \dot{\tilde{x}}_{e}+\tilde{y}_{e} \dot{\tilde{y}}_{e}+\frac{1}{\gamma_{1}} \tilde{\theta}_{1} \dot{\tilde{\theta}}_{1}+\frac{1}{\gamma_{2}} \tilde{\theta}_{2} \dot{\tilde{\theta}}_{2}= \\ \tilde{x}_{e} \dot{\tilde{x}}_{e}+\tilde{y}_{e} \dot{\tilde{y}}_{e}-\frac{1}{\gamma_{1}} \tilde{\theta}_{1} \dot{\hat{\theta}}_{1}-\frac{1}{\gamma_{2}} \tilde{\theta}_{2} \dot{\hat{\theta}}_{2}-k_{x} \tilde{x}_{e}^{2}+ \\ \tilde{x}_{e} U\left[\cos \left(\psi-\gamma_{p}\right) \tilde{\theta}_{1}-\sin \left(\psi-\gamma_{p}\right) \tilde{\theta}_{2}\right]-\\ k_{y} \tilde{y}_{e}^{2}+\tilde{y}_{e} U\left[\sin \left(\psi-\gamma_{p}\right) \tilde{\theta}_{1}+\cos \left(\psi-\gamma_{p}\right) \tilde{\theta}_{2}\right]- \\ \frac{1}{\gamma_{1}} \tilde{\theta}_{1} \gamma_{1} U\left[\cos \left(\psi-\gamma_{p}\right) \tilde{x}_{e}+\sin \left(\psi-\gamma_{p}\right) \tilde{y}_{e}\right]- \\ \frac{1}{\gamma_{2}} \tilde{\theta}_{2} \gamma_{2} U\left[-\sin \left(\psi-\gamma_{p}\right) \tilde{x}_{e}+\cos \left(\psi-\gamma_{p}\right) \tilde{y}_{e}\right]= \\ -k_{x} \tilde{x}_{e}^{2}-k_{y} \tilde{y}_{e}^{2} \leqslant 0 \end{array} $ | (21) |
根据李雅普诺夫稳定性定理,可知预测误差和跟踪误差是全局一致渐近稳定的。
3 基于侧滑角补偿的LOS导引本节基于前述的自适应侧滑角参数估计值,对LOS导引进行实时侧滑补偿,以求更好的全垫升气垫船路径跟踪效果。为稳定切向误差xe,设计控制输入up为:
| $ u_{p}=U_{d} \cos \left(\psi-\gamma_{\mathrm{p}}\right) \hat{\theta}_{1}-U_{d} \sin \left(\psi-\gamma_{\mathrm{p}}\right) \hat{\theta}_{2}+\kappa_{1} \hat{x}_{e} $ | (22) |
由式(8)可得路径参数更新律:
| $ \dot{\vartheta}=\frac{U_{d} \cos \left(\psi-\gamma_{\mathrm{p}}\right) \hat{\theta}_{1}-U_{d} \sin \left(\psi-\gamma_{\mathrm{p}}\right) \hat{\theta}_{2}+\kappa_{1} \hat{x}_{e}}{\sqrt{x_{p}^{\prime 2}({\vartheta})+y_{p}^{\prime 2}({\vartheta})}} $ | (23) |
式中κ1∈R, κ1>0为导引律的参数增益。
根据观测模型(17)和路径参数更新率(23),可得:
| $ \hat{x}_{e}=-\kappa_{1} \hat{x}_{e}+k_{x} \tilde{x}_{e}+\dot{\gamma}_{p} \hat{y}_{e} $ | (24) |
由于路径当前参考点的旋转角度γp(ϑ) 为已知量,并且路径跟踪误差可测,设计导引角度为:
| $ \psi_{d}=\gamma_{p}(\vartheta)+\arctan \left(-\frac{1}{\varDelta}\left(\hat{y}_{e}+\alpha_{y}\right)\right) $ | (25) |
式中αy为待设计控制输入。
由于
| $ \left\{\begin{array}{l} \sin \left(\arctan \left(-\frac{\hat{y}_{e}}{\varDelta}-\alpha_{y}\right)\right)=-\frac{\hat{y}_{e}+\alpha_{y}}{\sqrt{\left(\hat{y}_{e}+\alpha_{y}\right)^{2}+\varDelta^{2}}} \\ \cos \left(\arctan \left(-\frac{\hat{y}_{e}}{\varDelta}-\alpha_{y}\right)\right)=\frac{\varDelta}{\sqrt{\left(\hat{y}_{e}+\alpha_{y}\right)^{2}+\varDelta^{2}}} \end{array}\right. $ | (26) |
那么,式(17)中的法向误差估计模型可化为:
| $ \begin{array}{c} \hat{y}_{e}=U\left(\frac{-\left(\hat{y}_{e}+\alpha_{y}\right) \hat{\theta}_{1}}{\sqrt{\left(\hat{y}_{e}+\alpha_{y}\right)^{2}+\varDelta^{2}}}+\frac{\varDelta \hat{\theta}_{2}}{\sqrt{\left(\hat{y}_{e}+\alpha_{y}\right)^{2}+\varDelta^{2}}}\right)+ \\ \dot{\gamma}_{p} \hat{x}_{e}-k_{w 2} \tilde{y}_{e} \end{array} $ | (27) |
取虚拟控制输入
| $ \hat{y}_{e}=-\kappa_{2} \hat{y}_{e}+\dot{\gamma}_{p} \hat{x}_{e}+k_{y} \tilde{y}_{e} $ | (28) |
式中:
| $ \kappa_{2}=\frac{U \hat{\theta}_{1}}{\sqrt{\left(\hat{y}_{e}+\varDelta \hat{\theta}_{2} / \hat{\theta}_{1}\right)^{2}+\varDelta^{2}}} \geqslant 0 $ | (29) |
综上,模型(17)转化为:
| $ \left\{\begin{array}{l} \hat{x}_{e}=-\kappa_{1} \hat{x}_{e}+k_{x} \tilde{x}_{e}+\dot{\gamma}_{p} \hat{y}_{e} \\ \hat{y}_{e}=-\kappa_{2} \hat{y}_{e}+k_{y} \tilde{y}_{e}-\dot{\gamma}_{p} \hat{x}_{e} \end{array}\right. $ | (30) |
导引律(25)化为:
| $ \psi_{d}=\gamma_{p}({\vartheta})+\arctan \left(-\frac{\hat{y}_{e}}{\varDelta}-\frac{\hat{\theta}_{2}}{\hat{\theta}_{1}}\right) $ | (31) |
定理2 以状态
证明:取李雅普诺夫函数:
| $ V_{2}=\left(\hat{x}_{e}^{2}+\hat{y}_{e}^{2}\right) / 2 $ | (32) |
对上述李雅普诺夫函数求导:
| $ \begin{array}{c} \dot{V}_{2}=\hat{x}_{e}\left(-\kappa_{1} \hat{x}_{e}+k_{x} \tilde{x}_{e}+\dot{\gamma}_{p} \hat{y}_{e}\right)+ \\ \hat{y}_{e}\left(-\kappa_{2} \hat{y}_{e}+\dot{\gamma}_{p} \hat{x}_{e}+k_{y} \tilde{y}_{e}\right) \leqslant \\ -\kappa_{1} \hat{x}_{e}^{2}-\kappa_{2} \hat{y}_{e}^{2}+\frac{k_{x}}{2 \varepsilon_{1}} \hat{x}_{e}^{2}+\frac{k_{x} \varepsilon_{1}}{2} \tilde{x}_{e}^{2}+\frac{k_{y}}{2 \varepsilon_{2}} \hat{y}_{e}^{2}+ \\ \frac{k_{y} \varepsilon_{2}}{2} \tilde{y}_{e}^{2} \leqslant-m V_{2}+\frac{k_{x} \varepsilon_{1}}{2} \tilde{x}_{e}^{2}+\frac{k_{y} \varepsilon_{2}}{2} \tilde{y}_{e}^{2} \leqslant \\ \frac{-h}{2} V_{2}-\left(\frac{h}{2} V_{2}-\frac{k_{x} \varepsilon_{1}}{2} \tilde{x}_{e}^{2}-\frac{k_{y} \varepsilon_{2}}{2} \tilde{y}_{e}^{2}\right) \end{array} $ | (33) |
式中:h=min{κ1-kx/2ε1, κ2-ky/2ε2}>0;ε1、ε2>0,通过设计适当的参数ε1、ε2可使:
| $ \frac{h}{2} V_{2}-\frac{k_{x} \varepsilon_{1}}{2} \tilde{x}_{e}^{2}-\frac{k_{y} \varepsilon_{2}}{2} \tilde{y}_{e}^{2} \geqslant 0 $ | (34) |
那么:
| $ \dot{V}_{2} \leqslant \frac{-h}{2} V_{2} $ | (35) |
因此,系统(30)是输入状态稳定的。
定理3 在更新律(18)与导引律(31)下,系统(30)与系统(19)构成的级联系统是全局一致渐近稳定的。
证明:定理1和定理2表明导引子系统(30)是输入输出稳定的,侧滑角估计子系统(19)是全局一致渐近稳定的,由级联系统稳定性理论可知,闭环级联系统是全局一直渐近稳定的。从而,路径跟踪的实际误差
为验证设计方法的有效性,以某型全垫升气垫船为例,在外界风干扰下对气垫船的直线和曲线路径分别进行了路径跟踪仿真实验。仿真环境设置为:风速为10 m/s,风向为30°,其相对风速为:
| $ \left\{\begin{array}{l} x_{\text {wind }}=u+10 \cos \left(30^{\circ}-\psi\right) \\ y_{\text {wind }}=v+10 \sin \left(30^{\circ}-\psi\right) \end{array}\right. $ | (36) |
因此,相对于船体来说随着航向和速度的变化,风干扰是非线性时变的。
仿真案例1:直线路径跟踪,其航路点信息如表 1所示。初始位置及艏向为(0 m, 150 m,0°);直线路径的起点(0 m, 0 m),终点(4 000 m, 4 000 m),初始航速为0 kn,目标航速20 kn,仿真参数设置为κ1=0.5;kx=1;ky=1;γ1=γ2=0.2;仿真结果如图 2~7所示。
| 表 1 直线路径航路点信息 Table 1 The way points data for line path |
|
Download:
|
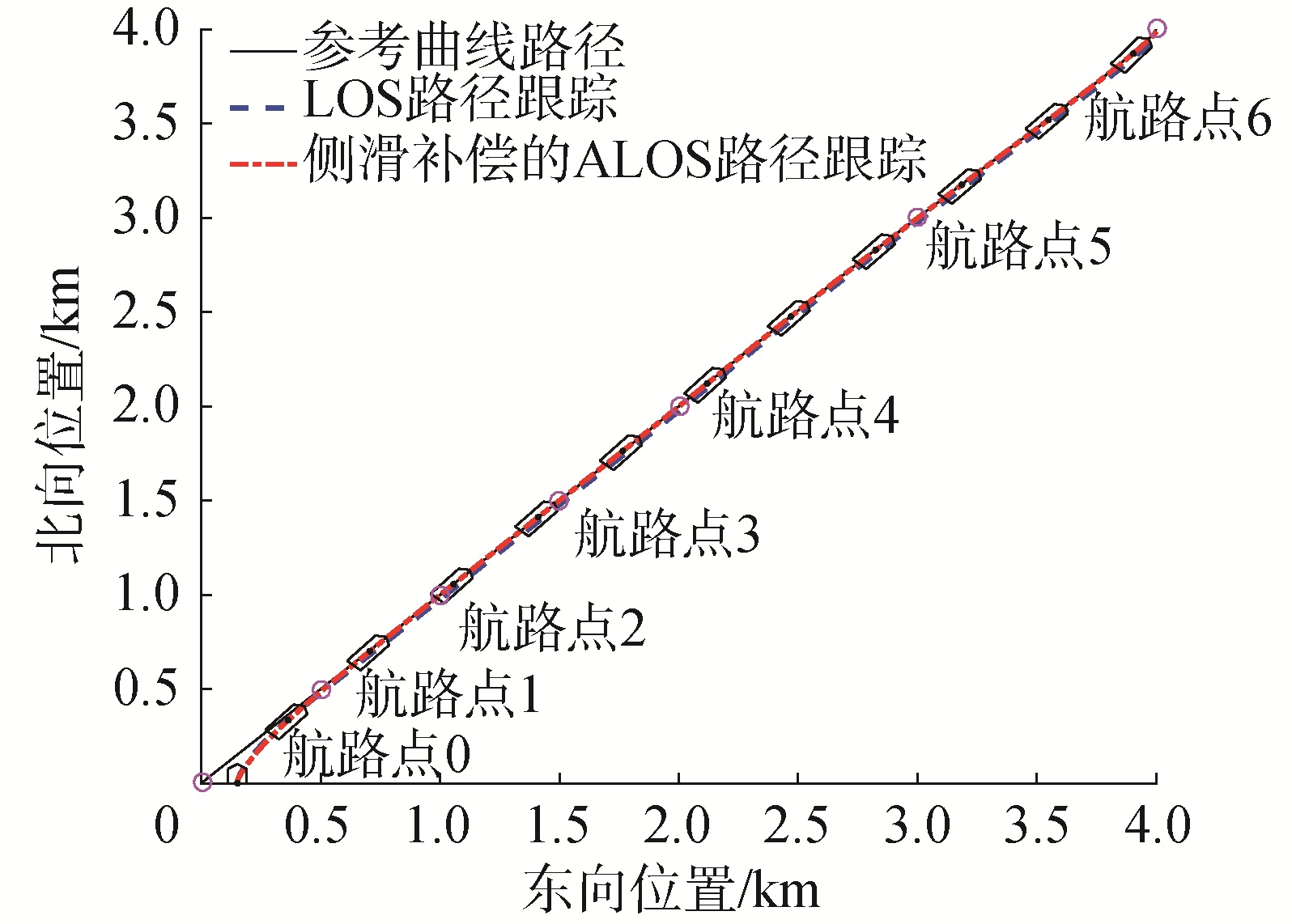
| 图 2 气垫船直线路径跟踪结果 Fig. 2 The curve of linear path tracking of hovercraft | |
|
Download:
|
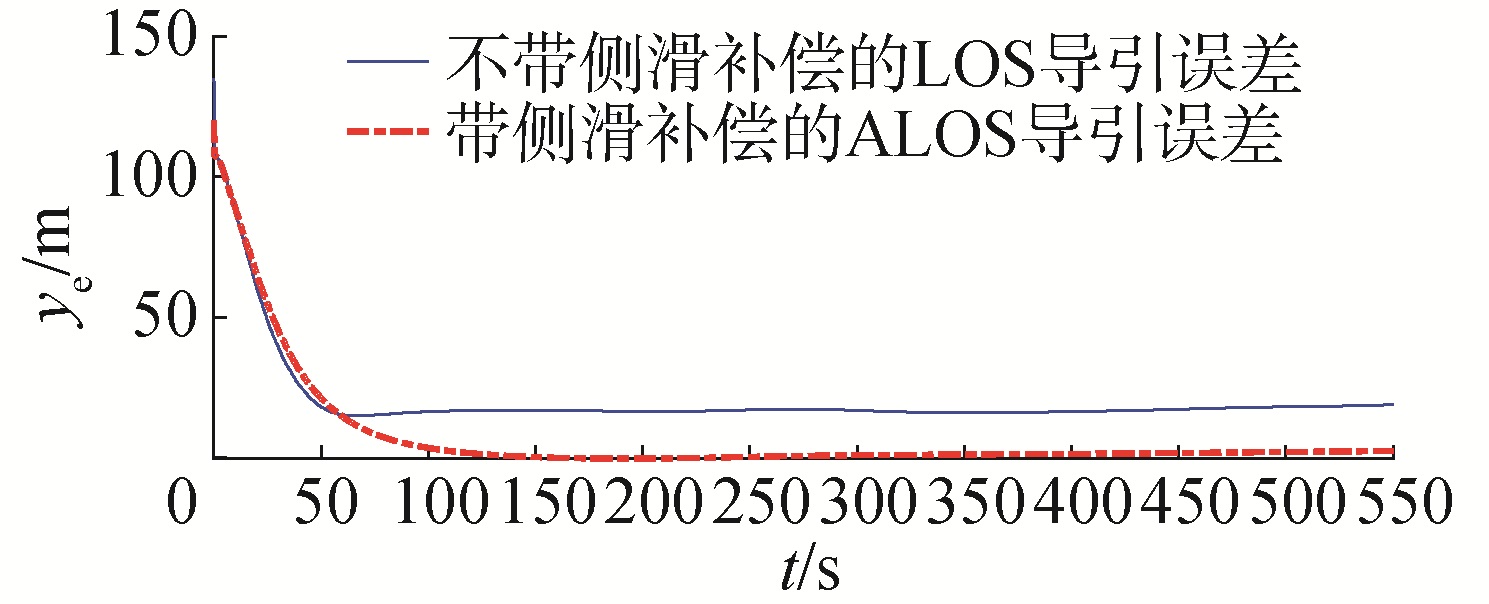
| 图 3 气垫船直线路径跟踪实际法向误差比较 Fig. 3 The comparison of cross-error of path following of hovercraft | |
|
Download:
|
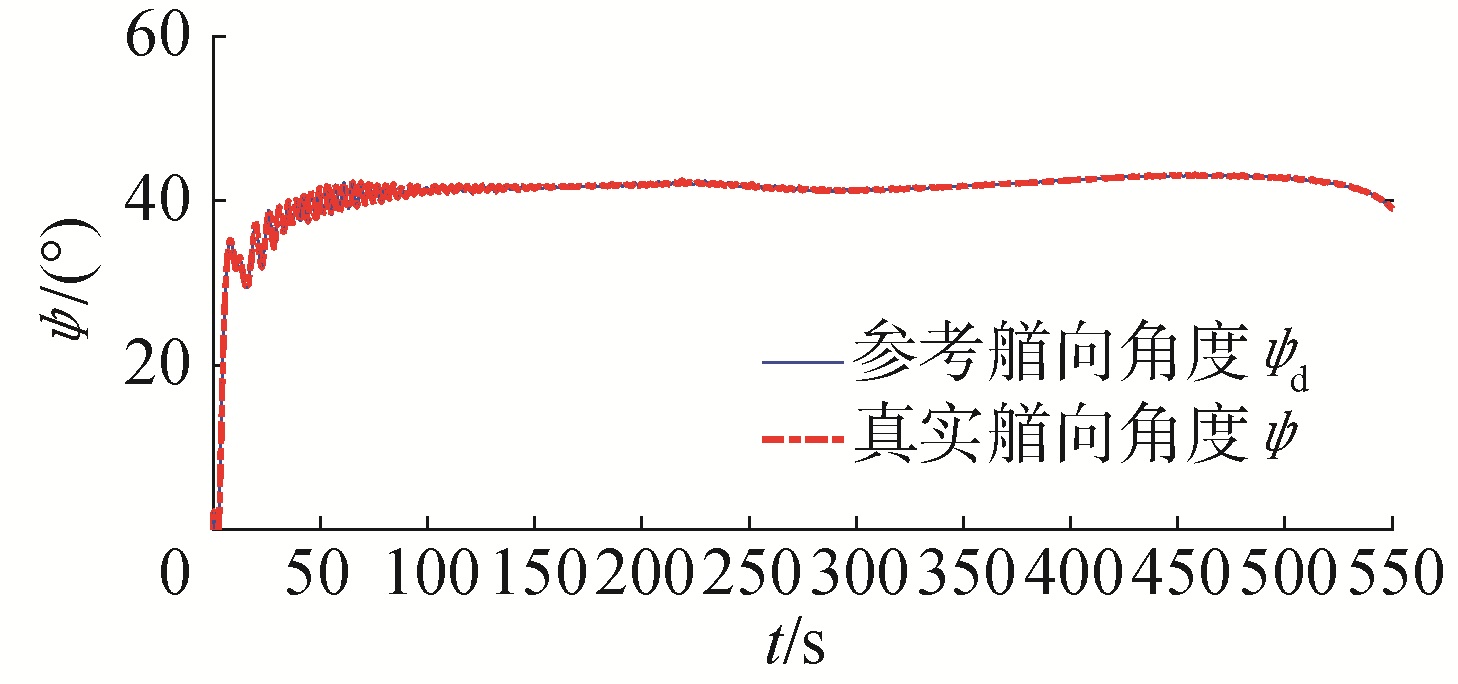
| 图 4 气垫船艏向角度的参考值与实际值 Fig. 4 The reference heading and true heading of hovercraft | |
|
Download:
|
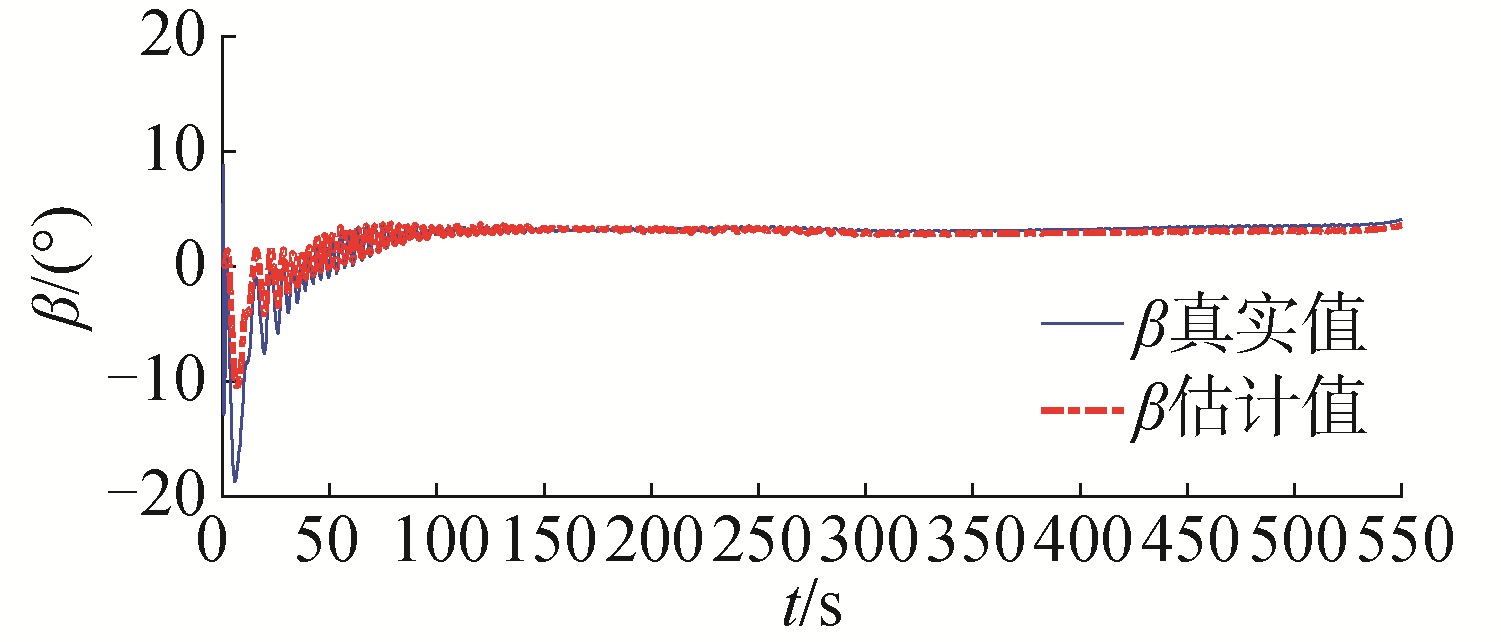
| 图 5 气垫船直线路径跟踪过程中侧滑角的实际值与估计值 Fig. 5 The estimated value and the true value of hovercraft during line path following | |
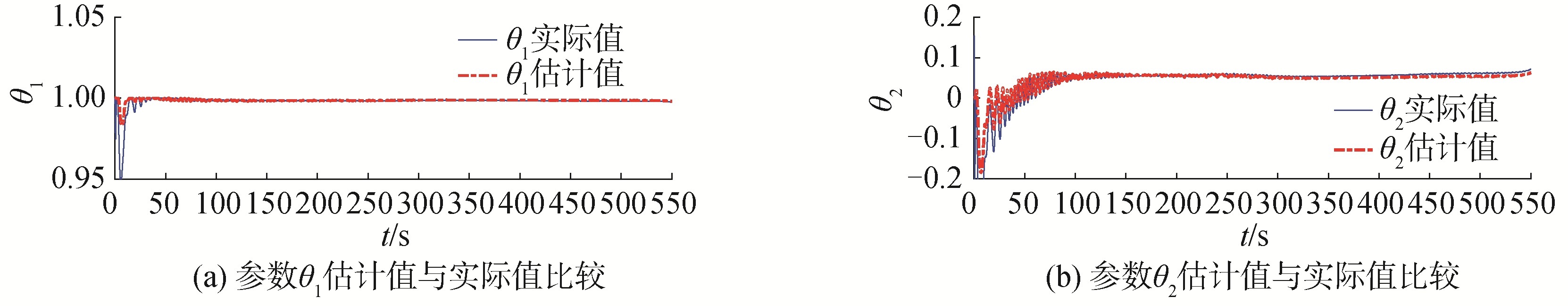
|
Download:
|
| 图 6 气垫船直线路径跟踪的参数估计值 Fig. 6 The estimated parameters for line path following of hovercraft | |
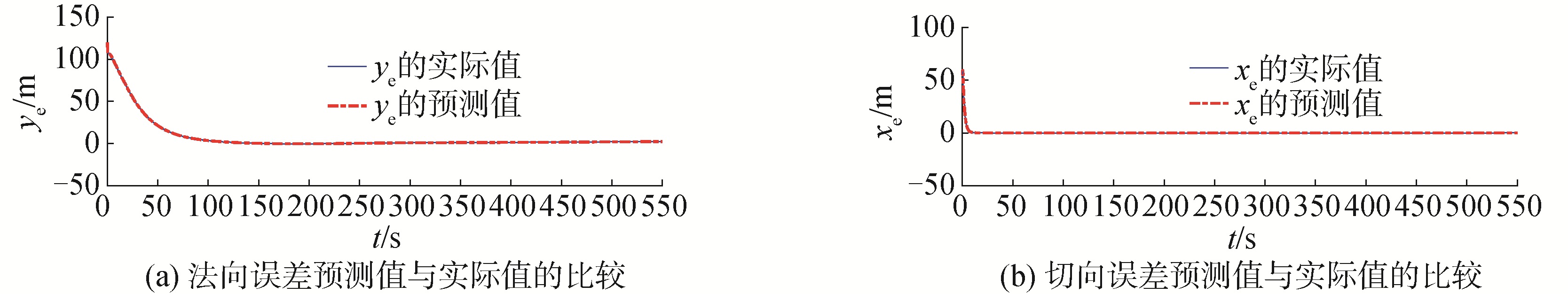
|
Download:
|
| 图 7 气垫船直线路径跟踪误差的实际值与预测值 Fig. 7 The true and predicted value of following errors of hovercraft | |
图 2和图 3表明:带有自适应侧滑补偿的ALOS导引的全垫升气垫船直线路径跟踪效果优于LOS导引的路径跟踪结果。图 3给出了直线路径跟踪的法向误差比较曲线,说明无侧滑补偿的路径跟踪为有差跟踪,稳态误差保持在22 m左右,而带有侧滑补偿的路径跟踪误差收敛于零。图 4表明:艏向控制系统能够跟踪导引系统给出的参考艏向。
图 5和图 6表明:本文提出的方法能够估计到较大的时变侧滑角度,本方法将Fossen等[17]的小侧滑角度假设取缔,能够估计到较大的侧滑角度范围。图 7表明:本文设计的预测器能够保证路径跟踪过程中的跟踪误差的预测值趋于跟踪误差实际值,并且趋于0,从而实现路径跟踪误差收敛的目的。
仿真案例2:曲线路径跟踪,其航路点信息如表 2所示。初始位置及艏向为(0 m, 150 m, 0°);初始航速为0 kn,目标航速20 kn,仿真参数设置为κ1=0.5;kx=1;ky=1;γ1=γ2=0.2;仿真结果如图 8~图 13所示。
| 表 2 曲线路径航路点信息 Table 2 The way points data for cure path |

|
Download:
|
| 图 8 气垫船曲线路径跟踪结果 Fig. 8 The curve of path tracking of hovercraft | |
|
Download:
|
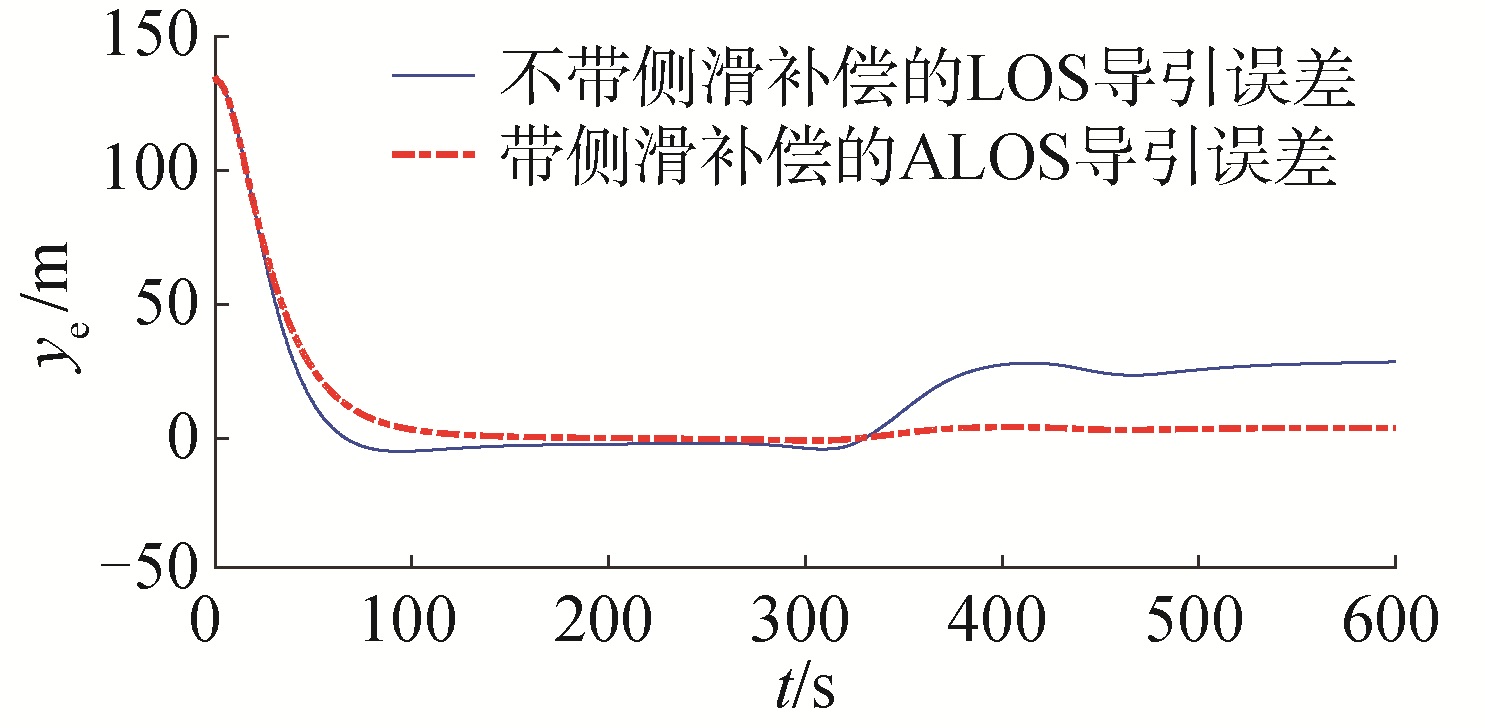
| 图 9 气垫船曲线路径跟踪实际法向误差比较 Fig. 9 The comparison of cross-error for curve path following of hovercraft | |
|
Download:
|
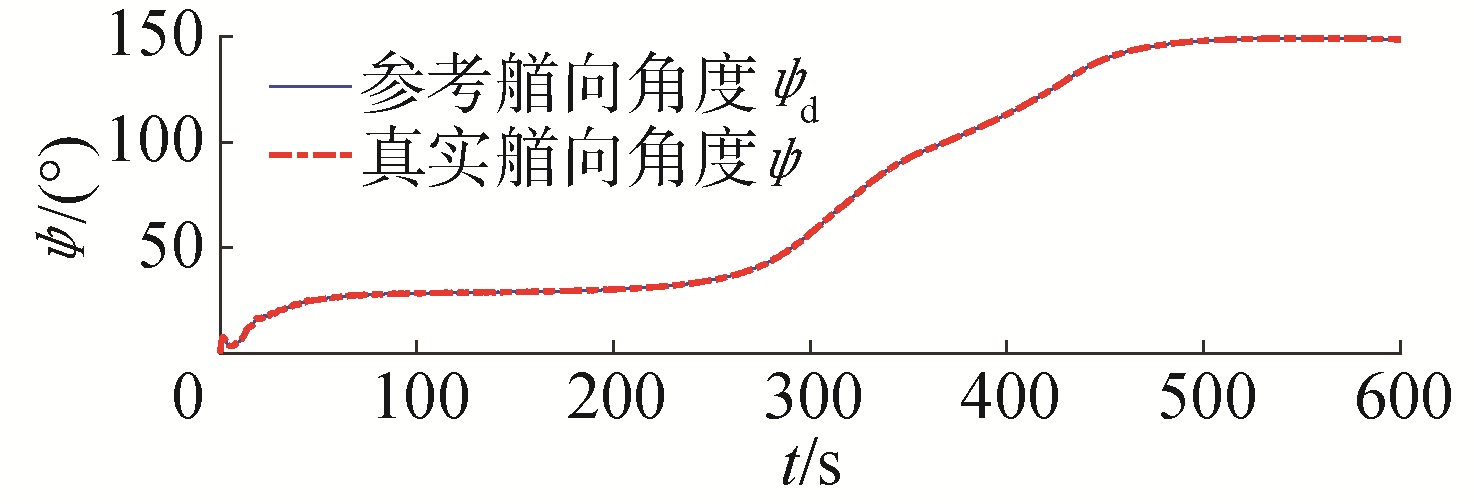
| 图 10 气垫船艏向角度的参考值与实际值 Fig. 10 The reference heading and true heading of hovercraft | |
|
Download:
|
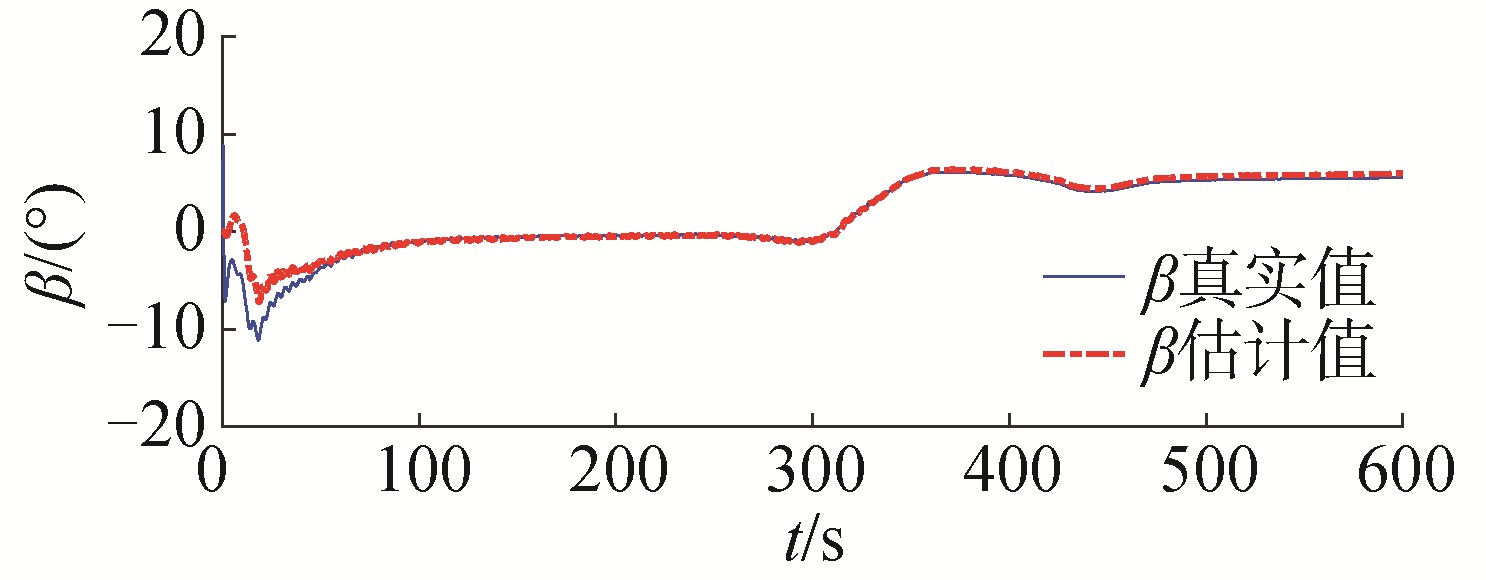
| 图 11 气垫船曲线路径跟踪过程中侧滑角的实际值与估计值 Fig. 11 The estimated value and the true value of hovercraft during curve path following | |
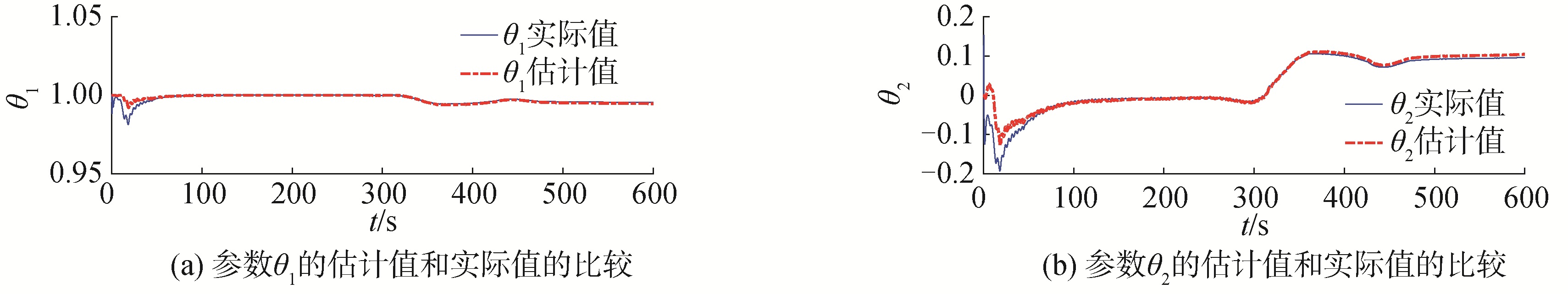
|
Download:
|
| 图 12 气垫船曲线路径跟踪的参数的估计值 Fig. 12 The estimated parameters for curve path following of hovercraft | |

|
Download:
|
| 图 13 气垫船曲线路径跟踪误差的实际值与预测值 Fig. 13 The actual and predicted value of following errors of hovercraft | |
图 8和图 9表明无侧滑补偿的路径跟踪为有差跟踪,在曲线路径的后半段稳态误差约为25 m,而带有侧滑补偿的ALOS路径跟踪稳态误差收敛于0。图 10表明:艏向控制系统能够控制艏向到由导引系统给出的艏向参考值。
图 11和图 12表明:气垫船在曲线路径跟踪过程中,其侧滑角为时变大侧滑角,本文提出的基于预测器的侧滑角估计方法能够估计到气垫船的时变大侧滑角值,并且能够在LOS导引方法中对时变大侧滑角进行补偿。图 13表明:本文设计的预测器能够保证气垫船曲线路径跟踪过程中的跟踪误差估计值趋于跟踪误差实际值,并且趋于零,实现路径跟踪的目的。
综上,本文提出的基于预测模型的时变大侧滑角补偿自适应LOS导引方法能够估计到时变大侧滑角值,并在LOS导引系统中对侧滑角进行补偿,进而实现气垫船在未知侧漂力下的路径跟踪收敛目标。
5 结论1) 提出的基于预测器的侧滑角自适应估计律能够准确地估计到未知时变大侧滑角度值。
2) 设计的预测器是基于位置跟踪误差对侧滑角进行估计和预测,不依赖于模型精确度。
3) 提出的基于时变大侧滑角估计补偿的自适应LOS导引策略能够有效地提高气垫船在未知侧漂力存在情况下路径跟踪精度。
| [1] |
付明玉, 张洪雨, 施小成, 等. 气垫船操纵性能理论分析[J]. 中国造船, 2006, 47(3): 14-21. FU Mingyu, ZHANG Hongyu, SHI Xiaocheng, et al. Theoretical analysis on the operation performance of air cushion vehicle[J]. Shipbuilding of China, 2006, 47(3): 14-21. DOI:10.3969/j.issn.1000-4882.2006.03.002 (  0) 0)
|
| [2] |
YU Yalei, GUO Chen, YU Haomiao. Finite-time PLOS-based integral sliding-mode adaptive neural path following for unmanned surface vessels with unknown dynamics and disturbances[J]. IEEE transactions on automation science and engineering, 2019, 16(4): 1500-1511. DOI:10.1109/TASE.2019.2925657 (  0) 0)
|
| [3] |
XIA Yingkai, XU Kan, LI Ye. Improved line-of-sight trajectory tracking control of under-actuated AUV subjects to ocean currents and input saturation[J]. Ocean engineering, 2019, 174: 14-30. DOI:10.1016/j.oceaneng.2019.01.025 (  0) 0)
|
| [4] |
SHOJAEI K, DOLATSHAHI M. Line-of-sight target tracking control of underactuated autonomous underwater vehicles[J]. Ocean engineering, 2017, 133: 244-252. DOI:10.1016/j.oceaneng.2017.02.007 (  0) 0)
|
| [5] |
MOE S, PETTERSEN K Y. Set-based Line-of-Sight (LOS) path following with collision avoidance for underactuated unmanned surface vessel[C]//Proceedings of the 2016 24th Mediterranean Conference on Control and Automation, Athens, Greece, 2016: 402-409.
(  0) 0)
|
| [6] |
JIN Xu. Fault tolerant finite-time leader-follower formation control for autonomous surface vessels with LOS range and angle constraints[J]. Automatica, 2016, 68: 228-236. DOI:10.1016/j.automatica.2016.01.064 (  0) 0)
|
| [7] |
LEKKAS A M, FOSSEN T I. A quaternion-based LOS guidance scheme for path following of AUVs[J]. IFAC proceedings volumes, 2013, 46(33): 245-250. DOI:10.3182/20130918-4-JP-3022.00070 (  0) 0)
|
| [8] |
LEKKAS A M, FOSSEN T I. Line-of-sight guidance for path following of marine vehicles[M]//GAL O. Advanced in Marine Robotics. Saarbrücken: LAP LAMBERT Academic Publishing, 2013: 63-92.
(  0) 0)
|
| [9] |
ROUT R, CUI Rongxin, HAN Zhengqing. Modified line-of-sight guidance law with adaptive neural network control of underactuated marine vehicles with state and input constraints[J]. IEEE transactions on control systems technology, 2020, 28(5): 1902-1914. DOI:10.1109/TCST.2020.2998798 (  0) 0)
|
| [10] |
WAN Lili, SU Yixin, ZHANG Huajun, et al. An improved integral light-of-sight guidance law for path following of unmanned surface vehicles[J]. Ocean engineering, 2020, 205: 107302. DOI:10.1016/j.oceaneng.2020.107302 (  0) 0)
|
| [11] |
MIAO Jianming, WANG Shaoping, TOMOVIC M M, et al. Compound line-of-sight nonlinear path following control of underactuated marine vehicles exposed to wind, waves, and ocean currents[J]. Nonlinear dynamics, 2017, 89(4): 2441-2459. DOI:10.1007/s11071-017-3596-9 (  0) 0)
|
| [12] |
LIU Fengxu, SHEN Yue, HE Bo, et al. Drift angle compensation-based adaptive line-of-sight path following for autonomous underwater vehicle[J]. Applied ocean research, 2019, 93: 101943. DOI:10.1016/j.apor.2019.101943 (  0) 0)
|
| [13] |
BREIVIK M, FOSSEN T I. Principles of guidance-based path following in 2D and 3D[C]//Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 2005: 627-634.
(  0) 0)
|
| [14] |
FOSSEN T I, PETTERSEN K Y. On uniform semiglobal exponential stability (USGES) of proportional line-of-sight guidance laws[J]. Automatica, 2014, 50(11): 2912-2917. DOI:10.1016/j.automatica.2014.10.018 (  0) 0)
|
| [15] |
BORHAUG E, PAVLOV A, PETTERSEN K Y. Integral LOS control for path following of underactuated marine surface vessels in the presence of constant ocean currents[C]//Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 2008: 4984-4991.
(  0) 0)
|
| [16] |
LEKKAS A M, FOSSEN T I. Integral LOS path following for curved paths based on a monotone cubic hermite spline parametrization[J]. IEEE transactions on control systems technology, 2014, 22(6): 2287-2301. DOI:10.1109/TCST.2014.2306774 (  0) 0)
|
| [17] |
FOSSEN T I, PETTERSEN K Y, GALEAZZI R. Line-of-sight path following for dubins paths with adaptive sideslip compensation of drift forces[J]. IEEE transactions on control systems technology, 2015, 23(2): 820-827. DOI:10.1109/TCST.2014.2338354 (  0) 0)
|
| [18] |
LIU Lu, WANG Dan, PENG Zhouhua, et al. Predictor-based LOS guidance law for path following of underactuated marine surface vehicles with sideslip compensation[J]. Ocean engineering, 2016, 124: 340-348. DOI:10.1016/j.oceaneng.2016.07.057 (  0) 0)
|
| [19] |
王浩铎, 王钦若, 吴小泽. 船舶全局一致渐进路径跟踪变积分增益导航策略[J]. 控制理论与应用, 2015, 32(6): 849-856. WANG Haoduo, WANG Qinruo, WU Xiaoze. Uniformly globally asymptotically stable path following with integral gain-variable guidance law for ships[J]. Control theory & applications, 2015, 32(6): 849-856. (  0) 0)
|
| [20] |
FOSSEN T I. Handbook of marine craft hydrodynamics and motion control[M]. United Kingdom: Wiley, 2011.
(  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


