随着多源信息组合导航技术的发展,导航对系统容错性的需求也日益提高[1]。传统多传感器组合导航系统容错技术以联邦滤波结合故障检测方法为主要技术手段,以故障检测函数与隔离门限判断各子滤波器是否发生故障,隔离故障子滤波器,提高系统可靠性与精度[2-4]。传统容错技术将量测信息分为“有故障”与“无故障”2种状态,对联邦滤波器进行隔离式重构,对于小幅值或斜坡慢变故障的检测灵敏度差,滤波器可能受到污染,且在检测门限附近存在组合模式切换频繁的情况,降低了系统稳定性[5],除此之外,传统的故障检测技术,以子滤波器为检测对象,有害量测发生时,对该子滤波器的所有量测信息实行无差别隔离处理,降低了有效信息利用率[6]。
集中滤波往往被认为不具备容错能力,因此对多源信息组合导航系统来说适用性低于联邦滤波[7]。文献[8]提出了一种矢量故障检测方法,通过引入故障检测矢量函数,以量测信息为检测对象,实现对故障观测信息的定位,为故障隔离提供依据,但这种硬切换方式仍然采用隔离式重构方法。自适应集中滤波器也具有一定的容错能力,其中,部分自适应滤波方法在滤波过程中不断修正或估计噪声统计特性或利用可靠状态实现信息预测,实现变权控制提升估计精度[9-11]。抗差卡尔曼滤波[12-14]作为自适应滤波的一种,以提升滤波算法实际抗差性能与估计结果可靠性为主要目标,通过抗差估计原理实时检测信息质量,控制观测异常,对强突变噪声(阶跃噪声或冲击噪声)的检验具有较高灵敏度,并通过构建等价权函数,对有害信息进行降权处理,抑制突变噪声对估计精度和可靠性的影响,但抗差卡尔曼滤波以量测信息的标准化残差为对象评价观测信息质量并构建自适应因子,对状态向量的一步预测依赖性强,无法抑制诸如斜坡噪声、小幅慢变低频量测噪声。
针对上述问题,本文提出一种应用于多传感器融合组合导航技术的集中容错卡尔曼滤波算法,提升导航系统精度与可靠性。该算法以广义极大似然型抗差估计(M估计)为基础,基于系统动力学模型预测信息与量测信息构建量测残差,借助量测信息先验概率密度与极大后验概率准则,建立涵盖量测粗差、及小幅噪声、慢变噪声等低频噪声的量测信息质量评估函数,基于量测信息质量评估值对量测信息进行分类,并设计权函数与自适应因子,通过调节滤波参数实现有害信息降权处理与隔离,避免硬隔离的同时降低存疑信息对滤波器的污染,充分利用有效量测信息保证滤波效率,达到提升导航系统稳定性、可靠性与精度的目的。
1 集中式自适应容错卡尔曼滤波递推方程假设离散化后的组合导航滤波器动力学模型与观测模型为:
| $ \left\{\begin{array}{l} \boldsymbol{X}_{k}={\mathit{\pmb{{\Phi}}}}_{k, k-1} \boldsymbol{X}_{k-1}+\boldsymbol{\varGamma}_{k} \boldsymbol{W}_{k} \\ \boldsymbol{Z}_{k}=\boldsymbol{H}_{k} \boldsymbol{X}_{k}+\boldsymbol{V}_{k} \end{array}\right. $ | (1) |
式中:Xk为k时刻系统n×1维状态向量,主要包括惯性导航系统误差、惯性器件主要误差参数和量测信息主要误差参数;Φk, k-1为系统n×n维状态一步转移矩阵;Γk为动力学模型系统噪声矩阵;Wk为系统噪声向量;Zk为m×1维量测信息向量;Hk为m×n维量测矩阵;Vk为量测噪声向量。在组合导航中,通常假设系统噪声Wk与量测噪声Vk为零均值高斯白噪声。量测残差rk为:
| $ \boldsymbol{r}_{k}=\boldsymbol{Z}_{k}-\boldsymbol{H}_{k} \hat{\boldsymbol{X}}_{k, k-1} $ | (2) |
式中
根据抗差M估计原则构造自适应容错卡尔曼滤波的极值条件:
| $ \varOmega=\boldsymbol{r}_{k}^{\mathrm{T}} \overline{\boldsymbol{R}}_{k}^{-1} \boldsymbol{r}_{k}+\left(\hat{\boldsymbol{X}}_{k}-\hat{\boldsymbol{X}}_{k, k-1}\right)^{\mathrm{T}} \overline{\boldsymbol{P}}_{k}^{-1}\left(\hat{\boldsymbol{X}}_{k}-\hat{\boldsymbol{X}}_{k, k-1}\right)=\min $ | (3) |
根据极值条件,可得到自适应卡尔曼滤波的递推方程:
| $ \hat{\boldsymbol{X}}_{k, k-1}=\boldsymbol{\varPhi}_{k, k-1} \hat{\boldsymbol{X}}_{k-1} $ | (4) |
| $ \boldsymbol{P}_{k / k-1}=\boldsymbol{\varPhi}_{k, k-1} \boldsymbol{P}_{k-1} \boldsymbol{\varPhi}_{k, k-1}^{\mathrm{T}}+\boldsymbol{\varGamma}_{k-1} \boldsymbol{Q}_{k-1} \boldsymbol{\varGamma}_{k-1}^{\mathrm{T}} $ | (5) |
| $ \boldsymbol{K}_{k}=\overline{\boldsymbol{P}}_{k / k-1} \boldsymbol{H}_{k}^{\mathrm{T}}\left(\boldsymbol{H}_{k} \overline{\boldsymbol{P}}_{k / k-1} \boldsymbol{H}_{k}^{\mathrm{T}}+\overline{\boldsymbol{R}}_{k}\right)^{-1} $ | (6) |
| $ \hat{\boldsymbol{X}}_{k}=\hat{\boldsymbol{X}}_{k / k-1}+\boldsymbol{K}_{k}\left(\boldsymbol{Z}_{k}-\boldsymbol{H}_{k} \hat{\boldsymbol{X}}_{k / k-1}\right) $ | (7) |
| $ \overline{\boldsymbol{P}}_{k}=\left(\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right) \overline{\boldsymbol{P}}_{k / k-1}\left(\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right)^{\mathrm{T}}+\boldsymbol{K}_{k} \overline{\boldsymbol{R}}_{k} \boldsymbol{K}_{k}^{\mathrm{T}} $ | (8) |
式中:Rk为量测信息的等价噪声方差矩阵,当量测信息中存在有害信息,通过Rk调节量测更新在滤波更新中所占权重,实现抗差估计;Rk为状态一步预测的等价方差-协方差矩阵,当动力学模型存在较大扰动异常,可以膨胀过程噪声方差,实现对动力学模型的自适应估计。本文主要针对量测信息异常噪声抑制问题展开研究,通过对量测信息等价噪声协方差矩阵进行自适应调节,提升系统容错性。
在组合导航实际应用中,容错卡尔曼滤波算法通过对量测信息质量进行评价,建立适当的量测信息等价权函数,平衡新息对状态估计的贡献,充分利用有效量测信息,屏蔽有害量测信息,从而达到提升导航系统容错性的目的,因此量测信息质量评价方法与等加权函数的设计十分重要,是决定滤波算法容错性能的关键因素之一。
2 质量评价函数与量测噪声等价权函数 2.1 基于先验概率分布的量测信息质量评价函数为了实现对斜坡慢变噪声的识别与抑制,引入量测信息先验概率分布,设计量测信息质量评价函数,再基于质量评价函数设计量测噪声等价权函数与自适应因子,实时调节量测信息权重,提高组合导航系统容错性。
对于i时刻的量测信息,借助i时刻的量测残差ri及量测残差统计特性对该量测信息进行质量评价。根据量测信息统计特性进行假设,假设健康量测信息的残差均值为μ=μ0,则量测信息的残差均值包含2个样本类型:
H0:待检测信息健康,μ=μ0;
H1:待检测信息异常,μ=μ1。
量测信息也对应属于以上2个样本类型。H0与H1样本的条件概率密度分别为P(rij|H0)与P(rij|H1),其中rij为第i次量测残差ri向量中的第j个元素,即第i次量测信息向量中的第j个量测残差。根据最大后验概率准则,可得2种样本类型的后验概率为:
| $ \left\{\begin{array}{l} P\left(H_{0} \mid r_{i j}\right)=\frac{P\left(r_{i j} \mid H_{0}\right) P\left(H_{0}\right)}{P\left(r_{i j}\right)} \\ P\left(H_{1} \mid r_{i j}\right)=\frac{P\left(r_{i j} \mid H_{1}\right) P\left(H_{1}\right)}{P\left(r_{i j}\right)} \end{array}\right. $ | (9) |
式中:P(H0) 为正常状态的先验概率;P(H1) 为故障状态的先验概率。样本发生判断准则为:
| $ \begin{array}{l} \frac{P\left(H_{1} \mid r_{i j}\right)}{P\left(H_{0} \mid r_{i j}\right)}>1, \quad H_{1} \text { 成立 } \\ \frac{P\left(H_{1} \mid r_{i j}\right)}{P\left(H_{0} \mid r_{i j}\right)}<1, \quad H_{0} \text { 成立 } \end{array} $ |
由于
| $ \begin{array}{c} \frac{P\left(H_{1} \mid r_{i j}\right)}{P\left(H_{0} \mid r_{i j}\right)}=\frac{P\left(r_{i j} \mid H_{1}\right) P\left(H_{1}\right) / P\left(r_{i j}\right)}{P\left(r_{i j} \mid H_{0}\right) P\left(H_{0}\right) / P\left(r_{i j}\right)}= \\ \frac{P\left(r_{i j} \mid H_{1}\right)}{P\left(r_{i j} \mid H_{0}\right)} \frac{P\left(H_{1}\right)}{P\left(H_{0}\right)} \end{array} $ | (10) |
定义似然比公式为:
| $ L=\frac{P\left(r_{i j} \mid H_{1}\right)}{P\left(r_{i j} \mid H_{0}\right)} $ | (11) |
此时,样本发生判断准则可以被改写为对似然比值大小的判断。预先设计门限值TD,可得到:
| $ \left\{\begin{array}{ll} L>\frac{P\left(H_{0}\right)}{P\left(H_{1}\right)} T_{D}, & H_{1} \text { 成立 } \\ L<\frac{P\left(H_{0}\right)}{P\left(H_{1}\right)} T_{D}, & H_{0} \text { 成立 } \end{array}\right. $ |
式中门限TD值与判断误警率、漏检率相关。
对于待检测的第k次获得的量测信息rkj,考虑从第1到k次逐次获取的量测信息序列r1j, r2j, …, rkj,则rkj的样本似然比L(k) 为:
| $ L(k)=\frac{P\left(r_{1 j}, r_{2 j}, \cdots, r_{k j} \mid H_{1}\right)}{P\left(r_{1 j}, r_{2 j}, \cdots, r_{k j} \mid H_{0}\right)}=\prod\limits_{i=1}^{k} \frac{P\left(r_{i j} \mid H_{1}\right)}{P\left(r_{i j} \mid H_{0}\right)} $ | (12) |
对似然比L(k) 取对数变换,定义对数似然比为量测信息质量评价函数,得到质量评价函数递推公式:
| $ \begin{array}{*{20}{c}} {\lambda (k) = \ln [L(k)] = \ln \left[ {\prod\limits_{i = 1}^k {\frac{{P\left( {{r_{ij}}\mid {H_1}} \right)}}{{P\left( {{r_{ij}}\mid {H_0}} \right)}}} } \right] = }\\ {\ln \left[ {\prod\limits_{i = 1}^{k - 1} {\frac{{P\left( {{r_{ij}}\mid {H_1}} \right)}}{{P\left( {{r_{ij}}\mid {H_0}} \right)}}} } \right] + \ln \left[ {\frac{{P\left( {{r_{kj}}\mid {H_1}} \right)}}{{P\left( {{r_{kj}}\mid {H_0}} \right)}}} \right] = }\\ {\lambda (k - 1) + \Delta \lambda (k)} \end{array} $ | (13) |
应用于组合导航量测信息评价时,量测信息近似服从正态分布,则在H0与H1下待评价量测信息的条件概率密度分别为:
| $ \left\{ {\begin{array}{*{20}{l}} {P\left( {{r_{ij}}\mid {H_0}} \right) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}{\sigma _i}} }}\exp \left[ { - \frac{{\left( {{r_{ij}} - {\mu _0}} \right)}}{{{\sigma _i}^2}}} \right]}\\ {P\left( {{r_{ij}}\mid {H_1}} \right) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}{\sigma _i}} }}\exp \left[ { - \frac{{\left( {{r_{ij}} - {\mu _1}} \right)}}{{{\sigma _i}^2}}} \right]} \end{array}} \right. $ | (14) |
样本似然比L(k) 为:
| $ L(k)=\exp \left[\sum\limits_{i=1}^{k} \frac{\left(r_{i j}-\mu_{0}\right)-\left(r_{i j}-\mu_{1}\right)}{\sigma_{i}{}^{2}}\right] $ | (15) |
其质量评价函数λ(k) 的递推公式为:
| $ \begin{array}{c} \lambda(k)=\ln [L(k)]=\sum\limits_{i=1}^{k} \frac{\left(r_{i j}-\mu_{0}\right)-\left(r_{i j}-\mu_{1}\right)}{\sigma_{i}{}^{2}}= \\ \lambda(k-1)+\Delta \lambda(k) \end{array} $ | (16) |
其中:
| $ \Delta \lambda(k)=\frac{\left(r_{k j}-\mu_{0}\right)-\left(r_{k j}-\mu_{1}\right)}{\sigma_{k}{}^{2}}, i=1,2, \cdots, k。$ |
量测新息服从正态分布,检验统计量与待检测信号的低频噪声实时幅值相关,因此质量评价函数值的大小可以反映被检测量测信息实时质量,且由于先验概率的引入与新观察数据的不断填充,除了突变粗差外,小幅慢变噪声也可以被检测,对量测信息质量的评价可以反映小幅慢变噪声的影响。
2.2 等价权函数与自适应因子构造理想的权函数可以根据量测信息质量,实现对量测信息权重的合理调节,有较强的容错能力(有效过滤有害观测信息),且具有较高的滤波估计效率(合理利用有效信息)。得到广泛应用的权函数有2段函数式和3段函数式,2段函数法包括常用的Huber法,丹麦法或选权法,3段函数法包括常用的IGG方案[11]。
考虑到对小幅慢变噪声的检测与抑制,量测信息根据质量评价值被划分为3个区间:有效信息、存疑信息、有害信息,质量评价采用IGG方案,构建权函数:
| $ \alpha_{k j}=\left\{\begin{array}{lc} 1, & \left|\lambda_{k j}\right| \leqslant c_{0} \\ \frac{c_{0}}{\left|\lambda_{k j}\right|}\left(\frac{c_{0}-\left|\lambda_{k j}\right|}{c_{1}-c_{0}}\right)^{2}, & c_{0}<\left|\lambda_{k j}\right|<c_{1} \\ 0, & \left|\lambda_{k j}\right| \geqslant c_{1} \end{array}\right. $ | (17) |
式中:|λk|≤c0时H0成立;|λk|≥c1时H1成立。因此,c0与c1的取值与H0及H1样本判定的误警率Pf及漏检率Pm有关,通常情况下,1.0 < c0 < 1.5,3.0 < c1 < 4.5,本文取c0=1.3,c1=3.5。
αkj为第k次量测信息矢量的第j个分量对应的权值,也可被视为自适应因子,基于权函数,可实时得到该量测信息的等价噪声方差
| $ \bar{R}_{k j}=R_{k j} / \alpha_{k j} $ | (18) |
由式(18)依次求得量测信息向量中所有元素对应的等价噪声协方差,更新量测噪声协方差矩阵,代入式(4)~(8)中,即可完成集中式容错卡尔曼滤波器滤波更新。
3 仿真实验及分析本文提出集中式自适应容错卡尔曼滤波目的在于提高多源导航信息融合的组合导航系统的可靠性,因此,以某惯性/多普勒/超短基线组合导航系统为例,开展仿真实验,验证算法性能。
3.1 惯性/多普勒/超短基线组合导航滤波模型选取惯性导航系统姿态、速度、位置误差为主要待估计状态量,选取多普勒计程仪速度信息、超短基线相对位置信息(斜距R、航向角α、俯仰角β) 为量测信息,建立组合导航模型。此处,采用文献[8]中已被验证的极区格网惯性/声学组合导航滤波模型,其系统状态模型为:
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{\dot x}}_{{\rm{SINS}}}}}\\ {{{\boldsymbol{\dot x}}_{{\rm{DVL}}}}}\\ {{{\boldsymbol{\dot x}}_{{\rm{USBL}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{F}_{{\rm{SINS}}}}} &{{{\bf{0}}_{15 \times 3}}}&{{{\bf{0}}_{15 \times 6}}}\\ {{{\bf{0}}_{3 \times 15}}}&{{\boldsymbol{F}_{{\rm{DVL}}}}}&{{{\bf{0}}_{3 \times 6}}}\\ {{{\bf{0}}_{6 \times 15}}}&{{{\bf{0}}_{6 \times 3}}}&{{\boldsymbol{F}_{{\rm{USBL}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{x}_{{\rm{SINS}}}}}\\ {{\boldsymbol{x}_{{\rm{DVL}}}}}\\ {{\boldsymbol{x}_{{\rm{USBL}}}}} \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{G}_{{\rm{SINS}}}}}&{{{\bf{0}}_{15 \times 3}}}&{{{\bf{0}}_{15 \times 2}}}\\ {{{\bf{0}}_{3 \times 6}}}&{{\boldsymbol{G}_{{\rm{DVL}}}}}&{{{\bf{0}}_{3 \times 2}}}\\ {{{\bf{0}}_{6 \times 6}}}&{{{\bf{0}}_{6 \times 3}}}&{{\boldsymbol{G}_{{\rm{USBL}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{w}_{{\rm{SINS}}}}}\\ {{\boldsymbol{w}_{{\rm{DVL}}}}}\\ {{\boldsymbol{w}_{{\rm{USBL}}}}} \end{array}} \right]} \end{array} $ |
观测模型为:
| $ \left[\begin{array}{c} \boldsymbol{z}_{\mathrm{DVL}} \\ \boldsymbol{z}_{\mathrm{USBL}} \end{array}\right]=\left[\begin{array}{c} \boldsymbol{H}_{\mathrm{DVL}} \\ \boldsymbol{H}_{\mathrm{USBL}} \end{array}\right]\left[\begin{array}{c} \boldsymbol{x}_{\mathrm{SINS}} \\ \boldsymbol{x}_{\mathrm{DVL}} \\ \boldsymbol{x}_{\mathrm{USBL}} \end{array}\right]+\left[\begin{array}{c} \boldsymbol{v}_{\mathrm{DVL}} \\ \boldsymbol{v}_{\mathrm{USBL}} \end{array}\right] $ |
式中各矩阵见文献[8]。
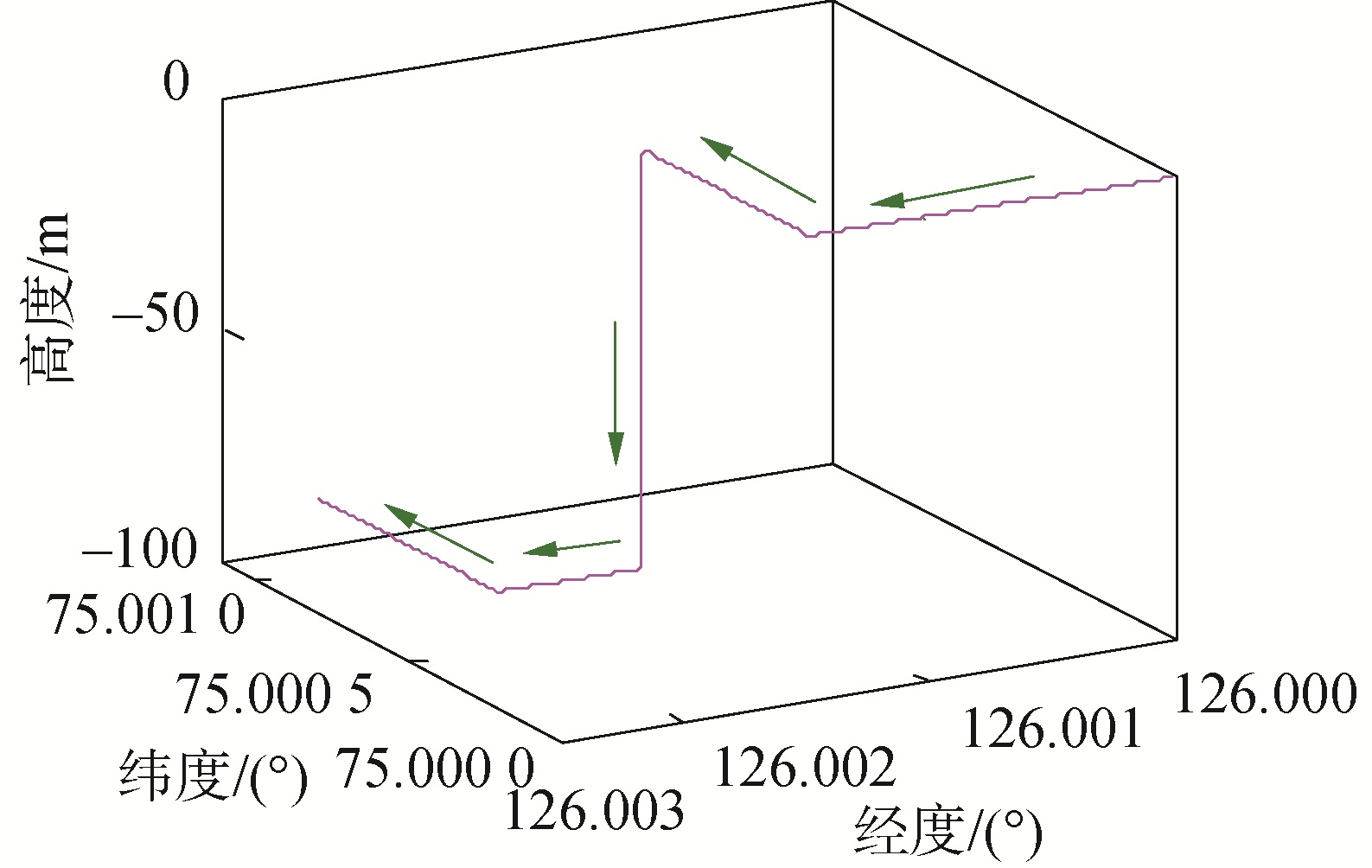
3.1 仿真实验条件及实验结果分析设载体的初始位置为东经126°,北纬75°,载体在仿真实验过程中,具有静止,匀加速、匀速、匀减速、下潜等运动状态,其中,加速度为0.2 m/s2,最大速度为5 m/s,载体运动轨迹如图 1所示。
|
Download:
|
| 图 1 载体运动轨迹 Fig. 1 Description of the vehicle trajectory | |
陀螺常值漂移为0.05(°)/h,加速度计零偏为6×10-5 g,多普勒计程仪测速误差小于0.3 m/s,超短基线测距误差小于20 m,测向误差小于1.5°。为了验证滤波算法的容错性能,分别在如表 1所示时间段内,向不同量测信息加入不同性质的异常噪声。仿真时长为4 h,仿真结果如图 2~5所示。
| 表 1 多普勒计程仪量测信息异常噪声起止时间 Table 1 The starting and termination times of Doppler velocity log (DVL) abnormal measurements |

|
Download:
|
| 图 2 量测噪声与权值 Fig. 2 Description of measurement noise and weights | |
|
Download:
|
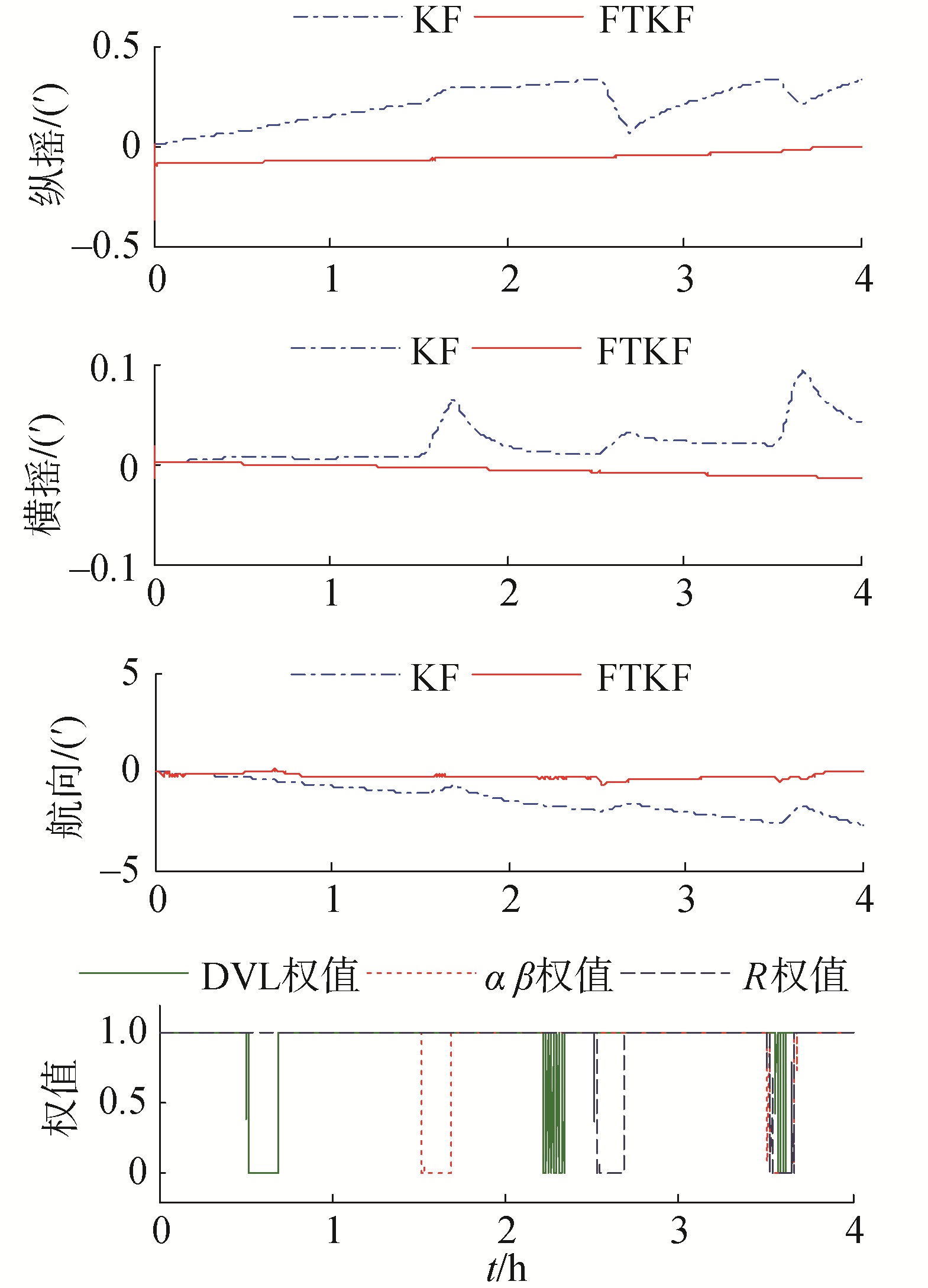
| 图 3 组合导航姿态误差 Fig. 3 Description of the attitude errors | |
|
Download:
|
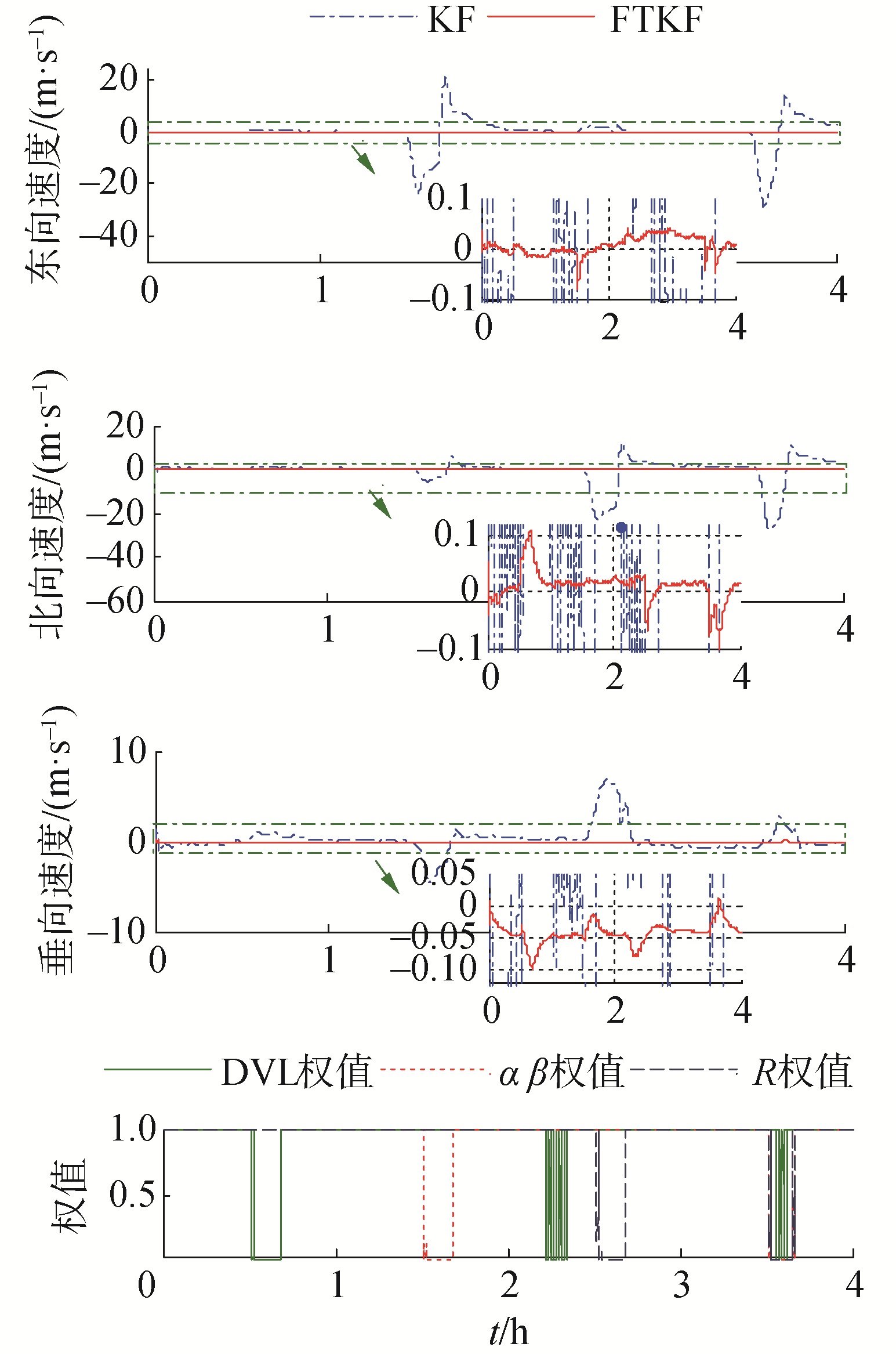
| 图 4 组合导航速度误差 Fig. 4 Description of the velocity errors | |
|
Download:
|
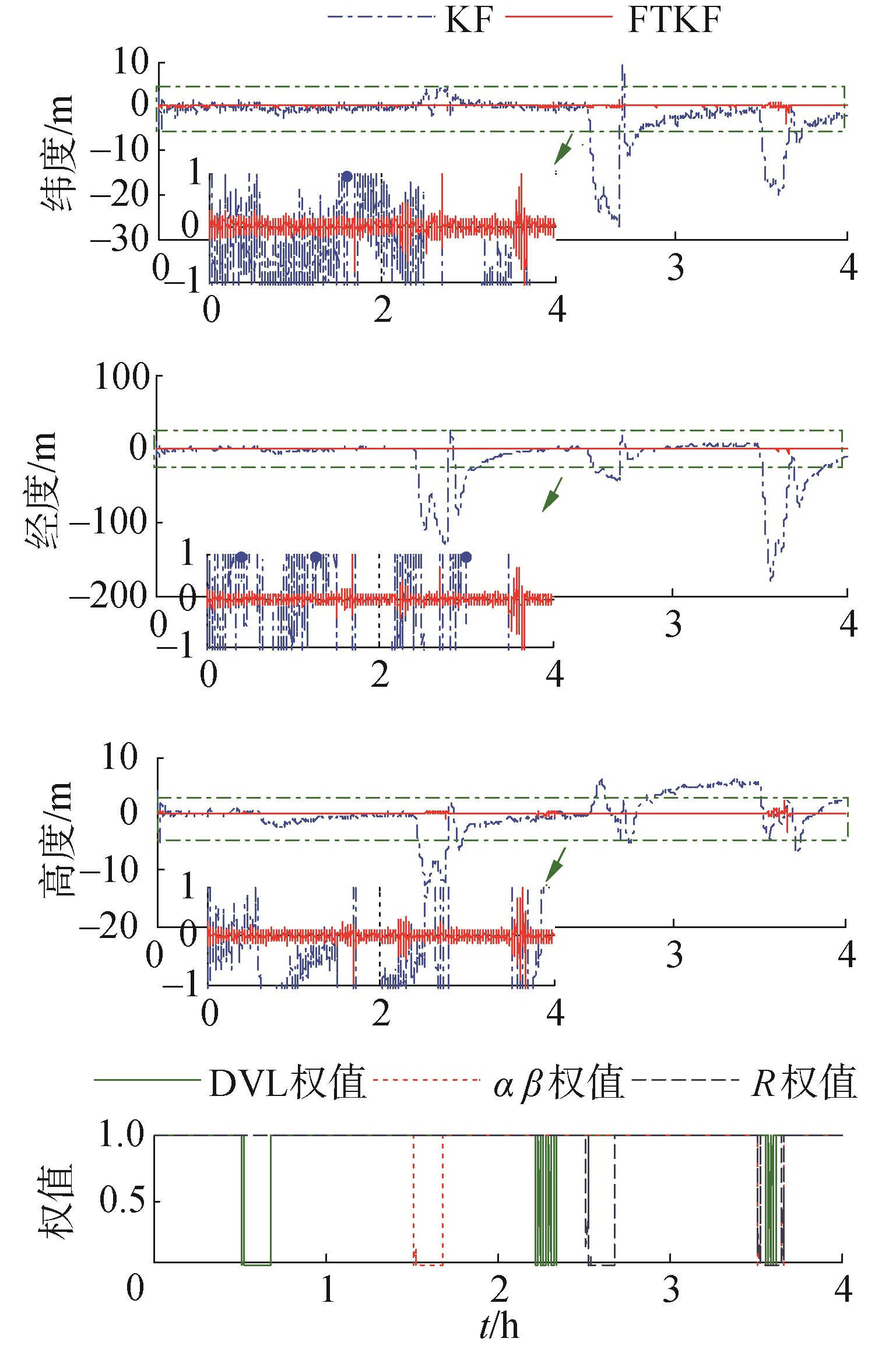
| 图 5 组合导航位置误差 Fig. 5 Description of the position errors | |
组合导航系统量测噪声情况如表 1、表 2及图 2所示。图 2~5中的权值变化曲线即为不同观测量相应自适应调节因子变化曲线。由图 2可知,量测信息出现异常噪声时,量测信息权值可得到实时有效调节。对高频量测粗差,量测信息权重可以得到有效调节。对于呈现斜坡增长的噪声,在噪声幅值较小时,量测信息对应权重值由α=1下降至0 < α < 1,当量测噪声幅值增长到一定程度后,权值下降至0,该量测信息不再参与量测更新。此外,当超短基线测向信息αβ异常时,若测距信息R输出不包含异常噪声,则仅测向信息被降权处理,测距信息权重不受影响;若测距信息R也含有异常噪声,则所有超短基线信息被降权处理。可见,以量测信息为对象的容错集中滤波算法不仅可以有效抑制有害量测信息,还可以保证有效量测信息得到充分利用,保证滤波效率。
| 表 2 超短基线量测信息异常噪声起止时间 Table 2 The starting and termination times of ultra-short base line (USBL) abnormal measurements |
由图 3~5可知,使用传统卡尔曼滤波算法时,量测信息异常噪声无法被有效抑制,有害观测信息被引入组合导航系统,导致导航精度与可靠性下降。容错卡尔曼滤波通过质量评价函数实时调节量测信息的权重值,由表 1、表 2及图 3~5可知,基于普通卡尔曼滤波的组合导航系统,纬度最大误差为37.36,均方差5.47;经度最大误差为179.33,均方差33.11;高度最大误差为12.80,均方差3.28。基于容错卡尔曼滤波的组合导航系统,纬度最大误差为3.78,均方差0.11;经度最大误差为5.41,均方差0.12;高度最大误差为5.42,均方差0.11。由此可见,本文提出的容错卡尔曼滤波算法可以有效提高组合导航系统的可靠性和精度。
4 结论1) 该滤波算法通过引入量测信息的先验概率分布,基于极大后验准则,建立了量测信息质量评价函数,并借助质量评价值设计了量测信息权函数与自适应因子,通过调节滤波参数,实时调节了量测信息在滤波更新中所占权重。
2) 该滤波算法充分利用有效信息,降权使用存疑信息并有效隔离有害信息,最终实现了提高组合导航系统容错性、可靠性和精度的目的。
3) 通过仿真实验,充分验证了容错卡尔曼滤波在提高组合导航精度与可靠性方面的有效性。量测信息受污染时,降低了量测信息权重,对状态一步预测给予了更多信任。
考虑到系统动力学模型存在不确定性,如何对状态一步预测的等价方差-协方差矩阵进行自适应调节,更加精确有效的平衡状态更新与量测更新之间的相对权重,将是本文将来的研究方向。
| [1] |
BIBULI M, PASCOAL A, RIDAO P, et al. Introduction to the special section on navigation, control, and sensing in the marine environment[J]. Annual reviews in control, 2015, 40: 127-128. DOI:10.1016/j.arcontrol.2015.09.007 (  0) 0)
|
| [2] |
熊智, 邵慧, 华冰, 等. 改进故障隔离的容错联邦滤波[J]. 航空学报, 2015, 36(3): 929-938. XIONG Zhi, SHAO Hui, HUA Bing, et al. An improved fault tolerant federated filter with fault isolation[J]. Acta aeronautica et astronautica sinica, 2015, 36(3): 929-938. (  0) 0)
|
| [3] |
韩强, 李保国, 陈克川. 改进的量测一致性的联邦滤波器两级故障检测[J]. 导航与控制, 2017, 16(3): 61-65, 104. HAN Qiang, LI Baoguo, CHEN Kechuan. The Improvement two levels of fault detection algorithm based on the consistency between the measurement of federal filter[J]. Navigation and control, 2017, 16(3): 61-65, 104. DOI:10.3969/j.issn.1674-5558.2017.03.011 (  0) 0)
|
| [4] |
LI Shengnan, MEI Jinsong, QU Qiang, et al. Research on SINS/GPS/CNS fault-tolerant integrated navigation system with air data system assistance[C]//2016 IEEE Chinese Guidance, Navigation and Control Conference. Nanjing, China, 2016: 2366-2370.
(  0) 0)
|
| [5] |
BHATTI U I, OCHIENG W Y, FENG Shaojun. Performance of rate detector algorithms for an integrated GPS/INS system in the presence of slowly growing error[J]. GPS solutions, 2012, 16(3): 293-301. DOI:10.1007/s10291-011-0231-y (  0) 0)
|
| [6] |
王其, 徐晓苏. 系统容错技术在水下航行器组合导航系统中的应用[J]. 中国惯性技术学报, 2008, 16(2): 167-170. WANG Qi, XU Xiaosu. Application of fault-tolerant technology to integrated navigation system of underwater vehicle[J]. Journal of Chinese inertial technology, 2008, 16(2): 167-170. (  0) 0)
|
| [7] |
ALLERTON D J, JIA Huamin. A review of multisensor fusion methodologies for aircraft navigation systems[J]. The journal of navigation, 2005, 58(3): 405-417. DOI:10.1017/S0373463305003383 (  0) 0)
|
| [8] |
ZHAO Lin, KANG Yingyao, CHENG Jianhua, et al. A fault-tolerant polar grid SINS/DVL/USBL integrated navigation algorithm based on the centralized filter and relative position measurement[J]. Sensors, 2019, 19(18): 3899. DOI:10.3390/s19183899 (  0) 0)
|
| [9] |
范晓亮. 基于自适应滤波的SINS/DVL组合导航算法研究[D]. 哈尔滨: 哈尔滨工程大学, 2018. FAN Xiaoliang. Research on integrated navigation algorithm of SINS/DVL based on adaptive filtering[D]. Harbin: Harbin Engineering University, 2018 (  0) 0)
|
| [10] |
高社生, 宋飞彪, 姜微微. 抗差自适应模型预测滤波及其在组合导航中的应用[J]. 中国惯性技术学报, 2011, 19(6): 701-705. GAO Shesheng, SONG Feibiao, JIANG Weiwei. Robust adaptive model predictive filtering algorithm and application to integrated navigation[J]. Journal of Chinese inertial technology, 2011, 19(6): 701-705. (  0) 0)
|
| [11] |
杨元喜, 任夏, 许艳. 自适应抗差滤波理论及应用的主要进展[J]. 导航定位学报, 2013, 1(1): 9-15. YANG Yuanxi, REN Xia, XU Yan. Main progress of adaptively robust filter with applications in navigation[J]. Journal of navigation and positioning, 2013, 1(1): 9-15. DOI:10.3969/j.issn.2095-4999.2013.01.003 (  0) 0)
|
| [12] |
WU Mouyan, DING Jicheng, ZHAO Lin, et al. Design and performance evaluation of an adaptive hybrid coherent and non-coherent GNSS vector tracking loop[C]//Proceedings of the 2017 International Technical Meeting of the Institute of Navigation. Monterey, California, 2017: 1129-1146.
(  0) 0)
|
| [13] |
KANG Yingyao, ZHAO Lin, CHENG Jianhua, et al. A novel grid SINS/DVL integrated navigation algorithm for marine application[J]. Sensors, 2018, 18(2): 364. DOI:10.3390/s18020364 (  0) 0)
|
| [14] |
郭斐. GPS精密单点定位质量控制与分析的相关理论和方法研究[D]. 武汉: 武汉大学, 2013. GUO Fei. Theory and methodology of quality control and quality analysis for GPS precise point positioning[D]. Wuhan: Wuhan University, 2013. (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


