空间信号到达方向估计(direction of arrival, DOA)是阵列信号处理研究的一个重要问题[1-4]。最早的DOA估计都是基于点信源理想模型的假设,然而实际阵列接收的信号往往具有一定的角度扩展[5],此时若采用传统的点信源模型估计性能将严重恶化。因此,有学者提出了空间分布源的概念[6]并根据散射分量的特点将分布源分为相干分布源(coherently distributed, CD)和非相干分布源(incoherently distributed,ID)2种。非相干分布源的各散射分量不相关,其协方差矩阵大特征值的个数大于信源数,此时空间谱估计较为困难。文献[6]通过对多重信号分类(multiple signal classification, MUSIC)算法的阵列流形进行改进从而提出了针对分布式信源的分布源参数估计(distributed signal parameter estimator, DSPE)算法。文献[7]中提出,虽然非相干信源存在秩多的情况,但大部分能量都集中于最大的少数特征值中并据此提出了伪子空间的概念。文献[8]利用泰勒展开的GAM模型提出了一种基于旋转不变子空间原理的非相干分布式信源空间谱估计方法(ESPRIT-ID)。然而这些方法并未消除多径信号,只是采用空间重新划分的方法尽量消除散射信号造成的影响。测向处理后的一个重要的目标就是定位,最常用的方法就是单站定位或多站定位。单站定位一般要求测向站相对待测向目标处于运动当中[9-10]。传统多站定位一般为2步定位,对信号进行角度解算[11-13]后利用相应方法进行目标位置的估计。2步定位会引入额外误差[14],为了解决这个问题有学者提出了数据域直接定位算法[15-19]。但大部分的多站定位都要求测向站的数量大于信源数。此时会造成资源的浪费。
针对非相干分布源,本文利用2个较远阵列之间接收信号的信号特性,利用主径信号之间的强相关性和散射径之间的不相关性,极大地消除散射径信号对测向结果的影响。同时,利用阵列接收信号之间的角度关联性,对信号子空间进行重构,完成2阵列测向角度之间的匹配,从而实现了利用2个阵列对多个信源进行无模糊的交叉定位。
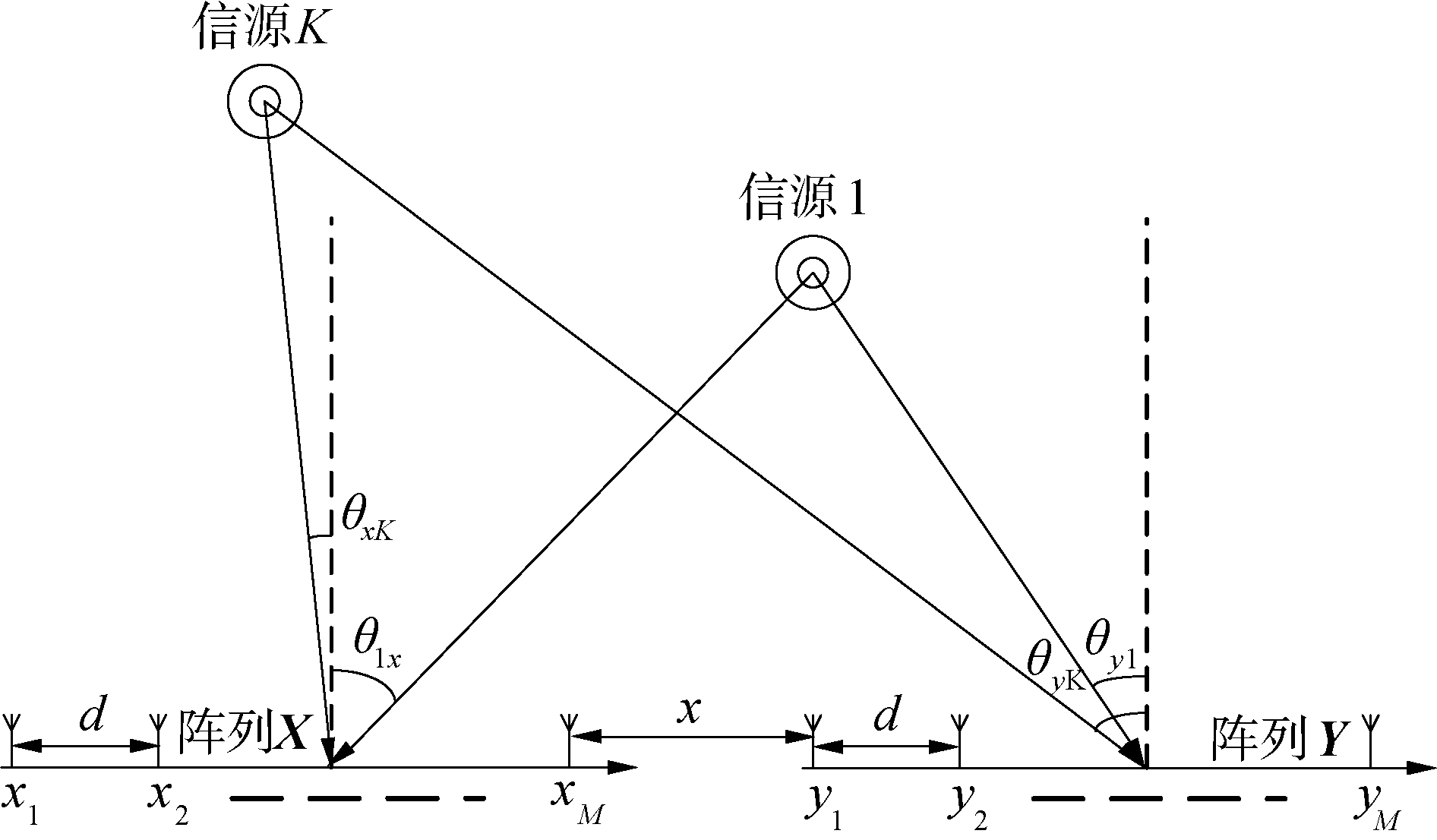
1 阵列信号模型将2个完全相同的均匀线阵X和Y摆放成图 1所示,每个线阵均有M个阵元,阵列中阵元的间距为d,2个阵列位于同一水平线,阵列间的间距为x且有x≫d。假设存在K个非相干分布式信号分别入射到2个阵列上,信号的波长为λ且λ≥2d,可以得到t时刻时2个阵列输出的信号矢量分别为:
|
Download:
|
| 图 1 阵列空间 Fig. 1 Array space | |
| $ \left\{\begin{array}{l} \boldsymbol{X}(t)=\sum\limits_{k=1}^{K} \sum\limits_{l=1}^{L_{X}} \gamma_{x k, l}(t) \boldsymbol{s}_{k}\left(t-\tau_{k l x}\right) \boldsymbol{\alpha}\left[\bar{\theta}_{x k, l}(t)\right]+\boldsymbol{n}_{x}(t) \\ \boldsymbol{Y}(t)=\sum\limits_{k=1}^{K} \sum\limits_{l=1}^{L_{Y}} \gamma_{y k, l}(t) \boldsymbol{s}_{k}\left(t-\tau_{k l y}\right) \boldsymbol{\alpha}\left[\bar{\theta}_{y k, l}(t)\right]+\boldsymbol{n}_{y}(t) \end{array}\right. $ | (1) |
式中:t为采样时间;θxk, l(t)和θyk, l(t)分别为第k个信源第l径对应于X和Y阵列的入射角;γxk, l(t)和γyk, l(t)为入射路径的随机复增益;LX和LY分别为第k个信源对应2个阵列的入射的多径数;sk(t)为第k个信源发射的信号;τklx代表第k个信源入射到X阵列的第l条径的随机延时;nx(t)和ny(t)是方差为σ2的加性高斯白噪声。对于非相干分布式信源,不同传播路径增益之间增益互不相关,即γxk, l(t)和γyk, l(t)均为时域独立同分布的复值零均值变量。M×1维的阵列方向矢量α[θxk, l(t)]的第m个元素表示为:
| $ \boldsymbol{\alpha}\left[\bar{\theta}_{x k, l}(t)\right]=\exp \left(\mathrm{j} \frac{2 {\rm{ \mathsf{ π} }}}{\lambda}(m-1) d \sin \left(\bar{\theta}_{x k, l}(t)\right)\right) $ | (2) |
式中:λ为信号波长;d表示阵元间距;入射角θxk, l(t)可以表示为:
| $ \bar{\theta}_{x k, l}(t)=\theta_{x k}+\varphi_{x k, l}(t) $ | (3) |
式中:θxk对应第k个信源对应X阵列的中心DOA;φxk, l(t)为入射到X阵列的第l径信号的随机角度偏差,其均值为0,方差为待估计的角度扩展。
阵列流型α[θxk, l(t)]的一阶泰勒展开为:
| $ \boldsymbol{\alpha}\left[\bar{\theta}_{x k, l}(t)\right]=\boldsymbol{\alpha}\left(\theta_{x k}\right)+\boldsymbol{\alpha}^{\prime}\left(\theta_{x k}\right) \varphi_{x k, l}(t) $ | (4) |
式中α′(θxk)为α(θxk)的偏导数。由于角度扩展通常比较小,因此省略泰勒展开中的余项,接收信号重新表示为:
| $ \left\{\begin{aligned} \boldsymbol{X}(t)=& \sum\limits_{k=1}^{K}\left[\boldsymbol{\alpha}\left(\theta_{x k}\right) \boldsymbol{g}_{x k, 0}(t)+\right.\\ &\left.\boldsymbol{\alpha}^{\prime}\left(\theta_{x k}\right) \boldsymbol{g}_{x k, 1}(t)\right]+\boldsymbol{n}_{x}(t) \\ \boldsymbol{Y}(t)=& \sum\limits_{k=1}^{K}\left[\boldsymbol{\alpha}\left(\theta_{y k}\right) \boldsymbol{g}_{y k, 0}(t)+\right.\\ &\left.\boldsymbol{\alpha}^{\boldsymbol{\alpha}}\left(\theta_{y k}\right) \boldsymbol{g}_{y k, 1}(t)\right]+\boldsymbol{n}_{x}(t) \end{aligned}\right. $ | (5) |
式中: α(θxk)=
为了节约多信源情况下交叉定位方法的空间资源和阵列数量,本文通过利用2个相隔较远阵列之间非相干信源散射信号之间的不相关性,很大程度上消除了散射信号对主径信号测向的影响,同时利用2个阵列间同一信号之间的相关性,利用左右奇异向量对应的信号子空间来求解出每个信源对应于2个阵列的分别的入射角,实现利用2个阵列来实现多信源(大于2个)的交叉定位。
2.1 基于互相关测向方法阵列X和Y接收信号的互相关矩阵为:
| $ \boldsymbol{R}_{x y}=\mathrm{E}\left[\boldsymbol{X}(t) \cdot(\boldsymbol{Y}(t))^{\mathrm{H}}\right] $ | (6) |
由于发射信号、阵列路径增益及2阵列角度扩展之间全部互不相关,同时2个阵列的折射径信号的增益互相之间也互不相关,因此可以得到:
| $ \mathrm{E}\left\{\boldsymbol{g}_{x k, 0} \boldsymbol{g}_{y k, 0}^{*}\right\}=\mathrm{E}\left\{\boldsymbol{s}(t) \boldsymbol{s}^{*}\left(t-\tau_{k}\right)\right\} \sigma_{\gamma x k} \sigma_{\gamma y k} $ | (7) |
| $ \left\{\begin{array}{l} \mathrm{E}\left\{\boldsymbol{g}_{x k, n} \boldsymbol{g}_{y k^{\prime}, n^{\prime}}^{*}\right\}=\mathrm{E}\left\{\boldsymbol{g}_{x k, 1} \boldsymbol{g}_{y k, 1}^{*}\right\}=0, \\ \forall k \neq k^{\prime} \text { 或 } n \neq n^{\prime} \end{array}\right. $ | (8) |
式中:τk=τklx- τkly,代表 2阵列接收的第k个信号主径信号间的延时。
同时,由于2个阵列接收的噪声均为高斯白噪声,两者之间相互独立,因此接收信号互相关中不包含噪声分量,避免了噪声分量对于参数估计的影响。因此,两阵列接收信号的互相关矩阵可以表示为:
| $ \begin{aligned} \boldsymbol{R}_{x y} &=\mathrm{E}\left\{\boldsymbol{X}(t) \cdot \boldsymbol{Y}(t)^{\mathrm{H}}\right\}=\\ & \mathrm{E}\left\{\left(\sum\limits_{k=1}^{K} \boldsymbol{a}\left(\theta_{x k}\right) \boldsymbol{g}_{x k, 0}(t)\right) \cdot\left(\sum\limits_{k=1}^{K} \boldsymbol{a}\left(\theta_{y k}\right) \boldsymbol{g}_{y k, 0}(t)\right)^{*}\right\}=\\ &\mathrm{E}\left\{\sum\limits_{k=1}^{K} \boldsymbol{a}\left(\theta_{x k}\right) \boldsymbol{g}_{x k, 0}(t) \boldsymbol{g}_{y k, 0}^{*}(t) \boldsymbol{a}^{*}\left(\theta_{y k}\right)\right\}=\\ &\mathrm{E}\left\{\sum\limits_{k=1}^{K} \boldsymbol{a}\left(\theta_{x k}\right) \boldsymbol{s}(t) \boldsymbol{s}^{*}\left(t-\tau_{k}\right) \sigma_{\gamma x k} \sigma_{\gamma y k} \boldsymbol{a}^{*}\left(\theta_{y k}\right)\right\}=\\ &\mathrm{E}\left\{\sum\limits_{k=1}^{K} \boldsymbol{a}\left(\theta_{x k}\right)\left|\boldsymbol{s}(t)^{2}\right| \sigma_{\gamma x k} \sigma_{\gamma y k} \mathrm{e}^{-\mathrm{j} \tau_{k}} \boldsymbol{a}^{*}\left(\theta_{y k}\right)\right\}=\\ &\boldsymbol{A}\left(\boldsymbol{\theta}_{x}\right) \boldsymbol{R}_{S} \boldsymbol{B}^{\mathrm{H}}\left(\boldsymbol{\theta}_{y}\right) \end{aligned} $ | (9) |
式中:
| $ \left\{\begin{array}{l} \boldsymbol{R}_{s}=\mathrm{E}\left[\boldsymbol{s}(t) \boldsymbol{s}^{\mathrm{H}}(t) \sigma_{\gamma x k} \sigma_{\gamma y k}\right] \\ \boldsymbol{B}\left(\theta_{y}\right)=\left[\begin{array}{llll} \boldsymbol{b}\left(\theta_{y 1}\right) & \boldsymbol{b}\left(\theta_{y 2}\right) & \cdots & \boldsymbol{b}\left(\theta_{y k}\right) \end{array}\right] \\ \boldsymbol{b}\left(\theta_{y k}\right)=\left[\begin{array}{llll} \mathrm{e}^{-\mathrm{j} \tau_{k}} & \mathrm{e}^{-\mathrm{j} \tau_{k}} \mathrm{e}^{-\mathrm{j} 2 {\rm{ \mathsf{ π} }} d \operatorname{lin} \theta / \lambda} & \cdots & \mathrm{e}^{-\mathrm{j} \tau_{k}} \mathrm{e}^{-\mathrm{j} 2 {\rm{ \mathsf{ π} }} d(m-1) \sin \theta / \lambda} \end{array}\right] \end{array}\right. $ |
对接收信号互相关矩阵进行奇异值分解可以得到:
| $ \begin{gathered} \boldsymbol{R}_{x y}=\boldsymbol{U} \boldsymbol{\varLambda} \boldsymbol{V}^{\mathrm{H}}=\left[\begin{array}{ll} \boldsymbol{U}_{1} & \boldsymbol{U}_{2} \end{array}\right] \cdot \\ {\left[\begin{array}{cc} \boldsymbol{\varLambda}_{K} & {\bf{0}}_{K \times(M-K)} \\ {\bf{0}}_{(M-K) \times K} & {\bf{0}}_{(M-K) \times(M-K)} \end{array}\right]\left[\begin{array}{ll} \boldsymbol{V}_{1} & \boldsymbol{V}_{2} \end{array}\right]^{\mathrm{H}}} \end{gathered} $ | (10) |
式中:ΛK对应奇异值分解得到的K个大奇异值组成的对角阵;U1和V1分别为K个大奇异值ΛK所对应的M×K维的左右奇异向量矩阵。根据信号空间理论,U1和V1分别对应阵列X和Y的信号子空间,因此可以得到:
| $ \left\{\begin{array}{c} \operatorname{span}\left(\boldsymbol{U}_{1}\right)=\operatorname{span}\left(\boldsymbol{A}\left(\theta_{x}\right)\right) \\ \operatorname{span}\left(\boldsymbol{V}_{1}\right)=\operatorname{span}\left(\boldsymbol{B}\left(\theta_{y}\right)\right) \end{array}\right. $ | (11) |
由式(11)可知必定存在唯一的、非奇异的K×K维的满秩矩阵T1、T2满足:
| $ \left\{\begin{array}{l} \boldsymbol{U}_\mathit{\pmb{1}}=\boldsymbol{A}\left(\theta_{x}\right) \times \boldsymbol{T}_{1} \\ \boldsymbol{V}_\mathit{\pmb{1}}=\boldsymbol{B}\left(\theta_{y}\right) \times \boldsymbol{T}_{2} \end{array}\right. $ | (12) |
由于均匀线阵具有的旋转不变一致性,可以将信号子空间分解为2部分,为了尽可能提高测量的精度,将信号子空间U1分解为2个(M-1)×K维的矩阵:
| $ \boldsymbol{U}_{1}=\left[\begin{array}{l} \boldsymbol{U}_{11} \\ \boldsymbol{U}_{12} \end{array}\right]=\left[\begin{array}{c} \boldsymbol{A} \boldsymbol{T} \\ \boldsymbol{A} \boldsymbol{\varPhi} \boldsymbol{T} \end{array}\right] $ | (13) |
式中:U11和U12分别为U1的第1~M-1行和第2~M行所组成的矩阵;A和Φ分别为:
| $ \left\{\begin{array}{l} \boldsymbol{A}=\left[\boldsymbol{\alpha}\left(\theta_{x 1}\right), \boldsymbol{\alpha}\left(\theta_{x 2}\right), \cdots, \boldsymbol{\alpha}\left(\theta_{x k}\right)\right] \\ \boldsymbol{\varPhi}=\operatorname{diag}\left(\mathrm{e}^{\mathrm{j} 2 {\rm{ \mathsf{ π} }} d \sin \theta_{x 1}{/ \lambda}}, \mathrm{e}^{\mathrm{j} 2 {\rm{ \mathsf{ π} }} d \sin \theta_{x 2} / \lambda}, \cdots, \mathrm{e}^{\mathrm{j} 2 {\rm{ \mathsf{ π} }} d \sin \theta_{x k} /\lambda}\right) \end{array}\right. $ | (14) |
由式(13)可以得到:
| $ \boldsymbol{U}_{12}=\boldsymbol{U}_{11} \boldsymbol{T}^{-1} \boldsymbol{\varPhi} \boldsymbol{T}=\boldsymbol{U}_{11} \boldsymbol{\varPsi} $ | (15) |
此时利用最小二乘准则,即寻找一个矩阵:
| $ \boldsymbol{F}=\left[\begin{array}{l} \boldsymbol{F}_{0} \\ \boldsymbol{F}_{1} \end{array}\right] \in {\bf{C}}^{2 K \times K} $ | (16) |
使得
| $ \boldsymbol{V}=\left\|\left[\begin{array}{cc} \hat{\boldsymbol{U}}_{11} & \hat{\boldsymbol{U}}_{12} \end{array}\right] \boldsymbol{F}\right\|_{F}^{2} $ | (17) |
达到最小,并且满足:
| $ \boldsymbol{F}^{\mathrm{H}} \boldsymbol{F}=\boldsymbol{I} $ | (18) |
显然矩阵F为
| $ \hat{\boldsymbol{\varPsi}}_{T L S}=-\boldsymbol{F}_{0} \boldsymbol{F}_{1}^{-1} $ | (19) |
对
| $ \theta_{x k}=\arcsin \left(\frac{c \cdot \operatorname{angle}\left(\lambda_{k}\right)}{\omega_{0} d}\right) $ | (20) |
同理,对阵列Y对应的信号子空间V1进行同样的处理即可得到相应的阵列Y的DOA的估计值。
虽然通过对2个信号子空间直接进行估计可以快速的得到2个阵列的入射角信息,但当空间中的信源数大于1时,左右阵列的角度并不一一对应,此时交叉定位在空间中会出现多个交汇点。当信源数为K时,空间中会出现个K2交汇点,此时虚假点的个数为K2-K。传统的交叉定位方法在解决虚假点问题时多采用多站定位的方法,即增加空间中观测站的数量,通过相应的算法剔除虚假点,还原信号的真实位置信息,此时计算的复杂度随着信源数的增多而提高。
2.2 多信源角度匹配由2.1节可知U1和V1分别对应阵列X和Y的信号子空间。虽然空间相同,但对2个空间进行处理后的角度并不能一一对应,因此需要对U1和V1进行一定的处理。
由前面的推导可知:
| $ \boldsymbol{R}_{x y}=\boldsymbol{A}\left(\theta_{x}\right) \boldsymbol{R}_{s} \boldsymbol{B}\left(\theta_{y}\right)=\boldsymbol{U}_{1} \boldsymbol{\varLambda} \boldsymbol{V}_{1}^{\mathrm{H}} $ | (21) |
由式(12)可知,存在K×K维满秩矩阵T使得:
| $ \boldsymbol{U}_{1}=\boldsymbol{A}\left(\boldsymbol{\theta}_{x}\right) \cdot \boldsymbol{T} $ | (22) |
代入式(22)中可以得到:
| $ \boldsymbol{R}_{s} \boldsymbol{B}^{\mathrm{H}}\left(\theta_{y}\right)=\boldsymbol{T} \boldsymbol{\varLambda} \boldsymbol{V}_{1}^{\mathrm{H}} $ | (23) |
将左右两端分别进行转置可以得到:
| $ \boldsymbol{B}\left(\theta_{y}\right) \boldsymbol{R}_{S}=\boldsymbol{V}_{1} \boldsymbol{\varLambda} \boldsymbol{T}^{\mathrm{H}} $ | (24) |
式中:RS与Λ均为对角阵,因此其转置不变;RS对角线上元素表示发射信号的功率;Λ对角线上元素表示接收信号的功率。
B(θy)为Y阵列的阵列流形,对其进行处理时需要的是每一列元素相邻两元素之间的相位信息。RS对角线上元素为发射信号的功率,因此均为实数。两者相乘的结果为:
| $ \begin{aligned} \boldsymbol{B}^{\prime}\left(\theta_{y}\right)&=\boldsymbol{B}\left(\theta_{y}\right) \boldsymbol{R}_{S}= \\ &{\left[\begin{array}{llll} \rho_{1} \boldsymbol{b}\left(\theta_{1}\right) & \rho_{2} \boldsymbol{b}\left(\theta_{2}\right) & \cdots & \rho_{K} \boldsymbol{b}\left(\theta_{K}\right) \end{array}\right]} \end{aligned} $ | (25) |
式中ρK表示第K个信号的发射功率。
由于ρ1到ρK均为实数,相当于对B(θ)的幅度进行了处理而对其相位并无影响。因此,利用相应方法对B(θy)和B′(θy)进行测向的结果相同。对U1和V1进行处理如下:首先对U1进行空间分解并进行TLS估计得到阵列X的DOA估计。将得到的阵列X的入射角重构阵列流型向量Â(θx),利用信号子空间U1和重构的阵列流型向量Â(θx)可以求解出非奇异的×K维的满秩矩阵T的估计值:
| $ \hat{\boldsymbol{T}}=\hat{\boldsymbol{A}}\left(\theta_{x}\right)^{-1} \boldsymbol{U}_{1} $ | (26) |
利用估计得到的
| $ \overset\frown{\boldsymbol{B}}{}^{\prime}\left(\theta_{y}\right)=\boldsymbol{V}_{1} \boldsymbol{\varLambda} \boldsymbol{T}^{\mathrm{H}}=\boldsymbol{V}_{1} \boldsymbol{\varLambda} \boldsymbol{U}_{1}^{\mathrm{H}}\left(\hat{\boldsymbol{A}}\left(\theta_{x}\right)^{-1}\right)^{\mathrm{H}} $ | (27) |
此时对重构的阵列流型
利用前面求得的2个阵列的角度信息即可以得到信源的空间位置,通过简单推导即可得出第k个信源与两阵列间的距离lkx和lky分别为:
| $ \left\{\begin{array}{l} l_{k x}=\frac{x \cos \theta_{k y}}{\sin \left(\theta_{k x}-\theta_{k y}\right)} \\ l_{k y}=\frac{x \cos \theta_{k x}}{\sin \left(\theta_{k x}-\theta_{k y}\right)} \end{array}\right. $ | (28) |
算法步骤总结如下:
1) 由2个阵列接收信号得到互相关矩阵Rxy的估计值
2) 对
3) 将
| $ \boldsymbol{U}_{x}^{\mathrm{H}} \boldsymbol{U}_{x}=\left[\begin{array}{l} \boldsymbol{U}_{11}^{\mathrm{H}} \\ \boldsymbol{U}_{12}^{\mathrm{H}} \end{array}\right]\left[\begin{array}{ll} \boldsymbol{U}_{11} & \boldsymbol{U}_{12} \end{array}\right]=\boldsymbol{U} \boldsymbol{\varLambda} \boldsymbol{U}^{\mathrm{H}} $ |
4) 将U分解成K×K维的子矩阵:
| $ \boldsymbol{U}=\left[\begin{array}{ll} \boldsymbol{u}_{11} & \boldsymbol{u}_{12} \\ \boldsymbol{u}_{21} & \boldsymbol{u}_{22} \end{array}\right] $ |
5) 计算Ψ=-u12u22-1的特征值λk;
6) 利用式(20)计算阵列X到达角的估计值
7) 利用阵列X到达角的估计值重构阵列X的阵列流型Â(θx)并将相应矩阵代入式(27)中得到阵列Y的阵列流型的估计值
8) 对
9) 将
定义均方根误差(root mean square error, RMSE)作为衡量估计精度的指标,RMSE的计算公式为:
| $ \mathrm{RMSE}=\frac{1}{K} \sum\limits_{k=1}^{K} \sqrt{\frac{1}{p} \sum\limits_{p=1}^{P}\left(\hat{\theta}_{k, p}-\theta_{k}\right)} $ | (29) |
式中:P表示蒙特卡洛仿真次数;
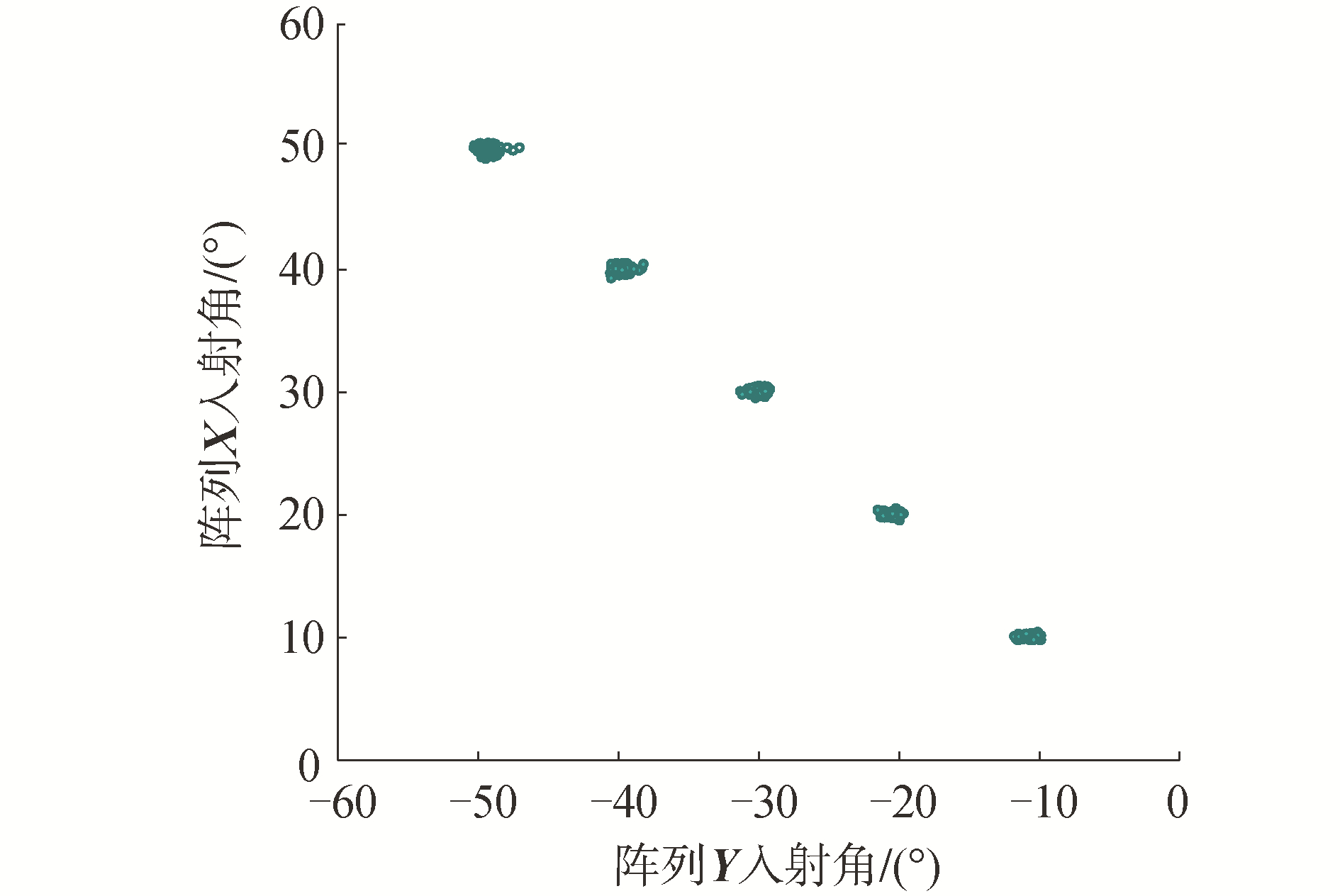
仿真1 验证算法有效性。假设空间中存在5个非相干分布式信源,5个信源的入射角分别为(10°, -10°)、(20°, -20°)、(30°, -30°)、(40°, -40°)、(50°, -50°);信噪比(signal to noise ratio,SNR)为15 dB。左右2个角度分别对应阵列X和阵列Y的入射角,进行100次独立实验,测量结果如图 2所示。由图 2可以看出,本算法可以很好的将2个阵列的入射角相对应,可以实现多个信源(大于2个)同时入射时的交叉定位测向。
|
Download:
|
| 图 2 算法有效性仿真结果 Fig. 2 Simulation results of algorithm effectiveness | |
仿真2 算法性能对比。将所提算法与广义ESPRIT算法[18]及DSPE算法[8]进行性能对比。实验中均采用均匀线阵作为接收阵列,阵元间距为λ/2;信号拍数N=500;角度扩展σ=2°;入射路径数L=100;分布方式采用高斯分布。
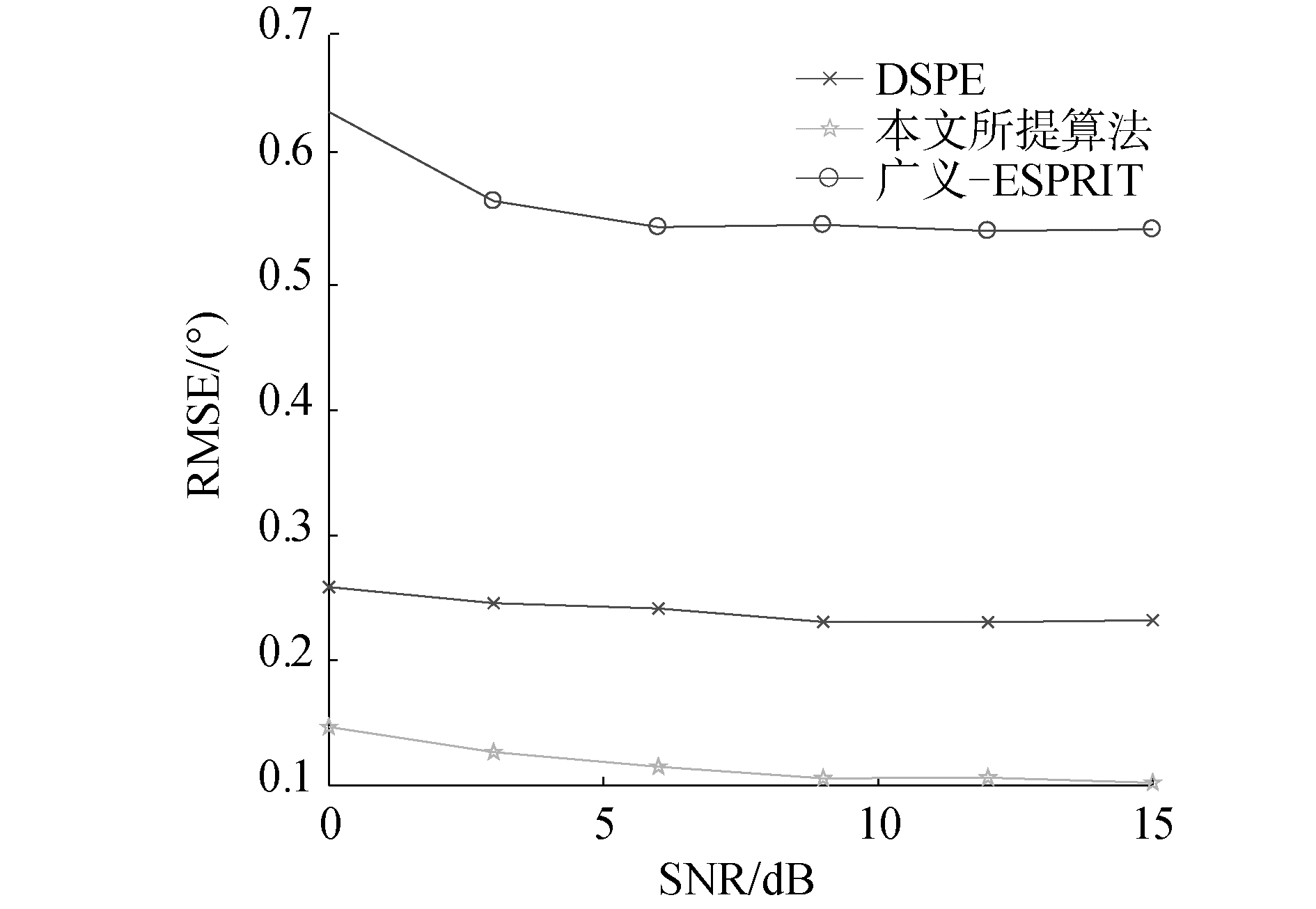
图 3为信噪比对3种算法测向性能的影响,仿真时阵元数K=16;左右阵列入射角分别为(-10°, 10°)。1 000次蒙特卡洛仿真结果如图 3所示。
|
Download:
|
| 图 3 RMSE随信噪比SNR变化 Fig. 3 RMSE varies with SNR | |
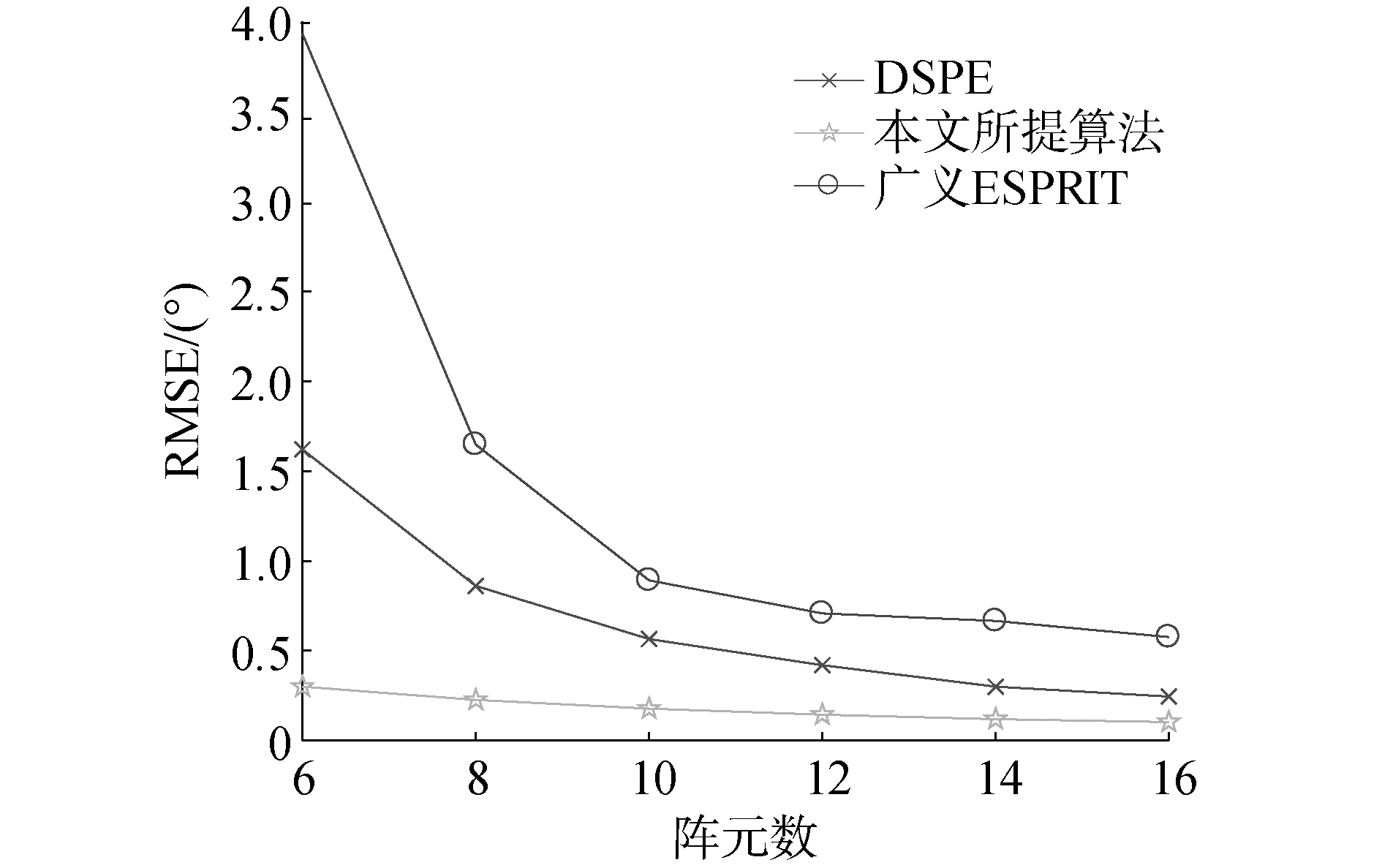
图 4为阵元数对3种算法测向性能的影响,仿真时信号信噪比SNR=15 dB;左右阵列入射角分别为(-10°, 10°)。1 000次蒙特卡洛仿真结果如图 4所示。
|
Download:
|
| 图 4 RMSE随阵元数变化 Fig. 4 RMSE varies with the number of array elements | |
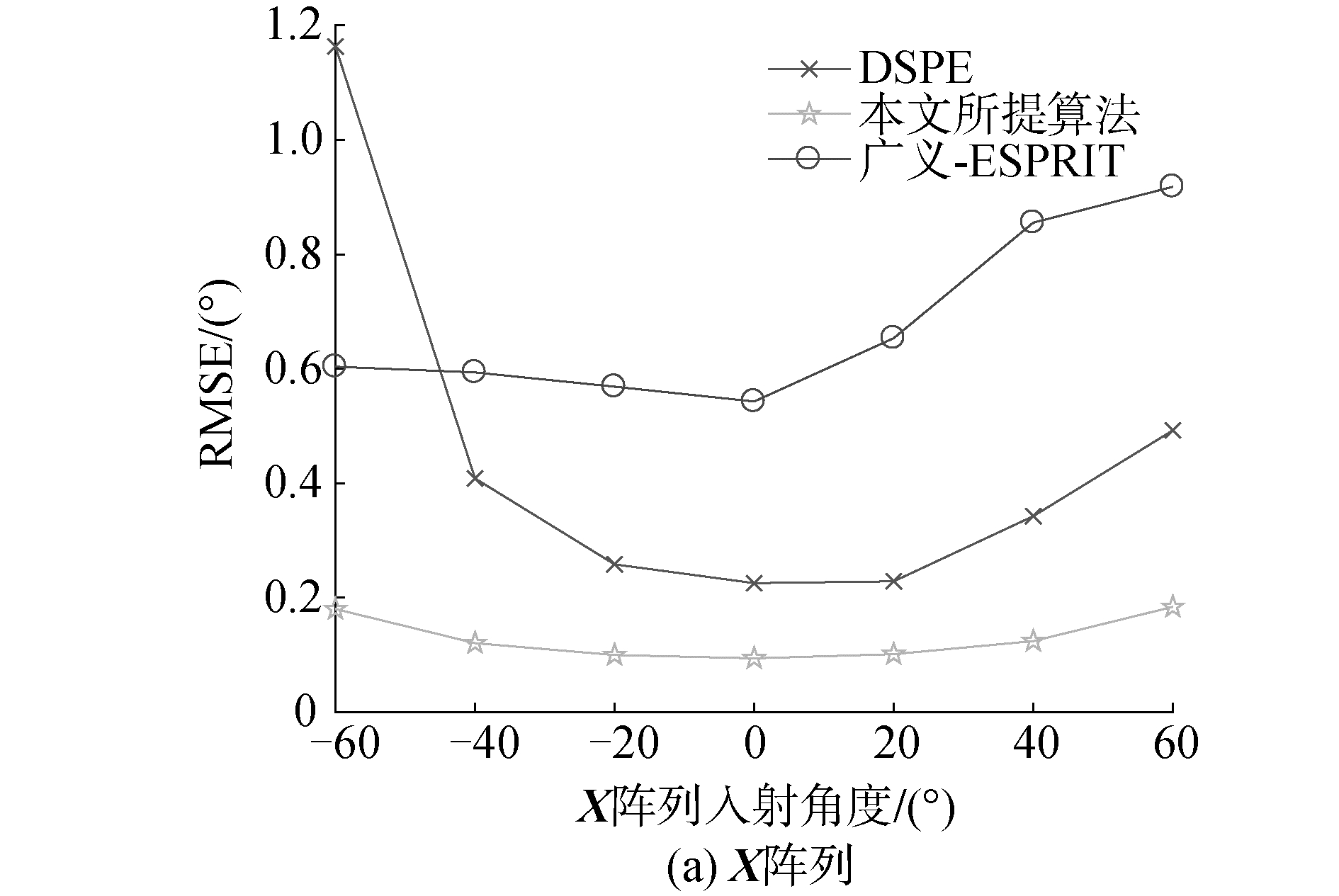
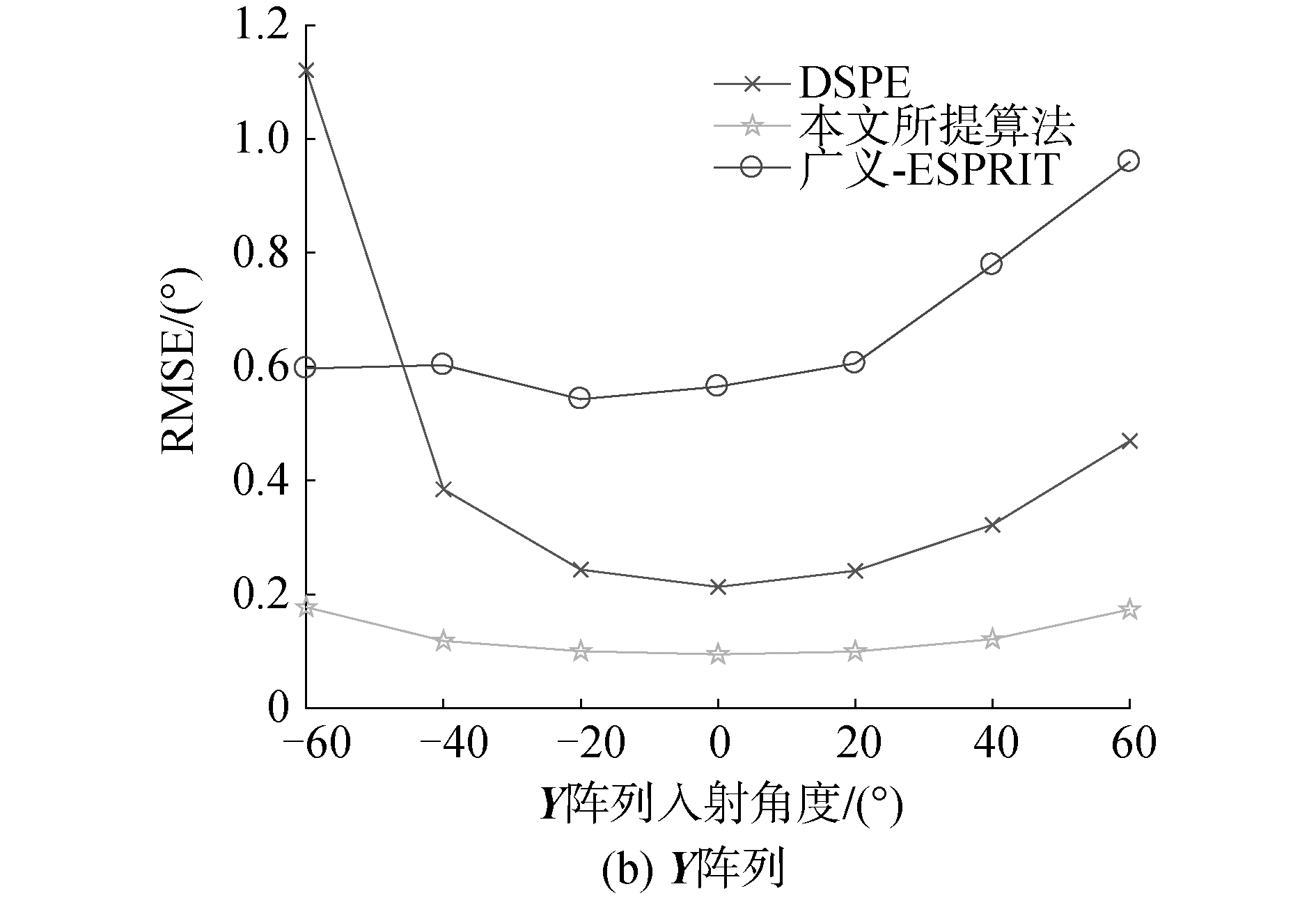
图 5为阵列入射角度变化对3种算法测向性能的影响。仿真时信号信噪比SNR=15 dB;阵元数K=16;图 5(a)为X阵列入射角度变化对测向性能的影响,此时Y阵列的入射角度固定为0°;图 5(b)为Y阵列入射角度变化对测向性能的影响,此时X阵列的入射角度固定为0°。1 000次蒙特卡洛仿真结果分别如图 5所示。
|
Download:
|
| 图 5 RMSE随阵列入射角变化 Fig. 5 RMSE varies with incident angle of array | |
从图 5中可以看出,本文算法的测向精度与DSPE算法相当,同时优于广义ESPRIT,这是因为本文算法通过利用多径信号之间的不相关性,通过取阵列的互相关从而减弱了多径信号对测向的影响,同时由于不同阵列之间的噪声互不相关。因此,互相关也削弱了高斯噪声对测向误差的影响。
仿真3 算法复杂度。将本文的方法与广义ESPRIT和DSPE算法进行复杂度的对比,复杂度的对比标准为复数乘法的运算次数。假设阵列个数为M,快拍数为N,信源数为K。广义ESPRIT算法主要的运算在于一个M阶矩阵的协方差矩阵及特征值分解运算、再加上需要进行搜索函数的构建以及谱峰搜索,因此复杂度可以表示为O(M2N+M3+l(2MK)),其中l为谱峰搜索的次数;DSPE算法主要运算为M阶矩阵的协方差矩阵及特征值分解运算、再加上需要进行搜索函数的构建以及谱峰搜索,因此复杂度可以表示为O(M2N+M3+l1l2×M(M-K)),其中l1和l2分别为对中心DOA和角度扩展谱峰搜索的次数;本文算法主要为一个M×M阶矩阵的互协方差和奇异值分解、最小二乘估计、计算满秩矩阵T以及阵列流形的重构,因此本文算法的复杂度可以表示为O(M2N+M3+K2+MK+K3),各算法复杂度如表 1所示。
| 表 1 复杂度对比 Table 1 Comparison of complexity |
假设空间中信源数量为5;快拍数为500;方位角搜索范围为-90°~90°; 角度扩展搜索范围为-5°~5°;搜索步进为0.1°。此时各算法的复数乘法运算复杂度对比如图 6所示。
|
Download:
|
| 图 6 算法复杂度对比 Fig. 6 Algorithm complexity comparison diagram | |
可以看出,本文算法的复杂度较低,这是因为本文算法无需进行谱峰搜索,因此大大减少了计算量,提升了测向的实时性。
本文算法的缺点在于虽然算法的复杂度较低,但由于特定的阵列结构,造成了阵列孔径的缺失,使得相同阵元数的情况下可同时测向的目标数减少。
4 结论1) 本文利用泰勒级数展开的方法建立非相干分布式信源的模型,通过2个较远阵列之间的互协方差来消除不相关散射信号对测向造成的影响,提升了测向结果的精度。
2) 利用2个阵列之间的相关性,通过角度匹配的方法解决了交叉定位中由于测向角与信源失配造成的模糊点问题。仿真结果表明,在多信源情况下,所提算法可以很好的实现信源测向角的对应问题。
3) 本文算法的缺点在于虽然算法的复杂度较低,但由于特定的阵列结构,造成了阵列孔径的缺失,使得相同阵元数的情况下可同时测向的目标数减少。
| [1] |
TIAN Quan, QIU Tianshuang, LI Jingchun, et al. Robust adaptive DOA estimation method in an impulsive noise environment considering coherently distributed sources[J]. Signal processing, 2019, 165: 343-356. DOI:10.1016/j.sigpro.2019.07.014 (  0) 0)
|
| [2] |
崔维嘉, 代正亮, 巴斌, 等. 基于互相关抽样分解的分布式非圆信号DOA快速估计[J]. 电子与信息学报, 2018, 40(5): 1226-1233. CUI Weijia, DAI Zhengliang, BA Bin, et al. Fast DOA estimation of distributed noncircular sources by cross-correlation sampling decomposition[J]. Journal of electronics & information technology, 2018, 40(5): 1226-1233. (  0) 0)
|
| [3] |
朝乐蒙, 邱天爽, 李景春, 等. 广义复相关熵与相干分布式非圆信号DOA估计[J]. 信号处理, 2019, 35(5): 795-801. CHAO Lemeng, QIU Tianshuang, LI Jingchun, et al. Generalized complex correntropy and DOA estimation for coherently distributed noncircular sources[J]. Journal of signal processing, 2019, 35(5): 795-801. (  0) 0)
|
| [4] |
CHENG Qianlin, ZHANG Xiaofei, CAO Renzheng. Fast parallel factor decomposition technique for coherently distributed source localization[J]. Journal of systems engineering and electronics, 2018, 29(4): 667-675. DOI:10.21629/JSEE.2018.04.01 (  0) 0)
|
| [5] |
JANTTI T P. The influence of extended sources on the theoretical performance of the MUSIC and ESPRIT methods: narrow-band sources[C]//IEEE International Conference on Acoustics, Speech, and Signal Processing. San Francisco, CA, USA, 1992: 429-432.
(  0) 0)
|
| [6] |
SHAHBAZPANAHI S, VALAEE S, BASTANI M H. Distributed source localization using ESPRIT algorithm[J]. IEEE transactions on signal processing, 2001, 49(10): 2169-2178. DOI:10.1109/78.950773 (  0) 0)
|
| [7] |
MENG Y, STOICA P, WONG K M. Estimation of the directions of arrival of spatially dispersed signals in array processing[J]. IEE proceedings-radar, sonar and navigation, 1996, 143(1): 1-9. DOI:10.1049/ip-rsn:19960170 (  0) 0)
|
| [8] |
王鼎, 张瑞杰, 张涛. 一种阵列互耦影响下的目标直接定位算法及其理论性能分析[J]. 电子学报, 2017, 45(5): 1130-1138. WANG Ding, ZHANG Ruijie, ZHANG Tao. A direct position determination approach for radio emitters in presence of mutual coupling[J]. Acta electronica sinica, 2017, 45(5): 1130-1138. DOI:10.3969/j.issn.0372-2112.2017.05.016 (  0) 0)
|
| [9] |
YANG Xuemin, ZHENG Zhi, HU Bin. Off-grid DOA estimation of incoherently distributed non-circular sources via generalised approximate message passing[J]. Electronics letters, 2016, 52(4): 262-264. DOI:10.1049/el.2015.1973 (  0) 0)
|
| [10] |
宋海亮, 付永庆. 基于迭代UH_∞的单站无源定位算法[J]. 哈尔滨工程大学学报, 2013, 34(10): 1334-1338. (  0) 0)
|
| [11] |
WEISS A J. Direct position determination of narrowband radio frequency transmitters[J]. IEEE signal processing letters, 2004, 11(5): 513-516. DOI:10.1109/LSP.2004.826501 (  0) 0)
|
| [12] |
蒋伊琳, 刘梦楠, 郜丽鹏, 陈涛. 运动多站无源时差/频差联合定位方法[J]. 系统工程与电子技术, 2019, 41(7): 1441-1449. (  0) 0)
|
| [13] |
吴龙文, 王宝莹, 魏俊杰, 何胜阳, 赵雅琴. 基于AOA的双机无源定位模型及其解算方法[J]. 系统工程与电子技术, 2020, 42(5): 978-986. (  0) 0)
|
| [14] |
AMAR A, WEISS A J. Direct position determination of multiple radio signals[C]//IEEE International Conference on Acoustics, Speech, and Signal Processing. Montreal, QC, Canada, 2004.
(  0) 0)
|
| [15] |
AMAR A, WEISS A J. Direct position determination in the presence of model errors-known waveforms[J]. Digital signal processing, 2006, 16(1): 52-83. DOI:10.1016/j.dsp.2005.03.003 (  0) 0)
|
| [16] |
OISPUU M, NICKEL U. Direct detection and position determination of multiple sources with intermittent emission[J]. Signal processing, 2010, 90(12): 3056-3064. DOI:10.1016/j.sigpro.2010.05.010 (  0) 0)
|
| [17] |
逯志宇, 王建辉, 秦天柱, 等. 基于对称旋转不变性的非圆相干分布源直接定位算法[J]. 电子与信息学报, 2019, 41(3): 537-543. LU Zhiyu, WANG Jianhui, QIN Tianzhu, et al. Direct position determination for coherently distributed noncircular source based on symmetric shift invariance[J]. Journal of electronics & information technology, 2019, 41(3): 537-543. (  0) 0)
|
| [18] |
王大鸣, 任衍青, 逯志宇, 等. 分布式信源数据域直接位置估计方法[J]. 电子与信息学报, 2018, 40(2): 371-377. WANG Daming, REN Yanqing, LU Zhiyu, et al. Direct position determination of the distributed source[J]. Journal of electronics & information technology, 2018, 40(2): 371-377. (  0) 0)
|
| [19] |
ZOUBIR A, WANG Yide, CHARGÉ P. Efficient subspace-based estimator for localization of multiple incoherently distributed sources[J]. IEEE transactions on signal processing, 2008, 56(2): 532-542. DOI:10.1109/TSP.2007.907877 (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


