2. 哈尔滨工业大学 空间科学与应用技术研究院, 广东 深圳 518055
2. Institute of Space Science and Applied Technology, Harbin Institute of Technology, Shenzhen 518055, China
光学成像小卫星在空间图像获取、灾害应急救援等方面展现出极大的应用价值和广阔的应用前景,逐渐成为航天领域重要发展方向[1]。为提高光学成像小卫星的性价比,结构优化和轻量化设计以提高微小卫星有效载荷比成为有效的手段。近些年,许多文献介绍了结构优化设计方面的进展,推出了如Nastran、Adina等众多结构分析软件供卫星设计者应用。对于优化模型方面的问题,许多文献也多有涉猎。陈昌亚等[2]结合卫星结构的特点和卫星结构设计方面的经验,提出了以等效板为主的建模方法,简化了蜂窝夹层板设计变量选取工作,为卫星结构优化工作提供了重要参考。文献[3-5]也提出了一些参数化建模方法对形状、材料等对加筋板固有频率进行分析。这些参数不仅包括用于描述结构几何形状的参数,还包括对结构进行有限元分析的其他参数,如描述网格划分情况的参数、描述材料特性的参数、描述载荷类型和数值的参数等等[6-7]。在强度校核方面,目前卫星蜂窝夹层结构强度校核基本不依赖参数化设计,而是就材料选择和埋件形状进行优化[8-9]。但夹层板的动力学特性优化可选参数较多,是影响卫星结构重量的主要因素,也是目前轻量化设计的难点[10-11]。根据文献调研,国内外光学载荷卫星结构分系统占比约为22%~29%。本文所设计的小卫星总重不大于500 kg,有效载荷占比高达50%,对结构分系统提出了质量占比不大于15%的约束。本文对卫星结构参数进行分析整理,得到了关键优化参数,并且在改进的有限元等效模型下对卫星结构进行优化设计,最终得到满足刚度和强度要求的卫星结构设计方案。
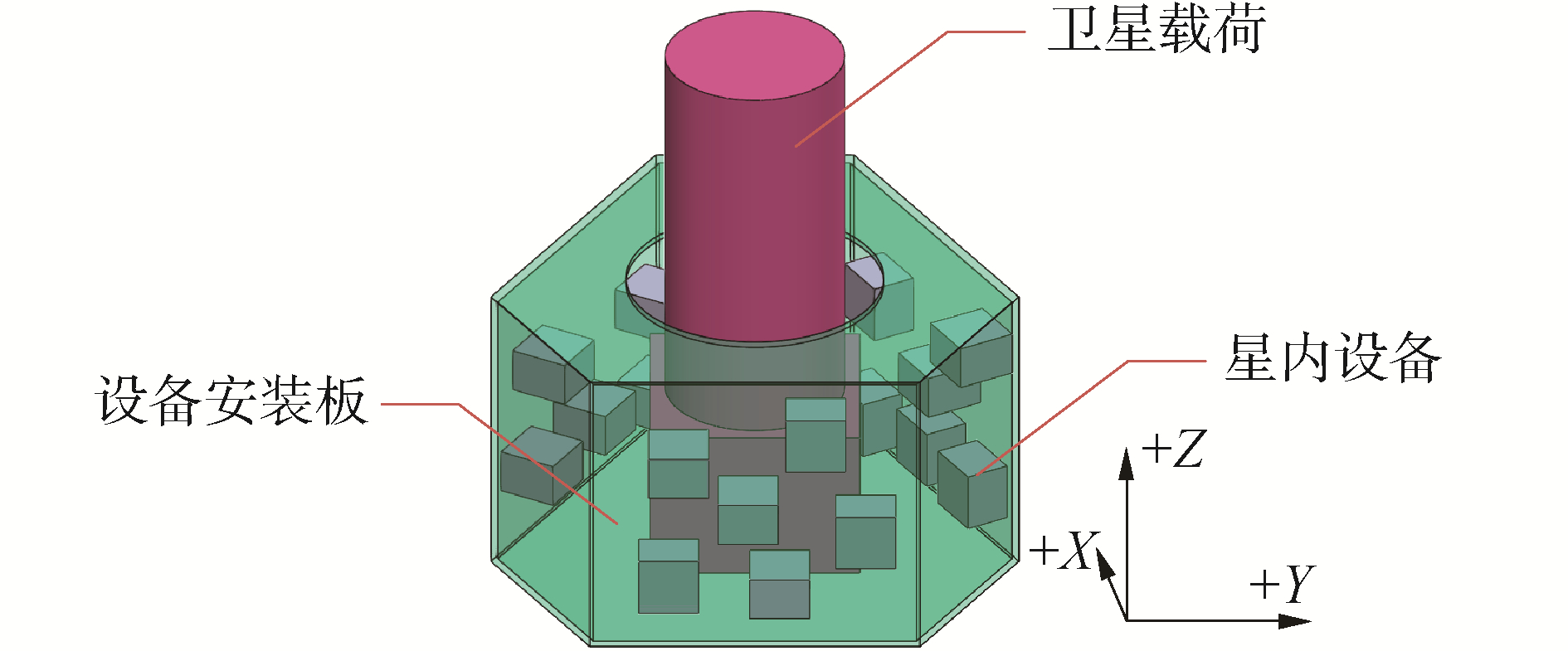
1 高载荷比卫星结构组成本文所研究卫星构型如图 1所示,卫星以载荷为中心,形成六棱柱构型,3个长边结构板作为单机安装板;3个短边结构板作为连接结构,同时安装少量设备,下部安装板作为星箭对接面。
|
Download:
|
| 图 1 卫星构型 Fig. 1 The overall structure of the satellite | |
根据卫星工程常用设计参数,统计出卫星结构分系统重量上下设计阈值,如表 1所示。
| 表 1 卫星结构可选参数统计表 Table 1 Statistic of optional parameters of satellite structure |
可以看出,卫星结构板设计重量约在54.5~117.5 kg。对于卫星结构参数优化,强度校核问题属于必须满足条件,本文所述设计参数均能满足蜂窝内部埋件和整体屈曲等静力强度要求,不再赘述计算过程。
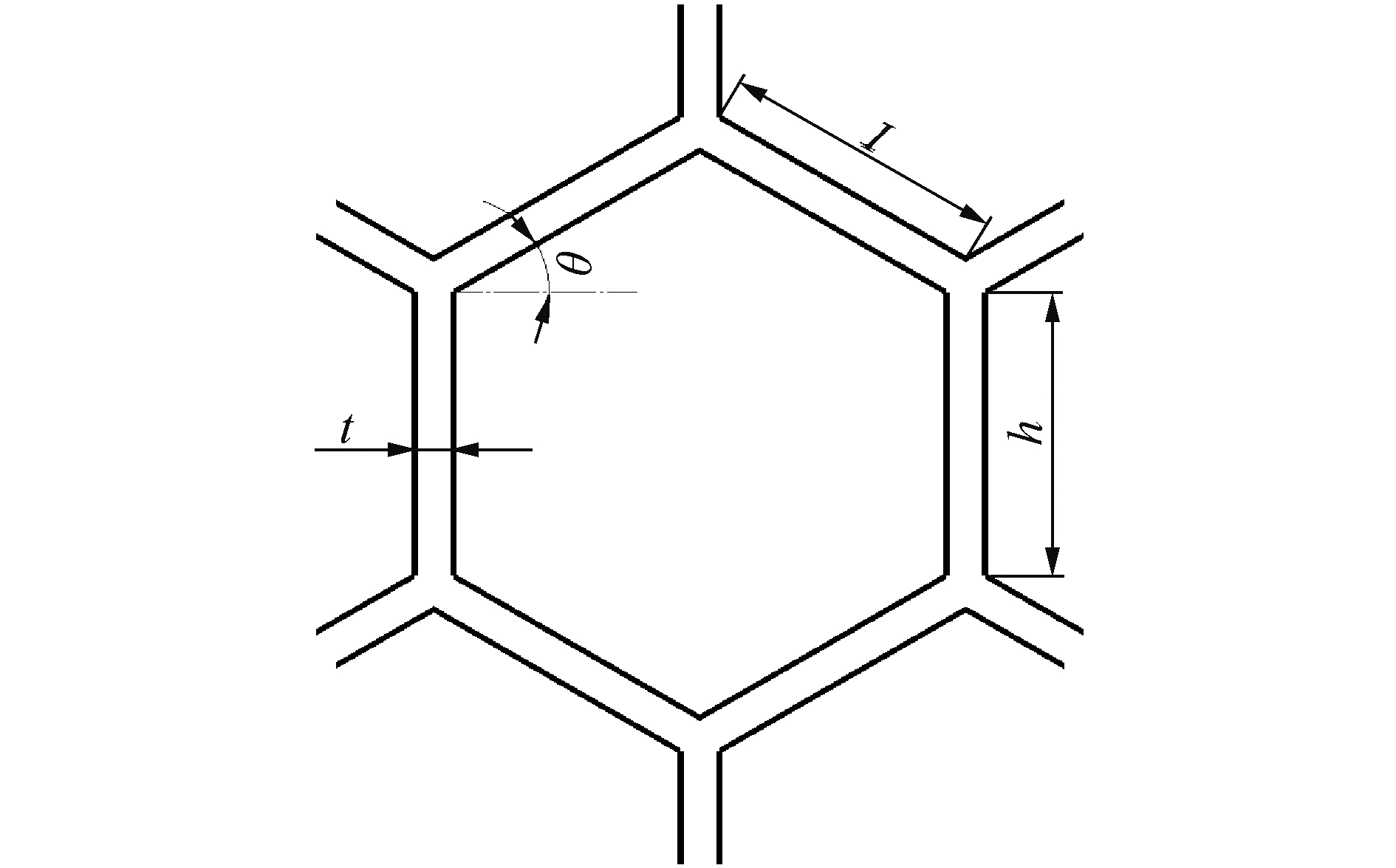
2 蜂窝夹层结构等效模型修正为确定最终蜂窝夹层结构各个参数,利用Kirchhoff基本理论假设[12]。卫星结构板中蜂窝结构为正六边形蜂窝芯子,蜂窝芯子材料的弹性模量为ES,剪切模量为GS,泊松比μ,密度为ρ,芯子壁厚为t,蜂窝芯子边长为l,蜂窝芯子直臂长度为h,θ为蜂窝芯子斜臂与水平轴的夹角,如图 2所示。
|
Download:
|
| 图 2 蜂窝芯格参数 Fig. 2 Schematic of honeycomb core parameters | |
根据蜂窝夹层本构关系,在哈密尔顿基本理论下,根据动力学原理可将蜂窝夹层结构等效为尺寸相同,等效前后夹层板刚度相同的正交各向异性板。利用经典蜂窝模量等效公式得:
| $ \left\{\begin{array}{l} E_{c x}=\frac{4 \sqrt{3}}{3} E_{s}\left(1-3 \frac{t^{2}}{l^{2}}\right) \frac{t^{3}}{l^{3}} \\ E_{c y}=\frac{4 \sqrt{3}}{3} E_{s}\left(1-\frac{5 t^{2}}{3 l^{2}}\right) \frac{t^{3}}{l^{3}} \\ E_{c z}=\frac{2}{\sqrt{3}} E_{s} \frac{t}{l} \\ G_{c x y}=\frac{E_{s}}{\sqrt{3}}\left(\frac{t}{l}\right)^{3} \\ G_{c x z}=\frac{\gamma G_{s}}{\sqrt{3}} \frac{t}{l} \\ G_{c y z}=\frac{G_{s} \gamma \sqrt{3}}{2} \frac{t}{l} \\ \rho_{c}=\frac{8 \sqrt{3}}{9} \frac{t}{l} \rho_{s} \end{array}\right. $ | (1) |
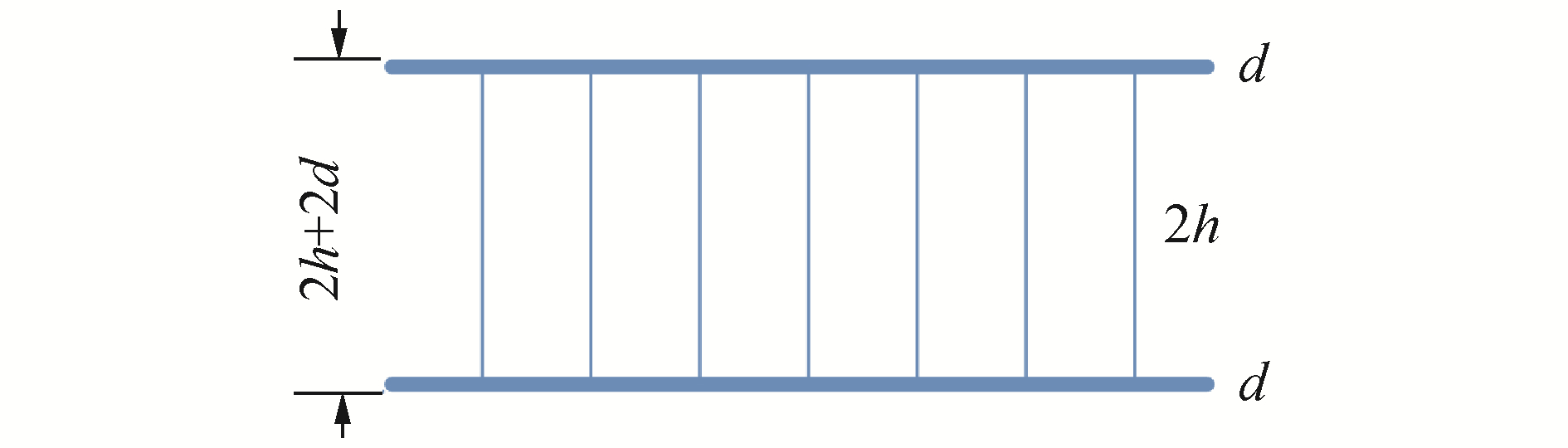
如图 3所示,蜂窝蒙皮厚度为d,芯子高度为2h,根据蜂窝夹层界面位移连续性,得:
| $ \left\{\begin{array}{l} u(x, y, z, t)=z \varphi_{x}(x, y, t) \\ v(x, y, z, t)=z \varphi_{y}(x, y, t) \\ w(x, y, z, t)=z \varphi_{z}(x, y, t) \end{array}\right. $ | (2) |
|
Download:
|
| 图 3 蜂窝夹层板分层结构 Fig. 3 Honeycomb sandwich structure | |
式中:u、v、w代表位移分量;φx、φy表示夹层板中层面外法线绕x轴和y轴的转角,通过建立蜂窝夹层板各层几何方程、物理方程和动力学本构关系的基本方程,得到关系:
| $ \left\{\begin{array}{l} E_{x}=\frac{e_{11} e_{12}-e_{12}^{2}}{e_{22}} \\ E_{y}=\frac{e_{11} e_{22}-e_{12}^{2}}{e_{11}} \\ G_{x z}=e_{44} \\ G_{y z}=e_{55} \\ G_{x y}=e_{66} \\ \mu_{x y}=\frac{e_{12}}{e_{22}} \\ \rho=\frac{\rho_{f} d+h \rho_{c}}{h+d} \end{array}\right. $ | (3) |
其中:
| $ \left\{\begin{array}{l} e_{11}=\frac{\left[(h+d)^{3}-h^{3}\right] e_{f 11}+h^{3} e_{c 11}}{(h+d)^{3}} \\ e_{22}=\frac{\left[(h+d)^{3}-h^{3}\right] e_{f 22}+h^{3} e_{c 22}}{(h+d)^{3}} \\ e_{12}=\frac{\left[(h+d)^{3}-h^{3}\right] e_{f 12}+h^{3} e_{c 12}}{(h+d)^{3}} \\ e_{44}=\frac{d}{h+d} e_{f 44}+\frac{d}{h+d} e_{c 44} \\ e_{55}=\frac{d}{h+d} e_{f 55}+\frac{d}{h+d} e_{c 55} \\ e_{66}=\frac{\left[(h+d)^{3}-h^{3}\right] e_{f 66}+h^{3} e_{c 66}}{(h+d)^{3}} \\ \rho=\frac{\rho_{f} d+h \rho_{c}}{h+d} \end{array}\right. $ | (4) |
其中与蜂窝芯子参数有关等式:
| $ \left\{\begin{array}{l} e_{c 11}=e_{c 22}=\frac{1}{1-\mu_{c x y}^{2}} E_{c x} \\ e_{c 12}=\frac{\mu_{c x y}}{1-\mu_{c x y}^{2}} E_{c y} \\ e_{c 44}=G_{c x z} \\ e_{c 55}=G_{c y z} \\ e_{c 66}=G_{c x y} \end{array}\right. $ | (5) |
与蒙皮有关的等式:
| $ \left\{\begin{array}{l} e_{f 11}=e_{f 22}=\frac{1}{1-\mu_{f}^{2}} E_{f} \\ e_{f 12}=\frac{\mu_{f}}{1-\mu_{f}^{2}} E_{f} \\ e_{f 44}=e_{f 55}=K G \\ e_{f 66}=G \end{array}\right. $ | (6) |
式中:efij、ecij分别表示蜂窝板上下蒙皮和蜂窝芯子在坐标系中的刚度系数;Ef和μf为蜂窝板蒙皮的弹性模量和泊松比;Ecx、Ecy、Gcxy、Gcxz和Gcyz分别为蜂窝芯子沿不同方向的弹性模量和剪切模量。K为影响系数,表示蜂窝夹层板蒙皮受横向剪切影响,取值在0~1,理论值取1。根据蜂窝板实际材料选用情况,可计算出相应的夹层板力学参数,用于有限元计算使用。
再根据Hoff基本假设理论,由于夹层板上下蒙皮相对于蜂窝芯子很薄,蜂窝芯子的厚度相对于蒙皮刚度很小,既假设蜂窝芯子在xy平面内的应力忽略不计,可以将蜂窝夹层结构等效为各向同性薄板结构,根据基本弯曲理论假设,可得等效后的弹性模量,厚度和密度等:
| $ \left\{\begin{array}{l} t_{e q}=\sqrt{h_{f}^{2}+3\left(h_{c}+h_{f}\right)^{2}} \\ E_{e q}=\frac{2 E h_{f}}{t_{e q}} \\ \rho_{e q}=\frac{2 \rho_{f} h_{f}+\rho_{c} h_{c}}{t_{e q}} \end{array}\right. $ | (7) |
式中teq、Eeq和ρeq分为等效后的面板厚度、弹性模量和密度。
经过长期的工程实践,可以确认,利用式(7)计算出的等效蜂窝板模态频率误差在3%左右。在此引入2个修正系数,能够有效提高计算精度,将式(7)修改为:
| $ \left\{\begin{array}{l} t_{e q}=\sqrt{h_{f}^{2}+3\left(h_{c}+h_{f}\right)^{2}} \\ E_{e q}=\frac{2 K_{s} E h_{f}}{t_{e q}} \\ \rho_{e q}=\frac{2 \rho_{f} h_{f}+\rho_{c} h_{c}}{t_{e q}}+K_{\lambda} \end{array}\right. $ | (8) |
式中:Ks为刚度弱化系数,取值范围0.98~1;Kλ为密度强化系数,取值范围在0.5~1。修正后的模态频率计算结果误差为1%左右,效果明显。
3 蜂窝夹层板有限元数学建模根据上述蜂窝夹层板的力学参数,采用经典薄板弯曲理论假定如下[13-14]:
1) 可以忽略板厚度方向的正应力,并假设薄板的厚度没有变化;
2) 薄板的法线在产生弯曲后,仍然保持为薄板的弹性曲面的法线;
3) 薄板中面上的各点没有平行于中面的位移。
假设1)中信息可得:εz=∂w/∂z=0,这样在单元中w=w(x, y),即挠度w仅是x和y的函数,与z无关。
由假设2)可知:板内不存在剪应变,即γyz=∂ν/∂z+∂w/∂y=0,γyx=∂w/∂x+∂u/∂z=0。可以从中推得:
| $ \frac{\partial v}{\partial z}=-\frac{\partial w}{\partial y}, \quad \frac{\partial u}{\partial z}=-\frac{\partial w}{\partial x} $ | (9) |
对于式(9)进行积分,并注意到由于∂w/∂x和∂w/∂y也与z无关,因此可得:
| $ v=-z \frac{\partial w}{\partial y}+f_{1}(x, y), \quad u=-z \frac{\partial w}{\partial x}+f_{x}(x, y) $ | (10) |
式中f1(x, y)和f2(x, y)是关于x和y的任意函数。
由假设3)可知uz=0=vz=0=0,因此由式(10)可知f1(x, y)=f2(x, y)=0,式(10)可简化为:
| $ v=-z \frac{\partial w}{\partial y}, \quad u=-z \frac{\partial w}{\partial x} $ | (11) |
综上所述,在受弯薄板中只有2个应变分量εx, εy和γxy不为零:
| $ \left\{\begin{array}{l} \varepsilon_{x}=\frac{\partial u}{\partial x}=-z \frac{\partial^{2} w}{\partial x^{2}} \\ \varepsilon_{y}=\frac{\partial v}{\partial y}=-z \frac{\partial^{2} v}{\partial y^{2}} \\ \gamma_{x y}=\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}=-2 z \frac{\partial^{2} w}{\partial x y} \end{array}\right. $ | (12) |
在式(12)中含有z,可以通过引入广义的应变和广义应力的概念来得到更简洁的形式[15]。对于各项同性材料,在不考虑σz的平面情况下有如下应力应变关系:
| $ \left\{\begin{array}{l} \sigma_{x}=\frac{E}{1-\mu^{2}}\left(\varepsilon_{x}+\mu \varepsilon_{y}\right) \\ \sigma_{y}=\frac{E}{1-\mu^{2}}\left(\mu \varepsilon_{x}+\varepsilon_{y}\right) \\ \tau_{x y}=\frac{E}{2(1-\mu)} \gamma_{x y} \end{array}\right. $ | (13) |
将式(12)代入式(13)得:
| $ \left\{\begin{array}{l} \sigma_{x}=-\frac{E}{1-\mu^{2}} z\left(\frac{\partial^{2} w}{\partial x^{2}}+\mu \frac{\partial^{2} w}{\partial y^{2}}\right) \\ \sigma_{y}=-\frac{E}{1-\mu^{2}} z\left(\mu \frac{\partial^{2} w}{\partial x^{2}}+\frac{\partial^{2} w}{\partial y^{2}}\right) \\ \tau_{x y}=-\frac{E}{2(1+\mu)} z \frac{\partial^{2} w}{\partial x \partial y} \end{array}\right. $ | (14) |
上述应力将在板内分别合称为薄板的内力:
| $ \left\{\begin{array}{l} m_{x}=\int\limits_{-t / z}^{t / z} z \sigma_{x} \mathrm{~d} z=-\frac{E t^{3}}{12\left(1-\mu^{2}\right)}\left(\frac{\partial^{2} w}{\partial x^{2}}+\mu \frac{\partial^{2} w}{\partial y^{2}}\right) \\ m_{y}=\int\limits_{-t / z}^{t / z} z \sigma_{y} \mathrm{~d} z=-\frac{E t^{3}}{12\left(1-\mu^{2}\right)}\left(\mu \frac{\partial^{2} w}{\partial x^{2}}+\frac{\partial^{2} w}{\partial y^{2}}\right) \\ m_{x y}=\int\limits_{-t / z}^{t / z} z \sigma_{x y} \mathrm{~d} z=-\frac{E t^{3}}{12(1-\mu)} \cdot \frac{\partial^{2} w}{\partial x \partial y} \end{array}\right. $ | (15) |
式(15)以矩阵形式表达为:
| $ \boldsymbol{m}=\left[\begin{array}{c} m_{x} \\ m_{y} \\ m_{y} \end{array}\right]=\frac{E t^{3}}{12\left(1-\mu^{2}\right)}\left[\begin{array}{ccc} 1 & \mu & 0 \\ \mu & 1 & 0 \\ 0 & 0 & \frac{1-\mu}{2} \end{array}\right]\left[\begin{array}{c} -\frac{\partial^{2} w}{\partial x^{2}} \\ -\frac{\partial^{2} w}{\partial y^{2}} \\ -2 \frac{\partial^{2} w}{\partial x \partial y} \end{array}\right] $ | (16) |
将式(16)简写为:
| $ \boldsymbol{m}=\boldsymbol{D} \boldsymbol{\kappa} $ | (17) |
式(17)即受弯薄板中的广义应力应变关系。
其中:
| $ \boldsymbol{\kappa}=\left[\begin{array}{c} -\frac{\partial^{2} w}{\partial x^{2}} \\ -\frac{\partial^{2} w}{\partial y^{2}} \\ -2 \frac{\partial^{2} w}{\partial x \partial y} \end{array}\right]=\boldsymbol{L} w $ | (18) |
| $ \boldsymbol{D}=D_{0}\left[\begin{array}{ccc} 1 & \mu & 0 \\ \mu & 1 & 0 \\ 0 & 0 & \frac{1-\mu}{2} \end{array}\right] $ | (19) |
式中
利用有限元理论将薄板划分为若干单元,每个单元上的节点有3个自由度:挠度w、法线绕x轴转动θx和法线绕y轴转动θy:
| $ \left[a_{i}\right]=\left[\begin{array}{c} w_{i} \\ \varphi_{x i} \\ \varphi_{y i} \end{array}\right]=\left[w_{i} \quad\left(\frac{\partial w}{\partial y}\right)_{i}\quad-\left(\frac{\partial w}{\partial x}\right)_{i}\right]^{T} $ | (20) |
单元节点位移向量为:
| $ \boldsymbol{a}^{e}=\left[\begin{array}{llll} a_{1} & a_{2} & \cdots & a_{n} \end{array}\right]^{\mathrm{T}} $ | (21) |
式中n为单元的节点数量。
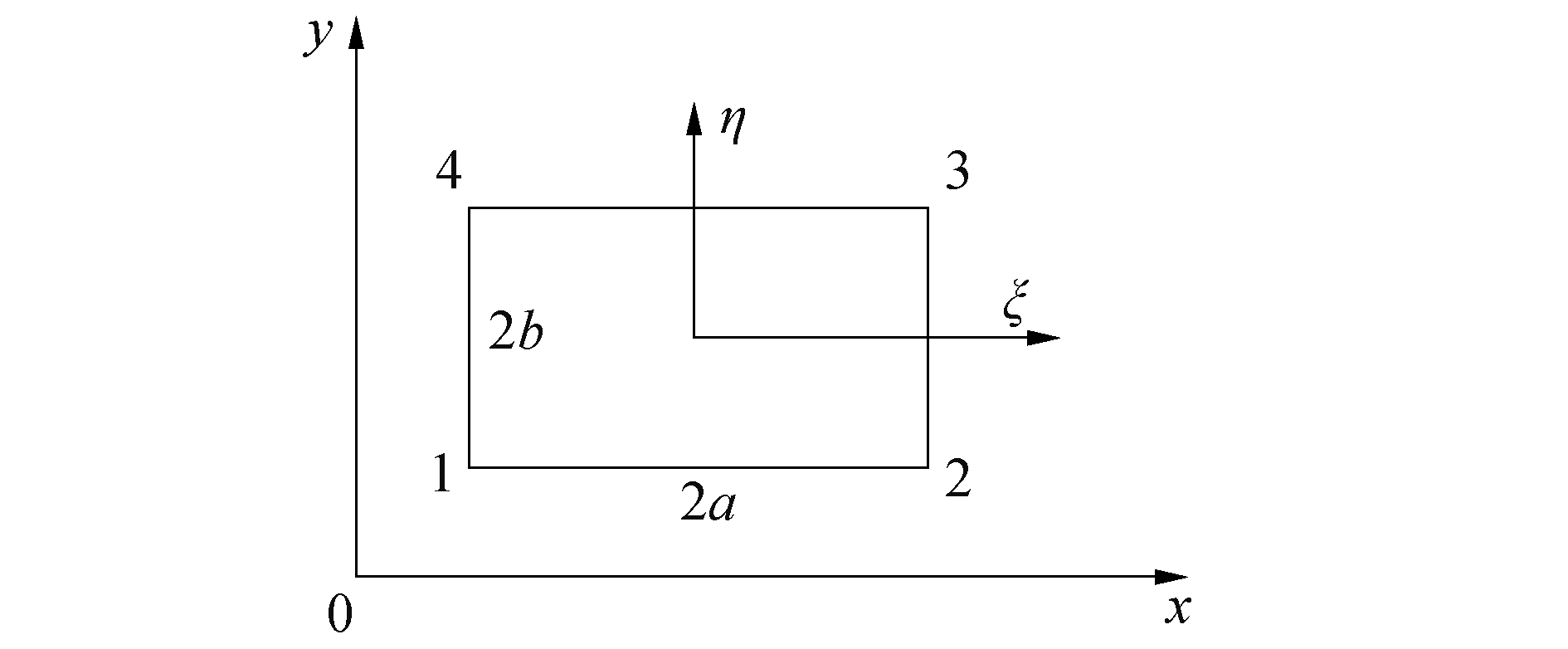
本文利用有限元法建立厚度为0.025 m,长宽均为1.1 m的矩形薄板,单元采用矩形单元(如图 4)。已经推导出式(16)和式(21),只需建立单元形函数即可求出刚度矩阵和质量矩阵,求得整板的模Me=∫VeρNTNdV态等结果。
|
Download:
|
| 图 4 四节点矩形单元无量纲坐标 Fig. 4 Four-node rectangular element coordinate | |
矩形单元任意一点的挠度可以运用形函数Ni(x, y)和单元节点位移[ai]表示为:
| $ w=\sum\limits_{i=1}^{4}\left(N_{i} w_{i}+N_{i x} \varphi_{x i}+N_{i y} \varphi_{y i}\right)=\sum\limits_{j=1}^{4}\left[N_{j}\right]\left[a_{j}\right] $ | (22) |
其中
| $ \left[N_{j}\right]=\left[\begin{array}{lll} N_{j} & N_{j x} & N_{j y} \end{array}\right] $ | (23) |
矩形单元形函数为:
| $ \left\{\begin{array}{l} N_{i}=\frac{1}{8}\left(1+\xi \xi_{i}\right)\left(1+\eta \eta_{i}\right)\left(2+\xi \xi_{i}+\eta \eta_{i}-\xi^{2}-\eta^{2}\right) \\ N_{i x}=-\frac{1}{8} b \eta_{i}\left(1+\xi \xi_{i}\right)\left(1+\eta \eta_{i}\right)\left(1-\eta^{2}\right) \\ N_{i y}=\frac{1}{8} a \xi_{i}\left(1+\xi \xi_{i}\right)\left(1+\eta \eta_{i}\right)\left(1-\xi^{2}\right) \end{array}\right. $ | (24) |
式中:i=1, 2, 3, 4
可以将式(22)变成矩阵形式:
| $ w = \mathit{\boldsymbol{N}}{\mathit{\boldsymbol{a}}^e} $ | (25) |
将式(25)代入式(18)中得:
| $ \boldsymbol{\kappa}=\boldsymbol{L} \boldsymbol{w}=\boldsymbol{L} \boldsymbol{N a}^{e}=\boldsymbol{B} \boldsymbol{a}^{e} $ | (26) |
其中B为3×12阶矩阵:
| $ \boldsymbol{B}=-\left[\begin{array}{ccccc} \frac{\partial^{2} N_{1}}{\partial x^{2}} & \frac{\partial^{2} N_{1 x}}{\partial x^{2}} & \frac{\partial^{2} N_{1 y}}{\partial x^{2}} & \cdots & \frac{\partial^{2} N_{4 y}}{\partial x^{2}} \\ \frac{\partial^{2} N_{1}}{\partial y^{2}} & \frac{\partial^{2} N_{1 x}}{\partial y^{2}} & \frac{\partial^{2} N_{1 y}}{\partial y^{2}} & \cdots & \frac{\partial^{2} N_{4 y}}{\partial y^{2}} \\ 2 \frac{\partial^{2} N_{1}}{\partial x \partial y} & 2 \frac{\partial^{2} N_{1 x}}{\partial x \partial y} & 2 \frac{\partial^{2} N_{1 y}}{\partial x \partial y} & \cdots & 2 \frac{\partial^{2} N_{4 y}}{\partial x \partial y} \end{array}\right] $ | (27) |
根据单元刚度矩阵定义可知:
| $ \boldsymbol{K}^{e}=\int_{V^{e}} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{B} \mathrm{d} V $ | (28) |
根据质量矩阵定义,协调质量矩阵为:
| $ \boldsymbol{M}^{e}=\int_{V^{e}} \rho \boldsymbol{N}^{\mathrm{T}} \boldsymbol{N }{\rm{d}} V $ | (29) |
再根据结构动力学方程可以求出矩形板模态和应力的结果:
| $ \mathit{\boldsymbol{M\ddot \delta }} + \mathit{\boldsymbol{\dot C\dot \delta }} + \mathit{\boldsymbol{K\delta }} = \mathit{\boldsymbol{F}} $ | (30) |
将式(8)代入式(28)即可得到蜂窝板单元刚度矩阵,再利用式(30)即可求出蜂窝板的结构频率与模态阵型。
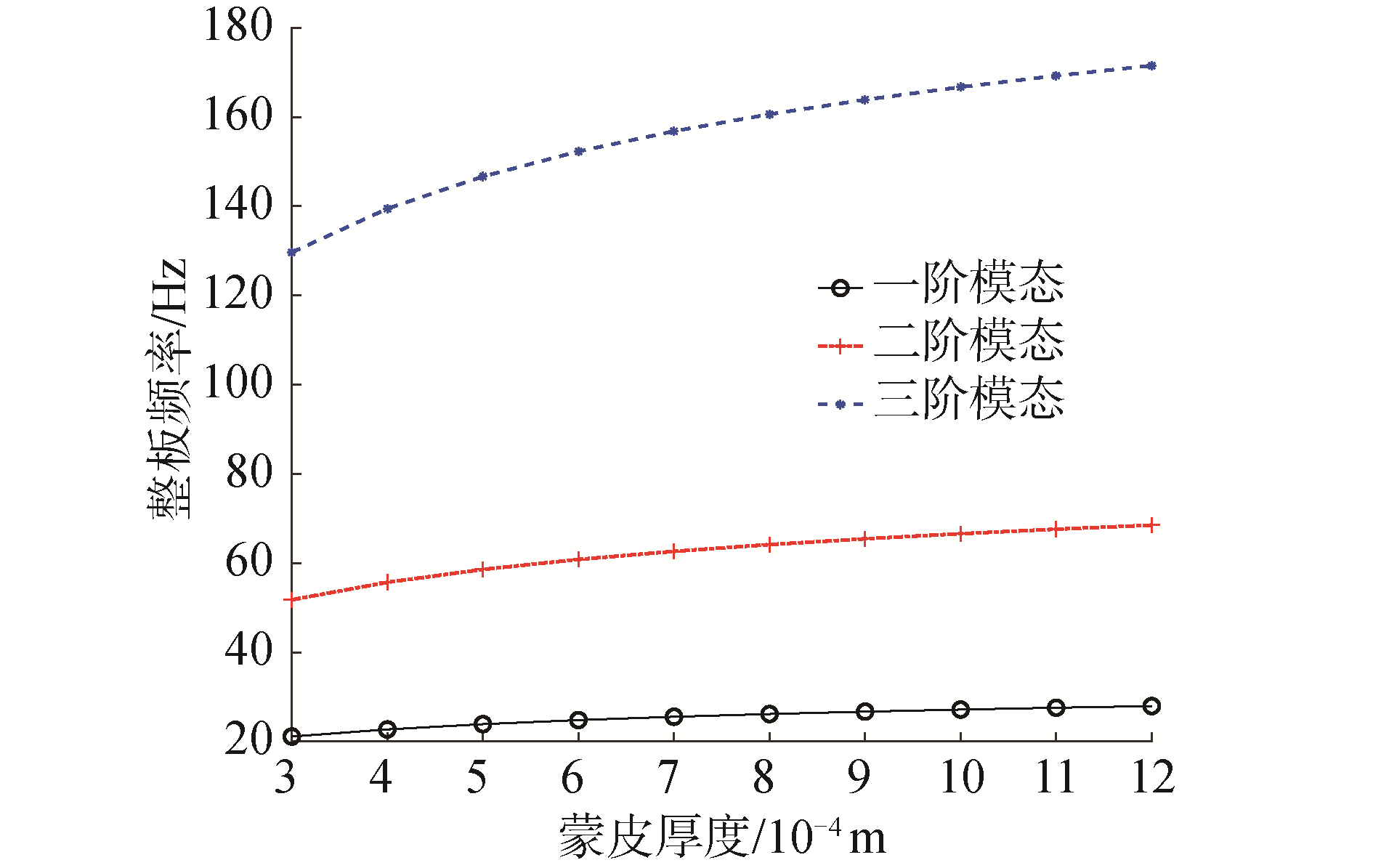
4 基于灵敏度的结构参数优化 4.1 整星蜂窝结构参数优化可以看出蜂窝芯子高度对蜂窝板刚度影响更大,并且蜂窝芯子密度远小于蒙皮密度,所以选择蒙皮最薄厚度为0.3 mm,蜂窝芯子厚度为24.4 mm,该厚度即能满足蜂窝板刚度要求,同时能够适应常规24.4 mm双工热管的厚度。蜂窝夹层结构参数与刚结构关系如图 5、6所示。
|
Download:
|
| 图 5 蜂窝板前3阶模态频率随蒙皮厚度变化曲线 Fig. 5 Frequency vs. thickness of skin variation curve | |
|
Download:
|
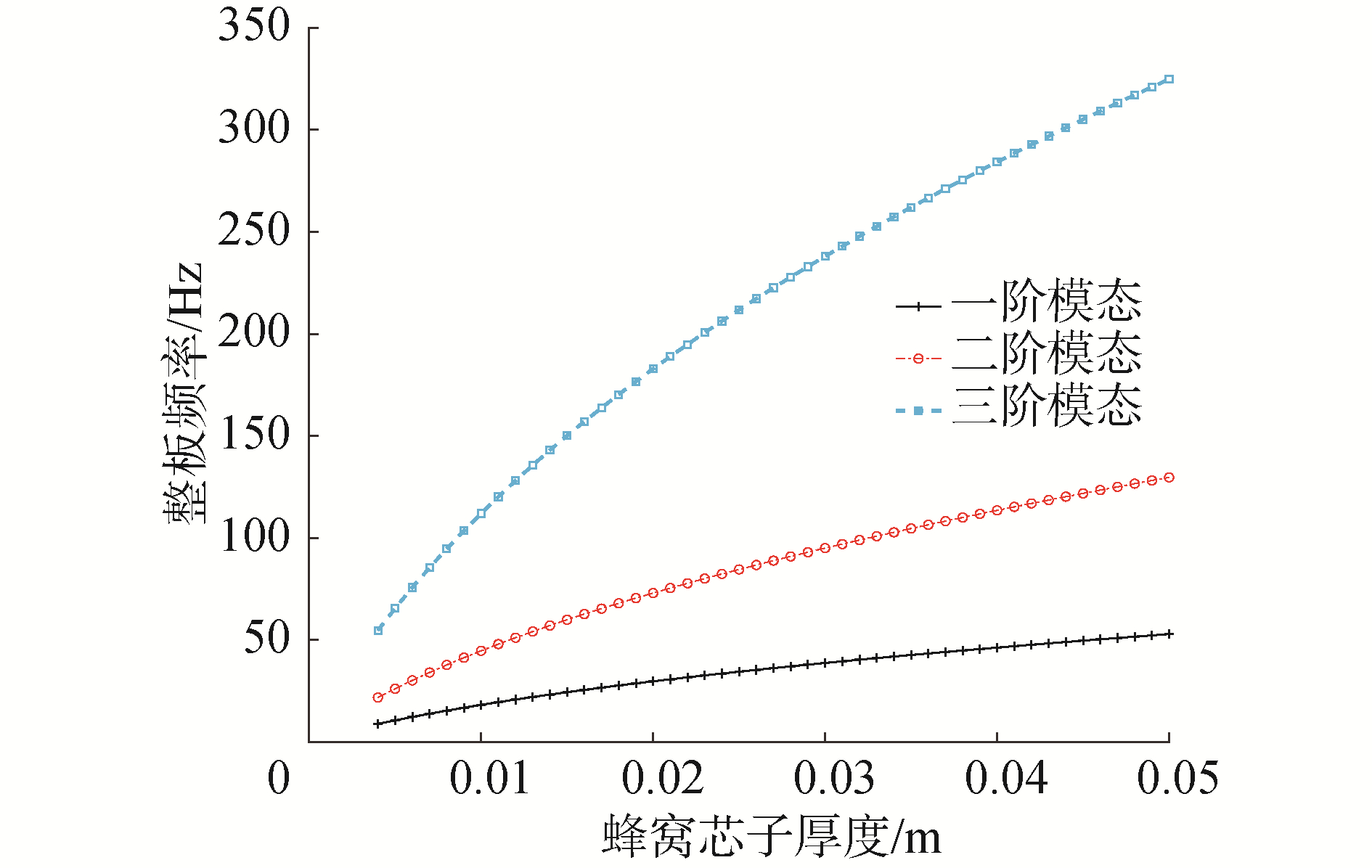
| 图 6 蜂窝板前3阶模态频率随芯子壁厚变化曲线 Fig. 6 Frequency vs. thickness of honeycomb core | |
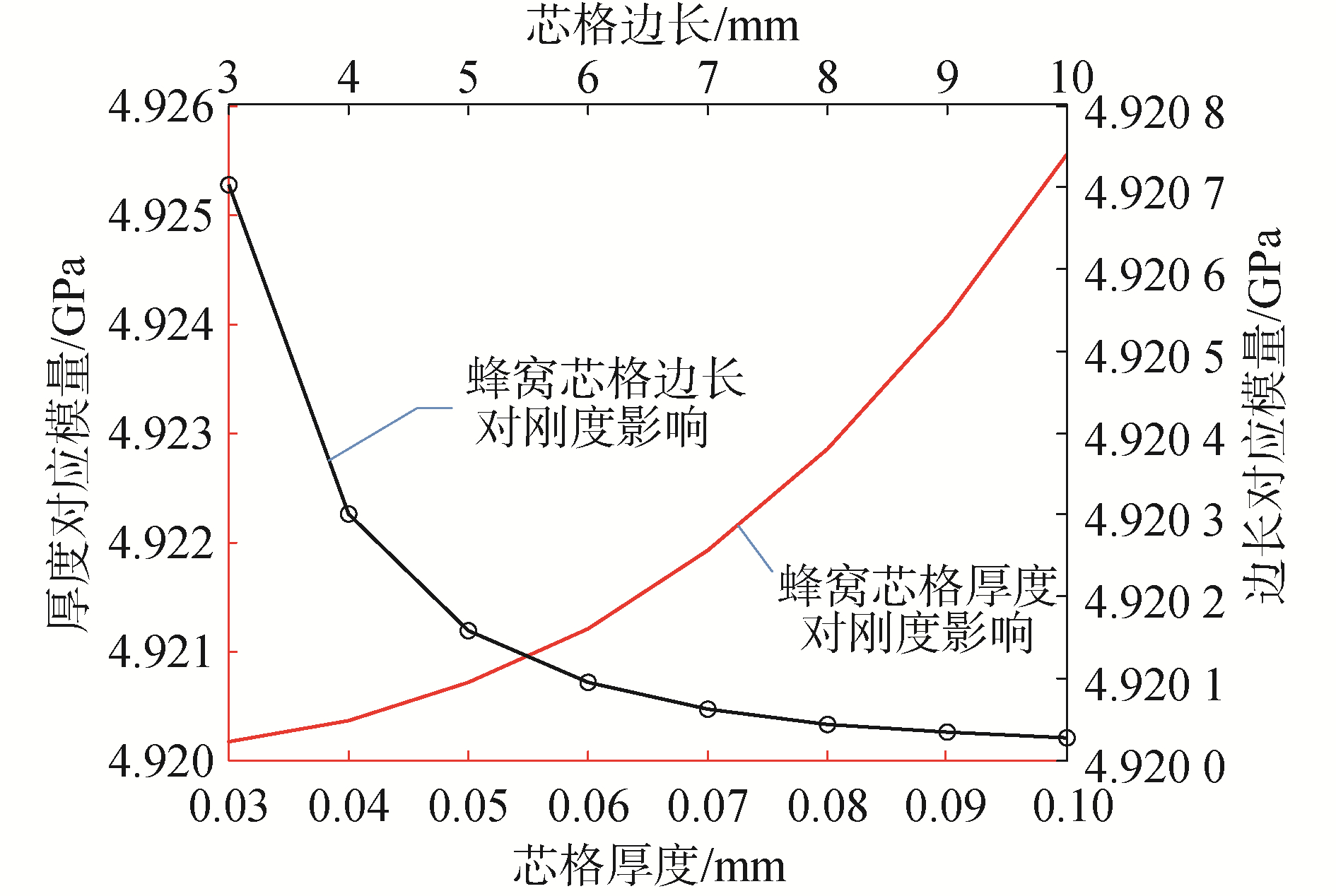
由图 7所示,蜂窝芯格的壁厚越厚,边长越短,整板刚度越高[16]。工程上选用3×0.05芯格较多,但该型号密度最大,设计余量过多。在单机安装板中选用5×0.05芯格,该型号既保留了常用芯格壁厚,同时增加芯格边长,减少结构重量,力学性能在同等条件下比4×0.04型号更高。最后在星箭对接面,采用4×0.05 mm蜂窝芯格提高对接面刚度和埋件胶结强度。最终得出卫星结构板各参数如表 2所示。
|
Download:
|
| 图 7 蜂窝板前3阶模态频率随芯子高度变化曲线 Fig. 7 Frequency vs. height of honeycomb core | |
| 表 2 卫星结构最终设计参数表 Table 2 The final design parameters of the satellite structure |
经过对蜂窝夹层结构的参数分析,实际卫星结构板总重量为59 kg,质量占比11.8%,结构重量接近最优方案。
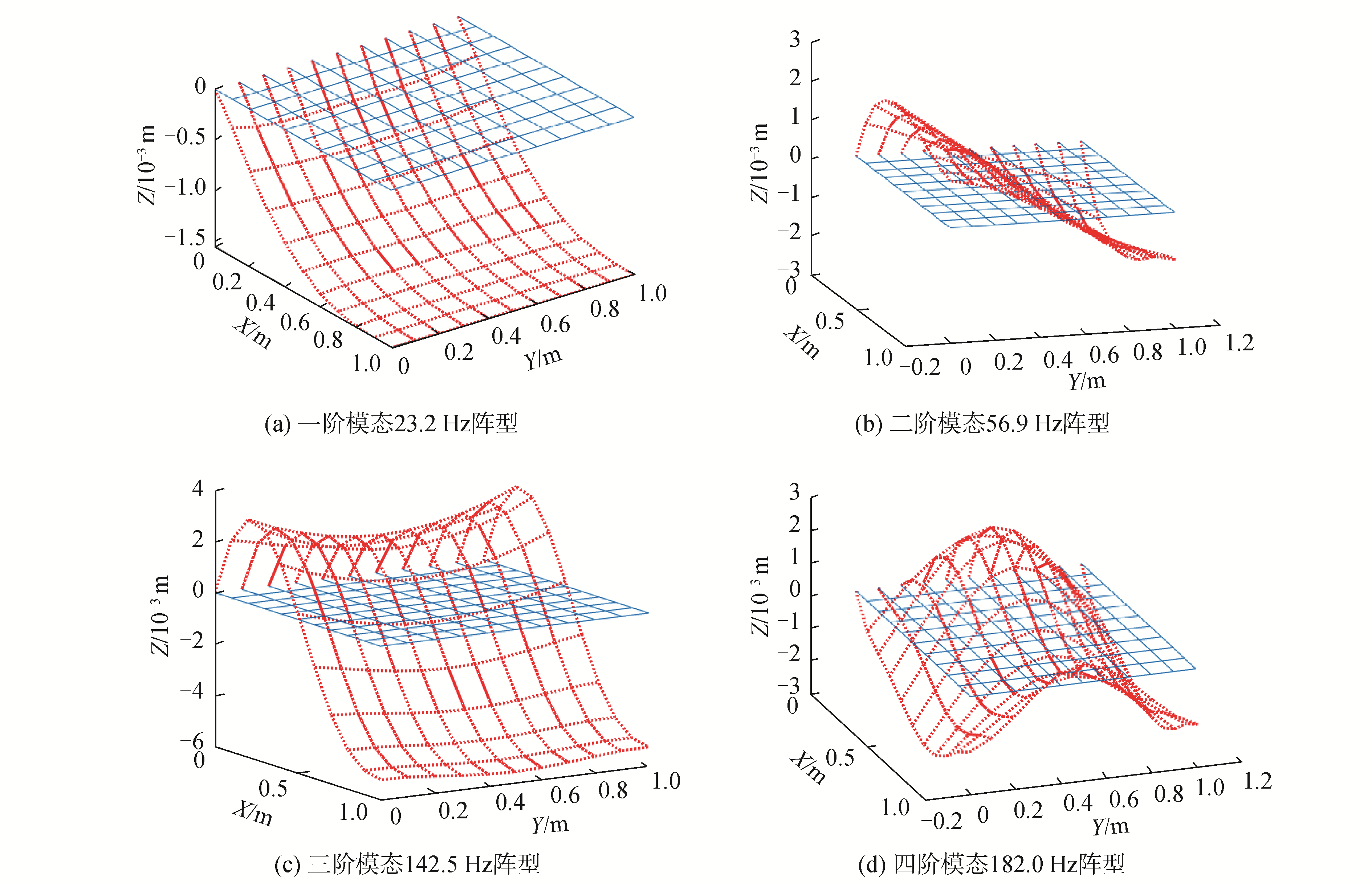
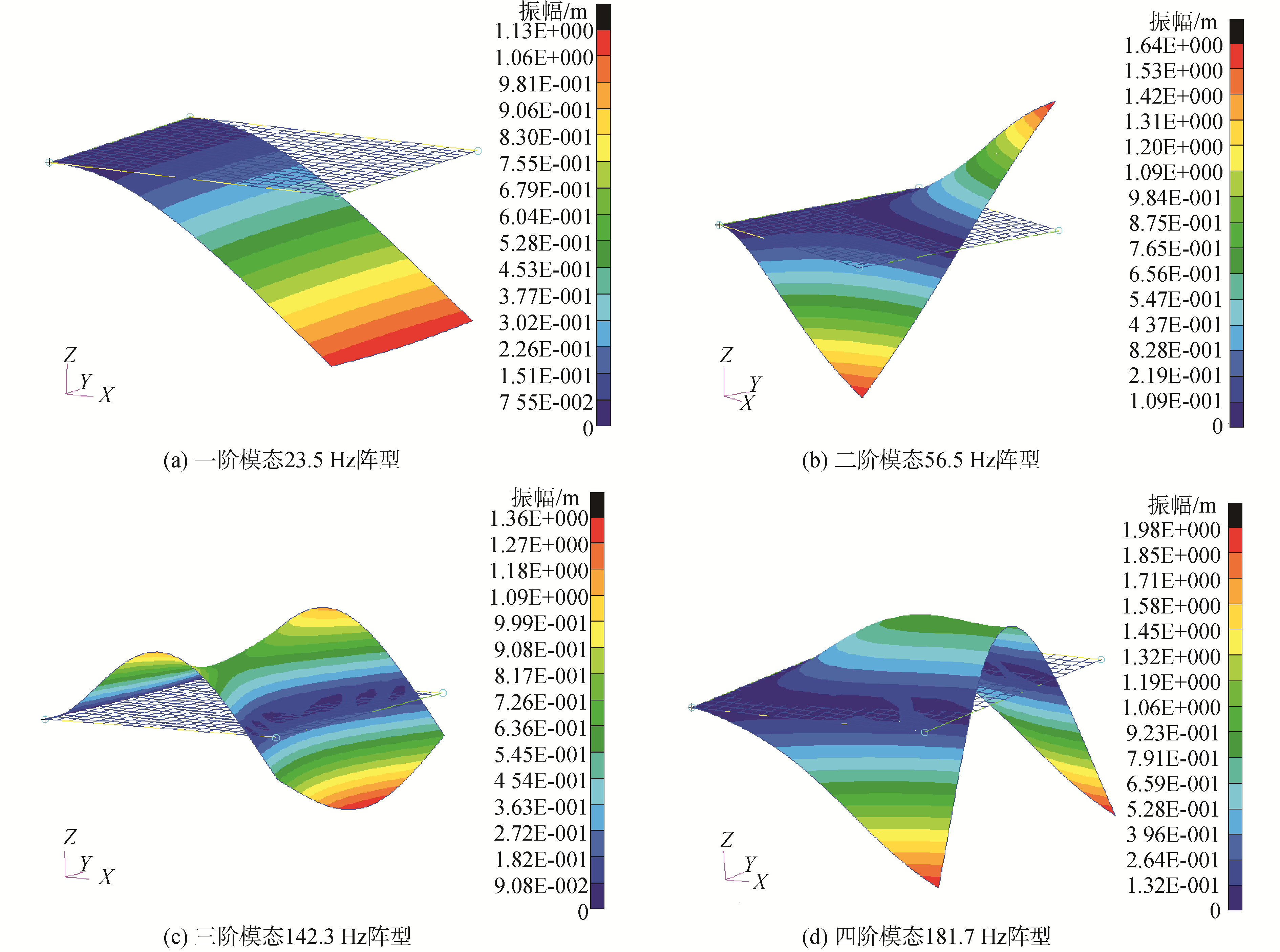
为验证上述理论计算与优化结果的正确性,选取单机安装板,尺寸为1.1 m×1.1 m的蜂窝夹层板,一边固支,构成悬臂结构,选用5×0.05芯格,0.3 mm厚铝蒙皮,蜂窝板厚度为25 mm。建立有限元数学模型,将薄板划分为20×20的单元网格,利用式(28)和式(29)计算出刚度矩阵和质量矩阵,在利用式(30)计算出薄板的结构频率和阵型。利用工程有限元软件建立同样模型,计算前4阶模态结果进行对比(如图 8、9所示)。
|
Download:
|
| 图 8 数学仿真的模态阵型结果 Fig. 8 Mode shapes of mathematical simulation | |
|
Download:
|
| 图 9 Nastran仿真阵型 Fig. 9 Mode shapes of Nastran simulation | |
可以看出,数学仿真计算结果与工程有限元软件仿真结果基本一致,能够说明上述蜂窝板理论研究正确性。所选蜂窝板参数接近工程最小值,为整星减重起到关键作用。
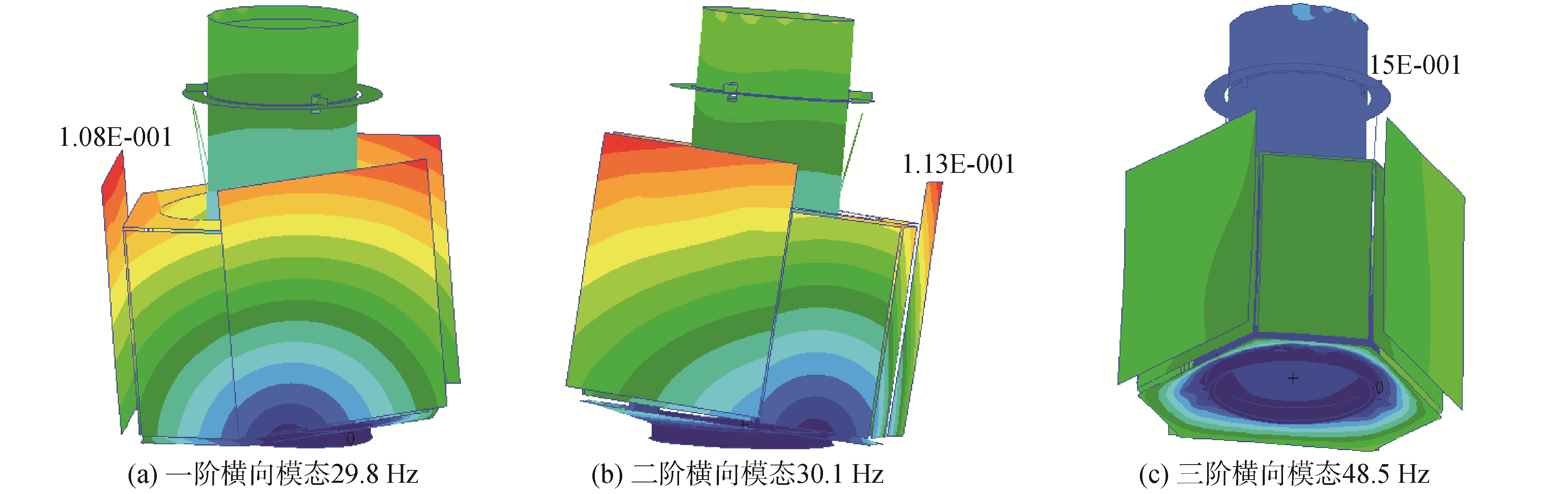
4.2 整星有限元分析与验证根据上述参数优化结果,设计出了“新技术试验E卫星”结构,并进行了力学分析工作,卫星前3阶模态振型如图 10所示。
|
Download:
|
| 图 10 整星模态分析阵型 Fig. 10 Mode shapes of satellite | |
根据上述结构优化设计结果,研制出了“新技术试验E卫星”,并通过了力学环境试验等各项验证工作,整星力学试验测得基频结果与分析结果对比如表 3所示。表 3中数据表明卫星结构分析结果与试验结果基本吻合。基于该方法设计的“新技术试验E卫星”于2020年在西昌卫星发射中心成功发射入轨,进一步验证了本文卫星结构参数优化方法的工程可行性与正确性。
| 表 3 卫星力学试验基频结果与分析值对比表 Table 3 Comparison between the results of the mechanical test and the analysis |
1) 本文针对高达50%载荷占比小卫星对结构分系统的质量严苛约束问题,分析了影响卫星结构板刚度和重量的关键设计参数,针对蜂窝夹层板等效模型进行了适当修正,并利用修正模型对夹层板的刚度灵敏度进行分析,设计出占比仅为11.8%的轻量化卫星结构,达到了目前小卫星结构设计的较高水平。
2) 整星测试数据进一步验证了轻量化设计方法的有效性和可靠性,目前国际发射成本约为每千克1万美元,经过结构轻量化设计后,可节省约41万美元发射成本。为后续的工程应用提供了一定的参考。
3) 本文没有利用已有的成熟优化算法进行参数优化,而是直接根据工程实际需求与经验对各参数进行选取。后续将开展这方面的研究。
| [1] |
叶秀芬, 于淼, 郭书祥, 等. 遥感图像中细弱目标分割方法[J]. 哈尔滨工程大学学报, 2020, 41(11): 1689-1694. YE Xiufen, YU Miao, GUO Shuxiang, et al. Segmentation method of thin and weak targets in remote sensing images[J]. Journal of Harbin Engineering University, 2020, 41(11): 1689-1694. (  0) 0)
|
| [2] |
陈昌亚, 郑晓亚, 姜晋庆. 卫星结构优化设计的建模问题[J]. 机械科学与技术, 2005, 24(1): 66-69. CHEN Changya, ZHENG Xiaoya, JIANG Jinqing. On some modeling problems in the optimization of satellite structures[J]. Mechanical science and technology, 2005, 24(1): 66-69. (  0) 0)
|
| [3] |
李真. 飞机偏心受载加筋板结构的有限元简化建模方法[J]. 科学技术与工程, 2011, 11(30): 7467-7470, 7475. LI Zhen. Simplified finite element model building method for stiffened-panel airframe structure under eccentricity load[J]. Science technology and engineering, 2011, 11(30): 7467-7470, 7475. DOI:10.3969/j.issn.1671-1815.2011.30.030 (  0) 0)
|
| [4] |
孙士平, 凌龙平. 多相材料格栅加筋板性能的参数化分析[J]. 机械设计与制造, 2013(10): 191-193. SUN Shiping, LI Longping. Parametric analysis of performance of multi-material stiffened panel[J]. Machinery design & manufacture, 2013(10): 191-193. (  0) 0)
|
| [5] |
卿光辉, 邱家俊, 塔娜. 弹性体的正则方程和加筋板的固有频率分析[J]. 力学学报, 2004, 36(6): 749-756. QING Guanghui, QIU Jiajun, TA Na. Hamilton canonical equation for elastic bodies and natural frequencies analysis of integral stiffened plates[J]. Acta mechanica sinica, 2004, 36(6): 749-756. DOI:10.3321/j.issn:0459-1879.2004.06.016 (  0) 0)
|
| [6] |
李磊. 基于结构完整性分析的固体火箭发动机药形改进与优化设计[D]. 长沙: 国防科学技术大学, 2011. LI Lei. Shape improvement and optimization of solid rocket motor grain based on structural integrity analysis[D]. National University of Defense Technology, Changsha: 2011. (  0) 0)
|
| [7] |
谢志刚. 基于异形封头(平盖加筋结构)参数化建模与优化设计的研究[D]. 南昌: 南昌大学, 2006. XIE Zhigang. The study on parametric-modeling and optimization of special head (flat head with ribs)[D]. Nanchang: Nanchang University, 2006. (  0) 0)
|
| [8] |
李莺歌, 关鑫, 陈维强, 等. 蜂窝夹层结构及其埋件的力学性能研究[J]. 宇航材料工艺, 2018, 48(4): 41-45. LI Yingge, GUAN Xin, CHEN Weiqiang, et al. Mechanical performances of honeycomb sandwich structure and inserts[J]. Aerospace materials & technology, 2018, 48(4): 41-45. (  0) 0)
|
| [9] |
窦明月, 王显峰, 张冬梅, 等. Nomex蜂窝芯静态压缩屈曲与后屈曲分析[J]. 南京航空航天大学学报, 2019, 51(1): 69-74. DOU Mingyue, WANG Xianfeng, ZHANG Dongmei, et al. Buckling and post-buckling of nomex honeycomb cores under compression[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2019, 51(1): 69-74. (  0) 0)
|
| [10] |
陈昊, 郭宁, 朱振涛, 等. 蜂窝夹层结构等效动力学建模方法对比研究[J]. 强度与环境, 2020, 47(1): 17-25. CHEN Hao, GUO Ning, ZHU Zhentao, et al. Comparative study on simplified dynamics modeling method of honeycomb sandwich structure[J]. Structure & environment engineering, 2020, 47(1): 17-25. (  0) 0)
|
| [11] |
肖潭, 胡森, 吴伟, 等. 蜂窝夹层铝建筑模板的几何优化与试验研究[J]. 工程力学, 2019, 36(2): 195-204. XIAO Tan, HU Sen, WU Wei, et al. Geometrical optimization and experimental study of aluminum honeycomb sandwich construction formworks[J]. Engineering mechanics, 2019, 36(2): 195-204. (  0) 0)
|
| [12] |
阚文广, 尹维龙. 可变形蜂窝结构设计与力学分析[J]. 哈尔滨工程大学学报, 2017, 38(9): 1406-1412. KAN Wenguang, YIN Weilong. Design and mechanical analysis of deformable honeycomb structures[J]. Journal of Harbin Engineering University, 2017, 38(9): 1406-1412. (  0) 0)
|
| [13] |
荣万崇, 周娜, 张体南, 等. 悬臂边界下带粘弹性层的纤维增强复合薄板固有特性研究[J]. 哈尔滨工程大学学报, 2019, 40(11): 1911-1916. RONG Wanchong, ZHOU Na, ZHANG Tinan, et al. Inherent characteristics of fiber-reinforced composite thin plate with viscoelastic layer under cantilever boundary condition[J]. Journal of Harbin Engineering University, 2019, 40(11): 1911-1916. (  0) 0)
|
| [14] |
孙林峰, 王冰松, 王立凯, 等. 蜂窝夹芯结构剪切性能参数工程化计算方法研究[J]. 工程与试验, 2018, 58(4): 8-11. SUN Linfeng, WANG Bingsong, WANG Likai, et al. Study on engineering calculation method for shear performance parameter of honeycomb core[J]. Engineering & test, 2018, 58(4): 8-11. (  0) 0)
|
| [15] |
章妮, 卢克非, 崔文龙. 芯子宽厚比对铝蜂窝夹层结构平压强度的影响[J]. 宇航材料工艺, 2016, 46(2): 36-38. ZHANG Ni, LU Kefei, CUI Wenlong. Effection of ratio of width to thickness of aluminum honeycomb sandwich structure of flatwise compression stress[J]. Aerospace materials & technology, 2016, 46(2): 36-38. (  0) 0)
|
| [16] |
金迪, 乔凌云, 凡玉. 芯层高度对复合材料蜂窝夹层结构总体稳定性的影响[J]. 机械强度, 2017, 39(5): 1164-1168. JIN Di, QIAO Lingyun, FAN Yu. Effect of core height on general stability of honeycomb sandwich structure[J]. Journal of mechanical strength, 2017, 39(5): 1164-1168. (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


