2. 哈尔滨工程大学 核安全与仿真技术国防重点学科实验室, 黑龙江 哈尔滨 150001
2. Fundamental Science on Nuclear Safety and Simulation Technology Laboratory, Harbin Engineering University, Harbin 150001, China
核电厂中存在有大量的旋转机械,如各类泵、汽轮机、电机、风机等,而轴承是旋转机械中较为薄弱的环节,由于受到安装、载荷、润滑等因素的影响,轴承在运行过程中会发生各种类型的失效[1]。据统计,旋转机械的故障中30%以上来自于轴承[2],因此,需要采用有效的检测技术对核电厂轴承的运行状态进行评估。核电厂一般采用在线的方式对旋转机械的振动幅值进行监测,一旦超出阈值将采用频谱分析技术对设备的振动信号进行分析并确定故障原因[3],但是只有在故障程度发展到足够大的时候才会被检测出来,加大了被动停机的风险。因此轴承的早期故障检测是关键,并在此基础上制定预测性的维护策略。
在轴承故障早期,周期性的冲击脉冲信号非常微弱,由于环境噪声的影响,难以提取出故障特征[4]。根据工程实践经验,机械振动响应是多频特征信号的叠加,因此可以采用信号分解和滤波的方式来提取故障特征,常用的信号分解方法主要有小波分解[5]、小波包分解[6]、经验模态分解(empirical mode decomposition, EMD)[7]和局部均值分解(local mean decomposition, LMD)[8]等。但是小波和小波包是一种非自适应的分解方法,需要提前确定小波基函数和分解层数。虽然EMD和LMD能够对信号进行自适应的分解,但是模态混叠现象使其应用受到了限制。集成经验模态分解(ensemble empirical mode decomposition, EEMD)通过添加辅助白噪声在一定程度上缓解了模态混叠问题[9],但计算量急剧增加,添加的白噪声无法完全被中和,不具有完备性。相对于递归式的模态分解方法,变分模态分解(variational mode decomposition,VMD)可以将信号分解成一组有限带宽的固有模态函数(intrinsic mode function, IMF),并在线估计其中心频率,可以有效抑制模态混叠现象。
由于模态数和带宽控制参数对VMD的分解效果具有显著的影响,并且在传统的VMD方法中,参数的取值是预先给定的,因此本文以最大加权峭度指标为目标函数,采用ABC算法对VMD参数进行优化,并对加权峭度指标最大的敏感分量进行分析,从而提取轴承的早期故障特征。由于核电厂中的轴承数据较难获取,因此本文采用仿真和实验数据进行分析。
1 基于人工蜂群优化的变分模态分解方法 1.1 变分模态分解VMD是一种新的信号分解方法[10],它的分解过程就是求解K个模态函数μk(t),k∈{1, 2, …, K},使其估计带宽之和最小,且各模态函数之和为输入信号f(t),因此,利用VMD对信号进行分解的过程可以用约束变分模型表示:
| $ \left\{\begin{array}{l} \min \limits_{\left\{\mu_{k}\right\},\left\{\omega_{k}\right\}}\left\{\sum\limits_{k=1}^{K}\left\|\partial_{t}\left[\left(\delta(t)+\frac{j}{{\rm{ \mathsf{ π} }} t}\right) * \mu_{k}(t)\right] \mathrm{e}^{-\mathrm{j} \omega_{k} t}\right\|_{2}^{2}\right\} \\ \text { s. t. } \quad \sum\limits_{k=1}^{K} \mu_{k}(t)=f(t) \end{array}\right. $ | (1) |
式中:μk(t)为各模态函数;ωk为各模态函数的中心频率;δ(t)为冲激函数。
为了求解上述的约束变分问题,引入二次惩罚因子α和Lagrange乘法算子λ(t)。其中α可以保证在高斯噪声存在的情况下信号重构的精度,λ(t)可以保证约束条件的严密性,则扩展的Lagrange表达式为:
| $ \begin{gathered} L\left(\mu_{k}(t), \omega_{k}, \lambda(t)\right)= \\ \alpha \sum\limits_{k=1}^{K}\left\|\partial_{t}\left[\left(\delta(t)+\frac{j}{{\rm{ \mathsf{ π} }} t}\right) * \mu_{k}(t)\right] \mathrm{e}^{-\mathrm{j} \omega_{k^{t}}}\right\|_{2}^{2}+ \\ \left\|f(t)-\sum\limits_{k=1}^{K} \mu_{k}(t)\right\|_{2}^{2}+\left\langle\lambda(t), f(t)-\sum\limits_{k=1}^{K} \mu_{k}(t)\right\rangle \end{gathered} $ | (2) |
采用交替方向乘子法(alternate direction method of multipliers,ADMM)对μkn+1(t)、ωkn+1、λn+1(t)进行交替更新迭代,求取扩展的Lagrange表达式的鞍点,即原变分问题的最优解。
每个模态函数μk(t)和相应的中心频率ωk的更新迭代过程为:
| $ \hat{\mu}_{k}^{n+1}(\omega)=\frac{\hat{f}(\omega)-\sum\limits_{i \neq k} \hat{\mu}_{i}(\omega)+\frac{\hat{\lambda}(\omega)}{2}}{1+2 \alpha\left(\omega-\omega_{k}\right)^{2}} $ | (3) |
| $ \omega_{k}^{n+1}=\frac{\int_{0}^{\infty} \omega\left|\hat{\mu}_{k}(\omega)\right|^{2} \mathrm{~d} \omega}{\int_{0}^{\infty}\left|\hat{\mu}_{k}(\omega)\right|^{2} \mathrm{~d} \omega} $ | (4) |
式中:
| $ \hat{\lambda}^{n+1}(\omega)=\hat{\lambda}^{n}(\omega)+\tau\left[\hat{f}(\omega)-\sum\limits_{k=1}^{K} \hat{\mu}_{k}^{n+1}(\omega)\right] $ | (5) |
式中:τ为更新步长。直到满足:
| $ \sum\limits_{k=1}^{K} \frac{\left\|\hat{\mu}_{k}^{n+1}-\hat{\mu}_{k}^{n}\right\|_{2}^{2}}{\left\|\hat{\mu}_{k}^{n}\right\|_{2}^{2}}<\varepsilon $ | (6) |
上述的迭代过程停止,最终得到K个具有独立频带成分的模态函数。
从上述过程可以看出,VMD在分解过程中需要预先设置4个参数,分别为模态数K、带宽控制参数(二次惩罚因子)α、更新步长τ和收敛误差ε。其中模态数和带宽控制参数对VMD的分解效果影响较大,而其他2个参数一般取默认值。
1.2 人工蜂群算法人工蜂群(artificial bee colony, ABC)是根据蜜蜂觅食原理提出的群智能优化算法[11]。ABC算法中将蜂群分为雇佣蜂、跟随蜂和侦查蜂。在每一次食物源的搜寻过程中,雇佣蜂先发现食物源并记录食物源的信息,然后跟随蜂根据雇佣蜂提供的食物源信息按一定的概率选择一个食物源。当一个食物源经过有限次搜寻之后仍然没有被更新,那么该食物源将会被舍弃,相应的雇佣蜂变成侦查蜂并随机寻找新的食物源。
每个食物源代表优化问题的一个可能解,食物源的花蜜量代表相应解的质量,即适应度值fiti。在ABC算法求解优化问题时,首先初始化种群,随机产生SN个d维的初始解xi(i=1, 2, …, SN):
| $ \boldsymbol{x}_{i}=\mathrm{lb}+(\mathrm{ub}-\mathrm{lb}) \cdot \operatorname{rand}(0,1) $ | (7) |
式中:ub、lb分别为xi取值的上限和下限,其中xi=[xi1 xi2 … xid]T。初始化之后,整个种群将进行雇佣蜂、跟随蜂和侦查蜂的循环搜寻过程,直到满足误差要求或达到最大迭代次数。
雇佣蜂首先进行领域搜索,在已有食物源附近更新食物源位置:
| $ x_{i j}^{\prime}=x_{i j}+\phi_{i j}\left(x_{i j}-x_{k j}\right) $ | (8) |
计算新解的适应度值fiti:
| $ \text { fit}_{i}= \begin{cases}1 /\left(1+f_{i}\right), & f_{i} \geqslant 0 \\ 1+\operatorname{abs}\left(f_{i}\right), & f_{i}<0\end{cases} $ | (9) |
如果新解的适应度值优于旧解,则雇佣蜂接受新解,否则将保留旧解。跟随蜂再依据适应度值计算每个解被选择的概率:
| $ \mathrm { prob }_{i}=\mathrm{fit}_{i} / \sum\limits_{i=1}^{\mathrm{SN}} \mathrm{fit}_{i} $ | (10) |
式中:k∈{1, 2, …, SN},且k≠i;j∈{1, 2, …, d};ϕij∈[-1, 1]的随机数;fi为第i个解的目标函数值;probi为第i个解被选择的概率。随后在区间[0, 1]内产生一个随机数,如果probi大于该随机数,则跟随蜂将按照式(8)产生新解并计算新解的适应度值fiti,若新解的fiti优于旧解,则跟随蜂接受新解,否则将保留旧解。如果一个解经过有限次循环后仍然没有被更新,为了防止陷入局部最优,该解将会被舍弃,相对应的雇佣蜂将变成侦查蜂并产生新解:
| $ x_{i j}=x_{\min j}+\operatorname{rand}(0,1) \cdot\left(x_{\max j}-x_{\min j}\right) $ | (11) |
式中xmaxj、xminj分别为第j维上的最大值和最小值。
1.3 基于改进VMD的轴承故障特征提取方法本文以最大加权峭度指标为目标函数,采用ABC算法对VMD分解过程中的模态数K和带宽控制参数α进行优化,对加权峭度指标最大的敏感模态分量进行包络谱分析并识别故障特征。在机械振动信号分析和特征提取过程中,采用的特征指标主要有熵、峭度、相关系数、振动烈度等,其中峭度和相关系数2个指标应用最为广泛。峭度是一种无量纲指标,对振动信号中的冲击分量极为敏感,因此它适用于冲击测量,并已广泛应用于机械设备的损伤监测中。然而峭度只依赖冲击信号的分布密度,如果以最大峭度指标为目标函数对VMD参数进行优化,可能会忽略一些振幅较大但分布较为分散的冲击分量。相关系数可以表征信号间的相似程度,但在冲击信号检测中容易受到噪声的影响。因此,考虑到峭度和相关系数这2个指标的优缺点,采用加权峭度指标作为目标函数对VMD参数进行优化,加权峭度指标KCI定义为:
| $ \mathrm{KCI}=\mathrm{KI} \cdot \mid C \mid $ | (12) |
| $ \mathrm{KI}=\frac{\frac{1}{N} \sum\limits_{n=1}^{N} x^{4}(n)}{\left(\frac{1}{N} \sum\limits_{n=1}^{N} x^{2}(n)\right)^{2}} $ | (13) |
| $ C=\frac{\left.\sum\limits_{n=1}^{N}(x(n)-\bar{x})\right)(y(n)-\bar{y})}{\sqrt{\sum\limits_{n=1}^{N}(x(n)-\bar{x})^{2} \sum\limits_{n=1}^{N}(y(n)-\bar{y})^{2}}} $ | (14) |
式中:KI为信号序列x(n)零均值下的峭度值;N是信号长度;C为信号x(n)和y(n)之间的相关系数,文中表示各IMFs与原始信号之间的相关系数,其取值范围是|C|≤1。考虑到ABC算法以最大适应度值fiti为优化目标,按照式(9)中fiti的定义,优化目标即为目标函数的最小值,因此本文以最小-KCI为优化目标,则本文提出的基于参数自适应VMD的轴承故障特征提取方法的原理如图 1所示。
|
Download:
|
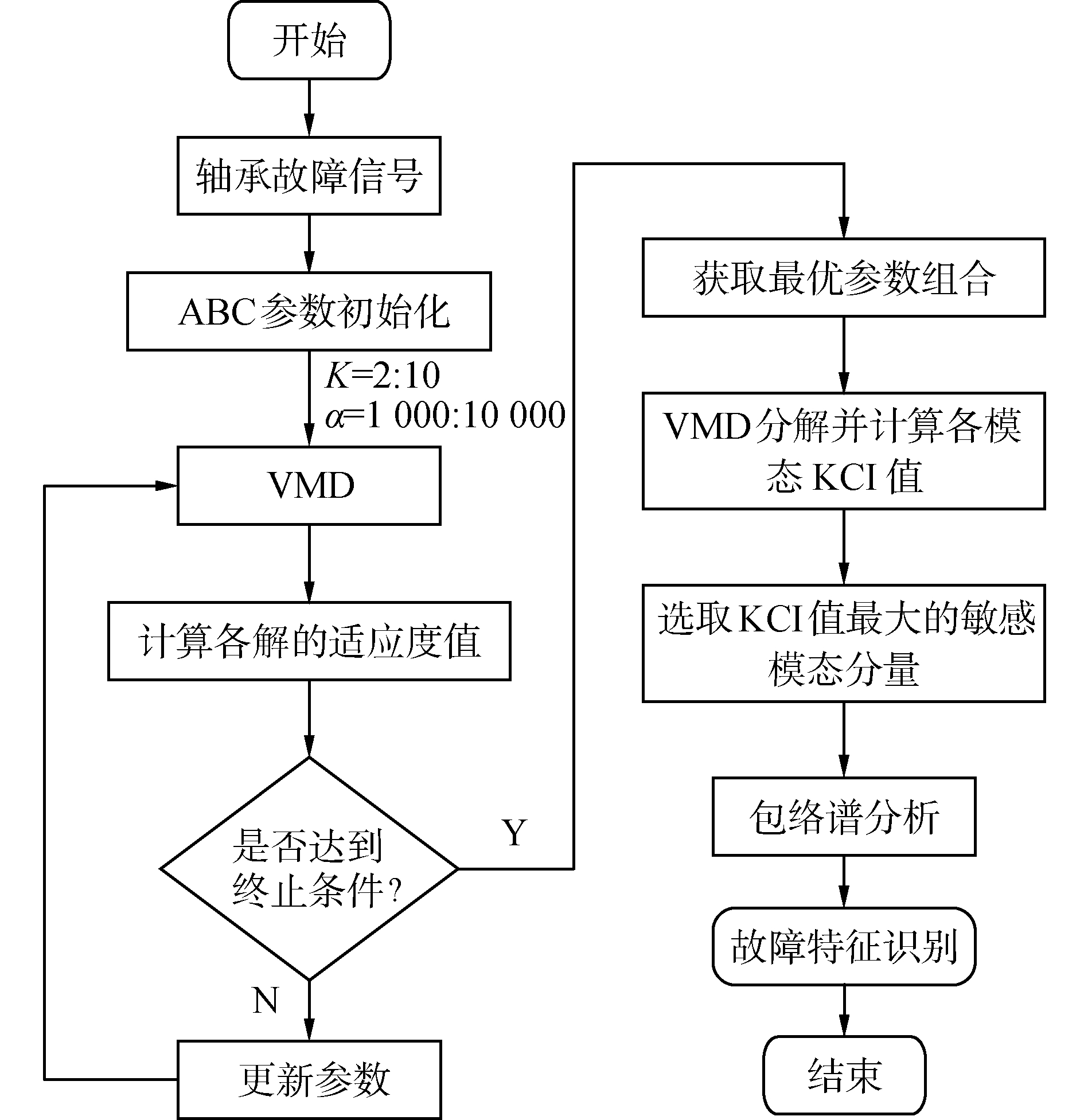
| 图 1 基于参数自适应VMD的轴承故障特征提取方法 Fig. 1 Flowchart of bearing fault feature extraction based on parameter adaptive VMD | |
首先,输入轴承故障信号,初始化ABC算法参数,并且设置优化参数的范围;然后,对信号进行VMD分解,计算各解的适应度值。判断是否达到迭代终止条件,如果没有则更新参数继续进行迭代,如果满足终止条件,则输出最优的参数组合;最后,利用最优参数组合对信号进行VMD分解,并对KCI值最大的敏感模态进行包络谱分析,从而对故障特征进行识别。
2 轴承仿真信号分析当核电厂中大型旋转机械的轴承出现点蚀或缺陷故障时,零件之间的碰撞会产生周期性指数衰减的正弦冲击信号。在故障早期,冲击信号较为稀疏且微弱,很容易被强噪声淹没。为了对提出的轴承故障特征提取方法的有效性进行验证,本文利用轴承内圈故障的仿真信号进行分析:
| $ \left\{\begin{array}{l} x(t)=s(t)+n(t) \\ s(t)=\sum A_{i} h\left(t-i T-\tau_{i}\right) \\ h(t)=\exp (-C t) \sin \left(2 {\rm{ \mathsf{ π} }} f_{n} t\right) \\ A_{i}=1+A_{0} \sin \left(2 {\rm{ \mathsf{ π} }} f_{r} t\right) \end{array}\right. $ | (15) |
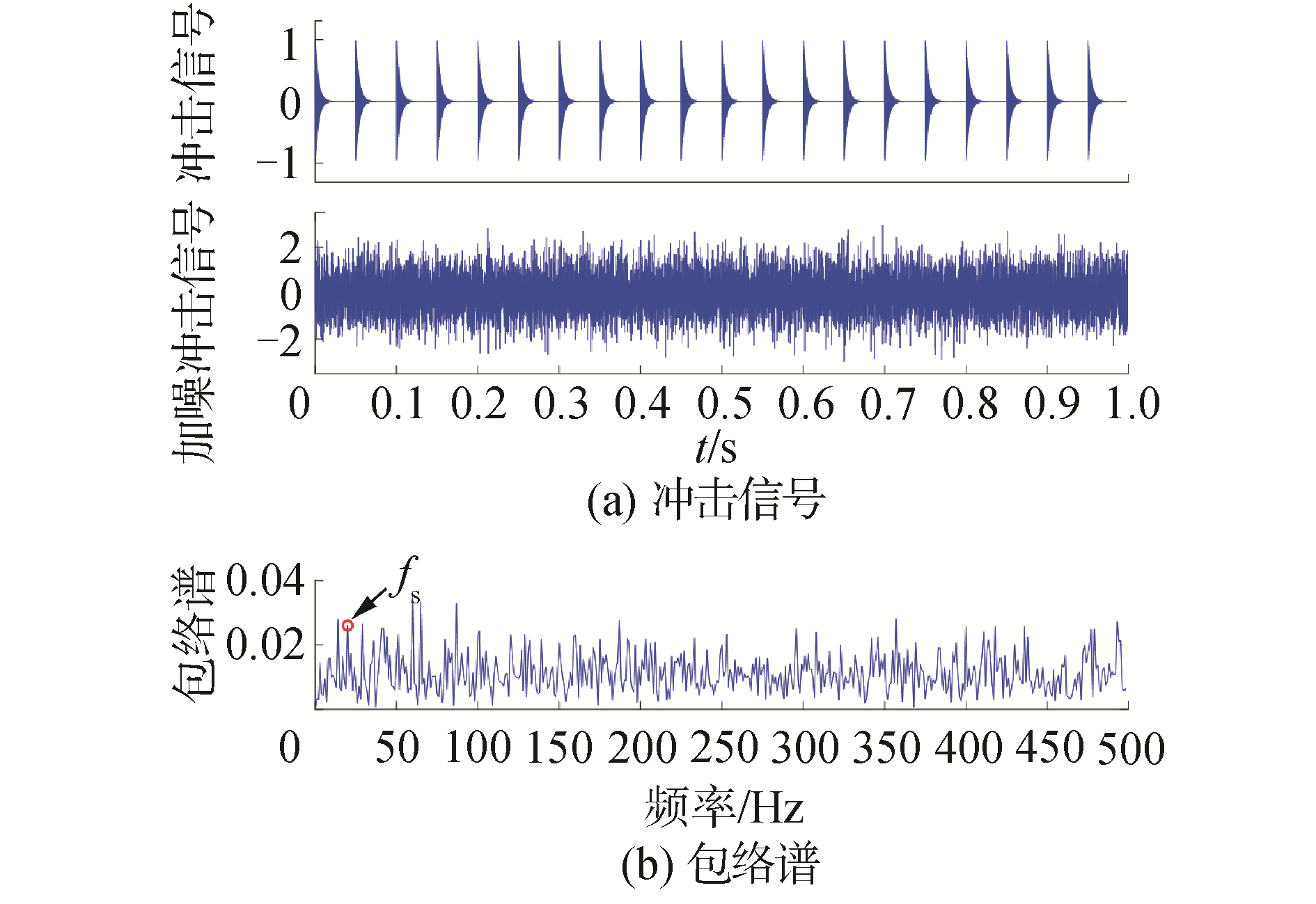
式中:x(t)为带噪声的模拟冲击信号;s(t)为周期性冲击信号;n(t)为高斯白噪声;Ai为第i次冲击信号的幅值,初始幅值A0=0.5,转频fr=10 Hz;h(t)为指数衰减的正弦信号,阻尼系数C=250,系统固有频率fn=3 000 Hz,平均脉冲周期T=0.05 s; τi为第i次冲击相对于周期T的微小波动,服从均值为零,标准差为0.5%倍转频的正态分布;轴承的故障特征频率fs=1/T=20 Hz;加噪冲击信号的信噪比SNR=-15 dB;信号的采样频率为12 000 Hz。则轴承内圈故障的仿真信号及其包络谱如图 2所示。
|
Download:
|
| 图 2 轴承内圈故障仿真信号及其包络谱 Fig. 2 Simulation signal of bearing inner race fault and its envelope spectrum | |
从图 2可以看出,周期性脉冲信号幅值较小,基本淹没在强背景噪声中,从时域波形图中很难观察到冲击分量,可以用来模拟轴承早期故障的微弱振动响应。虽然加噪信号的包络谱中可以观察到故障特征频率fs,但是周围干扰分量较多,在故障未知的前提下很难得出准确的诊断结果。因此利用本文提出的方法对加噪冲击信号进行处理,设置ABC的食物源数量SN=10,最大迭代次数为10,则以最小-KCI为目标,求VMD分解最优参数组合的ABC收敛曲线如图 3所示。
|
Download:
|
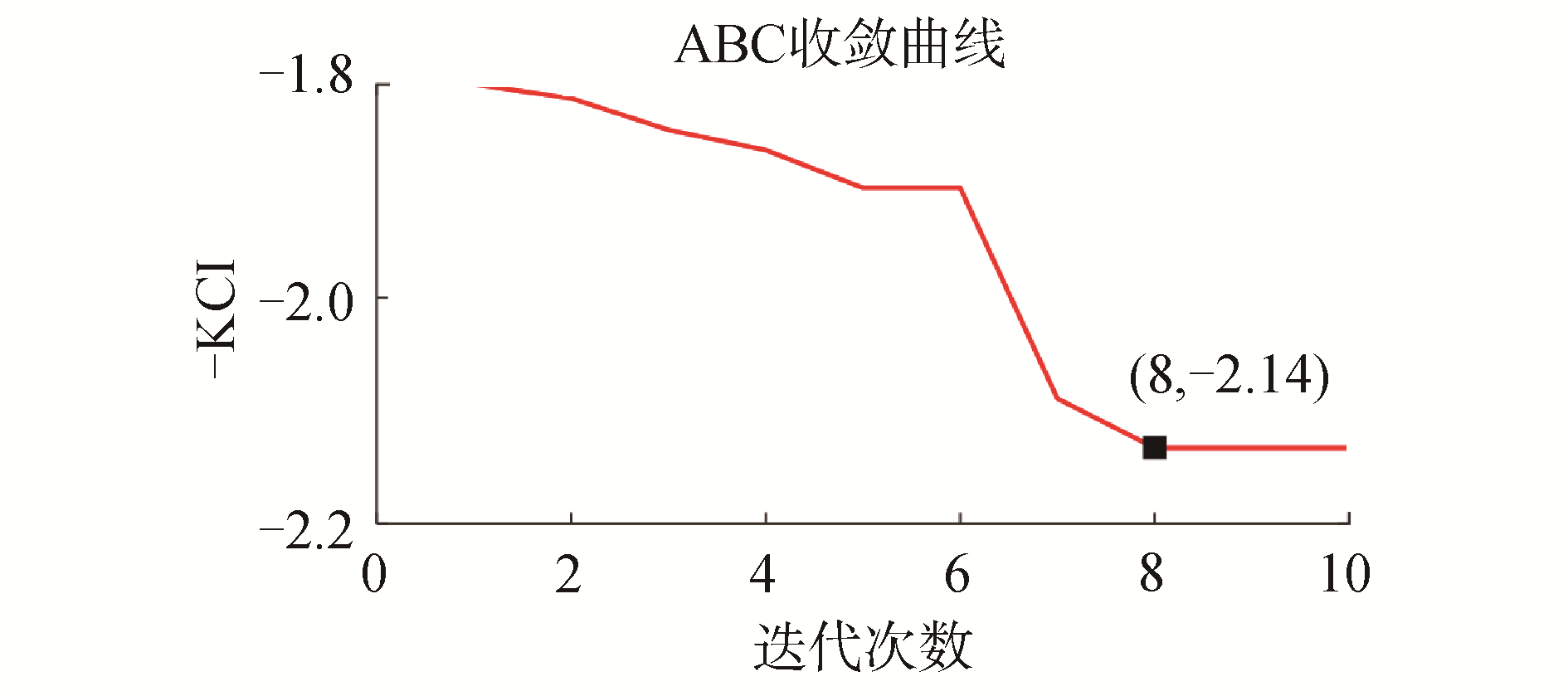
| 图 3 ABC收敛曲线 Fig. 3 ABC convergence curve | |
从图 3可以看出,ABC优化的最大KCI值为2.14,相对应的模态数K和带宽控制参数α的取值分别为2和1 500。采用最优参数组合的VMD方法对加噪冲击信号进行分解并计算各模态的KCI值,结果如图 4所示。将KCI值最大的IMF2作为敏感分量并对其进行包络谱分析,从而提取故障特征。为了对KCI作为敏感分量选择依据的有效性进行验证,还对其他模态分量进行了包络谱分析,结果如图 5所示。

|
Download:
|
| 图 4 模态函数及其KCI值 Fig. 4 Modes decomposed by the optimal VMD and the corresponding KCI values | |
|
Download:
|
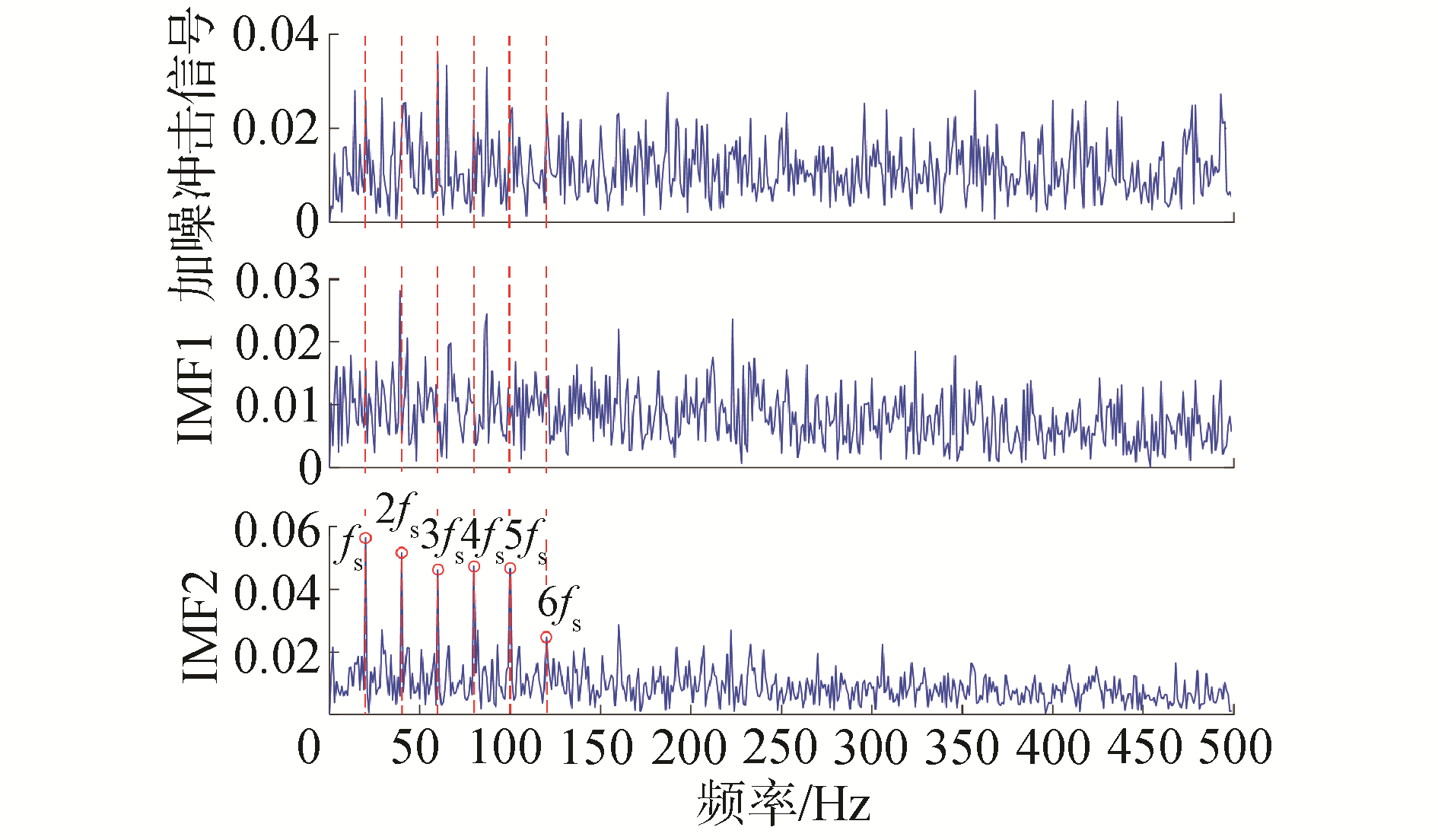
| 图 5 加噪冲击信号及各模态的包络谱 Fig. 5 Envelope spectrums of noisy impact signal and each modes | |
通过对比可以看出,IMF2几乎包含了所有特征信息,与原始加噪冲击信号相比故障特征频率更为显著,能够清晰地观察到故障频率fs及其谐波(2fs、3fs、4fs、5fs、6fs),而IMF1主要为噪声分量,包络谱中没有观察到明显的故障特征。分析结果表明,将KCI作为敏感模态分量的选择依据是有效的,该方法能够有效地分析振动信号,提取出强背景噪声中的微弱故障特征。
为进一步评估本文方法的特征提取效果,将该方法与EEMD、LMD和固定参数VMD的信号处理效果进行比较,将原加噪冲击信号分别进行EEMD、LMD和固定参数VMD分解,其中VMD分解中模态数K和带宽控制参数α分别取默认值4和2 000。然后以最大KCI值为依据选取敏感模态分量进行包络谱分析,结果如图 6所示。

|
Download:
|
| 图 6 敏感模态分量的包络谱 Fig. 6 Envelope spectrums of sensitive modes | |
EEMD、LMD和固定参数VMD方法均能够在不同程度上识别出故障频率fs及其谐波分量,但是3种方法故障特征频率的幅值与本文方法相比要小,且均无法识别谐波分量6fs。其中EEMD方法中谐波分量2fs无法识别,LMD方法低频处存在有大量的干扰分量,故障频率fs和谐波分量2fs无法清晰观察到。因此,本文方法针对冲击信号的特征提取方面与EEMD、LMD、固定参数VMD方法相比具有更好的效果,为了进一步验证该方法的有效性和工程应用价值,下一节将采用该方法对轴承故障的实验数据进行分析。
3 实验验证轴承内圈故障数据来自于XJTU-SY轴承加速寿命测试平台[12],实验台和故障轴承内圈如图 7所示,测试轴承的主要参数如表 1所示。驱动轴转速为2 400 r/m,采样频率为25.6 kHz,计算得到轴承外圈和内圈的理论故障频率分别为123.32 Hz和196.68 Hz。

|
Download:
|
| 图 7 实验台及故障轴承内圈 Fig. 7 The testbed and the bearing inner race with defect | |
| 表 1 测试轴承参数 Table 1 The specification of test bearing |
轴承内圈故障信号的时域波形和包络谱如图 8所示,由于轴承处于早期故障阶段,冲击脉冲的幅值并未大量超出正常值,因此核电厂中的幅值监测手段将很难检测出故障,并且包络谱中也未能获取故障信息。然后利用本文提出的方法对轴承故障信号进行处理,ABC的参数设置与上文相同,则以最小-KCI为目标,求VMD分解最优参数组合的ABC收敛曲线如图 9所示。

|
Download:
|
| 图 8 轴承内圈故障信号及其包络谱 Fig. 8 Fault signal of bearing inner race and its envelope spectrum | |
|
Download:
|
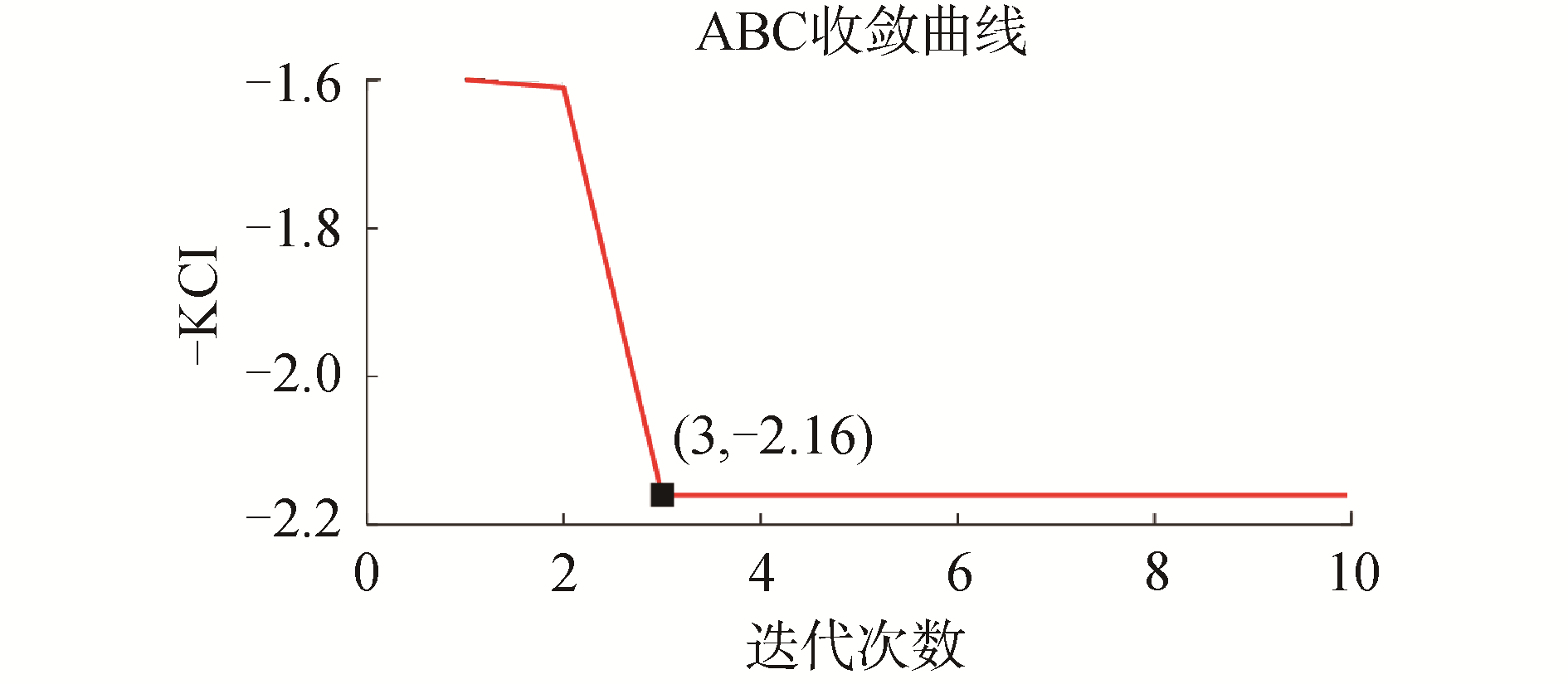
| 图 9 ABC收敛曲线 Fig. 9 ABC convergence curve | |
从图 9可以看出,ABC优化的最大KCI值为2.16,相对应的模态数K和带宽控制参数α的取值分别为5和1 000。采用最优参数组合的VMD方法对轴承故障信号进行分解并计算各模态的KCI值,结果如图 10所示。
|
Download:
|
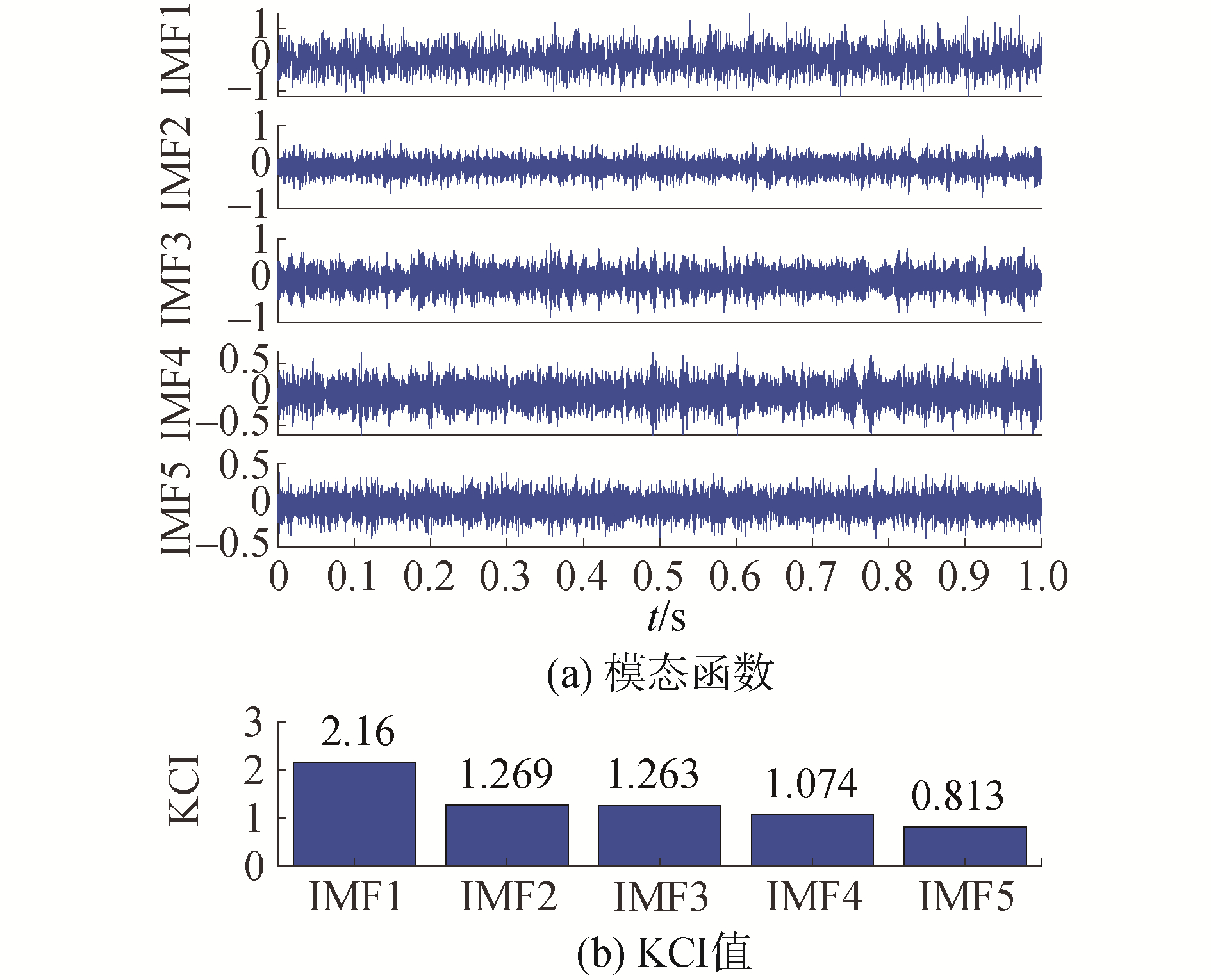
| 图 10 模态函数及其KCI值 Fig. 10 Modes decomposed by the optimal VMD and the corresponding KCI values | |
将KCI值最大的IMF1作为敏感分量并对其进行包络谱分析。同样,为了对KCI作为敏感分量选择依据的有效性进行验证,还对其他模态分量进行了包络谱分析,结果如图 11所示。
|
Download:
|
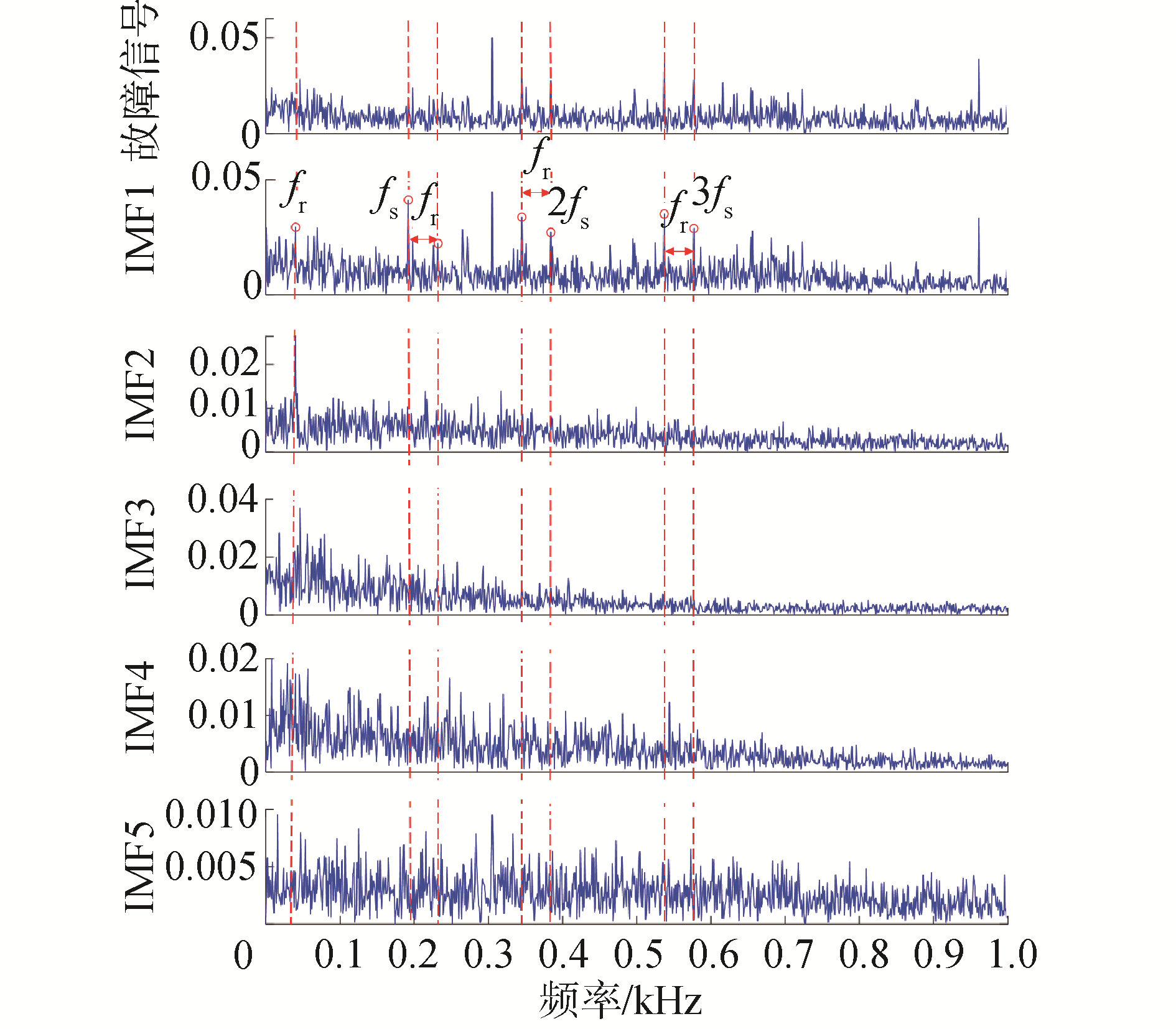
| 图 11 轴承故障信号及各模态的包络谱 Fig. 11 Envelope spectrums of bearing fault signal and each modes | |
可以看出设备运行状态的信息集中于所选的IMF1中,再次表明了将KCI作为敏感模态分量的选择依据是有效的。与原始轴承信号相比,IMF1的包络谱中故障特征频率更为显著,能够清晰地观察到转频fr、故障频率fs及其谐波(2fs、3fs),并且在fs、2fs、3fs附近均出现了转频fr的边频带,表明故障特征频率受转频fr的调制,轴承的内圈出现了局部缺陷故障,这与实验结果是一致的。
将本文方法与EEMD、LMD和固定参数VMD的信号处理效果进行比较,各种方法获取的敏感模态分量的包络谱如图 12所示。EEMD和LMD方法均无法识别出故障频率fs,而固定参数VMD方法能够有效识别出转频fr、故障频率fs及其转频fr的边频带,但是无法识别故障频率fs的谐波分量。因此,进一步验证了本文方法在轴承内圈的早期故障识别方面比EEMD、LMD、固定参数VMD方法具有更好的效果。

|
Download:
|
| 图 12 敏感模态分量的包络谱 Fig. 12 Envelope spectrums of sensitive modes | |
1) 该方法克服了VMD的参数选择问题,能够自适应地获取与待分解信号相匹配的模态数K和带宽控制参数α。
2) ABC优化过程中以加权峭度指标KCI为目标函数,不仅考虑了各分解模态的冲击特性,还考虑了模态与原信号的相关性,可以有效避免重要特征信息的泄漏。
3) 采用该方法分别对轴承内圈早期故障的仿真和实验信号进行分析,均成功识别出故障特征频率。通过与EEMD、LMD和固定参数VMD方法的比较,进一步验证了该方法在早期故障特征提取方面的优势。
该方法对核电厂轴承的早期故障检测具有一定的工程参考价值,在满足高频振动信号采集、传输和存储要求的前提下,该方法可用于核电厂轴承在线故障检测。下一步将针对该方法的故障可检测范围进行研究,以确定该方法在一定故障程度和噪声强度下的适用性。
| [1] |
王志超, 夏虹, 朱少民, 等. EWT-GG聚类的核电厂轴承故障诊断方法研究[J]. 哈尔滨工程大学学报, 2020, 41(6): 899-906. WANG Zhichao, XIA Hong, ZHU Shaomin, et al. Bearing fault diagnosis method in nuclear power plants based on EWT-GG clustering[J]. Journal of Harbin Engineering University, 2020, 41(6): 899-906. (  0) 0)
|
| [2] |
IMMOVILLI F, BELLINI A, RUBINI R, et al. Diagnosis of bearing faults in induction machines by vibration or current signals: a critical comparison[J]. IEEE transactions on industry applications, 2010, 46(4): 1350-1359. DOI:10.1109/TIA.2010.2049623 (  0) 0)
|
| [3] |
孙健, 刘道和, 吕群贤. 振动监测与分析技术在核电站中的应用[J]. 核动力工程, 2000, 21(5): 477-480. SUN Jian, LIU Daohe, LYU Qunxian. Application of vibration monitoring and analysis technique in nuclear power station[J]. Nuclear power engineering, 2000, 21(5): 477-480. DOI:10.3969/j.issn.0258-0926.2000.05.021 (  0) 0)
|
| [4] |
PAN Yubin, HONG Rongjing, CHEN Jie, et al. Incipient fault detection of wind turbine large-size slewing bearing based on circular domain[J]. Measurement, 2019, 137: 130-142. DOI:10.1016/j.measurement.2019.01.033 (  0) 0)
|
| [5] |
LI Zong, FENG Zhipeng, CHU Fulei. A load identification method based on wavelet multi-resolution analysis[J]. Journal of sound and vibration, 2014, 333(2): 381-391. DOI:10.1016/j.jsv.2013.09.026 (  0) 0)
|
| [6] |
WANG Yi, XU Guanghua, LIANG Lin, et al. Detection of weak transient signals based on wavelet packet transform and manifold learning for rolling element bearing fault diagnosis[J]. Mechanical systems and signal processing, 2015, 54-55: 259-276. DOI:10.1016/j.ymssp.2014.09.002 (  0) 0)
|
| [7] |
GROVER C, TURK N. Rolling element bearing fault diagnosis using empirical mode decomposition and Hjorth parameters[J]. Procedia computer science, 2020, 167: 1484-1494. DOI:10.1016/j.procs.2020.03.359 (  0) 0)
|
| [8] |
WANG Lei, LIU Zhiwen, MIAO Qiang, et al. Time-frequency analysis based on ensemble local mean decomposition and fast kurtogram for rotating machinery fault diagnosis[J]. Mechanical systems and signal processing, 2018, 103: 60-75. DOI:10.1016/j.ymssp.2017.09.042 (  0) 0)
|
| [9] |
WU Zhaohua, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in adaptive data analysis, 2009, 1(1): 1-41. DOI:10.1142/S1793536909000047 (  0) 0)
|
| [10] |
DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE transactions on signal processing, 2014, 62(3): 531-544. DOI:10.1109/TSP.2013.2288675 (  0) 0)
|
| [11] |
KARABOGA D. An idea based on honey bee swarm for numerical optimization. Technical Report-tr06[R]. Kaiseri: Erciyes University, 2005. WANG Biao, LEI Yaguo, LI Naipeng, et al. A hybrid prognostics approach for estimating remaining useful life of rolling element bearings[J]. IEEE transactions on reliability, 2020, 69(1): 401-412. DOI:10.1109/TR.2018.2882682 (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


