2. 黑龙江东方学院 基础教学研究部, 黑龙江 哈尔滨 150066;
3. 山东科技大学 计算机科学与工程学院, 山东 青岛 266590
2. The Department of Basic Education, East University of Heilongjiang, Harbin 150066, China;
3. College of Computer Science and Engineering, Shandong University of Science and Technology, Qingdao 266590, China
随着科学技术的发展,通过各种智能设备搜集和存储数据的能力越来越强,对这些数据进行分析挖掘可以很好的为人们的生活服务。但是这些数据往往包含敏感的个人信息,如果直接将数据发布出去,将会泄露个人隐私。平衡发布数据的可用性和隐私性的研究成为近些年研究的热点,隐私保护的数据发布就是将原始数据进行变换使得发布的数据能够满足人们用来分析挖掘的需求并且避免隐私泄露。
隐私保护技术有匿名方法、抑制方法等,但都容易遭受具有背景知识的攻击,而差分隐私可以抵抗攻击者具有任何背景知识的攻击,差分隐私是将原始数据加入随机噪声,从概率意义上使得攻击者无法区分原始输入数据,因此,基于差分隐私的数据发布机制的研究成为近年来研究的热点[1-5]。
大数据时代搜集到的数据具有量大,维度高且有相关性等特点,通常所用的主成分分析(principal component analysis, PCA)方法是利用降维的思想,研究如何通过少数几个综合隐变量来解释原来变量的绝大多数信息的一种多元统计分析方法,是非概率的方法,其对应的生成式方法叫做概率主成分分析(probabilistic PCA,PPCA),可以构建一个概率模型,得到原始高维变量和低维隐变量之间的关系式。Dwork[6]中提出差分隐私,其思想是将数据中加入随机噪声,由于差分隐私具有严谨的数学形式,所以无论攻击者有什么样的背景知识都能提供强大的隐私保护,因此差分隐私成为近年的研究热点,在隐私保护领域有着广泛的应用,目前对于数据隐私保护,差分隐私算法根据添加噪声扰动的方式分为输入扰动、目标扰动、算法扰动和输出扰动。
高维数据之间具有相关性,如果数据之间存在相关性,则差分隐私可能无法保证针对任意对手的隐私[7];如果对高维相关数据的每一维度特征都加入噪声确保差分隐私,那么随着隐私预算的减少,加入的噪声变大,发布数据的效用将会明显降低,甚至导致发布数据不可用[8]。因此,先对高维数据进行降维处理,在低维的综合隐变量中加入噪声,这相当于在不降低隐私保护级别的情况下,将噪声添加到更少但最重要的部分数据中,从而可以提高发布数据的效用。文献[9-17]基于主成分分析的差分隐私数据发布方法已有一些研究成果。目前大多数方法都是基于输入扰动,基于输出扰动的研究比较少,但是随着数据维数的增多,特征之间存在关联性,直接对输入进行扰动,会导致重复加噪和发布数据的效用过低等问题。
基于以上研究,本文提出2种隐私保护数据发布方法:
1) 基于概率主成分分析(probabilistic principal component analysis,PPCA)模型的隐私数据发布方法,将原始高维变量降维为少数综合隐变量,利用概率主成分分析模型生成新的数据集发布,发布的数据集保持原数据集的统计特性;
2) 基于概率主成分分析的差分隐私(probability principal component analysis of differential privacy,PPCA-DP)数据发布方法,将原始变量降维,得到原始数据集的投影矩阵,在投影矩阵中加入拉普拉斯随机噪声,再利用概率主成分分析模型生成新的数据集发布,提高发布数据集的效用。
1 差分隐私及主成分分析差分隐私为敏感信息提供了可用数学公式量化的、严格的隐私保护,差分隐私的本质是随机扰动,有Laplace机制[18]和指数机制[19],Laplace机制适用于数值型查询,指数机制适用于非数值型查询,本文采用Laplace机制。
定义1 差分隐私[6]:给定2个数据集D和D′,两者至多相差一条记录,给定一个隐私算法A,Rang(A)为A的取值范围,若算法A在2个相邻数据集D和D′上的任意输出结果O满足:
| $ P_{r}\{A(D)=0\} \leqslant \exp (\varepsilon) P_{r}\left\{A\left(D^{\prime}\right)=O\right\} $ | (1) |
称算法A满足ε差分隐私,ε为隐私预算,取值越小表示隐私保护度越高。
定义2 全局敏感度[20]:对于任意一个函数f: D→Rd,函数f的全局敏感度为:
定义3 拉普拉斯机制[20]:对于任意一个函数f: D→Rd,若算法A的输出满足等式:
| $ A(D)=f(D)+\operatorname{Lap}\left(\frac{\Delta f}{\varepsilon}\right) $ | (2) |
式中算法A满足ε差分隐私,其中Lap(Δf/ε)是拉普拉斯变量。
主成分分析[21]是一种简化数据集的技术,其思想是对协方差矩阵Σ进行特征分解得:
| $ \boldsymbol{\varSigma}=\boldsymbol{U}^{\mathrm{T}} \boldsymbol{\varLambda} \boldsymbol{U} $ | (3) |
式中:Λ为对角矩阵,对角线上的元素为Σ的特征值;U为正交矩阵,由Σ的特征值所对应的特征向量构成,将特征值降序排列λ1≥λ2≥…≥λp≥0;p为原始变量的维数,由主成分的累积贡献率
主成分分析是非概率形式的方法,对应的概率形式称为概率主成分分析。图 1所示的隐变量模型中,将p维观测向量x与相应的k维隐变量s联系起来。最常见的这种模型是因子分析模型:
| $ \boldsymbol{x}=\boldsymbol{W} \boldsymbol{s}+\boldsymbol{\mu}+\boldsymbol{\xi} $ | (4) |
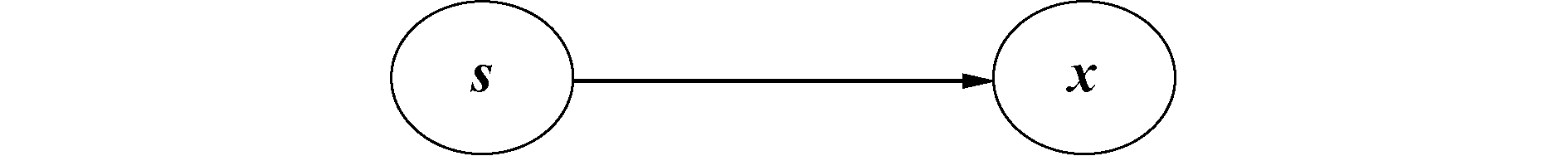
|
Download:
|
| 图 1 因子分析图模型 Fig. 1 Graphical model for factor analysis | |
式中:x是p维观测变量;s为k维隐变量,主成分分析可以看作是具有各向同性协方差矩阵的因子分析模型的最大似然解。
定理1[22]:由图 1和因子分析模型所定义的模型中,当ξ~N(0,σ2I), s~N(0, Ik)时:
| $ \boldsymbol{x} \mid \boldsymbol{s} \sim N\left(\boldsymbol{W} \boldsymbol{s}+\boldsymbol{\mu}, \sigma^{2} \boldsymbol{I}_{p}\right), $ | (5) |
式中:σ>0, W∈Rp×k;参数W、μ、σ2的最大似然估计为:
| $ \hat{\boldsymbol{\mu}}=\tilde{\boldsymbol{\mu}} $ | (6) |
| $ \hat{\boldsymbol{W}}=\boldsymbol{U}_{k}\left(\boldsymbol{\varLambda}_{k}-\hat{{\sigma}}^{2} \boldsymbol{I}\right)^{\frac{1}{2}} $ | (7) |
| $ \hat{{\sigma}}^{2}=\frac{1}{p-k} \sum\limits_{{i}=k+1}^{p} \lambda_{i} $ | (8) |
式中:
定理2[22]:由图 1和因子分析模型所定义的隐变量模型中在给定观测变量x的情况下,s的条件分布为:
| $ \boldsymbol{s} \mid \boldsymbol{x} \sim N\left(\boldsymbol{M}^{-1} \boldsymbol{W}^{\mathrm{T}}(\boldsymbol{x}-\boldsymbol{\mu}), \sigma^{2} \boldsymbol{M}^{-1}\right) $ | (9) |
其中s|x已知x的情况下σ的条件分布;M=WTW+σ2I,W, σ2的极大似然估计为:
| $ \hat{\boldsymbol{W}}=\boldsymbol{U}_{k}\left(\boldsymbol{\varLambda}_{k}-\hat{\sigma}^{2} \boldsymbol{I}\right)^{\frac{1}{2}} $ | (10) |
| $ \hat{\sigma}^{2}=\frac{1}{p-k} \sum\limits_{i=k+1}^{p} \lambda_{i} $ | (11) |
基于此本节提出2种隐私数据发布方法,分别是基于概率主成分分析模型的隐私数据发布方法及基于概率主成分分析的差分隐私数据发布方法。
2.1 基于PPCA模型的隐私数据发布方法基于PPCA模型的隐私数据发布方法其原理是利用主成分分析将原始高维变量降维为低维隐变量,再根据定理1和定理2中的模型,由低维隐变量得到原始高维变量的概率分布,然后依分布抽样生成与原始数据集具有相同规模的合成数据集发布,发布的合成数据集与原始数据集具有相近的统计特征,所以该方法既保护了原始数据集的隐私又提高了发布数据集的效用。PPCA模型的算法如下:
算法1:基于PPCA模型的隐私数据发布方法。
输入:原始数据集Xn×p为n行p列的矩阵,每一行是一个样本,每个样本具有p维特征。
输出:与原始数据具有相近概率分布的数据集X′n×p。
算法过程为:
1) 输入数据集Xn×p;
2) 数据规范化处理,将数据变换在[0, 1]取值;
3) 计算样本均值和样本协方差阵:
| $ \mathrm{E}(\boldsymbol{X})=\bar{\boldsymbol{X}}, $ | (12) |
| $ \boldsymbol{\varSigma}=\frac{1}{n}\left(\boldsymbol{X}^{\mathrm{T}} \boldsymbol{X}-n \overline{\boldsymbol{X}} \overline{\boldsymbol{X}}^{\mathrm{T}}\right) $ | (13) |
4) 对Σ分解得Σ=UTΛU,U的各列由矩阵Σ的特征值λ1≥λ2≥…≥λp所对应的特征向量构成,选取U的前k列得到Uk;
5) 计算Xn×p在k个主成分空间的主成分得分矩阵:
| $ \boldsymbol{S}_{n \times k}=(\boldsymbol{X}-\mathrm{E}(\boldsymbol{X})) \boldsymbol{U}_{k} $ | (14) |
6) 由定理2求隐变量s的条件均值E(s|x)和方差Var(s|x),从而得到条件分布P(s|x);
7) 依分布P(s|x)抽取样本s;
8) 依分布x|s~N(Ws+μ, σ2Ip)抽取样本x;
9) 生成新的数据集X′n×p。
基于PPCA模型的隐私数据发布方法没有引入差分隐私,而是利用PPCA模型生成新的与原始数据集具有相近概率分布的数据集发布,从而使得原始数据的隐私信息得到保护。
2.2 基于PPCA-DP模型的隐私数据发布方法差分隐私可以抵御具有任何背景知识的攻击,由于数据的高维特性,直接在原始数据中加入噪声或者在协方差矩阵中加入噪声将会影响发布数据的效用,尤其当高维数据之间存在相关性的时候,存在重复加噪的问题,导致发布数据效用过低,甚至不可用,因此本方案主要分2步: 1)利用主成分分析将高维数据降维后得到低维隐变量,在低维隐变量中加入噪声,这相当于在比较重要的独立的变量中加入噪声,在同等隐私保护度下可以提高发布数据的效用;2)利用定理1和定理2生成与原始数据具有相近概率分布的合成数据集发布,既提高了发布数据的效用又保护了原始数据的隐私。具体PPCA-DP算法如下:
算法2:基于PPCA-DP的隐私数据发布方法。
输入:原始数据集Xn×p。
输出:加入拉普拉斯噪声的与原始数据具有相近概率分布的数据集X′n×p。
1) 输入数据集Xn×p;
2) 数据规范化处理,将数据变换在[0, 1]取值;
3) 计算样本均值和样本协方差阵;
4) 对Σ分解得Σ=UTΛU,U的各列由矩阵Σ的特征值λ1≥λ2≥…≥λp所对应的特征向量构成,选取U的前k列得到Uk;
5) 计算Xn×p在k个主成分空间的主成分得分矩阵:
| $ \boldsymbol{K}=(\boldsymbol{X}-\mathrm{E}(\boldsymbol{X})) \boldsymbol{U}_{k} $ | (15) |
6) 在主成分得分矩阵中加入拉普拉斯噪声:
| $ \boldsymbol{W}=(\boldsymbol{X}-E(\boldsymbol{X})) \boldsymbol{U}_{k}+\operatorname{Lap}\left(\frac{\sqrt{k p}}{\varepsilon}\right) $ | (16) |
7) 由定理2求隐变量s的条件均值E(s|x)和方差Var(s|x),从而得到条件分布P(s|x);
8) 依分布P(s|x)抽取样本s;
9) 依分布x|s~N(Ws+μ, σ2Ip)抽取样本;
10) 生成新的数据集X′n×p;
在PPCA-DP算法中,加入了差分隐私,所以对原始数据集起到了更加严格的隐私保护作用,以下是PPCA-DP算法的隐私分析。
定理3:算法PPCA-DP满足ε差分隐私。
证明:由拉普拉斯机制可知,只需证明函数f=Xn×pUp×k的敏感度为
由向量范数的定义知:
| $ \begin{gathered} \left\|\left(\boldsymbol{X}_{(1)}-\boldsymbol{X}_{(2)}\right) \boldsymbol{U}_{p \times k}\right\|_{1}^{2}=\left(\sum\limits_{i=1}^{k}\left|\left(\boldsymbol{X}_{(1)}-\boldsymbol{X}_{(2)}\right) \boldsymbol{u}_{i}\right|\right)^{2} \leqslant \\ k \sum\limits_{i=1}^{k}\left|\left(X_{(1)}-X_{(2)}\right) u_{i}\right|^{2}= \\ k\left\|\left(\boldsymbol{X}_{(1)}-\boldsymbol{X}_{(2)}\right) \boldsymbol{U}_{p \times k}\right\|_{2}=k\left[\left(\boldsymbol{X}_{(1)}-\boldsymbol{X}_{(2)}\right) \boldsymbol{U}_{p \times k}\right] \\ {\left[\left(\boldsymbol{X}_{(1)}-\boldsymbol{X}_{(2)}\right) \boldsymbol{U}_{p \times k}\right]^{\mathrm{T}}=k\left\|\left(\boldsymbol{X}_{(1)}-\boldsymbol{X}_{(2)}\right)\right\|_{2}^{2}} \end{gathered} $ | (17) |
故有:
| $ \begin{gathered} \left\|\left(\boldsymbol{X}_{(1)}-\boldsymbol{X}_{(2)}\right) \boldsymbol{U}_{p \times k}\right\|_{1} \leqslant \\ \sqrt{k\left\|\left(\boldsymbol{X}_{(1)}-\boldsymbol{X}_{(2)}\right)\right\|_{2}^{2}}=\sqrt{k p} \end{gathered} $ | (18) |
因此PPCA-DP算法满足ε差分隐私。
3 低秩近似误差及SVM分类实验实验的2个数据集分别为Adult数据集和Magic04数据集,均来自UCI数据集。利用Python实现本文算法,每组实验进行5次,取5次实验结果的平均值。Adult数据集中每个数据具有15个特征维度,在本节实验中删除Adult数据集的部分特征,保留其中的age、workclass、education-num、race、gender、capital-gain、capital-loss、hours-per-week、income 9个特征维度,其中有些是非数值特征,经过特征转换后得到具有21维特征的数据集,以income≤50k和income>50k为分类目标。Magic04数据集中每个数据具有11个特征维度,数据属于2个分类。
针对2种方法,本节与文献[8]提出的PCA-based PPDP方法做了对比实验,从矩阵低秩近似误差MSE值和SVM分类准确率2方面分别比较这3种方法发布数据集的功效。
Adult和Magic04数据集的特征值占比如图 2所示,可看出Adult数据集的前9个主成分的累积贡献率可以达到90%以上,Magic04数据集的前4个主成分的累积贡献率可以达到90%以上。

|
Download:
|
| 图 2 特征值占比 Fig. 2 Proportion of eigenvalues | |
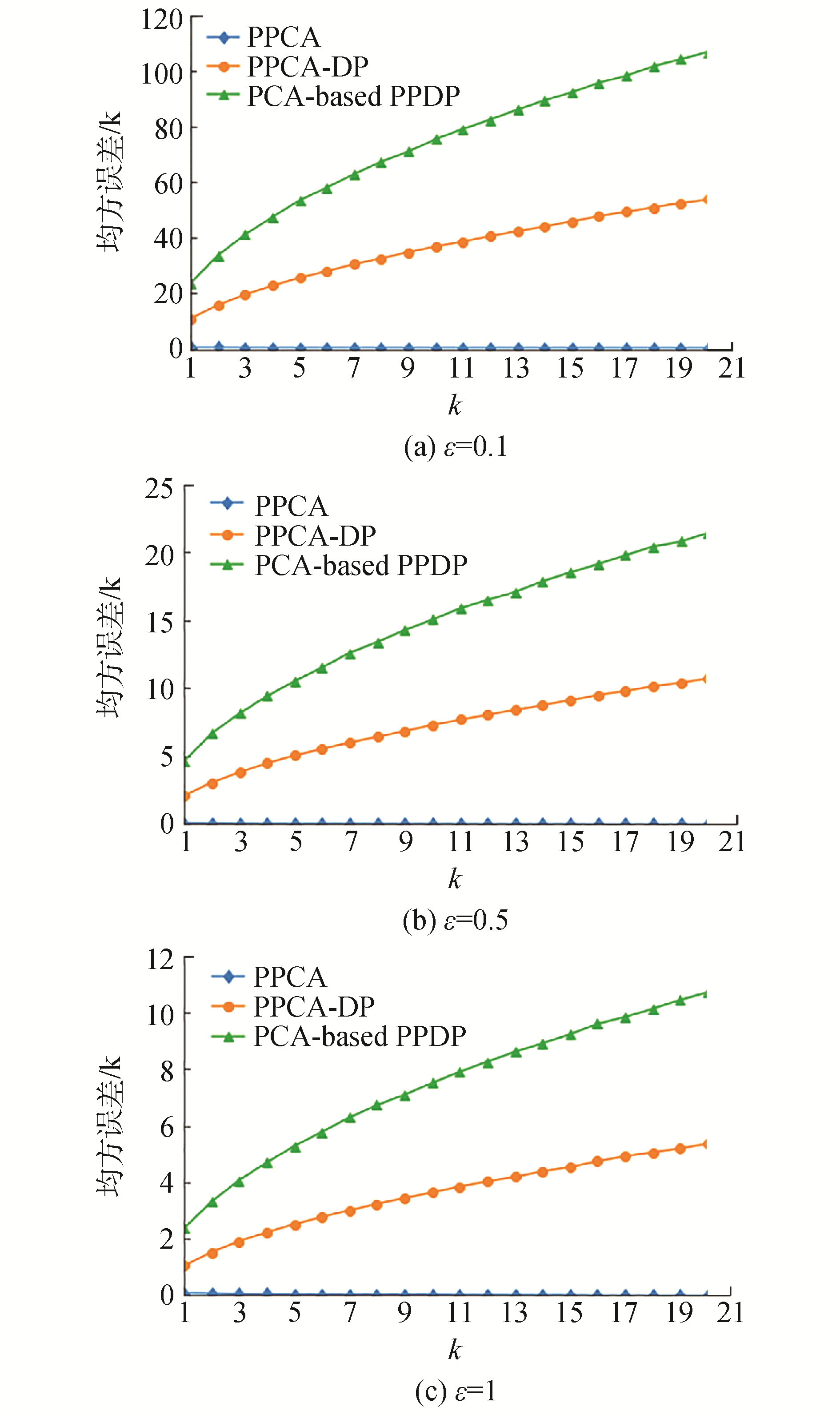
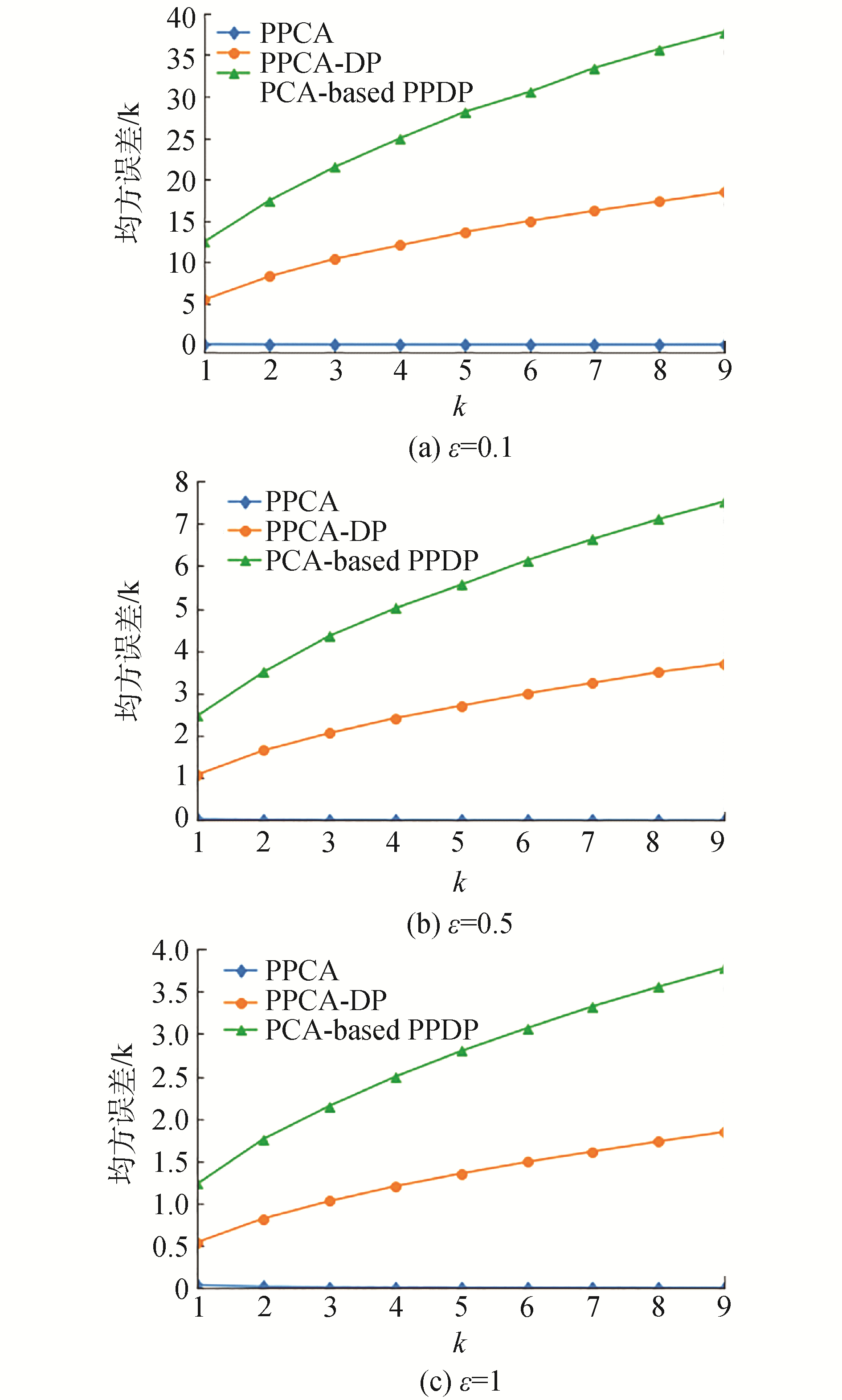
本节利用发布数据集和原始数据集之间的矩阵低秩近似误差MSE的值衡量本文提出的PPCA方法和PPCA-DP方法发布数据集的效用,并与PCA-based PPDP方法作比较。图 3和图 4分别表示2个数据集的实验结果,每个数据集分别在隐私预算ε取值为0.1、0.5、1下进行实验,从图 3和图 4可以看出本文所提出的2种方法PPCA与PPCA-DP发布数据集的矩阵低秩近似误差MSE的值均低于PCA-based PPDP方法发布数据集的矩阵低秩近似误差MSE的值,这说明本文的PPCA与PPCA-DP方法发布数据集的效用均高于PCA-based PPDP方法发布数据集的效用。
|
Download:
|
| 图 3 不同ε取值下的均方误差值比较(Adult数据集) Fig. 3 Comparison of mean squared errors values under different ε values (Adult dataset) | |
|
Download:
|
| 图 4 不同ε取值下的均方误差值比较(Magic04数据集) Fig. 4 Comparison of mean squared errors values under different ε values (Magic04 dataset) | |
从图 3和图 4中还可以看出对于PPCA数据发布方法,由于没有引入差分隐私,所以其发布数据集与原始数据集的矩阵低秩近似误差MSE值非常小,并与其余2种方法的MSE值不在一个数量级别,并且其MSE值随着保留主成分个数k的增大而减小,这说明随着保留主成分个数k的增多,保留下来的原始变量的信息越多,进而发布数据集的概率分布就越接近原始数据集的概率分布。
从2个数据集的实验结果还可以看出,在同等隐私保护度下,PPCA-DP方法发布数据集的MSE值低于PCA-based PPDP方法发布数据集的MSE值,这说明在同等隐私保护度下,本文PPCA-DP方法发布数据集的效用高于PCA-based PPDP方法发布数据集的效用。同时可以看出两者的MSE值均受2个因素的影响,一个是主成分保留个数k,另一个是隐私保护预算ε,当固定k的时候,MSE值随着隐私预算ε的减小而增大,说明随着隐私保护度的增高,加入的噪声增多,所以MSE值变大,即发布数据的效用变低;当固定隐私预算ε的时候,MSE值随着k的增大而增大,这是因为保留的主成分个数越多,加入的噪声就越多,所以MSE值变大,因此当前k个主成分已经占有原始变量90%以上信息的时候,再过多的保留主成分所带来的信息有限但势必导致整体加入的噪声变多,从而影响发布数据的效用。
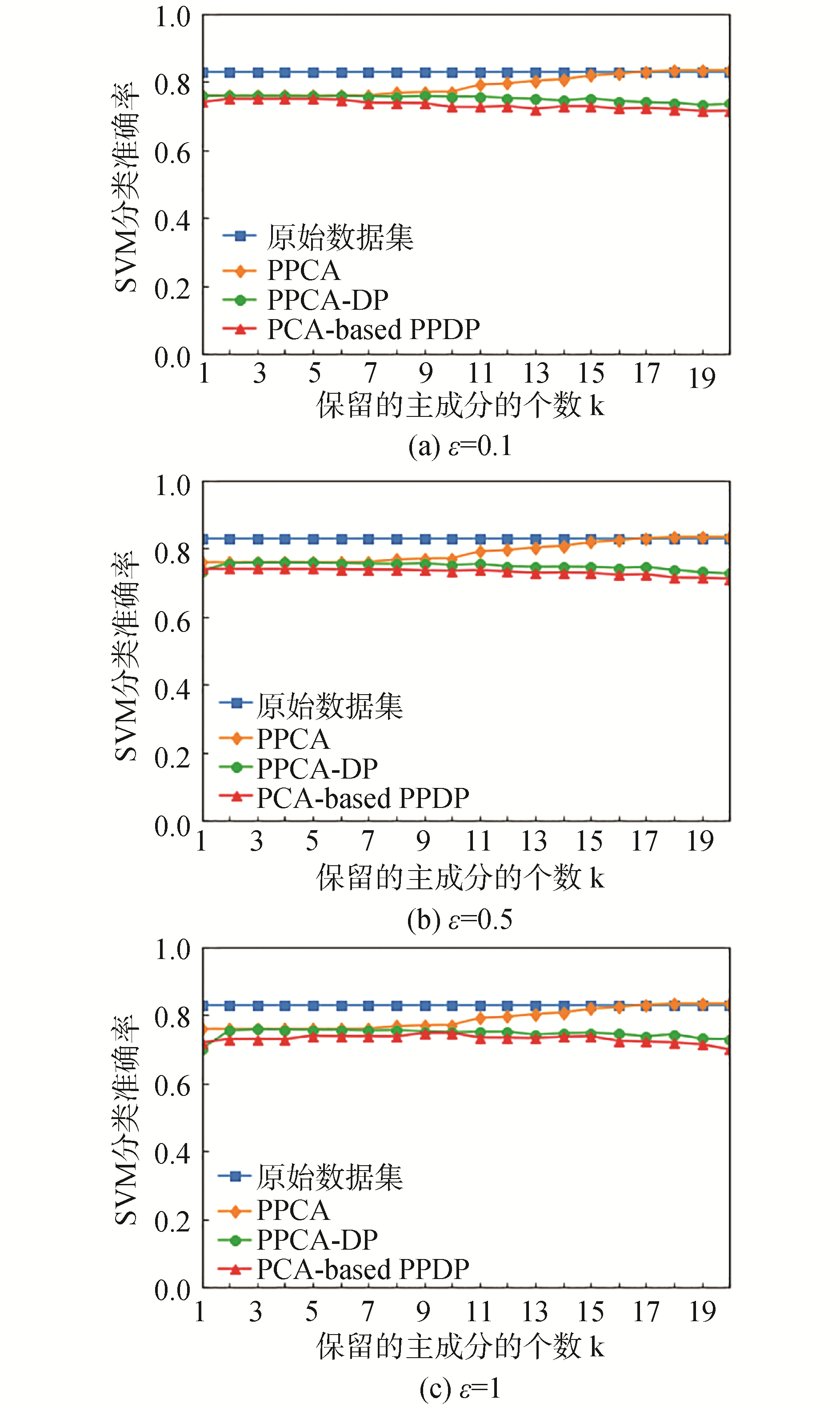
3.2 SVM分类准确率的比较本节利用SVM分类准确率衡量本文的PPCA方法和PPCA-DP方法发布数据集的效用,并与PCA-based PPDP方法作比较。图 5和图 6分别为2个数据集上的实验结果,每个数据集分别在隐私预算ε取值为0.1、0.5、1进行实验。
|
Download:
|
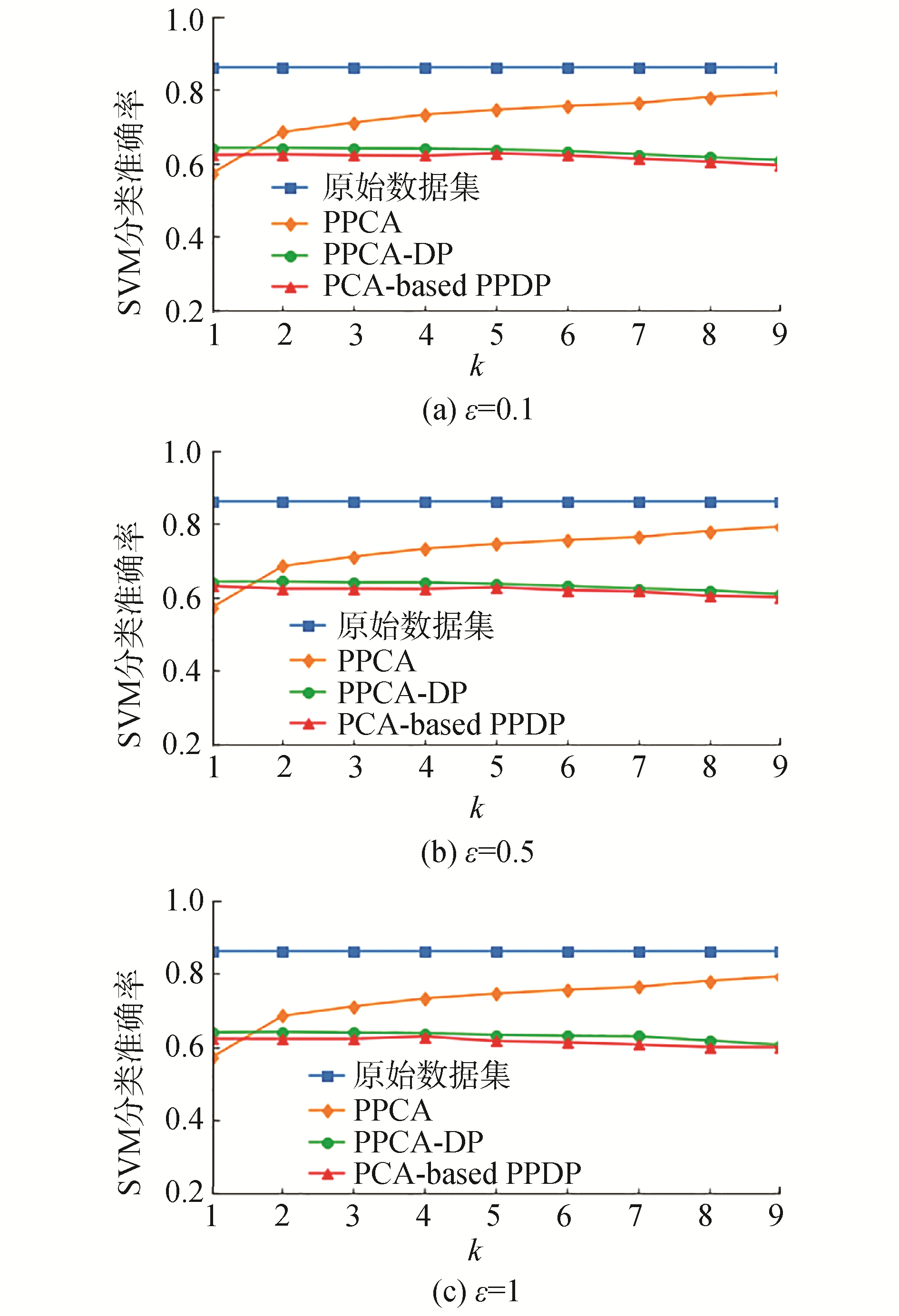
| 图 5 不同ε取值下SVM分类准确率比较(Adult数据集) Fig. 5 Comparison of SVM prediction accuracy at different ε values (Adult dataset) | |
|
Download:
|
| 图 6 不同ε取值下SVM分类准确率比较(Magic04数据集) Fig. 6 Comparison of SVM prediction accuracy at different ε values (Magic04 dataset) | |
从图 5和图 6可以看出,PPCA方法和PPCA-DP方法发布数据集的SVM分类准确率均高于PCA-based PPDP方法发布数据集的SVM分类准确率,这说明PPCA方法和PPCA-DP方法发布数据集的效用均高于PCA-based PPDP方法发布数据集的效用。PPCA方法发布数据集的SVM分类准确率随着保留的主成分个数k的增大而增大,当k接近原变量个数的时候,其SVM分类准确率接近原数据集的SVM分类准确率,这是因为PPCA方法没有加入差分隐私,而随着k的增大保留的原始数据集的信息增多,因此发布数据集的概率分布就越接近原始数据集的概率分布。
PPCA-DP方法引入了差分隐私,有较强的隐私保护效果,从图 5和图 6看出在同等隐私保护度下,其发布数据集的SVM分类准确率略高于PCA-based PPDP方法发布数据集的SVM分类准确率,两者的共同点是随着主成分个数k的增多,SVM分类准确率均在下降,这是因为随着保留的主成分个数的增多,加入的噪声增多,导致发布数据的效用下降。
4 结论1) 针对数据的高维度,相关性等特点,本文提出了2种隐私保护数据发布方法PPCA方法和PPCA-DP方法,其中PPCA-DP方法解决了相关数据的重复加噪问题,使得发布数据满足差分隐私的同时提高了发布数据的效用。
2) 理论和实验结果表明,从发布数据的矩阵低秩近似均方误差和SVM分类准确率2方面衡量发布数据的效用时,在相同隐私预算下,PPCA-DP方法发布数据的效用高于PCA-based PPDP方法发布数据的效用。
然而本文也有不足之处,主成分分析主要是针对高维数据的线性相关关系进行降维,在下一步研究工作中将开展非线性关系数据的降维,另外,本文方法适用于数据拥有方为单方时,发布数据的隐私保护,在下一步研究中将扩展为当数据被多个数据拥有方所拥有时,如何能在保护数据隐私的情况下整合多方数据以供人们分析和利用。
| [1] |
HAN Chao, WANG Ke. Sensitive disclosures under differential privacy guarantees[C]//2015 IEEE International Congress on Big Data. New York, NY, USA: IEEE, 2015: 110-117.
(  0) 0)
|
| [2] |
WANG Qian, ZHANG Yan, LU Xiao, et al. RescueDP: real-time spatio-temporal crowd-sourced data publishing with differential privacy[C]//IEEE INFOCOM 2016-the 35th Annual IEEE International Conference on Computer Communications. San Francisco, CA, USA: IEEE, 2016: 1-9.
(  0) 0)
|
| [3] |
KANG Haiyan, ZHANG Shuxuan, JIA Qianqian. A method for time-series location data publication based on differential privacy[J]. Wuhan University Journal of Natural Sciences, 2019, 24(2): 107-115. DOI:10.1007/s11859-019-1375-9 (  0) 0)
|
| [4] |
WANG Hao, XU Zhengquan. CTS-DP: Publishing correlated time-series data via differential privacy[J]. Knowledge-based systems, 2017, 122: 167-179. DOI:10.1016/j.knosys.2017.02.004 (  0) 0)
|
| [5] |
聂熠文. 基于差分隐私的数据发布技术研究[D]. 合肥: 中国科学技术大学, 2019. NIE Yiwen. Research on data publishing technology based on differential privacy[D]. Hefei: University of Science and Technology of China, 2019. (  0) 0)
|
| [6] |
DWORK C. Differential privacy[C]//International Colloquium on Automata, Languages, and Programming. Berlin, Heidelberg: Springer, 2006: 1-12.
(  0) 0)
|
| [7] |
YANG Bin, SATO I, NAKAGAWA H. Bayesian differential privacy on correlated data[C]//Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data. New York, NY, USA: ACM, 2015.
(  0) 0)
|
| [8] |
JIANG Xiaoqian, JI Zhanglong, WANG Shuang, et al. Differential-private data publishing through component analysis[J]. Transactions on data privacy, 2013, 6(1): 19-34. (  0) 0)
|
| [9] |
BLUM A, DWORK C, MCSHERRY F, et al. Practical privacy: the SuLQ framework[C]//Proceedings of the Twenty-Fourth ACM Sigmod-Sigact-Sigart Symposium on Principles of Database Systems. New York, NY, USA: ACM, 2005: 128-138.
(  0) 0)
|
| [10] |
CHAUDHURY K, SARWATE A D, SINHA K. A near-optimal algorithm for differentially-private principal components[J]. The journal of machine learning research, 2013, 14(9): 2905-2943. (  0) 0)
|
| [11] |
KAPRALOV M, TALWAR K. On differentially private low rank approximation[C]//Proceedings of the Twenty-Fourth Annual ACM-Siam Symposium on Discrete Algorithms. New York, NY, USA: SIAM, 2013: 1395-1414.
(  0) 0)
|
| [12] |
KALAI A, VEMPALA S. Efficient algorithms for online decision problems[J]. Journal of computer and system sciences, 2005, 71(3): 291-307. DOI:10.1016/j.jcss.2004.10.016 (  0) 0)
|
| [13] |
DWORK C, TALWAR K, THAKURTA A, et al. Analyze gauss: optimal bounds for privacy-preserving principal component analysis[C]//Proceedings of the Forty-Sixth Annual ACM Symposium on Theory of Computing. New York, NY, USA: ACM, 2014: 11-20.
(  0) 0)
|
| [14] |
JIANG Wuxuan, XIE Cong, ZHANG Zhihua. Wishart mechanism for differentially private principal components analysis[C]//Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence. Phoenix, Arizona, USA: AAAI, 2016.
(  0) 0)
|
| [15] |
XU Chugui, REN Ju, ZHANG Yaoxue, et al. DPPro: differentially private high-dimensional data release via random projection[J]. IEEE transactions on information forensics and security, 2017, 12(12): 3081-3093. DOI:10.1109/TIFS.2017.2737966 (  0) 0)
|
| [16] |
彭长根, 赵园园, 樊玫玫. 基于最大信息系数的主成分分析差分隐私数据发布算法[J]. 信息网络安全, 2020, 20(2): 37-48. PENG Changgen, ZHAO Yuanyuan, FAN Meimei. A differential private data publishing algorithm via principal component analysis based on maximum information coefficient[J]. Netinfo security, 2020, 20(2): 37-48. (  0) 0)
|
| [17] |
唐朋. 满足差分隐私的多方数据发布技术研究[D]. 北京: 北京邮电大学, 2019. TANG Peng. Research on differentially private multi-party data publishing[D]. Beijing: Beijing University of Posts and Telecommunications, 2019. (  0) 0)
|
| [18] |
DWORK C, ROTH A. The algorithmic foundations of differential privacy[M]. New York, NY, USA: Now Publishers Inc., 2014.
(  0) 0)
|
| [19] |
MCSHERRY F, TALWAR K. Mechanism design via differential privacy[C]//48th Annual IEEE Symposium on Foundations of Computer Science (FOCS'07). Providence, RI, USA: IEEE, 2007: 94-103.
(  0) 0)
|
| [20] |
DWORK C, MCSHERRY F, NISSIM K, et al. Calibrating noise to sensitivity in private data analysis//Proceedings of the 3th Theory of Cryptography Conference (TCC). New York, NY, USA: Springer, 2006: 363-385.
(  0) 0)
|
| [21] |
WOLD S. Principal component analysis[J]. Chemometrics and Intelligent Laboratory Systems, 1987, 2. (  0) 0)
|
| [22] |
TIPPING M E, BISHOP C M. Probabilistic principal component analysis[J]. Journal of the royal statistical society, series B, 1999, 61(3): 611-622. DOI:10.1111/1467-9868.00196 (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


