目前船用舵机多采用液压和电动2种驱动方式, 液压驱动具有驱动力大、功率密度高、结构紧凑等优点,但亦存在效率低、噪声大、结构复杂、频响低的缺点;相较液压驱动,电机驱动则驱动力相对较小,其传动效率高、频响快、布置方便,在小型船舶中应用较为广泛。电动舵机主要由电动缸作为驱动单元,通过活塞杆的伸缩运动间接实现舵机的转角运动。针对电动舵机,文献[1-3]运用指数趋近率滑膜控制器、自抗扰控制器等方法实现了舵机的高精度位置控制,张阳阳等[4-5]分别针对电动缸中的滚珠丝杠振动和行星滚柱丝杠承载力、刚度、使用寿命等问题展开了相应研究,为电动缸的技术进步作出了一定的贡献。针对船用舵机结构和负载特点,陈潇等[6]提出基于速度限幅的功率同步控制策略进行双缸驱动舵机的同步控制研究,实现了船舶装配的工程基础。高长虹等[7]针对冗余并联机构的内力问题,提出了基于误差最小控制综合算法的内力抑制策略,并通过实验平台验证了控制策略的有效性。张连朋等[8]通过分析冗余振动台的内力产生机理,并结合动力学关系,设计了比例积分振动台内力抑制策略,仿真结果验证了内力抑制器的有效性。电动缸控制器虽可提高电动缸的控制精度,但并不能够实现对指令信号的零相差控制,舵机系统的装配误差,使得电动缸在实际运动轨迹与理论轨迹间存在一定的偏差。由于舵机系统为刚性连接,较小的位移便可产生较大的力。此力的存在并不能够进行舵机驱动,且极易降低电动缸的驱动能力,此力即为系统内力。由于电动缸位移与舵机转角间存在三角函数关系,若在三角函数中引入相应的相位超前操作,便可补偿系统的相位滞后,从而提高舵机系统的位置控制精度。
本文以电动直驱舵机为研究对象,建立以伺服电机转角、活塞杆位移和舵机转角为变量的运动学方程,并进一步分析了位置控制模式下电机转角误差与舵机系统内力之间的数学关系,提出舵机转角的自适应控制算法和基于力补偿方法的内力抑制策略。通过仿真对比常规PID控制器和自适应控制器下的舵机转角曲线、运用力补偿器前后的驱动力曲线。
1 内力形成机理电动直驱舵机如图 1所示,整个舵机系统主要由行星滚柱丝杠、交流伺服电机、减速机构、舵柄和相应附件构成。在运动过程中,通过两交流伺服电机的协调控制,使舵柄绕其轴线转动,进而实现舵叶摆动的目的。

|
Download:
|
| 图 1 电动直驱舵机 Fig. 1 Electric direct drive steering gear 注:1、6为行星滚柱丝杠,2、4为交流伺服电机,3、4为减速机构,7为舵柄 | |
图 2所示为舵机结构简图,其中E、F分别为电动缸两端铰接中心点,O为舵柄旋转中心点。

|
Download:
|
| 图 2 舵机结构 Fig. 2 Structure diagram of steering gear | |
令β表示两电动缸轴线平行时∠EOF值,则
| $ \beta=\operatorname{atan}(d / b) $ | (1) |
式中:θ表示舵机转角,则舵机转角θ与电动缸位移ci(i=1, 2)的关系为:
| $ \cos (\beta+\theta)=\frac{a^{2}+b^{2}-c_{1}^{2}}{2 a b} $ | (2) |
| $ \cos (\beta-\theta)=\frac{a^{2}+b^{2}-c_{2}^{2}}{2 a b} $ | (3) |
则丝杠转速为:
| $ n_{2}=\frac{n_{0}}{i_{0} i_{1}} $ | (4) |
则电动缸输出速度为:
| $ v=\frac{n_{2} P_{a}}{60} $ | (5) |
则各传动扭矩为:
| $ T_{0}-\tau_{1}=J_{0} \dot{\omega}_{0} $ | (6) |
| $ T_{1}=\tau_{1}-\tau_{2}=J_{1} \dot{\omega}_{1} $ | (7) |
| $ T_{2}=\tau_{2}-\tau_{3}=J_{2} \dot{\omega}_{2} $ | (8) |
进而推得:
| $ T_{0}=J_{0} \dot{\omega}_{0}+J_{1} \dot{\omega}_{1}+J_{2} \dot{\omega}_{2}+\tau_{3} $ | (9) |
| $ \tau_{3}=\frac{F_{D} P_{a}}{2 \pi \eta} $ | (10) |
式中:a为O、E两点之间的距离;b为O、F两点之间的距离;i0为电机轴齿轮与过度齿轮间的传动比;i1为过度齿轮与滚柱丝杠间的传动比;n0、n1和n2分别表示电机轴齿轮、过渡齿轮和丝杠输出转速;T0、T1和T2分别表示电机轴齿轮、过渡齿轮和丝杠扭矩;J0、J1和J2分别表示电机轴、过渡齿轮和丝杠转动惯量;ω0、ω1和ω2分别表示电机轴、过渡齿轮和丝杠的角速度;τ1为过度齿轮对电机轴齿轮阻力矩;τ2为丝杠对过度齿轮阻力矩;τ3为丝杠螺母驱动力对丝杠的阻力矩;FD为丝杠螺母驱动力;Pa为丝杠导程;η为丝杠效率。
由于丝杠螺母与电动缸活塞杆固联,丝杠螺母驱动力即为电动缸驱动力。由此可得,电机轴驱动扭矩与电动缸驱动力间的关系为:
| $ F_{D}=\left[T_{0}-\left(J_{0} \dot{\omega}_{0}+J_{1} \dot{\omega}_{1}+J_{2} \dot{\omega}_{2}\right)\right] \frac{2 \pi \eta}{P_{a}} $ | (11) |
令FD1、FD2分别表示电动缸1和电动缸2驱动力,结合电动缸尺寸关系可得总驱动扭矩为:
| $ \begin{aligned} T=& F_{D_{1}} b \sin \left(\arccos \left(\frac{b-a \cos (\beta+\theta)}{\sqrt{a^{2}+b^{2}-2 a b \cos (\beta+\theta)}}\right)\right)+\\ &F_{D_{2}} b \sin \left(\arccos \left(\frac{b-a \cos (\beta-\theta)}{\sqrt{a^{2}+b^{2}-2 a b \cos (\beta-\theta)}}\right)\right) \end{aligned} $ | (12) |
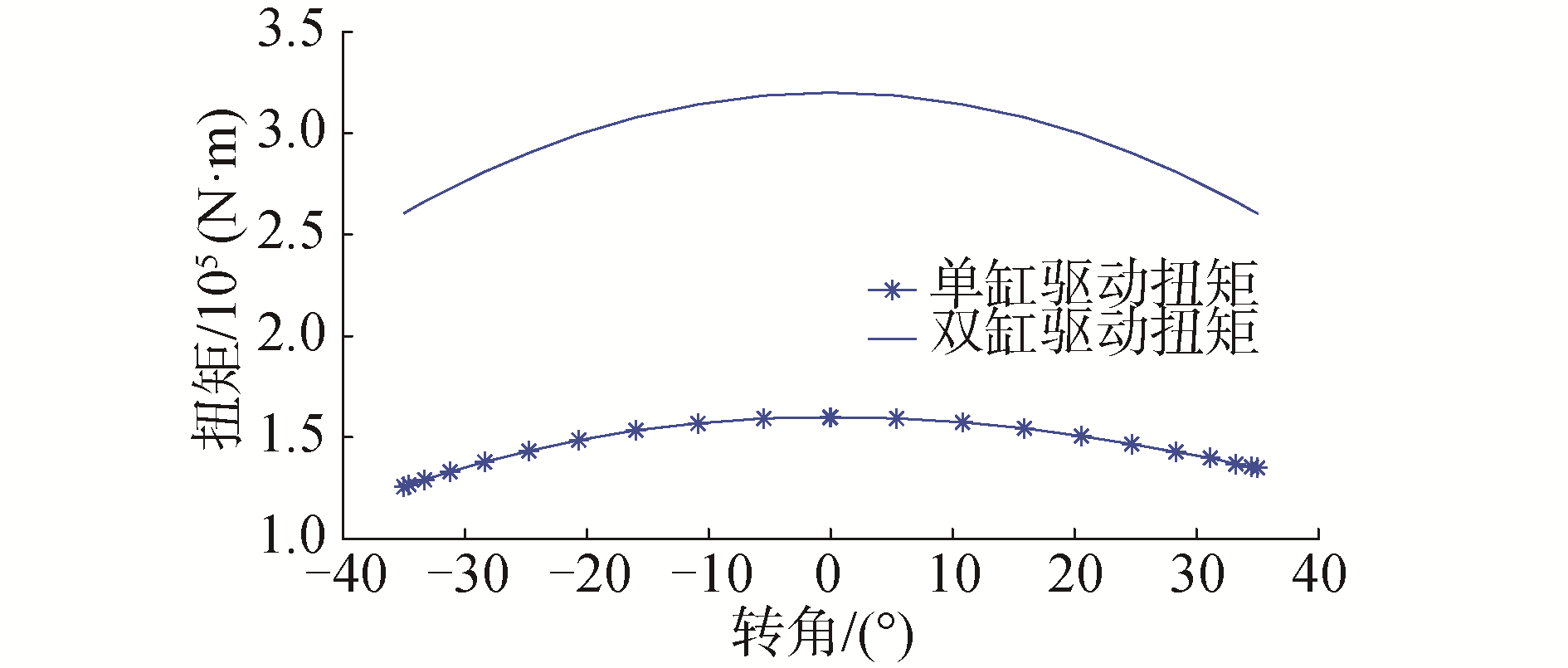
由式(12)可知,电动缸输出力与驱动扭矩为非线性关系。当电动缸驱动力为3.478×105 N时,可得图 3所示电动缸驱动扭矩与舵机转角关系曲线。
|
Download:
|
| 图 3 电动缸驱动扭矩曲线 Fig. 3 Drive torque curves of electric cylinder | |
理想情况下,通过舵机运动学方程便可依据舵机转角指令规划出2个伺服电机转角指令。假设舵机在运动过程中机械结构无变形。在位置控制模式下,若某一时刻电动缸1伸出过程中输出位移c1在实际运动过程中产生一定的位移误差Δc1(Δc1为正数),由式(2)可知,Δc1势必引起舵机转角误差Δθ(Δθ为正数)。令Δc21(Δc21为正数)表示电动缸2对应于电动缸1位移误差Δc1的输出量,Δc2(Δc2为正数)表示电动缸2输出位移误差。由电动舵机空间几何关系可知,电动缸1伸出(缩回)对应电动缸2缩回(伸出)。
令某一时刻电动缸2实际位移D为:
| $ D=c_{2}-\Delta c_{2}^{1}+\Delta c_{2} $ | (13) |
则当Δc21=Δc2,电动缸1和电动缸2便可协调运动,无内力发生,电动缸1产生推力,电动缸2产生拉力;当Δc21>Δc2,电动缸2缩回速度滞后于理想速度,电动缸1产生推力,电动缸2亦产生推力,舵机有效驱动扭矩降低;当Δc21 < Δc2,电动缸2缩回速度大于理想速度,电动缸1受到拉力,电动缸2亦产生拉力,舵机有效驱动扭矩亦降低。由此可知,若2个电动缸出现非协调运动,即会产生一定的内力,使得舵机有效驱动扭矩降低,进而降低舵机的静动态性能。
同时,由于舵机电动缸为刚性连接,较小的位移误差,便可产生较大的力(力矩)误差,极易造成电机过载,甚至会引起舵机结构破坏。
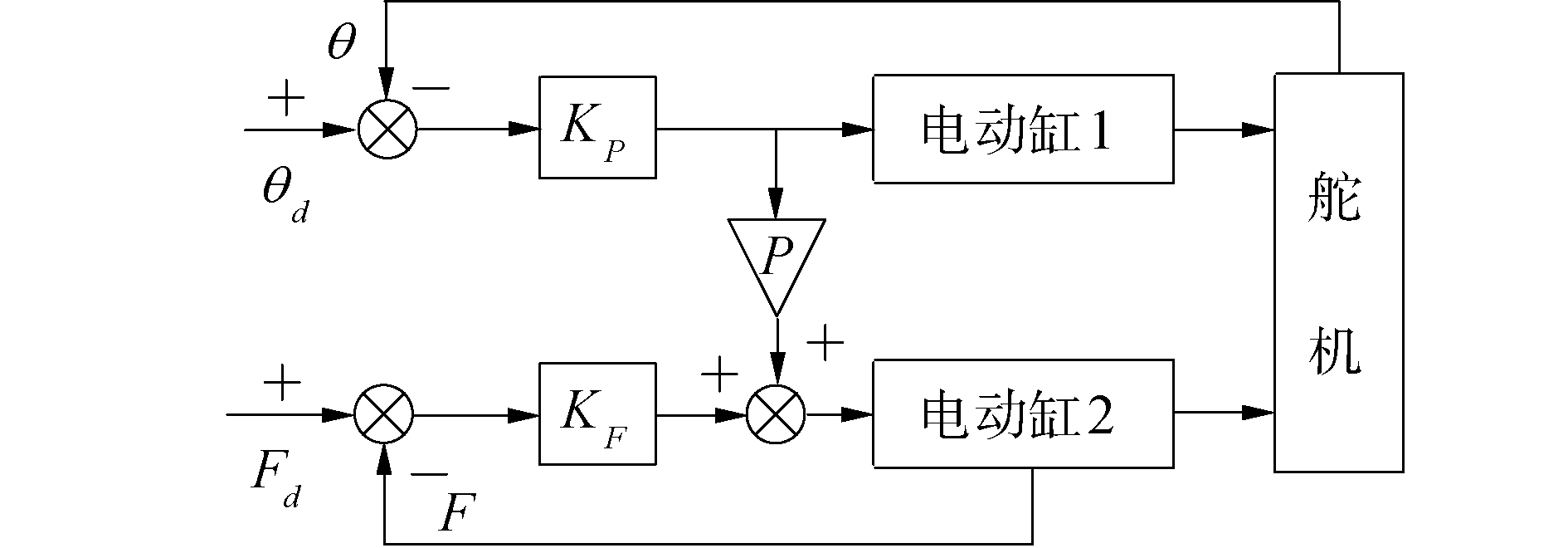
2 内力抑制控制器设计内力抑制控制如图 4所示,主要包括位置控制器和力补偿器。图中θd为舵机转角指令信号,θ为舵机实际转角反馈信号,Fd为舵机电动缸2参考力信号,其取值与电动缸1实际驱动力大小相等、符号相反。F为电动缸2反馈力信号,KP为舵机转角控制器,KF为力补偿控制器,P转换系数,此处取P=-1。由于组成舵机的2个电动缸并联布置,电动缸1伸出、电动缸2缩回,反之亦然。使得组成舵机的电动缸2接收的舵机转角指令总是大小相等符号相反。因此,电动缸1直接接收经转角控制器输出信号,电动缸2则需经转换系数P接收部分指令信号。若Fd与F相异,力补偿器KF输出补偿信号,以调整电动缸2转角,进而消除内力。
|
Download:
|
| 图 4 内力抑制控制 Fig. 4 Internal force suppression control block diagram | |
舵机转角控制器KP可保证舵机按照期望转角进行动作,因此高精度转角控制是舵机控制器的前提。
式(2)和式(3)可进一步写为:
| $ c_{1}=\sqrt{a^{2}+b^{2}-2 a b \cos (\beta+\theta)} $ | (14) |
| $ c_{2}=\sqrt{a^{2}+b^{2}-2 a b \cos (\beta-\theta)} $ | (15) |
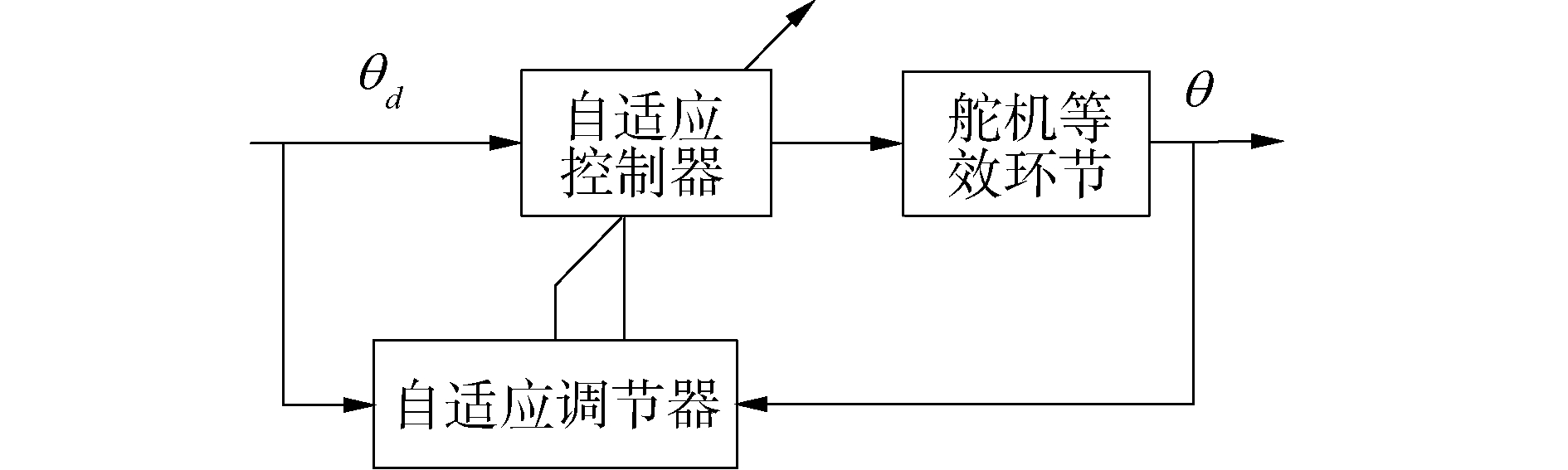
由于舵机转角与电动缸位移存在三角函数关系,而舵机系统运动过程中存在一定的相位滞后,若在余弦函数中引入一定的相位超前量,便可有效降低系统的相位滞后。考虑到舵机系统参数变化,位置控制器KP采用自适应控制器,其原理图如图 5所示。
|
Download:
|
| 图 5 自适应控制 Fig. 5 Adaptive control block diagram | |
自适应控制原理图如图 6表示。图中n为滤波器阶数,r(k)为滤波器输入,Wi(k)(i=0, 1, …,n-1)为滤波器权因子,d(k)为期望输出,y(k)为滤波器实际输出,期望输出与实际输出偏差e(k)及代价函数J(k)为:
| $ e(k)=d(k)-y(k) $ | (16) |
| $ J(k)=E\left\{e^{2}(k)\right\} $ | (17) |

|
Download:
|
| 图 6 横向滤波器 Fig. 6 Transverse filter | |
若在求解过程中能够保证代价函数J(k)最小,此时滤波器便为最优滤波器,均方误差梯度算子定义为:
| $ \nabla_{i} \cdot J=-2 E\{r(n-i) e(n)\} \quad i=0,1, \cdots, n-1 $ | (18) |
若▽i·J为零,此时式(17)便获取最小值,即滤波器工作在最优状态。
横向滤波器输出可表示为:
| $ y(k)=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{r}(k) $ | (19) |
式中:w=[w0 w1 … wn-2 wn-1]T,r(k)=[r(k) r(k-1) … r(k-n+2) r(k-n+1)]T。
则代价函数变为:
| $ \begin{aligned} \boldsymbol{J}(k)=& \mathrm{E}\left\{\left[d(k)-\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}(k)\right]^{2}\right\}=\\ & \mathrm{E}\left\{d^{2}(k)\right\}-2 \mathrm{E}\left\{\boldsymbol{x}^{\mathrm{T}}(k) d(k) \boldsymbol{w}\right\}+\\ & \mathrm{E}\left\{\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}(k) \boldsymbol{x}^{\mathrm{T}}(k) \boldsymbol{w}\right\} \end{aligned} $ | (20) |
滤波器输入矩阵定义为:
| $ \begin{aligned} \boldsymbol{R}=&\mathrm{E}\left[\boldsymbol{r}(k) \boldsymbol{r}^{\mathrm{H}}(k)\right]=\\ &\left[\begin{array}{cccc} r(0) & r(1) & \cdots & r(n-1) \\ r(1) & r(0) & \cdots & r(n-2) \\ \vdots & \vdots & \ddots & \vdots \\ r(n-1) & r(n-2) & \cdots & r(0) \end{array}\right] \end{aligned} $ | (21) |
定义互相关矩阵P为:
| $ \boldsymbol{P}=\mathrm{E}[\boldsymbol{r}(k) \boldsymbol{d}(k)]=\mathrm{E}\left[\begin{array}{c} r(k) d(k) \\ \vdots \\ r(k-n+1) d(k) \end{array}\right] $ | (22) |
则代价函数可进一步表示为:
| $ \begin{aligned} J(k)=& \mathrm{E}\left\{\left[d(k)-\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}(k)\right]^{2}\right\}=\\ &\left.\mathrm{E}\left\{d^{2}(k)\right\}-2 \boldsymbol{P}^{\mathrm{T}} \boldsymbol{w}+\boldsymbol{w}^{\mathrm{T}} \boldsymbol{R} \boldsymbol{w}\right\} \end{aligned} $ | (23) |
对式(23)两端求导得:
| $ \frac{\partial J(k)}{\partial \boldsymbol{w}}=-2 \boldsymbol{P}+\boldsymbol{R} \boldsymbol{w} $ | (24) |
假设R为非奇异矩阵,令式(23)为零,则得最优滤波器权系数为:
| $ \boldsymbol{w}_{0}=\boldsymbol{R}^{-1} \boldsymbol{P} $ | (25) |
式(25)即为维纳-霍夫方程,其解w0成为维纳解,应用维纳解所得的滤波器为维纳滤波器,其求解过程已有成熟理论,本文不再赘述。
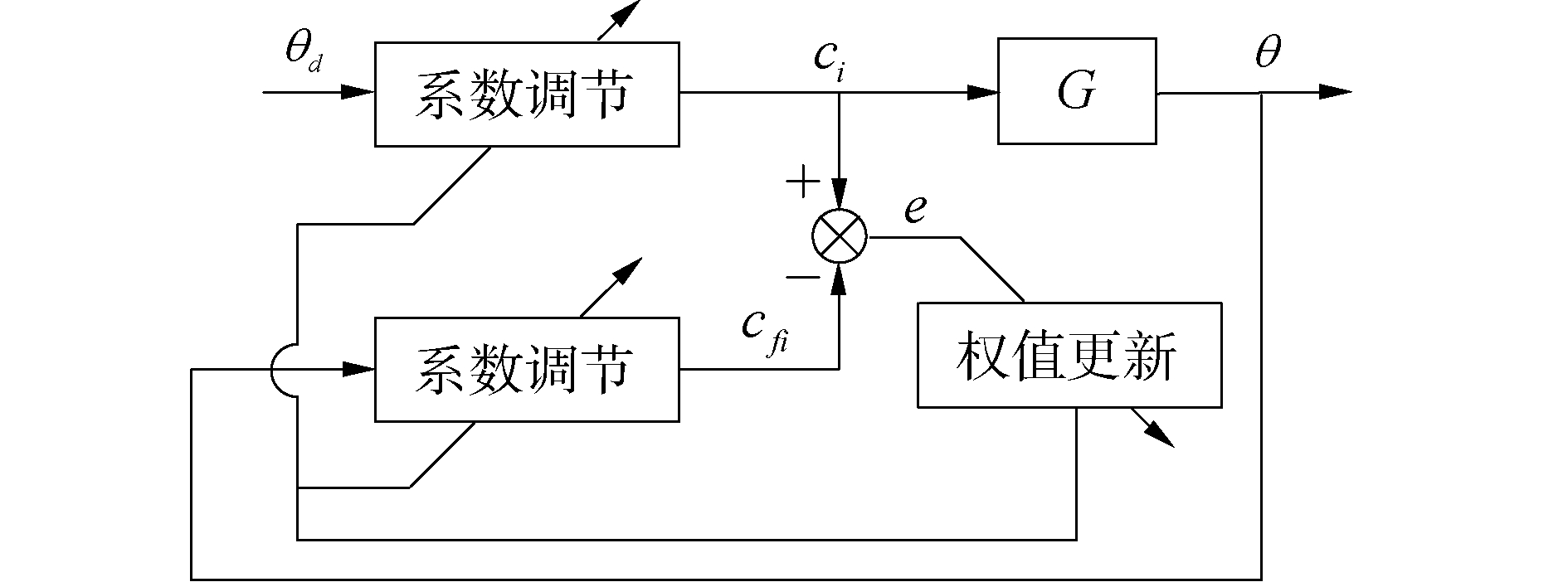
自适应控制器的核心是滤波器权值的调整,本文采用最小均方算法进行调整,考虑算法实现性,现对图 5所示的调节器进行相应修改得图 7所示的自适应补偿器。
|
Download:
|
| 图 7 自适应补偿器 Fig. 7 Adaptive compensator | |
由图 7可知,若ci能够跟踪cfi,则系统输出便可跟踪系统输入[9-14],从而实现系统精确补偿。
理想情况下,电动推杆伸出时电动缸提供推力,电动推杆缩回时电动缸产生拉力。由于电动缸正反行程最大驱动力值相同,在控制过程中可使两电动缸驱动力大小相同。力补偿控制器采用比例、积分控制器。
3 联合仿真对比分析为验证控制策略的有效性,运用Matlab和ADAMS联合仿真平台对电动直驱舵机转舵机构进行了仿真分析。运用Matlab进行舵机控制系统建模,运用ADAMS平台进行机械结构模拟,ADAMS中仿真模型如图 8所示。

|
Download:
|
| 图 8 电动舵机仿真模型 Fig. 8 Simulation model of electric steering gear | |
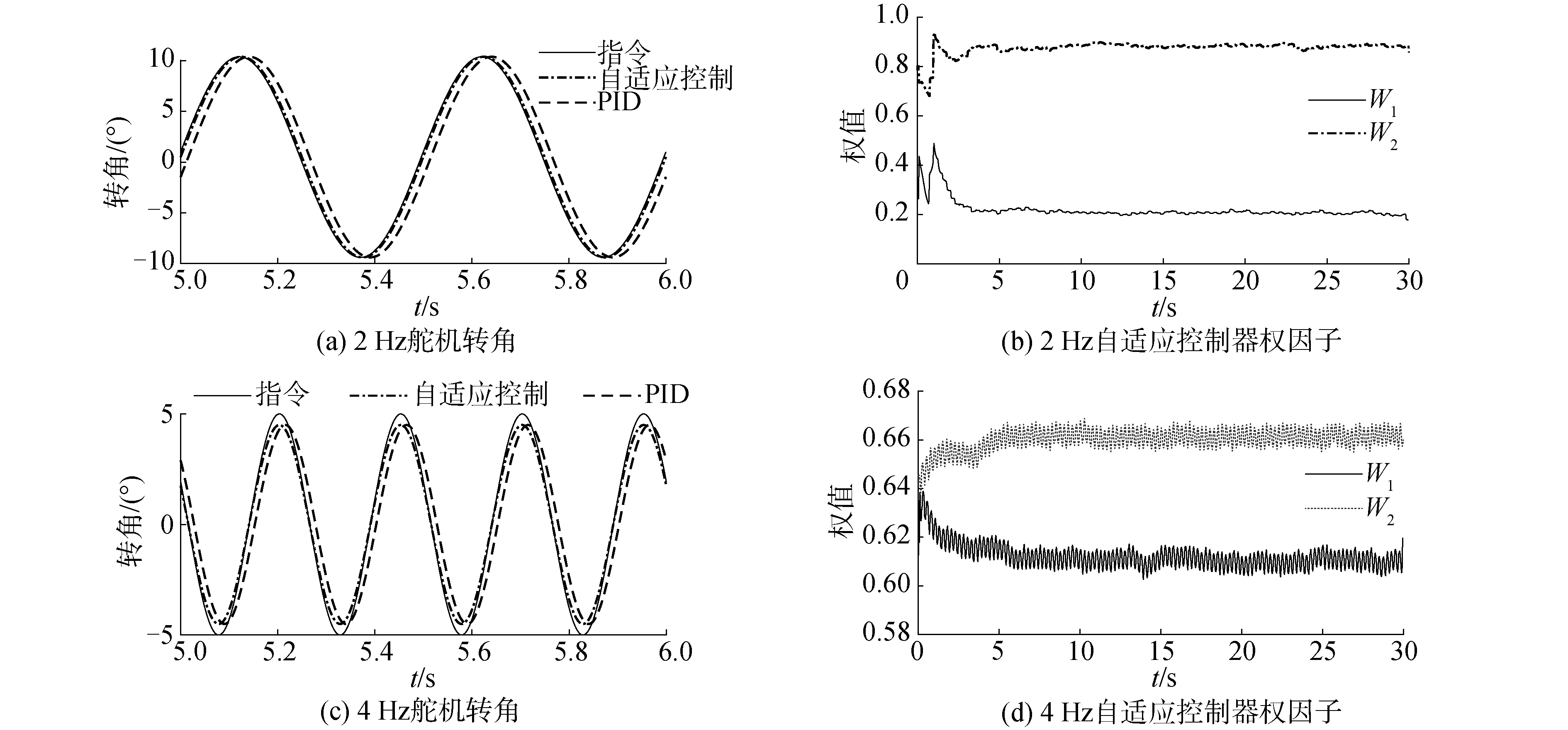
在推舵机构转角跟踪仿真过程中未对电动缸驱动力进行限制。图 9分别为2 Hz指令信号和4 Hz指令信号下系统响应曲线。其中图 9(a)、9(c)中的常规PID控制器中比例、积分和微分系数分别为200、120、0。
|
Download:
|
| 图 9 舵机转角响应及自适应控制器权因子曲线 Fig. 9 Steering gear angle response and adaptive controller weight factor curves | |
由图 9中2种频率的舵角正弦信号指令和舵机实际舵角的跟踪响应以及自适应控制器调节因子曲线可知,在激励信号为2 Hz条件下,自适应控制器可以保证舵机舵角的响应信号对指令信号的无差跟踪,而舵机系统在采用PID控制器的情况下系统的幅值衰减小于10%,相位滞后7.2°。当舵角指令信号为4 Hz条件下时,在自适应控制器控制情况下,舵机系统的幅值衰减4%,相位滞后14.4°,而在同样的指令情况下由PID控制器进行控制时,舵机系统的幅值衰减为6%,相位滞后达到35°,由此可以说明采用自适应控制器相比PID控制器更能够有效提高舵机系统的性能。
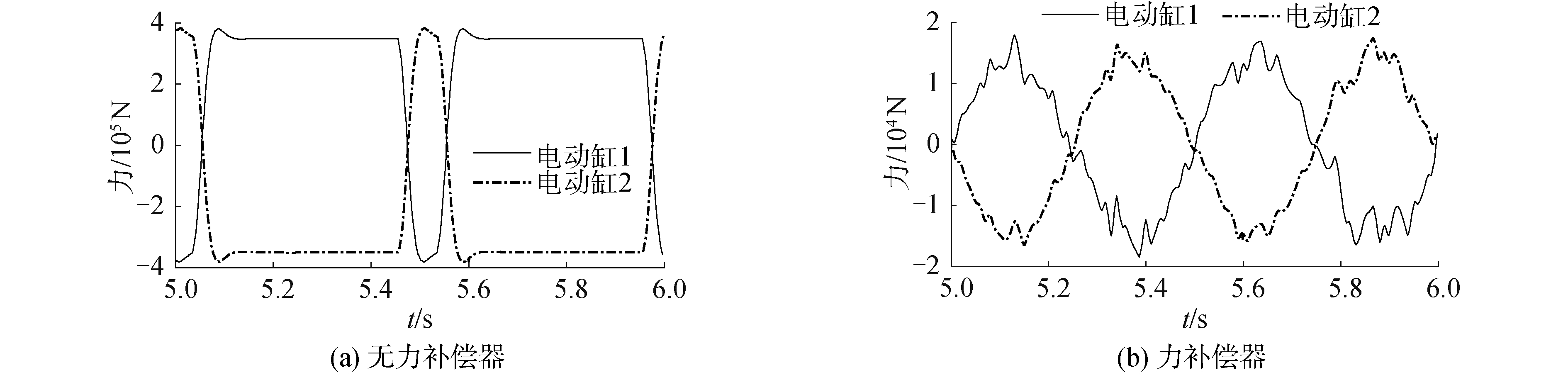
3.2 内力仿真分析图 10和图 11分别为2 Hz指令信号和4 Hz指令信号下电动缸驱动力曲线,其中曲线1和曲线2分别对应电动缸1和电动缸2驱动力曲线。
|
Download:
|
| 图 10 2 Hz电动缸驱动力曲线 Fig. 10 Electric cylinder driving force curves of 2 Hz excitation signal | |

|
Download:
|
| 图 11 4 Hz电动缸驱动力曲线 Fig. 11 Electric cylinder driving force curves of 4 Hz excitation signal | |
由图 9、10和11可知,虽然自适应控制器可以获得较高的位置控制精度,但系统仍存在较大内力,无力补偿器时,电动缸驱动力较大,已达到力饱和,而引入力补偿器后的2个电动缸驱动力较小,最大幅值仅为2×104 N和3×104 N。说明了力补偿控制器能有效消除转舵时电动缸的内力。
4 结论1) 转角相位滞后以及加工装配误差均会使舵机产生较大内力,从而导致电机输出力矩增大甚至过载以及系统结构破坏。
2) 舵机转角自适应控制算法和基于力补偿方法的内力抑制策略可大幅减小舵机系统内力,为电动直驱舵机的工程应用夯实了理论基础。
| [1] |
潘大夫. 电动舵机系统建模及控制算法[J]. 四川兵工学报, 2013, 34(9): 1-4. PAN Dafu. Electromechanical actuator system model and control method research[J]. Journal of Sichuan ordnance, 2013, 34(9): 1-4. (  0) 0)
|
| [2] |
骆光照. 电动舵机的鲁棒控制研究[D]. 西安: 西北工业大学, 2003. LUO Guangzhao. Robust control application in electromechanical actuator[D]. Xi'an: Northwestern Polytechnical University, 2003. (  0) 0)
|
| [3] |
闫飞飞, 陈圣东, 刘亚丽. 基于自抗扰控制器的船舶电动舵机控制系统设计[J]. 舰船科学技术, 2013, 35(12): 88-91. YAN Feifei, CHEN Shengdong, LIU Yali. Design for steering gear control system based on ADRC[J]. Ship science and technology, 2013, 35(12): 88-91. DOI:10.3404/j.issn.1672-7649.2013.12.019 (  0) 0)
|
| [4] |
张阳阳, 邢继峰, 彭利坤, 等. 电动舵机用电动缸滚珠丝杠振动特性[J]. 舰船科学技术, 2013, 35(12): 29-31, 41. ZHANG Yangyang, XING Jifeng, PENG Likun, et al. Ball screw vibration characteristic of electric cylinder used in electric helm[J]. Ship science and technology, 2013, 35(12): 29-31, 41. DOI:10.3404/j.issn.1672-7649.2013.12.006 (  0) 0)
|
| [5] |
谢俊超, 肖清, 花靖. 船用新型电动舵机可行性研究[J]. 舰船科学技术, 2013, 35(10): 78-81. XIE Junchao, XIAO Qing, HUA Jing. Research on the new marine electro-mechanical actuator feasibility[J]. Ship science and technology, 2013, 35(10): 78-81. DOI:10.3404/j.issn.1672-7649.2013.10.018 (  0) 0)
|
| [6] |
陈潇, 邓攀, 安宁, 等. 双缸推动型船舶电动舵机的同步控制技术[J]. 船舶工程, 2018, 40(5): 68-71, 76. CHEN Xiao, DENG Pan, AN Ning, et al. Synchronous control method for marine electric steering engine of dual-cylinder propulsion[J]. Ship engineering, 2018, 40(5): 68-71, 76. (  0) 0)
|
| [7] |
高长虹, 杨志东, 丛大成, 等. 液压驱动冗余并联机构内力分析及抑制[J]. 中南大学学报(自然科学版), 2017, 48(11): 2897-2905. GAO Changhong, YANG Zhidong, CONG Dacheng, et al. Internal force analysis and rejection of hydraulically driven redundant parallel mechanism[J]. Journal of Central South University (science and technology), 2017, 48(11): 2897-2905. DOI:10.11817/j.issn.1672-7207.2017.11.038 (  0) 0)
|
| [8] |
张连朋, 杨炽夫, 杨志东, 等. 冗余驱动液驱振动台台阵系统内力分析及其抑制方法研究[J]. 振动与冲击, 2017, 36(3): 83-92. ZHANG Lianpeng, YANG Chifu, YANG Zhidong, et al. Inner coupling force analysis and suppression for redundant-drive hydraulic shaking tables[J]. Journal of vibration and shock, 2017, 36(3): 83-92. (  0) 0)
|
| [9] |
孙桂涛, 邵俊鹏, 赵新通, 等. 液压机器人作动器建模及关节转角跟踪控制[J]. 仪器仪表学报, 2015, 36(3): 584-591. SUN Guitao, SHAO Junpeng, ZHAO Xintong, et al. Hydraulic robot actuator modeling and joint angle tracking control[J]. Chinese journal of scientific instrument, 2015, 36(3): 584-591. (  0) 0)
|
| [10] |
YAO Jianjun, DI Duotao, JIANG Guilin, et al. Acceleration amplitude-phase regulation for electro-hydraulic servo shaking table based on LMS adaptive filtering algorithm[J]. International journal of control, 2012, 85(10): 1581-1592. DOI:10.1080/00207179.2012.694081 (  0) 0)
|
| [11] |
YAO Jianjun, JIANG Guilin, DI Duotao, et al. Acceleration harmonic identification for an electro-hydraulic servo shaking table based on the normalized least-mean-square adaptive algorithm[J]. Journal of vibration and control, 2013, 19(1): 47-55. DOI:10.1177/1077546311429151 (  0) 0)
|
| [12] |
LIU Huajian, HUANG Qitao, TONG Zhizhong. Simulation and analysis of a full-active electro-hydrostatic powered ankle prosthesis[C]//Proceedings of the 19th International Conference on Advanced Robotics. Belo Horizonte, Brazil, 2019.
(  0) 0)
|
| [13] |
LIU Yi, WANG Tao, GONG Guofang, et al. Present status and prospect of high-frequency electro-hydraulic vibration control technology[J]. Chinese journal of mechanical engineering, 2019, 32(1): 93. DOI:10.1186/s10033-019-0406-y (  0) 0)
|
| [14] |
GUAN Guangfeng, PLUMMER A R. Acceleration decoupling control of 6 degrees of freedom electro-hydraulic shaking table[J]. Journal of vibration and control, 2019, 25(21/22): 2758-2768. (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


