近年来,水下无人航行器技术发展迅速,应用于海底环境监测、海底地形探测、水下管道检查等领域,这些海洋探索依赖于先进的水下探测技术,其中水下图像处理是其中重要的一部分,但水下的浮游生物、可见颗粒物等物质会对太阳光有吸收和散射作用[1],针对不同波长的太阳光水的吸收程度不同,其中水对红色光的吸收作用最强,水下图像多呈蓝绿色调,与陆地上的图像相比水下图像会存在颜色畸变、对比度低、噪声大等问题,因此水下图像增强对于水下图像的信息恢复、质量提升有重要意义[2]。水下图像增强技术分为基于物理模型的方法和基于非物理模型的方法2种[3],基于非物理模型的方法不考虑水下图像退化的物理过程,经典方法是基于Retinex的增强方法[4],融合对比度和颜色校正的方法[5],这类方法通常是直接改变像素值,容易发生过度校正和过饱和。基于物理模型的方法对水下成像过程建模,文献[6]利用水下图像的散射模型对水下图像增强,因其需要对背景光预先标定而不适用于背景光变化的水下场景。He等[7]提出的针对空气中有雾图像的暗通道去雾方法(dark channel prior,DCP)可应用于水下图像,但由于水下光的散射和吸收传统暗通道方法作用不明显。谢昊伶等[8]利用波长和散射系数的关系分别估计了三通道的透射率,通过导向滤波细化透射率,但该方法需获得相机的拍摄深度,限制了其实际应用。汤忠强等[9]改进了DCP方法,通过亮暗通道的视差估计背景光和透射率。以上均是基于物理模型的方法,在先验信息的基础上估计模型参数,反向计算出未退化的水下图像。在图像去雾中,He等[7]提出了暗通道先验构建透射率的方法;Park等[10]提出利用熵信息和保真率结合的方式构建雾天透射率;Zhu等[11]提出利用亮度和饱和度之差构建透射率。
借鉴雾天图像增强的分析方法,本文对水下浑浊图像直接进行分析。考虑物理模型法增强图像会获得更好的效果,同时减少模型参数估计带来的复杂程度,本文对水下浑浊图像直接进行分析。考虑物理模型法增强图像会获得更好的效果,同时减少模型参数估计带来的复杂程度,本文提出的水下图像增强方法仅通过单幅图像,不需要模型先验参数就能实现水下浑浊图像的自适应增强,以恢复水下图像损失的细节,实现水下浑浊图像清晰化。
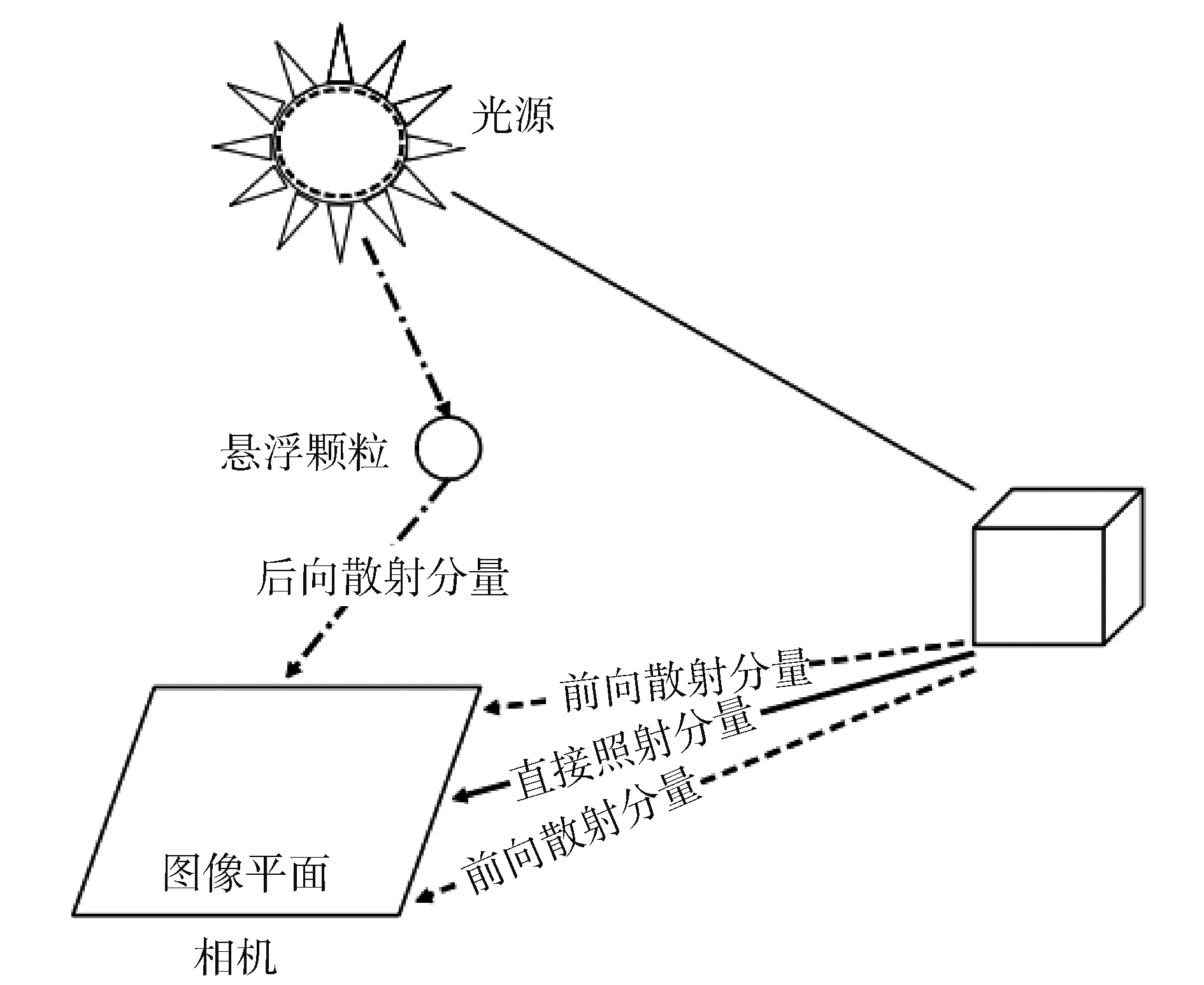
1 水下视觉成像模型建立水下图像受光照不足、亮度不均、水体的散射和吸收、悬浮颗粒物等因素的影响损失了很多信息,针对水下的特殊环境,Jaffe-McGlamery定义的水下光传播经典模型[12],到达相机的光是前向散射、后向散射和直接光三部分的线性叠加,前向散射是水下物体的反射光又经散射的光,后向散射是环境光被水中的颗粒、生物等散射后进入相机的光,直接光是相机直接接受到的光。在距离较短时可以忽略前向散射,用直接光和后向散射近似描述到达相机的总光:
| $ A_{n}(x, \lambda)=A_{\infty}(\lambda)\left(1-\mathrm{e}^{-\alpha(\lambda) \mathrm{x}}\right) $ | (1) |
式中:x为光传播距离;A∞(λ)为背景光;λ为波长;α(λ)为由于吸收和散射的总的衰减系数。场景直接光散射Ad(x, λ)可以表示为:
| $ A_{d}(x, \lambda)=J_{0}(\lambda) \mathrm{e}^{-\alpha(\lambda) \mathrm{x}} $ | (2) |
式中:x表示传播的距离;λ表示波长;为由于吸收和散射的总的衰减系数;J0(λ)是未被水下环境衰减的光,就是需要被恢复的清晰图像。水下摄像机成像模型为:
| $ \begin{gathered} I=A_{d}(x, \lambda)+A_{n}(x, \lambda)=J_{0}(\lambda) \mathrm{e}^{-\alpha(\lambda) x}+ \\ A_{\infty}(\lambda)\left(1-\mathrm{e}^{-\alpha(\lambda) x}\right) \end{gathered} $ | (3) |
近距离下,认为水对光的吸收和散射作用相同,将α视为常数,忽略波长的影响,水下成像模型为:
| $ I=J_{0} \mathrm{e}^{-\alpha x}+A_{\infty}\left(1-\mathrm{e}^{-\alpha x}\right)=J_{0} t(x)+A_{\infty}(1-t(x)) $ | (4) |
式中t(x)为透射率。将等式两边对距离x求导,可得:
| $ \frac{\partial I}{\partial x}=\alpha\left(A_{\infty}-J_{0}\right) \mathrm{e}^{-\alpha x} $ | (5) |
当背景光大于自然光,光强随距离增加而减小且衰减速度越来越慢,当背景光小于自然光,光强随距离增加而增加且增加速度越来越慢,符合人眼观察到的水下图像景深越深场景越模糊大的特点。
|
Download:
|
| 图 1 水下光散射模型 Fig. 1 Underwater light scattering model | |
依据式(4),进行移项可得水下图像复原公式:
| $ J_{0}=\frac{I-A_{\infty}}{t(x)}+A_{\infty} $ | (6) |
式中:A∞为背景光;t(x)为透射率。式(6)可以得到增强后的水下场景清晰图像。随着相机离物体距离的增加,观察到的信息越少,图像越模糊,通过一些评价指标如熵、平均梯度、逼真度等可以量化水下图像的信息。
2.1 背景光估计文献[7-9]将传统的暗通道先验去雾方法改进后估计水下图像背景光用于水下图像复原,但暗通道先验去雾方法是基于一种统计规律,水下图像的统计规律和空气中图像有差异。本文针对水下图像的特性对背景光的大小进行分析,利用水下图像的局部区域熵信息估计背景光。
通过式(5)和前文的分析,水下物体模糊的一部分原因为景深的增加,景深增加带来了更严重的吸收、散射、颜色畸变等问题,背景光的区域景深最大因而信息也最少,视觉上看起来是最模糊的,用熵来衡量水下图像的信息,局部区域信息熵越大证明信息越多。后向散射带来的水下图像的模糊主要是因为距离远的物体在光的传播过程中造成了熵大的衰减,用熵描述景深为:
| $ f_{\text {entropy }}=-\sum\limits_{i=0}^{L} P(i) \log (P(i)) $ | (7) |
式中P(i)某个灰度在该图像中出现的概率,可由灰度直方图计算。
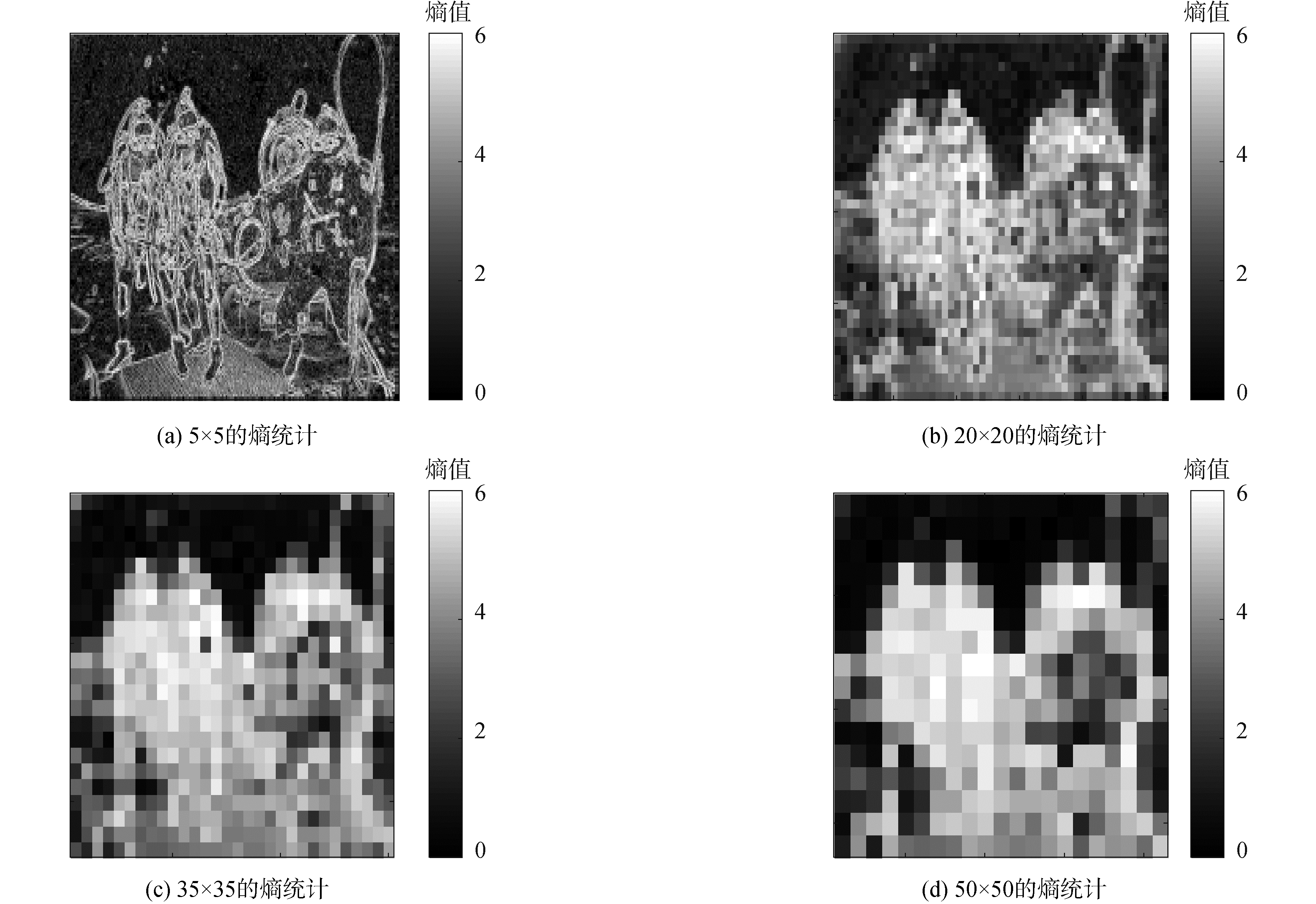
对图 2的背景光进行估计,在计算信息熵前先将图像分成互不重叠的小块,局部区域块的大小会影响最后的估计结果。本文选取4组不同的局部区域块尺寸(5×5,20×20,35×35,50×50),按区域块统计熵,不同尺寸区域块的熵统计图如图 3所示。

|
Download:
|
| 图 2 水下原始图像 Fig. 2 Underwater original image | |
|
Download:
|
| 图 3 不同尺寸熵统计结果 Fig. 3 Entropy statistical results of different block sizes | |
根据图 3的熵统计结果可知,水下图像不同区域块信息熵的大小随景深而变化,熵和光在水下的吸收和散射程度密切相关。观察4种分块尺寸的熵值图,分块大小为50×50的熵值图较模糊,由于分块过大已经不能完整地描述景深,局部区块大小为5×5的熵统计图因为区块选取过小又弱化了水下散射和熵值的相关性,使相同景深下物体的不同细节熵值有较大差异(例如潜水员衣服上的细节),故局部区域块尺寸为20×20,35×35能较好地描述景深,综合对景深的细化处理和算法的快速性,本文选取的局部区域块大小为35×35。
利用局部区域块大小为35×35的熵值图估计背景光,参照熵对水下信息的表述能力,熵值越大代表图像的信息越多,景深越小,而背景光区域出现在景深较大处,相对于整幅图像熵值最低,因此选取熵值较低的20%的区域作为估计背景光的候选区域,在候选区域中选择出现频率最高的灰度作为水下图像的背景光,这样就能在候选区域中降低误判的可能性,提高背景光估计的准确性。
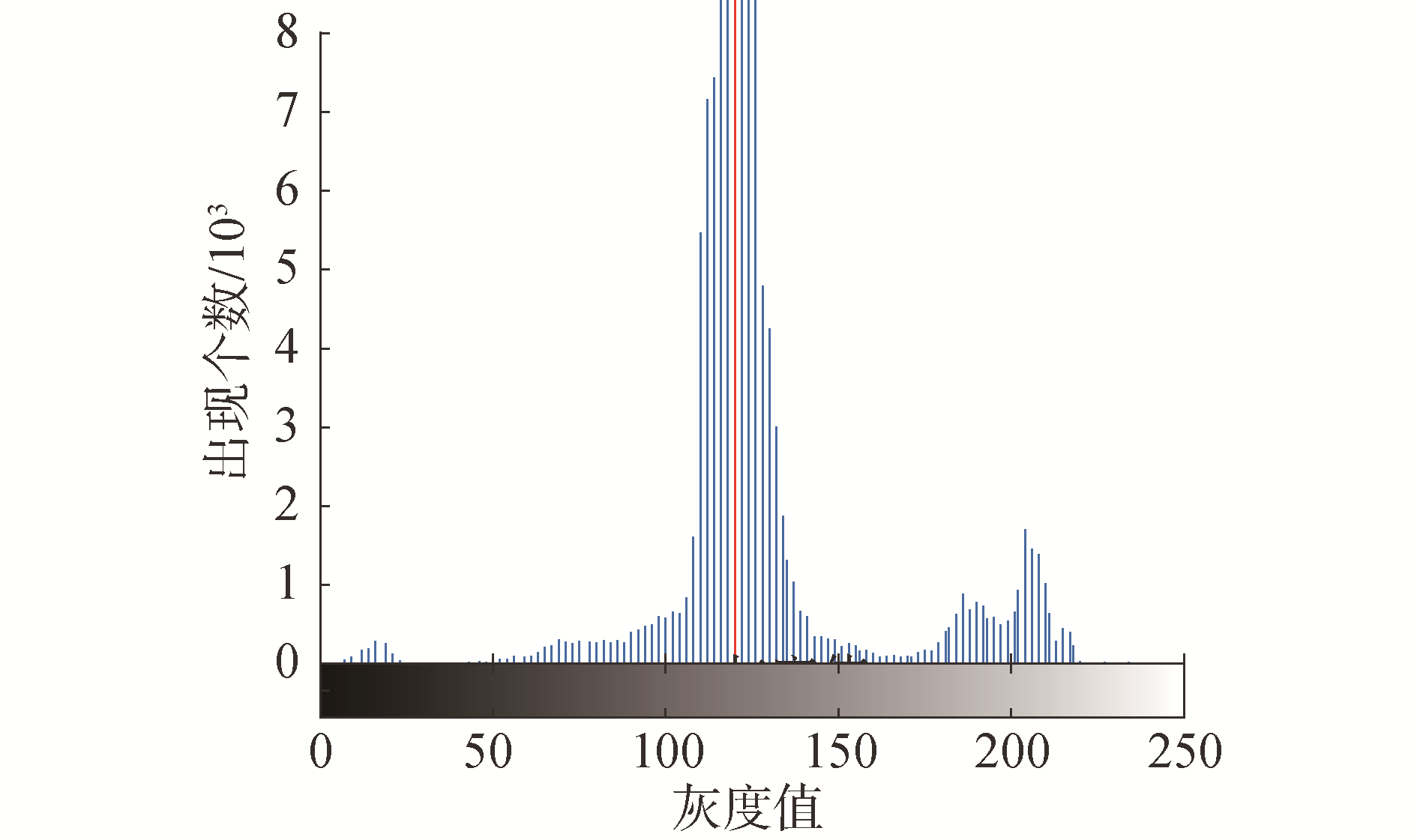
具有较低强度的前20%的熵统计图如图 4所示,原图中此区域为水体背景,由此可以看出本方法估计背景光较为合理,背景光候选区域的灰度直方图如图 5所示,选取出现频率最高的灰度值作为背景光,数值为122。

|
Download:
|
| 图 4 具有较低强度的前20%熵的统计量 Fig. 4 Statistics of the first 20% entropy with higher intensity | |
|
Download:
|
| 图 5 具有较低强度的前20%熵的直方图统计 Fig. 5 Histogram statistics of the first 20% entropy with higher intensity | |
假设水下图像局部区域透射率连续不变且水下图像的真实场景与透射率无关,为准确估计水下图像的局部透射率,本文根据图像的平均梯度和图像的逼真度提出了一个代价函数。图像的局部区域清晰度可以用梯度衡量,具有最大平均梯度的局部区域对应局部最佳透射率,衡量图像的平均梯度的代价函数为:
| $ f_{\text {gradient }}(r)=\frac{1}{M N} \sum\limits_{1}^{M} \sum\limits_{1}^{N} \sqrt{\left(\frac{\partial J_{0}(i, j)}{\partial x}\right)^{2}+\left(\frac{\partial J_{0}(i, j)}{\partial y}\right)^{2}} $ | (8) |
式中:M、N分别表示区域图像的宽度和高度;r为某局部区域;
由式(6)复原后的清晰图像可能会出现失真的像素,即像素值大于255或小于0,在计算平均梯度之前通过阈值处理先去除掉一些失真像素,当像素大于255时上界取255,当像素小于0时取下界0。逼真度为:
| $ f_{\text {fidelity }}(r)=\frac{1}{M N} \delta(p) $ | (9) |
| $ \delta(p)=\left\{\begin{array}{cc} 1, & 0<J_{0}(p)<255 \\ 0, & \text { 其他 } \end{array}\right. $ | (10) |
式中:δ(p)表示在透射率为r时当前区域块内没有失真的像素占总像素的比例。δ(p)越小图像的逼真度越低,δ(p)越大失真像素比例越小,图像的逼真度越高,图像增强的效果越好。因此需最大化代价函数以获得好的图像增强效果。综合水下图像清晰度和逼真度两方面,计算透射率的代价函数为:
| $ f_{\text {final }}(r)=f_{\text {gradient }}(r) \cdot f_{\text {fidelity }}(r) $ | (11) |
计算该代价函数的最大值可计算出最佳透射率,透射率为:
| $ r=\operatorname{argmax}\left(f_{\text {final }}(r)\right) $ | (12) |
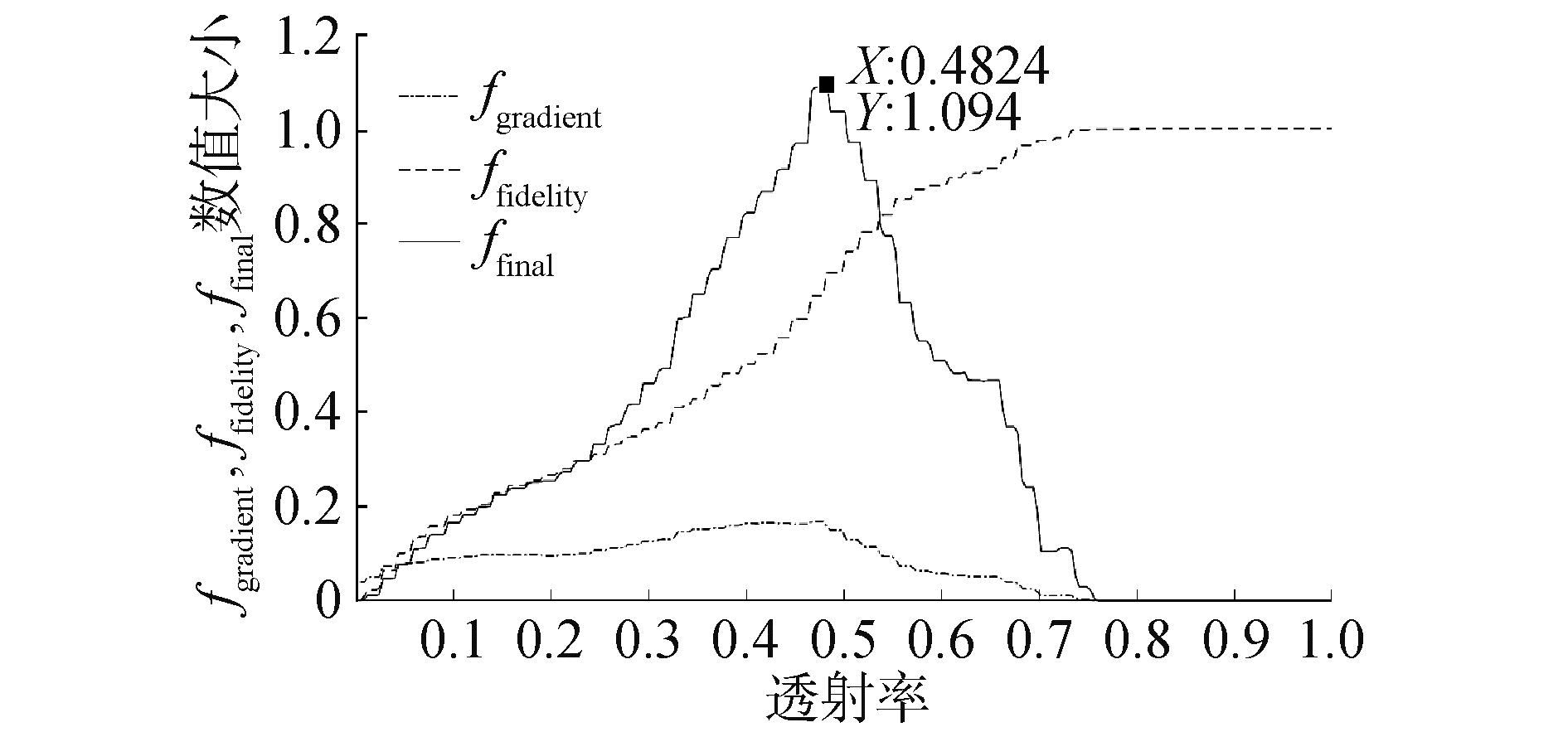
如图 6所示,图中显示了ffidelity(r)、fgradient(r)和ffinal(r)的结果,最佳透射率为最大化ffinal(r)所对应的结果,透射率为0.48。
|
Download:
|
| 图 6 最优透射率计算函数 Fig. 6 The graph of the function for calculating the optimal transmission | |
通过计算可以得到局部区域的透射率,由于透射率是分块计算的,所以在区块的连接处透射率图不够连续,恢复出的水下图像在块的连接处也会出现块效应,因此需要减弱透射图区块边缘的影响,利用改进的最改进加权最小二乘的保边滤波算法细化透射图。未改进的最小二乘保边滤波算法为[12]:
| $ B=\left((t-\tilde{t})^{2}+\lambda\left(w_{x}(t)\left(\frac{\partial t}{\partial x}\right)^{2}+w_{y}(t)\left(\frac{\partial t}{\partial y}\right)^{2}\right)\right) $ | (13) |
式中:t是经细化的透射图;
| $ K=\left((t-\tilde{t})^{2}+\lambda\left(w_{x}(g)\left(\frac{\partial t}{\partial x}\right)^{2}+w_{y}(g)\left(\frac{\partial t}{\partial y}\right)^{2}\right)\right) $ | (14) |
式中:wx(g)为原图像经高斯滤波后x方向梯度值;wy(g)为原图像经高斯滤波后y方向梯度值。改进后的最小二乘保边滤波算法可通过增大λ平滑透射图的区块边缘,同时也能起到增强原图边缘细节的作用,但λ过大也会削弱不同局部块之间透射率的差异,需在合理范围内。
改进后的最小二乘保边滤波算法细化前后的透射图如图 7所示,从图中可以看出未处理前的透射图局部区块连接处不够平滑,细化后的透射图局部区块间平滑过渡,物体的边界也被增强。

|
Download:
|
| 图 7 细化前后的透射图像 Fig. 7 Transmission image before and after refining | |
通过2.3节方法计算出背景光和透射率可以用于图像增强,但在进行透射率计算时设计的代价函数权衡了图像细节和图像失真,仍然存在一些失真的像素,为解决此问题设计自适应调节因子μ,经式(6)计算出增强后的图像为J0,统计增强图像中相对于原始图像像素的失真比μ,设计新的图像复原为:
| $ J_{\text {final }}=\frac{I-A_{\infty}}{\max (t(x), \mu \max t(x))}+A_{\infty} $ | (15) |
式中:A∞为背景光;t(x)为透射率;μ是原始像素失真比。
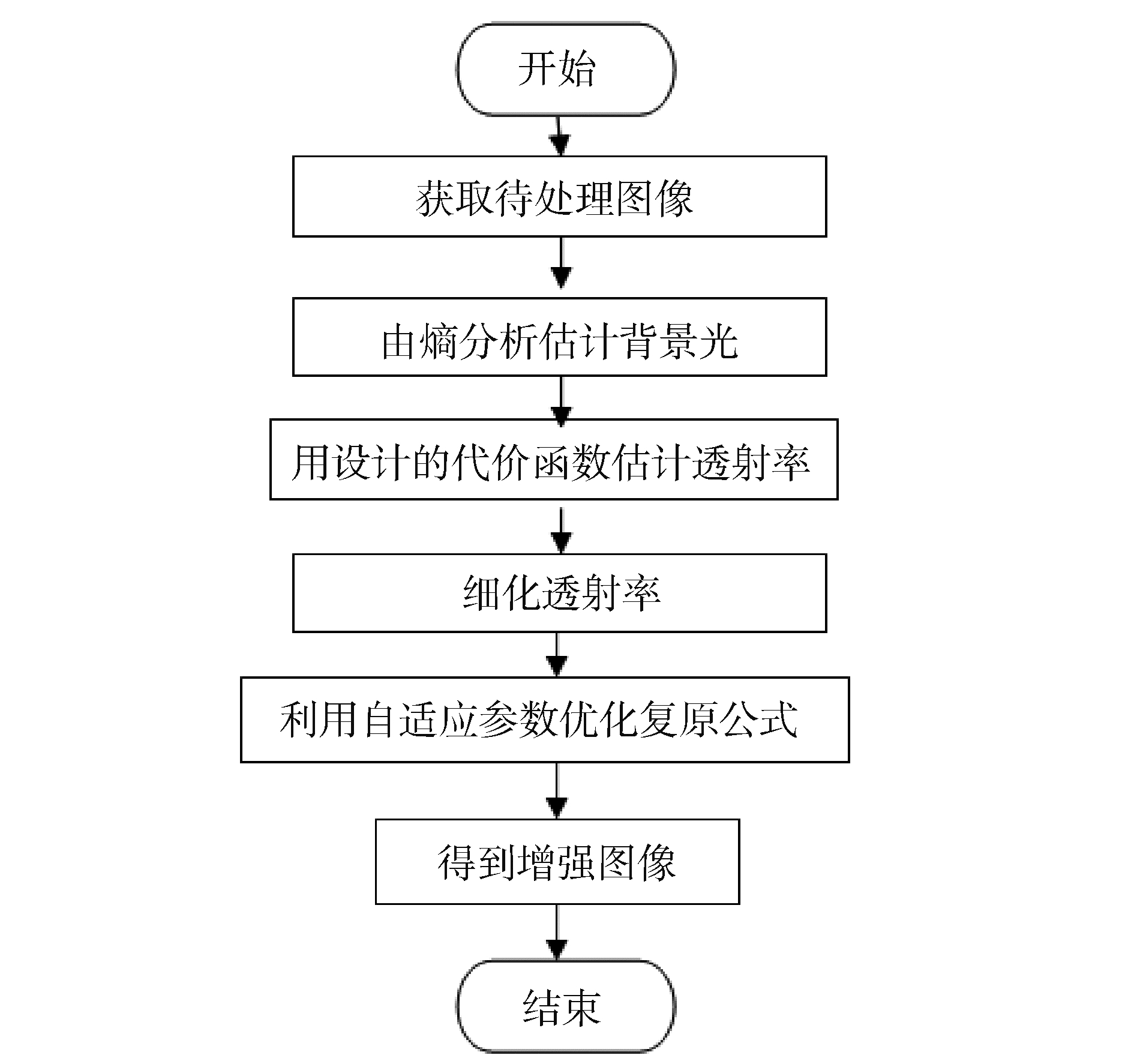
该自适应调节方法可以减少图像复原后部分像素的失真情况。算法总体流程如图 8。
|
Download:
|
| 图 8 算法整体流程 Fig. 8 Algorithm overall flow chart | |
为了验证本文所提算法的有效性,本为选取水下灰度图像作为测试图像,按照本文方法进行图像增强,计算客观评价指标验证所提算法的有效性,并与传统暗通道先验去雾算法和文献[6]所提方法进行比较。
3.1 客观评价指标图像的客观评价方法主要有2种,一种是全参考,一种是无参考,本文采用全参考评价,可视化边角比率[13]。可视化边角比率是增强图像中恢复的可见边与原始图像中可见边的比率,对于水下的图像,由于光的吸收和散射效应等问题而丢失了一些可见边,采用这个度量可以衡量给定图像增强方法所带来的可见边数量以及图像细节的改变,仅仅计算增强图像的可见边并不能反映算法的有效性,系数e为:
| $ e=\frac{n_{r}-n_{0}}{n_{0}} $ | (16) |
式中:nr是增强图像Ir中可见边的数目;n0是原始图像I0中可见边的数目, 图像中的边可以定义为找到一组连接像素的2个相邻区域之间的边界,如果e>1则图像的可视边缘增加,这里使用的边缘检测算法是Sobel边缘检测器。e的值可以评估该方法恢复在I0中不可见但在Ir中不可见的边的能力。
对于非周期目标,其可见度与发光对比度相关,其定义为:
| $ C=\frac{\Delta L}{\Delta L_{b}}=\frac{L_{t}-L_{b}}{L_{b}} $ | (17) |
式中:ΔL是目标和背景的亮度差;Lt是目标亮度;Lb是背景的亮度。当目标和背景之间的亮度差是阈值亮度差ΔLthreshold时,目标以高概率被感知,目标的可见性水平可通过以下比率量化:
| $ V_{L}=\frac{C_{\text {actual }}}{C_{\text {threshold }}} $ | (18) |
式中:Cactual为实际对比度;Cthreshold为阈值处的对比度。
在阈值处,目标的可见性水平为:
| $ V_{L}=\frac{\Delta L_{\text {actual }}}{\Delta L_{\text {threshold }}} $ | (19) |
对于复杂图像计算ΔLthreshold并不简单,有必要检测和分割多个目标对象,这对于复杂对象的图像是十分困难的。为了评估图像增强算法的性能不需要分割图像,对于可见边缘的每个像素,计算恢复图像和原始图像梯度的比率:
| $ r=\frac{\Delta L_{r}}{\Delta L_{o}}=\frac{\Delta I_{r}}{\Delta I_{o}} $ | (20) |
式中:ΔIr是恢复图像中的梯度;ΔI0是原始图像中的梯度。
计算r的平均值r表示所提出方法的对比度恢复质量, 不同场景恢复的可见边如图 9所示。
| $ \bar{r}=\frac{1}{n_{r}} \sum\limits_{P_{i} \in I_{r}} \log r_{i} $ | (21) |

|
Download:
|
| 图 9 不同方法恢复的可见边 Fig. 9 Corresponding visible edge maps of the recovered images | |
结构相似性理论从高层次上模拟人眼视觉系统的整体功能,因此对结构信息的度量可以作为图像感知质量的近似,文献[14]提出了结构相似度指数SSIM,但传统的SSIM指数存在一些缺点,本文采用改进的SSIM算法,计算基于结构信息提取的SIExt指数作为图像增强的评价指标。
3.2 实验效果比较对于不同场景的e和r结果如表 1所示,不同场景的图像增强结果10所示。该参数可以评估所提方法对比度的恢复质量,从表中数据可以看出所提方法恢复的可见边优于DCP方法恢复的可见边,视觉上有更多的细节,对比度得到提升。在用DCP方法恢复的图像中整体灰度级较低,改变了原始图像的灰度级分布,目标与背景之间的灰度差别过小导致了细节的隐藏,整体对比度较低,目标的轮廓周围有明亮光晕,使得图像的整体亮暗程度极不自然。通过e参数和r参数的分析,本文所提方法优于DCP方法。
| 表 1 不同场景下的参数e、r结果 Table 1 Coefficient e, r compared on four images |

|
Download:
|
| 图 10 不同算法的图像增强效果 Fig. 10 Image enhancement with different algorithms | |
在场景2中,DCP方法的暗背景几乎隐藏了后方的对象,地面上的细小物体周围均存在光晕,对于目标过多的图像DCP方法明显会带来较多光晕,本文所提方法并不存在此问题。在场景3中DCP方法左上角的对象十分模糊,本文所提方法很好地复原了原始图像中的该部分。场景4中虽然目标轮廓的光晕不明显,但是位于中间和右侧的对象几乎看不到任何细节,从e参数也可以看出场景4的可见边数目相比原图没有增加反而减少,虽然对比度相差不大,但是由于可见边的丢失使得视觉效果远不如本文所提方法。
该方法能够评估基于视觉描述的图像增强算法的性能,但是并不能评价图像增强算法的保真度,只测量对象的可见性。相应地,计算基于结构信息提取的图像质量评价,在频域不同频率的成分对图像信息起到了不同的作用,局部区域的基本灰度等级主要由低频成分决定,中频部分影响着图像的结构,高频部分构成图像的一些边缘细节。并且同一频率成分,能量越大, 重要程度越大,视觉注意力也就越大,基于以上分析,本文将结构信息解释为图像中能量足够大的中高频成分。SIExt各部分参数设置如下:wl=0.1,ws=0.8,wn=0.1,表 2给出了SIExt评价结果。
| 表 2 不同场景SIExt结果 Table 2 The SIExt compared on four images |
从实验结果获得的数据可以看到本文所提方法的结构相似性优于DCP方法,在场景2中,DCP方法的结构相似性优于本文方法。中频成分是人眼所能感知的主要成分,是图像中最重要的频率成分,故结构信息系数设置为最大,根据文献[8]的结论,SIExt在各分量取不同权重时变化并不敏感,故基于结构信息提取的图像质量评价准则更好地验证了前文的结论。
本文对文献[6]中的图像进行处理,计算标定后的背景光和透射率,将本文方法与文献[6]方法、暗通道先验去雾算法[9](DCP)比较,实验结果如表 3和图 11所示。
| 表 3 不同方法的e、r参数比较 Table 3 Coefficient e, r compared on different algorithms |

|
Download:
|
| 图 11 不同算法的图像增强效果 Fig. 11 Image enhancement with different algorithms | |
计算e值可知,文献[6]中算法和暗通道先验去雾算法均丢失了可见边,从视觉效果上算法[6]的灰度分布最为均匀,对比度和亮度提升适当,相应地r参数值最大,但是算法[6]丢失的可见边最多。DCP方法也丢失了一些可见边,使得复原图像的可见性水平变低,只有一部分物体的对比度提高,但图像整体上失真较多,亮暗分布不均。本文所提方法针对大面积的高灰度场合有一定的细节损失,对于场景4没有恢复过多的可见边,与原始图像相比可见边数目大体相当,保持了原始图像的可见性,提升了大部分的细节,亮度和对比度增强幅度合适。比文献[6]中方法相比不需要事先标定,有更大的适用性。
4 结论1) 本文所提出的算法合理地估计了水下图像的背景光和透射率,通过实验对比分析,有良好的效果,恢复图像丢失的可见边,提升了水下图像对比度。
2) 解决了水下浑浊图像失真的问题,恢复了场景信息。算法有更广泛的适用性,针对陆地上的雾天图像可考虑应用本文算法去雾。在未来的研究中,可对散射模型研究和改进。
3) 本文算法建立在忽略前向散射的模型基础上,若能较准确地建立前向散射模型,可以更好地解决光照不均匀的问题,增强算法的普适性。
| [1] |
LU Huimin, LI Yujie, ZHANG Yudong, et al. Underwater optical image processing: a comprehensive review[J]. Mobile networks and applications, 2017, 22(6): 1204-1211. DOI:10.1007/s11036-017-0863-4 (  0) 0)
|
| [2] |
ZHANG Weidong, PAN Xipeng, XIE Xiwang, et al. Color correction and adaptive contrast enhancement for underwater image enhancement[J]. Computers & electrical engineering, 2021, 91: 106981. (  0) 0)
|
| [3] |
郭继昌, 李重仪, 郭春乐, 等. 水下图像增强和复原方法研究进展[J]. 中国图象图形学报, 2017, 22(3): 273-287. GUO Jichang, LI Chongyi, GUO Chunle, et al. Research progress of underwater image enhancement and restoration methods[J]. Journal of image and graphics, 2017, 22(3): 273-287. (  0) 0)
|
| [4] |
HOU Guojia, LI Jingming, WANG Guodong, et al. A novel dark channel prior guided variational framework for underwater image restoration[J]. Journal of visual communication and image representation, 2020, 66: 102732. DOI:10.1016/j.jvcir.2019.102732 (  0) 0)
|
| [5] |
ANCUTI C, ANCUTI C O, HABER T, et al. Enhancing underwater images and videos by fusion[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence, USA: IEEE, 2012: 81-88.
(  0) 0)
|
| [6] |
边信黔, 王晓娟. 基于散射模型的水下图像复原[J]. 机器人, 2010, 32(6): 721-725. BIAN Xinqian, WANG Xiaojuan. Scattering model based underwater image restoration[J]. Robot, 2010, 32(6): 721-725. (  0) 0)
|
| [7] |
HE Kaiming, SUN Jian, TANG Xiaoou, et al. Single image haze removal using dark channel prior[J]. IEEE transactions on pattern analysis and machine intelligence, 2011, 33(12): 2341-2353. DOI:10.1109/TPAMI.2010.168 (  0) 0)
|
| [8] |
谢昊伶, 彭国华, 王凡, 等. 基于背景光估计与暗通道先验的水下图像复原[J]. 光学学报, 2018, 38(1): 0101002. XIE Haoling, PENG Guohua, WANG Fan, et al. Underwater image restoration based on background light estimation and dark channel prior[J]. Acta optica sinica, 2018, 38(1): 0101002. (  0) 0)
|
| [9] |
汤忠强, 周波, 戴先中, 等. 基于改进DCP算法的水下机器人视觉增强[J]. 机器人, 2018, 40(2): 222-230. TANG Zhongqiang, ZHOU Bo, DAI Xianzhong, et al. Underwater robot visual enhancements based on the improved DCP algorithm[J]. Robot, 2018, 40(2): 222-230. (  0) 0)
|
| [10] |
PARK D, PARK H, HAN D K, et al. Single image dehazing with image entropy and information fidelity[C]//2014 IEEE International Conference on Image Processing (ICIP). Paris, France: IEEE, 2014: 4037-4041.
(  0) 0)
|
| [11] |
ZHU Qingsong, MAI Jiaming, SHAO Ling. A fast single image haze removal algorithm using color attenuation prior[J]. IEEE transactions on image processing, 2015, 24(11): 3522-3533. DOI:10.1109/TIP.2015.2446191 (  0) 0)
|
| [12] |
FARBMAN Z, FATTAL R, LISCHINSKI D, et al. Edge-preserving decompositions for multi-scale tone and detail manipulation[J]. ACM transactions on graphics, 2008, 27(3): 67. (  0) 0)
|
| [13] |
LAI Weisheng, HUANG Jiabin, HU Zhe, et al. A comparative study for single image blind deblurring[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, USA: IEEE, 2016: 1701-1709.
(  0) 0)
|
| [14] |
叶盛楠, 苏开娜, 肖创柏, 等. 基于结构信息提取的图像质量评价[J]. 电子学报, 2008, 36(5): 856-861. YE Shengnan, SU Kaina, XIAO Chuangbai, et al. Image quality assessment based on structural information extraction[J]. Acta electronica sinica, 2008, 36(5): 856-861. DOI:10.3321/j.issn:0372-2112.2008.05.005 (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


