跳频信号通信频率受跳频图案控制,随时间不断改变,所以其具有出色的抗干扰性能和抗截获性能,多数应用在民用无人机上行数据链以及军用通信数据链中,因此跳频信号的频谱感知在认知无线电以及军用侦察领域应用广泛。然而多数研究集中于定频信号的频谱感知问题,对于跳频信号的研究较少,所以跳频信号感知模型的建立和理论分析是比较重要的问题。
自Mitola[1]提出认知无线电的概念,作为其核心技术,频谱感知能有效地识别授权用户信号是否存在,为次级用户接入提供先验信息,从而提高频谱利用率。Urkowitz[2]基于能量检测提出了确定性信号在高斯白噪声下的感知方法,该方法不需要任何先验信息,计算简单但受噪声影响较大,而且实际接收信号往往为不确定性信号,所以适用性并不强。Digham等[3]在上述研究基础上探究了能量检测在Rayleigh、Nakagami等多径衰落信道的感知性能,并通过组合和分集等方式来提升感知性能,但该研究仍针对确定性信号。基于接收信号的随机性与不确定性,Atapattu等[4]提出不确定性信号能量感知方法,在平坦衰落信道下得到了检测概率的数学表达式,并推导了在低信噪比下的渐进最优门限。
Djurović等[5-7]针对非平稳信号提出一种基于S方法以及Wigner-Ville分布的感知方法,并通过蒙特卡洛仿真得出其感知性能。Shaghayegh等[8]基于时频分析以及压缩感知技术进行感知,在保持一定感知性能的同时降低了信号在时频平面的采样率。颜雨等[9]根据滑动相关判断跳频信号出现区域,在初步确定跳频区域后再利用小波变换进行精确搜索,从而实现跳频信号检测。张萌等10]利用HOG特征提取和SVM支持向量机实现跳频信号的检测,但机器学习的方法针对性强,检测环境的变化会给训练模型带来较大的影响。刘旭波等[11-12]以传统的功率谱分段对消方法作为研究基础,通过构造阈值判决参数实现跳频信号检测,并可以在一定程度上减弱干扰信号产生的影响。郑洋等[13]通过小波变换去除信号背景噪声,并利用希尔伯特-黄变换实现跳频信号检测。但上述研究均通过蒙特卡洛仿真得到某个检测阈值或门限,且需要已知跳频图案或跳频速率等参数,在实际应用中需根据不同的检测环境分别进行仿真,计算量大、特异性强,且复杂度较高。
基于上述问题,本文针对跳频信号建立了感知数学模型,并利用了短时傅里叶变换方法,在不能同步跳频图案的情况下同时对跳点位置以及信号存在性进行感知。此外,本文在AWGN、Rayleigh和Nakagami-m 3种不同衰落信道下推导了检测概率和虚警概率的理论闭环表达式,提供了跳频信号在不同衰落信道下感知的理论基础,并通过最小化误差概率得到最优门限,最终通过仿真结果验证了其正确性。
1 跳频信号频谱感知数学模型频谱感知即一个二元假设问题,包含2个假设:假设H1为主用户信号存在,假设H0为主用户信号不存在。则接收信号y(n)的二元假设表示为:
| $ y(n)=\left\{\begin{array}{ll} w(n), & H_{0} \\ h x(n)+w(n), & H_{1} \end{array}\right. $ | (1) |
式中:x(n)为主用户信号;h为无线信道增益;w(n)为满足零均值,方差为σw2的加性高斯白噪声。当信号x(n)为未知形式时(假定为PSK信号),一般被认为服从零均值,方差为σs2的高斯分布。则若给定信道增益h,则接收机的瞬时信噪比γ=|h|2σs2/σw2。
本文考虑AWGN、Rayleigh衰落和Nakgami-m衰落信道,这3种衰落可以对实际无线信道中变化的衰落影响进行建模。若无线信道增益h满足Nakagami-m分布且接收信号平均信噪比为
| $ f_{\lambda \mathrm{Nak}}(x)=\frac{(m / \bar{\gamma})^{m}}{\varGamma(m)} x^{m-1} \mathrm{e}^{-\frac{m}{\bar{\gamma}}^{\gamma}} $ | (2) |
若主用户信号x(n)为跳频信号,其离散形式数学表达式为:
| $ x(n) = d(n) \cdot \cos \left[ {2{\rm{ \mathsf{ π} }}\left( {{f_0} + {f^\prime }} \right)/{f_s} + {\varphi _n}} \right] $ | (3) |
式中:d(n)为调制信号;f0为跳频起始频率;f′=[f1, f2, …,fN](N=1, 2, 3,…)为跳频频率集;fs为采样率;φn为初始相位。
跳频信号与定频信号相比,在通信频带内存在多个通信频段,并且通信频段在时间轴上以某种规律变化。在H1假设下,若某跳频信号瞬时跳点在fj(fj∈f′)处,感知出的跳点在fi(fi∈f′)处,则在给定信道衰落h后,平均检测概率
| $ \bar{P}_{d}=\int_{-\infty}^{\infty} P\left\{(i=j), \varLambda \geqslant \lambda \mid\left(H_{1}, \gamma\right)\right\} f(\gamma) \mathrm{d} \gamma $ | (4) |
式中:Λ为某感知算法构造的检测统计量;λ为该算法的感知门限。因为事件i=j和事件Λ≥λ二者相互独立,所以式(4)可以展开为:
| $ \begin{array}{c} \bar{P}_{d}=\int_{-\infty}^{\infty} P\{(i=j) \mid(H, \gamma)\} \cdot\\ P\{(\varLambda \geqslant \lambda) \mid(H, \gamma)\} f(\gamma) \mathrm{d} \gamma \end{array} $ | (5) |
在H0假设下,由于仅存在噪声,所以信道衰落无影响,虚警概率Pf表示为:
| $ P_{f}=P\left\{(\varLambda \geqslant \lambda) \mid H_{0}\right\} $ | (6) |
若给定信号x(t)∈L2(R),则连续时间短时傅里叶变换定义为:
| $ \begin{array}{l} {{\mathop{\rm STFT}\nolimits} _x}(t,f) = \int_{ - \infty }^\infty x (\tau ) \cdot {g^*}(\tau - t){{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}ft}}{\rm{d}}\tau = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\langle {x(\tau ),g(\tau - t){{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}ft}}} \right\rangle \end{array} $ | (7) |
式中:g(τ)为窗函数而且一般取对称函数,且‖g(τ)‖=1。
对于离散信号,若对连续信号采样时间为Δt,则式(7)又可表示为:
| $ \begin{array}{*{20}{c}} {{{{\mathop{\rm STFT}\nolimits} }_x}(t,f) = \int_{ - \infty }^\infty x (\tau ) \cdot {g^*}(\tau - t){{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}ft}}{\rm{d}}\tau \approx }\\ {\sum\limits_{m = - \infty }^\infty x (m\Delta t){g^*}((m - n)\Delta t){{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}m\Delta tf}}\Delta t} \end{array} $ | (8) |
令x(n)=x(nΔt), w=2πfΔt,则离散形式短时傅里叶变换表示为:
| $ \operatorname{STFT}_{x}(n, \omega)=\sum\limits_{m=-\infty}^{m=\infty} x(m) g^{*}(m-n) \mathrm{e}^{-\mathrm{j} m \omega} $ | (9) |
对式(9)等号两端分别取平方,可得:
| $ \begin{aligned} \left|\operatorname{STFT}_{x}(n, \omega)\right|^{2}=&\left|\sum\limits_{m=-\infty}^{m=\infty} x(m) g^{*}(m-n) \mathrm{e}^{-\mathrm{j} m \omega}\right|^{2}=\\ & S_{x}(n, \omega) \end{aligned} $ | (10) |
式中Sx(n, ω)称为谱图,表示信号能量的分布。
2.2 算法描述根据式(1)中主用户信号模型及式(9)短时傅里叶变换定义可得,在H0假设下,由于仅存在噪声,所以接收信号y(n)的谱图表示为:
| $ \begin{aligned} S_{H_{0}}(n, \omega)=&\left|\mathrm{STFT}_{H_{0}}\right|^{2}=\left|\operatorname{STFT}_{H_{0}}(n, \omega)\right|^{2}=\\ &\left|\sum\limits_{m=-\infty}^{\infty} \omega(m) g^{*}(m-n) \mathrm{e}^{-\mathrm{j} m \omega}\right|^{2} \end{aligned} $ | (11) |
在H1假设下,接收信号y(n)的短时傅里叶变换表示为:
| $ \begin{array}{l} S_{H_{1}}(n, \omega)=\left|\operatorname{STFT}_{H_{1}}\right|^{2}=\left|\operatorname{STFT}_{H_{1}}(n, w)\right|^{2}= \\ \quad\left|\sum\limits_{m=-\infty}^{\infty}[x(m)+\omega(m)] g^{*}(m-n) \mathrm{e}^{-\mathrm{j} m \omega}\right|^{2} \end{array} $ | (12) |
根据时频分布的能量性质,信号在固定时频区域内的能量可以表示为:
| $ E=\sum\limits_{\omega=\omega_{1}}^{\omega_{2}} \sum\limits_{n_{1}}^{n_{2}} S(n, \omega) $ | (13) |
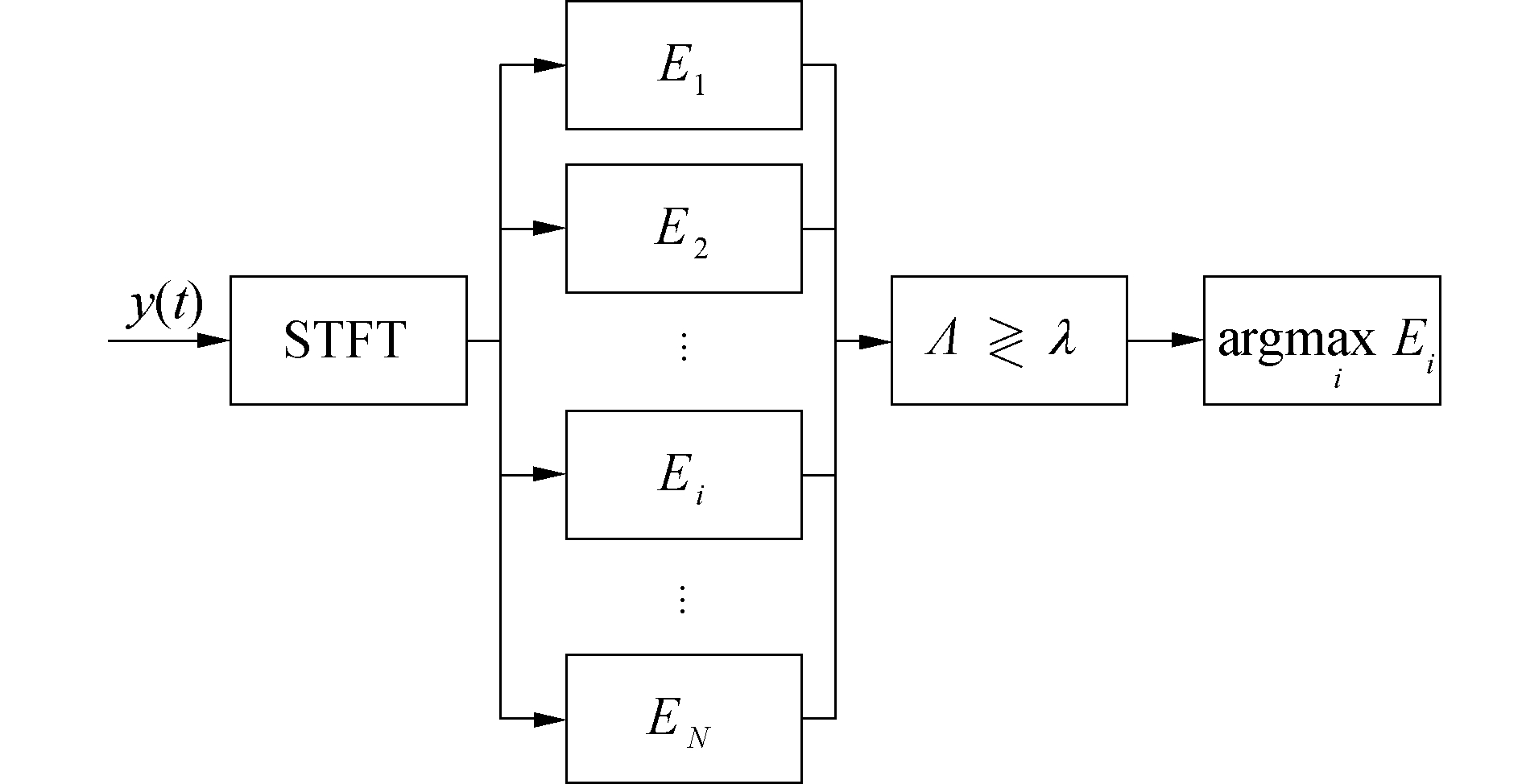
式中:[ω1, ω2]为待感知跳点频率区间;[n1, n2]为时间区间。由式(10)可知谱图为短时傅里叶变换模值的平方,所以SH1(n, ω)>SH0(n, ω)恒成立,因此E|H1>E|H0也恒成立。则可利用信号在固定时频区域的累积能量对跳点位置和存在性进行检测,其流程如图 1所示。
|
Download:
|
| 图 1 基于STFT的跳频信号频谱感知方法流程 Fig. 1 Diagram of spectrum sensing of frequency hopping signals based on STFT | |
首先对接收信号y(n)进行短时傅里叶变换,然后在固定时间区域[n1, n2], Δn=n2-n1内,分别对个跳点所在频率区域[ω2i-1, ω2i], Δω=ω2i-ω2i-1的谱图求和,设检测统计量Λ=max(Ei),并与检测门限对比进行存在性检测,若确定信号存在,之后根据能量最大值所在频率区域确定跳点。
注意,需满足[ω2i-1, ω2i]∩[ω2i+1, ω2i+2]=
在H0和H1 2种假设下,接收信号y(n)均服从独立高斯分布,由于短时傅里叶变换为线性变换,所以其变换结果仍服从独立高斯分布。
在H0假设下,STFTH0的数学期望和方差可分别表示为:
| $ \left.\mathrm{E}\left[\mathrm{STFT}_{H_{0}}\right]=\mathrm{E}\left[\sum\limits_{m=-\infty}^{\infty} \omega(m) g^{*}(m-n) \mathrm{e}^{-\mathrm{j}m\omega}\right]\right]=0 $ | (14) |
| $ \begin{array}{c} \mathrm{E}\left[\sum\limits_{u=-\infty}^{\infty} \omega(u) g^{*}(u-n) \mathrm{e}^{-\mathrm{j} u \omega} \sum\limits_{v=-\infty}^{\infty} \omega^{*}(v) g(v-n) \mathrm{e}^{\mathrm{j} v \omega}\right]= \\ \sum\limits_{v=-\infty }^{\infty} \sum\limits_{u=-\infty}^{\infty}(u-n) g(v-n) \mathrm{e}^{\mathrm{j} \omega(v-u)} \delta(u-v) \sigma_{\omega}^{2}= \\ \sigma_{\omega}^{2}\|g(u-n)\|=\sigma_{\omega}^{2} \end{array} $ | (15) |
根据式(14)和(15)可得,STFTH0服从零均值,方差为σω2的复高斯分布,根据随机变量的函数关系可得,能量Ei服从自由度为M=ΔωΔn2/2πΔt的中心卡方分布。当M数值比较大时,根据中心极限定理,能量可以渐进认为服从均值为Mσω2,方差为2Mσω4的高斯分布。虚警概率Pf在AWGN信道与平坦衰落信道2种信道中相同,表示为:
| $ \begin{aligned} P_{f}=P\{(\varLambda&\left.\geqslant \lambda) \mid H_{0}\right\}=P\left\{\left(\max \left(E_{i}\right) \geqslant \lambda\right) \mid H_{0}\right\}=\\ 1 &-P\left\{\left(\max \left(E_{i}\right)<\lambda\right) \mid H_{0}\right\}=\\ & 1-\prod\limits_{i=1}^{N} P\left\{\left(E_{i}<\lambda\right) \mid H_{0}\right\}=\\ 1-& \prod\limits_{i=1}^{N}\left(1-P\left\{\left(E_{i} \geqslant \lambda\right) \mid H_{0}\right\}\right)=\\ & 1-Q^{N}\left(\frac{M \sigma_{\omega}^{2}-\lambda}{\sqrt{2 M} \sigma_{\omega}^{2}}\right)=\xi_{1}^{N}(\lambda) \end{aligned} $ | (16) |
式中:
| $ \lambda=\sigma_{\omega}^{2}\left[M-\sqrt{2 M} Q^{-1}\left(\sqrt[N]{1-p_{f}}\right)\right] $ | (17) |
在H1假设下,在非第j个跳点的时频区域内,均可视为假设,即只有第j个跳点所在时频区域内为H1假设。STFTH1的数学期望同式(14)可轻易求得为零,方差可表示为:
| $ \begin{array}{c} \operatorname{Var}\left[\mathrm{STFT}_{H_{1}}\right]=\mathrm{E}\left[\mathrm{STF} \mathrm{T}_{H_{1}}^{2}\right]-\mathrm{E}\left[\mathrm{STFT}_{H_{1}}\right]^{2}= \\ \mathrm{E}\left\{\sum\limits_{u=-\infty}^{\infty}[x(u)+\omega(u)] g^{*}(u-n) \mathrm{e}^{-\mathrm{j} u \omega} \cdot\right. \\ \left.\sum\limits_{v=-\infty}^{\infty}\left[x^{*}(v)+\omega^{*}(v)\right] g(v-n) \mathrm{e}^{-\mathrm{j} v \omega}\right\}=\\ \sum\limits_{v=-\infty}^{\infty} \sum\limits_{u=-\infty}^{\infty} g^{*}(u-n) g(v-n) \mathrm{e}^{\mathrm{j} \omega(v-u)} \mathrm{E}\left[x(u) x^{*}(v)+\right. \\ \left.x(u) \omega^{*}(v)+\omega(v) x^{*}(u)+\omega(u) \omega^{*}(v)\right]= \\ \left(\sigma_{\omega}^{2}+\sigma_{s}^{2}\right)\|g(u-n)\|=\sigma_{\omega}^{2}+\sigma_{s}^{2} \end{array} $ | (18) |
根据式(18)可得,STFTH1服从零均值,方差为σω2+σs2的复高斯分布。根据中心极限定理可得,能量Ei渐进满足均值为
| $ \begin{array}{c} P_{1}=P\left\{(\varLambda \geqslant \lambda) \mid H_{1}\right\}= \\ 1-Q^{N}\left(\frac{M \sigma_{\omega}^{2}(1+\gamma)-\lambda}{\sqrt{2 M} \sigma_{\omega}^{2}(1+\gamma)}\right)=1-\xi_{2}^{N}(\lambda, \gamma) \end{array} $ | (19) |
P2为感知出的跳点与真实跳点相符时的概率,在前文提出的算法下,其可以表述为:
| $ \begin{array}{*{20}{c}} {{P_2} = P\left\{ {\arg \mathop {\max }\limits_i {E_i} = j} \right\} = P\left\{ {{E_i} < {E_j},i \ne j} \right\} = }\\ {\prod\limits_{i \ne j} P \left\{ {{E_i} < {E_j}} \right\}\mathop \to \limits^{z = {E_j} - {E_i}} \prod\limits_{i \ne j} {\left\{ {{z_i} > 0} \right\}} = }\\ {{P^{N - 1}}\left\{ {{z_i} > 0} \right\}} \end{array} $ | (20) |
根据高斯变量的函数关系,可求得zi满足均值为
| $ \begin{array}{c} P_{2}=P^{N-1}\left\{z_{i}>0\right\}= \\ Q^{N-1}\left(-\sqrt{\frac{M \gamma^{2}}{2\left(1+(1+r)^{2}\right)}}\right)=\xi_{3}^{N-1}(\gamma) \end{array} $ | (21) |
在H1假设下,检测概率由Pd=P1P2可求得。
3.2 衰落信道下感知性能分析虚警概率Pf与AWGN信道下相同,见式(16)。
因为无线信道中存在衰落,根据式(19)和式(21)则在H1假设下,检测概率
| $ \begin{array}{c} \bar{P}_{d}^{\mathrm{NaK} }=\int_{0}^{\infty} P_{1}(\gamma) \cdot P_{2}(\gamma) f_{\gamma \mathrm{NaK}}(\gamma) \mathrm{d} \gamma= \\ \frac{(m / \bar{r})}{\varGamma(m)} \int_{0}^{\infty} \gamma^{m-1} \mathrm{e}^{-\frac{m}{\gamma} \gamma}\left[1-\xi_{2}^{N}(\lambda, \gamma)\right] \xi_{3}^{N-1}(\gamma) \mathrm{d} \gamma \end{array} $ | (22) |
当衰落系数m=1时,Nakagami-m分布退化为Rayleigh分布,检测概率
| $ \begin{array}{c} \bar{P}_{d}^{\mathrm{NaK}}=\int_{0}^{\infty} P_{1}(\gamma) P_{2}(\gamma) f_{\gamma \text { Ray }}(\gamma) \mathrm{d} \gamma= \\ \frac{1}{\gamma} \int_{0}^{\infty} \mathrm{e}^{-\frac{1}{\bar{\gamma}} \gamma}\left[1-\xi_{2}^{N}(\lambda, \gamma)\right] \xi_{3}^{N}(\gamma) \mathrm{d} \gamma \end{array} $ | (23) |
频谱感知往往通过误差概率来评价误差性能,误差概率Pe(λ)定义为:
| $ \begin{aligned} P_{e}(\lambda)=& P_{f}(\lambda)+P_{m d}(\lambda)=1+P_{f}(\lambda)-P_{d}(\lambda)=\\ & 2-\xi_{1}^{N}(\lambda)-\xi_{3}^{N}\left(1-\xi_{2}^{N}(\lambda)\right) \end{aligned} $ | (24) |
最优门限λ*为误差概率达到最小值时的门限:
| $ {\lambda ^*} = \arg \mathop {min}\limits_\lambda {P_e}(\lambda ) $ | (25) |
当λ=λ*时,误差概率Pe(λ)对门限λ的偏导数
| $ \frac{{N\xi _3^{N - 1}\xi _2^{N - 1}(\lambda ){{\rm{e}}^{ - \frac{{{v^2}}}{2}}}}}{{\sqrt {2M} \sigma _\omega ^2(1 + \lambda )}} = \left. {\frac{{N\xi _1^{N - 1}(\lambda ){{\rm{e}}^{ - \frac{{{u^2}}}{2}}}}}{{\sqrt {2M} \sigma _\omega ^2}}} \right|_{u = \frac{{M\sigma _\omega ^2 - \lambda }}{{\sqrt {2M} \sigma _\omega ^2}}}^{v = \frac{{M\sigma _\omega ^2(1 + \lambda ) - \lambda }}{{\sqrt {2M} \sigma _\omega ^2(1 + \lambda )}}} $ | (26) |
式(26)为超越方程不能求出常规解,只能通过Matlab等数学工具进行数值分析求解。考虑当
| $ \begin{array}{c} \left(\gamma^{2}+2 \gamma\right) \lambda^{2}-2 M \sigma_{\omega}^{2}\left(\gamma^{2}+\gamma\right) \lambda- \\ 4 M \sigma_{\omega}^{4}(1+\gamma)^{2} \ln \left(\frac{1+\gamma}{\xi_{3}^{N-1}}\right)=0 \end{array} $ | (27) |
由于门限λ恒大于零,舍掉负数解,最终得到最优门限λ*表达式为:
| $ \lambda^{*}=\frac{\gamma+1}{\gamma+2} M \sigma_{\omega}^{2}\left[1+\sqrt{1+4 M^{-1}\left(1+2 \gamma^{-1}\right) \ln \left(\frac{1+\gamma}{\xi_{3}^{N-1}}\right)}\right] $ | (28) |
由于假设
| $ \lambda^{*}=M \sigma_{\omega}^{2}\left[1+\sqrt{1-4 M^{-1}\left(1+2 \gamma^{-1}\right) \ln \left(\frac{1+\gamma}{\xi_{3}^{N-1}}\right)}\right] $ | (29) |
在Nakagami-m衰落信道下,同式(25)求偏导为零时的最优门限,可得:
| $ \int_{0}^{\infty} \psi(\gamma) \frac{N \xi_{3}^{N-1} \xi_{2}^{N-1}(\lambda, \gamma) \mathrm{e}^{-\frac{v^{2}}{2}}}{\sqrt{2 M} \sigma_{\omega}^{2}(1+\lambda)} \mathrm{d} \gamma=\frac{N \xi_{1}^{N-1}(\lambda) \mathrm{e}^{-\frac{u^{2}}{2}}}{\sqrt{2 M} \sigma_{\omega}^{2}} $ | (30) |
式中:
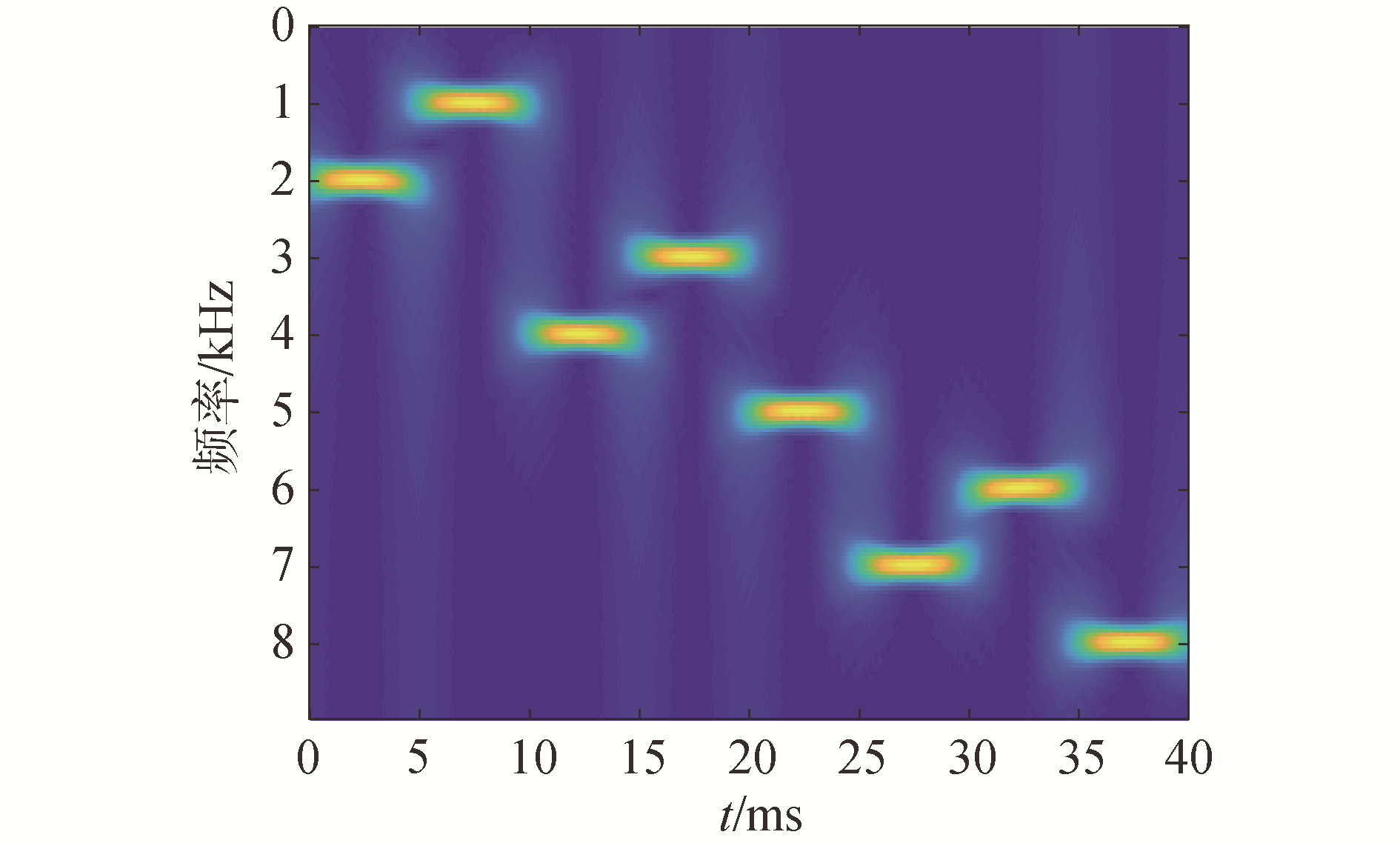
图 2为仿真信源FH-BPSK信号经过短时傅里叶变换得到的谱图。仿真条件为:跳点N=8,码元速率Rb=200 bd,采样率fs=18 kHz,跳速5 ms。
|
Download:
|
| 图 2 FH-BPSK信号的谱 Fig. 2 Spectrogram of FH-BPSK signals | |
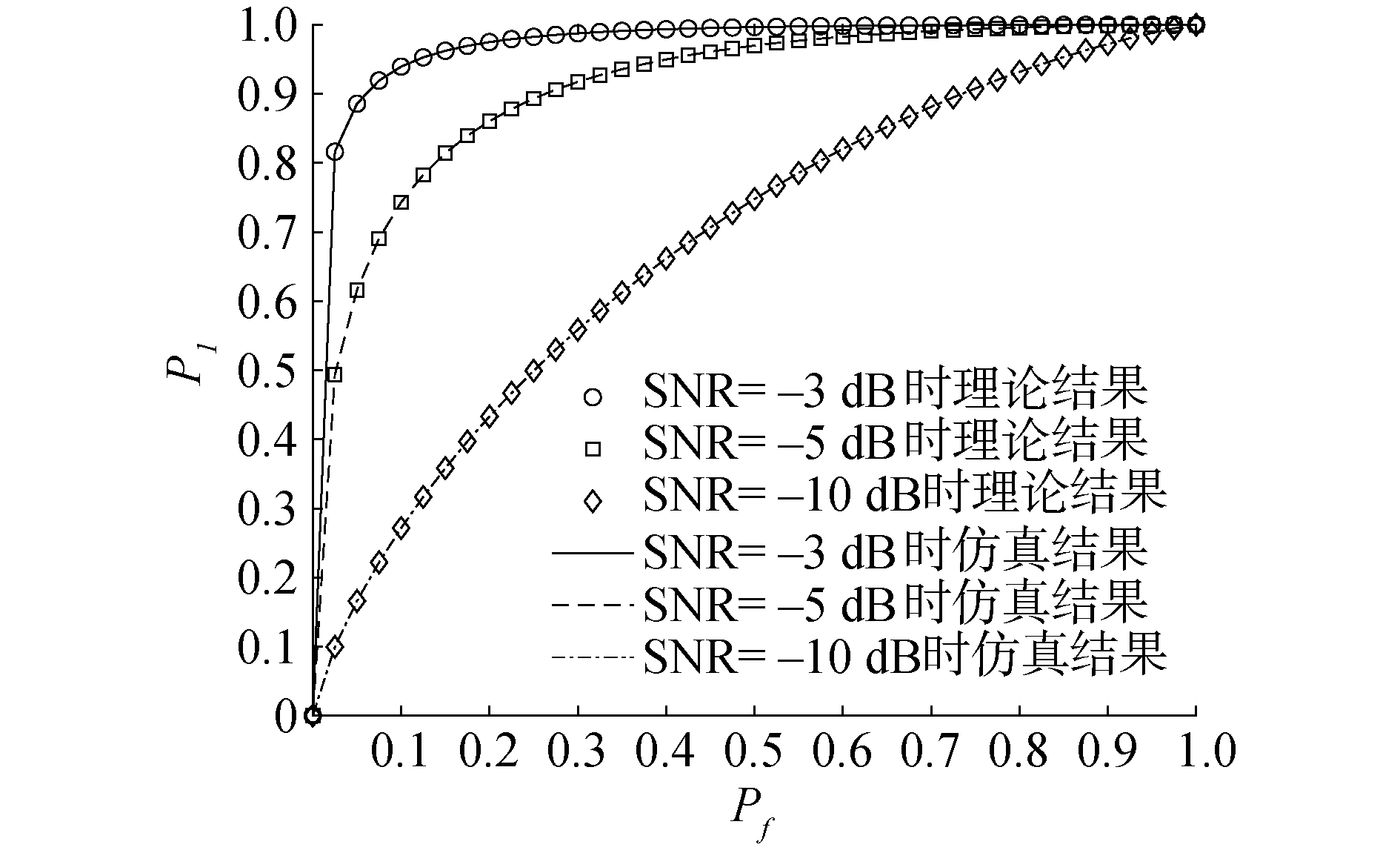
图 3为AWGN信道下概率P1与虚警概率Pf在3种不同信噪比下的理论与仿真ROC曲线。仿真条件:检测点数M=16,蒙特卡洛仿真次数5 000。其余条件上同。由图可见理论曲线和仿真曲线较好地重合,证明了理论推导的正确性。随着虚警概率Pf由0增长到1,概率P1体现出相同的变化趋势。
|
Download:
|
| 图 3 AWGN信道下Pf与Pf的理论与仿真曲线 Fig. 3 Curves of Pf and Pf of theory and simulations under AWGN channels | |
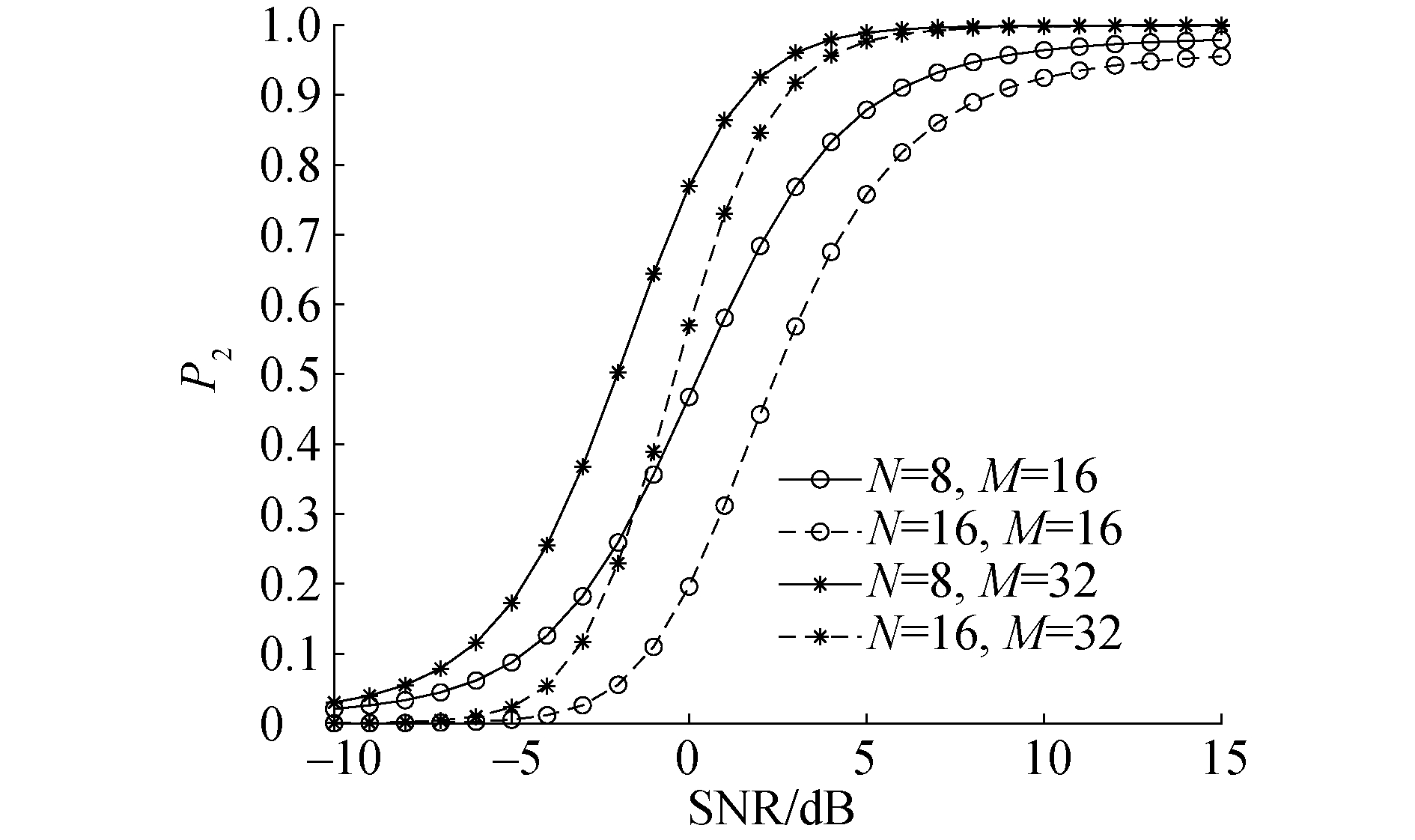
图 4为AWGN信道下跳点检测概率P2与虚警概率Pf在不同检测点数和跳点数下的关系曲线。跳点概率P2仅仅与信噪比有关,随着信噪比的增大,概率N=8, M=32逐渐增长到1。当N=8, M=32时,信噪比取5 dB即可以0.98左右的概率水平确定跳点位置。当检测点数确定之后,跳点个数的提升也会明显降低跳点位置检测概率,但通过增加检测点数可以有效地提升P2。例如当信噪比仍取5 dB时,当检测点数为32时,跳点数为16点的概率与跳点数为8点的概率接近;而在检测点数为16时二者却相差0.15左右。
|
Download:
|
| 图 4 AWGN信道下Pd=P1·P2与SNR的关系曲线 Fig. 4 Curves of Pd=P1·P2 and SNR under AWGN Channels | |
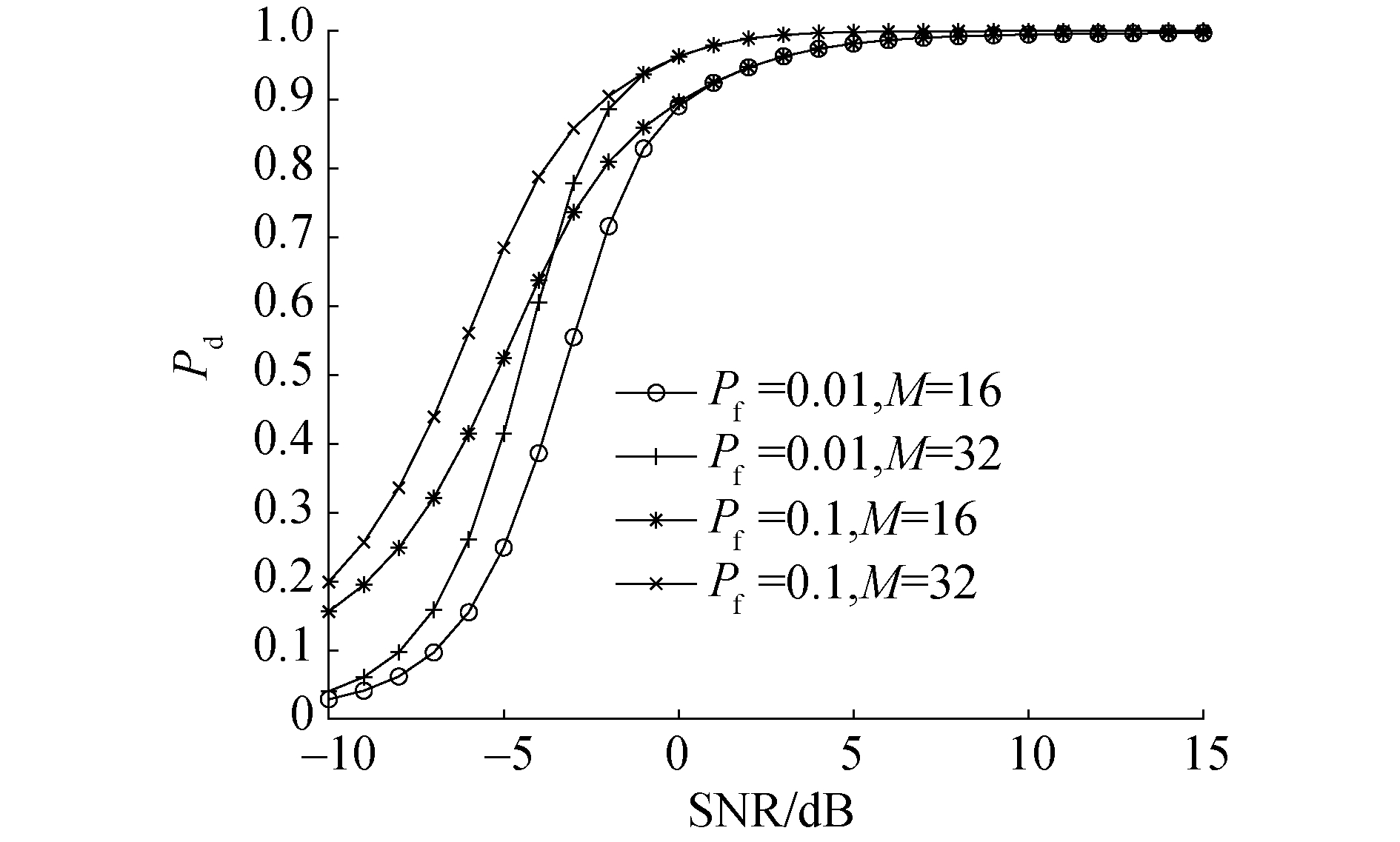
图 5为AWGN信道下检测概率Pd=P1P2与信噪比SNR的ROC曲线。检测概率同时受2个概率的影响,最终随信噪比的增大趋近于1。在信噪比小于0 dB时,相同的检测点数下,检测概率在虚警概率水平较低时明显较低。但当信噪比大于0 dB时检测概率基本不受虚警概率影响。信噪比在0~10 dB时检测概率仍受检测点数增大而增大,在10 dB以上即处于较高信噪比水平时检测概率最终均趋近于1。
|
Download:
|
| 图 5 AWGN信道下M=16与SNR的ROC曲线 Fig. 5 ROC curves of M=16 and SNR under AWGN channels | |
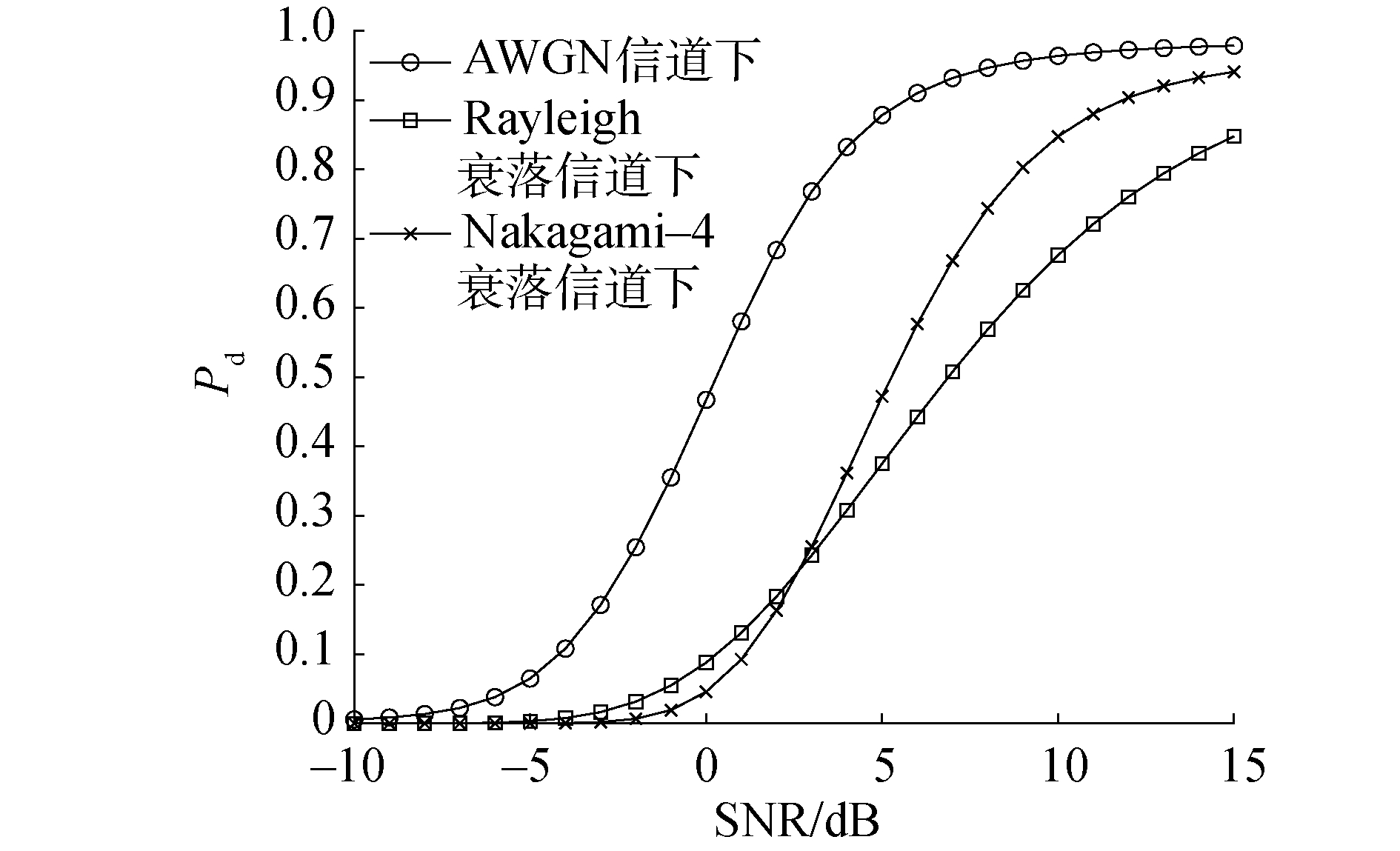
图 6为当检测点数M=16且虚警概率Pf=0.1时检测概率与信噪比在3种衰落信道下的ROC曲线。在如图所示的信噪比区间(-10 dB~15 dB),检测概率在AWGN信道的性能高于Nakgami-4衰落信道以及Rayleigh衰落信道,说明信道衰落会引起检测性能的下降。当信噪比取10 dB时,在AWGN信道下,虽然检测点数较低,但检测概率已逼近于1;在Nakagami-4衰落信道下,由于受到衰落影响,检测概率在0.85左右;而Rayleigh作为较为严重的衰落,检测概率在0.7左右,已经明显低于对于信号感知概率的标准。
|
Download:
|
| 图 6 衰落信道下M=1 000与SNR的ROC曲线 Fig. 6 ROC Curves of M=1 000 and SNR of under fading channels | |
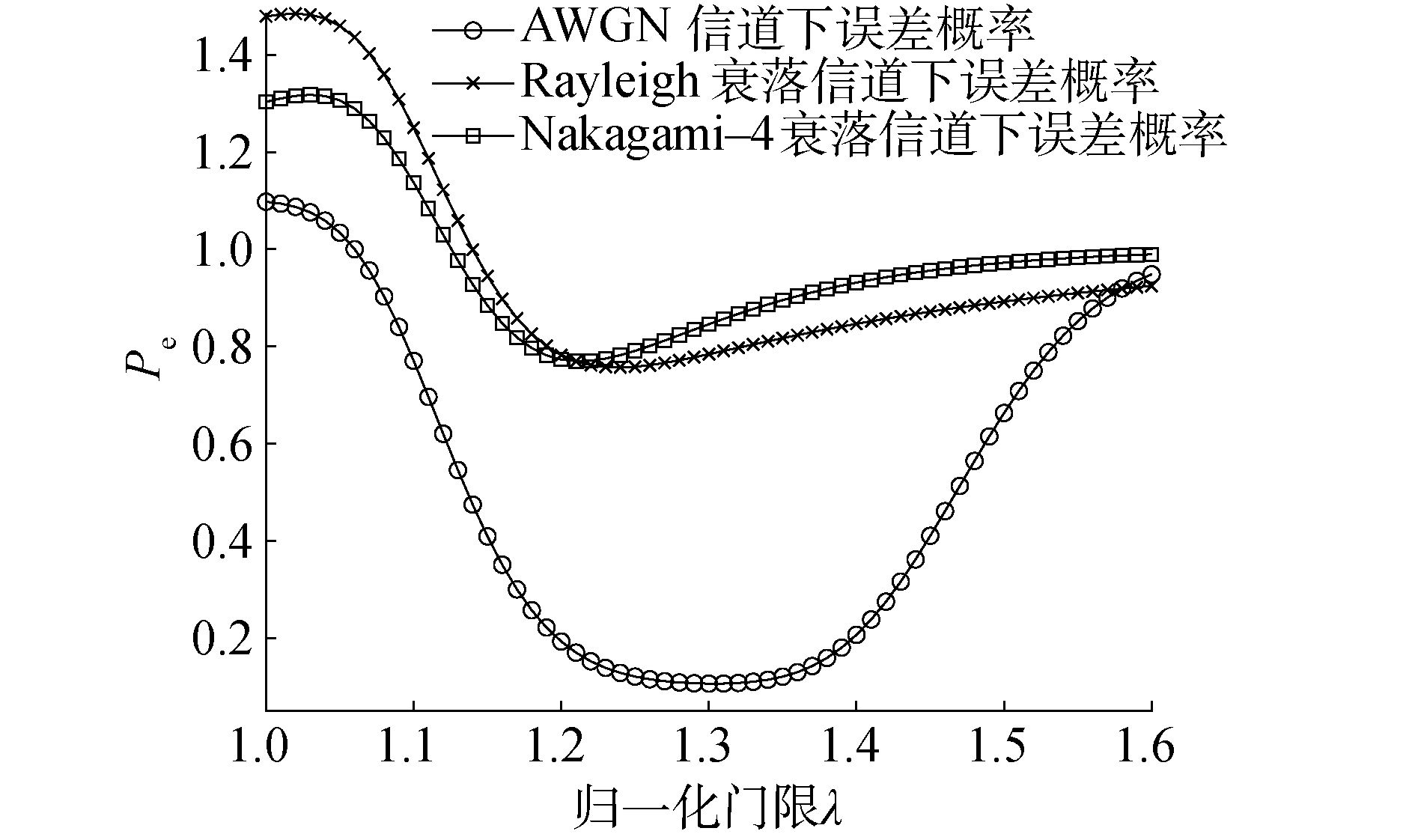
图 7为当检测点数M=1 000且信噪比为-5 dB时误差概率Pe与经过检测点数M归一化后的门限λ的关系曲线。由图可得,随着归一化门限由小到大增长的过程,3种信道下的误差概率都会逐渐降低,然后再升高,在某一门限取值上达到最优的误差概率。在Nakagami-4和Rayleigh衰落下,最优归一化门限均在1.2左右,而AWGN信道下该门限在1.3左右;前2种衰落引起的错误概率均在0.8左右,后者引起的错误概率在0.15左右,与式(30)验证结果基本相符。
|
Download:
|
| 图 7 衰落信道下Pe与归一化门限λ的ROC曲线 Fig. 7 ROC Curves of Pe and the normalized threshold λ under fading channels | |
1) 在对实际无线信道环境建立的3种不同衰落信道模型下,本文通过数学推导得出了检测概率和虚警概率的闭环表达式。
2) 通过最小化误差概率的方法得到了最优门限求解公式,提供了跳频信号在衰落信道下感知的理论依据。
3) 通过Matlab仿真工具对3种衰落信道下的概率曲线进行仿真,验证了其检测性能和理论正确性。
| [1] |
MITOLA J, MAGUIRE G Q. Cognitive radio: making software radios more personal[J]. IEEE personal communications, 1999, 6(4): 13-18. DOI:10.1109/98.788210 (  0) 0)
|
| [2] |
URKOWITZ H. Energy detection of unknown deterministic signals[J]. Proceedings of the IEEE, 1967, 55(4): 523-531. DOI:10.1109/PROC.1967.5573 (  0) 0)
|
| [3] |
DIGHAM F F, ALOUINI M S, SIMON M K. On the energy detection of unknown signals over fading channels[J]. IEEE transactions on communications, 2007, 55(1): 21-24. DOI:10.1109/TCOMM.2006.887483 (  0) 0)
|
| [4] |
ATAPATTU S, TELLAMBURA C, JIANG Hai. Spectrum sensing via energy detector in low SNR[C]//Proceedings of the 2011 IEEE International Conference on Communications. Kyoto, 2011: 1-5.
(  0) 0)
|
| [5] |
GUIBÈNE W, HAYAR A. Joint time-frequency spectrum sensing for Cognitive Radio[C]//Proceedings of the 2010 3rd International Symposium on Applied Sciences in Biomedical and Communication Technologies (ISABEL 2010). Rome, 2010: 1-4.
(  0) 0)
|
| [6] |
DJUROVIĆI, STANKOVIĆL. Time-frequency representation based on the reassigned S-method[J]. Signal processing, 1999, 71(1): 115-120. (  0) 0)
|
| [7] |
JAVED F, MAHMOOD A. The use of time frequency analysis for spectrum sensing in cognitive radios[C]//Proceedings of 2010 4th International Conference on Signal Processing and Communication Systems. Gold Coast, QLD, 2010: 1-7.
(  0) 0)
|
| [8] |
MONFARED S S M, TAHERPOUR A, KHATTAB T. Time-frequency compressed spectrum sensing in cognitive radios[C]//Proceedings of 2013 IEEE Global Communications Conference (GLOBECOM). Atlanta, GA, 2013: 1088-1094.
(  0) 0)
|
| [9] |
颜雨, 闫晓峰, 吴治霖. 一种复杂环境中跳频信号检测和参数估计改进方法[J]. 通信技术, 2020, 53(3): 572-577. YAN Yu, YAN Xiaofeng, WU Zhilin. Modified method for FH signal detection and parameter estimation in complex environment[J]. Communications technology, 2020, 53(3): 572-577. DOI:10.3969/j.issn.1002-0802.2020.03.007 (  0) 0)
|
| [10] |
张萌, 王文, 任俊星, 等. 基于HOG-SVM的跳频信号检测识别算法[J]. 信息安全学报, 2020, 5(3): 62-77. ZHANG Meng, WANG Wen, REN Junxing, et al. Detection and recognition algorithm for frequency hopping signals based on HOG-SVM[J]. Journal of cyber security, 2020, 5(3): 62-77. (  0) 0)
|
| [11] |
刘旭波. 基于功率谱分段对消算法的跳频信号检测[J]. 自动化技术与应用, 2017, 36(11): 69-73. LIU Xubo. Frequency hopping signal detection based on power spectrum cancellation algorithm[J]. Techniques of automation and applications, 2017, 36(11): 69-73. (  0) 0)
|
| [12] |
李敏. 关于无人机旋翼信号识别方法的研究[J]. 电子测试, 2018(22): 36-38. LI Min. Research on identification method of UAV rotor signal[J]. Electronic test, 2018(22): 36-38. (  0) 0)
|
| [13] |
郑洋, 陈西豪, 朱锐, 等. 基于小波分解与希尔伯特-黄变换的跳频信号检测[J]. 传感器与微系统, 2017, 36(9): 132-135. ZHENG Yang, CHEN Xihao, ZHU Rui, et al. Frequency hopping signals detection based on wavelet decomposition and HHT[J]. Transducer and microsystem technologies, 2017, 36(9): 132-135. (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


