轻度认知障碍(mild cognitive impairment, MCI)为阿尔茨海默病(Alzheimer′s disease, AD)的前期阶段。目前全球约有5000万痴呆症患者,其中2/3是阿尔茨海默病,据预测,到2050年,痴呆的人口可能会增加到1.52亿[1]。阿尔茨海默病是一种致死性疾病,轻度认知障碍患者一旦转化为阿尔茨海默病则不可逆转。相比之下,轻度认知障碍患者由于大脑病变程度较低,通过治疗可以延缓甚至阻止其向不可逆的阿尔茨海默病转化。但是,轻度认知障碍临床诊断困难重重,仅从结构上的影像检查结果来看,患者的病变不明显;病理检测敏感度不高且实施难度大;而最常用的神经心理学测试也存在主观性较强的问题。因此,研究如何对轻度认知障碍进行准确可靠的计算机辅助诊断可以使更多轻度认知障碍患者得到早诊断和早治疗,从而降低阿尔茨海默病的发病率,在老龄人口急剧增长的今天尤为重要。
近年来,功能磁共振成像(functional magnetic resonance imaging, fMRI)技术的快速发展为大脑疾病的研究提供了思路。其中,静息态功能磁共振成像(resting-state functional magnetic resonance imaging, rs-fMRI)是诊断轻度认知障碍等神经退行性疾病的一种重要手段,它可以有效、无创、安全地检测大脑各脑区的激活状态,有助于对因神经退行性疾病或其他原因难以执行复杂任务患者的大脑功能进行研究[2]。
极限学习机(extreme learning machine, ELM)是一种基于前馈神经网络的学习算法,相较于传统算法,具有学习速度快、泛化能力强、准确率高的特点。研究发现,使用极限学习机对于处理不平衡的数据能产生相较于支持向量机(support vector machine, SVM)算法更好的分类效果,且在参数选择及学习速度上也有较为明显的优势,目前极限学习机逐渐被应用于多领域研究中[3-10]。
目前已有研究运用复杂网络理论,基于功能磁共振图像构建脑网络,通过分析大脑各脑区间功能上的关联,进行阿尔茨海默病或轻度认知障碍的辅助诊断。其中大部分研究[11-12]采用的都是支持向量机算法,但结果表明,支持向量机算法应用于复杂疾病的辅助诊断时准确率较低,且该算法由于需要设置参数等原因,耗时较长。Jongin Kim的团队曾将极限学习机算法应用于阿尔茨海默病和轻度认知障碍的辅助诊断,准确率相比于支持向量机算法均有一定提升,但该团队只分析了结构磁共振图像,其轻度认知障碍分类准确率仅为78.28% [13]。
为解决目前轻度认知障碍疾病辅助诊断方法准确率低、耗时长的问题,本文综合考虑脑网络和轻度认知障碍疾病的各种特性,选择大脑静息态的功能磁共振图像运用复杂网络理论进行分析,提出一种基于极限学习机算法的轻度认知障碍辅助诊断方法。
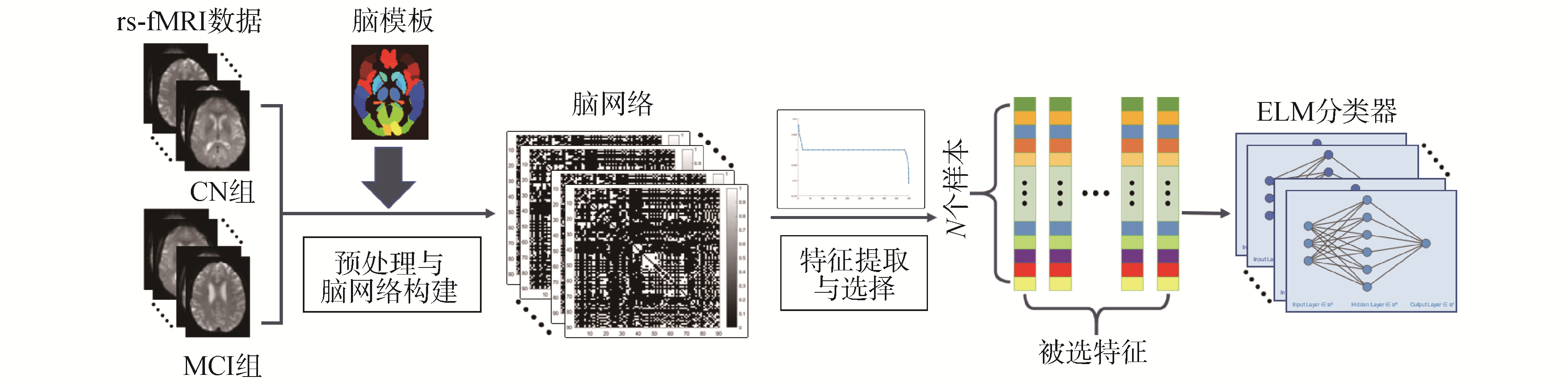
1 基于极限学习机的轻度认知障碍辅助诊断方法首先对静息态功能磁共振图像进行预处理,提取时间序列并构建脑网络,然后提取脑网络特征并进行特征选择,最后通过极限学习机算法训练分类模型并测试分类结果。基于极限学习机的轻度认知障碍辅助诊断过程如图 1所示。
|
Download:
|
| 图 1 基于极限学习机的轻度认知障碍辅助诊断过程 Fig. 1 Processing of computer-aided diagnosis of MCI based on ELM | |
对静息态功能磁共振图像进行预处理,其过程主要有以下5步:时间层校正、头动校正、噪声去除、空间标准化和平滑。对于每份预处理后的静息态功能磁共振图像,使用脑模板与其进行匹配,将大脑分割为大脑区和小脑区,常用的脑模板包括AAL(automated anatomical labeling)模板和Craddock模板。
将每个大脑区作为脑网络中的节点,求出所有节点的平均时间序列。把节点间的皮尔逊相关系数作为脑网络的边,从而得到相关矩阵,最后对相关矩阵进行阈值化得到脑网络。第k个被试的脑网络的节点i与节点j之间边的计算公式可表示为:
| $ r_{k}(i, j)=\frac{\sum\left(t_{i}-\bar{t}_{I}\right)\left(t_{j}-\bar{t}_{J}\right)}{\sqrt{\sum\left(t_{i}-\bar{t}_{I}\right)^{2} \sum\left(t_{j}-\bar{t}_{J}\right)^{2}}} $ | (1) |
式中:ti与tj分别为节点i与j的时间序列;tI与tJ分别是I与J节点的时间序列的平均值。
本文采用的阈值化方法是稀疏度阈值法,以脑网络的稀疏度作为阈值,通过阈值来控制矩阵中“0”与“1”的比例,得到不同阈值下的无权脑网络。
1.2 特征提取与选择本研究对构建好的脑网络进行网络分析,并提取出度中心性、介数中心性、聚类系数、效率、网页排名中心性、以及匹配特性6种特征,记为:F0={f1, f2, f3, f4, f5, f6}。
f1:度中心性。
节点的度是该节点与其他节点连接的边的个数,将度归一化可得度中心性,节点i的度中心性的定义为:
| $ f_{1}(i)=\frac{D_{i}}{N-1} $ | (2) |
式中:Di为节点i的度;N为网络中节点总数。
f2:介数中心性。
节点i介数中心性表现了该节点信息流向其他节点的效率,介数中心性越大表示该节点对网络中信息通信越重要。其定义为:
| $ f_{2}(i)=\sum\limits_{s \neq i \neq t} \frac{n_{s t}^{i}}{g_{s t}} $ | (3) |
式中:gst是指相隔的节点s与t之间存在的全部最短路径的条数;nsti表示这gst条路径中包含节点i的路径的数量。
f3:聚类系数。
节点i的聚类系数刻画了节点i与邻居节点聚集在一起的紧密程度。定义式为:
| $ f_{3}(i)=\frac{2 R_{i}}{k_{i}\left(k_{i}-1\right)} $ | (4) |
式中:Ri为节点i及其周边ki个临节点组成的网络的边数和。
为了表示整个网络节点的紧密程度,须将网络中的所有节点的聚类系数平均化,得到平均聚类系数。
f4:效率。
网络的效率衡量了网络中信息交换的效率。而针对节点i而言,则量化为i被移除时其邻居节点信息交流的效率,反映网络的局部信息传输能力。节点i的局部效率定义为:
| $ f_{4}(i)=\frac{1}{N_{G_{i}}\left(N_{G_{i}}-1\right)} \sum\limits_{i \neq k \in N_{G_{i}}} \frac{1}{d_{j k}} $ | (5) |
式中:Gi指节点i的邻居所构成的子图;NGi是子图中节点的个数;djk是节点j和节点k之间的最短路径长度。
f5:网页排名中心性。
网页排名中心性起初是用来根据网站的外部链接和内部链接的数量和质量来衡量网站的价值,该特征可以从概率的角度衡量一个节点在网络中的重要性。简而言之,某个节点的网页排名中心性越大,网络连接到该节点的可能性就越大,该节点在网络中的重要程度就越大。
| $ f_{5}(i)=\frac{1-\alpha}{N}+\alpha \sum\limits_{j \in N_{G i}} \frac{P R_{i}}{D_{j}^{\text {out }}} $ | (6) |
式中:α=0.85为常量;Djout是节点j的出度。
f6:匹配特性。
匹配特性是一个全局特征,计算了网络中所有节点度的相关系数,正向的匹配系数说明节点倾向于连接到具有一定相似程度的其他节点。
为了消除不同大脑间的个体随机差异,本方法计算匹配特性的标准分数:构造n个与样本脑网络节点数与边数相同的随机网络,计算它们的匹配特性,以及这些匹配特性的平均值u与方差σ,匹配特性的标准分数计算公式:
| $ f_{6}=\frac{A-u}{\sigma} $ | (7) |
其中A的计算式为:
| $ A=\frac{\left(\sum\limits_{i \in N} D_{i}\right)\left(2 \sum\limits_{i \neq j \in N} D_{i} D_{j}\right)-\left(\sum\limits_{i \in N} D_{i}^{2}\right)^{2}}{\left(\sum\limits_{i \in N} D_{i}\right)\left(\sum\limits_{i \in N} D_{i}^{3}\right)-\left(\sum\limits_{i \in N} D_{i}^{2}\right)^{2}} $ | (8) |
式中:Di为节点i的度;Dj为节点j的度;N为网络中节点总数。
需要注意的是,上述特征中,匹配特征f6是脑网络的全局特征,即每个脑网络只有一个取值,其余特征均是节点特征,即脑网络中的每一个节点都有一个取值。
在不同的阈值下,脑网络是不同的,从中提取出的特征值也不同。因此,为了综合考虑各个阈值下脑网络的特点,本文对于每个样本,计算一定阈值范围内所有脑网络的对应特征值,作出ROC曲线,以ROC曲线下面积作为最终从样本中提取出的特征集F'0。
计算出上述特征集F'0后,还需要进行特征选择,得到具有高区分度的特征子集F。此步骤对构建分类器至关重要,有效的特征选择能够降低数据处理量,节省时间,避免数据冗余,减轻噪声影响,有助于快速建立分类模型并提高分类效果。本文采用LASSO算子以实现特征选择。
1.3 基于极限学习机的轻度认知障碍辅助诊断 1.3.1 训练本文通过比较不同隐含层节点数和激活函数所得到的交叉验证准确率,最终选择准确率最高时的极限学习机参数作为训练步骤中的训练参数。
然后,将训练集的特征矩阵输入极限学习机中进行训练,如算法1所示。
算法1:训练极限学习机模型
//输入F, T, N, L, g(x):训练集特征矩阵、样本标签、样本数、隐含层节点数以及激活函数
//输出T:诊断结果
For i=1 to L Do
随机生成wi与b;
For i=1 to N Do
x=F[i];
For i=1 to L Do
For j=1 to N Do
H(i, j)=g(wi·xj+b);
β=TH-1;
return β
对于每一个隐含层节点,极限学习机会随机初始化权重wi和偏置项b,然后输入训练样本得到输出H,确定该隐含节点的输出权重β。式中g(x)是激活函数是满足极限学习机通用逼近能力定理得的非线性分段连续函数,常用的有sigmoid函数,tahn函数等。
与传统算法不同的是,极限学习机算法不需要在每次迭代的过程中不断地调整各项参数,而是在随机确定了输入权重wi和隐层的偏置b后,输出矩阵H就是唯一的,故其网络训练过程能够作为一个线性系统Hβ=T的求解,其最小二乘最优解即为输出权重:β=H†T。其中,“†”是矩阵的伪逆。
1.3.2 辅助诊断最后,上一步训练中得到了极限学习机模型中的各项参数。将待测样本的特征矩阵输入模型即可得到模型的预测T。如算法2所示。
算法2:测试极限学习机模型
//输入F, N, < wi, bi, L, β, g(x)>:测试集特征矩阵,样本数与极限学习机参数
//输出T:诊断结果
For i=1 to N Do
xj=F[i];
For i=1 to L Do
For j=1 to N Do
H(i, j)=g(wixj+b);
T=Hβ;
return T
算法中的g(x)是激活函数,是一个满足极限学习机通用逼近能力定理得的非线性分段连续函数,使得极限学习机拥有拟合非线性模型的能力,常用的有sigmoid函数,tanh函数等。
2 辅助诊断实验环境 2.1 实验数据本文的数据皆来源于阿尔茨海默病神经影像学倡议(alzheimer′s disease neuroimaging initiative, ADNI, http://adni.loni.usc.edu/)数据库,其中包括认知正常(cognitive normal, CN)组47例和轻度认知障碍(mild cognitive impairment, MCI)组53例,总共100例。所有数据都为Philips 3.0 T MR成像系统采集的rs-fMRI图像,且每位被试都经过专业的医师进行确诊。被试数据的各项基本信息如表 1所示。
| 表 1 被试基本信息 Table 1 The basic information of subjects |
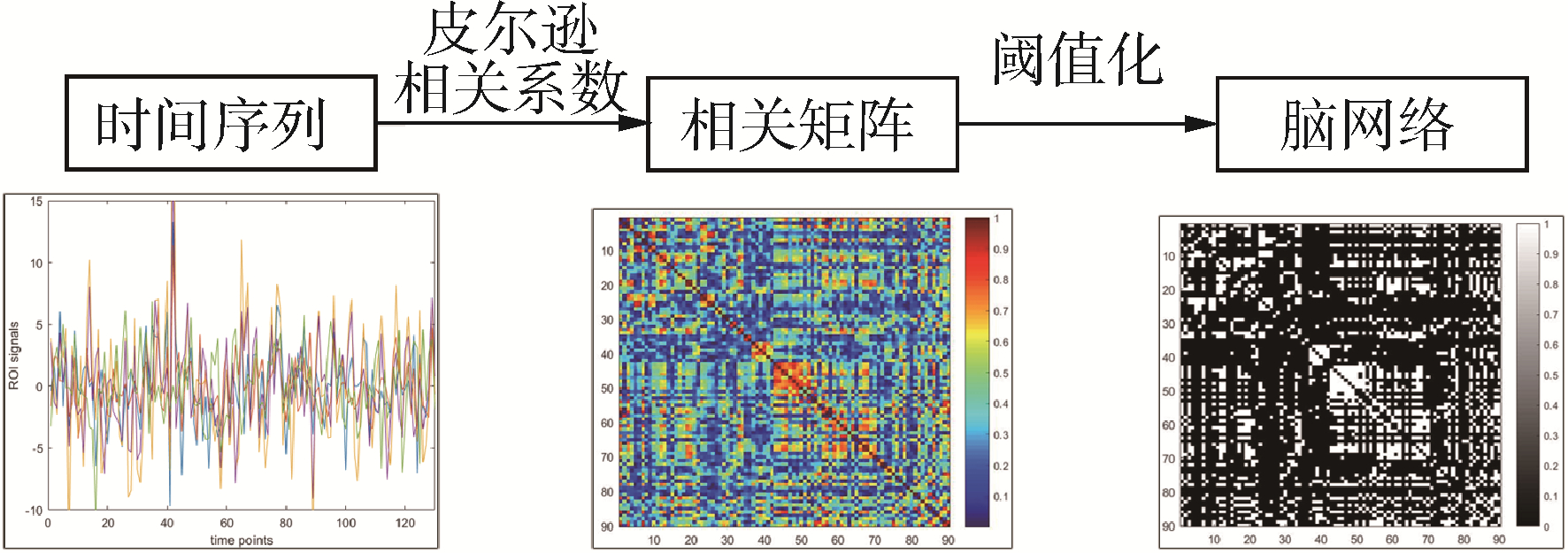
获取数据以后,本文基于DPABI(data processing & analysis for brain imaging)工具[14]对每份磁共振图像皆进行了预处理。对于每份预处理后的rs-fMRI图像,使用AAL脑模板与其进行匹配,根据蒙特利尔神经研究所(montreal neurological institute,MNI)给出的脑区坐标,AAL标准脑模板将大脑分割为116个脑区,其中26个区域为小脑区,其余90个左右对称的区域为大脑区,每个半球各45个。按照图 2方式构建脑网络,对于轻度认知障碍疾病,只需对大脑区进行分析,故取脑网络节点数N=90。由于在不同的阈值下会生成性质不同的脑网络,使得分类结果具有差异性,故本文参考Khazae等[15]的研究进行阈值选择,使得最终所得脑网络的稀疏度范围在thd∈[0.12, 0.4],步长σ=0.02。然后对不同阈值下的脑网络进行综合分析。
|
Download:
|
| 图 2 脑网络构建流程 Fig. 2 Procedure of brain network construction | |
对于每个样本的脑网络,按照本文1.2小节所述方法提取出特征集F'0。这样对于每个样本都可以提取出451个特征,包括5个节点特征:f1~f5与1个网络特征:f6。特征选择采用LASSO算子,选取正则化参数λ=0.02,最终计算出权重值非零的特征共有27个,作为用以分类的特征集F。
2.4 训练模型与辅助诊断提取出每个脑网络的特征矩阵后,本文按照7∶3的比例对100个实样本随机划分出训练集与测试集,并且确保每个数据集内认知正常与轻度认知障碍的比例相同。
在进行训练之前,首先要对极限学习机的参数进行选择,包括单隐层前馈网络隐层节点数与合适的激活函数。合适的参数对训练出高效准确的模型至关重要。本文除了不使用激活函数直接将线性叠加作为结果输出外,一共选择了3种非线性激活函数进行讨论:
sigmoid函数:
| $ g_{1}(x)=\frac{1}{1+\mathrm{e}^{-x}} $ | (9) |
tanh函数:
| $ g_{2}(x)=\frac{\mathrm{e}^{x}-\mathrm{e}^{-x}}{\mathrm{e}^{x}+\mathrm{e}^{-x}} $ | (10) |
RBF函数:
| $ g_{3}(x)=\mathrm{e}^{-\gamma\left\|x-x^{\prime}\right\|} $ | (11) |
其中值得一提的是,RBF作为激活函数时,x代入的是样本特征矩阵F。x′和γ是网络参数,相当于之前的权重w和偏置项b。式中‖x-x′‖计算的是F与w的距离,本文分别计算了L1距离和L2距离。
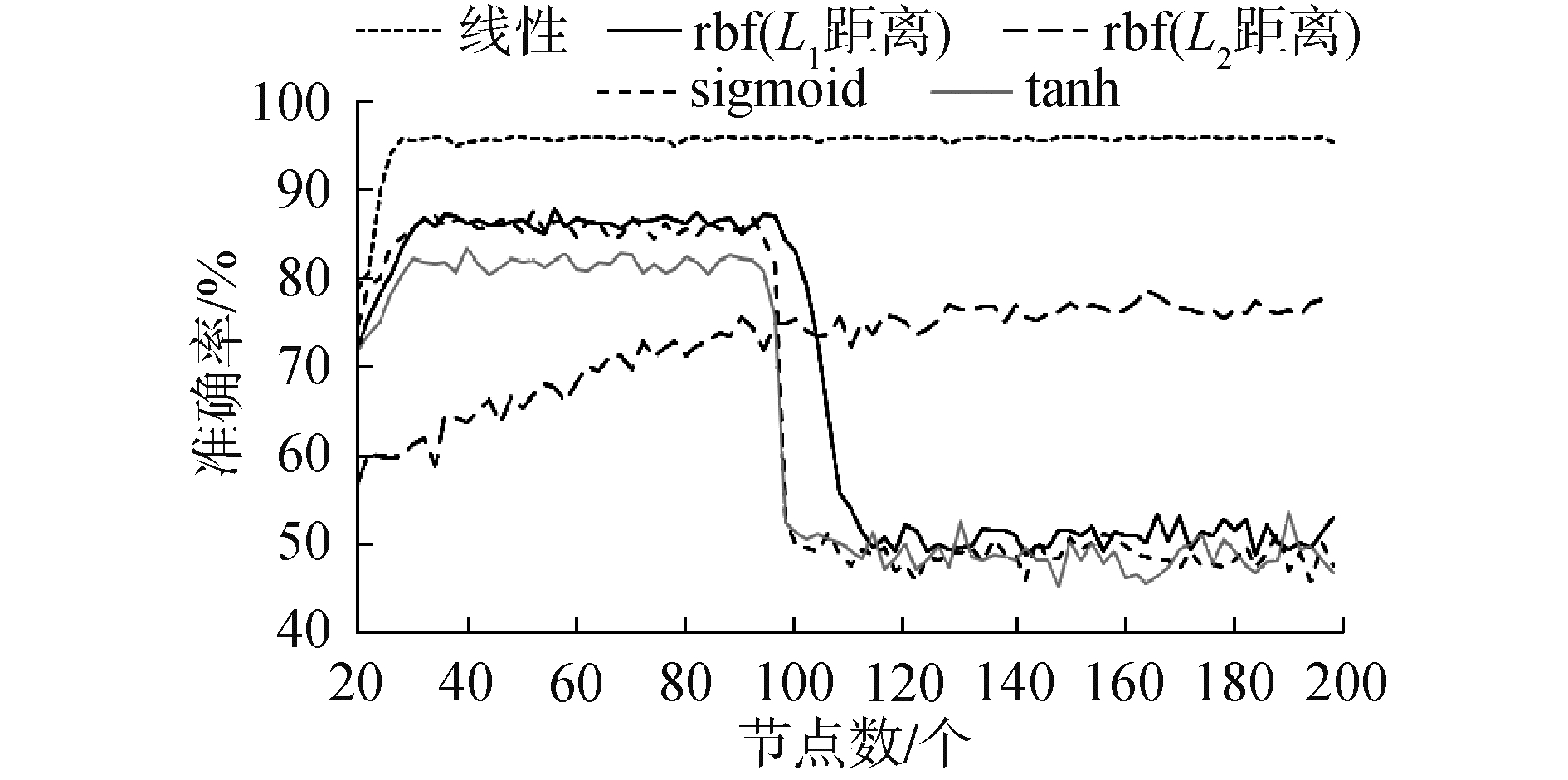
本文在训练集上使用留一法交叉验证来寻找合适的参数。首先在隐层节点数L∈[20,200]的范围内对极限学习机分类器进行验证,然后比较得到最优准确率对应的激活函数。使用不同激活函数进行分类的准确率对比如图 3所示。
|
Download:
|
| 图 3 不同参数下的分类准确率比较 Fig. 3 Comparison of accuracies with different parameters | |
通过对比可以看出对于轻度认知障碍的分类问题,直接将线性结果输出的效果最好,在70个样本的训练集中计算交叉验证准确率可以达到95%以上,且结果较为稳定,隐层节点数达到28个以后准确率便不再有大幅度变化。而其它的激活函数分类准确率均未超过90%。
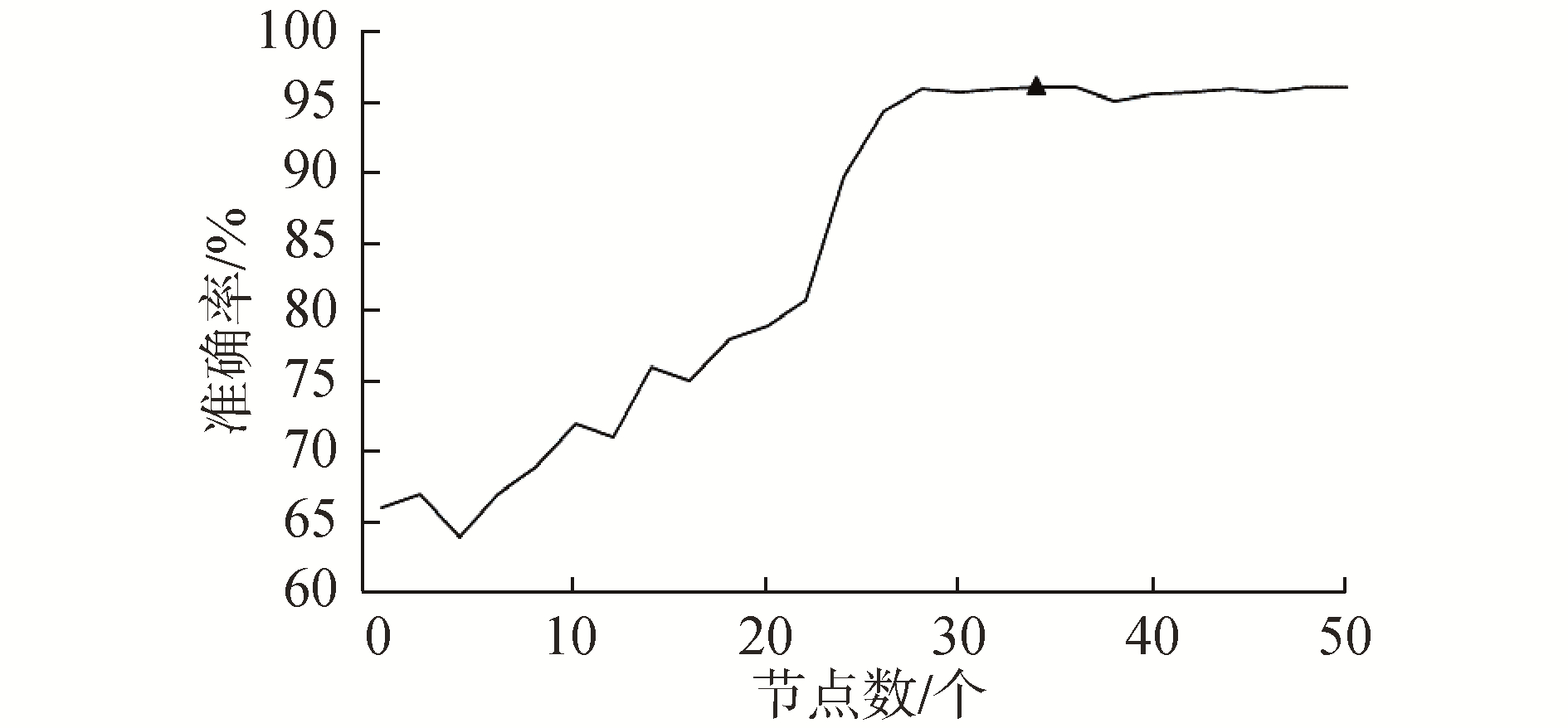
然后再对比线性的极限学习机的验证结果,选择隐层节点数为34时,交叉验证准确率最高为96%,该验证结果如图 4所示。
|
Download:
|
| 图 4 线性ELM在不同隐层节点数下的准确率 Fig. 4 The accuracy of linear ELM under different numbers of hidden layer nodes | |
按照算法1将训练集输入极限学习机进行训练,并按照算法2将测试集输入训练好的极限学习机模型进行诊断。同时进行两组对照实验,分别是使用同样的样本对支持向量机和BP神经网络进行训练和测试。其中,BP神经网络的学习率为0.2,迭代次数是10 000次。支持向量机的核函数为RBF函数。然后对比这3个模型的各项评价。
3 实验结果与分析 3.1 评价指标本文采用准确率(accuracy)、灵敏度(sensitivity)、特异度(specificity)、CN检出率(NPV)、MCI检出率(PPV),ROC曲线下面积(area under the curve,AUC)和训练耗时(time consumption)7项指标对测试结果进行评价,其中准确率、灵敏度、特异度,认知正常检出率和轻度认知障碍检出率的定义式如表 2所示。
| 表 2 部分评价指标 Table 2 A part of valuation indexes |
为了进一步证实极限学习机算法在轻度认知障碍辅助诊断中的优势,本文采用了和极限学习机辅助诊断实验中相同的训练集和测试集样本,分别对支持向量机模型和BP神经网络模型进行了训练以及测试,并在同一评价体系中对其结果进行评价和比较。其中,测试皆由搭载Intel(R) Core(TM) i5-7200 CPU 64位处理器的同一台MateBook D笔记本电脑完成,相关算法皆由Python实现。
3.2 实验结果本文的测试结果显示,极限学习机的准确率最高,高达93.3%,支持向量机为80%,BP神经网络为73.3%;敏感度最高的是BP神经网络,高达100%,极限学习机和支持向量机分别为94.4%和64.7%;支持向量机的特异度最高,为100%,极限学习机为92.3%,BP神经网络为61.9%;认知正常检出率最高的是BP神经网络,支持向量机和BP神经网络分别为68.4%和52.9%。支持向量机的轻度认知障碍检出率最高,极限学习机为94.4%,BP神经网络为52.9%。总体来看,仅有极限学习机的各项指标均达到90%,测试结果如表 3所示。
| 表 3 测试结果 Table 3 Test results |
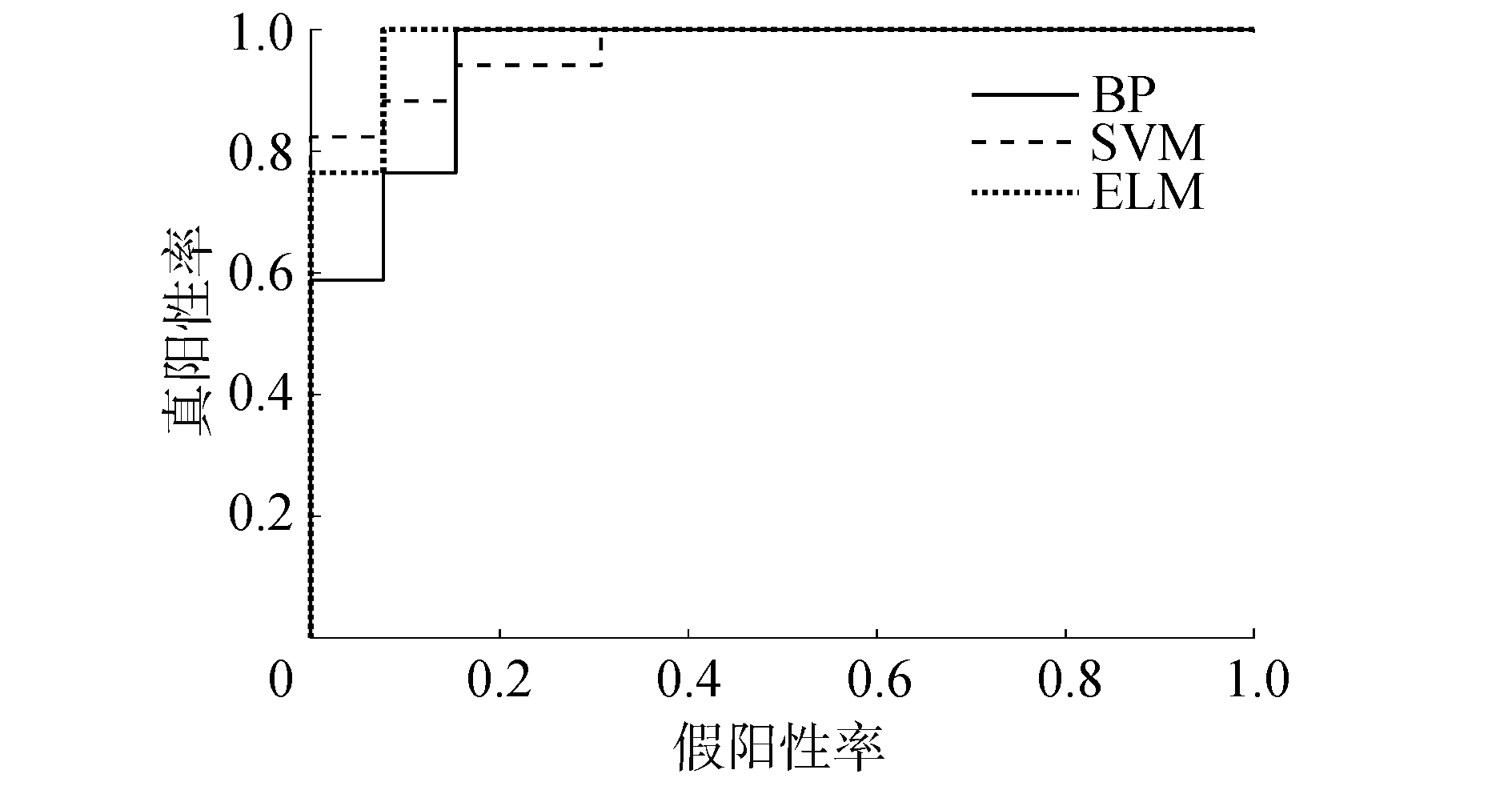
极限学习机的ROC曲线下面积为0.981,支持向量机的曲线下面积为0.968,BP神经网络的曲线下面积为0.951。结果表明,基于极限学习机算法与其他经典算法相比,其所构建的分类器取得了最佳表现。3种分类模型的ROC曲线见图 5。
|
Download:
|
| 图 5 分类模型的ROC曲线 Fig. 5 ROC of classification models | |
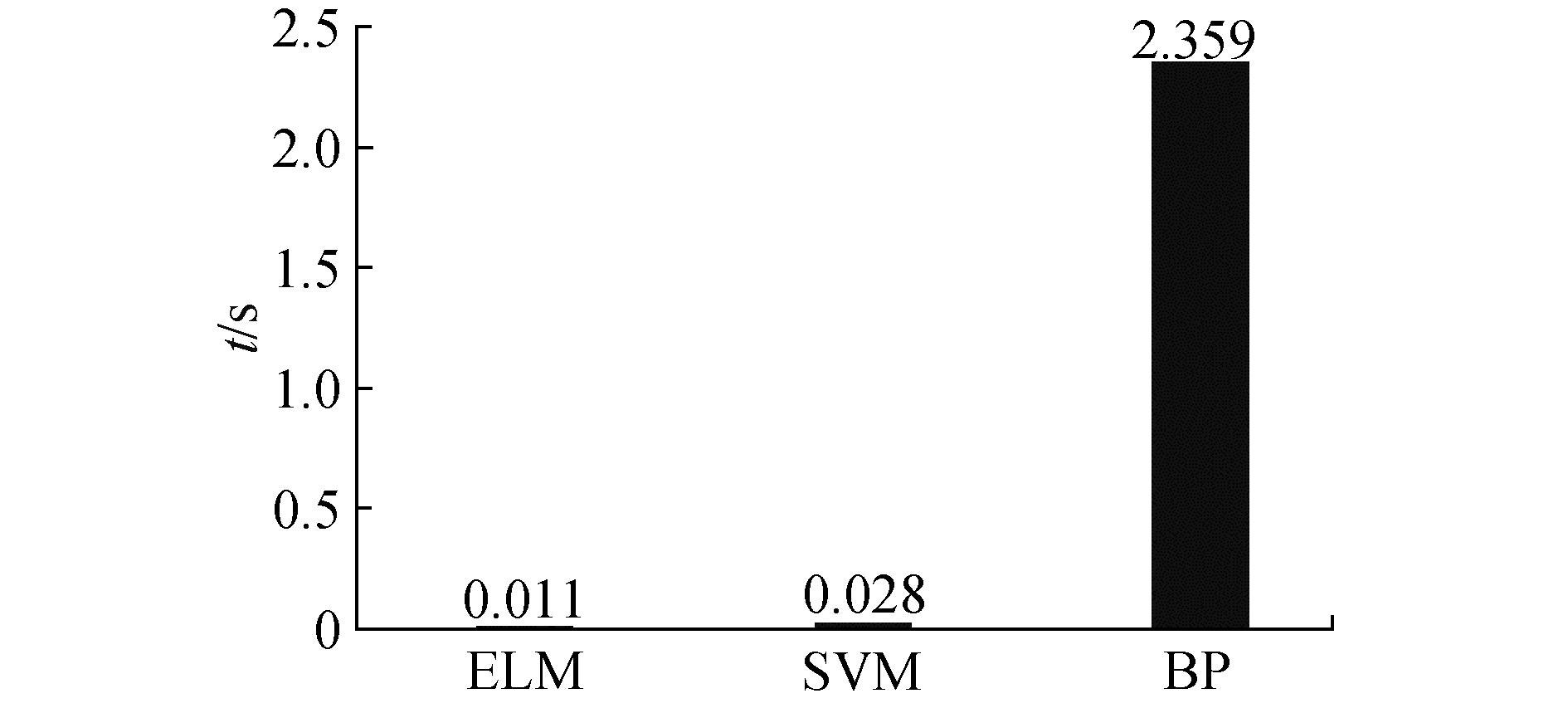
本文分别对3种算法测量了10组训练数据取平均值作为最终结果,结果显示,在样本总数70个的训练集上,极限学习机分类器的训练时间最短,耗时0.011 s。支持向量机训练速度次之,耗时0.028 s。BP神经网络运算速度较慢,耗时2.359 s。3种算法的训练时长见图 6。
|
Download:
|
| 图 6 训练时长 Fig. 6 Time consumption of three algorithm | |
从表 3的数据可以得出,3种方法中,仅有极限学习机应用于轻度认知障碍辅助诊断时,各项评价指标均高于92%,分类准确率更是达到3种算法的最高值93.3%,分别比支持向量机和BP神经网络方法高出13.3%和20.0%。值得一提的是,作为医学领域的重要指标,极限学习机的漏诊率(1-Sensitivity=5.6%)和误诊率(1-Specificity=7.7%)也都在8%以下,可以推断极限学习机对于推动轻度认知障碍辅助诊断的临床应用具有重要意义。
而支持向量机和BP神经网络虽然在个别指标上得分较高,却在其他指标上有所欠缺。例如,支持向量机的特异度虽高达100%,而灵敏度却只有64.7%,说明其更倾向于将被试诊断为正常人,这导致了支持向量机诊断具有较高的漏诊率。同理,BP神经网络则更倾向于将被试诊断为轻度认知障碍患者,拥有较高的误诊率。而极限学习机在各项评价指标上都在92%以上,漏诊率和误诊率都在8%以下,能更为准确地对被试进行分类,同时使特异度和敏感度在较高水平保持平衡。
在训练时间上(见图 5),极限学习机算法也是最快的,在训练集的样本数为70时,训练时间仅为0.011 s,分别只有支持向量机(0.028 s)的39.3%和BP神经网络(2.359 s)的0.5%。
综合上述研究结果表明,基于极限学习机的轻度认知障碍诊断方法与基于支持向量机和BP神经网络的诊断方法相比在多方面具有明显优势。
3.4 关于激活函数和隐含层节点设置的讨论非线性的激活函数可以使极限学习机可以拟合出非线性的数据模型,从而解决更复杂的问题,但根据图 3,本实验中不使用激活函数的线性模型分类效果是最好,可以推测利用脑网络特征解决轻度认知障碍分类问题的数据模型更接近于线性。对于隐含层节点的设置,理论上来说数量越多越可以更好地拟合训练数据,但由于数据的个体差异,过多的节点数会产生过拟合,降低模型的泛化能力,这就是图 1中部分曲线随着节点数的增加反而下降的原因。对于小样本的训练数据更容易产生过拟合的现象,所以需要通过测试集反映训练出的模型实际的分类状况。
4 结论1) 将极限学习机算法与复杂网络理论的分析方法应用于轻度认知障碍的辅助诊断,较大程度提高了辅助诊断的准确率和速度。
2) 对极限学习机分类器在不同的隐含层节点数和不同的激活函数时的分类准确率进行讨论,进一步提升分类器性能。
3) 将极限学习机算法与支持向量机和BP神经网络算法在轻度认知障碍辅助诊断中的性能差异进行分析,进一步证实基于极限学习机的轻度认知障碍辅助诊断方法的高效性。
然而,对于机器学习来说,训练样本量的大小对模型会产生一定影响。由于目前开源数据库中符合要求的样本有限,未来的研究将考虑与医院合作,获取更多的一手数据来验证本文的结果。在获得更优更多的数据进一步验证后,本文所述方法的应用将有效帮助实现轻度认知障碍的早发现、早诊断、早治疗,从而降低老年人罹患AD的风险。
| [1] |
PATTERSON C. World Alzheimer report 2018: the state of the art of dementia research: new frontiers[R]. London: Alzheimer's Disease International (ADI), 2018.
(  0) 0)
|
| [2] |
VAN DEN HEUVEL M P, POL H E H. Exploring the brain network: a review on resting-state fMRI functional connectivity[J]. European neuropsychopharmacology, 2010, 20(8): 519-534. DOI:10.1016/j.euroneuro.2010.03.008 (  0) 0)
|
| [3] |
许爱东, 李昊飞, 程乐峰, 等. PCA-PSO-ELM配网供电可靠性预测模型[J]. 哈尔滨工程大学学报, 2018, 39(6): 1116-1122. XU Aidong, LI Haofei, CHENG Lefeng, et al. Prediction model for power supply reliability of distribution network using PCA-PSO-ELM[J]. Journal of Harbin Engineering University, 2018, 39(6): 1116-1122. (  0) 0)
|
| [4] |
赵抢抢, 侯保林. 自动弹仓虚拟样机修正的故障定位与诊断[J]. 哈尔滨工程大学学报, 2017, 38(3): 440-445, 477. ZHAO Qiangqiang, HOU Baolin. Fault location and diagnosis for the modification of the virtual prototype of an automatic shell magazine[J]. Journal of Harbin Engineering University, 2017, 38(3): 440-445, 477. (  0) 0)
|
| [5] |
李强, 寇建华, 徐贺, 等. 基于极限学习机与模糊积分融合的机器人地面分类[J]. 哈尔滨工程大学学报, 2017, 38(4): 617-624. LI Qiang, KOU Jianhua, XU He, et al. Terrain classification for mobile robots based on extreme learning machine and fuzzy integral fusion[J]. Journal of Harbin Engineering University, 2017, 38(4): 617-624. (  0) 0)
|
| [6] |
吴建波, 王春艳, 洪华军, 等. 基于极限学习机的船舶柴油机故障诊断[J]. 计算机工程与应用, 2019, 55(15): 147-152. WU Jianbo, WANG Chunyan, HONG Huajun, et al. Fault diagnosis of marine diesel engine based on extreme learning machine[J]. Computer engineering and applications, 2019, 55(15): 147-152. (  0) 0)
|
| [7] |
田坤, 李冠, 赵卫东. 基于YOLO和极限学习机的驾驶员安全带检测模型研究[J]. 计算机应用与软件, 2019, 36(11): 196-201. TIAN Kun, LI Guan, ZHAO Weidong. Driver's seatbelt detection based on Yolo and extreme learning machine[J]. Computer applications and software, 2019, 36(11): 196-201. DOI:10.3969/j.issn.1000-386x.2019.11.032 (  0) 0)
|
| [8] |
马立勇, 袁统帅. 基于极限学习机的焊点质量检测[J]. 计算机工程与应用, 2018, 54(12): 214-218, 239. MA Liyong, YUAN Tongshuai. Quality inspection of solder joint based on extreme learning machine[J]. Computer engineering and applications, 2018, 54(12): 214-218, 239. DOI:10.3778/j.issn.1002-8331.1701-0149 (  0) 0)
|
| [9] |
陈林伟, 吴向平, 潘晨, 等. 极限学习机集成在骨髓细胞分类中的应用[J]. 计算机工程与应用, 2015, 51(2): 136-139. CHEN Linwei, WU Xiangping, PAN Chen, et al. Classification of bone marrow cells based on ensemble of extreme learning machine[J]. Computer engineering and applications, 2015, 51(2): 136-139. DOI:10.3778/j.issn.1002-8331.1303-0219 (  0) 0)
|
| [10] |
STEFENON S F, GREBOGI R B, FREIRE R Z, et al. Optimized ensemble extreme learning machine for classification of electrical insulators conditions[J]. IEEE transactions on industrial electronics, 2020, 67(6): 5170-5178. DOI:10.1109/TIE.2019.2926044 (  0) 0)
|
| [11] |
SØRENSEN L, NIELSEN M. Ensemble support vector machine classification of dementia using structural MRI and mini-mental state examination[J]. Journal of neuroscience methods, 2018, 302: 66-74. DOI:10.1016/j.jneumeth.2018.01.003 (  0) 0)
|
| [12] |
CHEN Sichong, JIANG Wenjiang, LIU Bingjia, et al. Computer-aided diagnosis of mild cognitive impairment based on SVM[M]//LIANG Qilian, WANG Wei, MU Jiasong, et al. Artificial Intelligence in China. Singapore: Springer, 2020: 442-451.
(  0) 0)
|
| [13] |
KIM J, LEE B. Automated discrimination of dementia spectrum disorders using extreme learning machine and structural T1 MRI features[C]//Proceedings of 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Jeju, Korea, 2017: 1990-1993.
(  0) 0)
|
| [14] |
YAN Chaogan, WANG Xindi, ZUO Xinian, et al. DPABI: data processing & analysis for (resting-state) brain imaging[J]. Neuroinformatics, 2016, 14(3): 339-351. DOI:10.1007/s12021-016-9299-4 (  0) 0)
|
| [15] |
KHAZAEE A, EBRAHIMZADEH A, BABAJANI-FEREMI A. Classification of patients with MCI and AD from healthy controls using directed graph measures of resting-state fMRI[J]. Behavioural brain research, 2017, 322: 339-350. DOI:10.1016/j.bbr.2016.06.043 (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


