2. 江苏省食品先进制造装备技术重点实验室, 江苏 无锡 214122
2. Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology, Wuxi 214122, China
系统动力学模型是机械系统设计分析以及优化和控制的重要工具,在传统机械系统动力学分析中,各运动关节均认作理想关节且不考虑关节间隙对于系统性能的影响[1-2],但由于制造和装配误差及磨损现象等因素,关节间隙不可避免,同时关节间隙是确保各构件相对运动的必要条件[3-5]。间隙的存在改变了间隙运动副关节元素间的自由度和受力状态,且随着关节元素的分离和接触产生碰撞力和冲击载荷,造成关节元素接触点的磨损和变形并引起机械系统的振动和噪声[6-7]。此外,随着系统的不断运行,非规则磨损间隙将进一步破坏系统动力学特性并加剧磨损现象,直至构件损坏和失效[8]。
目前国内外学者对含间隙机构关节磨损预测进行了大量的研究,Tasora等[9]基于Reye′s hypothesis模型对一转动副间隙磨损进行计算并通过与实验结果相对比验证了磨损计算的准确性。Mukras等[8, 10]提出了一种适用于多体系统动力学关节磨损分析的计算方法,并对弹性地基模型和接触力模型进行对比,以分析其在磨损计算过程中磨损深度和轮廓的差异。Flores等[11]基于连续接触模型和Archard磨损模型提出了一种转动副间隙磨损现象的分析方法并对其进行量化。Li等[12]将间隙定义为无质量杆,并基于弹性地基模型和Archard磨损模型提出了一种改进的转动副间隙磨损预测实用模型,通过实验数据对比验证了该模型的有效性。王庚祥等[13]基于Archard磨损模型对一含柔性构件平面五杆机构进行磨损预测分析,并对比分析不同程度的转动副磨损间隙对于机构动力学性能的影响。
机械系统在实际使用中,通常采用润滑剂以延长机体的使用寿命,提高系统的稳定性,目前已有大量文献对润滑条件下系统动力学进行了研究,Zhao等[14]对一含间隙曲柄摇杆机构进行分析,运用有限元方法求解润滑模型并通过拉格朗日方程建立含润滑关节及复杂接触力条件下系统动力学模型;Tian等[15]基于绝对节点坐标法建立了含柔性构件及润滑关节的系统动力学模型,并提出适用于该类问题的建模分析方法;Flores等[16]基于拉格朗日方程建立了含接触力及润滑力的系统动力学方程,并提出混合力模型以解决纯挤压油膜效应在碰撞计算过程中关节力不连续的问题。
综上所述不难发现,虽有大量文献致力于间隙关节磨损及关节润滑研究,但润滑条件下间隙关节磨损研究相对较少,因此本文以3-CPaR&R1R2混联机构为研究对象并在转动副中考虑间隙的存在,运用Flores接触力模型及修正Coulomb摩擦模型分别建立关节元素间接触点法向接触力及切向接触力模型,关节润滑力则通过Sommerfeld润滑条件下无限长轴颈-轴承的润滑力模型建立,最终运用拉格朗日方程建立了考虑转动副间隙及关节润滑的动力学数值仿真模型,通过实例计算分析不同的物理参数对于含间隙关节磨损预测的影响,并对比研究有无润滑条件下关节磨损特性。
1 转动副建模 1.1 间隙转动副建模 1.1.1 接触力模型在理想转动副关节中,轴与轴套间只有一个转动自由度,由于间隙的引入,轴与轴套分离且轴被约束在间隙范围内作不规则运动,随着轴与轴套间的碰撞和相对滑动,产生碰撞力和摩擦力,即转动副处的运动约束被力约束所替代。
鉴于含间隙关节元素间的不规则运动,接触力模型应满足复杂接触条件的计算且便于含间隙动力学方程的装配。文献[17]对Hetz接触理论的发展历程研究进行了系统的分析总结,讨论了5种纯弹性接触力模型以及8种考虑能量损耗的接触力模型,其中以Lankarani-Nikravesh接触力模型和Flores接触力模型应用最为广泛。Lankarani-Nikravesh接触力模型充分考虑了碰撞过程中内部阻尼做功导致的能量损失,但该模型受到恢复系数的限制仅适用于高恢复系数的接触碰撞问题研究。相比而言,Flores接触力模型(如图 1所示)更加精确并具有稳定的数值解,且无明显的限制条件,适用于一般的机械碰撞问题研究,此外,该模型能够同时反映完全塑性接触及弹性接触,更适合用于磨损模型的相关计算,故本文采用Flores接触力模型用于法向接触力计算[18]:
| $ F_{n}=K \delta^{n}\left[1+\frac{8\left(1-c_{r}\right)}{5 c_{r}} \frac{\dot{\delta}}{\dot{\delta}^{(-)}}\right] $ | (1) |
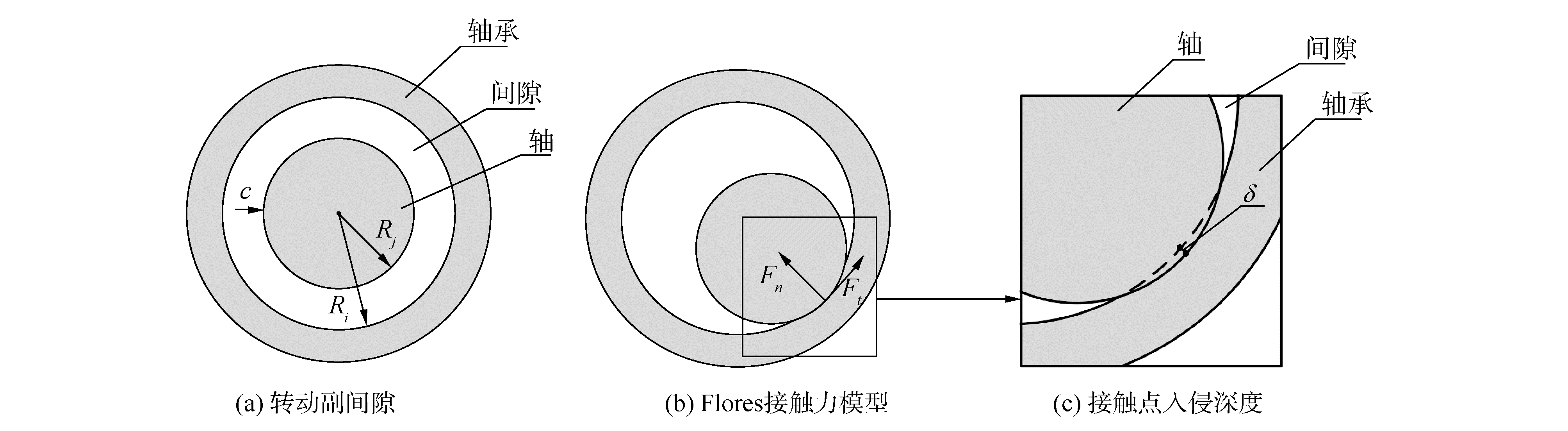
|
Download:
|
| 图 1 含间隙转动副关节模型 Fig. 1 Revolute joint model with clearance | |
式中:δ为接触变形量;
| $ {K = \frac{4}{{3{\rm{ \mathsf{ π} }}\left( {{\sigma _i} + {\sigma _j}} \right)}}{{\left( {\frac{{{R_i}{R_j}}}{{{R_i} - {R_j}}}} \right)}^{\frac{1}{2}}}} $ | (2) |
| $ {{\sigma _{(k = i,j)}} = \frac{{1 - v_k^2}}{{{\rm{ \mathsf{ π} }}{E_k}}}} $ | (3) |
式中:vk、Ek分别为关节元素的泊松比、弹性模量;下标i、j分别表示轴套和轴。
Coulomb摩擦模型大量应用于接触碰撞过程中的摩擦行为计算,该摩擦模型结构简单且便于嵌入含间隙多体系统动力学方程,但Coulomb摩擦力模型在切向速度为零时容易发生切向速度方向突变,使动力学仿真计算不收敛。为此,本文采用AMBRÓSIO[19]提出的修正Coulomb摩擦力模型:
| $ F_{t}=\left\{\begin{array}{lc} 0, & v_{t}<v_{0} \\ -\mu_{d} \frac{v_{t}-v_{0}}{v_{1}-v_{0}} F_{n} v_{t}, & v_{0} \leqslant v_{t} \leqslant v_{1} \\ -\mu_{d} F_{n} v_{t}, & v_{t}>v_{1} \end{array}\right. $ | (4) |
式中:ud为滑动摩擦系数;vt为切向速度;v0、v1为给定的速度界限。其摩擦系数为关节元素相对切向速度的函数,有效地解决了数值计算不稳定的问题,提高了数值积分的稳定性。基于式(1)、(4),故无润滑条件下轴对轴套的接触力可表示为:
| $ \boldsymbol{F}=F_{n} \boldsymbol{n}+F_{t} \boldsymbol{t}=\left(f_{x} \quad f_{y}\right)^{\mathrm{T}} $ | (5) |
大多数机械系统中,为减少磨损并延长机体的使用寿命,提高系统的稳定性,在实际设计使用中通常采用润滑剂。因此,为了准确地分析含间隙机构的动力学特性并提高磨损深度预测的有效性,建立含间隙转动副中的润滑模型极其重要。润滑间隙转动副的横截面模型如图 2所示。
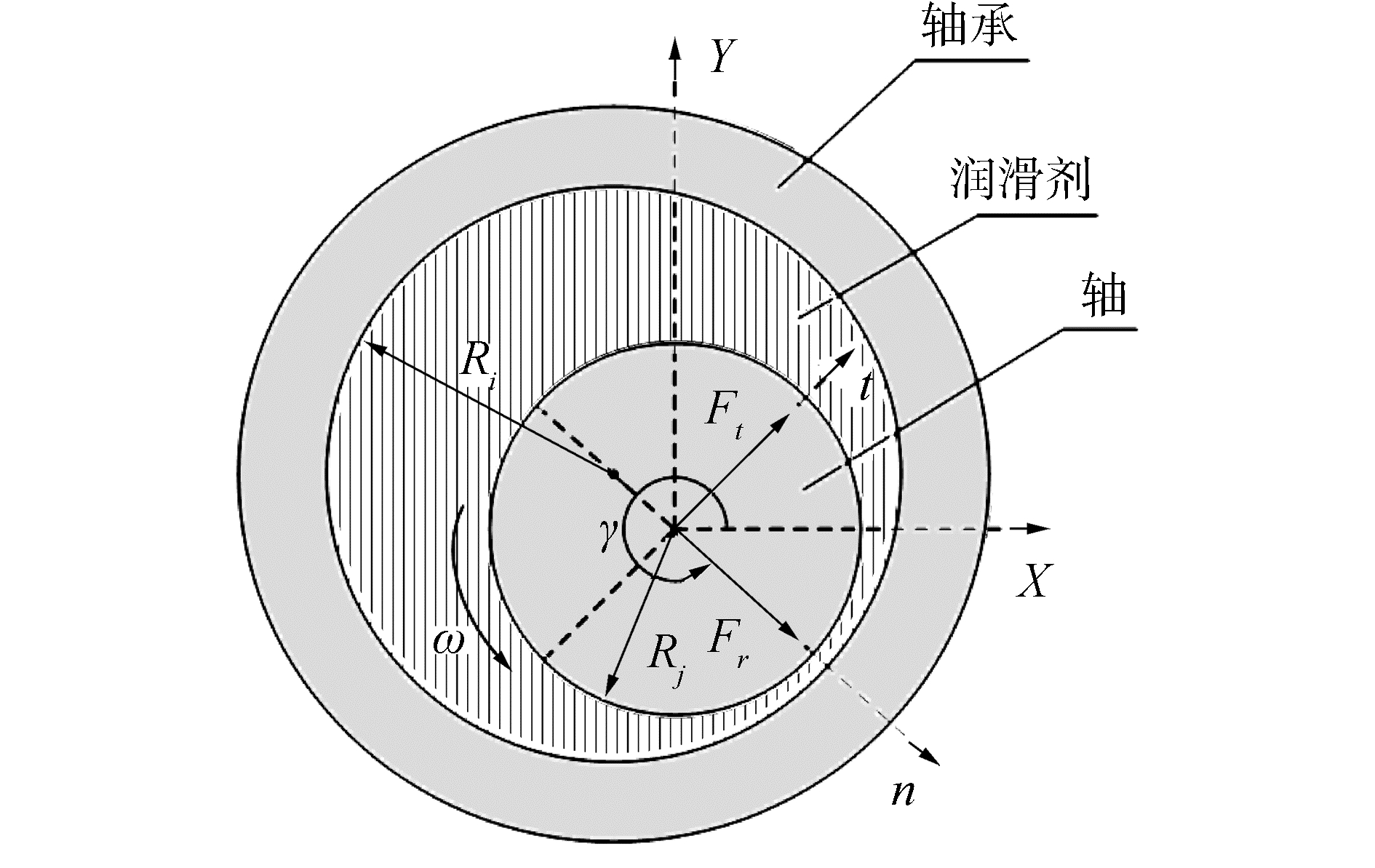
|
Download:
|
| 图 2 润滑轴颈-轴承横截面 Fig. 2 Cross section of a lubricated journal-bearing | |
润滑模型是基于润滑油膜效应建立的,其包括纯挤压油膜效应和楔形油膜效应,其中纯挤压油膜效应应用于轴和轴套间的相对径向速度远大于相对旋转速度的场合,而后者应用场合相反,假设该润滑间隙转动副油膜效应为纯挤压油膜效应。通常情况下,轴颈-轴承关节可以被视为无限长的轴颈-轴承模型(长度与直径比大于2),相应的润滑模型首先由Sommerfeld推导建立。根据文献[20],对于具有Sommerfeld润滑条件的无限长轴颈-轴承模型其润滑力可以表示为:
| $ \begin{array}{*{20}{c}} {}\\ {\left\{ {\begin{array}{*{20}{l}} {{F_r} = - \frac{{12{\rm{ \mathsf{ π} }}\mu LR_j^3\dot \varepsilon }}{{{c^2}{{\left( {1 - {\varepsilon ^2}} \right)}^{3/2}}}}}\\ {{F_t} = \frac{{12{\rm{ \mathsf{ π} }}\mu LR_j^3\varepsilon (\omega - 2\dot \gamma )}}{{{c^2}\left( {2 + {\varepsilon ^2}} \right){{\left( {1 - {\varepsilon ^2}} \right)}^{1/2}}}}}\\ {\dot \gamma = \frac{{\left( {{e_x}{{\dot e}_y} - {{\dot e}_x}{e_y}} \right)}}{{{e^2}}}} \end{array}} \right.} \end{array} $ | (6) |
式中:ω为轴与轴套间的相对角速度;L为轴和轴套的长度;μ为润滑油粘度;ε=e/c为偏心率,即轴和轴套的偏心距与间隙的比值;ex、ey为偏心距e在x、y方向上的分量。
在润滑条件下,间隙转动副关节经过一段时间的运行,会出现油膜厚度极小和干碰撞情况。由式(6)可知,当轴无限趋近于轴套表面时,ε趋近于1,导致润滑力不收敛且求解过程出现不连续现象。为解决上述问题,Flores等[16]提出了适用于从润滑力转换为干接触力过程的混合力模型,即存在一定厚度不可压缩的润滑油膜,且在该厚度范围内为润滑力和干接触力共同作用,当润滑力模型切换到干接触力模型时,该模型可确保润滑力求解的连续性。含润滑间隙转动副的关节力表示为:
| $ f=\left\{\begin{array}{ll} F_{\text {squeeze }}, & e_{i j} \leqslant c \\ \frac{\left(c+e_{0}\right)-e_{i j}}{e_{0}} F_{\text {squeeze }}+\frac{e_{i j}-c}{e_{0}} F_{\text {dry }}, & c \leqslant e_{i j} \leqslant c+e_{0} \\ F_{\text {dry }}, & e_{i j} \geqslant c+e_{0} \end{array}\right. $ | (7) |
式中:Fdry为轴与轴套干碰撞时的接触力;Fsqueeze为润滑力;e0为给定的偏心距容差且该参数值的选择取决于间隙尺寸及具体应用场合。
1.2 含间隙转动副磨损模型机械系统中由于关节间隙的存在,关节元素间发生接触碰撞及相对切向滑动,必然使接触体表层材料逐渐损失从而造成磨损,目前磨损预测方法大多基于Archard的磨损模型。该模型将磨损量与接触体的物理和几何特性包括施加载荷、滑动距离、材料硬度等因素相关联。此外,该模型已大量应用于磨损深度预测研究,如球面副旋转关节部件[22]和斜齿轮[23]磨损分析。本文将采用Archard磨损模型对机械系统中含间隙转动副进行磨损分析,其表达式为:
| $ \frac{V}{s}=\frac{k F_{n}}{H} $ | (8) |
式中:V为磨损体积;s为相对滑移距离;k为无量纲磨损常数;H为接触体中较软材料的硬度;Fn为法向接触力。
在对旋转关节的磨损预测分析中,磨损深度相比于磨损量,可更加直观地反映磨损对于部件尺寸及破坏程度的影响。为此,假设接触体接触表面为塑性变形且实际接触面积与接触力成正比,则式(8)可写为:
| $ \frac{V}{s}=k A_{a}=\frac{k F_{n}}{H} $ | (9) |
式中Aa为实际接触面积。则式(9)两边除以接触面积,可推导为:
| $ \frac{h}{s}=\frac{k P}{H} $ | (10) |
式中:h为磨损深度;P为法向接触应力。由该式表明,磨损深度与接触应力及相对滑移距离密切相关。在系统的运动过程中含间隙转动副关节元素之间接触应力和滑移距离均不断变化,且磨损计算过程中认为在一个碰撞瞬间接触条件保持不变,因此需将连续的接触过程离散化,则该方程的微分形式可写为:
| $ \frac{\mathrm{d} h}{\mathrm{~d} s}=\frac{k P}{H} $ | (11) |
当关节元素间相互接触碰撞,且完成接触应力和滑移距离的计算,即可基于Archard磨损模型计算磨损深度,其通过对时间离散化计算的累计深度为:
| $ h_{i}=h_{i-1}+k P \Delta s_{i} / H $ | (12) |
式中:hi、Pi、Δsi分别为第i个计算周期的磨损深度、接触应力以及相对滑移距离;hi-1为前一周期磨损深度。由此可通过计算单个周期内磨损深度而累计得到总磨损深度。
2 含间隙混联机构动力学建模本文对一含间隙3-CPaR&R1R2混联机构进行磨损预测分析,分析其在不同的驱动速度、间隙尺寸及考虑润滑条件下间隙关节磨损特性。如图 3所示,该混联机构由串联模块和并联模块组成,其中并联机构由3条相同的CPaR支链构成,使机构在X、Y、Z方向移动,其中C为圆柱副,Pa为平行四边形铰链,R为转动副,并联机构每条支链上相应的圆柱副C、平行四边形铰链Pa以及与Pa相连的转动副R轴线平行;串联机构由2个轴线呈空间垂直的转动副R1、R2构成,分别绕Y轴、X轴旋转。
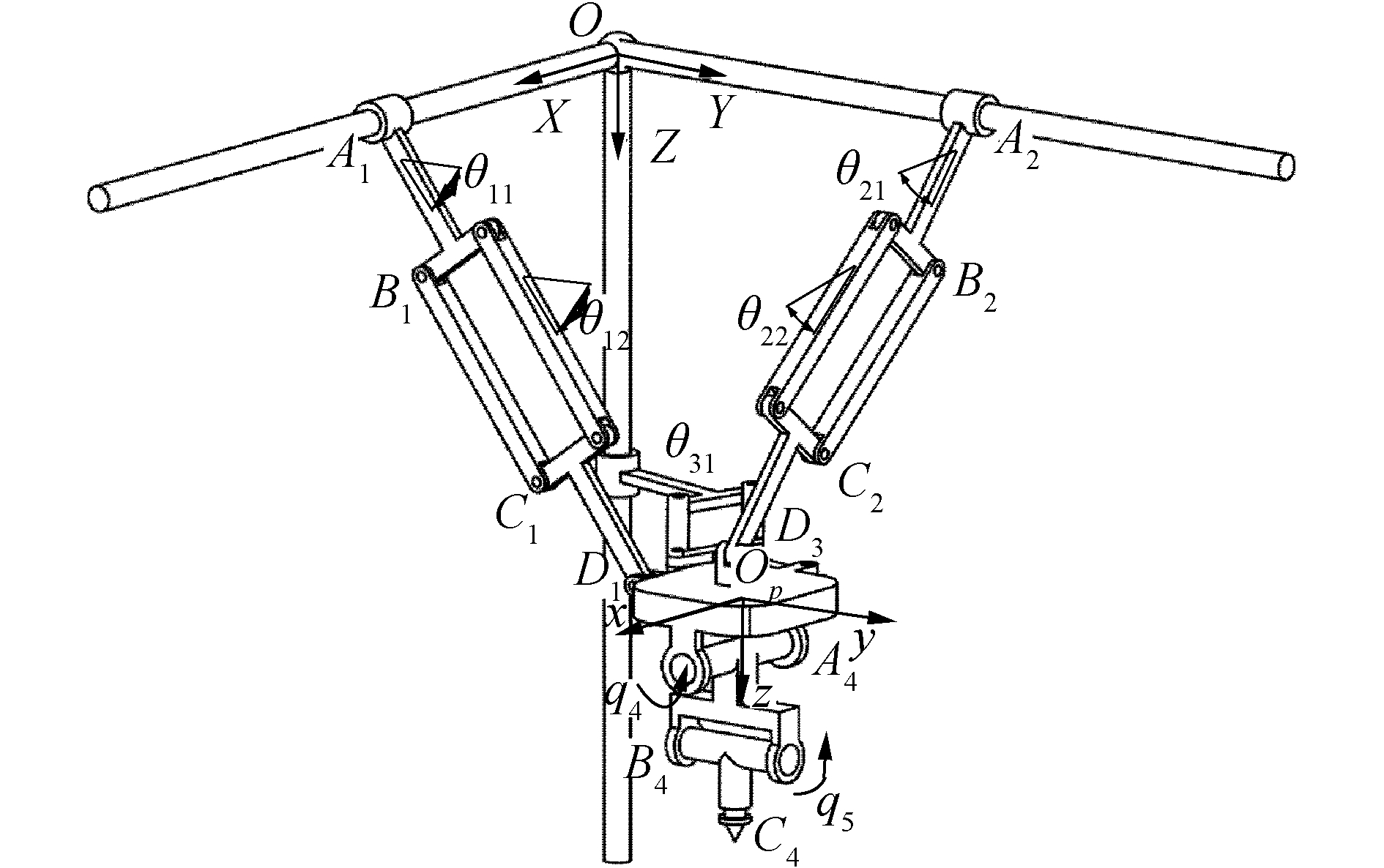
|
Download:
|
| 图 3 混联机构坐标系 Fig. 3 The coordinate system of the hybrid mechanism | |
混联机构系统坐标系如图 3所示,定坐标系O-XYZ以及动坐标系op-xyz分别设于定平台支架处与动平台几何中心且其坐标轴方向保持一致,串联模块在初始状态下沿重力方向(Z轴方向)自然下垂。构件AiBi、BiCi和CiDi的长度分别记为li1、li2、li3(i=1, 2, 3),动平台长宽高分别为lx、ly、lz,动平台下方串联模块部分,记杆件A4B4、B4C4长度分别为l41、l42。并联模块各支链中,构件A1B1、B1C1、A2B2、B2C2与平面XOY所成角度分别记为θ11、θ12、θ21、θ22,构件A3B3、B3C3与平面YOZ所成角度分别记为θ31、θ32。选取系统广义坐标为:并联模块3个支链上圆柱副的位移q1、q2、q3,串联模块中绕X轴转动和绕Y轴转动的转动副的旋转角度q4、q5。假设转动副D3处含有间隙。
碰撞点及接触力计算是进行磨损预测分析的首要条件,因此为研究含间隙及润滑条件下关节磨损特性,本文基于拉格朗日方程对该润滑条件下含间隙混联机构进行动力学建模。
含间隙机构中,由于理想运动约束被间隙关节元素间力约束所替代,其动力学方程由微分方程及运动约束方程组成,因此含间隙机构动力学方程可表示为:
| $ \left\{\begin{array}{l} \boldsymbol{M q}+\boldsymbol{C} \boldsymbol{q}+\boldsymbol{K}_{g} \boldsymbol{q}+\boldsymbol{\varPhi}_{q} \boldsymbol{\lambda}=\boldsymbol{F}+\boldsymbol{f}_{c} \\ \boldsymbol{\varPhi}(\boldsymbol{q}, \boldsymbol{t})=0 \end{array}\right. $ | (13) |
式中:M、C、Kg分别为系统质量矩阵、阻尼矩阵及刚度矩阵;Φq为该机构的Jacobian矩阵;矢量λ和F分别为拉格朗日乘子和广义驱动力;fc为混合力模型所计算的接触力及润滑力相对于广义坐标系q的广义力矩阵。
为了更加准确地分析该机构磨损特性,本文采用一种综合计算方法,该计算方法可反映磨损过程和机构动力学特性间的相互影响。在磨损计算过程中,磨损区域将由轴和轴承之间的碰撞点和滑移距离确定,运用Archard模型完成预测磨损深度计算后,根据磨损预测深度更新接触体的接触半径,重构接触体几何形状,其非规则磨损间隙将进一步影响系统的动态响应并导致磨损区域的变化。此外为提高计算效率,接触体表面被分为若干个扇区进行计算。该综合计算方法的主要迭代过程如下:
1) 定义系统的初始条件及间隙参数,给出碰撞力模型、摩擦模型、润滑模型及磨损模型的各项物理属性系数;
2) 开始进行数值仿真,计算间隙副关节元素间的相对运动状态并判定其是否接触,若接触则计算接触面积并依据式(7)计算其接触力,否则继续基于式(13)进行仿真计算;
3) 依据接触力及接触面积计算接触体表面应力分布,利用接触应力及相对滑移距离并基于式(11)、(12)计算当前及累计磨损深度;
4) 鉴于含间隙转动副关节元素间的磨损将造成接触体表面形貌改变,依据累计磨损深度对接触体表面几何形状进行重构;
5) 更新间隙运动学模型、接触力模型、摩擦模型及润滑模型,并与磨损前的混联机构动力学模型重新集成获得磨损后的机构动力学模型,并计算其各项动态输出参数;
6) 更新时间,使用全新的一组关节间隙参数继续步骤2),直至循环计算次数达到其预定的迭代周期。
3 数值分析为验证上述理论模型的正确性,分析不同的物理参数及有无润滑条件对于含间隙关节磨损预测的影响,以下将进行实例计算,3-CPaR&R1R2混联机构的各项结构参数如表 1所示,含间隙混联机构动力学仿真参数如表 2所示。值得指出的是:在仿真计算过程中,假设轴的硬度大于轴承硬度,则只考虑轴承的磨损深度且轴始终保持其初始尺寸形状,在40 ℃时润滑油的黏度为400 cP。
| 表 1 混联机构的结构参数 Table 1 Structural parameters of hybrid mechanism |
| 表 2 含关节间隙混联机构动力学仿真参数 Table 2 Dynamics simulation parameters of joint clearance |
为便于计算,给定机构各驱动关节的运动规律:q1=0.354-0.005sin(ωt),q2=0.409-0.005cos(ωt),q3= 0.415-0.005cos(ωt),q4=0.1sin(ωt),q5=0.2sin(ωt)。
3.1 无润滑条件下关节磨损驱动速度以及间隙尺寸是影响机构动态性能以及磨损现象的重要因素,本文在4种驱动速度(ω=4π,8π,16π,32π)及4种间隙尺寸(c=0.15,0.25,0.35,0.45 mm)下进行数值仿真,对比分析不同驱动速度及间隙尺寸对该机构间隙关节磨损的影响。
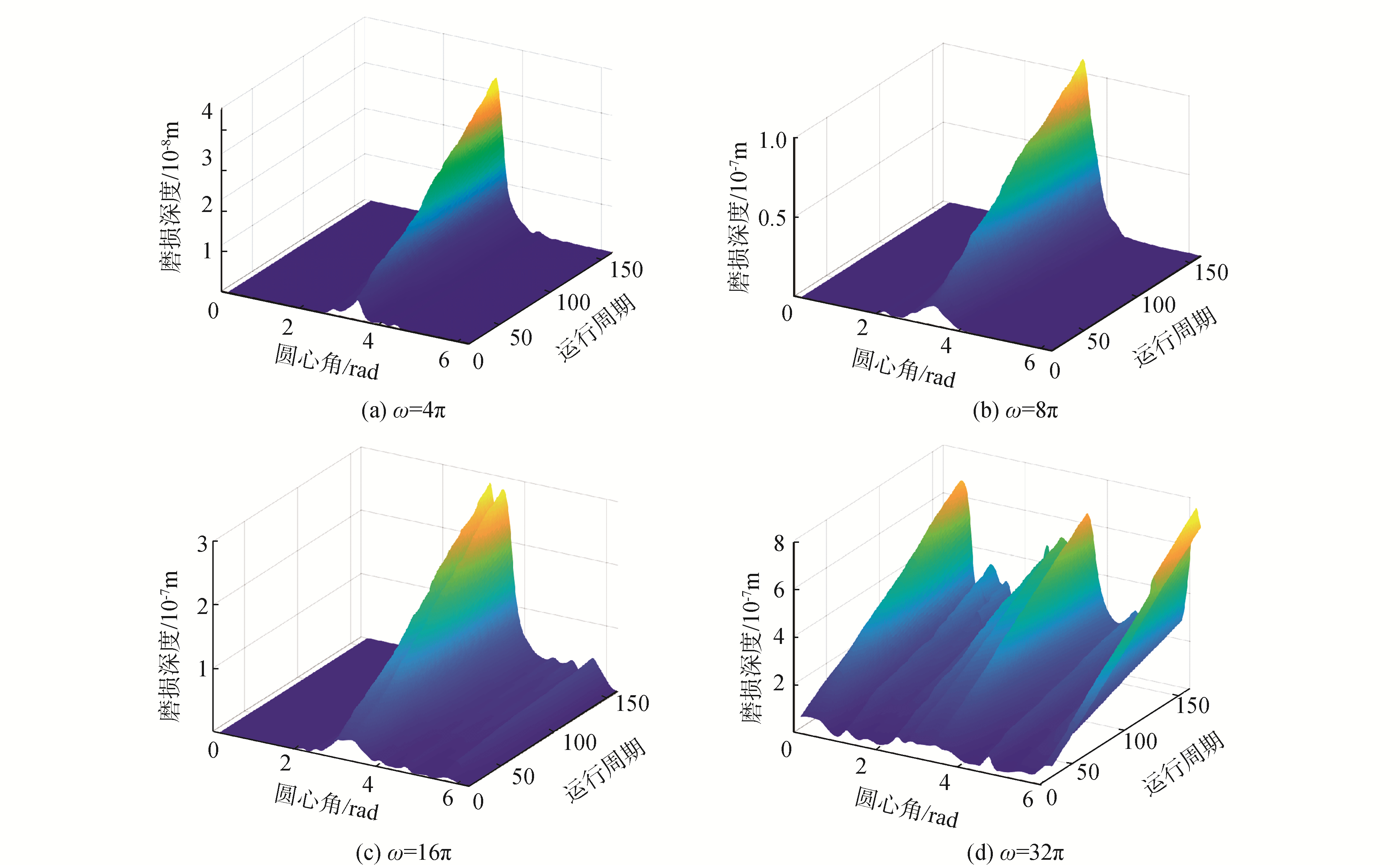
首先,依据表 1、表 2所列参数,并基于式(13),在给定的间隙尺寸c=0.25 mm、驱动速度ω=4π,8π,16π,32π条件下对其进行数值仿真,图 4给出了不同驱动速度下混联机构中含间隙关节轴心轨迹图,图 5是基于Archard磨损模型计算的轴承磨损深度,图 6为给定驱动速度及间隙尺寸条件下磨损深度随运行时间变化对比图。
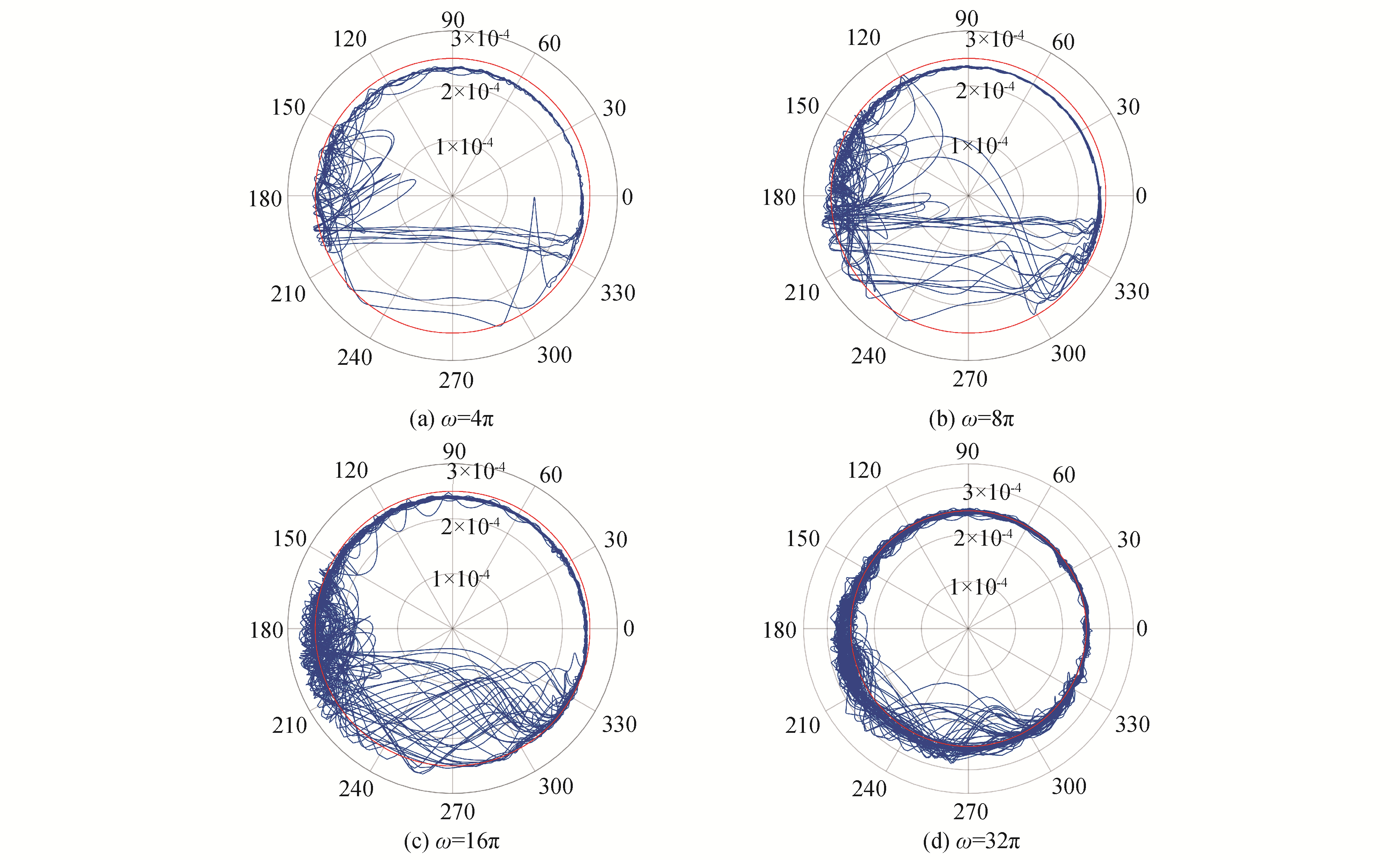
|
Download:
|
| 图 4 不同驱动速度下轴心轨迹 Fig. 4 Shaft center trajectory of the clearance joint with different driving velocities | |
|
Download:
|
| 图 5 不同驱动速度下磨损深度 Fig. 5 Wear depth of the clearance joint with different driving velocities | |
|
Download:
|
| 图 6 磨损深度变化曲线(c=0.25 mm, ω=32π) Fig. 6 Variation of wear depth (c=0.25 mm, ω=32π) | |
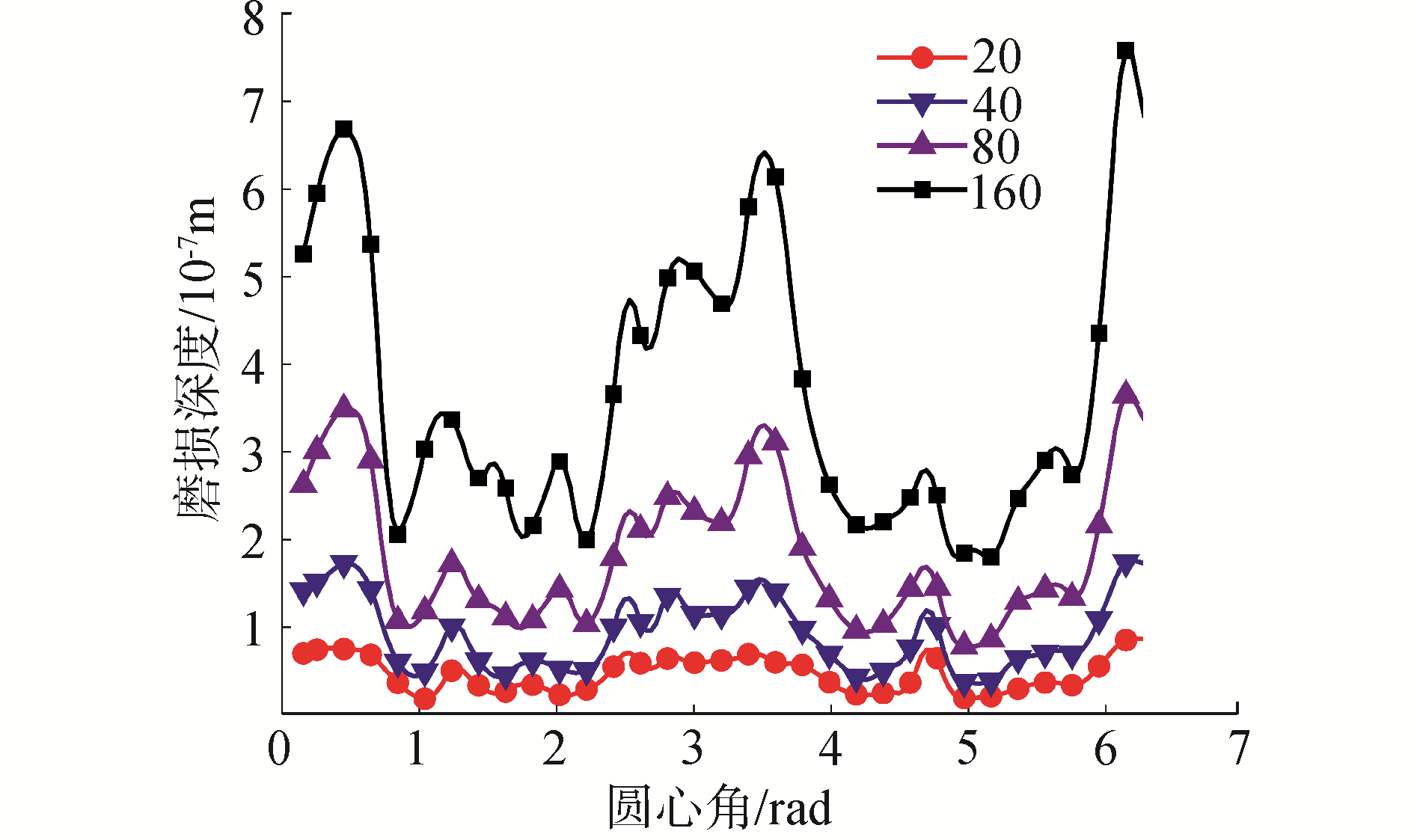
由图 4轴心轨迹图可知,在间隙尺寸为定值条件下,随着驱动速度的增加,含间隙关节元素间冲击碰撞现象减少,轴心轨迹逐渐变得较为规整且关节元素长时间处于连续接触状态,但其关节元素间侵入深度增加。由图 5磨损深度三维图可知,磨损过程中其接触表面的磨损深度并不是均匀磨损,且其磨损峰值区域与轨迹图 4中碰撞点分布区域相一致,此外,随着驱动速度的增加虽然磨损相对变得均匀但磨损深度显著加深;图 6为给定间隙尺寸c=0.25 mm及驱动速度ω=32π条件下,系统经过20、40、80、160运行周期后间隙关节轴承磨损深度,由图可知,随着运行时间的增长,其磨损峰值区域与其他磨损区域差距进一步增大,对轴承表面形状尺寸的破坏加剧,加速关节构件失效。
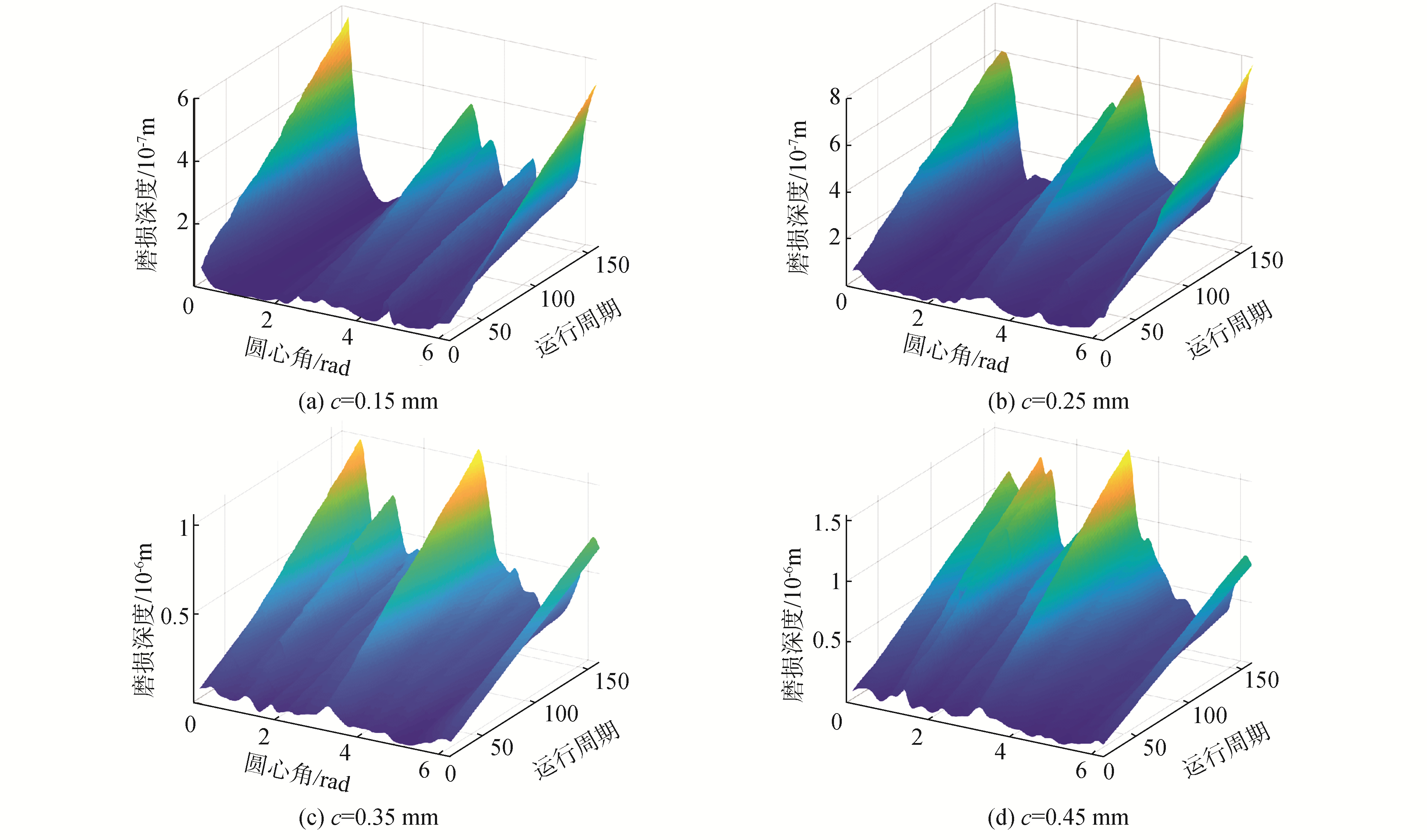
其次,令驱动速度为ω=30π,改变径向间隙尺寸,依次取c=0.15,0.25,0.35,0.45 mm,参照前述仿真方法,所得相应的磨损深度图像如图 7、图 8所示。
|
Download:
|
| 图 7 不同间隙尺寸下磨损深度 Fig. 7 Wear depth of the clearance joint with different clearance sizes | |
|
Download:
|
| 图 8 磨损深度变化曲线(ω=30π, n=80) Fig. 8 Variation of wear depth (ω=30π, n=80) | |
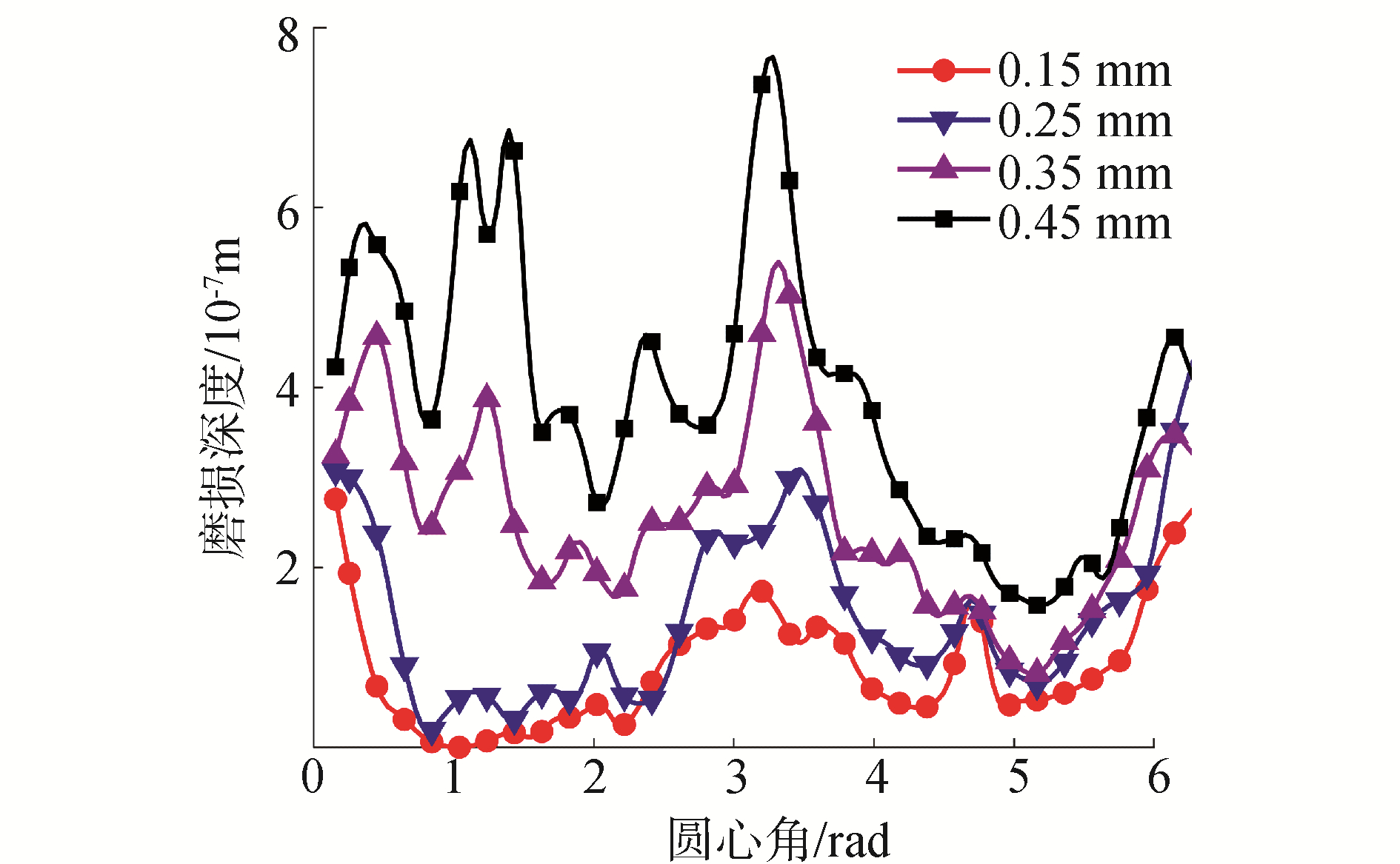
图 7为相同驱动速度及不同间隙尺寸下,磨损深度随运行时长的变化图像;图 8为给定驱动速度(ω=30π)及运行周期(n=80)条件下不同间隙尺寸磨损深度对比图像。由图 7、图 8可知,随着间隙尺寸的增加, 磨损深度也逐渐增加, 且磨损分布相对均匀,但间隙尺寸对于磨损深度的影响相对较小。
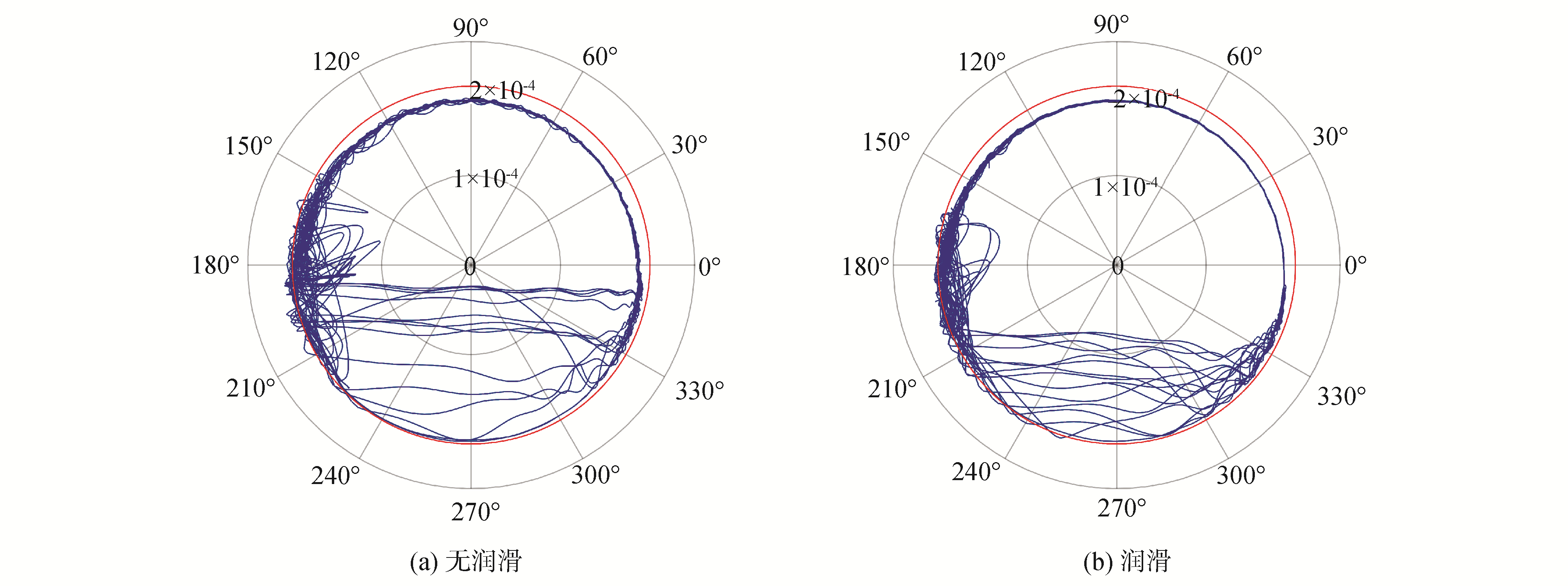
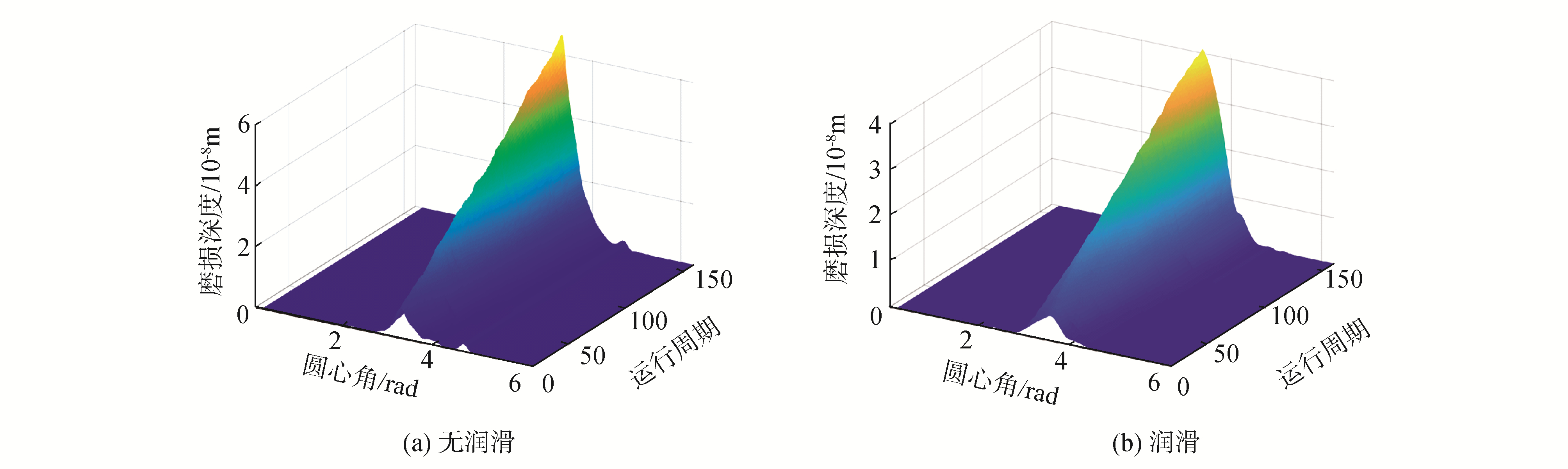
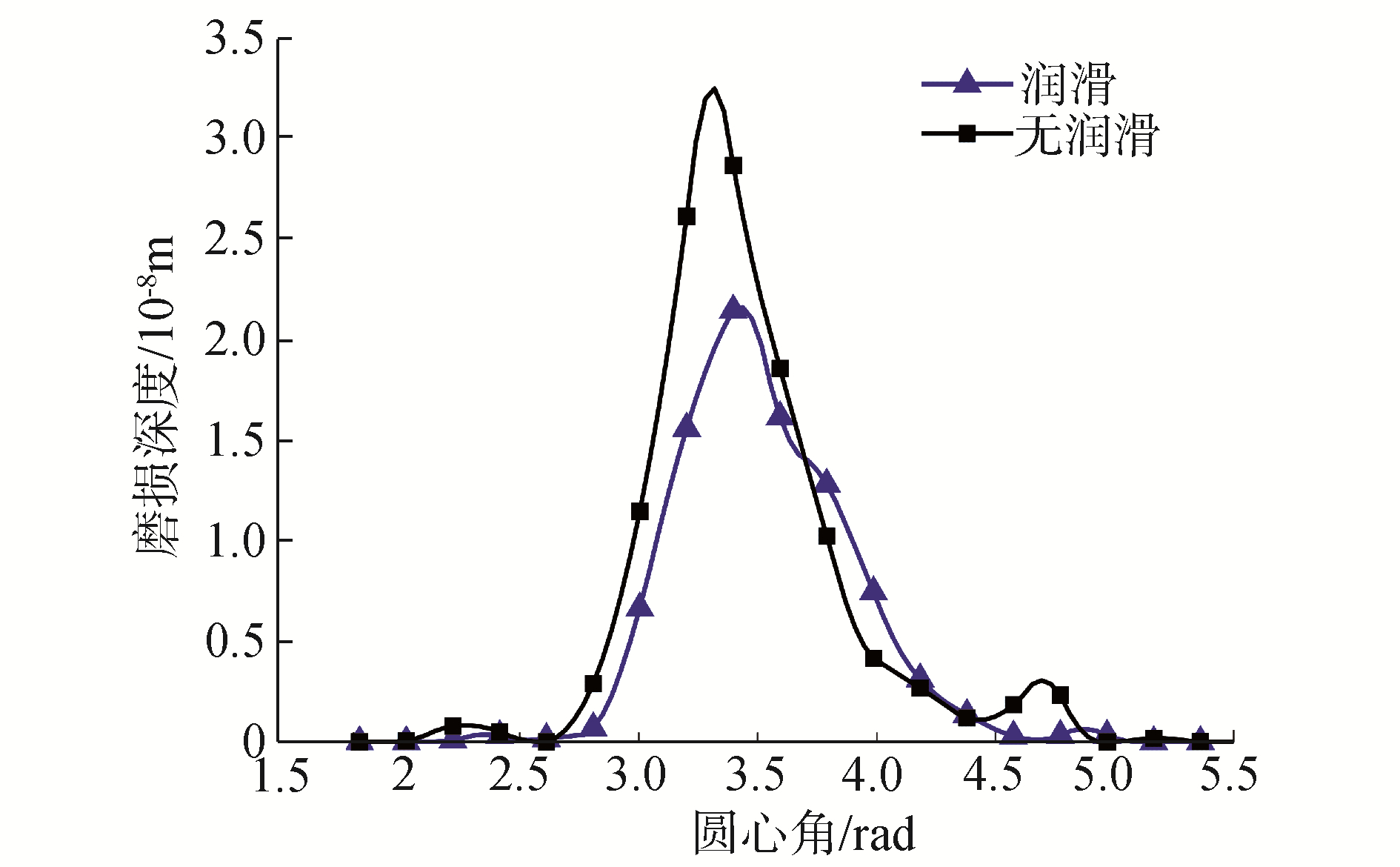
3.2 润滑条件下关节磨损大多数机械系统在实际使用中通常使用润滑剂,因此为研究关节润滑对于磨损深度的影响,本文对比分析了有无润滑条件下关节磨损深度。对于给定的间隙尺寸(c=0.20 mm)及驱动速度(ω=7π),图 9~11分别为有无润滑条件下含间隙关节轴心轨迹图及磨损深度。
|
Download:
|
| 图 9 轴心轨迹 Fig. 9 Shaft center trajectory | |
|
Download:
|
| 图 10 磨损深度 Fig. 10 Wear depth | |
|
Download:
|
| 图 11 磨损深度变化曲线 Fig. 11 Variation of wear depth | |
由图 9轴心轨迹可知,随着关节润滑的引入,间隙关节元素间冲击现象显著减轻且使侵入深度减小,轴心轨迹相对变得规整。由图 10、图 11可知,润滑条件下轴承磨损深度显著减小,但润滑因素对于磨损区域的分布影响较小。
4 结论1) 通过对4种不同驱动速度以及4种间隙尺寸下该3-CPaR&R1R2混联机构关节磨损研究可知,较高的驱动速度可使磨损分布均匀但会使磨损深度显著增加;间隙尺寸的增加会使磨损深度增加但其对磨损深度的影响相对较小。
2) 通过对有无润滑条件下含间隙关节磨损研究可知,含润滑条件下间隙关节磨损深度显著减小但其对于磨损区域的分布影响较小。
本文在考虑关节润滑条件下对含间隙3-CPaR&R1R2混联机构进行动力学建模及数值仿真,在后续的研究工作中将进行相应的样机实验研究,并考虑多间隙及不同的间隙位置对于该系统动力学及磨损特性的影响。
| [1] |
REIS V L, DANIEL G B, CAVALCA K L. Dynamic analysis of a lubricated planar slider-crank mechanism considering friction and Hertz contact effects[J]. Mechanism and machine theory, 2014, 74: 257-273. DOI:10.1016/j.mechmachtheory.2013.11.009 (  0) 0)
|
| [2] |
QUENTAL C, FOLGADO J, AMBRÓSIO J, et al. A new shoulder model with a biologically inspired glenohumeral joint[J]. Medical engineering & physics, 2016, 38(9): 969-977. (  0) 0)
|
| [3] |
CHEN Genliang, WANG Hao, LIN Zhongqin. A unified approach to the accuracy analysis of planar parallel manipulators both with input uncertainties and joint clearance[J]. Mechanism and machine theory, 2013, 64: 1-17. DOI:10.1016/j.mechmachtheory.2013.01.005 (  0) 0)
|
| [4] |
KOSHY C S, FLORES P, LANKARANI H M. Study of the effect of contact force model on the dynamic response of mechanical systems with dry clearance joints: computational and experimental approaches[J]. Nonlinear dynamics, 2013, 73(1/2): 325-338. DOI:10.1007%2Fs11071-013-0787-x (  0) 0)
|
| [5] |
PHAM H T, WANG D A. A constant-force bistable mechanism for force regulation and overload protection[J]. Mechanism and machine theory, 2011, 46(7): 899-909. DOI:10.1016/j.mechmachtheory.2011.02.008 (  0) 0)
|
| [6] |
DOPICO D, LUACES A, GONZALEZ M, et al. Dealing with multiple contacts in a human-in-the-loop application[J]. Multibody system dynamics, 2011, 25(2): 167-183. DOI:10.1007/s11044-010-9230-y (  0) 0)
|
| [7] |
DONG Xu, SONG Jin, YE Jin, et al. Kinetic uncertainty analysis of the reheat-stop-valve mechanism with multiple factors[J]. Mechanism and machine theory, 2010, 45(11): 1745-1765. DOI:10.1016/j.mechmachtheory.2010.06.001 (  0) 0)
|
| [8] |
MUKRAS S, KIM N H, MAUNTLER N A, et al. Analysis of planar multibody systems with revolute joint wear[J]. Wear, 2010, 268(5/6): 643-652. (  0) 0)
|
| [9] |
TASORA A, PRATI E, SILVESTRI M. Experimental investigation of clearance effects in a revolute joint[C]//Proceedings of 2004 AIMETA International Tribology Conference. Rome, 2004: 1-8.
(  0) 0)
|
| [10] |
MUKRAS S M. Analysis and design of planar multibody systems with revolute joint wear[D]. Florida: University of Florida, 2009.
(  0) 0)
|
| [11] |
FLORES P. Modeling and simulation of wear in revolute clearance joints in multibody systems[J]. Mechanism and machine theory, 2009, 44(6): 1211-1222. DOI:10.1016/j.mechmachtheory.2008.08.003 (  0) 0)
|
| [12] |
LI Pei, CHEN Wei, ZHU Aibin. An improved practical model for wear prediction of revolute clearance joints in crank slider mechanisms[J]. Science China technological sciences, 2013, 56(12): 2953-2963. DOI:10.1007/s11431-013-5401-4 (  0) 0)
|
| [13] |
WANG Gengxiang, LIU Hongzhao. Dynamic analysis and wear prediction of planar five-bar mechanism considering multiflexible links and multiclearance joints[J]. Journal of tribology, 2017, 139(5): 051606. DOI:10.1115/1.4035478 (  0) 0)
|
| [14] |
ZHAO Bo, ZHANG Zhinan, FANG Congcong, et al. Modeling and analysis of planar multibody system with mixed lubricated revolute joint[J]. Tribology international, 2016, 98: 229-241. DOI:10.1016/j.triboint.2016.02.024 (  0) 0)
|
| [15] |
TIAN Qiang, ZHANG Yunqing, CHEN Liping, et al. Simulation of planar flexible multibody systems with clearance and lubricated revolute joints[J]. Nonlinear dynamics, 2010, 60(4): 489-511. DOI:10.1007/s11071-009-9610-0 (  0) 0)
|
| [16] |
FLORES P, AMBRÓSIO J, CLARO J P. Dynamic analysis for planar multibody mechanical systems with lubricated joints[J]. Multibody system dynamics, 2004, 12(1): 47-74. DOI:10.1023/B:MUBO.0000042901.74498.3a (  0) 0)
|
| [17] |
MACHADO M, MOREIRA P, FLORES P, et al. Compliant contact force models in multibody dynamics: evolution of the Hertz contact theory[J]. Mechanism and machine theory, 2012, 53: 99-121. DOI:10.1016/j.mechmachtheory.2012.02.010 (  0) 0)
|
| [18] |
王庚祥, 刘宏昭. 考虑球面副间隙的4-SPS/CU并联机构动力学分析[J]. 机械工程学报, 2015, 51(1): 43-51. WANG Gengxiang, LIU Hongzhao. Dynamics analysis of 4-SPS/CU parallel mechanism with spherical joint clearance[J]. Journal of mechanical engineering, 2015, 51(1): 43-51. (  0) 0)
|
| [19] |
AMBRÓSIO J A C. Impact of rigid and flexible multibody systems: deformation description and contact models[M]//SCHIEHLEN W, VALÁŠEK M. Virtual Nonlinear Multibody Systems. Dordrecht: Springer, 2003: 57-81.
(  0) 0)
|
| [20] |
FLORES P, AMBRÓSIO J, CLARO J C P, et al. Lubricated revolute joints in rigid multibody systems[J]. Nonlinear dynamics, 2009, 56(3): 277-295. DOI:10.1007/s11071-008-9399-2 (  0) 0)
|
| [21] |
MUKRAS S, KIM N H, SAWYER W G, et al. Numerical integration schemes and parallel computation for wear prediction using finite element method[J]. Wear, 2009, 266(7/8): 822-831. (  0) 0)
|
| [22] |
FLODIN A, ANDERSSON S. A simplified model for wear prediction in helical gears[J]. Wear, 2001, 249(3/4): 285-292. (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


