挖掘机自动控制一直是工程领域研究的热点。文献[1-4]采用滑模变结构或其与模糊逻辑、自适应理论的结合,调节挖掘机输入转矩,使关节转角跟踪规划值,仿真结果证明了算法有效性。挖掘机工作装置由单活塞杆液压缸驱动,相较于电机驱动的机械臂,由于液压缸系统的非线性,采用关节转矩作为输入,控制不直接且控制精度低,使关节转角实际轨迹与规划轨迹存在很大误差,进而使铲斗斗尖在工作空间不能有效跟踪规划路径。为此,文献[5]分析了某机械臂系统液压伺服驱动空间与关节空间关系,以关节转矩为纽带,建立输入伺服电流与输出关节转角间的数学模型,从而将控制器设计转移到伺服驱动空间。
针对液压伺服系统的控制,阻抗滑模控制[6]、高阶滑模控制[7]、非连续投射[8-9]、及其与滑模控制的结合[10]、反馈线性化滑模控制[11-13], 被广泛应用并取得较好的仿真试验效果。然而上述控制方式需要采集活塞杆位移、速度或加速度,以及液压缸两腔压力信号,增加了控制成本。为降低传感器使用数量,观测器被引入至控制器的设计,用来对状态变量或干扰进行观测[14-19]。文献[14]基于投射法对干扰进行观测,文献[15]基于低通滤波对速度观测,文献[16]基于扩张观测器对状态变量及干扰观测,并采用反演法设计液压系统控制器。相较于上述观测器,高增益观测器能够对控制所需的所有状态信息进行有效估计,且设计更为简单,容易实现。文献[17]构造了基于高增益状态观测器的电液系统无源控制器,仿真与试验验证了控制输出活塞杆位移对目标位移信号优良的跟随性能。文献[18]设计了基于高增益观测器的积分滑模控制器,并采用奇异摄动理论证明了闭环系统的稳定性。文献[19]针对电液系统构造了基于高增益观测器的反演控制器,仿真与试验效果较好。
本文通过计算挖掘机关节空间与驱动空间的位移、速度与力之间的关系,得到控制输入伺服阀电压与关节转角之间的关系。采用基于高增益观测器的滑模控制理论,对驱动空间电液系统进行轨迹控制。并采用奇异摄动方法,将观测器状态观测误差与系统控制误差分别作为快变子系统变量与慢变子系统变量,基于李雅普诺夫函数,证明闭环系统稳定。相较于文献[18],本文采用文献[20]中高增益观测器的设计方法,只需调节观测器带宽参数,不需整定其他增益参数,因而观测器设计更加简便;在滑模控制中,采用滑模面函数代替符号函数,消除了抖振且对闭环系统稳定性有重要作用;在液压系统中引入匹配不确定项与非匹配不确定项,通过定义新的状态变量,对非匹配不确定项补偿。仿真结果表明本文设计的基于高增益观测器的滑模控制器效果较好,且对匹配与非匹配不确定项有良好的鲁棒性。
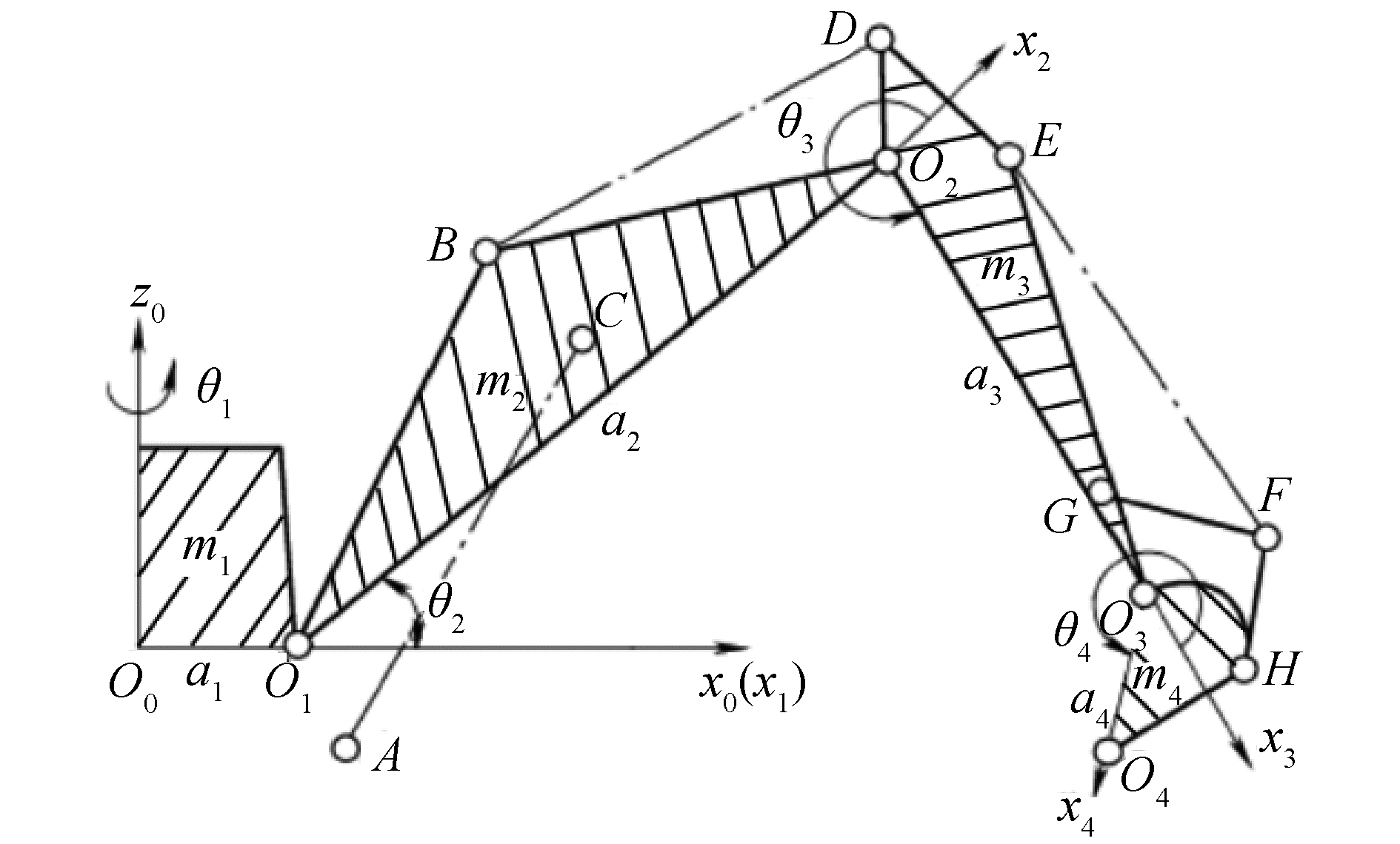
1 挖掘机规划轨迹生成 1.1 挖掘机驱动空间与关节空间关系图 1为挖掘机工作装置模型,采用D-H方法建立了系统坐标。
|
Download:
|
| 图 1 挖掘机工作装置模型 Fig. 1 Coordinate frames of the excavator | |
则挖掘机关节空间关节转角与驱动空间液压缸活塞杆长度之间的关系:
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{\theta _2} = \arccos \left( {\frac{{l_{{O_1}C}^2 + l_{{O_1}A}^2 - l_{AC}^2}}{{2{l_{{O_1}C}}{l_{{O_1}A}}}}} \right) - \angle C{O_1}{O_2} - \angle A{O_1}{x_1}}\\ {{\theta _3} = {\rm{ \mathsf{ π} }} - \arccos \left( {\frac{{l_{{O_2}D}^2 + l_{{O_2}B}^2 - l_{BD}^2}}{{2{l_{{O_2}D}}{l_{{O_2}B}}}}} \right) - \angle {O_1}{O_2}B - \angle D{O_2}{O_3}}\\ {{\theta _4} = {\rm{ \mathsf{ π} }} - \angle G{O_3}{O_2} - \angle G{O_3}F - \angle H{O_3}F - \angle H{O_3}{O_4}} \end{array}\\ \begin{array}{*{20}{l}} {\angle EGF = \arccos \left( {\frac{{l_{GE}^2 + l_{GF}^2 - l_{EF}^2}}{{2{l_{GE}}{l_{GF}}}}} \right)}\\ {\angle {O_3}GF = 2{\rm{ \mathsf{ π} }} - \angle EGF - \angle EG{O_2} - \angle {O_2}G{O_3}} \end{array}\\ \begin{array}{*{20}{l}} {{l_{{O_3}F}} = \sqrt {l_{{O_3}G}^2 + l_{FG}^2 - 2{l_{{O_3}G}}{l_{FG}}\arccos \angle {O_3}GF} }\\ {\angle G{O_3}F = \arccos \left( {\frac{{l_{{O_3}G}^2 + l_{{O_3}F}^2 - l_{GF}^2}}{{2{l_{{O_3}G}}{l_{{O_3}F}}}}} \right)}\\ {\angle H{O_3}F = \arccos \left( {\frac{{l_{{O_3}H}^2 + l_{{O_3}F}^2 - l_{FH}^2}}{{2{l_{{O_3}H}}{l_{{O_3}F}}}}} \right)} \end{array} \end{array} \right. $ | (1) |
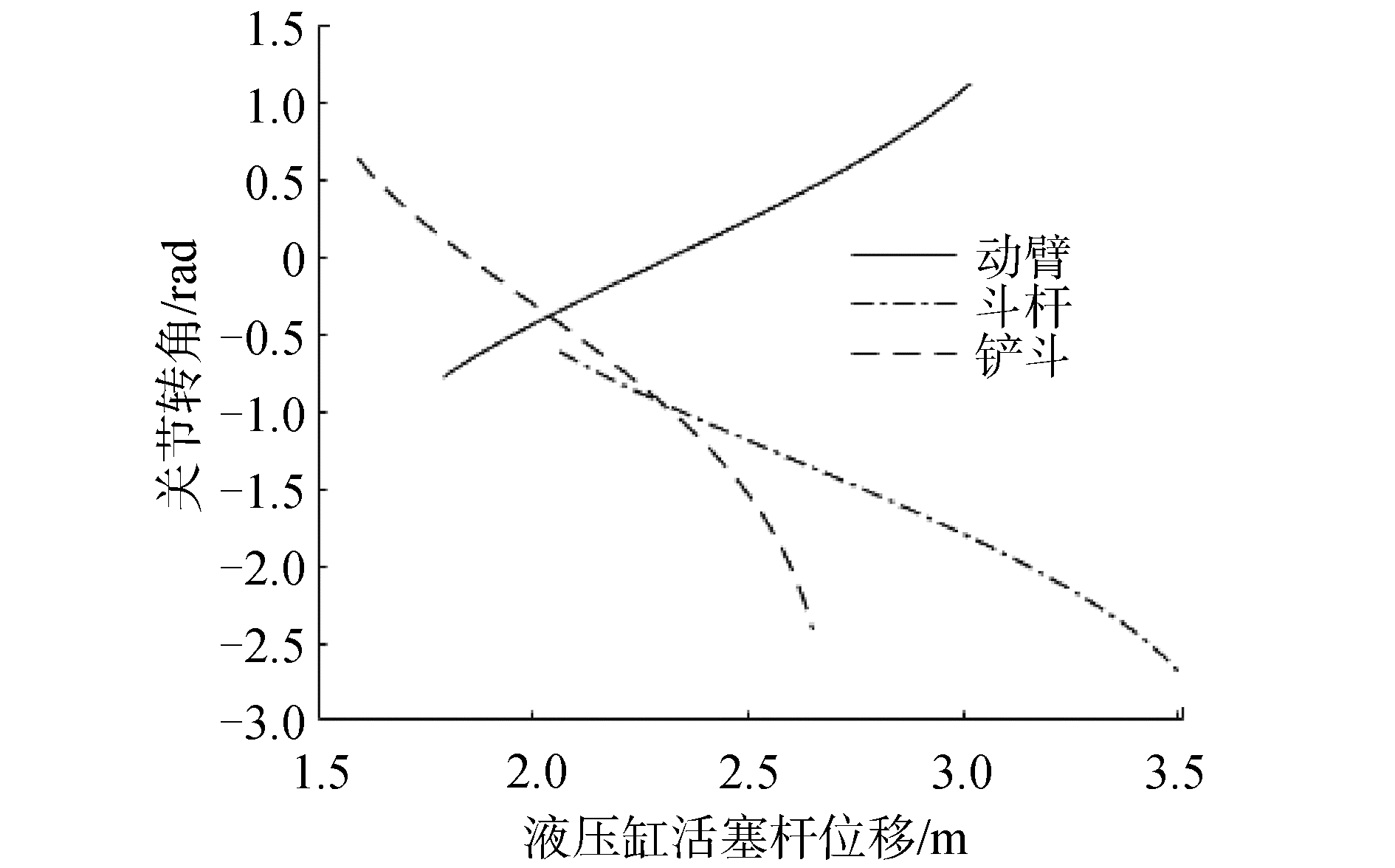
式中:∠CO1O2、∠AO1x1、∠O1O2B、∠DO2O3、∠GO3O2、∠HO3O4、∠EGO2、∠O2GO3与杆长lO1C、lO1A、lO2D、lO2B、lGE、lGF、lO3G、lO3H、lFG、lFH为常量,代入本文研究对象柳工某型液压挖掘样机参数,得到关节转角与对应液压缸活塞杆长度曲线如图 2所示。
|
Download:
|
| 图 2 液压挖掘机活塞杆位移与对应转角关系 Fig. 2 The relationship between piston rod displacement and corresponding rotation angle | |
由虚功原理,关节转矩与驱动力关系表示为:
| $ \left\{\begin{array}{l} \dot{\boldsymbol{\theta}}=\boldsymbol{J} \dot{\boldsymbol{l}} \\ \boldsymbol{\tau}=\boldsymbol{D}(\boldsymbol{\theta}) \boldsymbol{\theta}+\boldsymbol{C}(\boldsymbol{\theta}, \dot{\boldsymbol{\theta}}) \dot{\boldsymbol{\theta}}+\boldsymbol{G}(\boldsymbol{\theta}) \\ \boldsymbol{F}=\boldsymbol{J}^{\mathrm{T}} \boldsymbol{\tau} \end{array}\right. $ | (2) |
式中: θ=(θ2 θ3 θ4)T为关节转角向量;l=(lAC lBD lEF)T为活塞杆长度向量;τ=(τO1 τO2 τO3)T为对应关节转矩向量;D(θ)为关节空间惯性矩阵;
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{J}} = {\mathop{\rm diag}\nolimits} \left( {{J_1},\quad {J_2},\quad {J_3}} \right) = }\\ {{\mathop{\rm diag}\nolimits} \left( {\frac{{{l_{AC}}}}{{{l_{{O_1}C}}{l_{{O_1}A}}\sin {\varphi _2}}},\quad \frac{{{l_{BD}}}}{{{l_{{O_2}D}}{l_{{O_2}B}}\sin {\varphi _3}}},\quad \frac{{{l_{EH}}}}{{{l_{{O_3}E}}{l_{{O_3}H}}\sin {\varphi _4}}}} \right)} \end{array} $ | (3) |
式中:
挖掘机不考虑回转时,其铲斗末端轨迹在基坐标系O0x0y0z0(图 1)中表示为:
| $ \left\{\begin{array}{l} x_{0}=a_{4} c_{234}+a_{3} c_{23}+a_{2} c_{2}+a_{1} \\ z_{0}=a_{4} s_{234}+a_{3} s_{23}+a_{2} s_{2} \end{array}\right. $ | (4) |
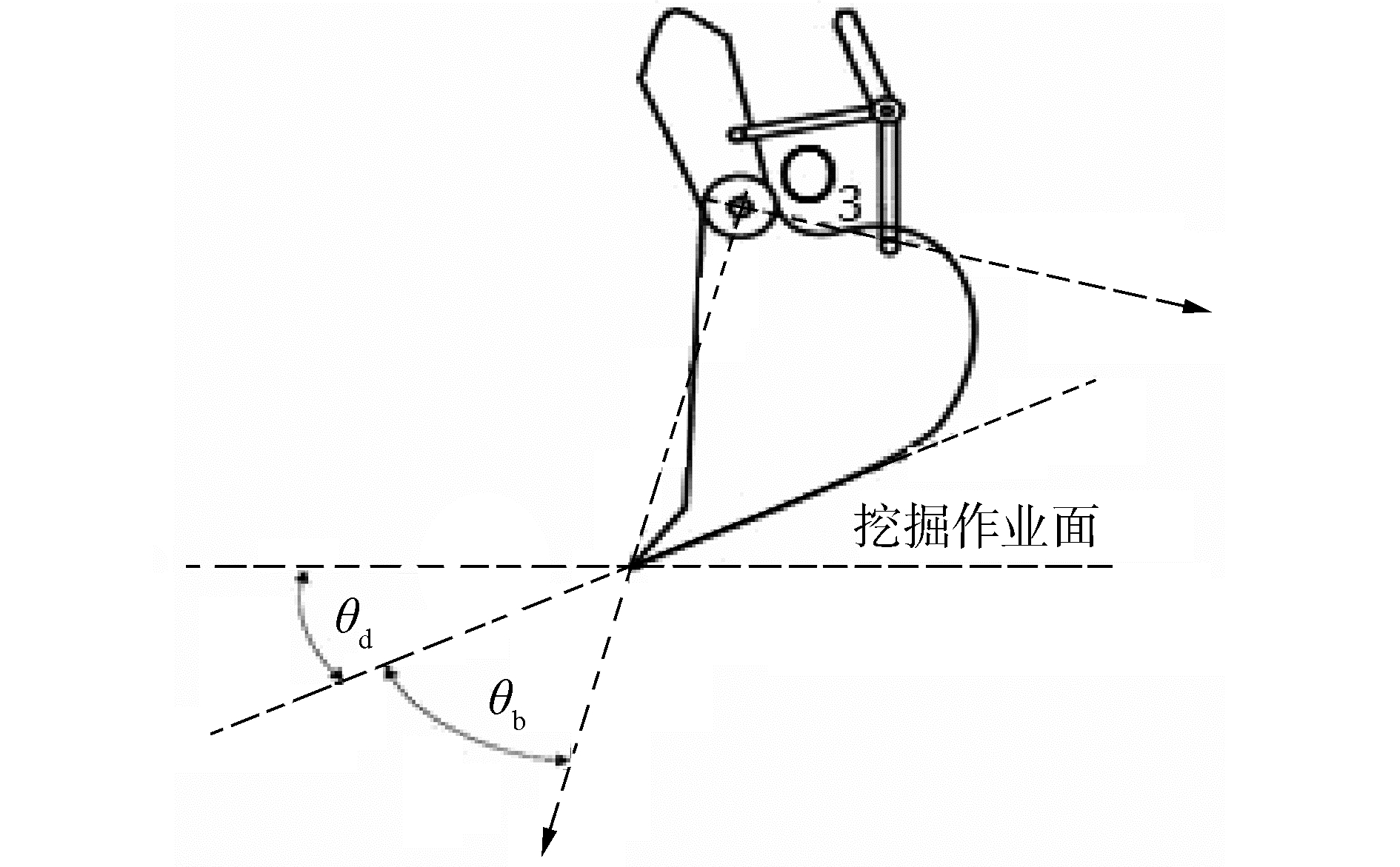
式中:a1为动臂铰接点水平长度,a2为动臂杆长,a3为斗杆杆长,a4为铲斗杆长,c234=cos(θ2+θ3+θ4),s234=sin(θ2+θ3+θ4)等。以挖掘机整平作业为例,实际中要求铲斗相对设定直线轨迹以固定的切削角进行工作。如图 3所示,θd为固定切削角,θb为铲斗齿尖与销轴的连线与切削板的夹角,则铲斗位姿角φ表示为:
| $ \varphi = {\theta _2} + {\theta _3} + {\theta _4} = {\theta _d} + {\theta _b} - {\rm{ \mathsf{ π} }} $ | (5) |
|
Download:
|
| 图 3 挖掘机整平作业铲斗位姿 Fig. 3 The bucket posture of the excavator during straight-line motion | |
即φ为固定值。
采用速度规划曲线[21]
| $ \left\{\begin{array}{l} \dot{x}_{0}=-0.4 t(\mathrm{m} / \mathrm{s}), \quad 0 \leqslant t \leqslant 1.5 \mathrm{~s} \\ \dot{x}_{0}=-0.6(\mathrm{m} / \mathrm{s}), \quad 1.5 \mathrm{~s}<t \leqslant 5.5 \mathrm{~s} \\ \dot{x}_{0}=-7.2+1.2 t(\mathrm{m} / \mathrm{s}), \quad 5.5 \mathrm{~s}<t \leqslant 6.0 \mathrm{~s} \end{array}\right. $ | (6) |
在水平作业面,以切削角θb=π/6进行整平作业(铲斗斗尖从机身远端移动至近端),由几何关系式:
| $ \left\{\begin{array}{l} \theta_{3} =-\arccos \left(\frac{\left(x_{0}-a_{1}-a_{4} \cos \varphi\right)^{2}}{2 a_{2} a_{3}}+\right.\\ \ \ \ \ \left.\frac{\left(z_{0}-a_{4} \sin \varphi\right)^{2}-a_{2}^{2}-a_{3}^{2}}{2 a_{2} a_{3}}\right) \\ \alpha =\arctan \left(\frac{z_{0}-a_{4} \sin \varphi}{x_{0}-a_{1}-a_{4} \cos \varphi}\right) \\ \beta =\arccos \frac{\left(x_{0}-a_{1}-a_{4} \cos \varphi\right)^{2}+\left(z_{0}-a_{4} \sin \varphi\right)^{2}+a_{2}^{2}-a_{3}^{2}}{2 a_{2} \sqrt{\left(x_{0}-a_{1}-a_{4} \cos \varphi\right)^{2}+\left(z_{0}-a_{4} \sin \varphi\right)^{2}}} \\ \theta_{2} =\alpha+\beta \\ \theta_{4} =\varphi-\theta_{2}-\theta_{3} \end{array}\right. $ | (7) |
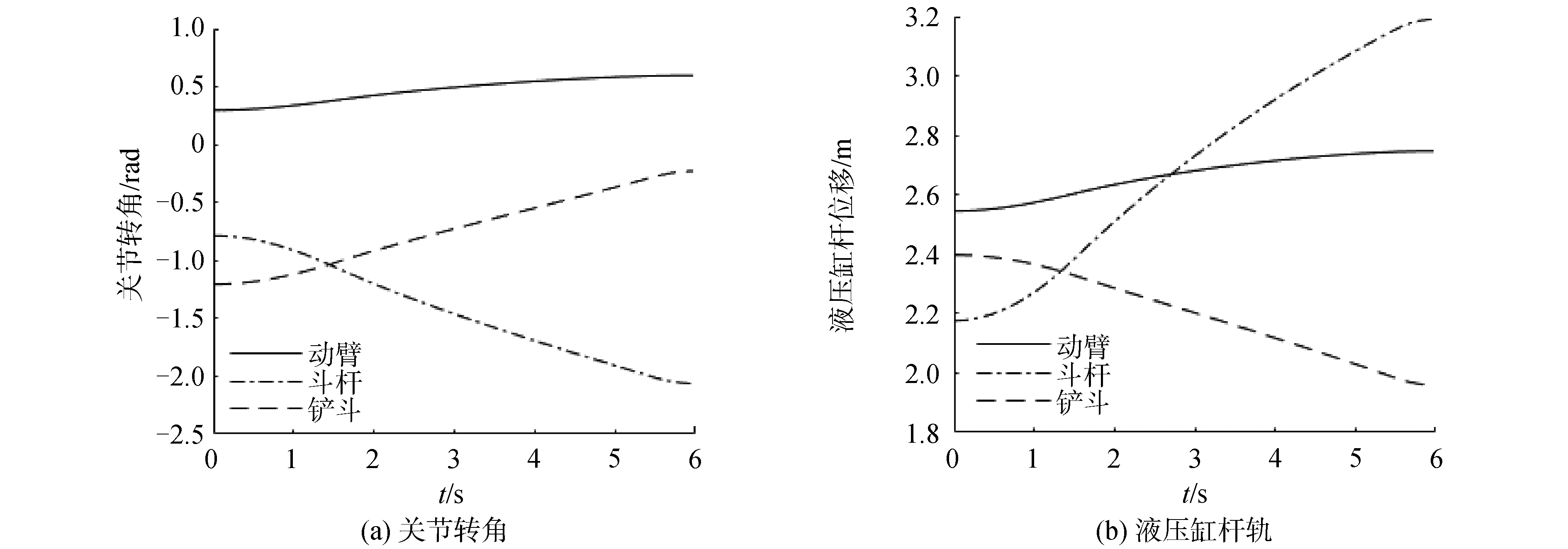
得到研究对象挖掘机动臂、斗杆与铲斗关节空间角度规划曲线及相应液压缸杆轨迹规划曲线,结果如图 4所示。
|
Download:
|
| 图 4 挖掘机作业面为水平面时的规划曲线 Fig. 4 Excavator planning curves with horizontal working surface | |
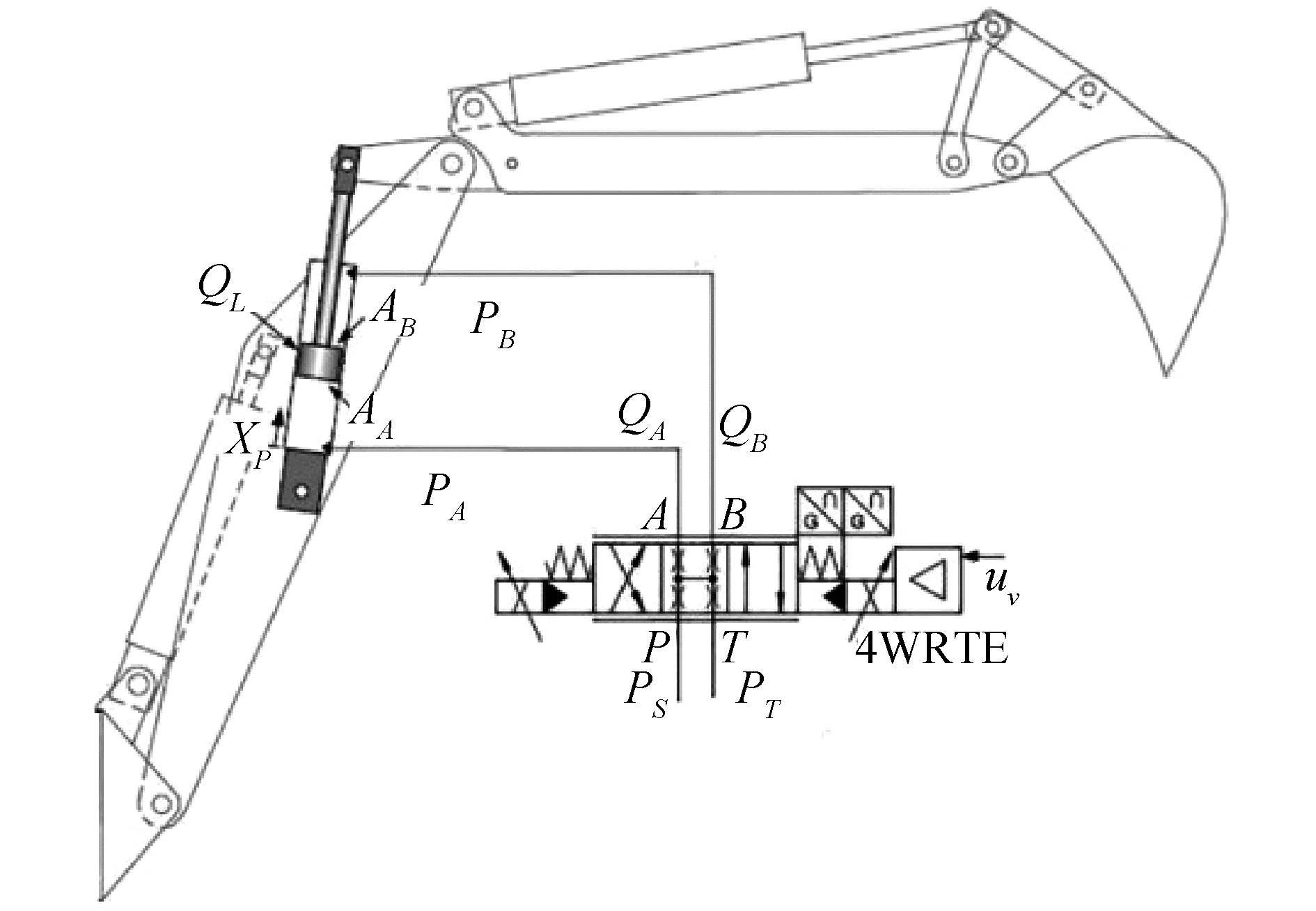
根据文献[22],对挖掘机进行电液比例改造,图 5为改造后斗杆阀控非对称液压缸结构框图。PS与PT分别为液压泵供油压力与回油压力,UV为电磁阀阀芯位移,xp=lBD为斗杆活塞杆长度,QA与QB分别表示流入非对称缸无杆腔的流量与流出有杆腔的流量,PA、AA与VA分别表示无杆腔压力,活塞面积与容积。PB、AB与VB则表示有杆腔压力,活塞面积与容积。
|
Download:
|
| 图 5 斗杆液压系统 Fig. 5 The schematic of the stick cylinder system | |
斗杆液压缸力平衡方程为:
| $ m \ddot{x}_{p}+c \dot{x}_{p}+k x_{p}+F_{B D}=P_{A} A_{A}-P_{B} A_{B} $ | (8) |
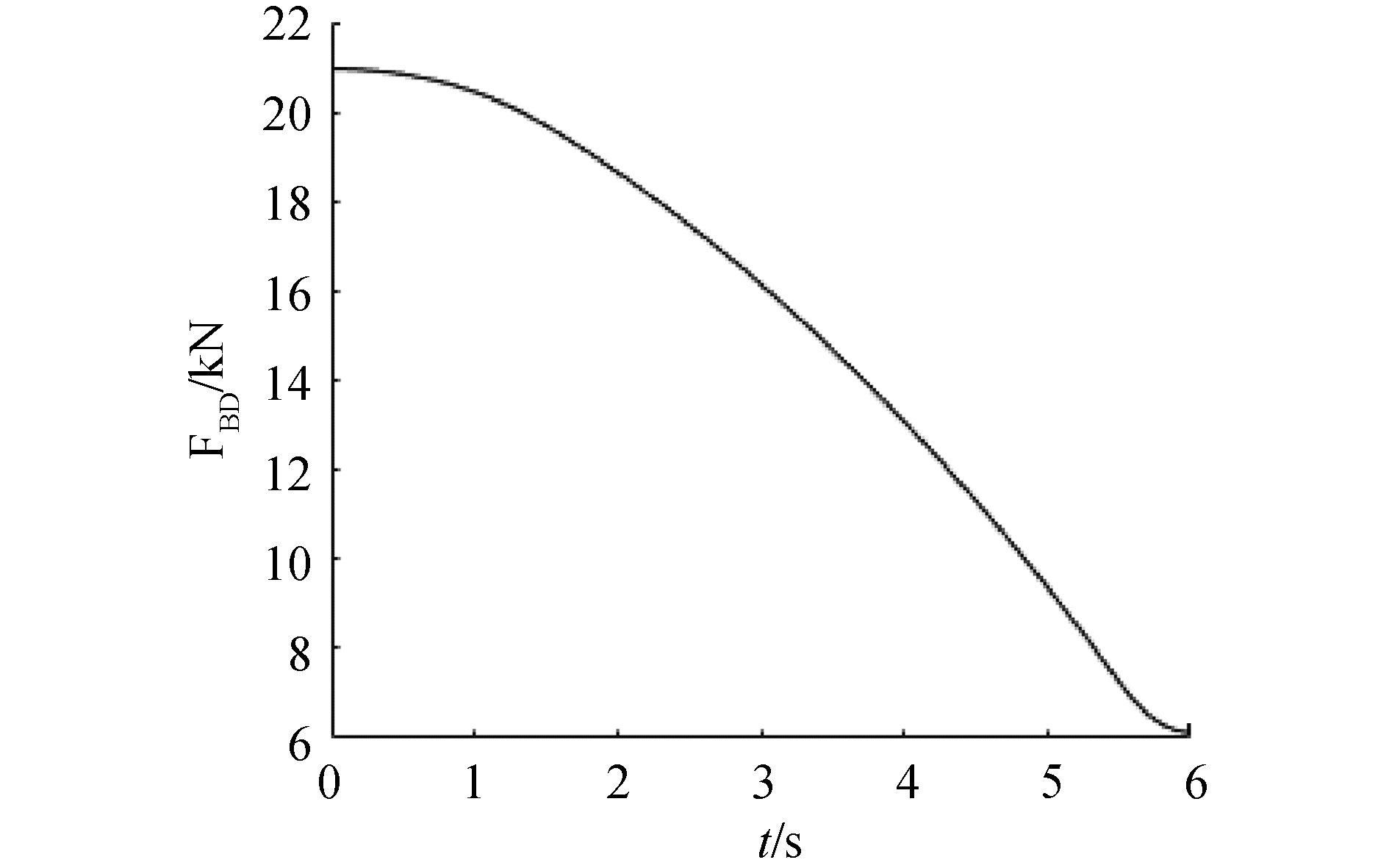
式中:m为活塞杆及腔内液体等效质量;c为活塞杆粘性阻尼系数;k为活塞杆刚度系数。FBD为式(2)中对应于斗杆的驱动力分量。挖掘机在水平作业面按照规划速度整平作业,考虑自重影响不计斗尖阻力时,FBD理论计算结果如图 6。
|
Download:
|
| 图 6 FBD的理论值 Fig. 6 Nominal value of FBD | |
斗杆阀控非对称液压缸在不考虑泄露因素条件下的流量连续性方程为:
| $ \left\{\begin{array}{l} Q_{A}=\frac{V_{A}}{\beta} \dot{P}_{A}+A_{A} \dot{x}_{p} \\ Q_{B}=-\frac{V_{B}}{\beta} \dot{P}_{B}+A_{B} \dot{x}_{p} \end{array}\right. $ | (9) |
式中:VA=VA0+AAxp为无杆腔容积,VB=VB0-ABxp有杆腔容积,VA0与VB0为各腔初始容积, β为液压油液弹性模量。阀的节流方程:
| $ \left\{\begin{array}{l} Q_{A}=h_{1} U_{V} \sqrt{\Delta P_{A}}, \Delta P_{A}=\left\{\begin{array}{l} P_{S}-P_{A}, U_{V} \geqslant 0 \\ P_{A}-P_{T}, U_{V}<0 \end{array}\right. \\ Q_{B}=h_{2} U_{V} \sqrt{\Delta P_{B}}, \Delta P_{B}=\left\{\begin{array}{l} P_{B}-P_{T}, U_{V} \geqslant 0 \\ P_{S}-P_{B}, U_{V}<0 \end{array}\right. \end{array}\right. $ | (10) |
式中h1与h2为流量增益系数。根据比例伺服阀特性曲线,流量QA和QB与伺服阀输入电压Vin的关系可线性化表示为[23]:
| $ \left\{\begin{array}{l} Q_{A}=\left\{\begin{array}{ll} K V_{\mathrm{in}}, & \dot{x}_{p} \geqslant 0 \\ \gamma K V_{\mathrm{in}}, & \dot{x}_{p}<0 \end{array}\right. \\ Q_{B}=\left\{\begin{array}{ll} \frac{K}{\gamma} V_{\mathrm{in}}, & \dot{x}_{p} \geqslant 0 \\ K V_{\mathrm{in}}, & \dot{x}_{p} <0 \end{array}\right. \end{array}\right. $ | (11) |
式中:K为流量信号增益,γ=AA/AB。令
| $ \left\{\begin{array}{l} \dot{x}_{1}=x_{2} \\ \dot{x}_{2}=-k_{1} x_{1}-k_{2} x_{2}+k_{3} x_{3}-T+d_{1}(t) \\ \dot{x}_{3}=-g_{1}\left(x_{1}\right) x_{2}+g_{2}\left(x_{1}\right) u+d_{2}(t) \end{array}\right. $ | (12) |
式中:
以斗杆液压缸活塞杆轨迹控制为例,挖掘机在水平作业面整平作业时,采用规划速度曲线得到的斗杆液压缸活塞杆规划轨迹如图 4(b)点划线所示。为了降低控制成本,减少传感器使用数量,仅使用位移传感器测量活塞杆实际长度,采用高增益观测器对其他控制状态变量进行观测。为对非匹配不确定项d1(t)补偿,定义状态变量:
| $ \left\{\begin{array}{l} z_{1}=x_{1} \\ z_{2}=x_{2} \\ z_{3}=-k_{1} x_{1}-k_{2} x_{2}+k_{3} x_{3}-T+d_{1}(t) \end{array}\right. $ | (13) |
则式(12)转换为:
| $ \left\{\begin{array}{l} \dot{z}_{1}=z_{2} \\ \dot{z}_{2}=z_{3} \\ \dot{z}_{3}=-\left[g_{1}\left(z_{1}\right) k_{3}+k_{1}\right] z_{2}-k_{2} z_{3}+ \\ \quad g_{2}\left(z_{1}\right) k_{3} u+d(t) \end{array}\right. $ | (14) |
式中
| $ \left\{\begin{array}{l} \dot{z}_{1}=\hat{z}_{2}+\frac{3}{\varepsilon}\left(y-\hat{z}_{1}\right) \\ \dot{z}_{2}=\hat{z}_{3}+\frac{3}{\varepsilon^{2}}\left(y-\hat{z}_{1}\right) \\ \dot{\hat{z}}_{3}=-\left[g_{1}\left(\hat{z}_{1}\right) k_{3}+k_{1}\right] \hat{z}_{2}-k_{2} \hat{z}_{3} \\ +g_{2}\left(\hat{z}_{1}\right) k_{3} u+\frac{1}{\varepsilon^{3}}\left(y-\hat{z}_{1}\right) \end{array}\right. $ | (15) |
式中:状态
| $ \left\| {\mathit{\boldsymbol{\hat z}}(t) - \mathit{\boldsymbol{z}}(t)} \right\| \le \lambda \frac{1}{{{\varepsilon ^2}}}{e^{ - {\mu _\varepsilon }t}}\left\| {\mathit{\boldsymbol{\hat z}}(0) - \mathit{\boldsymbol{z}}(0)} \right\| + {M_\varepsilon }\sigma $ | (16) |
式中σ为不确定项上界。且有
根据滑模变结构理论定义滑模面:
| $ \left\{\begin{array}{l} s=a^{2} e_{1}+2 a e_{2}+e_{3} \\ \hat{s}=a^{2} \hat{e}_{1}+2 a \hat{e}_{2}+\hat{e}_{3} \end{array}\right. $ | (17) |
式中:s为闭环系统实际滑模面;
| $ \begin{array}{c} \dot{\hat{s}}=a^{2} \dot{\hat{e}}_{1}+2 a \dot{\hat{e}}_{2}+\dot{\hat{e}}_{3}=a^{2} \hat{e}_{2}+2 a \hat{e}_{3}+\dddot{y}_{d}+ \\ {\left[g_{1}\left(\hat{z}_{1}\right) k_{3}+k_{1}\right] \hat{z}_{2}+k_{2} \hat{z}_{3}-g_{2}\left(\hat{z}_{1}\right) k_{3} u} \end{array} $ | (18) |
设计控制输入u为:
| $ \left\{ \begin{array}{l} u = {u_{eq}} + {u_{sw}}\\ {u_{eq}} = \frac{1}{{{g_2}\left( {{{\hat z}_1}} \right){k_3}}}\left( {{a^2}{{\hat e}_2} + 2a{{\hat e}_3} + {{\dddot y}_d} + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\left[ {{g_1}\left( {{{\hat z}_1}} \right){k_3} + {k_1}} \right]{{\hat z}_2} + {k_2}{{\hat z}_3}} \right)\\ {u_{sw}} = \frac{1}{{{g_2}\left( {{{\hat z}_1}} \right){k_3}}}\kappa {\mathop{\rm sign}\nolimits} (\hat s) \end{array} \right. $ | (19) |
式中:ueq为
| $ u_{s w}=\frac{1}{g_{2}\left(\hat{z}_{1}\right) k_{3}} \kappa\hat{s} $ | (20) |
因为
| $ \begin{array}{c} \dot{s}=\dot{\tilde{s}}+\dot{\hat{s}}=\dot{\tilde{s}}+a^{2} \hat{e}_{2}+2 a \hat{e}_{3}+\dddot{y}_{d}+k_{2} \hat{z}_{3}+ \\ {\left[g_{1}\left(\hat{z}_{1}\right) k_{3}+k_{1}\right] \hat{z}_{2}-g_{2}\left(\hat{z}_{1}\right) k_{3} u=\dot{\tilde{s}}-\kappa \hat{s}=} \\ \kappa \tilde{s}+\dot{\tilde{s}}-\kappa s=-\kappa s+f(\tilde{s}) \end{array} $ | (21) |
式中
| $ \left\{ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\tilde z}} = \mathit{\boldsymbol{z}} - \mathit{\boldsymbol{\hat z}} = \left[ {\begin{array}{*{20}{c}} {{{\tilde z}_1}}\\ {{{\tilde z}_2}}\\ {{{\tilde z}_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{z_1} - {{\hat z}_1}}\\ {{z_2} - {{\hat z}_2}}\\ {{z_3} - {{\hat z}_3}} \end{array}} \right]}\\ {\mathit{\boldsymbol{\eta }} = \left[ {\begin{array}{*{20}{l}} {{\eta _1}}\\ {{\eta _2}}\\ {{\eta _3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{1}{{{\varepsilon ^2}}}{{\tilde z}_1}}\\ {\frac{1}{\varepsilon }{{\tilde z}_2}}\\ {{{\tilde z}_3}} \end{array}} \right]} \end{array}} \right. $ | (22) |
则状态变量η与s可表示为奇异摄动标准形式:
| $ \left\{\begin{array}{l} \varepsilon \dot{\boldsymbol{\eta}}=\boldsymbol{A} \boldsymbol{\eta}+\boldsymbol{\varepsilon} \boldsymbol{\delta}(\boldsymbol{\eta}, \boldsymbol{z}, \hat{\boldsymbol{z}}, u) \\ \dot{s}=-\kappa s+f(\tilde{s}) \end{array}\right. $ | (23) |
式中:η为快变子系统状态变量;s为慢变子系统状态变量,且
| $ \boldsymbol{A}=\left[\begin{array}{c} A_{1} \\ A_{2} \\ A_{3} \end{array}\right]=\left[\begin{array}{lll} -3 & 1 & 0 \\ -3 & 0 & 1 \\ -1 & 0 & 0 \end{array}\right], $ |
| $ \begin{array}{c} \boldsymbol{\delta}(\eta, z, \hat{z}, u)=\left[\begin{array}{l} \delta_{1} \\ \delta_{2} \\ \delta_{3} \end{array}\right]= \\ \left[\begin{array}{c} 0 \\ 0 \\ g_{1}\left(\hat{z}_{1}\right) k_{3} \hat{z}_{2}-g_{1}\left(z_{1}\right) k_{3} z_{2}-k_{1} \varepsilon \eta_{2}+ \\ d-k_{2} \eta_{3}+\left(g_{2}\left(z_{1}\right)-g_{2}\left(\hat{z}_{1}\right)\right) k_{3} u \end{array}\right] \end{array} $ |
当
| $ \dot{s}=-\kappa $ | (24) |
定义李雅普诺夫函数:
| $ V=\frac{1}{2} s^{2} $ | (25) |
则有:
| $ \dot{V}=s \dot{s}=-\kappa s^{2}=-2 \kappa V \leqslant 0 $ | (26) |
易知V指数收敛,且在有限时间内
| $ \left[\begin{array}{c} \dot{e}_{1} \\ \dot{e}_{2} \end{array}\right]=\underbrace{\left[\begin{array}{cc} 0 & 1 \\ -a^{2} & -2 a \end{array}\right]}_{A_{e}}\left[\begin{array}{l} e_{1} \\ e_{2} \end{array}\right] $ | (27) |
因为Ae为Hurwitz,则跟踪误差e有限时间指数收敛。将式(23)时间尺度变换为τ=t/ε,则系统变换为:
| $ \left\{\begin{array}{l} \frac{\mathrm{d}}{\mathrm{d} \tau} \boldsymbol{\eta}=\boldsymbol{A} \boldsymbol{\eta}+\varepsilon \boldsymbol{\delta}(\boldsymbol{\eta}, \boldsymbol{z}, \hat{\boldsymbol z}, u) \\ \frac{\mathrm{d}}{\mathrm{d} \tau} s=-\varepsilon \kappa s+\varepsilon f(\tilde{s}) \end{array}\right. $ | (28) |
当ε→0,式(28)表示为:
| $ \frac{\mathrm{d}}{\mathrm{d} \tau} \boldsymbol{\eta}=\boldsymbol{A} \boldsymbol{\eta} $ | (29) |
因为A是Hurwitz,存在正定矩阵Pη使得:
| $ \boldsymbol{A}^{\mathrm{T}} \boldsymbol{P}_{\eta}+\boldsymbol{P}_{\eta} \boldsymbol{A}=-\boldsymbol{I} $ | (30) |
定义李雅普诺夫函数为:
| $ V_{\eta}=\boldsymbol{\eta}^{\mathrm{T}} \boldsymbol{P}_{\eta} \boldsymbol{\eta} $ | (31) |
则其对时间尺度τ的微分:
| $ \frac{\mathrm{d}}{\mathrm{d} \tau} V_{\eta}=\boldsymbol{\eta}^{\mathrm{T}}\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P}_{\eta}+\boldsymbol{P}_{\eta} A\right) \boldsymbol{\eta}=-\boldsymbol{\eta}^{T} \boldsymbol{\eta} \leqslant 0 $ | (32) |
以斗杆液压系统轨迹控制为例,活塞杆及腔内液体等效质量m=160 kg,c=600 N ·s/m,由于液压缸负载以惯性负载为主,弹性负载近似为0,设定k=0 N/m,
| $ \begin{array}{c} d(t)=\left(-89.1 t^{4}+1142.16 t^{3}-4\ 805.82 t^{2}+\right. \\ 7\ 149.8 t+157.09) / 160+100 \cos (2 t)+ \\ 100 \sin (5 t) / 160 \end{array} $ | (33) |
式中T的名义值
| $ \begin{array}{c} \hat T = \left( {17.82{t^5} - 285.54{t^4} + 1{\kern 1pt} {\kern 1pt} 601.94{t^3} - } \right.\\ \left. {3{\kern 1pt} {\kern 1pt} 574.90{t^2} - 157.09t + 20{\kern 1pt} {\kern 1pt} 816.56} \right)/160 \end{array} $ |
T的误差及干扰包含于非匹配不确定项, d1(t)=50sin(2t),设计匹配不确定项为d2(t)=100cos(5t)。考虑斗杆活塞杆工作范围[2.063 m 3.513 m]及初始位姿,初始状态设定为
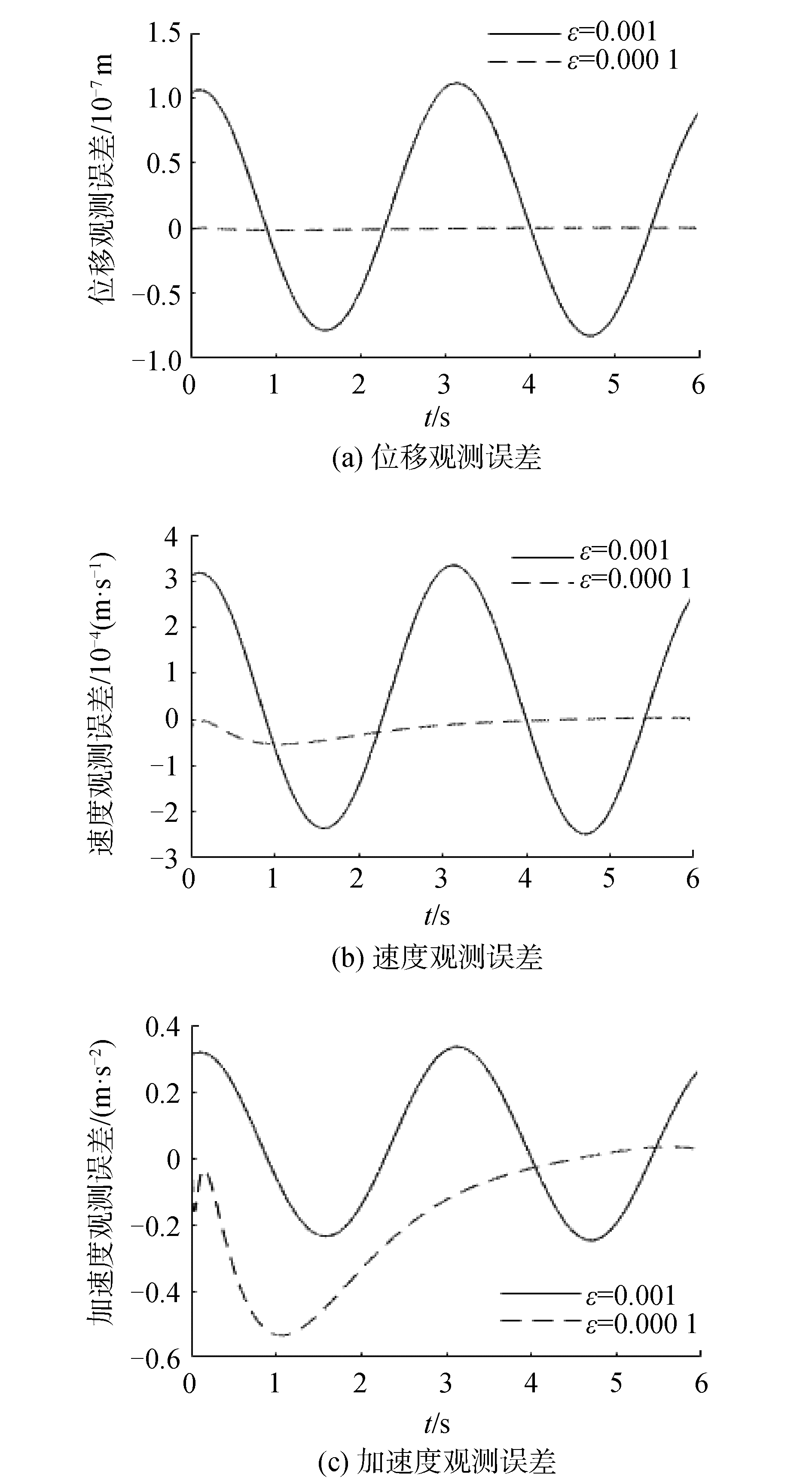
|
Download:
|
| 图 7 κ=100时ε对观测误差的影响 Fig. 7 The state estimation errors of high-gain observer with κ=100 | |
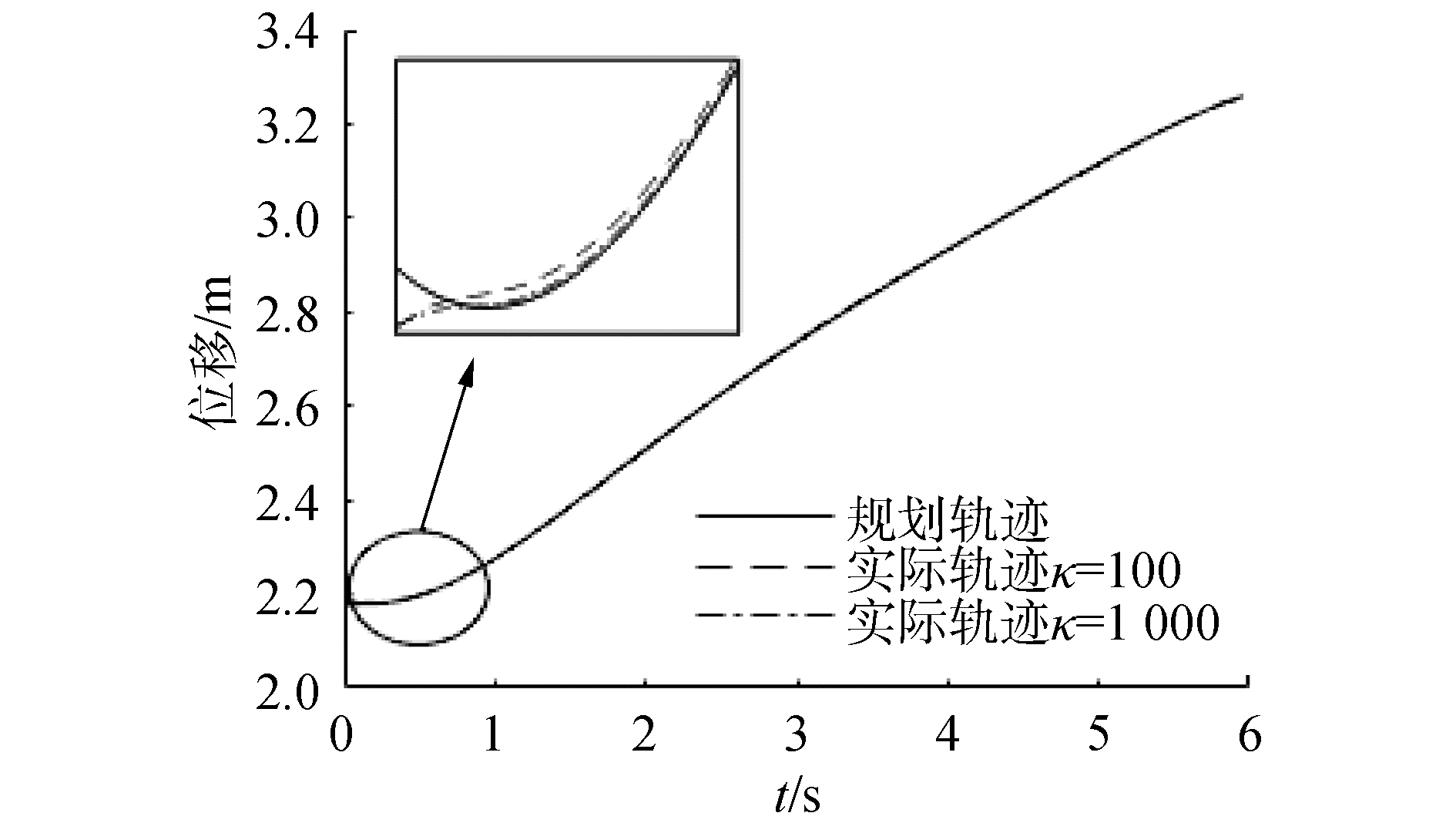
|
Download:
|
| 图 8 ε=0.001不同κ值的轨迹跟踪效果 Fig. 8 The tracking performance of the HOSMC with ε=0.001 | |
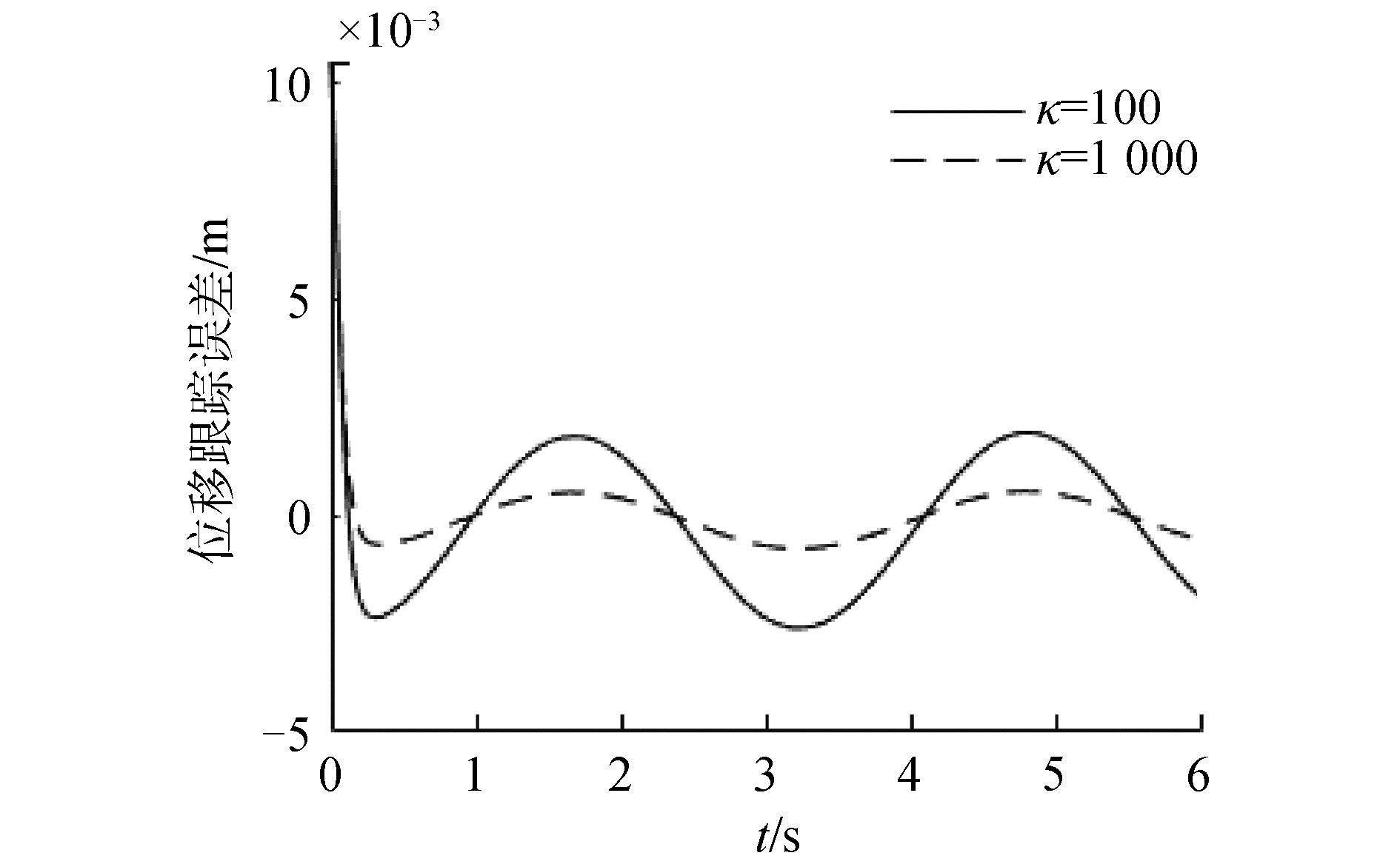
由图 7易知,在不考虑系统噪声环境下,ε值越小,对非匹配不确定项与匹配不确定项补偿效果越好,观测误差越小。由图 8和图 9,κ值越大,闭环系统收敛越快。
|
Download:
|
| 图 9 ε=0.001时不同κ值的轨迹跟踪误差 Fig. 9 The tracking error of the HOSMC with ε=0.001 | |
1) 通过建立挖掘机关节空间与驱动空间关系,以液压缸杆规划曲线为跟踪目标,伺服阀输入电压为控制输入,使控制方式更加直接,易于实践。
2) 以斗杆活塞杆轨迹控制为例,采用高增益观测器减少了传感器使用数量,降低了控制成本。观测器只需设计增益带宽ε,设计参数少,方法更为简便。在滑模控制中,通过对输入切换项的符号函数采用滑模面函数代替,消除了抖振。闭环系统通过奇异摄动理论验证了稳定性,跟踪误差有限时间收敛。
3) 对于式(12)型的一类系统,通过定义新的状态变量,采用基于高增益观测器的滑模控制时,可选择较小的带宽参数ε与较大的κ值,满足控制需要。对于挖掘机其他液压缸的控制,在进行流量分配后,可类似斗杆液压缸系统进行分析控制。
| [1] |
解培强. 模糊滑模控制在挖掘机控制中的应用[D]. 太原: 太原科技大学, 2014: 36-43. XIE Peiqiang. The application of fuzzy sliding mode control in the control of excavator[D]. Taiyuan: Taiyuan University of Science and Technology, 2014: 36-43. (  0) 0)
|
| [2] |
张金萍, 刘阔, 林剑峰, 等. 挖掘机的4自由度自适应模糊滑模控制[J]. 机械工程学报, 2010, 46(21): 87-92. ZHANG Jinping, LIU Kuo, LIN Jianfeng, et al. 4-DOF adaptive fuzzy sliding mode control of excavator[J]. Journal of mechanical engineering, 2010, 46(21): 87-92. (  0) 0)
|
| [3] |
黄茹楠, 顾波. 挖掘机轨迹跟踪的滑模变结构控制[J]. 控制工程, 2010, 17(2): 131-134. HUANG Runan, GU Bo. Sliding mode control for trajectory tracking of hydraulic excavator[J]. Control engineering of China, 2010, 17(2): 131-134. DOI:10.3969/j.issn.1671-7848.2010.02.002 (  0) 0)
|
| [4] |
刘阔, 郭大猛, 刘杰, 等. 液压挖掘机自适应模糊滑模控制的研究与仿真[J]. 东北大学学报(自然科学版), 2009, 30(11): 1649-1652. LIU Kuo, GUO Dameng, LIU Jie, et al. Research and simulation of hydraulic excavator's adaptive fuzzy sliding control[J]. Journal of Northeastern University (natural science), 2009, 30(11): 1649-1652. (  0) 0)
|
| [5] |
李元春, 王蒙, 盛立辉, 等. 液压机械臂基于反演的自适应二阶滑模控制[J]. 吉林大学学报(工学版), 2015, 45(1): 193-201. LI Yuanchun, WANG Meng, SHENG Lihui, et al. Adaptive second order sliding mode control for hydraulic manipulator based on backstepping[J]. Journal of Jilin University (engineering and technology edition), 2015, 45(1): 193-201. (  0) 0)
|
| [6] |
许颖, 刘阔. 挖掘机电液系统的滑模阻抗控制[J]. 机床与液压, 2015, 43(22): 138-141. XU Ying, LIU Kuo. Sliding mode impedance control for the excavator's electrohydraulic system[J]. Machine tool & hydraulics, 2015, 43(22): 138-141. DOI:10.3969/j.issn.1001-3881.2015.22.047 (  0) 0)
|
| [7] |
赵春红, 张洛平. 用于驱动液压缸活塞运动轨迹跟踪的二阶滑模控制[J]. 中国工程机械学报, 2019, 17(4): 311-315. ZHAO Chunhong, ZHANG Luoping. Two order sliding mode control for driving trajectory tracking of hydraulic cylinder piston[J]. Chinese journal of construction machinery, 2019, 17(4): 311-315. (  0) 0)
|
| [8] |
YAO Bin, BU Fanping, REEDY J, et al. Adaptive robust motion control of single-rod hydraulic actuators: theory and experiments[J]. IEEE/ASME transactions on mechatronics, 2000, 5(1): 79-91. DOI:10.1109/3516.828592 (  0) 0)
|
| [9] |
GUAN Cheng, PAN Shuangxia. Nonlinear adaptive robust control of single-rod electro-hydraulic actuator with unknown nonlinear parameters[J]. IEEE transactions on control systems technology, 2008, 16(3): 434-445. DOI:10.1109/TCST.2007.908195 (  0) 0)
|
| [10] |
GUAN Cheng, PAN Shuangxia. Adaptive sliding mode control of electro-hydraulic system with nonlinear unknown parameters[J]. Control engineering practice, 2008, 16(11): 1275-1284. DOI:10.1016/j.conengprac.2008.02.002 (  0) 0)
|
| [11] |
郑凯锋, 杨桂玲, 房加志, 等. 阀控非对称缸系统的反馈线性化滑模控制[J]. 机床与液压, 2017, 45(5): 151-154. ZHENG Kaifeng, YANG Guiling, FANG Jiazhi, et al. The control for vale-controlled asymmetrical cylinder based on feedback linearization and sliding mode control[J]. Machine tool & hydraulics, 2017, 45(5): 151-154. DOI:10.3969/j.issn.1001-3881.2017.05.036 (  0) 0)
|
| [12] |
杨俊, 谭建平. 阀控非对称缸系统鲁棒反馈线性化控制[J]. 华中科技大学学报(自然科学版), 2014, 42(2): 106-110. YANG Jun, TAN Jianping. Robust feedback linearization control of valve controlled asymmetric cylinder system[J]. Journal of Huazhong University of Science and Technology (nature science edition), 2014, 42(2): 106-110. (  0) 0)
|
| [13] |
LEI Junbo, WANG Xuanyin, PI Yangjun. Sliding mode control in position control for asymmetrical hydraulic cylinder with chambers connected[J]. Journal of Shanghai JiaoTong University, 2013, 18(4): 454-459. DOI:10.1007/s12204-013-1419-9 (  0) 0)
|
| [14] |
GUO Kai, WEI Jianhua, FANG Jinhui, et al. Position tracking control of electro-hydraulic single-rod actuator based on an extended disturbance observer[J]. Mechatronics, 2015, 27: 47-56. DOI:10.1016/j.mechatronics.2015.02.003 (  0) 0)
|
| [15] |
HA Q P, NGUYEN Q H, RYE D C, et al. Impedance control of a hydraulically actuated robotic excavator[J]. Automation in construction, 2000, 9(5/6): 421-435. (  0) 0)
|
| [16] |
WANG Chengwen, QUAN Long, JIAO Zongxia, et al. Nonlinear adaptive control of hydraulic system with observing and compensating mismatching uncertainties[J]. IEEE transactions on control systems technology, 2018, 26(3): 927-938. DOI:10.1109/TCST.2017.2699166 (  0) 0)
|
| [17] |
KIM W, WON D, SHIN D, et al. Output feedback nonlinear control for electro-hydraulic systems[J]. Mechatronics, 2012, 22(6): 766-777. DOI:10.1016/j.mechatronics.2012.03.008 (  0) 0)
|
| [18] |
WON D, KIM W, TOMIZUKA M. High-gain-observer-based integral sliding mode control for position tracking of electrohydraulic servo systems[J]. IEEE/ASME transactions on mechatronics, 2017, 22(6): 2695-2704. DOI:10.1109/TMECH.2017.2764110 (  0) 0)
|
| [19] |
GUO Qing, YU Tian, JIANG D. High-gain observer-based output feedback control of single-rod electro-hydraulic actuator[J]. IET control theory & applications, 2015, 9(16): 2395-2404. (  0) 0)
|
| [20] |
FARZA M, M'SAAD M, ROSSIGNOL L. Observer design for a class of MIMO nonlinear systems[J]. Automatica, 2004, 40(1): 135-143. DOI:10.1016/j.automatica.2003.08.008 (  0) 0)
|
| [21] |
CHANG P H, LEE S J. A straight-line motion tracking control of hydraulic excavator system[J]. Mechatronics, 2002, 12(1): 119-138. DOI:10.1016/S0957-4158(01)00014-9 (  0) 0)
|
| [22] |
杨艳慈. 液压挖掘机自动控制系统实现分析[J]. 液压与气动, 2012(7): 21-23. YANG Yanci. The analysis of hydraulic excavators automatic control systems[J]. Chinese hydraulics & pneumatics, 2012(7): 21-23. (  0) 0)
|
| [23] |
NAKKARAT P, KUNTANAPREEDA S. Observer-based backstepping force control of an electrohydraulic actuator[J]. Control engineering practice, 2009, 17(8): 895-902. DOI:10.1016/j.conengprac.2009.02.011 (  0) 0)
|
| [24] |
ZHANG D Q, PANDA S K. Chattering-free and fast-response sliding mode controller[J]. IEE proceedings-control theory and applications, 1999, 146(2): 171-177. DOI:10.1049/ip-cta:19990518 (  0) 0)
|
| [25] |
ATASSI A N, KHALIL H K. A separation principle for the stabilization of a class of nonlinear systems[J]. IEEE transactions on automatic control, 1999, 44(9): 1672-1687. DOI:10.1109/9.788534 (  0) 0)
|
| [26] |
KHALIL H K. High-gain observers in nonlinear feedback control[C]//Proceedings of 2008 International Conference on Control, Automation and Systems. Seoul, Korea (South), 2008.
(  0) 0)
|
| [27] |
YOUNG K K, KOKOTOVIC P, UTKIN V. A singular perturbation analysis of high-gain feedback systems[J]. IEEE transactions on automatic control, 1977, 22(6): 931-938. DOI:10.1109/TAC.1977.1101661 (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


