2. 上海船舶及海洋工程设计研究院, 上海 200011
2. Marine and Shipbuilding Design Institute of China, Shanghai 200011, China
气垫船是以静态空气压力支撑的一类高性能船[1],其中依靠全部静态空气压力支撑且速度较高的类型为全垫升式气垫船ACV。该类型气垫船在航行中的阻力绝大部分来自于兴波阻力,探究气垫面兴波的实质及与一般排水型船舶的异同,厘清其与航速、主尺度、气垫压力、喷气流量等参数之间的关系,建立求解兴波阻力的方法,对于气垫船快速性优化、及后续围裙动力学和气垫空气动力学[2]的研究具有重要意义。
研究气垫船兴波问题的方法主要有3大类:模型试验、理论方法及数值方法[3]。Newman等[4]提出了气垫做匀速直线运动的兴波阻力计算方法,将气垫简化为一个作用在水面上的压力面,面上压力分布均匀,并给出了相应工况下的兴波阻力系数图谱,后续学者研究多基于此来参照。Barratt[5]针对气垫底部不同压力分布时的情况,提出了浅水中的兴波阻力计算方法,结果表明兴波阻力的峰值随着流域的加深而提前发生,但是因其假设兴起的波浪是微幅波,其结果均较大于试验结果。Newman等[4]提供的图谱在中高速时与试验结果吻合良好,然而针对低速情况下的图谱结果出现了稠密的峰谷波动,与试验不符。Doctors[6]针对该问题提出了新的气垫底部压力分布方式,其假定底部为双曲正切分布,而非之前给定的均布压力,计算表明在阻力峰出现之前没有出现稠密的峰谷波动,弥补了Newman图谱的不足。同时,Doctors采用该方法研究了气垫船在浅水中直航的阻力性能,结果表明浅水会使兴波阻力增大。Lazauskas[7]采用线性理论方法预报了气垫船非匀速航行时的阻力性能。Mileewski[8]运用流体仿真软件计算分析了气垫船航行时船身四周的兴波波形。Nikseresht等[9]模拟了全垫升式气垫船气室内部气垫的空气流动,指出气垫的压力分布、航速等因素极大的影响了其兴波阻力与兴波波形。Bhushan[10]等运用线性理论和非线性理论2种方法对深浅水下不同压力面形状的气垫兴波阻力进行了计算分析,结果表明非线性理论更有利于计算浅水中的阻力性能。Kevin等[11]对线性方法和有限体积法这2种方法进行了对比,指出2种方法对计算较高速段的兴波阻力的准确性很高,而因低速时非线性影响的增强,线性方法不再稳定。刘宁[12]对全垫升式气垫船在波浪上航行的运动响应进行了研究,考虑若干非线性因素的影响,分析了围裙触水的影响。
前人的研究多是给定气垫面压力分布模拟兴波情况,而不同航速下适宜的压力分布情况较难把握,且实际情况中气垫船无法直接控制底部压力,而是通过控制风机流量来调整船体。本文介绍了求解全垫升式气垫船兴波阻力的基本假设及简化方法,建立了气室模型,并引入质量源模拟风机供气,运用STAR-CCM+商用软件,对兴波阻力进行了计算,并与多个文献计算结果进行对比,验证了该方法的有效性。此外,采用该方法研究了浅水中气垫船的兴波阻力变化情况。
1 气垫船兴波模型及数值计算气垫兴波数值模拟在一个三维数值水池中进行的,在出口处和远离船体的边界处设有人工阻尼消波区。以两相流假定为基础,自由面没有扰动时,其上部为空气,下部为水。
为模拟全垫升式气垫船在正常航行中的兴波情况,将其放置在一个以两相流假定为基础的三维数值水池中进行。采用固定在船上并随船以定常速度航行的参考坐标系来模拟计算兴波情况。因全垫升气垫船是一个多自由度非线性复杂系统,其中耦合了气垫、围裙、水面等多方面的影响,本文仅对兴波情况进行模拟,作如下简化假定:
1) 气垫船高速航行中,其水动阻力主要由气垫下表面与围裙触水的兴波阻力及围裙湿表面的摩擦阻力3部分构成,本文假设船体正常航行,围裙不触水,即水动阻力只有气垫的兴波阻力。同时将围裙视作刚性,简化气垫船上层建筑及船体结构。
2) 所研究的工况为气垫船稳定航行,不考虑船体姿态变化,且气垫底部压力分布达到稳态,在气室风机口加入质量源来模拟供气,从而达到垫升船体、作用水面的效果。
3) 因上述假定,气垫船稳定航行,船体与水没有接触,不存在水动摩擦阻力,因此不考虑粘性,视为理想流体,Bhushan等[9]的研究也表明在研究气垫船纯兴波问题时,不考虑粘性的结果与RANS方法差异相当小。
1.1 控制方程本计算模型中的流场是三维不可压缩理想流体,流场应满足连续性方程和欧拉方程:
| $ \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = q\left( {x,z,t} \right) $ | (1) |
| $ \left\{ \begin{array}{l} \frac{{\partial u}}{{\partial t}} + \mathit{\boldsymbol{\nabla}} \cdot \left( {u\mathit{\boldsymbol{c}}} \right) = - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + qu\\ \frac{{\partial v}}{{\partial t}} + \mathit{\boldsymbol{\nabla}} \cdot \left( {v\mathit{\boldsymbol{c}}} \right) = - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} + qv\\ \frac{{\partial w}}{{\partial t}} + \mathit{\boldsymbol{\nabla}} \cdot \left( {w\mathit{\boldsymbol{c}}} \right) = - \frac{1}{\rho }\frac{{\partial p}}{{\partial z}} + qw \end{array} \right. $ | (2) |
式中:(u, v, w)为质点速度;c=[u v w];g为重力加速度;ρ为流体密度;p为流体的压力;q为附加质量源项。
采用流体体积函数(volume of fluid,VOF)法追踪自由面。控制体内水的体积占控制体总体积之比定义为水的体积分数α,空气的体积分数即为(1-α)。该模型假定水和空气共享速度和压力场,可将其看作一种等效流体,故只要处理和单相流相同形式的质量、动量守恒方程,该等效流体的密度为:
| $ \rho {\rm{ = }}\alpha {\rho _w} + \left( {1 - \alpha } \right){\rho _a} $ | (3) |
式中下标w、a分别指代水和空气。体积分数满足连续性方程:
| $ \frac{{\partial \alpha }}{{\partial t}} + \frac{{\partial u\alpha }}{{\partial x}} + \frac{{\partial v\alpha }}{{\partial y}} + \frac{{\partial w\alpha }}{{\partial z}} = q $ | (4) |
方程(1)、(2)、(4)组成了气垫兴波模拟数值水池的控制方程。该方程组与一般的N-S方程相比,忽略了粘性项的影响,同时引入了附加质量源项q。
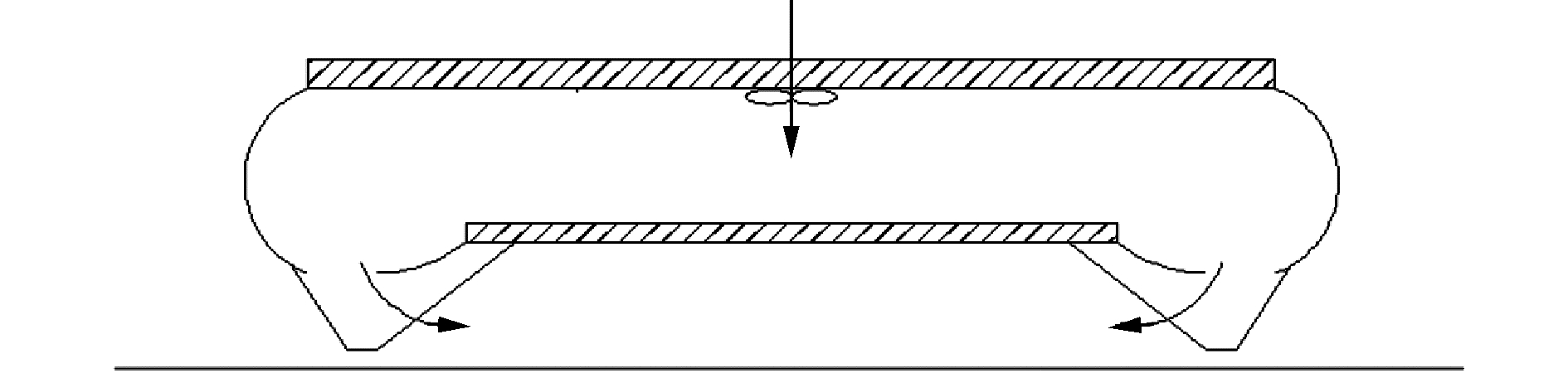
1.2 质量源模拟风机系统全垫升气垫船正常航行过程中,垫升风机向船体气道供气,气体经过围裙进入气室,形成气垫将船体全部托离水面,因垫升后船体距离水面有一段距离,气体会通过囊指下侧缝隙溢出,因此供气需持续稳定。图 1为气垫船横剖面的示意图。
|
Download:
|
| 图 1 气垫船横剖面示意 Fig. 1 Cross section diagram of ACV | |
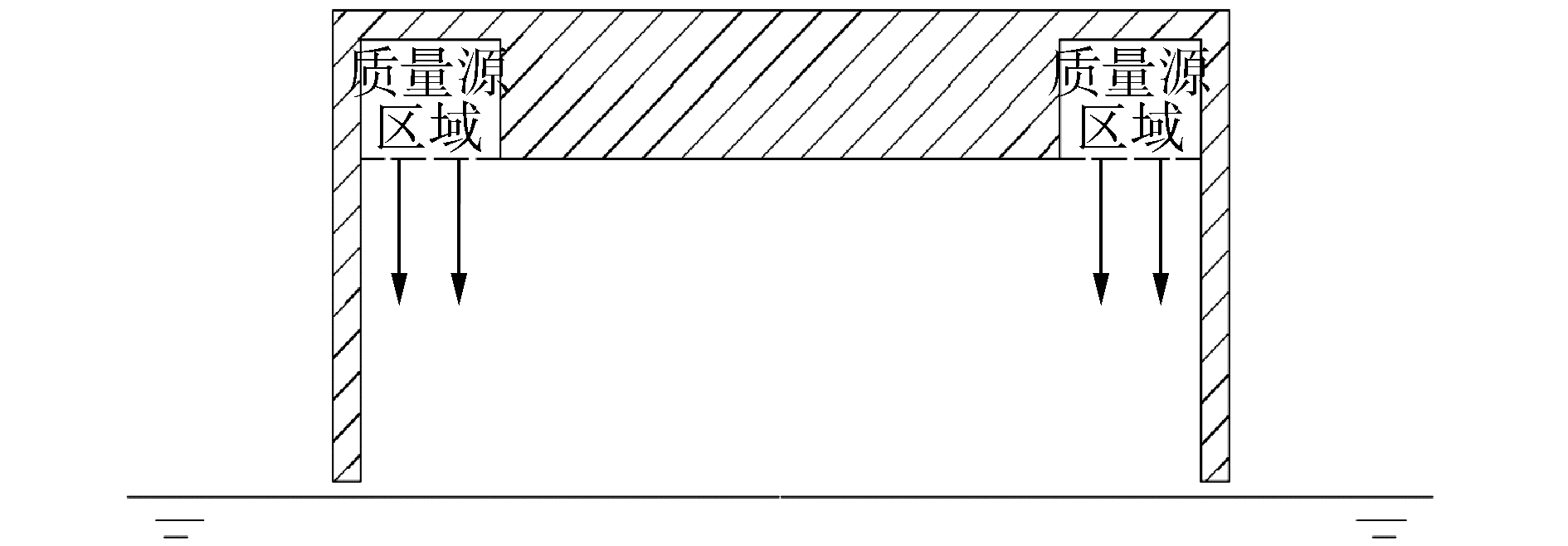
如前述假设2,为模拟出气垫施加于水面的效果,简化气垫船结构,仅对气室区域进行建模,如图所示为气室横剖面图。采用三维质量源方法[13]模拟风机不断给气室供气。
|
Download:
|
| 图 2 简化气室横剖面 Fig. 2 Cross section diagram of simplified chamber | |
式(1)、(2)中引入的质量源项q表达式为:
| $ q(x,y,z,t) = \left\{ {\begin{array}{*{20}{l}} {\frac{{2{v_{{\rm{air}}}}(x,y,t)}}{{\Delta z}},}&{(x,y,z) \in {\varOmega _s}}\\ {0,}&{(x,y,z) \notin {\varOmega _s}} \end{array}} \right. $ | (5) |
式中:Ωs为质量源区域,即图中虚线框住的部分;Δz为质量源区域的厚度;vair为模拟风机吹气口的空气速度;q的单位为s-1。通过在该区域添加与空气进气速度有关的质量源项,产生供气效果。
在本文的验证工作中,前人研究的前提多是给定压力分布情况,因此需要确定质量源项q的大小与气垫底部压长比的关系。
Bhushan等[14]给出了由伯努利方程得到的流量公式:
| $ Q = {C_d}{A_i}\sqrt {\frac{{2{p_c}}}{{{\rho _{{\rm{air}}}}}}} $ | (6) |
式中:pc为气垫面上实际压强减去标准大气压的压强由气垫压长比可得气垫相对压强;Q为模拟风机的出口流量,m3/s;Cd为泄漏系数,Faltine建议取为0.6~1.0;Ai为简化气室的四周边界最低点与水面的间隙形成的总面积;ρair为空气密度。质量源项可通过式q=Q/VΩ求出,其中VΩ为质量源区域的体积。
1.3 兴波阻力系数计算方法全垫升气垫船在正常航行中,船体并不与水面接触,难以采用排水型船体的表面压力积分法求得阻力。本文将简化气室和气垫视为一个整体,通过压力施加到水面,对气室正下方与气垫直接接触水面的形状及压力进行处理,求得内水面所受力,由牛顿第三定律即可得气垫船受到的兴波阻力。
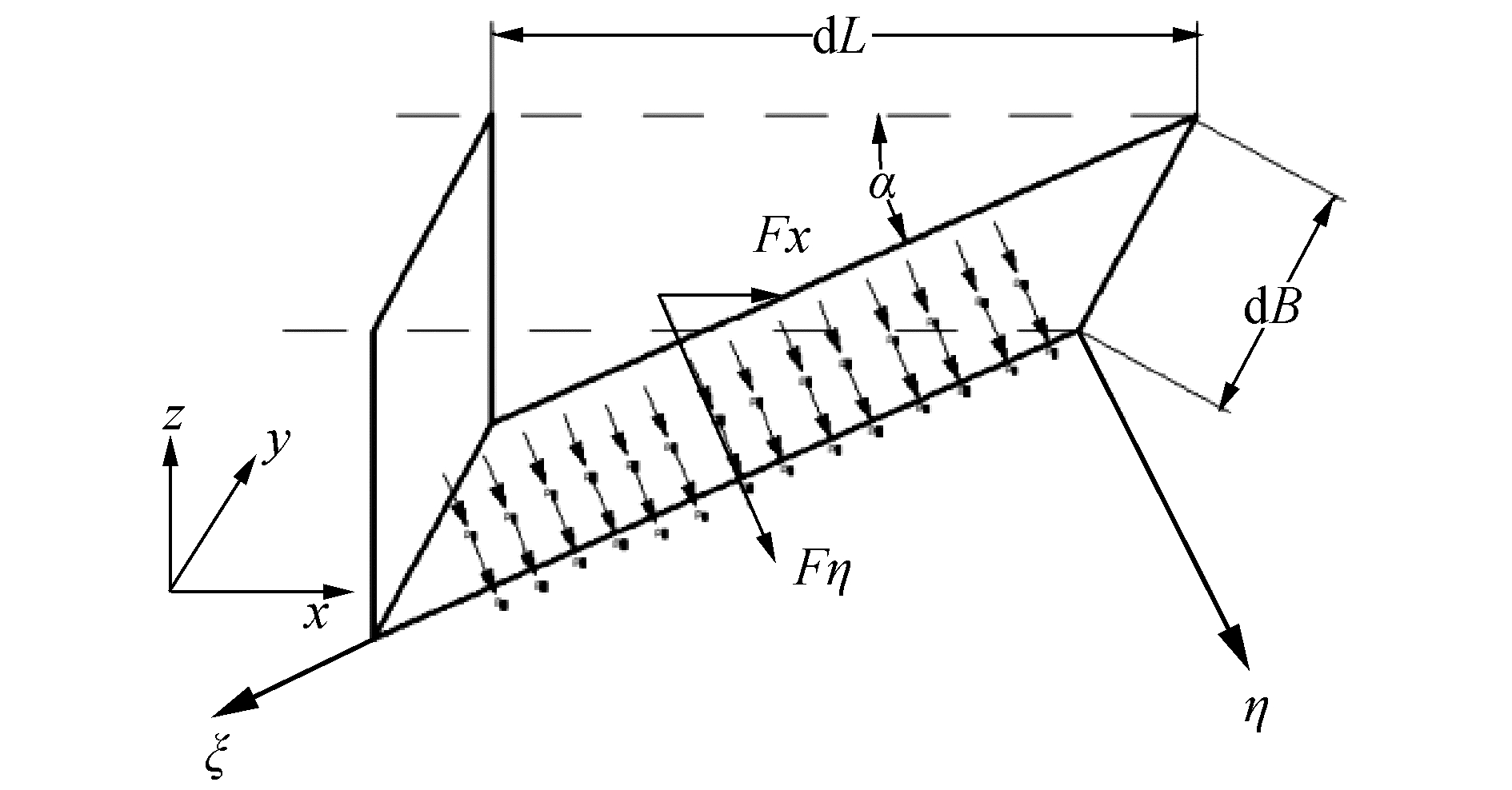
取气室正下方的水面上一矩形微元面,其长为dL,宽为dB,如图 3所示。
|
Download:
|
| 图 3 矩形微元面 Fig. 3 Rectangular infinitesimal element | |
该微元面与水平面夹角为αw,取直角坐标系ξOη, 其原点置于前端点O,Oξ轴沿航行方向向后为正,Oη轴垂直于Oξ轴,向下为正。因压力作用与作用面垂直,则微元面上的压力为:
| $ {F_\eta }{\rm{ = }}{p_c}(x,y){\rm{d}}B{\rm{d}}L $ | (7) |
该力沿船舶方向航行的分力为:
| $ {F_x} = {F_\eta }\sin {\alpha _w} = {p_c}(x,y)\frac{{{\rm{d}}{\xi _w}(x,y)}}{{{\rm{d}}x}}{\rm{d}}B{\rm{d}}L $ | (8) |
式中:dξw为微元面的波高;dx为微元面水平面投影的x方向距离。整个气室正下方水面上沿航行方向受到的总分力Rx可积分得到:
| $ {{R}_{x}}=\iint{{{p}_{c}}(x,y)\frac{\partial {{\xi }_{w}}(x,y)}{\partial x}\text{d}S} $ | (9) |
水面受到的力为气垫施加于其上的力,由牛顿第三定律,气室航行时的兴波阻力Rw为Rx的反作用力为:
| $ {{R}_{w}}=-{{R}_{x}}=-\iint{{{p}_{c}}(x,y)\frac{\partial {{\xi }_{w}}(x,y)}{\partial x}\text{d}S} $ | (10) |
具体求解采用将积分式离散求和的方法,表达式为:
| $ {R_w} = - \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{p_c}({x_m},{y_n})\frac{{\partial {\xi _w}({x_m},{y_n})}}{{\partial x}}} } \Delta x\Delta y $ | (11) |
在得到兴波阻力后,可根据纽曼-波尔的气垫船兴波阻力系数计算出兴波阻力系数:
| $ {C_w} = {R_w}\frac{{{\rho _w}g}}{{{{\bar p}_c}^2{B_c}}} $ | (12) |
式中:ρw为水的密度;pc为内水面上的平均阻力;Bc为气垫船宽。
2 气垫船的兴波波形及阻力计算验证影响气垫船阻力最主要的参数为压长比,其决定兴波阻力特别是越峰阻力的大小。许多学者在研究气垫船兴波问题时,多是指定气垫底面的压力分布,针对不同平面形状的气垫展开了广泛研究,其中较为广泛对照的是纽曼-波尔图谱,该图谱给出了指定压长比的气垫面在不同傅汝德数下的兴波阻力曲线。本文取一种压长比的气垫船模型在静水中航行的兴波情况进行研究,以验证该方法的有效性。
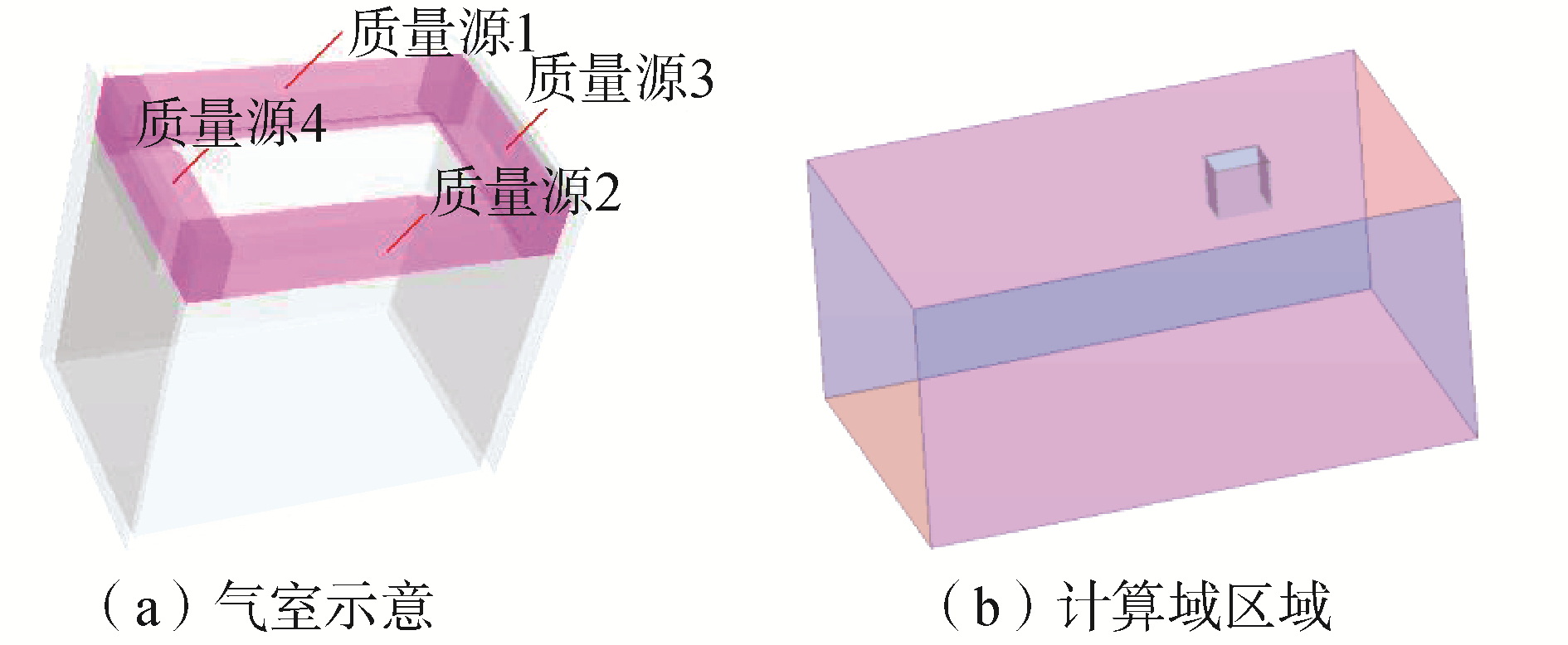
2.1 计算域及边界条件选取气垫船气室模型长LC=3 m,宽BC=2 m,气垫压长比PC=0.012 7ρgLC,如图 4(a),并置于图 4(b)所示的数值水池中。计算域原点位于气垫体的垂直中心线和静水面的交点处,x轴指向航行方向,沿船舶航行方向为正,y轴指向船宽方向,以船舶右舷为正,z轴向上为正。计算域范围为:-7LC < x < 3LC,-3LC < y < 3LC,-4LC < z < LC。如图 4所示,简化气室为内部中空的立方体,其顶部和四周封闭,底部开放。图 4(a)中质量源施加在阴影区域,气室最下沿离静止的自由面有一定距离,该缝隙可使气体溢出。
|
Download:
|
| 图 4 气室及计算域区域 Fig. 4 Air chamber and calculation domain | |
以船舶航行方向视角来定义计算域边界条件,前边界面及上下面设定为速度入口,左右面设定为对称边界,后边界面为压力出口,气室四壁及顶面为壁面。同时在左右面及后边界面设阻尼消波区,设定阻尼波长度大致为定常兴波波长的2倍,以消除波反射影响结果。
计算网格的划分如图 5所示,为在保证计算精度的同时提高计算效率,加密部分网格。在凯尔文波系范围内进行网格加密,精准捕捉波形,防止数值耗散,自由面垂向方向要保证足够网格,气室内部特别是质量源区域网格要加密,提高气体流场信息的准确度。
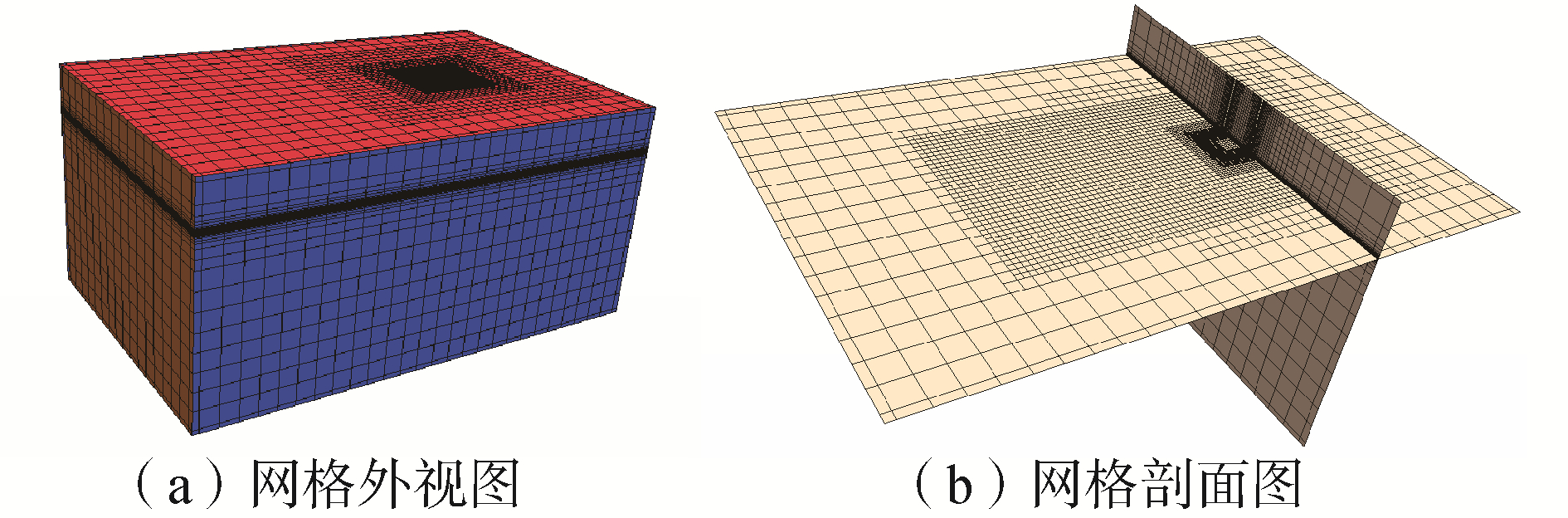
|
Download:
|
| 图 5 计算域网格划分 Fig. 5 Grid division of calculation domain | |
对气垫模型进行了12个傅汝德数下的静水航行兴波模拟计算,在确定质量源q大小时,先根据式(6)估算出大致范围,因气室与水面之间围合区域的面积随着自由面形状不同而异,在计算每种傅汝德数的情况时,需微调q的值,使气垫底面平均压强大致满足压长比的要求。
表 1给出了不同傅汝德数下气垫船静水航行中的兴波阻力及其系数,以及模拟所采用的质量源项的大小。将兴波阻力系数随傅汝德数变化的数据绘制成图 6。
| 表 1 气垫船兴波阻力及其系数计算结果 Table 1 Results of wave-making resistance and its coefficient of ACV |

|
Download:
|
| 图 6 气垫船兴波阻力系数随傅汝德数变化的曲线图 Fig. 6 Curve of wave making resistance coefficient of ACV changing with Froude number | |
由图 6可知,曲线有2个较为明显的阻力峰,第1个阻力峰发生在Fr为0.35时,第2个阻力峰发生在Fr为0.6附近时。气垫船底部与水面接触部分的压力减去大气压力,仅为大气压力的2%~6%,压力冲量相比一般排水型船舶产生的冲量很小。此外,随着航速提高,水面受到的压力也不会剧增,因而兴波阻力不会随之大量增加,反而可能会减弱,这是全垫升气垫船具有高速性能的原因之一。
图 6中给出了其他学者在相同工况下的模拟结果。本文的结果与Bhushan[7]的CFD方法较为吻合;与Everst等[15]的试验结果相比,曲线变化趋势尤其是2个阻力峰发生的傅汝德数基本一致。总体来看,本文计算气垫船兴波阻力的方法具有一定有效性和可靠性。
2.3 兴波波形分析图 7给出了5个不同傅汝德数时气垫船静水航行时的自由表面兴波波形。可以看出,低速时,凯尔文波系中的横波较为明显,随航速的增加,横波不再明显,凯尔文角逐渐减小,气垫压力中心逐渐后移。

|
Download:
|
| 图 7 气垫船自由面兴波 Fig. 7 Waveform inducing by ACV | |
图 8给出了4种工况下计算域中纵剖面上的自由面升高图。图中的横坐标x/LC为纵向长度和气垫船长的比值,0为气垫船纵向中点的位置。结合图 8,在航速较低(Fr=0.3)时,在气垫船区域有2个较为明显的波谷,随着航速增大,气垫区域第1个波谷的位置不断后移,当Fr为0.7时已处于船体后部。图中也可看出气垫深度随航速的变化,在Fr为0.7附近时有极大值,当傅汝德数偏离0.7时,气垫深度有减小的趋势。

|
Download:
|
| 图 8 气垫各航速下中纵剖面自由面升高曲线 Fig. 8 Free-form surface elevation curve of mid-longitudinal section at each speed of air cushion | |
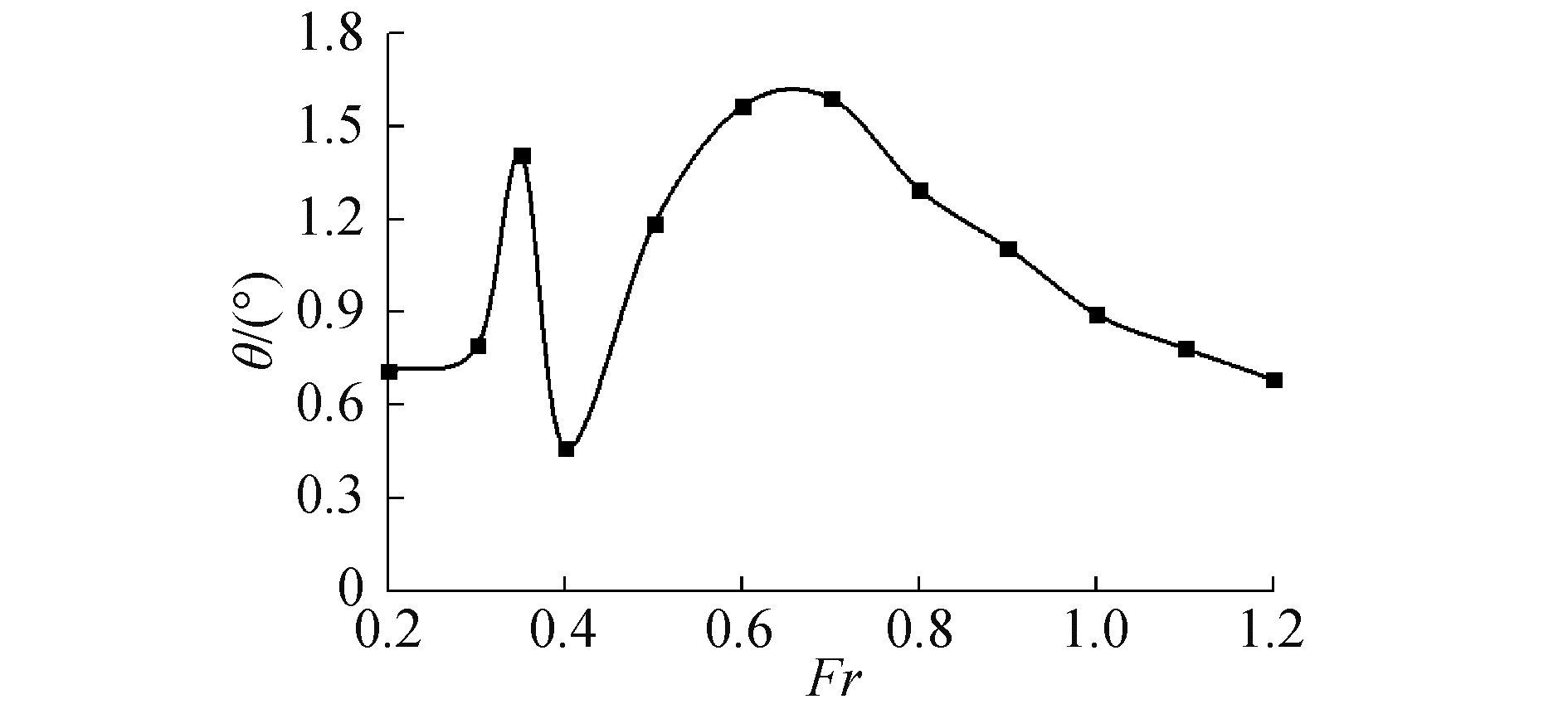
进一步分析波形,计算出各个航速下气垫正下方兴波水表面的平均纵倾角θw,如图 9所示。
|
Download:
|
| 图 9 气垫下方水表面平均纵倾角随航速的变化曲线 Fig. 9 Curve of average pitch angle of water surface under air cushion with speed | |
对比兴波阻力系数变化图(图 6)和平均纵倾角变化图(图 9)可见,两者变化趋势十分相似,平均纵倾角在Fr=0.35及Fr=0.6附近各有1个峰值。
因此,在气垫船底部压力一定的情况下,兴波阻力的主要影响因素之一是气垫下方水表面的平均纵倾角。气垫压力的强度与航速关系不密切,航速更多地影响底部波形分布,因此在后续对气垫船阻力性能研究中应着重关注设计航速下的气垫底部波形分布。
3 浅水中的气垫船兴波阻力变化气垫船因具有两栖性能,对浅水中气垫船的阻力特性进行研究具有研究意义。前文针对深水情况的气垫船兴波情况进行了计算研究,验证了该方法的有效性与可靠性,可运用该方法对浅水中气垫船的兴波阻力变化情况进行研究。
针对近似无限水深(d/Lc=4)和极浅水(d/Lc=0.25)2种情况,分别计算了10个傅汝德数下静水航行的兴波阻力系数。气垫及流域参数如表 2所示。
| 表 2 气垫船及流域参数 Table 2 Parameter of ACV and flow field |
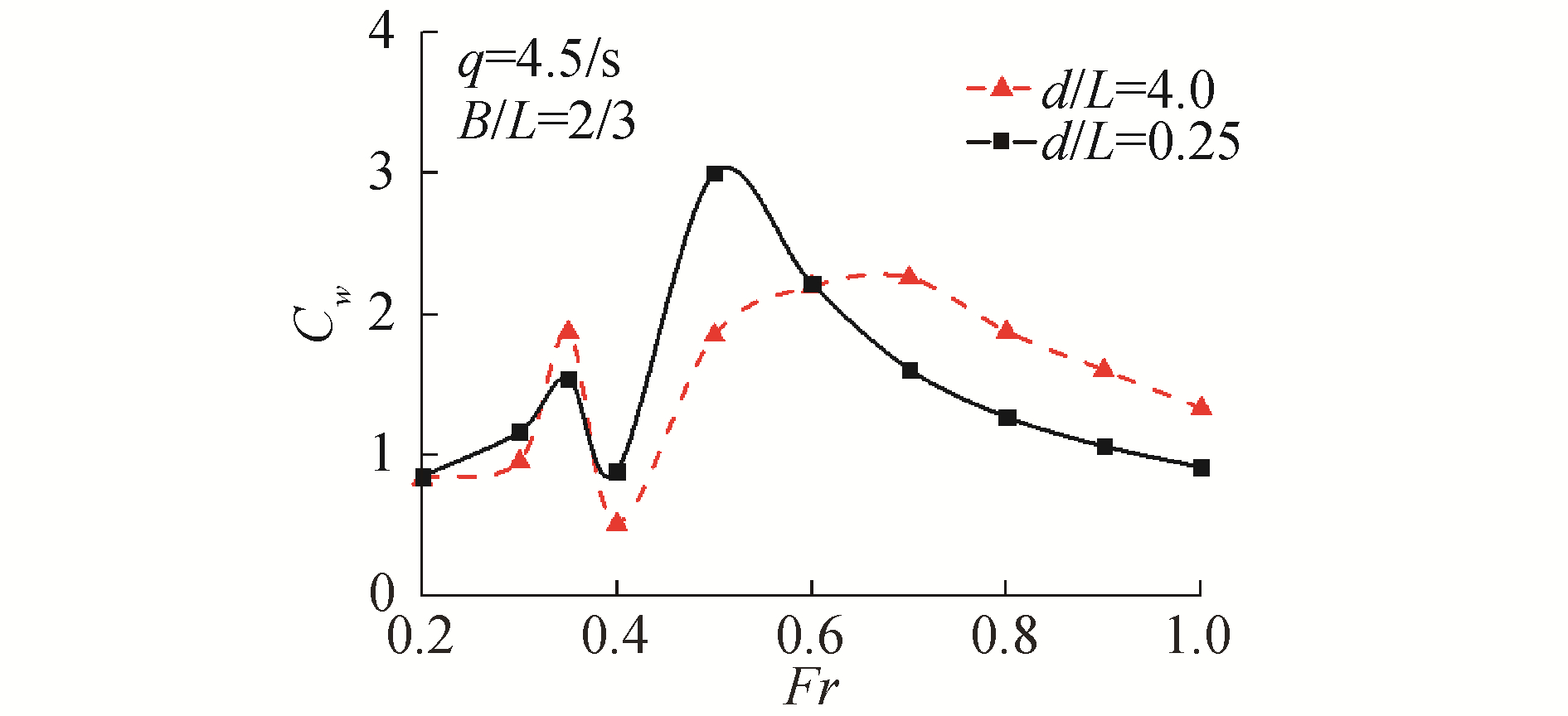
与第2节中控制底部压力分布情况不同,本节控制质量源项,即各航速下的进气流量保持一致,如此设置更接近真实情况,试验中控制风机流量较控制底部压力也更为便捷,方便对比结果。模拟得到的结果如图 10所示。
|
Download:
|
| 图 10 2种不同水深下的气垫船兴波阻力系数曲线 Fig. 10 Curve of wave resistance coefficient of ACV under two different water depths | |
由图 10可知,水域的深浅对兴波阻力影响很大,具有较为显著的浅水效应。浅水(d/L=0.25)与深水(d/L=4.0)下气垫船均有2个阻力峰,第1个阻力峰的位置两者基本相同,浅水的第1个阻力峰值较低,而浅水下的第2个阻力峰发生在Fr=0.5附近,深水发生在Fr=0.7左右,浅水的第2个阻力峰值显著大于深水的值。在越过阻力峰后,浅水下的阻力值较深水下要低。
产生该现象的原因本质是因为气垫船在浅水中航行时兴起波浪的波高、波速与深水情况不同,兴波图形也有明显变化。海佛洛克由兴波理论得出了不同水深下兴波阻力变化规律,浅水下阻力峰值对应的速度满足
因此气垫船的浅水效应大致与常规船型的规律一致,在临界速度附近阻力会出现极大值,一般为气垫船兴波的第2个阻力峰,在相关设计时需考虑该处影响。
4 结论1) 文中计算了不同航速下给定平均压力值的气垫船兴波阻力,结果准确给出了气垫船兴波阻力随速度变化的2个明显的阻力峰,与相关实验结果对比吻合良好。
2) 运用同一方法对浅水中的气垫船兴波阻力变化情况进行了研究,表明气垫船同样有浅水效应,在临界速度时兴波阻力会出现极大值,也是第2个阻力峰出现的位置。
综上可知,论文提出的质量源方法结合CFD平台可以模拟移动气垫引起的水表面变形,方法简单、计算稳定、高效,能够获得准确的兴波阻力,较为客观反映实际气垫船移动兴波特性。
| [1] |
马涛, 邬成杰. 气垫船总体性能与围裙气垫系统流体动力设计[M]. 北京: 国防工业出版社, 2012. MA Tao, WU Chengjie. Hovorcraft performance and skirt-cushion system dynamics design[M]. Beijing: National Defense Industry Press, 2012. (  0) 0)
|
| [2] |
曹林冲, 唐文勇, 张宗科, 等. 基于向量式有限元的气垫船围裙张力计算方法[J]. 中国造船, 2017, 58(2): 89-96. CAO Linchong, TANG Wenyong, ZHANG Zongke, et al. Calculation of skirt tension for air cushion vehicle based on vector form intrinsic finite element[J]. Shipbuilding of China, 2017, 58(2): 89-96. DOI:10.3969/j.issn.1000-4882.2017.02.010 (  0) 0)
|
| [3] |
冀楠. 全垫升气垫船运动特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2014. JI Nan. Research on motion characteristics of air cushion vehicle[D]. Harbin: Harbin Engineering University, 2014. (  0) 0)
|
| [4] |
NEWMAN J N, POOLE F A P. The wave resistance of a moving pressure distribution in a canal. RNC-TMB-648(Rev. 3-58)[R]. David Taylor Model Basin, 1962.
(  0) 0)
|
| [5] |
BARRATT M J. The wave drag of a hovercraft[J]. Journal of fluid mechanics, 1965, 22: 39-47. DOI:10.1017/S0022112065000563 (  0) 0)
|
| [6] |
DOCTORS L J, SHARMA S D. The wave resistance of air cushion vehicle in accelerated motion[J]. Journal of ship research, 1972, 16(4): 248-260. DOI:10.5957/jsr.1972.16.4.248 (  0) 0)
|
| [7] |
LAZAUSKAS L V. Hydrodynamics of advanced high-speed sealift vessels[D]. Adelaide, Australia: University of Adelaide, 2005.
(  0) 0)
|
| [8] |
MILEWSKI B, CONNELL B, WILSON J, et al. Dynamics of air cushion vehicles operating in a seaway[C]//Proceedings of the 9th International Conference on Numerical Ship Hydrodynamics. Ann Arbor, Michigan, 2007.
(  0) 0)
|
| [9] |
NIKSERESHT A H, ALISHAHI M M, EMDAD H. Complete flow field computation around an ACV (air-cushion vehicle) using 3D VOF with Lagrangian propagation in computational domain[J]. Computers & structures, 2008, 86(7/8): 627-641. (  0) 0)
|
| [10] |
BHUSHAN S, STERN F, DOCTORS L J. Verification and validation of URANS wave resistance for air cushion vehicles, and comparison with linear theory[J]. Journal of ship research, 2011, 55(4): 249-267. DOI:10.5957/jsr.2011.55.4.249 (  0) 0)
|
| [11] |
MAKI K J, BROGLIA R, DOCTORS L J, et al. Nonlinear wave resistance of a two-dimensional pressure patch moving on a free surface[J]. Ocean engineering, 2012, 39: 62-71. DOI:10.1016/j.oceaneng.2011.11.003 (  0) 0)
|
| [12] |
刘宁, 王晓强, 任慧龙, 等. 全垫升气垫船在波浪中运动的非线性理论研究[J]. 华中科技大学学报(自然科学版), 2014, 42(4): 91-95. LIU Ning, WANG Xiaoqiang, REN Huilong, et al. Nonlinear theory research on motion response of air cushion vehicle in waves[J]. Journal of Huazhong University of Science and Technology (nature science), 2014, 42(4): 91-95. (  0) 0)
|
| [13] |
杨云涛, 朱仁传, 蒋银, 等. 三维无反射数值波浪水池及波浪与结构物相互作用的模拟[J]. 上海交通大学学报, 2018, 52(3): 253-260. YANG Yuntao, ZHU Renchuan, JIANG Yin, et al. Simulation of 3-D viscous non-reflection numerical wave tank and the interactions of waves and structures[J]. Journal of Shanghai JiaoTong University, 2018, 52(3): 253-260. (  0) 0)
|
| [14] |
BHUSHAN S, MOUSAVIRAAD M, STERN F. Assessment of URANS surface effect ship models for calm water and head waves[J]. Applied ocean research, 2017, 67: 248-262. DOI:10.1016/j.apor.2017.07.013 (  0) 0)
|
| [15] |
EVEREST J T, HOCBEN N. Research on Hovercraft over calm water[J]. Trans royal institution of naval architects, 1967, 111(3): 343-365. (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


