2. 上海交通大学 船舶海洋与建筑工程学院, 上海 200240
2. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China
在实际海洋环境中,波流相互作用是一种非常普遍的现象,流的存在会使波浪的波高、波长等运动学特性发生显著变化。依照波浪理论,叠加规则波可以得到不规则波等实际波浪,可见研究规则波与流相互作用可为实际波浪与流相互作用研究打下基础,对模拟实际海域具有重要意义。
研究人员通常结合数值模拟和试验的方法对波浪及波流相互作用问题进行研究。胡捍红[1]选择四阶非线性薛定谔方程模拟了过渡水波在传播过程的非线性演变过程;贾岩等[2]基于波浪模式SWAN和海流模式POM研究了台风中的波流相互作用;Gao等[3]和Liu等[4]分别利用商业软件开发数值波浪水池,研究了规则波与水平圆柱相互作用问题。通过试验能够直观地验证模拟结果的准确性,Fernando等[5]、Qi等[6]开展试验研究了波浪与顺逆流的非线性相互作用;Soltanpour等[7]和Wei等[8]通过试验分别研究了波流相互作用下波浪在泥床上的耗散和桥梁基础的水动力响应特性;Jiang等[9]利用CFD软件模拟了不规则波与淹没式防波堤相互作用,并将模拟结果与实验进行了对比。然而,对比模拟结果与试验结果验证数值模型的有效性从本质上说是定性的。在第22届国际船模拖曳水池会议(ITTC)阻力委员会上推出了定量评估数值模拟结果的具体方法,即不确定度分析方法[10],至此相关学者开始关注如何定量评估计算流体力学数值模拟结果的可靠性。通常,数值模型的数值误差只能估计得到,Richardson外推法和网格收敛指数[11]因此被广泛应用于估计误差和数值不确定性。基于此Wu等[12]对船模阻力进行了不确定度分析,通过分析结果发现有效控制近船模表面第1层网格高度并选择合适湍流模型可大幅度降低船模阻力数值试验的不确定度。Zhu等[13]和Deng等[14]分别对船模横摇运动和小水线面双体船在波浪中的纵向运动进行了数值模拟与不确定度分析,给出了减小船舶运动参数数值模拟不确定度的有效建议。Silva等[15]、柏君励等[16]则对规则波和聚焦波的波参数进行了不确定分析。然而,文献[1-16]没有研究流对波浪模型不确定度的影响,这一问题的难点在于开展波流相互作用试验时很难保证造波精度。随着丁俊杰等[17]对上海交通大学风洞循环水槽消波装置的改进,该水槽能很好的满足试验要求。本文对均匀流作用下规则波的生成与演化进行了物理试验,然后基于RANS方程建立数值波浪水池进行波流相互作用下规则波特性研究,并依照ITTC规程开展计算结果的不确定度分析。给出了规则波的运动学特性随流速变化的一般规律,并讨论了顺流对波流相互作用数值模型不确定度的影响情况。
1 数值模型及验证 1.1 试验安排本文的试验在上海交通大学风洞循环水槽中进行,该循环水槽装置的工作原理如图 1所示。装置整体长24.6 m,宽4.5 m,高8.5 m,主要分为工作段、上游整流段、下游整流段、底部回流段以及动力段等部分。其中动力段能使循环水槽中的水体沿顺时针方向进行循环流动。工作段长为8.0 m,宽为3.0 m,高1.95 m,工作段的水深根据循环水槽工作状态的不同可小幅度调节,水深范围为1.60~1.63 m。安装于工作段前方的摇摆式造波机,可以生成规则波、JONSWAP谱不规则波与聚焦波等多类型波浪。实际造波时,根据试验需要设置造波机角度振幅和周期,即可造出目标波浪。当在静水中造波时水槽水深固定为1.63 m,而单独造流或同时造波和造流时水深固定为1.6 m。循环水槽能够实现长时间稳定的造流,稳定造流的流速范围为0.1~3.0 m/s。

|
Download:
|
| 图 1 循环水槽示意 Fig. 1 Diagram of circulating water channel | |
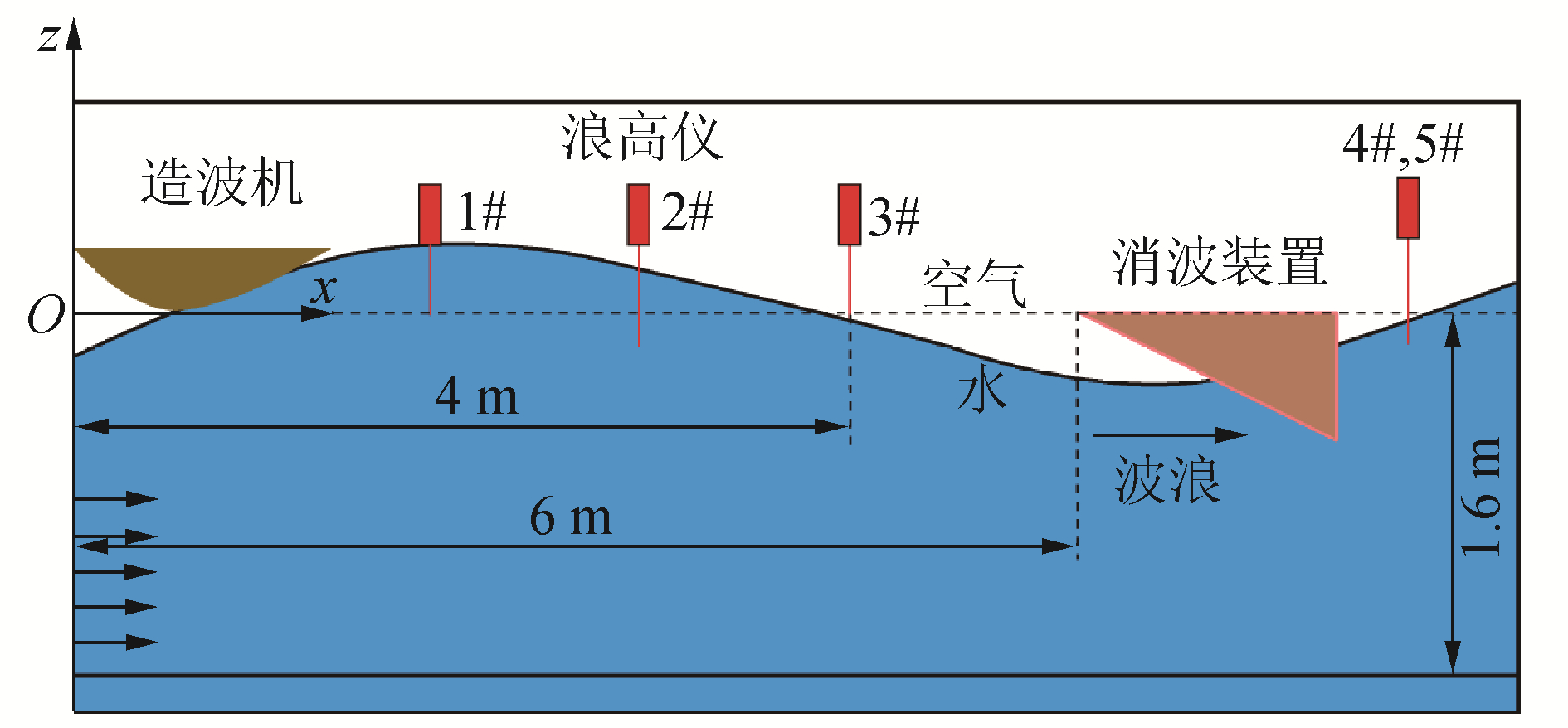
试验的目的是获取无流及有流情况下规则波自由液面处波高时历曲线,验证波流相互作用数值模型有效性,并分析流对规则波运动学特性的影响。试验布置如图 2所示,其中消波装置距造波端6 m。为满足试验需要,在水槽工作段共布置5个浪高仪,1#、2#和3#浪高仪布置在消波装置前侧,分别距造波端3.2、3.6、4 m。为了减小前方浪高仪对后方浪高仪的影响,1#、2#和3#浪高仪分别距水槽左端1、2、1.5 m;4#和5#浪高仪平行布置在消波装置后侧,距造波端6.7 m,且分别距左侧槽壁1、2 m,用于测试消波装置的性能。实验开始时,造波机生成的前5~10个波并不稳定,记录数据时将前10 s时间段内的波浪忽略。所有浪高仪量程为30 cm,测量频率为100 Hz,精度为0.5%。
|
Download:
|
| 图 2 试验布置示意 Fig. 2 The arrangement of wave experiments | |
本文利用计算流体力学商业软件STARCCM+建立数值模型[18],控制方程为Navier-Stokes方程:
| $ \rho \frac{{\partial {u_i}}}{{\partial t}} + \rho {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)} \right] + \rho {g_i} $ | (1) |
式中:ui为xi方向的速度分量;ρ为流体的密度;p为压强;μ为动力粘度;gi=g是重力加速度。本文关注湍流引起的流场在时间上的平均变化,主要采用雷诺平均的Navier-Stokes(RANS)方程:
| $ \begin{array}{l} \rho \frac{{{\rm{d}}{{\bar u}_i}}}{{{\rm{d}}t}} + \rho {{\bar u}_j}\frac{{\partial {{\bar u}_i}}}{{\partial {x_j}}} = - \frac{{\partial \bar p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\mu \left( {\frac{{\partial {{\bar u}_i}}}{{\partial {x_j}}} + \frac{{\partial {{\bar u}_j}}}{{\partial {x_i}}}} \right)} \right] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{\partial }{{\partial {x_j}}}\left( { - \rho \overline {u{_i^\prime}u{_j^\prime}} } \right) + \rho {g_i} \end{array} $ | (2) |
式中:ui是雷诺平均的xi方向速度分量;ui′是脉动速度;
| $ - \rho \overline {{u{_i^\prime}u{_j^\prime}}} = {\mu _t}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \frac{2}{3}\rho {\tau _{ij}}k $ | (3) |
式中:μt是湍流黏度;τij是Kronecker函数;k是湍动能。可采用Renormalization-Group(RNG)k-ε模型求解湍流黏度和湍动能,从而得到雷诺应力。
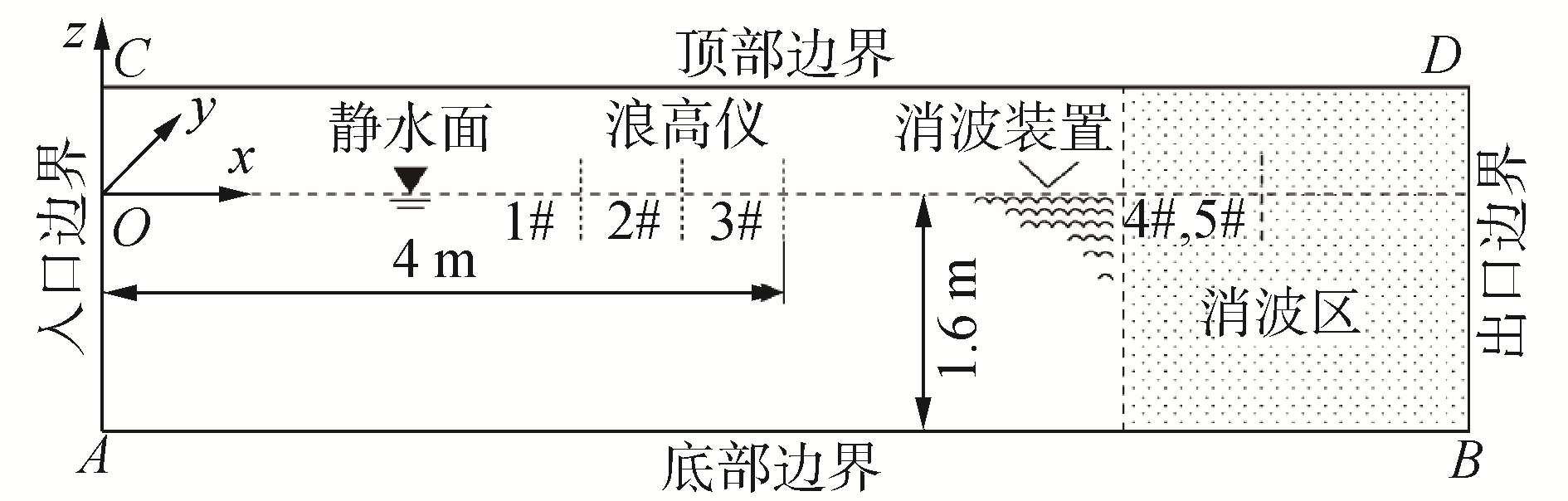
本文依照上海交通大学风洞循环水槽构建二维数值波浪水池。数值水池如图 3所示,主要分为工作段与消波段。由于只考虑波浪沿x方向的传播,数值水池的宽设为0.02 m,小于最小网格y方向的尺寸,采样点位置与试验中浪高仪位置对应。
|
Download:
|
| 图 3 数值波浪水池 Fig. 3 Numerical wave flume | |
网格划分时自由液面作为液相与气相交界面,造波过程中会发生明显的起伏运动。通常对自由液面处的网格进行多层加密,从而减少造波误差。计算域x、y、z方向对应的最小网格尺寸分别为0.01、0.1、0.002 m。主要采集x=4 m自由液面处波高信息作为输出数据,采样频率为100 Hz。
造波方法采用STARCCM+中造波模块的源项造波法;消波时,在尾部2 m添加阻尼项模拟阻尼消波段,并在阻尼消波段前加入一种多层变角度开孔折弯板透水消波装置[19]一同构成消波区。该消波板能够保证较高的透水效率的同时实现高效的消波。
采用STARCCM+库函数CURRENT设定水体速度造流。数值模型空间离散采用二阶迎风格式,压力和速度的耦合求解采用SIMPLE算法。自由液面捕捉采用流体体积(VOF)法。入口AC边界选择速度入口,出口BD边界为压力出口,底部AB边界为无滑移固壁边界而顶部边界CD为压力入口边界,两侧的边界选用对称边界。
按照Stokes波浪理论生成规则波,Stokes波浪理论与线性波类似,波浪运动也是势运动。对于弱非线性问题,可用摄动法进行求解,先假设势函数ϕ和波面曲线函数η都是某个小参数εs的幂级数,则:
| $ \phi = \sum\limits_{n = 1}^\infty {{\varepsilon _{\rm{s}}}} {\phi _n} $ | (4) |
| $ \eta = \sum\limits_{n = 1}^\infty {{\varepsilon _{\rm{s}}}} {\eta _n} $ | (5) |
当n=2,5时,代入自由表面条件泰勒展开式中,即可得到弱非线性的二阶和五阶Stokes波面方程和势函数。本文数值模拟的研究对象为Stokes五阶波,在软件中选择波浪类型并输入指定波高和周期,即可得到目标波浪。试验及模拟工况如表 1所示,其中C为流速,H为波高,L为波长,T为周期,EXP和NUM分别表示对该工况进行试验或者数值模拟。每个工况重复3组,每组试验或者模拟时长为50 s。
| 表 1 规则波试验与数值模拟工况 Table 1 Experimental and numerical cases of regular wave tests |
图 4为工况R1的波高时历曲线的数值模拟结果与理论(解析解)以及试验结果的对比情况。从图中可见工况R1的模拟结果与理论以及试验结果比较一致。表 2为数值模拟与试验数据得到的平均波高,其中hNUM, x=4 m和hEXP, x=4 m分别为在x=4 m自由液面处的平均波高模拟与试验结果。表 2表明,当C=0 m/s和C=0.3 m/s时,数值模拟和试验得到的平均波高相差不大,当顺流流速达到0.6 m/s时,平均波高试验值明显小于模拟值,造成这一误差的原因是因为数值模拟中未考虑造波机与流相互作用的影响。

|
Download:
|
| 图 4 工况R1数值模拟结果的验证 Fig. 4 Verification of simulation results of case R1 | |
| 表 2 数值模拟与试验数据的平均波高对比 Table 2 Experimental and numerical results of wave height |
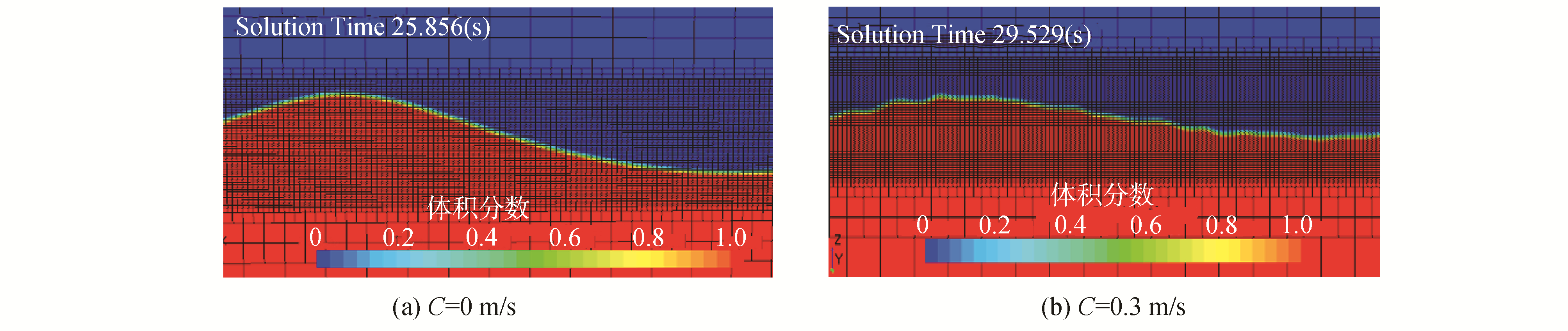
图 5给出了无流及顺流情况下规则波自由表面分布情况。从图 5可知,C=0 m/s时规则波的自由表面比较光滑;而在顺流(C=0.3 m/s)作用下,规则波波浪自由表面变得粗糙。
|
Download:
|
| 图 5 数值水池中波浪自由表面情况 Fig. 5 The water surface of waves in the numerical wave flume | |
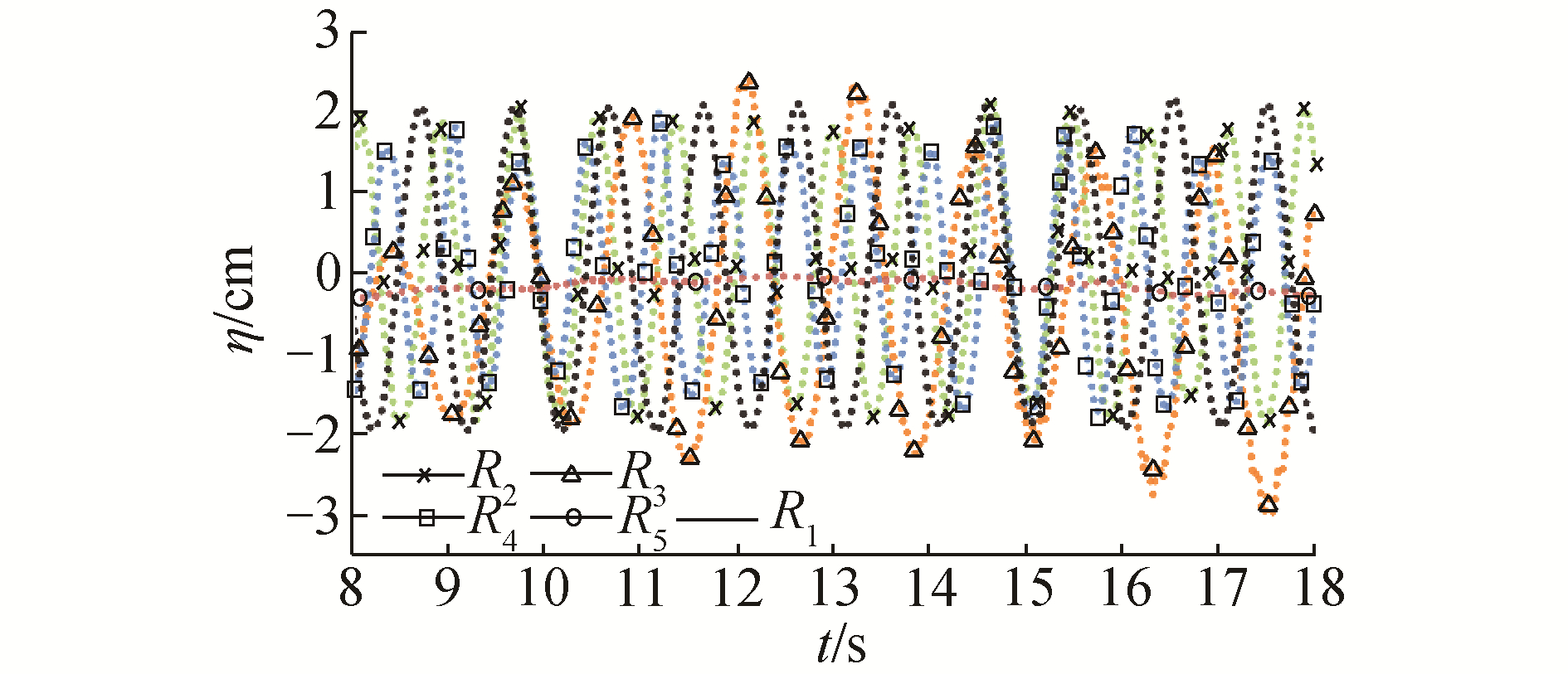
数值模拟得到的工况R1~R5波高时历曲线如图 6所示。图 6表明,随着均匀顺流流速增加,规则波波高降低,波峰和波谷相比于C=0 m/s时更平坦,逆流对规则波的影响与顺流工况的结果相反。
|
Download:
|
| 图 6 波高时历数值模拟结果 Fig. 6 Simulation results of the water surface elevations | |
从图 6也发现当逆流流速达到-0.3 m/s时,规则波传播变得缓慢,落后于无流及顺流工况;逆流流速过大时(C=-0.6 m/s),规则波波高几乎为0,这是由于当逆流流速过大时,规则波在传播时会在某个位置被阻隔。图 7给出了C=-0.6 m/s时波浪被阻隔的情况,被阻隔后规则波波面趋于平稳。

|
Download:
|
| 图 7 波浪阻隔现象 Fig. 7 The wave blocking | |
之前对数值模型的验证从本质上来说是定性的,无法定量评估数值模拟的误差。本节拟采用ITTC推荐的不确定度分析方法,定量评估数值模拟的误差。ITTC推荐的CFD数值模型的不确定度分析包括验证和确认2个部分,其中评估数值不确定度的过程称为验证,评估模型不确定度的过程称为确认,具体过程在ITTC规程中有详细介绍[6]。
评估数值不确定度时,需要对数值模型的参数进行收敛性分析。通常考虑的参数包括迭代次数、网格尺寸、时间步长和其他参数,本文规则波与流相互作用属于非稳态问题,网格尺寸和时间步长引起的误差比迭代次数等其他参数引起的误差要大,因此本节的不确定度分析将网格尺寸和时间步长作为主要因素加以考虑。
对数值模型的参数进行收敛性分析的一般过程是使用参数系列加细的多重解来估计参数引起的数值误差和不确定度,其中多重解的个数至少为3个。拟选取3套网格,网格参数加细比rG定为
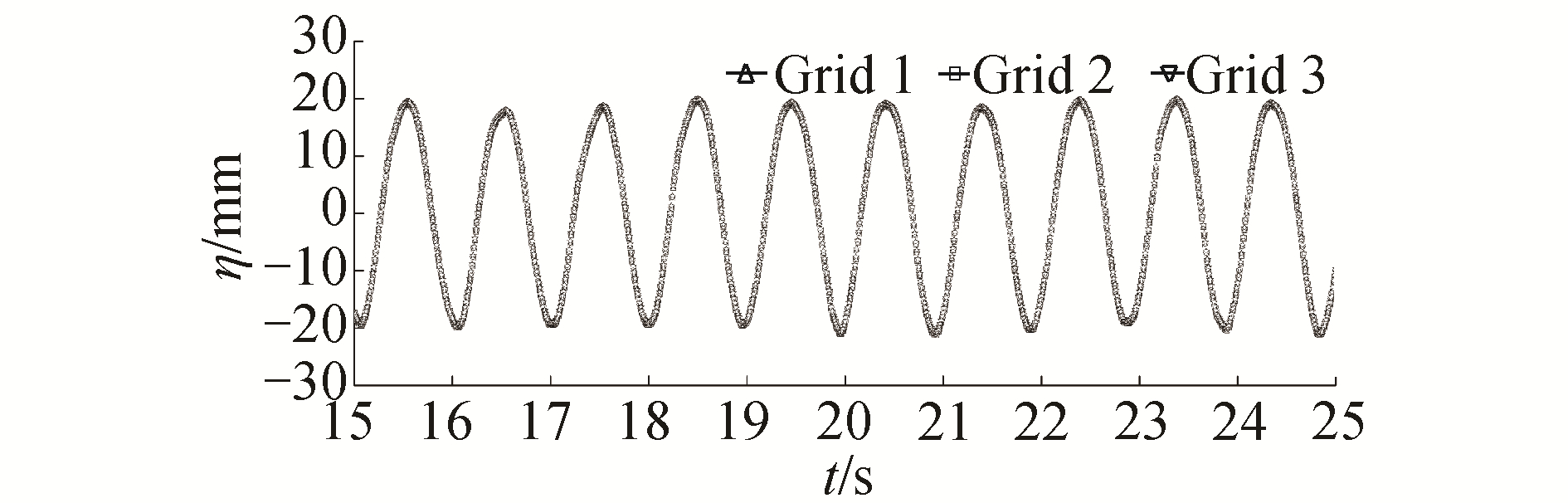
首先对工况R1中的网格参数进行收敛性研究,时间步长为0.001 s。用3套网格分别进行数值模拟后,得到3组波高时历曲线,如图 8所示。
|
Download:
|
| 图 8 不同网格对应的波高时历曲线 Fig. 8 Water surface elevations simulated with different grids | |
相邻网格参数波高时历之差的平均L2范数为:
| $ {\left\| {\left. {{\varepsilon _{{\rm{G21}}}}} \right\|} \right._2} = {[\frac{1}{N}\sum\limits_{i = 1}^N {({\eta _{{\rm{G2i}}}} - } {\eta _{{\rm{G1i}}}})^2}{]^{1/2}} = 0.000{\kern 1pt} 263 $ | (6) |
| $ {\left\| {\left. {{\varepsilon _{{\rm{G32}}}}} \right\|} \right._2} = {[\frac{1}{N}\sum\limits_{i = 1}^N {({\eta _{{\rm{G3i}}}} - } {\eta _{{\rm{G2i}}}})^2}{]^{1/2}} = 0.000{\kern 1pt} 859 $ | (7) |
其中ηG1i、ηG2i、ηG3i分别表示在细网格、中等网格和粗网格上模拟得到的波高时间序列中的第i个波高值,全局收敛因子为:
| $ \left\langle {{R_{\rm{G}}}} \right\rangle = \frac{{{{\left\| {\left. {{\varepsilon _{{\rm{G21}}}}}\;\; \right\|} \right.}_2}}}{{{{\left\| {\left. {{\varepsilon _{{\rm{G32}}}}}\;\; \right\|} \right.}_2}}} = 0.305 $ | (8) |
〈RG〉∈(0, 1),因此模拟结果单调收敛,可采用广义Richardson外推法估算准确度阶数pG和误差δREG*:
| $ {p_{\rm{G}}} = \frac{{\ln ({{\left\| {\left. {{\varepsilon _{{\rm{G32}}}}} \;\;\right\|} \right.}_2}/{{\left\| {\left. {{\varepsilon _{{\rm{G21}}}}}\;\; \right\|} \right.}_2})}}{{\ln ({r_{\rm{G}}})}} = 3.419 $ | (9) |
| $ \delta _{{\rm{R}}{{\rm{E}}_{\rm{G}}}}^* = \frac{{{{\left\| {\left. {{\varepsilon _{{\rm{G21}}}}} \;\;\right\|} \right.}_2}}}{{r_{\rm{G}}^{{p_{\rm{G}}}} - 1}} = 0.000{\kern 1pt} 116 $ | (10) |
网格收敛因子:
| $ {C_{\rm{G}}} = \frac{{r_{\rm{G}}^{{p_{\rm{G}}}} - 1}}{{r_{\rm{G}}^{{p_{{\rm{G,est}}}}} - 1}} = 2.270 $ | (11) |
式中pG, est是极限阶数的估计值,一般取2。由网格尺寸导致的数值模拟误差为:
| $ \delta _{\rm{G}}^* = {C_{\rm{G}}}\delta _{{\rm{R}}{{\rm{E}}_{\rm{G}}}}^* = 0.000{\kern 1pt} 263{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{m}} $ | (12) |
当CG远小于或远大于1时,网格尺寸引起的数值模拟不确定度为:
| $ {U_{\rm{G}}} = \left[ {9.6{{(1 - {U_{\rm{G}}})}^2} + 1.1} \right] \times \left| {\delta _{{\rm{R}}{{\rm{E}}_{\rm{G}}}}^*} \right| $ | (13) |
当|1-CG|≥0.25,网格尺寸引起的数值模拟不确定度为:
| $ {U_{\rm{G}}} = (1 + 2\left| {1 - {C_{\rm{G}}}} \right|) \times \left| {\delta _{{\rm{R}}{{\rm{E}}_{\rm{G}}}}^{\rm{*}}} \right| $ | (14) |
因此网格尺寸导致的数值模拟不确定度UG=1.080%H1,H1为工况R1的平均波高试验值。
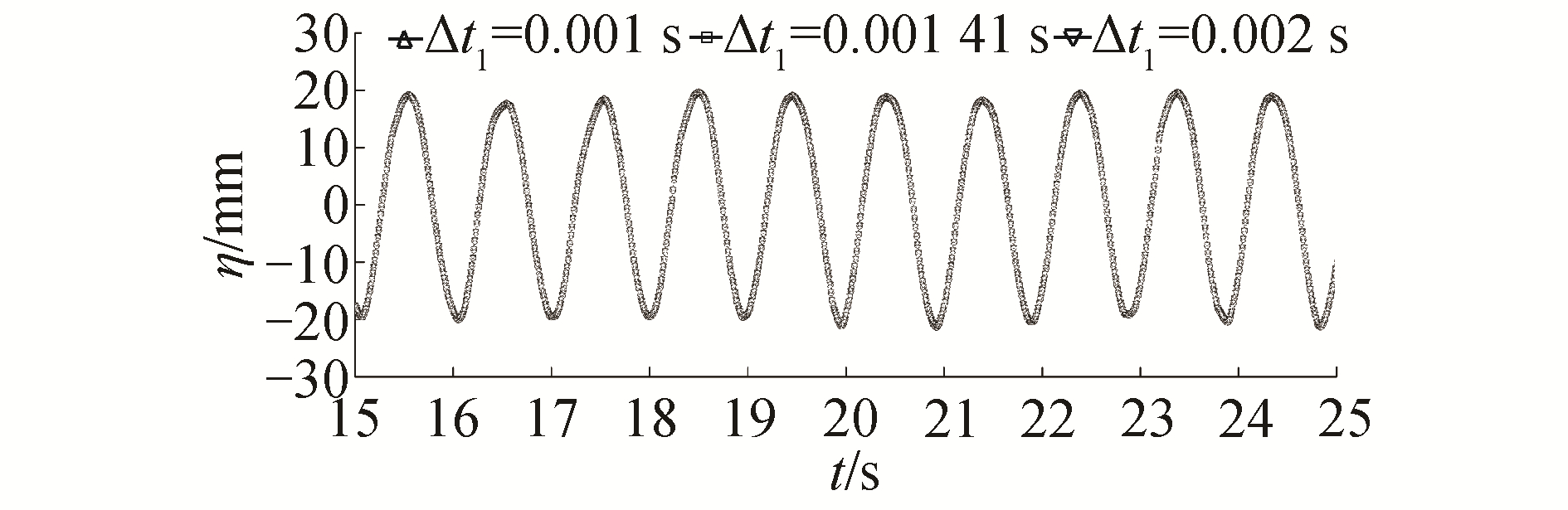
接下来在细网格Grid1上进行时间步长收敛性分析,得到3个时间步长对应的各个波高时历曲线,如图 9所示。
|
Download:
|
| 图 9 不同时间步长对应的波高时历 Fig. 9 Water surface elevations simulated with different time steps | |
相邻时间步长参数的波高时历之差的平均L2范数为:
| $ {\left\| {\left. {{\varepsilon _{{\rm{T21}}}}} \right\|} \right._2} = {\left[ {\frac{1}{N}\sum\limits_{i = 1}^N {({\eta _{{\rm{T2i}}}} - } {\eta _{{\rm{T1i}}}}{)^2}} \right]^{1/2}} = 0.000{\kern 1pt} 207 $ | (15) |
| $ {\left\| {\left. {{\varepsilon _{{\rm{T32}}}}} \right\|} \right._2} = {\left[ {\frac{1}{N}\sum\limits_{i = 1}^N {({\eta _{{\rm{T3i}}}} - } {\eta _{{\rm{T2i}}}}{)^2}} \right]^{1/2}} = 0.002{\kern 1pt} 18 $ | (16) |
其中ηT1i、ηT2i、ηT3i分别表示时间步长0.001 s、0.001 41 s、0.002 s时数值模拟得到的波高时间序列中的第i个波高值, 故全局收敛因子:
| $ \left\langle {{R_{\rm{T}}}} \right\rangle = \frac{{{{\left\| {\left. {{\varepsilon _{{\rm{T21}}}}} \;\;\right\|} \right.}_2}}}{{{{\left\| {\left. {{\varepsilon _{{\rm{T32}}}}} \;\;\right\|} \right.}_2}}} = 0.095{\kern 1pt} 0 $ | (17) |
〈RT〉∈(0, 1),结果也是单调收敛,采用广义Richardson外推法估算准确度阶数pT和误差δRET*:
| $ {p_{\rm{T}}} = \frac{{\ln ({{\left\| {\left. {{\varepsilon _{{\rm{T32}}}}} \;\;\right\|} \right.}_2}/{{\left\| {\left. {{\varepsilon _{{\rm{T21}}}}} \;\;\right\|} \right.}_2})}}{{\ln ({r_{\rm{T}}})}} = 6.792 $ | (18) |
| $ \delta _{{\rm{R}}{{\rm{E}}_{\rm{T}}}}^{\rm{*}} = \frac{{{{\left\| {\left. {{\varepsilon _{{\rm{T21}}}}} \;\;\right\|} \right.}_2}}}{{r_{\rm{T}}^{{p_{\rm{T}}}} - 1}} = 0.000{\kern 1pt} 021{\kern 1pt} 7 $ | (19) |
pT, est同样取2,时间步长修正因子:
| $ {C_{\rm{T}}} = \frac{{r_{\rm{T}}^{{p_{\rm{T}}}} - 1}}{{r_{\rm{T}}^{{p_{{\rm{T,est}}}}} - 1}} = 9.53 $ | (20) |
由时间步长导致的数值模拟误差为:
| $ \delta _{\rm{T}}^* = {C_{\rm{T}}}\delta _{{\rm{R}}{{\rm{E}}_{\rm{T}}}}^{\rm{*}} = 0.000{\kern 1pt} 207{\kern 1pt} {\kern 1pt} {\rm{m}} $ | (21) |
时间步长导致的数值模拟不确定度:
| $ {U_{\rm{T}}} = (1 + 2\left| {1 - {C_{\rm{T}}}} \right|)\left| {\delta _{{\rm{R}}{{\rm{E}}_{\rm{T}}}}^*} \right| = 1.034\% {{\bar H}_1} $ | (22) |
综上,在x=4 m自由液面处t∈ [15,25] s时间段内波高时历的数值模拟不确定度为:
| $ {U_{{\rm{SN}}}} = \sqrt {U_{\rm{G}}^2 + U_{\rm{T}}^2} = 1.495\% {{\bar H}_1} $ | (23) |
数值模拟误差估计值为:
| $ \delta _{{\rm{SN}}}^{\rm{*}} = \delta _{\rm{G}}^* + \delta _{\rm{T}}^{\rm{*}} = 0.000{\kern 1pt} 470{\kern 1pt} {\kern 1pt} {\rm{m}} $ | (24) |
至此工况R1的数值模拟验证过程结束,工况R2的验证与R1类似,2个工况的不确定度分析验证结果如表 3所示。其中H为对应工况测得的平均波高试验值。
| 表 3 数值模拟验证结果 Table 3 Numerical results of verification |
表 3给出,R1和R2 2个工况数值模拟的网格不确定度都大于时间步长不确定度,可知数值模拟无流及顺流情况下的规则波运动时,数值模拟结果对网格尺寸依赖程度大于时间步长,实际模拟时计算资源有限情况下应尽量满足网格精度要求。对比R1和R2工况数据可知,顺流工况R2数值模拟的网格不确定度是无流工况R1的3.46倍,时间步长不确定度是无流时的1.60倍,可见相比于无流工况R1,顺流提高了规则波时历曲线数值模拟结果对网格尺寸和时间步长的依赖程度。并且,顺流时规则波的平均波高小于无流工况,考虑顺流与规则波相互作用问题时,可适当减少自由液面加密区的高度,但需要注意选择合适的网格尺寸和时间步长,减小数值模拟带来的误差。
接下来根据ITTC规程,对数值模拟结果进行确认,工况R1中x=4 m自由液面处模拟的波高时历曲线确认不确定度UV为:
| $ {U_{\rm{V}}} = \sqrt {U_{{\rm{SN}}}^2 + U_{\rm{D}}^2} = \sqrt {{{1.495}^2} + {{2.5}^2}} \% {{\bar H}_1} = 2.913\% {{\bar H}_1} $ | (25) |
其中试验结果的不确定度UD假定为2.5%H1,波高时历模拟结果与试验测量结果比较误差的平均L2范数为:
| $ E = {\left\| {{\eta _{{\rm{EXP1,}}x{\rm{ = 4m}}}} - {\eta _{{\rm{NUM1,}}x{\rm{ = 4m}}}}} \;\;\right\|_2} = 1.425\% {{\bar H}_1} $ | (26) |
式中ηEXP1, x=4 m和ηNUM1, x=4 m分别表示工况R1在x=4 m自由液面处波高时历曲线的试验和模拟值。
工况R1和R2的数值模拟确认结果如表 4所示。从表 4可以看出,工况R1和工况R2在x=4 m处波高时历曲线的比较误差E都小于对应的确认不确定度UV,因此R1、R2工况在t∈ [15,25] s区间x=4 m自由液面处数值模拟的波高时历分别在2.913%H和4.791%H的程度上实现确认。
| 表 4 数值模拟确认结果 Table 4 Numerical results of validation |
1) 均匀顺流使规则波波高降低,传播速度加快,波峰和波谷与无流工况相比更平坦;逆流对规则波的影响与顺流的影响相反,逆流流速过大时,规则波会被阻隔。
2) 无流和顺流工况规则波波高时历曲线的比较误差都小于对应的确认不确定度,数值模拟结果得到确认,构建的数值波浪水池具有可靠性。
3) 无流及顺流情况下规则波的数值模拟结果对网格尺寸依赖程度大于时间步长,实际模拟时计算资源有限情况下应尽量满足网格精度要求。
4) 相比无流工况,顺流加剧了规则波波高时历曲线计算结果对网格尺寸和时间步长的依赖程度。
目前在循环水槽中进行逆流与规则波相互作用的试验时很难控制造波精度,下一步将从改善造波板水力传递函数等方面提高逆流中的造波质量,开展逆流与规则波相互作用的不确定度分析。
| [1] |
胡捍红. 考虑波流干扰的深水畸形波数值模拟研究[D]. 上海: 上海交通大学, 2012. HU Hanhong.Numerical simulation of rogue waves in deep water considering wave/current interaction[D].Shanghai: Shanghai Jiao Tong University, 2012. (  0) 0)
|
| [2] |
贾岩, 尹宝树, 杨德周. 东中国海浪流相互作用对水位和波高影响的数值研究[J]. 海洋科学, 2009, 33: 82-86. JIA Yan, YIN Baoshu, YANG Dezhou. A numerical study of the influence of wave-current interaction on water elevation and significant wave height in the East China Sea[J]. Marine science, 2009, 33: 82-86. (  0) 0)
|
| [3] |
GAO Ningbo, YANG Jianmin, LI Xin, et al. Wave forces on horizontal cylinder due to nonlinear focused wave groups[C]//Proceedings of the 25th International Ocean and Polar Engineering Conference. Hawaii, USA: ISOPE, 2015: 674-678.
(  0) 0)
|
| [4] |
LIU Shengnan, ONG M C, OBHRAI C, et al. Numerical simulations of regular and irregular wave forces on a horizontal semi-submerged cylinder[C]//Proceedings of the ASME 2017 36th International Conference on Ocean, Offshore and Arctic Engineering. Trondheim, Norway: OMAE, 2017.
(  0) 0)
|
| [5] |
FERNANDO P C, GUO Junke, LIN Pengzhi. Wave-current interaction at an angle 1:experiment[J]. Journal of hydraulic research, 2011, 49(4): 424-436. DOI:10.1080/00221686.2010.547036 (  0) 0)
|
| [6] |
QI Wengang, LI Changfei, JENG Dongsheng, et al. Combined wave-current induced excess pore-pressure in a sandy seabed: flume observations and comparisons with theoretical models[J]. Coastal engineering, 2019, 147: 89-98. DOI:10.1016/j.coastaleng.2019.02.006 (  0) 0)
|
| [7] |
SOLTANPOUR M, SAMSAMI F, SHIBAYAMA T, et al. Study of irregular wave-current-mud interaction[C]//Proceedings of the Coastal Engineering Conference. Seoul, Korea: ICCE, 2014: 01613782.
(  0) 0)
|
| [8] |
WEI C X, ZHOU D C, OU J P. Experimental study of the hydrodynamic responses of a bridge tower to waves and wave currents[J]. Journal of waterway, port, coastal and ocean engineering, 2017, 143(3): 04017002. DOI:10.1061/(ASCE)WW.1943-5460.0000381 (  0) 0)
|
| [9] |
JIANG Xuelian, ZOU Qingping, ZHANG Na. Wave load on submerged quarter-circular and semicircular breakwaters under irregular waves[J]. Coastal engineering, 2017, 121: 265-277. DOI:10.1016/j.coastaleng.2016.11.006 (  0) 0)
|
| [10] |
ITTC. 7.5-03-01-01, ITTC-recommended procedures and guidelines[S]. 2017.
(  0) 0)
|
| [11] |
ROACHE P J. Perspective: a method for uniform reporting of grid refinement studies[J]. Journal of fluids engineering, 1994, 116(3): 405-413. DOI:10.1115/1.2910291 (  0) 0)
|
| [12] |
吴乘胜, 邱耿耀, 魏泽, 等. 船模阻力数值水池试验不确定度评估[J]. 船舶力学, 2015, 19(10): 1197-1208. WU Chengsheng, QIU Gengyao, WEI Ze, et al. Uncertainty analysis on numerical computation of ship model resistance[J]. Journal of ship mechanics, 2015, 19(10): 1197-1208. DOI:10.3969/j.issn.1007-7294.2015.10.004 (  0) 0)
|
| [13] |
ZHU Renchuan, YANG Chunlei, MIAO Guoping, et al. Computational fluid dynamics uncertainty analysis for simulations of roll motions for a 3D ship[J]. Journal of Shanghai JiaoTong University (Science), 2015, 20(5): 591-599. DOI:10.1007/s12204-015-1666-z (  0) 0)
|
| [14] |
邓磊, 彭弘宇. 小水线面双体船耐波性能CFD不确定度分析[J]. 中国舰船研究, 2016, 11(3): 17-24. DENG Lei, PENG Hongyu. Uncertainty analysis in CFD for SWATH motions in regular head waves[J]. Chinese journal of ship research, 2016, 11(3): 17-24. DOI:10.3969/j.issn.1673-3185.2016.03.004 (  0) 0)
|
| [15] |
SILVA M C, VITOLA M A, EÇA L, et al. Numerical uncertainty analysis in regular wave modeling[J]. Journal of offshore mechanics and arctic engineering, 2018, 140(4): 041101. DOI:10.1115/1.4039260 (  0) 0)
|
| [16] |
柏君励, 马宁, 顾解忡. 畸形波的数值模拟及不确定度分析[J]. 上海交通大学学报, 2018, 23(4): 475-481. BAI Junli, MA Ning, GU Xiechong. Numerical simulation of focused wave and its uncertainty analysis[J]. Journal of Shanghai Jiao Tong University (Science), 2018, 23(4): 475-481. (  0) 0)
|
| [17] |
丁俊杰, 马宁, 顾解忡. 循环水槽多层孔板消波装置开发及消波特性数值模拟[J]. 上海交通大学学报, 2020, 54(1): 52-59. DING Junjie, MA Ning, GU Xiechong. Development of a wave-absorbing device with multiple porous plates for circulating water channel and simulation on its performance[J]. Journal of Shanghai JiaoTong University, 2020, 54(1): 52-59. (  0) 0)
|
| [18] |
PISTIDDA A, OTTENS H, ZOONTJES R. Using CFD to assess low frequency damping[C]//Proceedings of the ASME 201231st International Conference on Ocean, Offshore and Arctic Engineering. Rio de Janeiro, Brazil: OMAE, 2012: 657-665.
(  0) 0)
|
| [19] |
马宁, 丁俊杰, 顾解忡, 等. 多层变角度开孔折弯板透水消波装置: 中国, CN109100113A[P]. 2018-12-28. MA Ning, DING Junjie, GU Xiechong, et al. Multilayer variable angle perforated bending plate water-permeable wave absorbing device: CN, CN109100113A[P]. 2018-12-28. (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


