复杂的海洋环境对水下潜器带来巨大的挑战和威胁,各类水下潜器如水下机器人(autonomous underwater vehicle,AUV)在海试之前,一般需要在水池中测试其应急运动特性,而水中运动的姿态、速度和位移是非常关键的参数。
水下测量载体运动参数方式通常有声学导航、无线电导航、光学导航及惯性导航(inertia navigation system,INS)等[1],针对水池实验环境,采用INS是最合理的一种测量方式,因为INS测量信息全面、实时性好、频率快的优点,且不依赖任何外信息。但作为一种自主式导航,INS也存在误差随时间积累发散的缺点[2]。因此,要完成水下潜器模型在水池实验中的运动参数测量,需要采取一些创新的、工程上易于实现的有效措施。
为解决惯导精度随时间发散的问题,针对水池实验特殊应用环境,在大量试验的基础上,提出以下方法:首先对运动角速度和瞬时线速度的进行分析,判断潜器模型(AUV)的运动状态,如果模型基本处于静止,则实施精确的零速修正,估计陀螺和加速度计的误差;同时,考虑到水下载体转动的便利性,使用了方向调转的方案避免了陀螺北向等效漂移无法估计的问题。
1 捷联惯导误差与零速修正车载导航为了保证高精度,一般是在动力学约束基础上,每行进一段时间,进行短时间的停车,利用车辆静止状态下的零速度、零位移等信息修正捷联惯导系统误差[3]。对于水下运动测量,具有一定的借鉴意义。但由于水动力扰动等情况,水下不能像车载惯导一样,人为设置零速,此时可采用灵敏度高的陀螺信息和其他辅助信息,综合判断AUV是否处于静基座(发送“释放”命令前)或伪静基座(漂浮于水面)状态下。
1.1 载体机动状态的判断在使用惯导对AUV机动状态进行判断时,有2种选择方案,即使用角速度和加速度进行判断,或使用解算后的速度和姿态进行判断。
但由于惯导直接输出的器件信息对外界环境过于敏感且信号中含有高频随机噪声,不能真实反映AUV运动状态。当AUV匀速直线运动或静止时,AUV姿态信息变化很小,无法有效判别是否处于机动状态。同样,仅使用速度也无法区分AUV处于原地旋转还是静止状态。另外,在考虑捷联惯导解算出的速度在没有外界信息修正时易发散的情况,可选用解算的瞬时速度[4]和姿态信息,对AUV机动状态进行综合判断。即当一个AUV同时满足以下2点时可认为该载体未处于机动状态:
1) AUV综合速度V小于某阈值Vs;
2) AUV姿态变化角变换速度小于某阈值ωs。
其中Vs与ωs取值取决于AUV上所搭载的导航系统具体参数。
1.2 舒勒震荡对AUV瞬时速度量测影响根据速度误差状态传播方程[2]可知,造成惯导速度发散的主要误差源为惯性器件(陀螺和加速度计)的常值漂移和周期为24 h的地球震荡、周期为2π/ωiesinLh的傅科震荡和周期为84.4 min的舒勒震荡带来的误差等。由于地球震荡和傅科震荡周期远大于瞬时速度的量测时间,因此本文主要考虑舒勒震荡造成的影响。
图 1分别模拟了10 min内,幅值为0.6、周期为15 s的正弦信号X(图 1(a)),幅值为5、周期为84.4 min的类舒勒信号Y(图 1(b))和二者信号的叠加(图 1(c))。

|
Download:
|
| 图 1 正弦信号与舒勒周期信号的叠加 Fig. 1 The superposition of sinusoidal signal and Schuler signal | |
如图 1所示,原始信号的输出由于舒勒周期的存在而在短时间内具有发散特性。舒勒振荡项的存在使得加速度计的输出具有发散特性,由于从加速度信息到速度信息需要经过积分运算,因此这种发散特性还会增强[5-6]。如果要想得到较为准确的瞬时速度信息,就需要消除加速度计输出中的舒勒震荡项。利用不同信息频率的差异性,通过引入数字高通滤波器将高频的速度信息从叠加信号中分离出来。
1.3 高通滤波器的设计常用的数字滤波器有FIR和IIR滤波器,对于相同的设计指标,FIR滤波器所要求阶数比IIR滤波器高5~10倍[6]。因此本文出于工程化考虑选用了基于巴特沃兹的三阶IIR滤波器。
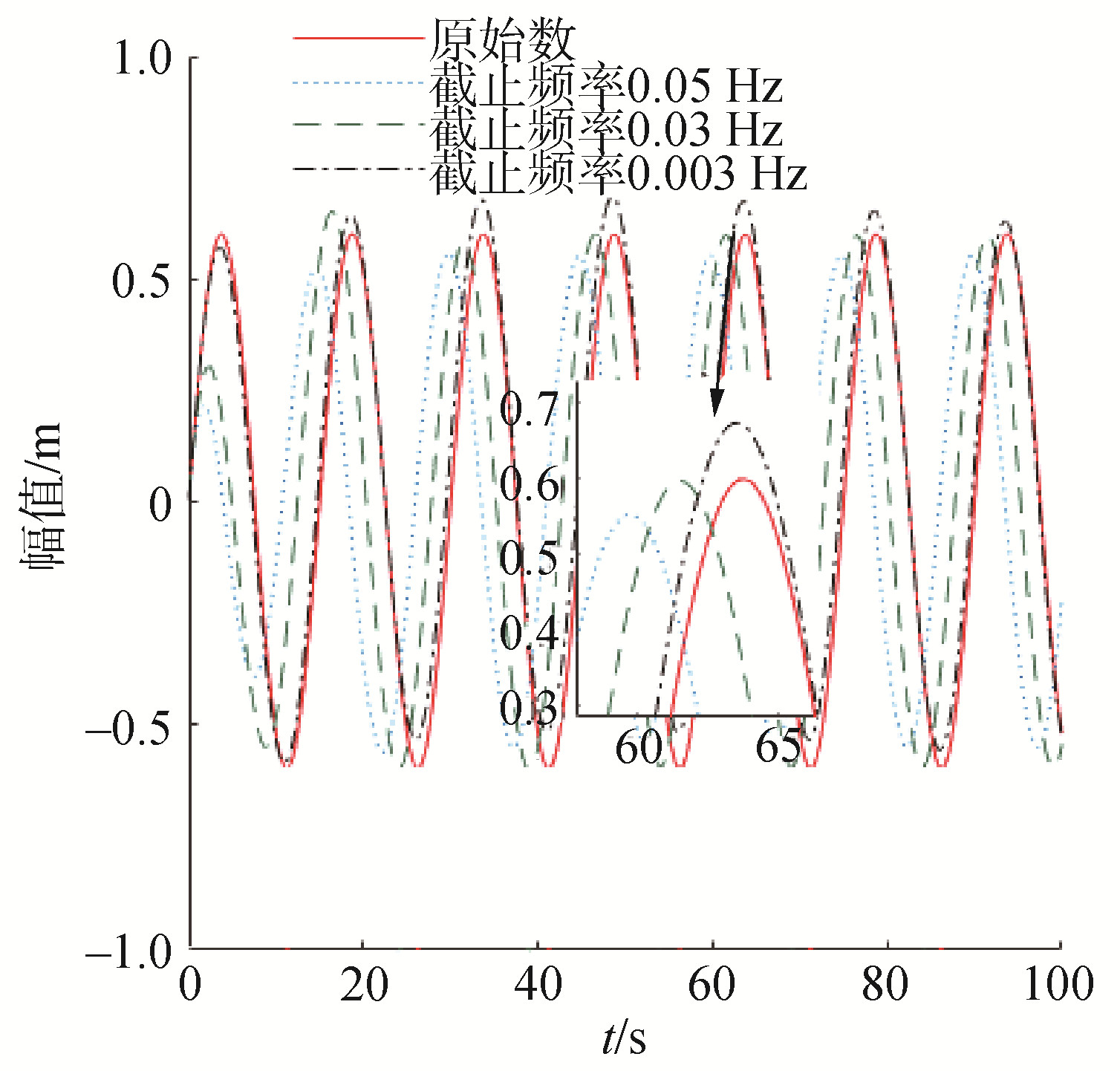
为得到较好的滤波结果,高通滤波器的截止频率一般应数倍高于目标信号频率,而高通滤波本身会导致相位超前的特性又决定了截止频率过高时会严重破坏原始信号,因此需针对滤波信号特点进行一定模拟来选定理想滤波参数。由于AUV不做运动时受水下扰动的通常周期为4~16 s[7],为了不损失数据真实性高通滤波器截止频率必须保证在0.06 Hz以下。图 2模拟了在不同截止频率下叠加信号的高通滤波结果,从对比上来看截止频率高低会直接影响滤波结果的幅值和超前时间。从图 2中可看出,当截止频率设置为0.03 Hz时,滤波结果在60 s内很快收敛到了理想结果,截止频率设为0.003 Hz时仍存在一个小幅正弦震荡,而0.05 Hz高通滤波下不仅滤波结果超前严重,对原始信号特性也造成了一定影响。综上,将高通滤波器截止频率设置为0.03 Hz是一个较好的结果。
|
Download:
|
| 图 2 不同截止频率下的高通滤波对叠加信号的处理结果 Fig. 2 The results of high-pass filtering at different cut-off frequency on superimposed signals | |
在选定高通滤波器截止频率后,AUV的瞬时速度即可按图 3所示方法解算得到。

|
Download:
|
| 图 3 基于高通滤波的瞬时速度计算方法 Fig. 3 The instantaneous velocity calculation method based on high pass filtering | |
将惯导误差模型的系统状态方程写为:
| $ \mathit{\boldsymbol{\dot X}} = \mathit{\boldsymbol{FX}} + \mathit{\boldsymbol{GW}} $ | (1) |
式中:状态量X=[δφ δv δp δw δf]T,δφ、δv、δp、δw、δf依次为姿态误差、速度误差、位置误差、陀螺仪等效漂移和加速度计等效偏置; 状态量噪声W=[ wgx wgy wgz wax way waz]T,为高斯白噪声; F和G分别为状态转移矩阵和噪声转移矩阵,在以东北天为指向的导航坐标系下为[2]:
| $ \mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_{aa}}}&{{\mathit{\boldsymbol{M}}_{av}}}&{{{\bf{0}}_{3 \times 3}}}&{{\mathit{\boldsymbol{I}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}} \\ {{\mathit{\boldsymbol{M}}_{va}}}&{{\mathit{\boldsymbol{M}}_{vv}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{\mathit{\boldsymbol{I}}_{3 \times 3}}} \\ {{{\bf{0}}_{3 \times 3}}}&{{\mathit{\boldsymbol{I}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}} \\ {{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{\mathit{\boldsymbol{M}}_g}}&{{{\bf{0}}_{3 \times 3}}} \\ {{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{\mathit{\boldsymbol{M}}_a}} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{M}}_{aa}} = \left[ {\begin{array}{*{20}{c}} 0&{{w_{ie}}{\text{sin}}L}&0 \\ { - {w_{ie}}{\text{sin}}L}&0&0 \\ {{w_{ie}}{\text{cos}}L}&0&0 \end{array}} \right],{\mathit{\boldsymbol{M}}_{va}} = \left[ {\begin{array}{*{20}{c}} 0&{ - g}&0 \\ g&0&0 \\ 0&0&0 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{M}}_{va}} = \left[ {\begin{array}{*{20}{c}} 0&{ - \frac{1}{{R + h}}}&0 \\ {\frac{1}{{R + h}}}&0&0 \\ {\frac{{{\text{tan}}L}}{{R + h}}}&0&0 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{M}}_{vv}} = \left[ {\begin{array}{*{20}{c}} 0&{2{w_{ie}}{\text{sin}}L}&{ - 2{w_{ie}}{\text{cos}}L} \\ { - 2{w_{ie}}{\text{sin}}L}&0&0 \\ {2{w_{ie}}{\text{cos}}L}&0&0 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{M}}_g} = \left[ {\begin{array}{*{20}{c}} { - \frac{1}{{{\tau _g}}}}&0&0 \\ 0&{ - \frac{1}{{{\tau _a}}}}&0 \\ 0&0&{ - \frac{1}{{{\tau _a}}}} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{M}}_a} = \left[ {\begin{array}{*{20}{c}} { - \frac{1}{{{\tau _a}}}}&0&0 \\ 0&{ - \frac{1}{{{\tau _a}}}}&0 \\ 0&0&{ - \frac{1}{{{\tau _a}}}} \end{array}} \right],\mathit{\boldsymbol{G = }}{\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{C}}_b^n}&{{{\bf{0}}_{3 \times 3}}} \\ {{{\bf{0}}_{3 \times 3}}}&{\mathit{\boldsymbol{C}}_b^n} \\ {{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}} \end{array}} \right]^{\text{T}}} $ |
式中:wie为地球自转角速度;g为当地重力加速度大小;L为当地纬度值;Cbn为载体系b到导航系n的转换矩阵;τg, τa分别为陀螺仪与加速度计马尔可夫时间常数。
2.2 量测方程及可观性分析静基座情况下可选用速度及位置误差作为系统观测量。对于姿态,由于对准误差等因素的存在,一般不适用于选用姿态误差作为系统观测量。此时,观测量与量测方程可写作:
| $ \begin{array}{l} \mathit{\boldsymbol{Z}} = \left[ {\mathit{\boldsymbol{\phi}} \mathit{\boldsymbol{v}}} \right],{\rm{ }}\mathit{\boldsymbol{H}} = [{{\bf{0}}_{3 \times 3}}\;\;{\mathit{\boldsymbol{I}}_{3 \times 3}}\;\;{{\bf{0}}_{3 \times 9}}]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{Z}} = {\rm{ }}\mathit{\boldsymbol{HX}} + \mathit{\boldsymbol{V}} \end{array} $ | (2) |
式中:ϕv为速度误差;V为观测量白噪声;式(1)与式(2)的可观性矩阵可写为[8]:
| $ \mathit{\boldsymbol{Q}} = {[{\mathit{\boldsymbol{H}}^{\rm{T}}}\;\;\;\;\;{\left( {\mathit{\boldsymbol{H}} \times \mathit{\boldsymbol{F}}} \right)^{\rm{T}}}\;\;\; \cdots \;\;\;{\rm{ }}{(\mathit{\boldsymbol{H}} \times {\mathit{\boldsymbol{F}}^{14}})^{\rm{T}}}]^{\rm{T}}} $ |
此时Q的秩为8 < 15,根据可观性定义整体系统为不完全可观状态,其中3个不可观量为位置误差δp,如在量测系统中引入当前时刻与静止初始时刻的位置差可一定程度上进行观测修正。此时状态空间中仍有4个不可观测量,对于这4个不可观测量的选取有不同的看法,但是所有观点均指出陀螺仪的东向等效漂移属于不可观测量[9-10]。
2.3 陀螺仪东向等效漂移的修正假设在某一时刻,惯导载体坐标系与导航坐标系水平面重合,方位相差α,导航系中的等效陀螺漂移可表示为:
| $ \delta {\mathit{\boldsymbol{w}}_1} = \left[ {\begin{array}{*{20}{c}} {\delta {w_{E1}}}\\ {\delta {w_{N1}}}\\ {\delta {w_{U1}}} \end{array}} \right]{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {\delta {w_x}{\rm{cos}}\alpha - \delta {w_y}{\rm{sin}}\alpha }\\ {\delta {w_y}{\rm{cos}}\alpha + \delta {\omega _x}{\rm{cos}}\alpha }\\ {\delta {w_z}} \end{array}} \right]{\rm{ }} $ | (3) |
若方位角转过α′时,则在第2个位置下导航系的等效陀螺漂移为:
| $ \delta {\mathit{\boldsymbol{w}}_2} = \left[ {\begin{array}{*{20}{c}} {\delta {w_{E2}}}\\ {\delta {w_{N2}}}\\ {\delta {w_{U2}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\delta {w_x}{\rm{cos}}\left( {\alpha + \alpha \prime } \right) - \delta {w_y}{\rm{sin}}\left( {\alpha + \alpha \prime } \right)}\\ {\delta {w_y}{\rm{cos}}\left( {\alpha + \alpha \prime } \right) + \delta {\omega _x}{\rm{cos}}\left( {\alpha + \alpha \prime } \right)}\\ {\delta {w_z}} \end{array}} \right] $ | (4) |
比较式(3)、(4)可发现:当α′=180°时,δω1+δω2的前2项为0,即可通过在静基座下绕方位轴旋转180°的方法来对北向及东向等效陀螺偏差进行估计[11]。
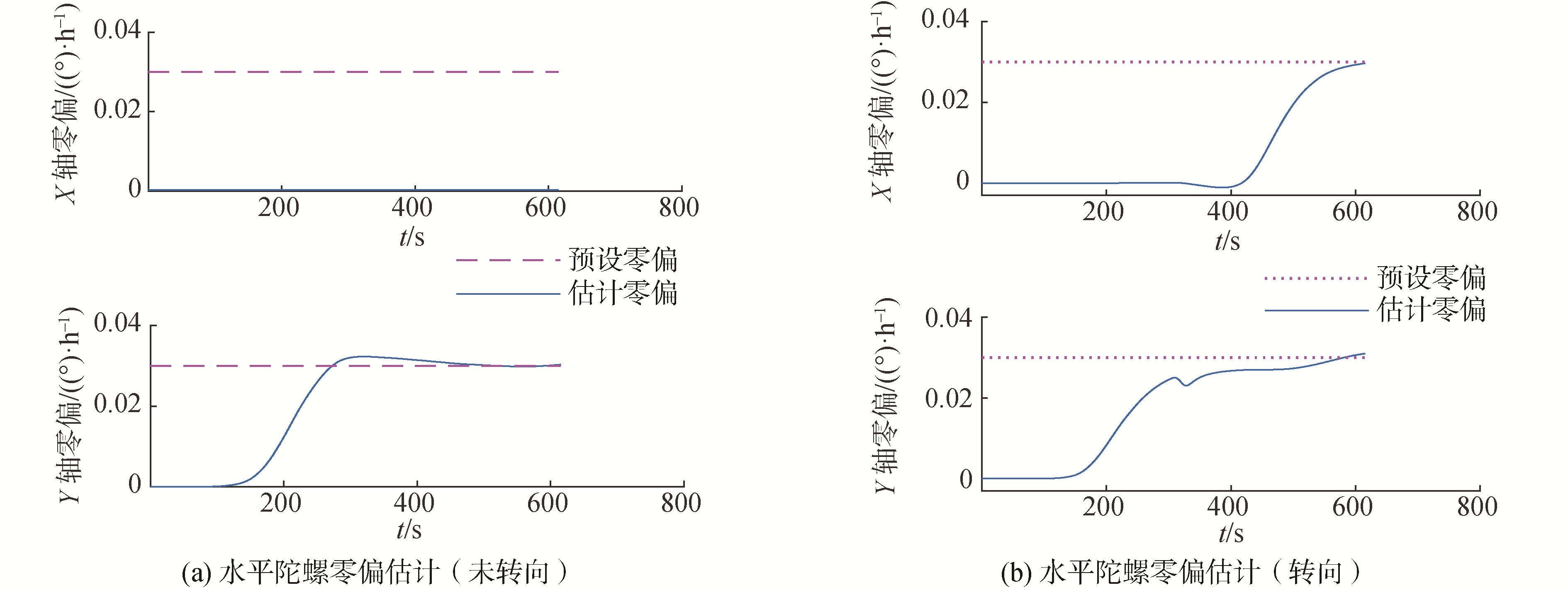
图 4模拟了在静基座条件下,惯导系统进行180°转向与静止下水平陀螺等效偏差估计结果。
|
Download:
|
| 图 4 X、Y轴陀螺零偏估计 Fig. 4 The bias estimation of the gyroscope in X & Y axis | |
其中陀螺零偏为0.03 (°)/h,起始方位角指北(此时东向陀螺可以等价于X轴陀螺),导航仪在300 s后进行了180 °转向,从对比中可以看出,未转向情况下无法对东向陀螺进行有效零偏估计,而在完成转向后其零偏则可以得到较为准确的估计值。
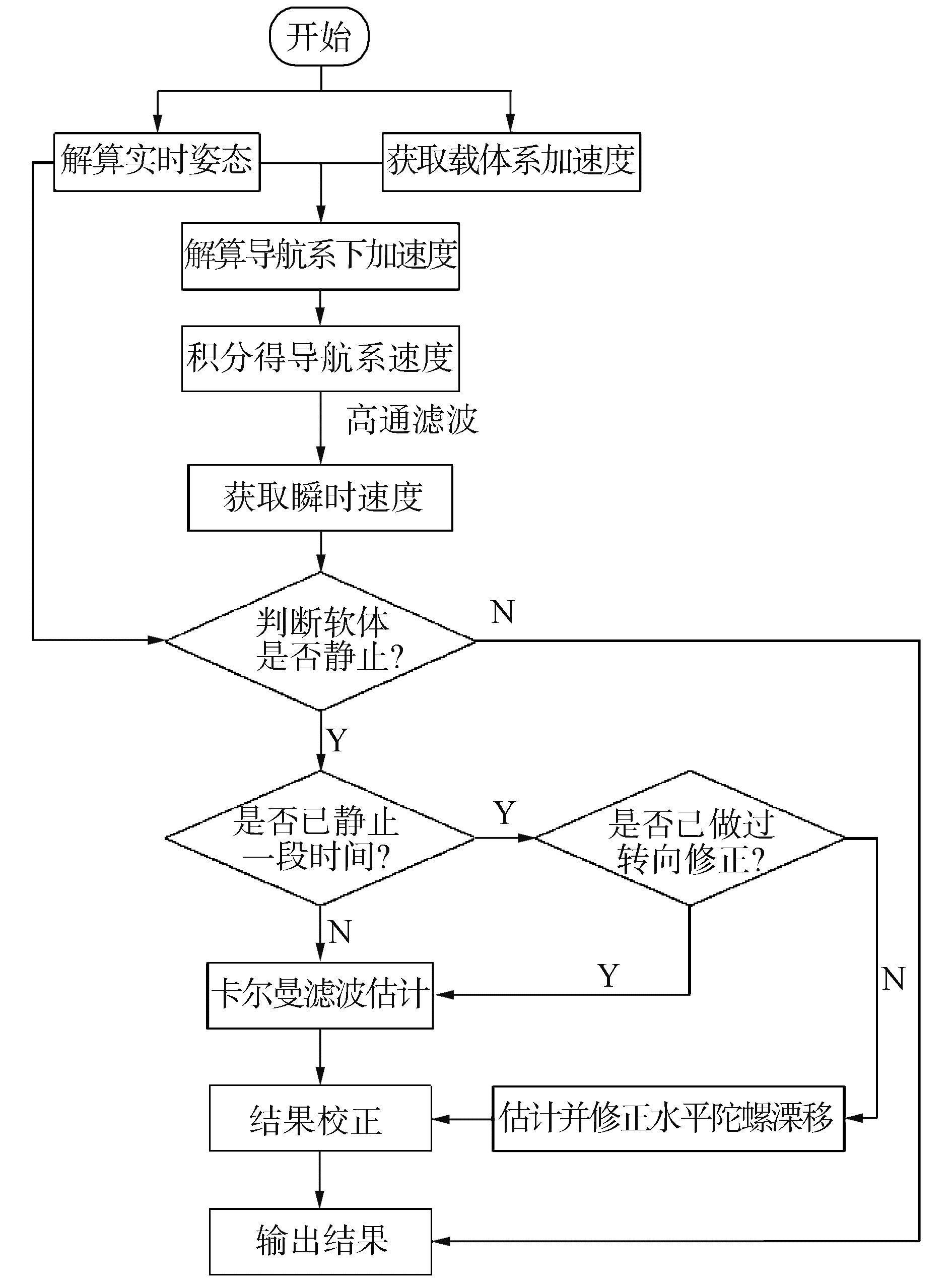
此时,可以根据递推的公式建立AUV运动轨迹量测的整体流程。如图 5所示,在惯导完成对准后,通过坐标转换和高通滤波得到非发散性的载体瞬时速度信息,之后可遵循1.1节中提出的准则对载体机动状态进行判断。若载体处于静态则利用量测误差对导航参数进行实时修正,以确保对AUV运动轨迹达到最优跟踪。
|
Download:
|
| 图 5 AUV运动轨迹量测流程 Fig. 5 The process of AUV trajectory measurement | |
为验证文中提出算法的可行性,根据试验的不同阶段分别进行了室内试验和水下试验。
3.1 试验设备验证试验选用了哈尔滨工程大学惯性导航与测控技术研究所研制的光纤捷联惯性导航仪(如图 6)。导航仪中加速度计量程范围为±25 g,零偏稳定性优于50 μg,标度系数稳定性优于30×10-6。所选用光纤陀螺角速度敏感范围为±600 (°)/s,常温下零偏稳定性优于0.01 (°)/h,标度因数稳定性优于5×10-6。

|
Download:
|
| 图 6 光纤捷联惯性导航仪 Fig. 6 FOG based SINS | |
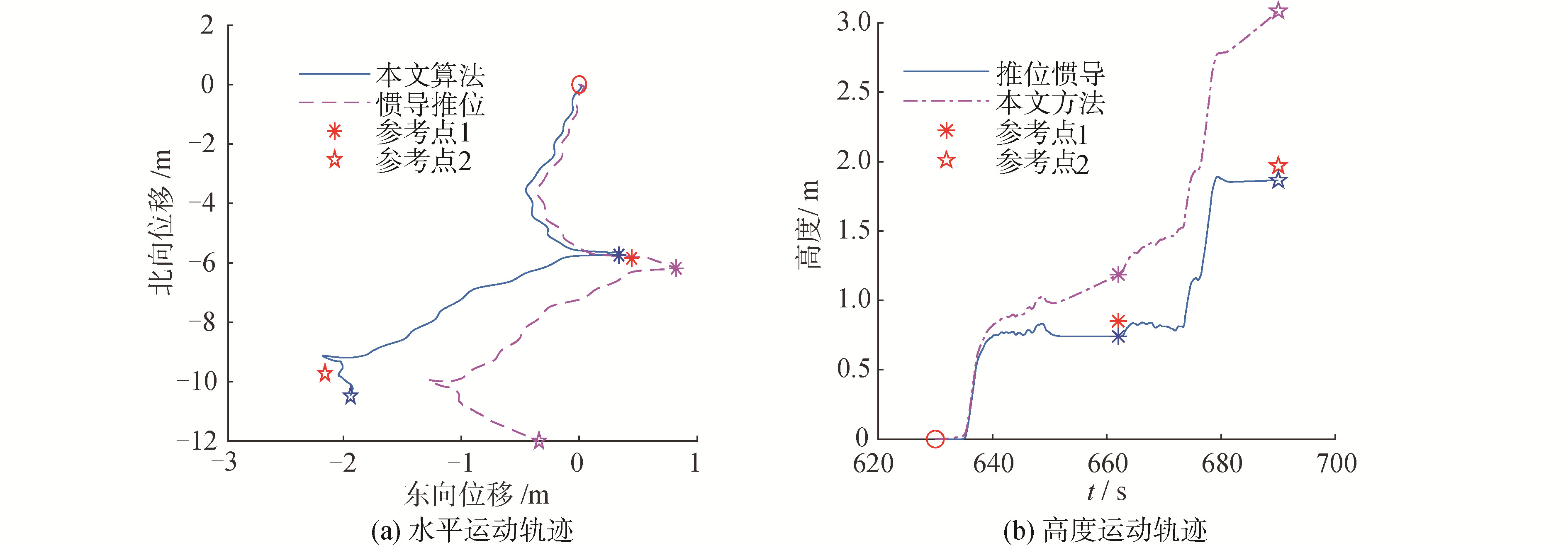
图 7为水池试验前先行进行的室内模拟试验结果,为模拟水下上浮行动及数据对比,室内试验采用二阶段式运动。
|
Download:
|
| 图 7 室内试验运动轨迹 Fig. 7 The trajectory of indoor experiment | |
惯导设备先在地面静置5 min后进行180 °转向,在转向后再次静置5 min,之后依次将设备搬至指定过渡点及终点,并分别停留10~15 s。其中过渡点与终点相对于起始点在东北天方向位置依次为0.44、-5.84、0.85、-2.15、-9.72及1.97 m。
由于室内试验不同于水下试验,其扰动因素较小,因此该试验结果中消去了关于机动判断的部分。图 7显示了室内试验中未经过机动判断与经过机动判断后的运动轨迹对比,圆圈为起始点位置,*号与☆号代表了中间点和终点相对于起始点的参考位置。
参考点解算距离对比如表 1,从表 1中可以看出,文中算法对室内试验移动距离解算明显优于惯导推位的结果,其平均导航精度约提升了75%。
| 表 1 参考点解算距离对比 Table 1 The position comparison of reference points |
试验地点选在哈尔滨工程大学的深水实验水池,深10 m,长10 m,宽5 m。光纤捷联惯性导航系统装在图 8中AUV密封舱内部,为了验证算法的有效性,将水下试验分为2个阶段:第1阶段采集AUV在水下静基座状态下的瞬时速度与姿态角变化来决定判断机动状态使用的Vs与ωs;第2阶段为上浮试验,将AUV分别从水深9、4 m处进行上浮试验,同时实时测量AUV的运动轨迹。

|
Download:
|
| 图 8 试验用水下机器人 Fig. 8 The AUV tested in experiment | |
试验分别采用捷联惯导解算AUV在水下的三维运动轨迹和深度传感器测量其深度的2种测量方法,把捷联惯导解算三维轨迹中的高度与深度传感器测量的深度进行对比。其中深度传感器分辨率约0.5 mm,量测噪声优于10 mm,因此可认为深度传感器测量的深度是比较准确的,即如果惯导解算三维轨迹中的高度与深度传感器测量的深度基本重合,那么可认为本文提出的方法在实际水下环境中也是有效的。
3.4 试验结果及分析在进行水池试验前先采集了AUV在水下静基座下采集并解算的瞬时速度与姿态角变化情况,由于在水下运动的特殊性,AUV在3个方向上的运动并无太大区分性,因而速度阈值Vs可由合成速度v来选定。数据显示瞬时速度的最大值约为0.001 8 m/s考虑到水下环境复杂度和后续可能发散情况可将阈值Vs选定为略高一个数量级的0.01 m/s,相对于瞬时速度由于姿态角变化较为缓慢平滑,同时姿态角变化值ωs大致选定为3倍静基座最高值的0.03 (°)/s。
图 9给出了AUV从水深9 m的深度进行上浮试验的情况,图 9(a)为试验中机动判断,*号之前代表了此时认为系统处于静基座,则进行零速修正估计惯导的偏差值,*号之后表示进入运动阶段。图 9(b)表示了文中算法与传统惯导推位算法运动参数计算结果与深度传感器的实时对比,可以看出文中算法与深度传感器所测结果基本一致,图 9(c)为文中算法与导航推位结果在深度上的误差,在最终误差上文中算法浮出水面时误差约为0.084 m,而使用了传统惯导推位算法的结果误差约为0.6 m。

|
Download:
|
| 图 9 水池试验结果 Fig. 9 The results of pool experiment | |
由于水池试验的特殊性,水下水平方向位移过程无法获取精确结果,此时可比较其浮出水面时的各方向位移进行粗估,在浮出水面时水下潜器相对于原始位置东向位移约11.5 m,北向位移约1.7 m,文中算法解得的东向位移为11.72 m,北向位移约1.67 m,相对于惯导推位结果的12.31 m与1.52 m更为接近量测结果。
同样,在4 m深度的上浮试验中,本文算法在深度值方向上误差0.067 m,明显优于纯惯导推位的0.4 m误差。因此,可认为使用了本文方法水下潜器运动参数量测可得到更到的精度。
4 结论1) 文中提出的运动参数辨识方法可有效判断水下潜器是否处于机动状态;
2) 室内试验精度较传统方法提高了75%;
3) 水池试验深度误差可有效控制在厘米内。
文中水池试验所采用的模型为实际水下潜器同比例缩小后模型,可认为该方法对水下潜器运动参数量测同样有效。
由于水池试验中实时水平位移获取较难,因此最终的精度对比只能由潜器模型深度和其浮出水面后的大概量测结果对三维运动中所有参数精度进行类比评估,这方面不足待后续量测参照方法改进后进行更为全方面的对比分析。
| [1] |
LYU Pengfei, HE Bo, GUO Jia, et al. Underwater navigation methodology based on intelligent velocity model for standard AUV[J]. Ocean engineering, 2020, 202: 107073. DOI:10.1016/j.oceaneng.2020.107073 (  0) 0)
|
| [2] |
秦永元. 惯性导航[M]. 2版. 北京: 科学出版社, 2014. QIN Yongyuan. Inertial navigation[M]. 2nd ed. Beijing: Science Press, 2014. (  0) 0)
|
| [3] |
YAO Yiqing, XU Xiaosu, XU Xiang. An IMM-aided ZUPT methodology for an INS/DVL integrated navigation system[J]. Sensors, 2017, 17(9): 2030. DOI:10.3390/s17092030 (  0) 0)
|
| [4] |
袁书明, 程建华, 马斌. 基于自适应频率估计的舰船瞬时线运动测量方法[J]. 中国惯性技术学报, 2016, 24(5): 565-570. YUAN Shuming, CHENG Jianhua, MA Bin. Measurement method for ship instantaneous linear movement based on adaptive frequency estimation[J]. Journal of Chinese inertial technology, 2016, 24(5): 565-570. (  0) 0)
|
| [5] |
孙伟, 孙枫. 基于惯导解算的舰船升沉测量技术[J]. 仪器仪表学报, 2012, 33(1): 167-172. SUN Wei, SUN Feng. Measurement technology of ship heave movement based on sins resolving[J]. Chinese journal of scientific instrument, 2012, 33(1): 167-172. DOI:10.3969/j.issn.0254-3087.2012.01.025 (  0) 0)
|
| [6] |
孙伟, 孙枫, 杨琳. 动态环境下舰船瞬时线运动测量方法研究[J]. 系统仿真学报, 2013, 25(4): 839-844. SUN Wei, SUN Feng, YANG Lin. Research on measurement method of warship instantaneous line motion under condition of dynamic motion[J]. Journal of system simulation, 2013, 25(4): 839-844. (  0) 0)
|
| [7] |
HU Keyong, GUO Zhongwen, CHE Zhaodong, et al. Composition model of complex virtual instrument for ocean observing[J]. Journal of software, 2014, 9(5): 1177-1188. (  0) 0)
|
| [8] |
HAM F M, BROWN R G. Observability, eigenvalues, and kalman filtering[J]. IEEE Transactions on Aerospace and Electronic Systems, 1983, AES-19(2): 269-273. DOI:10.1109/TAES.1983.309446 (  0) 0)
|
| [9] |
王新龙. 捷联式惯导系统动、静基座初始对准[M]. 西安: 西北工业大学出版社, 2013. WANG Xinlong. National defense monograph[M]. Xi'an: Northwestern Polytechnical University Press, 2013. (  0) 0)
|
| [10] |
王晓雪.光纤捷联惯导系统初始对准方法研究[D].哈尔滨: 哈尔滨工程大学, 2016. WANG Xiaoxue. Research on initial alignment method of fiber optic strapdpwn navigationg system[D]. Harbin: Harbin Engineering University, 2016. (  0) 0)
|
| [11] |
何昆鹏, 许德新, 吴简彤, 等. 船用捷联惯性导航系统在系泊状态下快速初始对准与标定[J]. 哈尔滨工程大学学报, 2008, 29(9): 944-950. HE Kunpeng, XU Dexin, WU Jiantong, et al. Initial rapid alignment/calibration of a marine strapdown inertial navigation system in moorage[J]. Journal of Harbin Engineering University, 2008, 29(9): 944-950. DOI:10.3969/j.issn.1006-7043.2008.09.010 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


