锅筒径向温差计算结果影响其热应力和锅筒疲劳寿命以及其他相关研究和应用的准确性。在固定式动力锅炉方面,我国在吸收国外先进标准和国内研究成果的基础上,制订了锅筒低周疲劳寿命国家标准计算方法[1-3],虽然历经2次修订,但是给出的锅筒径向温差计算公式没有改变,有必要对其准确程度进行探讨。在船舶动力锅炉方面,事实说明了船舶动力锅炉相关标准在制订时间上要滞后于固定式动力锅炉,并且船舶动力锅炉比固定式动力锅炉具有更高的机动性[4],因此固定式动力锅炉锅筒径向温差国家标准计算方法能否在船舶动力锅炉上应用是不容忽视的问题。另外,虽然现行固定式动力锅炉国家标准[3]规定,应力分析允许采用可靠的有限元分析计算软件,但应力分析结果必须与已有的解析解、数值解或实验结果相比较,以验证软件计算结果的准确性,然而目前能够为验证有限元分析软件计算结果准确性提供支撑的公开报道甚少,文献[5-6]等给出了锅筒体积平均温度与内壁温度之差的径向温差计算公式,但是该计算公式在表达上相对繁琐,而且也无法给出固定式动力锅炉锅筒径向温差国家标准计算公式的准确程度。
针对上述问题,本文主要建立符合工程实际的和更为准确的锅筒径向温差计算方法,用以验证固定式动力锅炉锅筒径向温差国家标准计算方法的相对计算误差及其产生原因和对船舶动力锅炉锅筒径向温差计算的适用性,以期该方法能够应用于固定式动力锅炉和船舶动力锅炉锅筒径向温差计算,从而为工程研究和应用奠定基础。
1 固定式动力锅炉国家标准法固定式动力锅炉国家标准[1-3]给出的锅筒径向温差计算式为:
| $ \Delta {t_1} = {t_{\rm{o}}} - {t_{\rm{i}}} = - \frac{{{C_{\rm{t}}}{\delta ^2}v}}{{{a_{\rm{t}}}}}[1 - {\rm{exp}}( - \chi t/\tau )] $ | (1) |
式中:Δt1为锅筒外壁与内壁的温差,℃;to为锅筒外壁绝热温度,℃;ti为锅筒内壁温度,取为锅筒内工质温度,℃;δ 为锅筒名义厚度,mm;v为锅筒内工质温度变化速率,℃/min。其中,升温为正值,降温为负值;at为锅筒材料热扩散率,mm2/min;t为锅筒内工质升温或降温所经历的时间,min。
Ct 为与按名义厚度确定的锅筒外径与内径的比值β有关的结构系数,可按式计算:
| $ {C_{\rm{t}}} = \frac{{2{\beta ^2}{\rm{ln}}\beta - {\beta ^2} + 1}}{{4{{(\beta - 1)}^2}}} $ | (2) |
式中χ为温度阻尼系数:
| $ \chi = \sqrt {\frac{{\beta - 1}}{{{\beta _1}}}} $ | (3) |
| $ \begin{array}{*{20}{l}} {{\beta _1} = \frac{{{\beta ^5} - 1}}{5} - 4{\beta ^2}\left( {\frac{{{\beta ^3}{\rm{ln}}\beta }}{3} - \frac{{{\beta ^3} - 1}}{9}} \right) + }\\ {{\kern 1pt} {\kern 1pt} 4{\beta ^4}[\beta {{({\rm{ln}}\beta - 1)}^2} + \beta - 2] + \beta - 1 + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2\left\{ {2{\beta ^2}[\beta ({\rm{ln}}\beta - 1) + 1] - \frac{{{\beta ^3} - 1}}{3}} \right\}} \end{array} $ | (4) |
式中τ为时间常数,min:
| $ \tau = \frac{{D_{\rm{i}}^2}}{{16{a_{\rm{t}}}}} $ | (5) |
式中Di为锅筒内直径,mm。
若|Δt1|>|vt|,则
| $ \Delta {t_1} = - vt $ | (6) |
可见,式(6)是式(1)的修正公式。
2 非常逼近解析解计算方法的建立文献[7]中“汽包温度场的解析解”给出了与固定式动力锅炉国家标准相同的锅筒导热方程和定解条件下的非稳态温度场推导过程,则根据该文献中的推导过程和计算结果,径向温差计算公式推导如下:
| $ \begin{array}{*{20}{c}} {\Delta {t_2} = \frac{v}{{4{a_{\rm{t}}}}}\left( {R_2^2 - R_1^2 - 2R_2^2{\rm{ln}}\frac{{{R_2}}}{{{R_1}}}} \right) + \frac{v}{{4{a_{\rm{t}}}}}(R_1^2 + }\\ {\left. {2R_2^2{\rm{ln}}\frac{{{R_2}}}{{{R_1}}} - R_2^2} \right){\rm{exp}}( - {a_{\rm{t}}}n_i^2t) = \frac{{vR_1^2}}{{4{a_{\rm{t}}}}}({\beta ^2} - }\\ {1 - 2{\beta ^2}{\rm{ln}}\beta )[1 - {\rm{exp}}( - {a_{\rm{t}}}n_i^2t)]} \end{array} $ | (7) |
式中:Δt2为按文献[7]计算出的锅筒外壁绝热温度与锅筒内壁温度之差,℃;R2为按名义厚度确定的锅筒外半径,mm;R1为锅筒内半径,mm;ni为特征方程式无穷多个正实根,且有n1 < n2 < n3 < …,由式(8)确定:
| $ {{\rm{J}}_0}({n_i}{R_1}){{\rm{Y}}_1}({n_i}{R_2}) - {{\rm{J}}_1}({n_i}{R_2}){{\rm{Y}}_0}({n_i}{R_1}) = 0 $ | (8) |
式中:J0为第一类零阶贝塞尔函数;Y0为第二类零阶贝塞尔函数;J1为第一类一阶贝塞尔函数;Y1为第二类一阶贝塞尔函数。
设式(1)和式(7)相等,并使:
| $ { - \frac{{{C_{\rm{t}}}{\delta ^2}v}}{{{a_{\rm{t}}}}} = \frac{{vR_1^2}}{{4{a_{\rm{t}}}}}({\beta ^2} - 1 - 2{\beta ^2}{\rm{ln}}\beta )} $ | (9) |
则:
| $ {1 - {\rm{exp}}( - \chi t/\tau ) = 1 - {\rm{exp}}( - {a_{\rm{t}}}n_i^2t)} $ | (10) |
由式(9)和δ=R2-R1,得:
| $ {C_{\rm{t}}} = \frac{{2{\beta ^2}{\rm{ln}}\beta - {\beta ^2} + 1}}{{4{{(\beta - 1)}^2}}} $ | (11) |
可见,式(11)与式(2)相等。
将式(5)代入式(10),得:
| $ \chi = {\left( {\frac{{{n_i}{D_{\rm{i}}}}}{4}} \right)^2} = {\left( {\frac{{{n_i}{R_1}}}{2}} \right)^2} $ | (12) |
由式(9)可知,式(7)可改写成:
| $ \Delta {t_2} = - \frac{{{C_{\rm{t}}}{\delta ^2}v}}{{{a_{\rm{t}}}}}[1 - {\rm{exp}}( - {a_{\rm{t}}}n_i^2t)] $ | (13) |
文献[8]已证明,式(8)中ni仅取第1项n1时,式(7)就已非常逼近其解析解,且具有足够高的精度。这样,式(8)、(12)、(13)可以分别改写成:
| $ {{{\rm{J}}_0}({n_1}{R_1}){{\rm{Y}}_1}({n_1}{R_2}) - {{\rm{J}}_1}({n_1}{R_2}){{\rm{Y}}_0}({n_1}{R_1}) = 0} $ | (14) |
| $ {\chi = {{\left( {\frac{{{n_1}{R_1}}}{2}} \right)}^2}} $ | (15) |
| $ {\Delta {t_2} = - \frac{{{C_{\rm{t}}}{\delta ^2}v}}{{{a_{\rm{t}}}}}[1 - {\rm{exp}}( - {a_{\rm{t}}}n_1^2t)]} $ | (16) |
设n1R1=x,利用β=R2/R1,所以n1R2=βx。这样,式(14)可以写成:
| $ {{\rm{J}}_0}(x){{\rm{Y}}_1}(\beta x) - {{\rm{J}}_1}(\beta x){{\rm{Y}}_0}(x) = 0 $ | (17) |
文献[9]给出了当x≥3时,式(17)的计算关联式为:
| $ {{{\rm{J}}_0}(x) = {x^{ - 0.5}}{f_0}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\theta _0}} $ | (18) |
| $ {{{\rm{Y}}_0}(x) = {x^{ - 0.5}}{f_0}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\theta _0}} $ | (19) |
| $ \begin{array}{*{20}{l}} {\;\:{f_0} = 0.797{\kern 1pt} {\kern 1pt} {\kern 1pt} 884{\kern 1pt} {\kern 1pt} {\kern 1pt} 56 - 0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 000{\kern 1pt} {\kern 1pt} {\kern 1pt} 77(3/x) - }\\ {0.005{\kern 1pt} {\kern 1pt} {\kern 1pt} 527{\kern 1pt} {\kern 1pt} {\kern 1pt} 40{{(3/x)}^2} - 0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 095{\kern 1pt} {\kern 1pt} {\kern 1pt} 12{{(3/x)}^3} + }\\ {0.001{\kern 1pt} {\kern 1pt} {\kern 1pt} 372{\kern 1pt} {\kern 1pt} {\kern 1pt} 37{{(3/x)}^4} - 0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 728{\kern 1pt} {\kern 1pt} {\kern 1pt} 05{{(3/x)}^5} + }\\ {0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 144{\kern 1pt} {\kern 1pt} {\kern 1pt} 76{{(3/x)}^6} + \varepsilon (|\varepsilon | < 1.6 \times {{10}^{ - 8}})} \end{array} $ | (20) |
| $ \begin{array}{*{20}{l}} {{\theta _0} = x - 0.785{\kern 1pt} {\kern 1pt} {\kern 1pt} 398{\kern 1pt} {\kern 1pt} {\kern 1pt} 16 - 0.041{\kern 1pt} {\kern 1pt} {\kern 1pt} 663{\kern 1pt} {\kern 1pt} {\kern 1pt} 97(3/x) - }\\ {0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 039{\kern 1pt} {\kern 1pt} {\kern 1pt} 54{{(3/x)}^2} + 0.002{\kern 1pt} {\kern 1pt} {\kern 1pt} 625{\kern 1pt} {\kern 1pt} {\kern 1pt} 73{{(3/x)}^3} - }\\ {0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 541{\kern 1pt} {\kern 1pt} {\kern 1pt} 25{{(3/x)}^4} - 0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 293{\kern 1pt} {\kern 1pt} {\kern 1pt} 33{{(3/x)}^5} + }\\ {0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 135{\kern 1pt} {\kern 1pt} {\kern 1pt} 58{{(3/x)}^6} + \varepsilon (|\varepsilon | < 7 \times {{10}^{ - 8}})} \end{array} $ | (21) |
| $ {{{\rm{J}}_1}(x) = {x^{ - 0.5}}{f_1}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\theta _1}} $ | (22) |
| $ {{{\rm{Y}}_1}(x) = {x^{ - 0.5}}{f_1}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\theta _1}} $ | (23) |
| $ \begin{array}{*{20}{c}} {{f_1} = 0.797{\kern 1pt} {\kern 1pt} {\kern 1pt} 884{\kern 1pt} {\kern 1pt} 56 + 0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 001{\kern 1pt} {\kern 1pt} {\kern 1pt} 56(3/x) + }\\ {0.016{\kern 1pt} {\kern 1pt} {\kern 1pt} 596{\kern 1pt} {\kern 1pt} {\kern 1pt} 67{{(3/x)}^2} + 0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 171{\kern 1pt} {\kern 1pt} {\kern 1pt} 05{{(3/x)}^3} - }\\ {0.002{\kern 1pt} {\kern 1pt} {\kern 1pt} 495{\kern 1pt} {\kern 1pt} {\kern 1pt} 11{{(3/x)}^4} + 0.001{\kern 1pt} {\kern 1pt} {\kern 1pt} 136{\kern 1pt} {\kern 1pt} {\kern 1pt} 53{{(3/x)}^5} - }\\ {0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 200{\kern 1pt} {\kern 1pt} {\kern 1pt} 33{{(3/x)}^6} + \varepsilon (|\varepsilon | < 4 \times {{10}^{ - 8}})} \end{array} $ | (24) |
| $ \begin{array}{*{20}{c}} {{\theta _1} = x - 2.356{\kern 1pt} {\kern 1pt} {\kern 1pt} 194{\kern 1pt} {\kern 1pt} 49 + 0.124{\kern 1pt} {\kern 1pt} 996{\kern 1pt} {\kern 1pt} {\kern 1pt} 12(3/x) + }\\ {0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 056{\kern 1pt} {\kern 1pt} {\kern 1pt} 50{{(3/x)}^2} - 0.006{\kern 1pt} {\kern 1pt} {\kern 1pt} 378{\kern 1pt} {\kern 1pt} {\kern 1pt} 79{{(3/x)}^3} + }\\ {0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 743{\kern 1pt} {\kern 1pt} {\kern 1pt} 48{{(3/x)}^4} + 0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 798{\kern 1pt} {\kern 1pt} 24{{(3/x)}^5} - }\\ {0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 291{\kern 1pt} {\kern 1pt} {\kern 1pt} 66{{(3/x)}^6} + \varepsilon (|\varepsilon | < 9 \times {{10}^{ - 8}})} \end{array} $ | (25) |
因为在式(17)中β为已知量,所以将式(18)~(25)代入式(17),即可求得x,并由n1R1=x,进而可以求出n1。
3 实例计算分析 3.1 对于固定式动力锅炉 3.1.1 基本参数固定式动力锅炉国家标准[1]给出的锅筒基本参数:内直径Di为1 743 mm,名义厚度δ为203 mm,外径与内径比值β为1.233,结构参数Ct为0.537和温度阻尼系数χ为11.68。
3.1.2 计算结果固定式动力锅炉国家标准[1]中锅筒径向温差计算实例与采用非常逼近解析解法的计算结果如表 1所示。
| 表 1 固定式动力锅炉锅筒径向温差计算结果 Table 1 Calculation results of radial temperature difference for the steam drum of a fixed power boiler |
由表 1可知,固定式动力锅炉国家标准法中式(1)或式(6)与非常逼近解析解法相比,总是存在一定的相对计算误差,通过式(6)的修正能够降低由式(1)带来的计算误差。
相对计算误差的存在说明了固定式动力锅炉国家标准法中式(1)和式(6)这2个公式本身是一个近似计算公式,可见固定式动力锅炉国家标准法是一种近似的计算方法。
3.2 对于船舶动力锅炉 3.2.1 锅筒材料物理性能和基本参数1) 文献[10]给出的锅筒材料BHW35的热扩散率at随温度变化的数据:20 ℃时为648 mm2/min,100 ℃时为618 mm2/min,200 ℃时为576 mm2/min,300 ℃时为534 mm2/min;
2) 锅筒内直径Di为1 300 mm,名义厚度δ为75 mm。这样,外径与内径比值β为1.115 4,按式(2)或式(11)得到的结构系数Ct为0.519,按式(3)和式(4)得到的温度阻尼系数χ为49.383,按式(17)~(25)得到的参数n1为20.74 m-1。
3.2.2 船舶动力锅炉典型工况1) 锅炉冷态启动工况。
锅筒工作压力由0 MPa升为6.47 MPa,则锅筒工质饱和温度由99.63 ℃升为281.61℃[11];锅炉启动时间在10 min以内[4],计算时取为10 min。这样,锅筒内工质平均变化速率为18.20 ℃/min。
2) 锅炉热备用启动和停炉工况。
① 锅炉启动时间为50 s[12],锅筒工作压力由3.5 MPa升为6.47 MPa,则锅筒内工质饱和温度由244.22 ℃升为281.61℃[11]。这样,锅筒内工质平均变化速率为44.868 ℃/min;
② 锅炉停炉时间为30 s[12],锅筒工作压力由6.47 MPa降为3.5 MPa,则锅筒内工质饱和温度由281.61 ℃降为244.22℃[11]。这样,锅筒内工质平均变化速率为-74.78 ℃/min。
3.2.3 计算结果和分析1) 对于锅炉冷态启动工况。
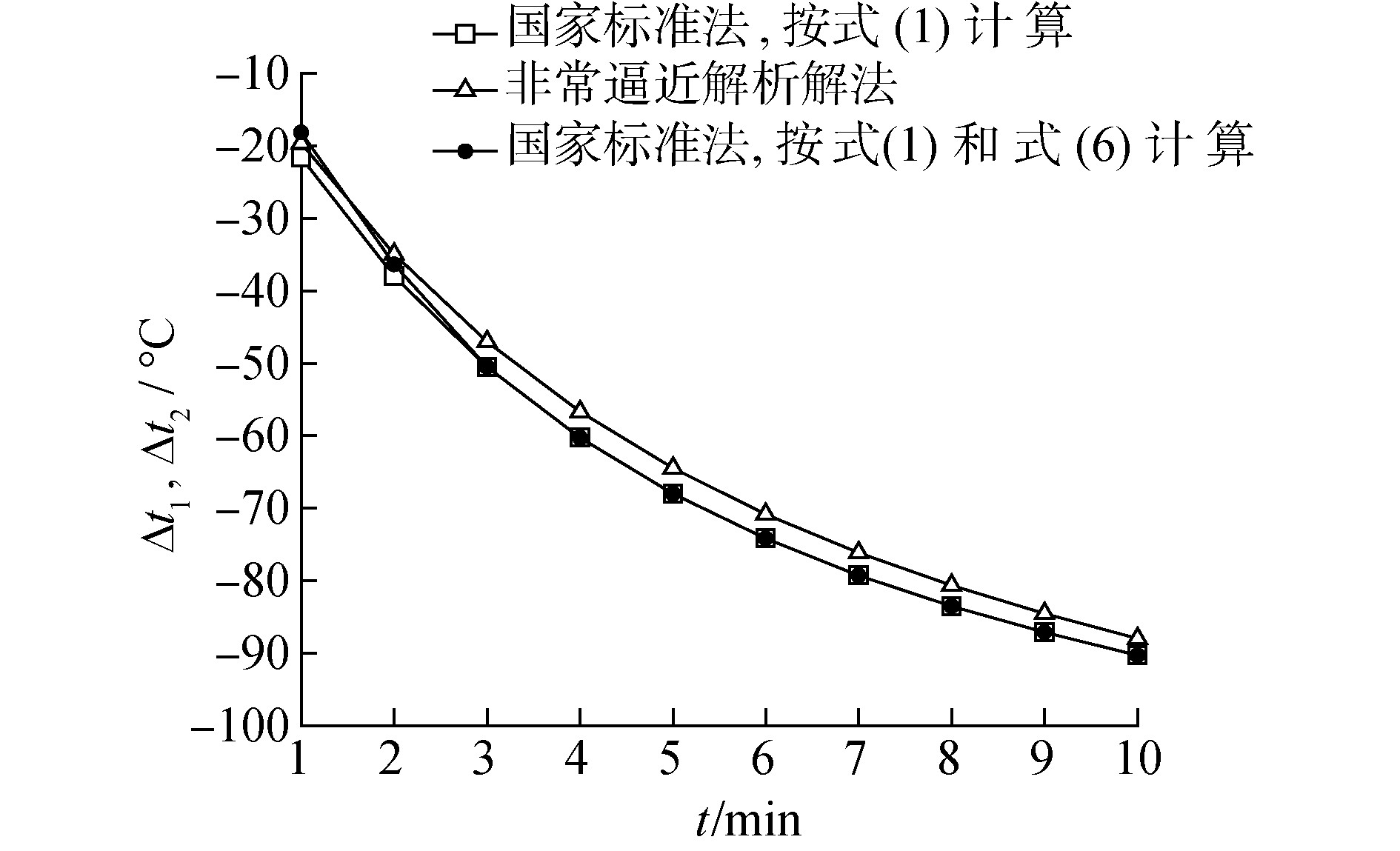
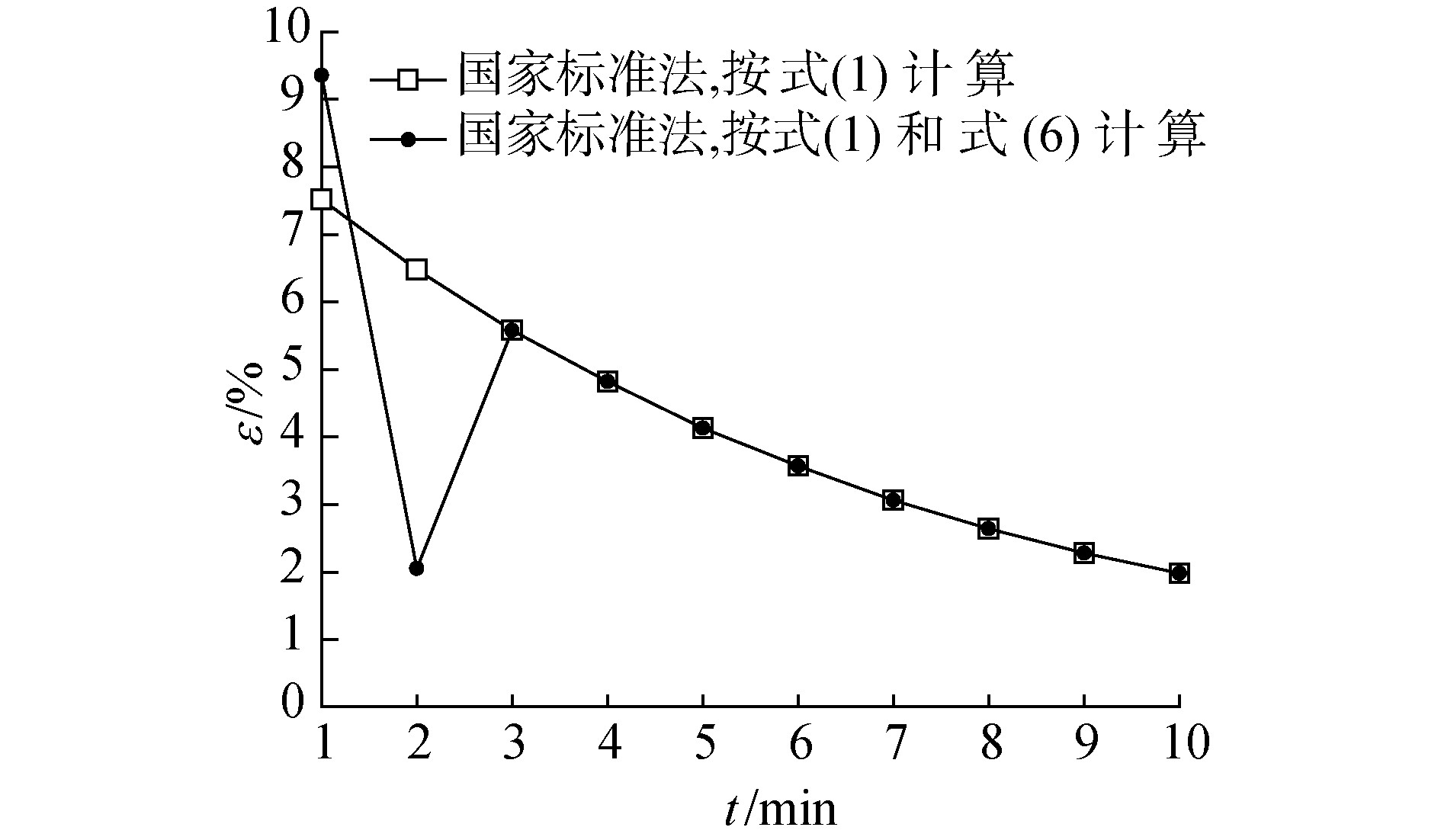
由固定式动力锅炉国家标准法和非常逼近解析解法得到的径向温差Δt1或Δt2随启动时间t的变化规律如图 1所示,相应的相对计算误差ε随启动时间t的变化规律如图 2所示。
|
Download:
|
| 图 1 冷态启动时的t-Δt1或t-Δt2 Fig. 1 The relation of t-Δt1 or t -Δt2 during the start-up of cold state | |
|
Download:
|
| 图 2 冷态启动时的t-ε Fig. 2 The relation of t-ε during the start-up of cold state | |
由图 1可见,按固定式动力锅炉国家标准法中式(1)计算出的船舶动力锅炉锅筒径向温差总是高于非常逼近解析解法,且由图 2可见,虽然相对计算误差能够随锅炉启动时间增加而降低,但是在锅炉启动的一段时间内仍有较大相对计算误差。
由图 1和图 2均能看出,固定式动力锅炉国家标准中式(6)对式(1)的修正计算仅发生在船舶动力锅炉启动开始的一小部分时间内(3 min以内),且由图 1可以看出,修正后的船舶动力锅炉锅筒径向温差有时低于非常逼近解析法(如1 min时刻),有时高于非常逼近解析法(如2 min时刻)。但由图 2可见,通过式(6)对式(1)修正后,有时使较高的相对计算误差进一步增大(如1 min时刻),有时能够大幅度降低相对计算误差(如2 min时刻)。
总之,由于固定式动力锅炉国家标准法计算出的船舶动力锅炉在冷态启动过程中的锅筒径向温差仍然存在较高的相对计算误差,使计算结果失去意义,所以不适用于所计算的工况。
2) 对于锅炉热备用启动和停炉工况。
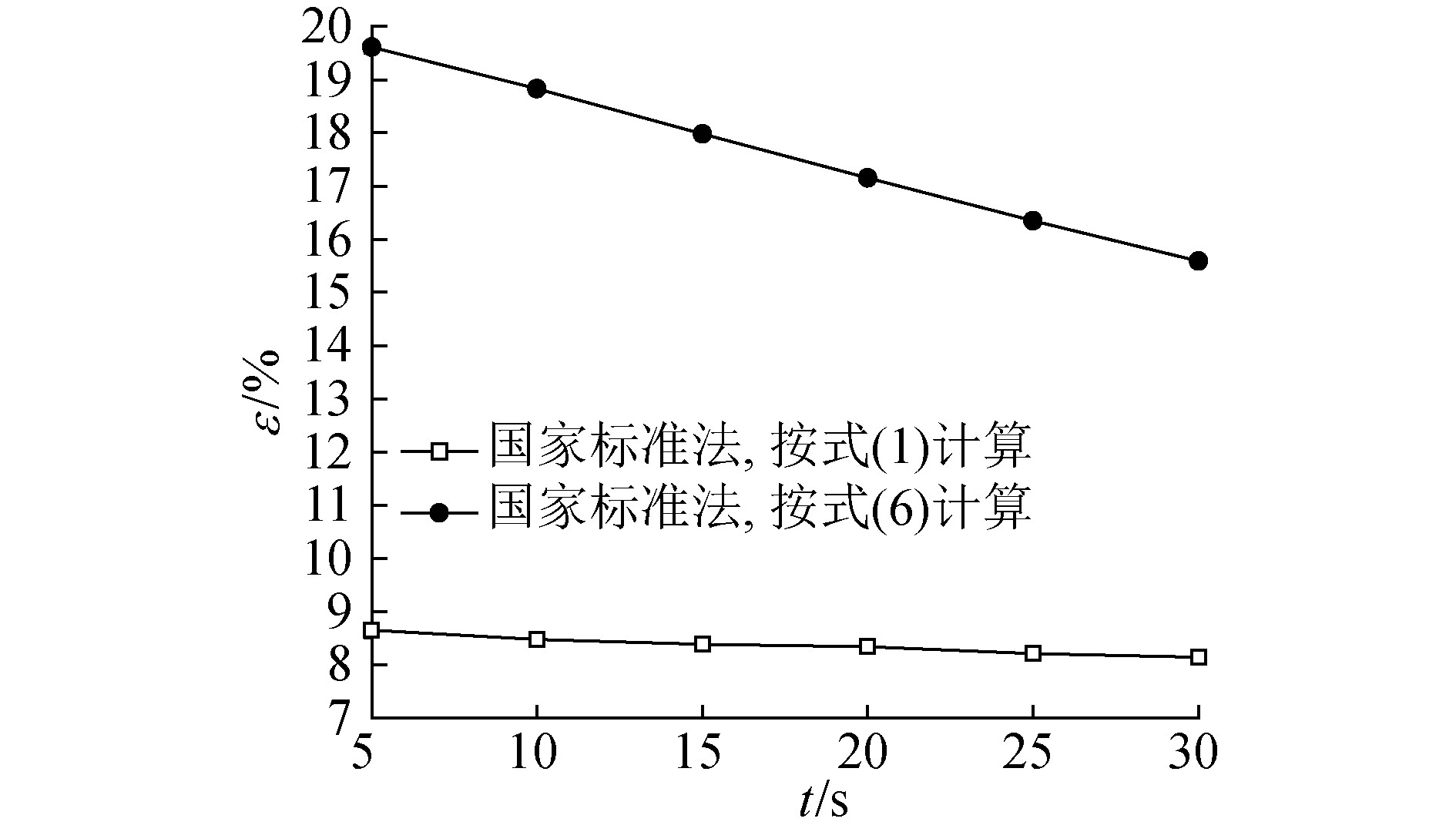
由固定式动力锅炉国家标准法和非常逼近解析解法得到的径向温差Δt1或Δt2随时间t的变化规律分别如图 3和图 5所示,相应的相对计算误差ε随时间t的变化规律分别如图 4和图 6所示。

|
Download:
|
| 图 3 热备用启动时的t-Δt1或t-Δt2 Fig. 3 The relation of t-Δt1 or t-Δt2during the start-up of stand-by heat | |

|
Download:
|
| 图 5 热备用停炉时的t-Δt1或t-Δt2 Fig. 5 The relation of t-Δt1 or t -Δt2 during the furnace shut down of stand-by heat | |

|
Download:
|
| 图 4 热备用启动时的t-ε Fig. 4 The relation of t-ε during the start-up of stand-by heat | |
|
Download:
|
| 图 6 热备用停炉时的t-ε Fig. 6 The relation of t-ε during the furnace shut down of stand-by heat | |
由图 3和图 5可见,按固定式动力锅炉国家标准法中式(1)计算出的船舶动力锅炉锅筒径向温差总是高于非常逼近解析解法,但经该标准中式(6)的修正后而计算出的结果低于非常逼近解析解法。
由图 3和图 5或图 4和图 6均可见,式(6)能够在船舶动力锅炉热备用启动或停炉的整个过程中,对式(1)计算出的船舶动力锅炉锅筒径向温差计算结果进行修正。
由图 4和图 6可见,虽然按固定式动力锅炉国家标准法中式(1)和修正式(6)均使相对计算误差随船舶动力锅炉启动或停炉时间的增加而降低,但经式(6)修正后的相对计算误差进一步增大,且按式(1)和式(6)所得出的相对计算误差均处于较高范围。
总之,由于固定式动力锅炉国家标准法计算出的船舶动力锅炉在热备用启动或停炉过程中的锅筒径向温差存在较高的相对计算误差,使计算结果失去意义,所以不适用于所计算的工况。
3.2.4 国家标准法对其他计算工况的适用性与分析不可否认的是,船舶动力锅炉一定存在一些运行工况是可以采用固定式动力锅炉国家标准法对锅筒径向温差进行计算的。然而,由于固定式动力锅炉国家标准法是一种近似计算方法,本身无法回答解决具体问题的准确程度,因而无法确定适用的船舶动力锅炉运行工况,所以对于船舶动力锅炉这些工况的计算还是推荐采用本研究提出的非常逼近解析解的方法。
事实上,非常逼近解析解法得到的式(15)可作为固定式动力锅炉国家标准法中式(3)表达的温度阻尼系数的应达值。当式(15)与式(3)相比较时,能够反映固定式动力锅炉国家标准计算方法中式(1)接近式(16)的程度。当二者相等时,式(1)就变成了式(16),此时的固定式动力锅炉国家标准计算方法中式(1)的修正式(6)也就可以被省略。
4 结论1) 当船舶动力锅炉与固定式动力锅炉具有相同的锅筒导热方程和定解条件情况下,提出的基于非常逼近解析解的锅筒径向温差计算公式和计算方法对固定式动力锅炉和船舶动力锅炉锅筒径向温差计算结果都具有足够高的计算精度;
2) 现行固定式动力锅炉国家标准法中的锅筒径向温差计算的2个公式是近似公式,该方法是一种近似计算方法,导致无法对船舶动力锅炉锅筒在任何可能工况下的径向温差进行合理计算;
3) 得到了基于非常逼近解析解的锅筒径向温差计算中的锅筒温度阻尼系数计算公式,明确指出了其在应用上的价值。
| [1] |
上海发电设备成套设计研究所. GB/T 9222-1988, 水管锅炉受压元件强度计算[S].北京: 机械工业出版社, 1989. Shanghai Power Equipment Research Institute. GB/T 9222-1988, Strength calculation of pressure parts for watertube boilers[S]. Beijing: China Machine Press, 1989. (  0) 0)
|
| [2] |
上海发电设备成套设计研究院. GB/T 9222-2008, 水管锅炉受压元件强度计算[S].北京: 中国标准出版社, 2008. Shanghai Power Equipment Research Institute.GB/T 9222-2008, Strength calculation of pressure parts for watertube boilers[S]. Beijing: China Standard Press, 2008. (  0) 0)
|
| [3] |
上海发电设备成套设计研究院. GB/T 16507.4-2013, 水管锅炉第4部分: 受压元件强度计算[S].北京: 中国标准出版社, 2013. Shanghai Power Equipment Research Institute. GB/T 16507.4-2013, Water-tube boilers-Part 4: Strength calculation of pressure parts[S]. Beijing: China Standard Press, 2013. (  0) 0)
|
| [4] |
李章, 张宁, 刘祥源, 等. 舰用增压锅炉装置[M]. 北京: 海潮出版社, 2000: 3. LI Zhang, ZHANG Ning, LIU Xiangyuan, et al. Naval supercharged boiler installation[M]. Beijing: Haichao Press, 2000: 3. (  0) 0)
|
| [5] |
郑心伟, 孙瑜, 王晓军. 增压锅炉汽包低周疲劳寿命计算方法研究[J]. 热能动力工程, 2010, 25(2): 184-189. ZHENG Xinwei, SUN Yu, WANG Xiaojun. Study of the methods for calculating the low-cycle fatigue life of a supercharged boiler drum[J]. Journal of engineering for thermal energy and power, 2010, 25(2): 184-189. (  0) 0)
|
| [6] |
ZHENG Xinwei, LI Zheng, WANG Hao, et al. Comparison of the computing method for the radial temperature difference of a supercharged boiler steam drum shell based on the approximate solution and the current Chinese standard[J]. Advanced materials research, 2011, 383-390: 5496-5503. DOI:10.4028/www.scientific.net/AMR.383-390.5496 (  0) 0)
|
| [7] |
吕邦泰, 沈月芬. 锅炉承压部件强度及寿命[M]. 北京: 水利电力出版社, 1992: 79-83.
(  0) 0)
|
| [8] |
贾鸿祥, 沈月芬. 调峰机组锅炉汽包的温度场[J]. 热力发电, 1993(3): 3-12. JIA Hongxiang, SHEN Yuefen. The temperature field in the steam generator drum wall for cycle loading units[J]. Thermal power generation, 1993(3): 3-12. DOI:10.19666/j.rlfd.1993.03.001 (  0) 0)
|
| [9] |
ABRAMOWITZ M, STEGUN I A. Handbook of mathematical functions with formulas, graphs, and mathematical tables[M]. Washington D.C.: U.S. Government Printing Office, 1965: 369-370.
(  0) 0)
|
| [10] |
中国动力工程学会. 火力发电设备技术手册(第1卷)[M]. 北京: 机械工业出版社, 2003: 13-38.
(  0) 0)
|
| [11] |
严家马录, 余晓福, 王永青. 水和水蒸气热力性质图表(第2版)[M]. 北京: 高等教育出版社, 2004: 11, 13, 14.
(  0) 0)
|
| [12] |
刘长河. 船用增压锅炉技术的新进展[J]. 热能动力工程, 1999, 14(4): 241-245. LIU Changhe. New developments in marine supercharged boilers[J]. Journal of engineering for thermal energy and power, 1999, 14(4): 241-245. DOI:10.3969/j.issn.1001-2060.1999.04.001 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


