2. 哈尔滨工程大学 动力与能源工程学院, 黑龙江 哈尔滨 150001
2. College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China
强化对流换热一直是传热领域倍受瞩目的研究课题。近年来,通过引入特殊构型诱发流动的自发振荡,引发流动不稳定性,促使流体扰动和混合的换热通道成为新的研究热点。核心目的是在强化换热的同时不致引起较大的压损,其中波纹通道是实际应用较广的一种,其换热及阻力特性已经进行很多相关的实验和数值模拟研究。波纹通道形式多样,其中正弦型和三角型的应用比较广泛,因此进行了较为深入的研究。对于正弦型通道,Wang等[1]分析了正弦收敛发散通道中流体流动传热速率的变化,得出在增大振幅波长比的同时,通道汇聚段局部努塞尔数也会随之而增加。Zhang等[2]发现波纹通道上壁面波谷处形成的横向涡随着雷诺数与波纹纵横比的增加而增加,主流体与横向涡的相互流动使得流体混合更加剧烈,进而促成了涡的流动形态的产生。对于三角型波纹通道,Sparrow等[3]进行了可视化实验,得出在湍流流动中特征数的变化规律,并证明波纹通道越倾斜,越易引起流动分离和流动阻力的增大。马学虎等[4]研究得出,在低雷诺数时,相比于波纹倾角和波纹高度,板间距对换热的影响较大,对压降的影响较小。
一些学者对正弦型和三角型进行了性能对比研究,阴继翔等[5]对二维波纹通道内的周期性流动换热进行了数值模拟,得出正弦型比三角型波纹通道更易失稳而向湍流过渡,其表面换热性能更良好。杨刚[6]采用数值模拟分析了形状参数对三角型和正弦型板式换热器性能的影响,为得到最佳的性能因子提供了参考。Akbarzadeh等[7]对比了正弦型、三角型、梯型3种波纹通道,发现梯形波纹通道具有最大的回流区域,因此压降和平均努塞尔数最高,而三角型通道最低。
随着加工与制造技术的发展,所考虑波纹通道的结构更加全面并且趋于复杂化。其中Ramgada等[8]对上下壁面错位的波纹通道进行了数值模拟,发现相移对传热和压降特性具有较大影响,相位差为0°时具有最佳的传热特性,但也具有最高的阻力损失。Pati等[9]对相位差的影响规律做了进一步研究,发现对于波长较小时,通道的传热速率几乎相同,而波长较大时,环形通道的传热性能高于蛇形通道,并且雷诺数或波纹振幅较大时两者差异更加明显, 但环形通道相比于蛇形通道具有更高的压降。Alawadhi[10]研究了振幅呈线形增加的波纹通道,结果表明这种结构显著减小了通道内的压降,在振幅较大和低雷诺数下更加明显,而平均努塞尔数略微增加,强化传热并不显著。Harikrishnan等[11]分析了波纹倾角的影响,结果表明努塞尔数和摩擦系数分别在波纹倾角为35°和30°时存在极大值点。
已有的工作针对不同波纹形式(三角型、正弦型、梯型)以及不同结构参数(振幅、波长、波纹倾角以及相位移)进行了大量的研究。由上述研究可知,波纹通道的倒角连接处对于换热和阻力性能具有重要的影响,然而,针对波纹两侧倒角不同的非对称型波纹通道的流动特性鲜有研究。因此,本文拟针对不同雷诺数影响下对称型与非对称型波纹通道的流动与传热进行数值模拟研究。对比分析对称型与非对称型通道平均壁表面与局部壁表面特征数的变化规律,进而深入剖析2类型通道流动与传热参数的空间分布规律。
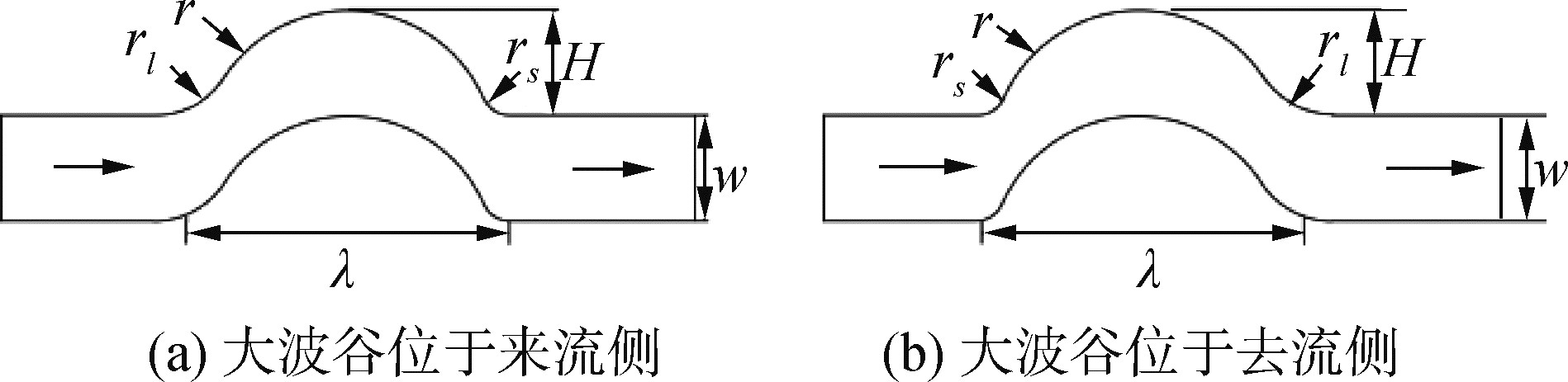
1 波纹通道流动与传热数值计算 1.1 物理模型及网格划分本文构建了非对称型波纹通道以及对称型波纹通道单元波节物理模型,如图 1和图 2所示。波纹通道的几何结构参数主要包括波纹板间宽度w,波纹高度H、波纹间距λ、波峰半径r,波谷半径(即2个波纹的连接处)。对于非对称型波纹通道波谷半径包括大波谷半径rl和小波谷半径rs。
|
Download:
|
| 图 1 非对称型波纹通道物理模型 Fig. 1 Asymmetrical corrugated channels physical model | |

|
Download:
|
| 图 2 对称型波纹通道物理模型 Fig. 2 Symmetrical corrugated channels physical model | |
本文考虑了2种非对称型波纹通道,分别为大波谷半径位于来流侧和去流侧。非对称型模型选取几何参数为波间宽度w=6 mm,波纹高度H=6 mm, 波纹间距λ=21.84 mm,大波谷半径rl=7 mm,小波谷半径rs=2 mm,波峰半径r=8.31 mm的波纹通道进行模拟(图 1)。对称型选取结构参数为波间宽度w=6 mm,波纹高度H=6 mm, 波纹间距λ=18.5 mm,rl=7 mm,波峰半径r=8.31 mm的波纹通道进行模拟(图 2),上、下壁面对应凹、凸壁面,同时选择在波纹通道模型的进口与出口处进行延伸扩展以尽量避免产生入口段效应以及出口处回流。
本文的网格划分如图 3所示,采用四面体非结构化网格对流动区域进行划分。

|
Download:
|
| 图 3 数学模型网格划分 Fig. 3 Meshing generation | |
如图 3(b)所示。波纹通道的壁面采用边界层网格处理[12],考虑到近壁面处存在较大的速度梯度和温度梯度,为了提高计算的准确性,对近壁面处的网格进行加密处理,保证壁面所有点的y+ < 1。
1.2 数学模型本文对波纹通道内流体的流动与换热建立数学模型,以水为工作介质。由于流体流动过程复杂多变,故进行如下假设:
1) 流体为不可压缩牛顿流体;
2) 流体流动选择定常流动;
3) 忽略重力与浮升力的影响;
4) 忽略流体流动时的粘性耗散热效应;
5) 流体通道周边与外界无任何热质交换。
建立连续性方程:
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} + \frac{{\partial {u_j}}}{{\partial {x_j}}} = 0 $ | (1) |
建立动量方程:
| $ \frac{{\partial (\rho {u_i}{u_j})}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_i}}} + \mu \left( {\frac{{{\partial ^2}{u_i}}}{{\partial x_i^2}} + \frac{{{\partial ^2}{u_j}}}{{\partial x_j^2}}} \right) + \frac{\partial }{{\partial {x_j}}}( - \rho \overline {u_i^\prime u_j^\prime } ) $ | (2) |
建立能量方程:
| $ \frac{\partial }{{\partial {x_i}}}[{u_i}(\rho E + p)] = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {k + \frac{{{c_p}{\mu _t}}}{{P{r_t}}}} \right)} \right]\frac{{\partial T}}{{\partial {x_j}}} $ | (3) |
由于本文模拟的是湍流流动,模型设置选取Realizable k-ε方程,且分子之间的粘性忽略不计[13]。
湍动能方程:
| $ \begin{array}{*{20}{l}} {\frac{\partial }{{\partial t}}(\rho k) + \frac{\partial }{{\partial x}}(\rho k{u_i}) = \frac{\partial }{{\partial y}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial y}}} \right] + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {G_k} + {G_b} - \rho \varepsilon - {Y_M} + {S_k}} \end{array} $ | (4) |
湍动能耗散率方程:
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} \frac{\partial }{{\partial t}}(\rho \varepsilon ) + \frac{{\partial (\rho \varepsilon {u_j})}}{{\partial {x_j}}} = \frac{\partial }{{\partial y}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial y}}} \right] + }\\ {\rho {C_1}{S_\varepsilon } - \rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {v\varepsilon } }} + {C_{1\varepsilon }}\frac{\varepsilon }{k}{C_{3\varepsilon }}{G_b} + {S_\varepsilon }} \end{array} $ | (5) |
式中:σk是湍动能方程湍度Prandtl数;σε是湍动能耗散率方程湍度Prandtl数;Gk是由层流速度梯度产生的湍动能;Gb表示为由浮力引起的湍动能,而YM表示为由过度的扩散引起的波动;C1ε、C2ε、C3ε则是常量;Sk、Sε则是用户自定义量。
本文所需计算参数定义:
1) 雷诺数:
| $ {Re = \frac{{uD\rho }}{\mu }} $ | (6) |
2) 努塞尔数:
| $ {Nu = \frac{{hD}}{\lambda }} $ | (7) |
3) 传热系数:
| $ {h = \frac{Q}{{\Delta {t_m}}}} $ | (8) |
4) 摩擦系数:
| $ {f = \frac{{2\Delta pD}}{{L\rho {u^2}}}} $ | (9) |
式中:u为工质流速;ρ为工质密度;μ为工质粘性系数;λ为工质导热系数;D为通道水力直径;Q为壁面热流密度。
1.3 数值求解条件设置由于整个过程温度变化不大,本文采用常物性的水作为介质,其中密度ρ=998.2 kg/m3,比热容Cp=4 182 J/(kg·K),热传导率k=0.6 W/(m·K),动力粘度μ=0.001 003 kg/(m·s)。
1) 本文主要目的是阐明波纹非对称结构对波纹通道流动与传热的影响,为简化条件,给定恒定的凹凸壁面温度Tw=360 K,且流体通道周边与外界不存在质与热的交换;
2) 边界条件设置速度入口,压力出口。流体进口速度根据雷诺数计算得到uin,且进口温度设置为300 K;
3) 壁面边界选择无滑移速度边界条件,其边界速度uw=0。
为了能够使求解器获得所需要的结果,对FLUENT设置一个初始化流场且初始值合理。其初始化方法为Standard Initialization。
为了与文献[14]中的实验数据对比,验证模型可靠性,本文对湍流状态下流道内流体的传热性能和摩擦阻力进行模拟。在研究湍流状态时,假设流动为定常充分发展湍流流动。
本文使用ANSYS FLUENT 15.0版本进行数值模拟研究。求解器类型选取基于压力求解器,计算模型采用Realizable的k-ε湍流模型,壁面函数采用增强壁面函数。压力与速度的耦合式算法采用的是SIMPLE算法。采用二阶迎风格式来进行各控制方程的离散。本文残差曲线设置:能量方程的相对残差值应小于10-6,其他的控制方程的残差值均应小于10-5,最后设置迭代步数为2 000步。
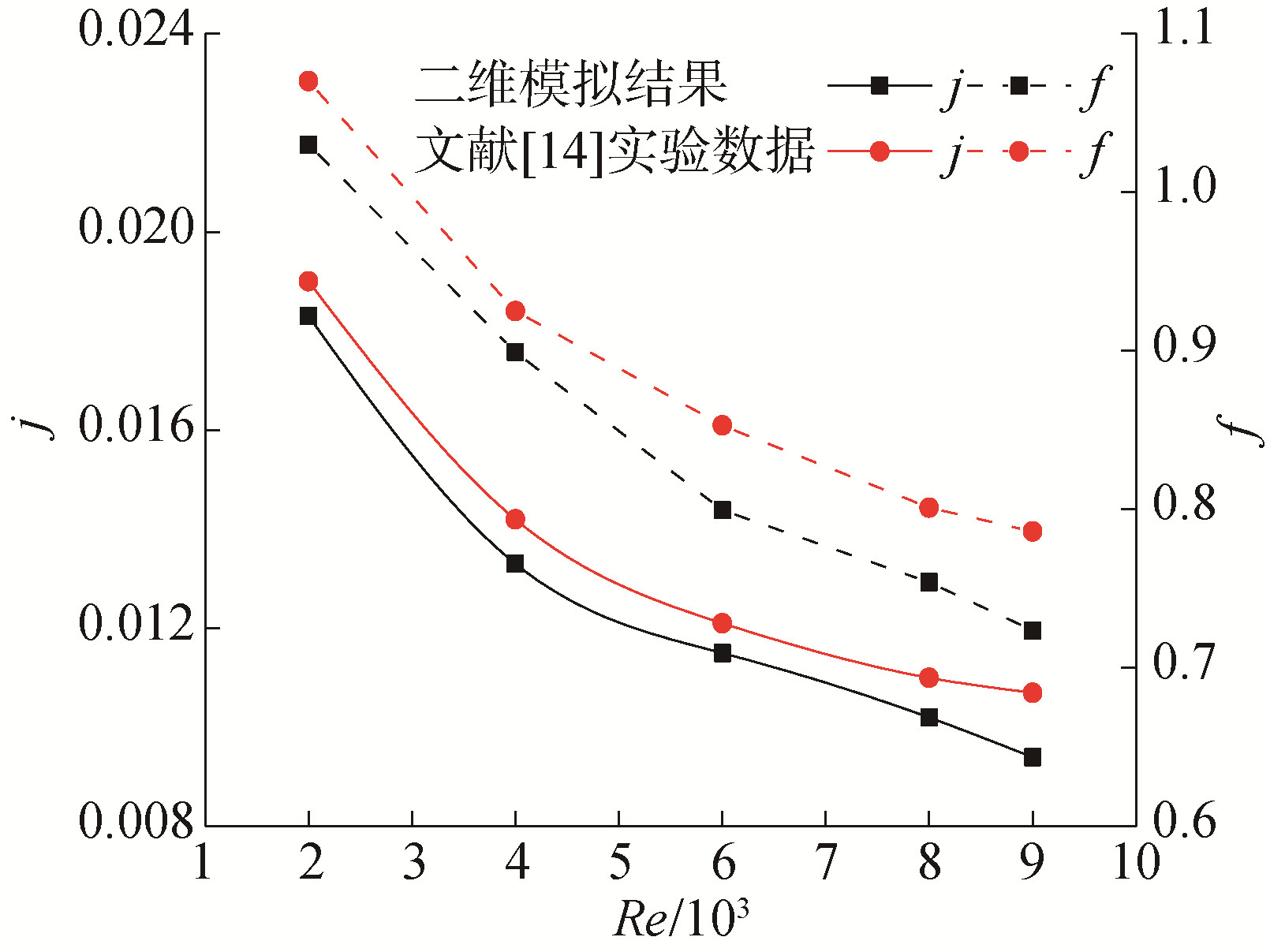
1.4 模型的验证 1.4.1 湍流模型验证本文数值模拟模型验证所用到的实验数据来自文献[14]。其中为了保持与文献[14]相似,模型选择波纹高度为3.8 mm,波纹间距为13.4 mm,流体介质为水,流体流动状态为湍流。
计算公式:
| $ j = \frac{{Nu}}{{Re \cdot P{r^{\frac{1}{3}}}}} $ | (10) |
式中:j为换热因子,表示流体的传热能力。
图 4为湍流状态下二维模拟得到的换热因子和摩擦系数与文献[14]实验数据的对比图。由图可知,本文的模拟与文献[14]实验数据对比误差均小于6%,误差在允许范围之内,说明模型的可靠性。
|
Download:
|
| 图 4 湍流状态下换热因子与摩擦系数对比 Fig. 4 Comparison of heat transfer factor and friction coefficient | |
本文主要研究波纹通道间流体传热特性的变化规律,因此计算网格在边界层的处理对计算结果的准确性十分重要,本节选取几何参数为λ=16 mm,H=6 mm的模型进行了网格无关性验证。图 6为波纹通道凹凸壁面平均努塞尔数Nu随网格数增加的变化曲线,在网格数为25 302、47 962、60 571、79 536、90 017、105 362时,凹凸壁面Nu先升高后基本保持不变,当网格数增加到79 536后,计算结果基本保持不变,故选用79 536的网格划分作为计算网格尺寸。

|
Download:
|
| 图 5 网格无关性验证 Fig. 5 Grid independence verification | |
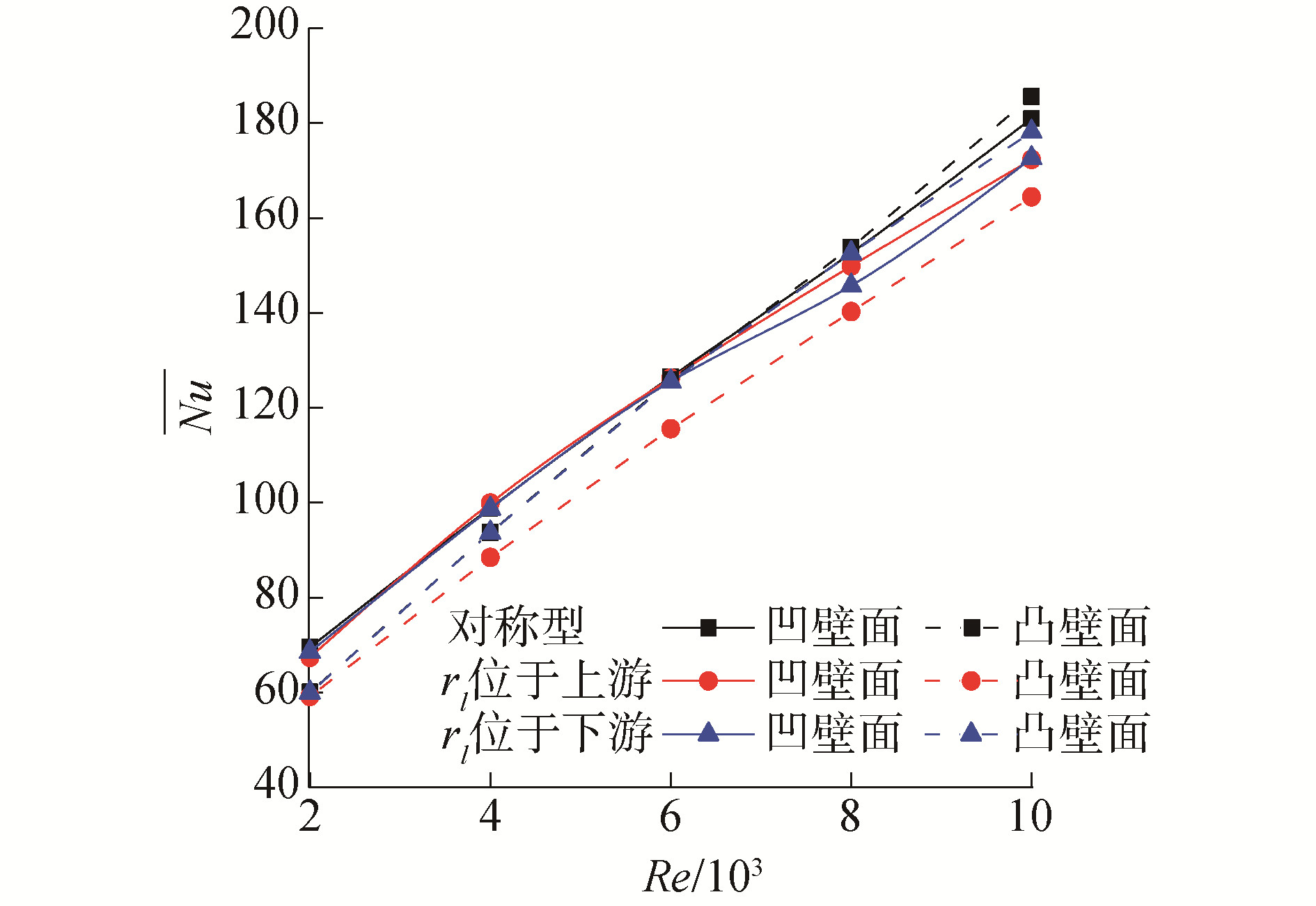
图 6为凹凸壁面的Nu随Re的变化曲线。由图可知,对称型与非对称型波纹通道Nu均随着Re的增加而增加,且对称型波纹通道凹凸壁面Nu增长速率均大于非对称型。这是由于随着Re的增加壁面流体流速逐渐增大,使得流体热边界层厚度变薄,并且壁面热阻减小,导致对流传热系数增大,且壁面Nu单调递增。对于凹壁面,在Re < 6 000时,非对称型与对称型波纹通道Nu数值相近;在Re>6 000时,对称型波纹通道Nu增长速率较大,而非对称型波纹通道大波谷位于来流侧增长速率略大于大波谷位于去流侧。对于凸壁面,大波谷位于去流侧非对称型波纹通道Nu与对称型波纹通道相差不大,而大波谷位于来流侧非对称型波纹通道则低于对称型波纹通道。
|
Download:
|
| 图 6 凹凸壁面Nu随Re变化曲线 Fig. 6 Variation of Nu along with various Re for concave and convex walls | |
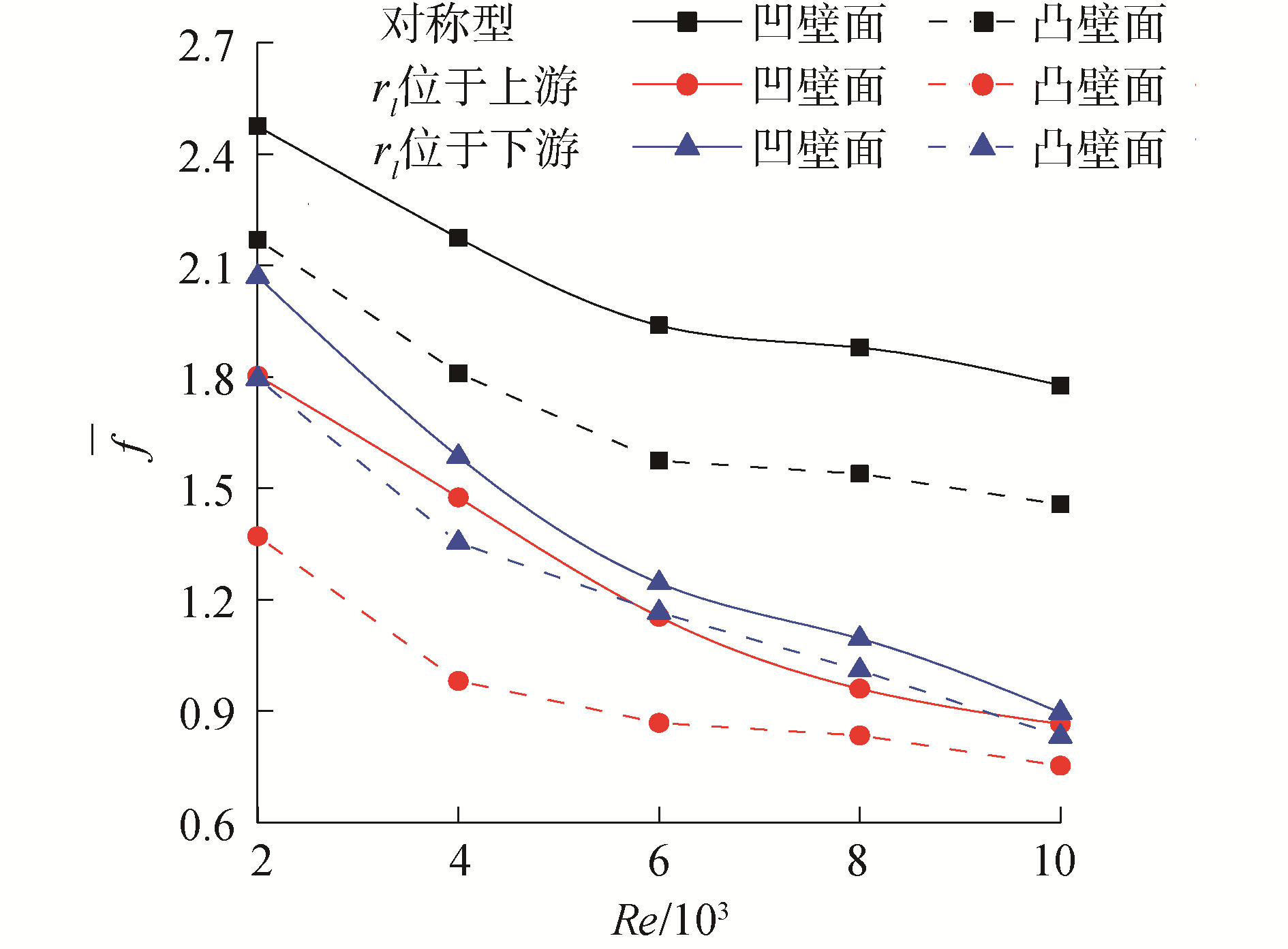
图 7为凹凸壁面的平均摩擦系数随Re的变化曲线。对称型与非对称型波纹通道凹凸壁面f均随着Re的增大而单调递减,且减缓速率越来越小,对称型波纹通道凹凸壁面平均摩擦系数整体上明显大于非对称型波纹通道。这是由于随着Re的增加,流体流速增大,使得流体壁面压降与剪切应力增大,且壁面压强增长速率更大。同时,相同Re下,非对称型波纹通道壁面f均小于对称型波纹通道,具有更小的阻力特性。当大波谷半径处于来流侧时,阻力性能相比于大波谷半径处于去流侧时更小,且凸壁面相比于凹壁面减小的更加明显。
|
Download:
|
| 图 7 凹凸壁面f随Re变化曲线 Fig. 7 Variation of f along with various Re for concave and convex walls | |
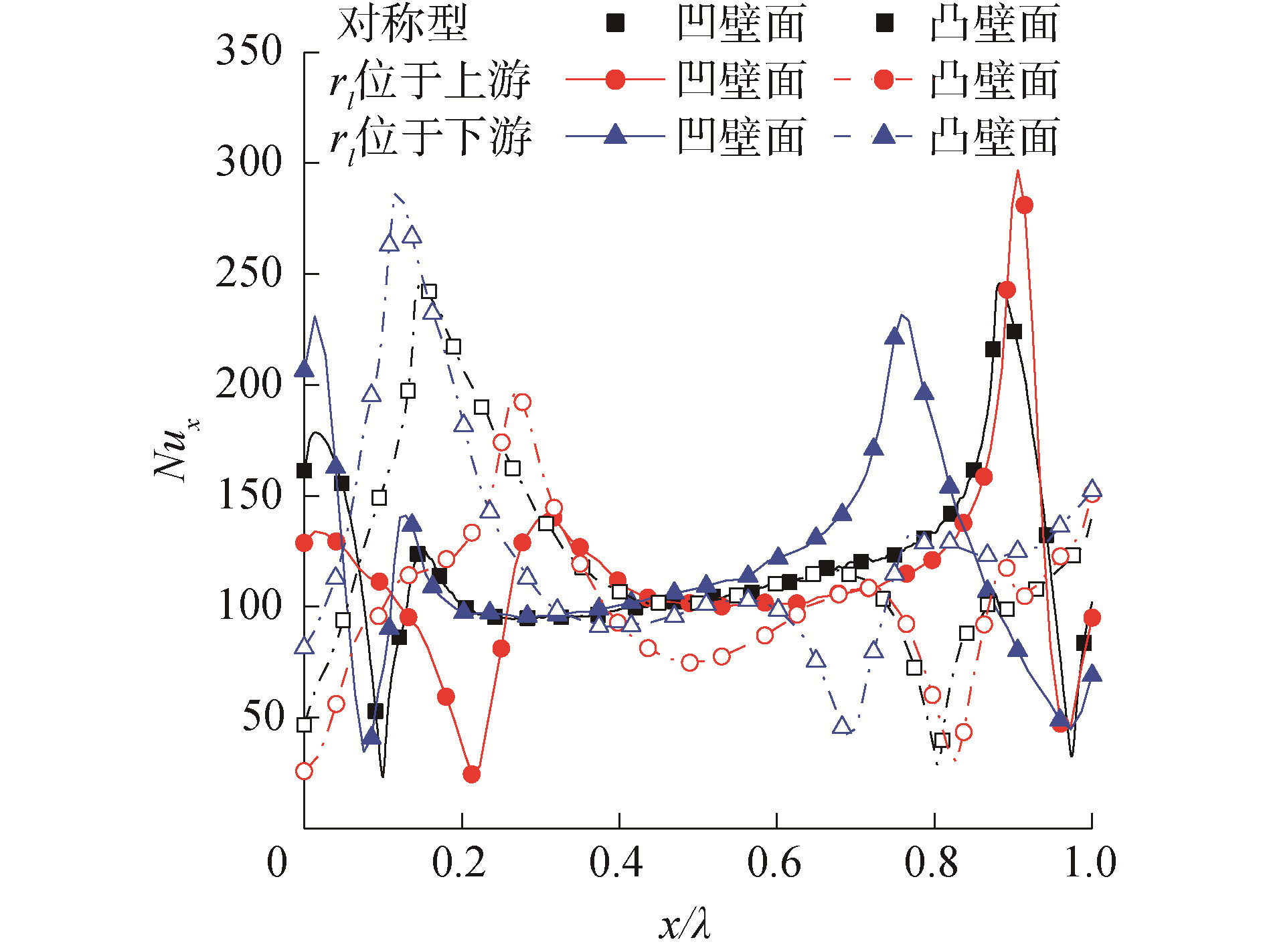
图 8为Re=6 000沿凹凸壁面Nux局部分布曲线图。Nux在凹壁面的上游区域近开始骤降至极小值,到达波峰处开始平缓增大,随后在凹壁面下游区域陡升至极大值并再次骤降,最终在进出口处出现一个极小值。图中极小值是由于涡流产生导致传热死区,而极大值的产生是由于流体对凹壁面的冲刷使温度边界层迅速变薄。对比3种通道类型可知3种通道的极大值和极小值略有差异,但综合来看差距不大,使得换热性能差距较小。Nux在凸壁面的趋势刚好相反,这是由于结构镜像导致。
|
Download:
|
| 图 8 Re=6 000沿凹壁面Nux局部分布 Fig. 8 Local Nux of concave wall in Re=6 000 | |
图 9为Re=6 000沿凹凸壁面fx局部分布曲线图。fx在凹壁面的上游逐渐增大至极大值,进入波峰区域后随着x的增大而逐渐降低,且降幅逐渐平缓,fx在凹壁面的下游再次陡升至极大值,下游的极大值相比于上游明显提升。比较3种结构可知,大波谷位于来流侧非对称型波纹通道fx整体最小,而大波谷位于去流侧非对称型波纹通道凹壁面fx最大。fx在凸壁面通道的上游区域快速增大至极大值,随后fx随着x的增大而缓慢降低,在下游区域略微向上浮动后再次缓慢降低。比较3种通道可知,大波谷位于来流侧非对称型波纹通道fx数值整体最小,大波谷位于去流侧最大。由以上可看出,大波谷位于来流侧时能够有效地降低阻力特性。

|
Download:
|
| 图 9 Re=6 000沿凹壁面fx局部分布 Fig. 9 Local fx of concave wall in Re=6 000 | |
图 10为Re=6 000时对称型与非对称型波纹通道的速度矢量图。流体进入波节后,流体流动速度开始增大,这种高流速主要集中于波纹通道中下部区域。近壁面处存在涡流,主要发生在凹壁面入口处和凸壁面出口处。比较3种波纹通道可知,大波谷半径位于去流侧时拥有更高整体流速,大波谷半径位于来流侧时流速较小。大波谷半径位于来流侧涡旋范围最小,另外2种通道涡旋范围相近。

|
Download:
|
| 图 10 Re=6 000时速度矢量图 Fig. 10 Velocity field in Re=6 000 | |
图 11为Re=6 000时对称与非对称型波纹通道温度分布图。对于凹凸壁面,在涡旋出现的区域热边界层增厚,随后重新发展。而流体直接冲刷的壁面区域,热边界层最薄。比较3种波纹通道可知,整体来看非对称型波纹通道温度边界层比对称型略厚,对于非对称型通道大波谷半径位于来流侧相比于位于去流侧略厚。局部来看凹壁面上游区域,大波谷位于去流侧时温度边界层最厚,凸壁面下游区域,大波谷位于来流侧时温度边界层最厚。非对称型波纹通道温度边界层比对称型略厚,对于非对称型通道大波谷半径位于来流侧相比于位于去流侧略厚。

|
Download:
|
| 图 11 Re=6 000时温度云图 Fig. 11 Temperature field in Re=6 000 | |
图 12为Re=6 000时对称型与非对称型波纹通道的压力分布图。流体进入通道后压力骤降,出现负压区,形成正压梯度,随后在波峰位置压力上升,出现逆压梯度,最后在下游区域骤降,再次形成正压梯度。这种压力梯度的不断转换导致阻力降的增加。凹壁面的上游和下游存在明显负压区;凸壁面波峰处存在负压区。比较3种波纹通道可知,对称型通道的压力梯度转换高于非对称型, 对于非对称型通道大波谷位于去流侧明显大于来流侧。

|
Download:
|
| 图 12 Re=6000时压力云图 Fig. 12 Pressure field in Re=6000 | |
图 13为Re=6 000时对称型与非对称型波纹通道的湍动能图。

|
Download:
|
| 图 13 Re=6 000时湍动能云图 Fig. 13 Turbulent kinetic energyfield in Re=6 000 | |
流体通道上游区域湍动能较小,波峰区域和流道下游区域湍动能较大。高湍流度集中在凹壁面侧的波峰以及凸壁面的下游区域。湍动能较大的原因主要是波峰处存在着涡流的出现,使得流体相互掺混,导致脉动速度增加。比较3种波纹通道可知,对称型波纹通道湍动能整体上大于非对称型,对于非对称型波纹通道大波谷位于去流侧要高于来流侧。
3 结论1) 对称型与非对称型波纹通道Nu均随着Re的增加而增加,且对称型波纹通道Nu增长速率均大于非对称型波纹通道。对称型与非对称型波纹通道f均随着Re的增大而单调递减,且减缓速率越来越小。3种波纹通道的Nu差距不大,而大波谷半径位于来流侧非对称型通道的f整体最小,对称型通道最大。大波谷半径位于来流侧非对称型通道在换热能力损失较小的情况下大大减少了摩擦阻力,在换热器设计上建议选择大波谷半径位于来流侧通道以提高整体性能系数。
2) 从Nux局部分布规律可以看出,对称型与非对称型波纹通道凹壁面近入口存在一个极小值,近出口处存在一个极大值,而凸壁面分布规律与之相反。从fx局部分布规律可知,凹壁面上游区域和下游区域均出现极大值,并且下游区域的峰值更高。而凸壁面的极值则出现在上游区域。
3) 大波谷半径位于去流侧时拥有更高整体流速且涡旋范围较大,位于来流侧时流速较小且涡旋范围较小。整体来看,非对称型波纹通道温度边界层比对称型略厚,对于非对称型通道大波谷半径位于来流侧相比于位于去流侧略厚。对称型通道的压力梯度转换高于非对称型,对于非对称型通道大波谷位于去流侧明显大于来流侧。对称型波纹通道湍动能整体上大于非对称型,对于非对称型波纹通道大波谷位于去流侧要高于来流侧。
| [1] |
WANG C C, CHEN C K. Forced convection in a wavy-wall channel[J]. International journal of heat and mass transfer, 2002, 45(12): 2587-2595. DOI:10.1016/S0017-9310(01)00335-0 (  0) 0)
|
| [2] |
ZHANG Jiehai, KUNDU J, MANGLIK R M. Effect of fin waviness and spacing on the lateral vortex structure and laminar heat transfer in wavy-plate-fin cores[J]. International journal of heat and mass transfer, 2004, 47(8/9): 1719-1730. (  0) 0)
|
| [3] |
O'BRIEN J E, SPARROW E M. Corrugated-duct heat transfer, pressure drop, and flow visualization[J]. Journal of heat transfer, 1982, 104(3): 410-416. DOI:10.1115/1.3245108 (  0) 0)
|
| [4] |
马学虎, 林乐, 兰忠, 等. 低Re下板式换热器性能的实验研究及热力学分析[J]. 热科学与技术, 2007, 6(1): 38-44. MA Xuehu, LIN Le, LAN Zhong, et al. Experimental investigation and thermodynamic analysis of performance of plate heat exchanger for low Reynolds number[J]. Journal of thermal science and technology, 2007, 6(1): 38-44. DOI:10.3969/j.issn.1671-8097.2007.01.007 (  0) 0)
|
| [5] |
阴继翔, 李国君, 丰镇平. 两种波纹通道内周期性充分发展对流换热的数值研究[J]. 热能动力工程, 2005, 20(3): 250-254. YIN Jixiang, LI Guojun, FENG Zhenping. Numerical study of periodically fully developed convection heat transfer in two kinds of wavy channels[J]. Journal of engineering for thermal energy and power, 2005, 20(3): 250-254. DOI:10.3969/j.issn.1001-2060.2005.03.008 (  0) 0)
|
| [6] |
杨刚.波纹板形状参数对换热器性能影响的数值研究[D].太原: 太原理工大学, 2012. YANG Gang. Numerical study of heat exchangers with different geometric parameters[D]. Taiyuan: Taiyuan University of Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10112-1012380725.htm (  0) 0)
|
| [7] |
AKBARZADEH M, RASHIDI S, ESFAHANI J A. Influences of corrugation profiles on entropy generation, heat transfer, pressure drop, and performance in a wavy channel[J]. Applied thermal engineering, 2017, 116: 278-291. DOI:10.1016/j.applthermaleng.2017.01.076 (  0) 0)
|
| [8] |
RAMGADIA A G, SAHA A K. Numerical study of fully developed unsteady flow and heat transfer in asymmetric wavy channels[J]. International journal of heat and mass transfer, 2016, 102: 98-112. DOI:10.1016/j.ijheatmasstransfer.2016.05.131 (  0) 0)
|
| [9] |
PATI S, MEHTA S K, BORAH A. Numerical investigation of thermo-hydraulic transport characteristics in wavy channels:comparison between raccoon and serpentine channels[J]. International communications in heat and mass transfer, 2017, 88: 171-176. DOI:10.1016/j.icheatmasstransfer.2017.09.001 (  0) 0)
|
| [10] |
ALAWADHI E M. Forced convection flow in a wavy channel with a linearly increasing waviness at the entrance region[J]. Journal of heat transfer, 2009, 131(1): 011703. DOI:10.1115/1.2977554 (  0) 0)
|
| [11] |
HARIKRISHNAN S, TIWARI S. Effect of skewness on flow and heat transfer characteristics of a wavy channel[J]. International journal of heat and mass transfer, 2018, 120: 956-969. DOI:10.1016/j.ijheatmasstransfer.2017.12.120 (  0) 0)
|
| [12] |
王福军. 计算流体动力学分析-CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004: 35. WANG Fujun. Computational fluid dynamics analysis CFD software principle and application[M]. Beijing: Tsinghua University Press, 2004: 35. (  0) 0)
|
| [13] |
JAIN S, JOSHI A, BANSAL P K. A new approach to numerical simulation of small sized plate heat exchangers with chevron plates[J]. Journal of heat transfer, 2007, 129(3): 291-297. DOI:10.1115/1.2430722 (  0) 0)
|
| [14] |
李晓亮.人字形板式换热器强化传热研究及场协同分析[D].济南: 山东大学, 2009. LI Xiaoliang. Research on heat transfer enhancement and field synergy principe of cheron-type plate heat exchanger[D]. Ji'nan: Shandong University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10422-2009246351.htm (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


